Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control
Abstract
1. Introduction
2. Chaotic Oscillator System with Hidden Attractor Design and Problem Formulation
2.1. Chaotic Oscillator System with Hidden Attractor Design
2.1.1. 2-D Chaotic Oscillator with Hidden Attractor Design
2.1.2. 4D-Chaotic System with Hidden Attractor
2.2. Problem Formulation
3. Adaptive Terminal Sliding Mode Controller Design
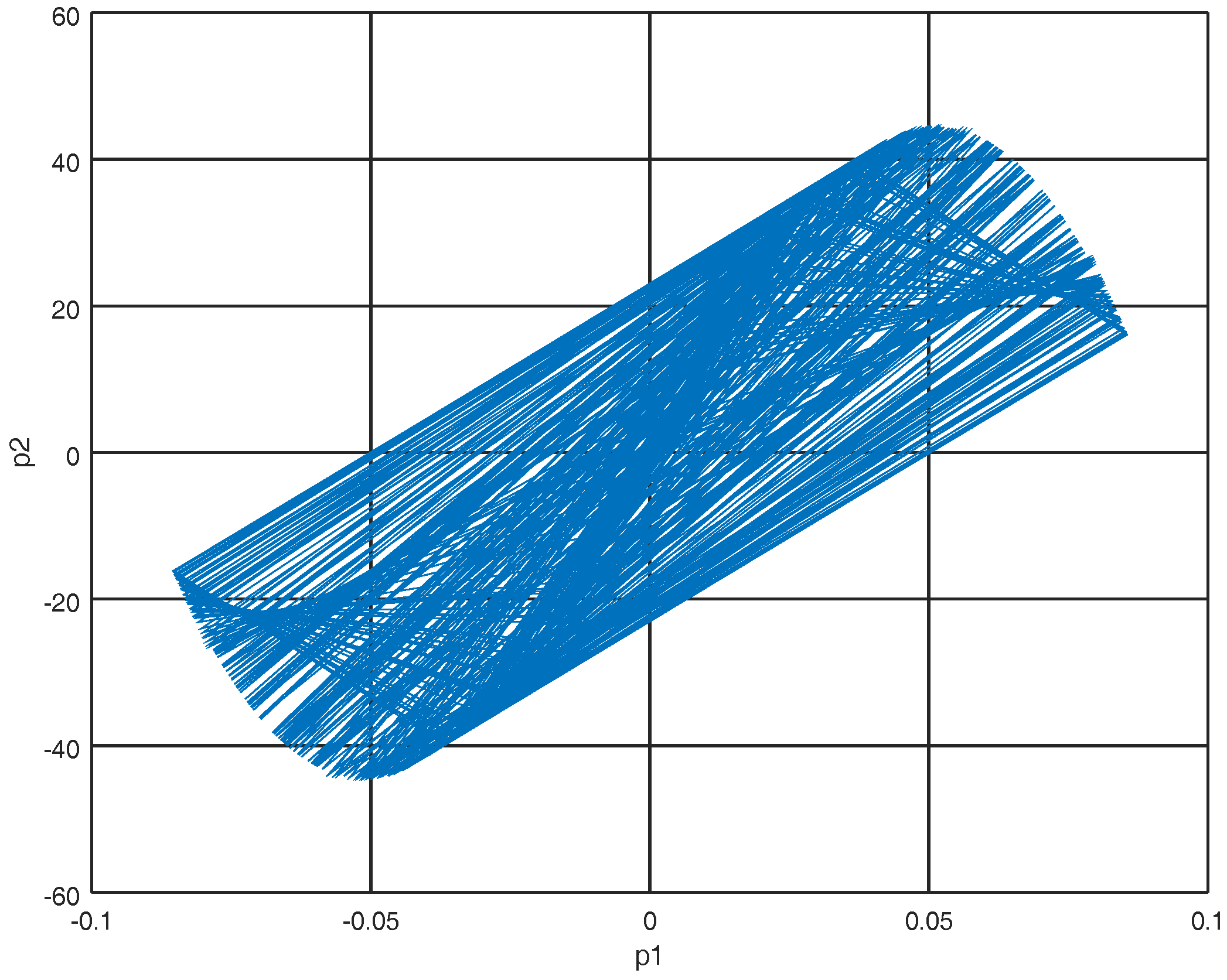
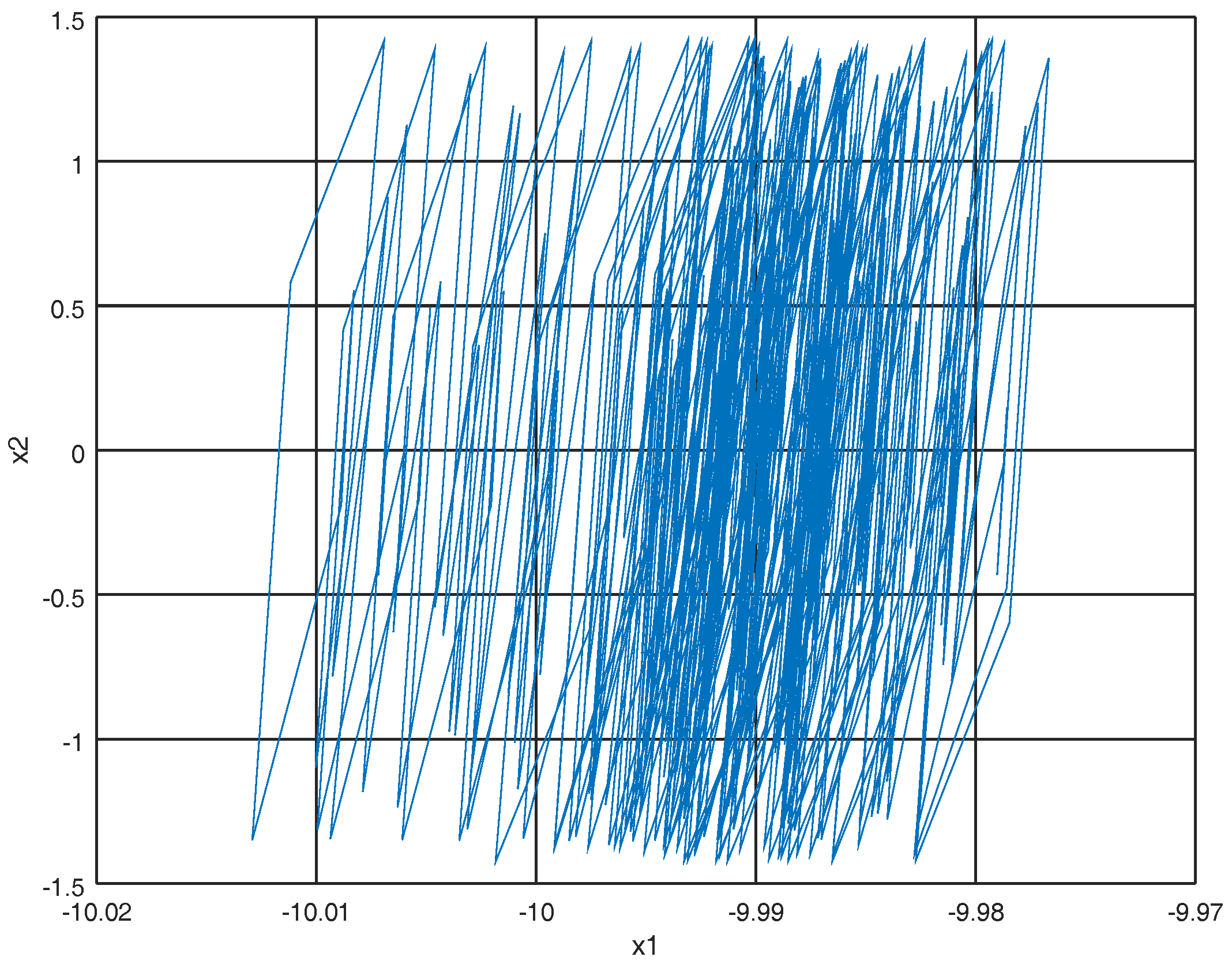
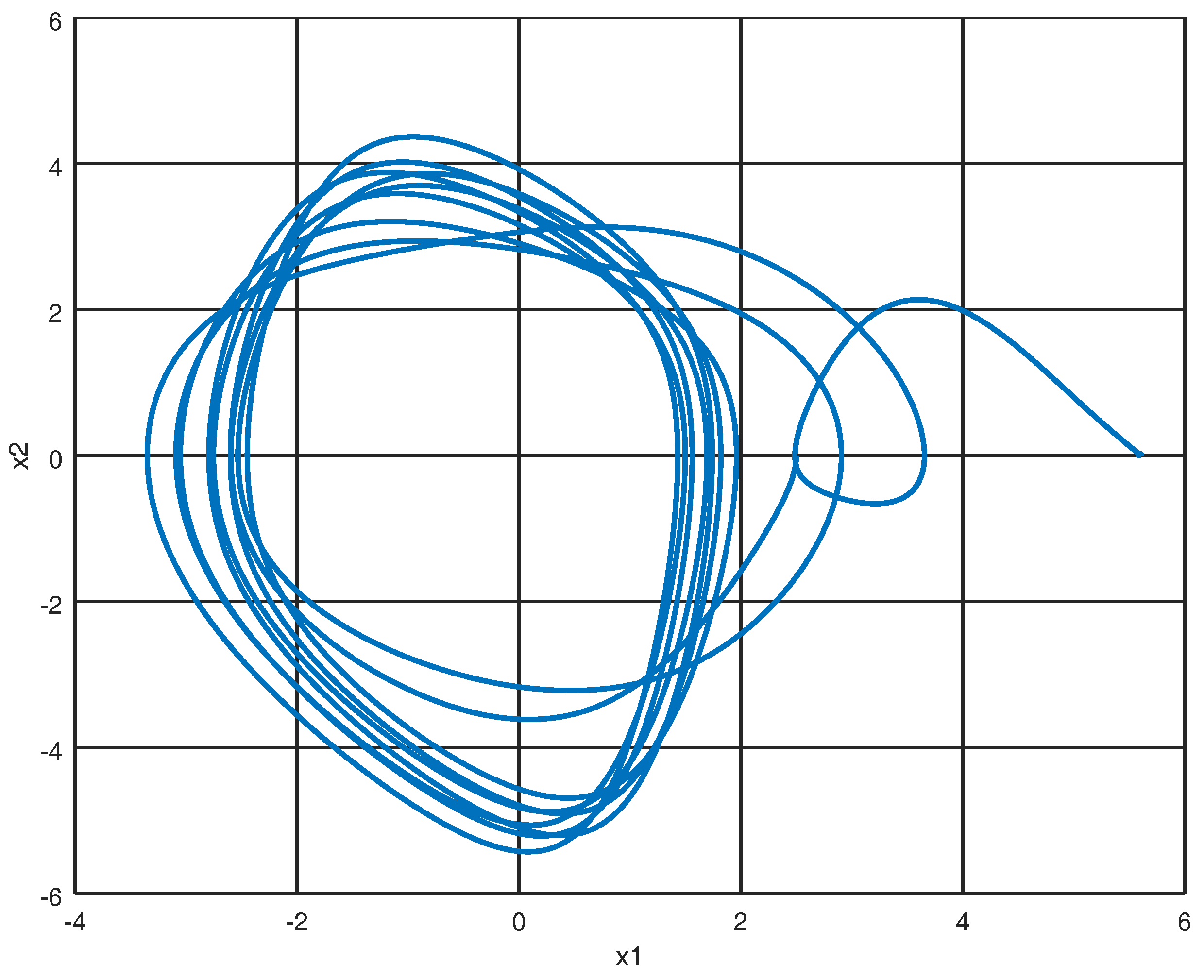
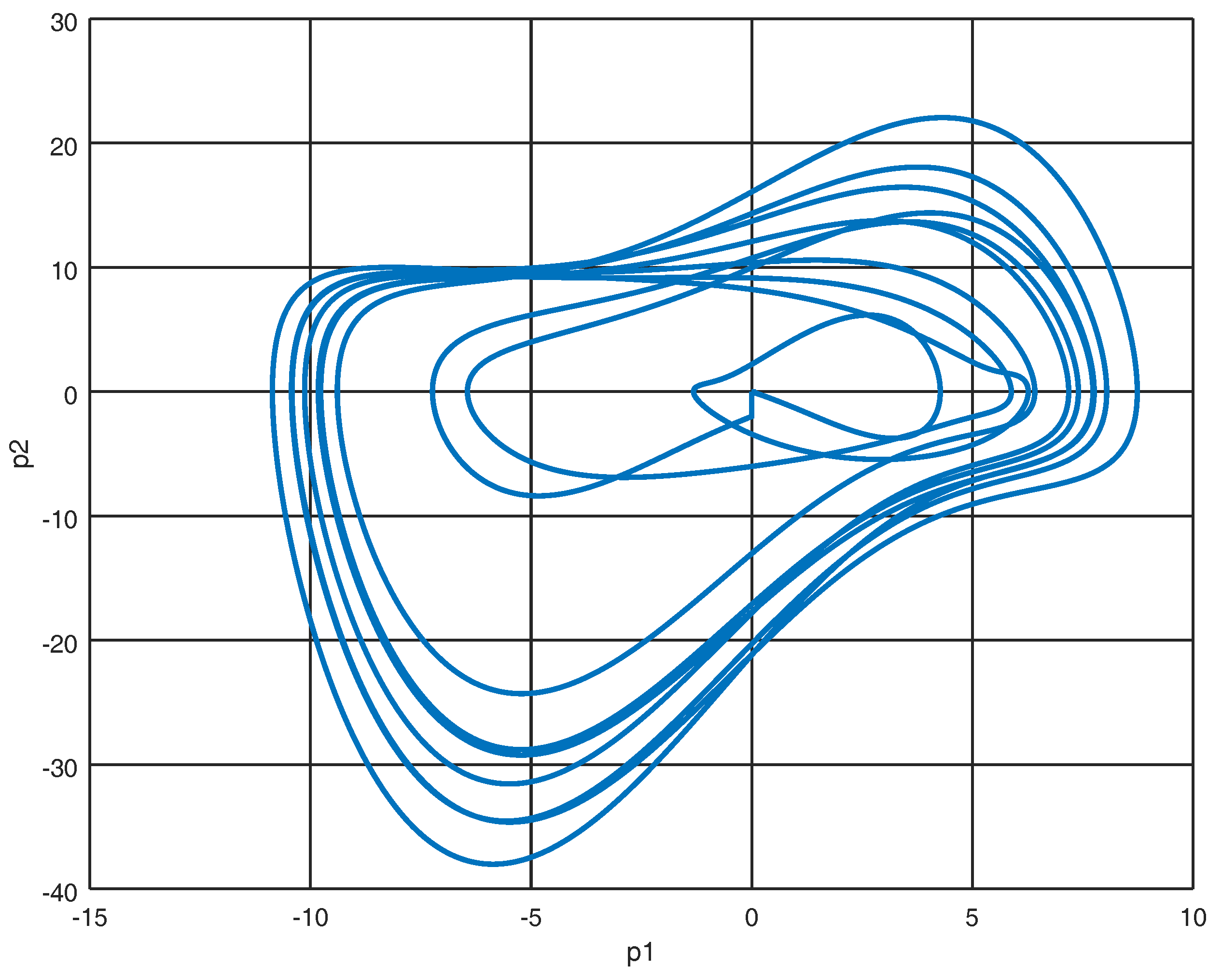
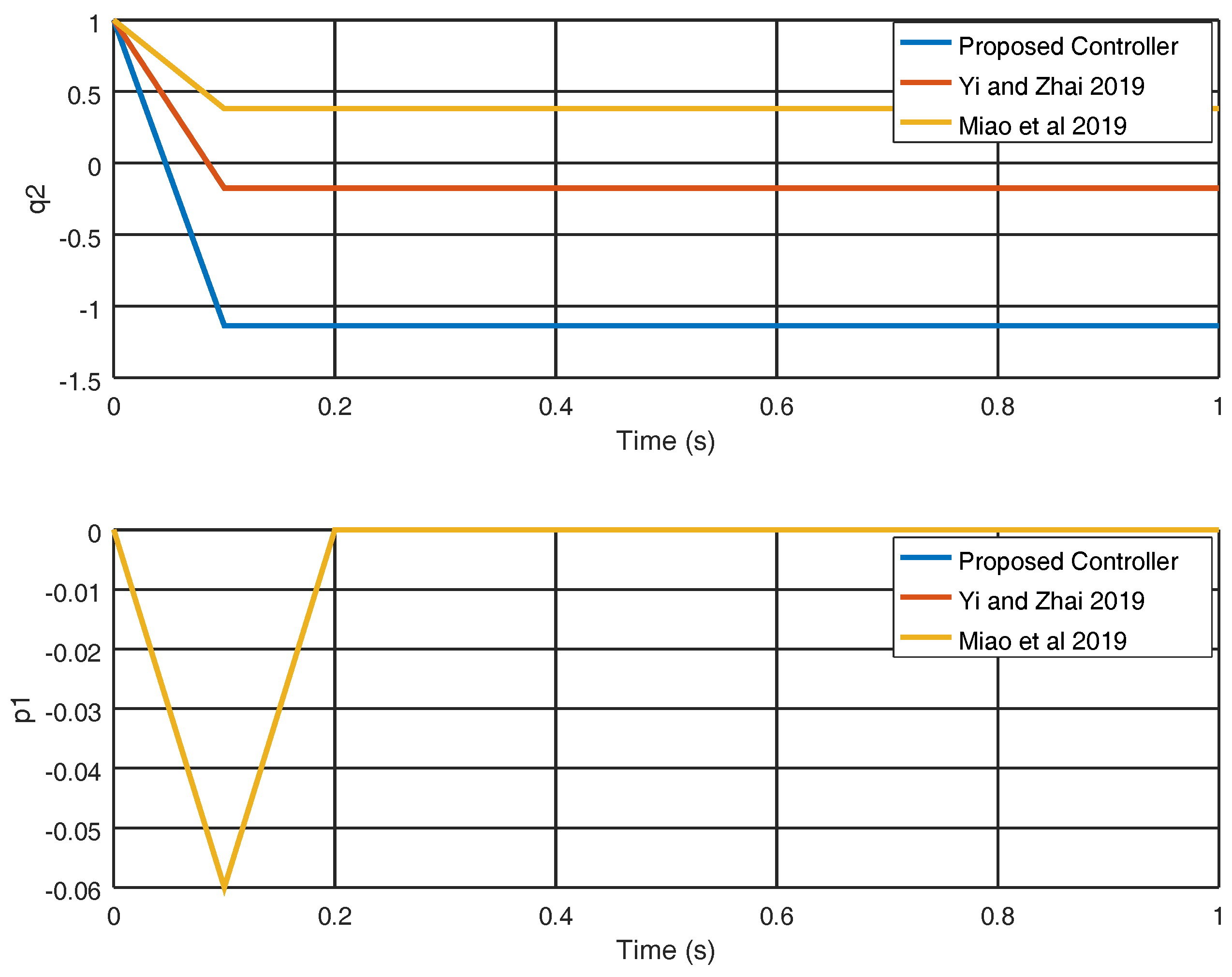
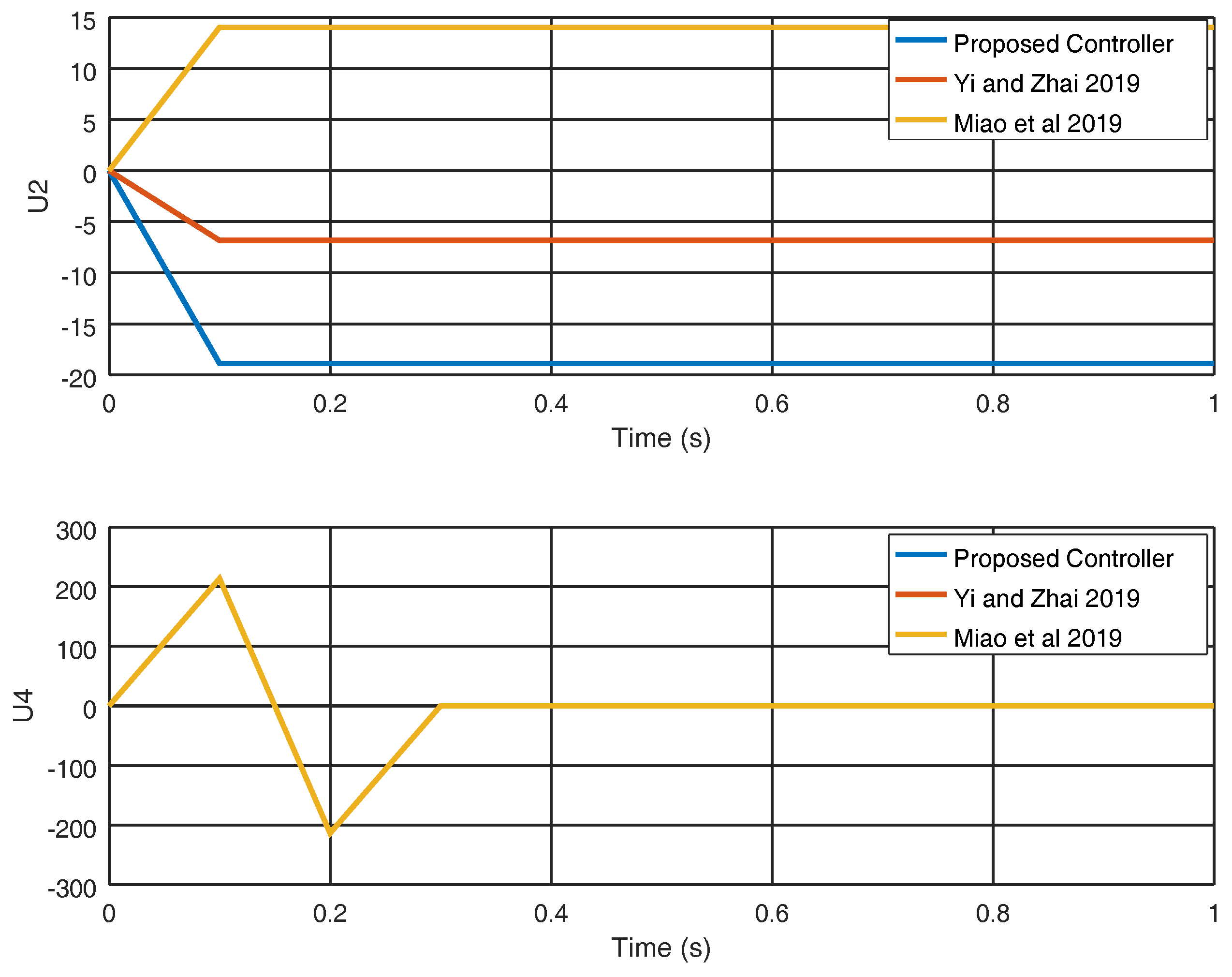
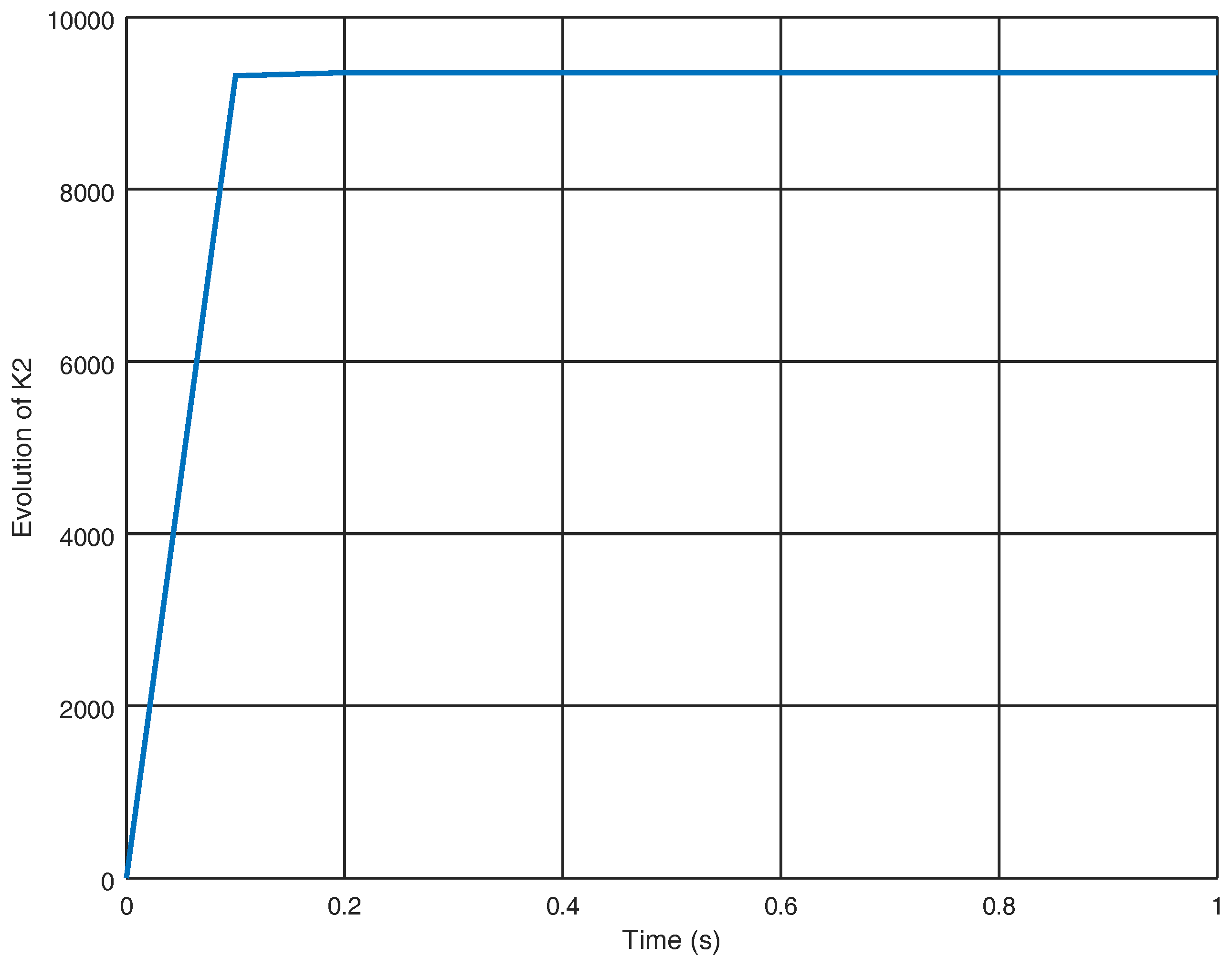
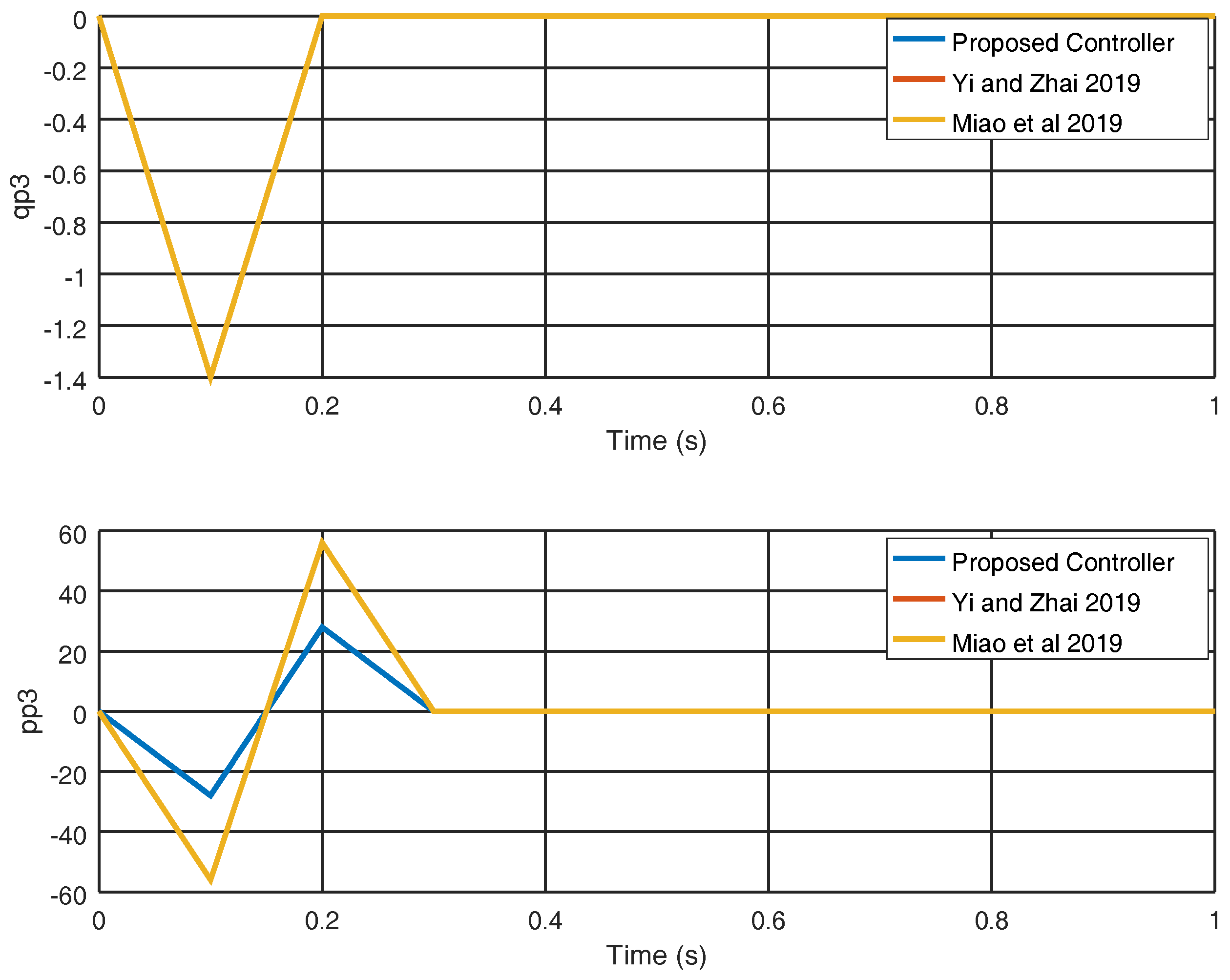
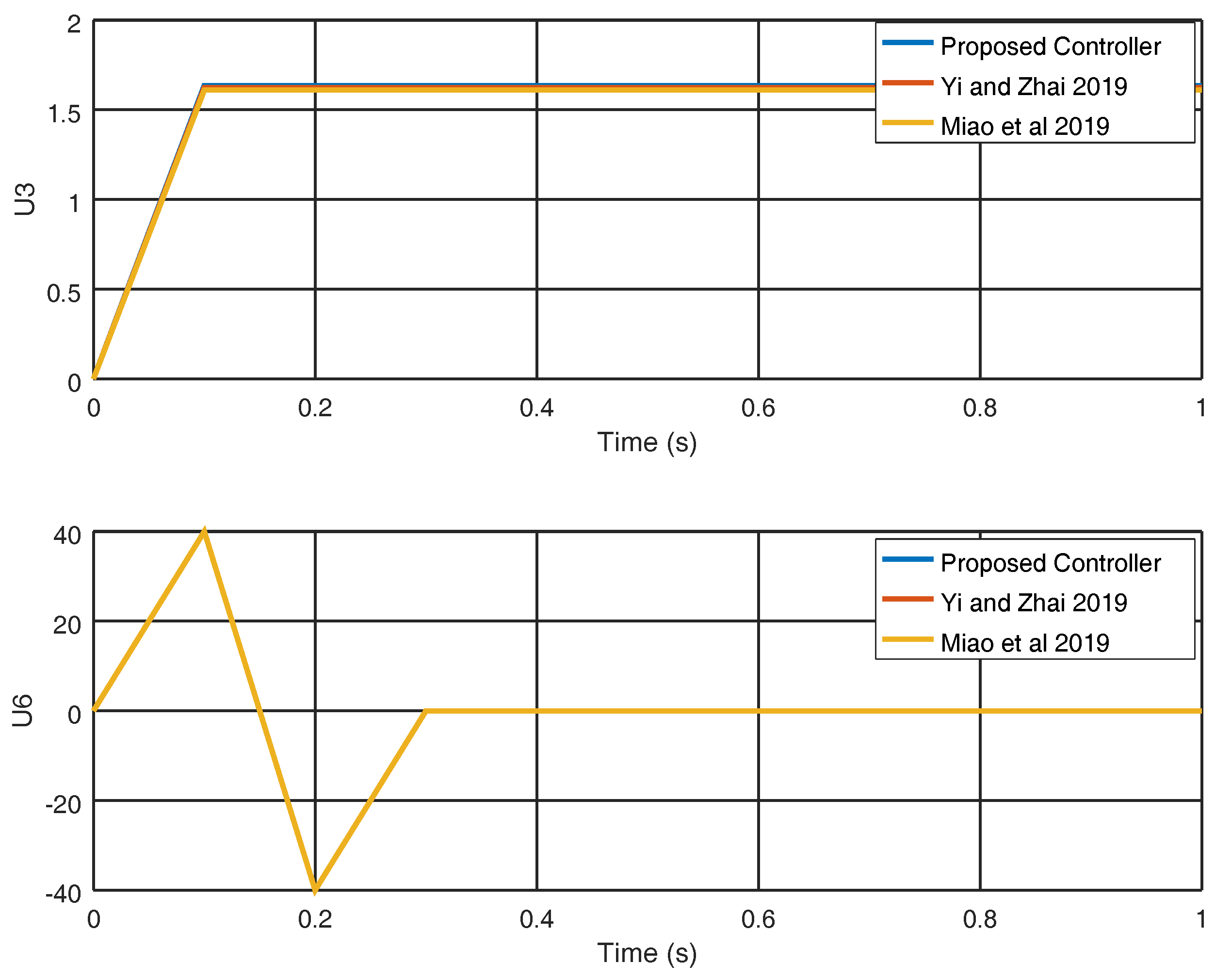
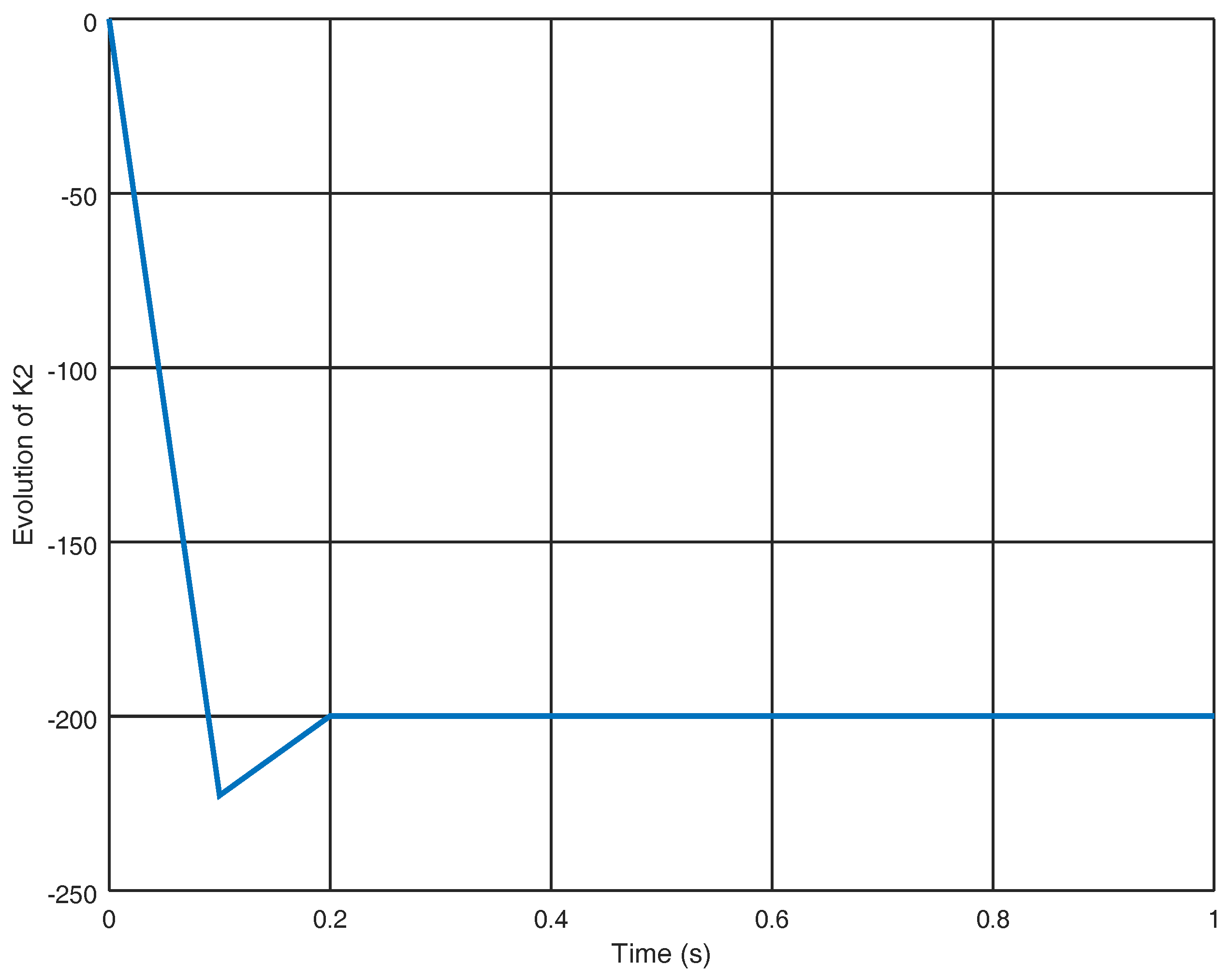
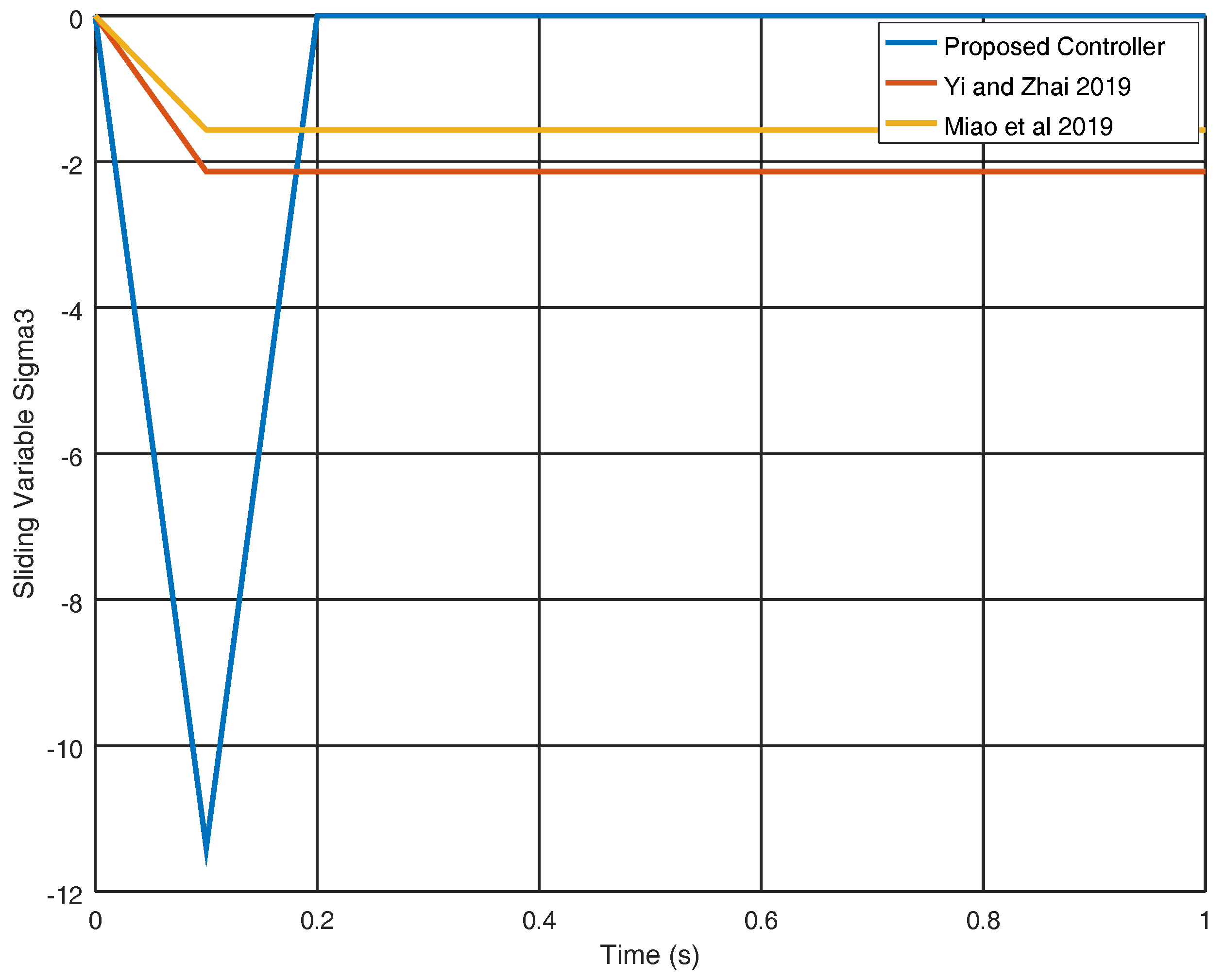
4. Numerical Experiments
4.1. Experiment 1
4.2. Experiment 2
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vaidyanathan, S.; Azar, A.T. Qualitative Study and Adaptive Control of a Novel 4-D Hyperchaotic System with Three Quadratic Nonlinearities. In Advances in Chaos Theory and Intelligent Control; Azar, A.T., Vaidyanathan, S., Eds.; Springer International Publishing: Cham, Germany, 2016; pp. 179–202. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T. Generalized projective synchronization of a novel hyperchaotic four-wing system via adaptive control method. In Advances in Chaos Theory and Intelligent Control; Springer: Berlin, Germany, 2016; pp. 275–290. [Google Scholar]
- Azar, A.T.; Volos, C.; Gerodimos, N.A.; Tombras, G.S.; Pham, V.T.; Radwan, A.G.; Vaidyanathan, S.; Ouannas, A.; Munoz-Pacheco, J.M. A Novel Chaotic System without Equilibrium: Dynamics, Synchronization, and Circuit Realization. Complexity 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Ouannas, A.; Azar, A.T.; Abu-Saris, R. A new type of hybrid synchronization between arbitrary hyperchaotic maps. Int. J. Mach. Learn. Cybern. 2017, 8, 1887–1894. [Google Scholar] [CrossRef]
- Azar, A.T.; Adele, N.M.; Alain, K.S.T.; Kengne, R.; Bertrand, F.H. Multistability analysis and function projective synchronization in relay coupled oscillators. Complexity 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T.; Sambas, A.; Singh, S.; Alain, K.S.T.; Serrano, F.E. A Novel Hyperchaotic System With Adaptive Control, Synchronization, and Circuit Simulation. In Advances in System Dynamics and Control; IGI Global: Philadelphia, PA, USA, 2018. [Google Scholar]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.K.; Azar, A.T.; Hoang, T.M.; Van Yem, V. A Three-Dimensional No-Equilibrium Chaotic System: Analysis, Synchronization and Its Fractional Order Form. In Fractional Order Control and Synchronization of Chaotic Systems; Azar, A.T., Vaidyanathan, S., Ouannas, A., Eds.; Springer International Publishing: Cham, Germany, 2017; pp. 449–470. [Google Scholar]
- Vaidyanathan, S.; Azar, A.T.; Akgul, A.; Lien, C.H.; Kacar, S.; Cavusoglu, U. A memristor-based system with hidden hyperchaotic attractors, its circuit design, synchronisation via integral sliding mode control and an application to voice encryption. Int. J. Autom. Control 2019, 13, 644–667. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Jafari, S.; Pham, V.T.; Azar, A.T.; Alsaadi, F.E. A 4-D chaotic hyperjerk system with a hidden attractor, adaptive backstepping control and circuit design. Arch. Control Sci. 2018, 28, 239–254. [Google Scholar]
- Pham, V.T.; Vaidyanathan, S.; Volos, C.K.; Jafari, S.; Gotthans, T. A Three-Dimensional Chaotic System with Square Equilibrium and No-Equilibrium. In Fractional Order Control and Synchronization of Chaotic Systems; Azar, A.T., Vaidyanathan, S., Ouannas, A., Eds.; Springer International Publishing: Cham, Germany, 2017; pp. 613–635. [Google Scholar]
- Wang, Z.; Volos, C.; Kingni, S.T.; Azar, A.T.; Pham, V.T. Four-wing attractors in a novel chaotic system with hyperbolic sine nonlinearity. Opt. Int. J. Light Electr. Opt. 2017, 131, 1071–1078. [Google Scholar] [CrossRef]
- Bayani, A.; Rajagopal, K.; Khalaf, A.; Jafari, S.; Leutcho, G.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2019, 383, 1450–1456. [Google Scholar] [CrossRef]
- Zuo, J.L.; Li, C.L. Multiple attractors and dynamic analysis of a no-equilibrium chaotic system. Optik 2016, 127, 7952–7957. [Google Scholar] [CrossRef]
- Signing, V.; Kengne, J.; Pone, J. Antimonotonicity, chaos, quasi-periodicity and coexistence of hidden attractors in a new simple 4-D chaotic system with hyperbolic cosine nonlinearity. Chaos Solitons Fractals 2019, 118, 187–198. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Jafari, S.; Ahmadi, A.; Khalaf, A.; Abdolmohammadi, H.; Pham, V.T.; Alsaadi, F. A new hidden chaotic attractor with extreme multi-stability. AEU Int. J. Electron. Commun. 2018, 89, 131–135. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Leonov, G. Hidden attractors in dynamical systems: Systems with no equilibria, multistability and coexisting attractors. IFAC Proc. Vol. 2014, 19, 5445–5454. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.; Mosekilde, E.; Rubanov, V.; Nabokov, R. Multistability and hidden attractors in a relay system with hysteresis. Phys. D Nonlinear Phenom. 2015, 306, 6–15. [Google Scholar] [CrossRef]
- Wei, Z.; Akgul, A.; Kocamaz, U.; Moroz, I.; Zhang, W. Control, electronic circuit application and fractional-order analysis of hidden chaotic attractors in the self-exciting homopolar disc dynamo. Chaos Solitons Fractals 2018, 111, 157–168. [Google Scholar] [CrossRef]
- Wang, M.; Liao, X.; Deng, Y.; Li, Z.; Su, Y.; Zeng, Y. Dynamics, synchronization and circuit implementation of a simple fractional-order chaotic system with hidden attractors. Chaos Solitons Fractals 2020, 130, 109406. [Google Scholar] [CrossRef]
- Dong, E.; Yuan, M.; Du, S.; Chen, Z. A new class of Hamiltonian conservative chaotic systems with multistability and design of pseudo-random number generator. Appl. Math. Model. 2019, 73, 40–71. [Google Scholar] [CrossRef]
- Qi, G.; Hu, J.; Wang, Z. Modeling of a Hamiltonian conservative chaotic system and its mechanism routes from periodic to quasiperiodic, chaos and strong chaos. Appl. Math. Model. 2020, 78, 350–365. [Google Scholar] [CrossRef]
- Cang, S.; Wu, A.; Wang, Z.; Chen, Z. On a 3-D generalized Hamiltonian model with conservative and dissipative chaotic flows. Chaos Solitons Fractals 2017, 99, 45–51. [Google Scholar] [CrossRef]
- Miao, Y.; Hwang, I.; Liu, M.; Wang, F. Adaptive fast nonsingular terminal sliding mode control for attitude tracking of flexible spacecraft with rotating appendage. Aerosp. Sci. Technol. 2019, 93, 105312. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; Serrano, F.E.; Vaidyanathan, S. Sliding Mode Stabilization and Synchronization of Fractional Order Complex Chaotic and Hyperchaotic Systems. In Mathematical Techniques of Fractional Order Systems; Advances in Nonlinear Dynamics and Chaos (ANDC); Azar, A.T., Radwan, A.G., Vaidyanathan, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Chapter 10; pp. 283–317. [Google Scholar]
- Azar, A.; Serrano, F.; Koubaa, A.; Kamal, N.; Vaidyanathan, S.; Fekik, A. Adaptive Terminal-Integral Sliding Mode Force Control of Elastic Joint Robot Manipulators in the Presence of Hysteresis. Adv. Intell. Syst. Comput. 2020, 1058, 266–276. [Google Scholar]
- Yi, S.; Zhai, J. Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators. ISA Trans. 2019, 90, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Azar, A.; Serrano, F.; Flores, M.; Vaidyanathan, S.; Zhu, Q. Adaptive neural-fuzzy and backstepping controller for port-Hamiltonian systems. Int. J. Comput. Appl. Technol. 2020, 62, 1–12. [Google Scholar] [CrossRef]
- Jost, J. Dynamical Systems; Springer: Berlin, Germany, 2005. [Google Scholar]
- Haddad, W.; Chellaboina, V. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azar, A.T.; Serrano, F.E. Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control. Entropy 2020, 22, 122. https://doi.org/10.3390/e22010122
Azar AT, Serrano FE. Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control. Entropy. 2020; 22(1):122. https://doi.org/10.3390/e22010122
Chicago/Turabian StyleAzar, Ahmad Taher, and Fernando E. Serrano. 2020. "Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control" Entropy 22, no. 1: 122. https://doi.org/10.3390/e22010122
APA StyleAzar, A. T., & Serrano, F. E. (2020). Stabilization of Port Hamiltonian Chaotic Systems with Hidden Attractors by Adaptive Terminal Sliding Mode Control. Entropy, 22(1), 122. https://doi.org/10.3390/e22010122




