1. Introduction
Decision trees are one of the efficient techniques that are widely used in various areas, like machine learning, image processing, and pattern recognition. Decision trees are good due to having better comprehensibility of classification in terms of extracting from feature-based samples [
1,
2,
3]. In addition, decision trees were not only proven efficient in many fields [
4], but also have less parameters [
5]. There are two main rules considered in the process of building decision trees [
6]. One is the stopping criterion to determine when to stop the growth of tree and generate leaf nodes [
7]. The other is how to assign class labels in leaf nodes [
8]. The first rule means that the growth of the tree should be ended [
9] if all samples belongs to the same class [
9]. The second rule emphasizes the importance of setting a threshold [
10]. There exist many methods of decision trees, such as ID3 [
7], C4.5 [
11,
12], and CART [
10].
However, all rules in the processing of decision trees are under certain situations; while the real world is filled with uncertainty [
13,
14,
15,
16]. Thus, when it deals with uncertain issues, all the rules should take uncertainty into consideration. Dempster-Shafer evidence theory (D–S) [
17,
18] is widely used in many applications such as decision making [
19,
20,
21,
22,
23,
24], evidential reasoning [
25,
26,
27,
28], information fusion [
29,
30], pattern recognition [
31,
32,
33], fault diagnosis [
34,
35,
36,
37], risk evaluation [
38,
39,
40], network analysis [
41], conflicting management [
42,
43,
44,
45], uncertainty modeling [
46,
47,
48,
49,
50], and so on [
51,
52,
53,
54]. In the D–S evidence theory, Basic Belief Assignment (BBA) measures the uncertainty. Deng entropy [
55] is proposed to quantify the uncertain measure of BBA.
Some works combined with evidence theory and decision trees are presented [
56,
57,
58,
59,
60], but, motivated by the idea of building decision tree based on Pearson correlation coefficient [
61] and the proposed Deng entropy instead of information entropy [
62,
63,
64,
65,
66], in this paper, the evidential decision tree is proposed for classification of fuzzy data sets using BBAs, which are applied directly for classification instead of using combination rules for classification indirectly. That is to say, the evidential decision tree is constructed for classification directly based on BBAs rather than using combination rules, which not only reduce the complexity of algorithm but also avoid designing the combination rules, which is always complicated. Moreover, the proposed evidential decision trees are much more efficient than traditional decision tree methods, illustrated by the analysis of experiments with the iris data set and wine data set.
The organization of this paper is introduced briefly as follows.
Section 2 presents the introduction of preliminaries. The building of the evidential decision tree is shown in
Section 3. Experiments are conducted in
Section 4. This paper ends with the conclusion in
Section 5.
2. Preliminaries
In this section, D–S evidence [
17,
18], Deng Entropy [
55], and Pearson’s correlation coefficient based on the decision tree (PCC-Tree) [
61] are briefly introduced. D–S evidence theory is introduced to present the definitions in terms of uncertain problems. Additionally, the Deng entropy is introduced to calculate the uncertain degree of BBAs. Finally, PPC-Tree is followed by the proposed method, replacing Pearson’s correlation coefficient with Deng entropy to build an evidential decision tree.
2.1. D–S Evidence Theory
Handling uncertainty is an open issue, and many methods have been developed [
67,
68,
69]. In D–S evidence theory [
17,
18],
is a frame of discernment.
represents the identification of every element in the framework.
Basic Belief Assignment (BBA), a mass function, is one of the most important definitions of D–S evidence theory and many operations are presented based on it such as negation [
70,
71], divergence measure [
72], and correlation [
73]. BBA has two features:
and
. It should be mentioned that the BBA of an empty set in classical evidence theory is zero [
74].
For the same evidence, different Basic Belief Assignments will be obtained due to different independent evidence sources. Assuming the frame of discernment is
,
are
n different BBAs which are all independent. According to Dempster’s combination rule, the result is presented as follows:
K is normalization factor, which is defined as follows:
The reliability factor
is given to construct the discounted mass function
,
m is one of the BBAs on the identification frame
:
2.2. Deng Entropy
Inspired by Shannon Entropy, a new uncertainty method called Deng Entropy is proposed [
55]:
As shown in the above definition, different from the classical Shannon entropy, the belief for each focal element
A is divided by
, which means the potential number of states in
A. Through a simple transformation, it is found that Deng entropy is actually a type of composite measure, as follows: If the quotient rule of logarithm transformation of Deng Entropy is carried out, it is actually a comprehensive measurement:
where the first term could be explained as a measure of total nonspecificity in the mass function
m, and the second term could be interpreted as the measure of discord of the mass function among distinct focal elements.
2.3. PCC-Tree
During building decision trees, the Pearson’s correlation coefficient can be used as the optimal splitting point—PCC-Tree [
61].
Following the idea of building the traditional decision tree, one new type of decision tree was reconstructed by Pearson’s correlation coefficient through a top-down recursive way. The detailed constructing process can be found in Algorithm 1.
| Algorithm 1 Constructing a PCC-Tree |
Require: A root node , where is the i th instance with n condition attributes and one decision attribute D; the stopping criterion . Ensure: A PCC-Tree. if the samples in X belong to some class then Mark X as a leaf node and assign the class as its label. return. end if for each attribute in X do for each value in do Compute the Pearson’s correlation coefficient P of two vectors: and , where P denotes Pearson’s correlation coefficient and V denotes one vector. end for . end for Get the best attribute and the splitting point , where . Suppose is the proportion of samples covered by X. if then Mark X as leaf node. Assign the maximum class of samples in X to this leaf node. return else Split X into two subsets and , based on and . if or then Mark X as a leaf node. Assign the maximum class of samples in X to this leaf node. return end if Recursively search the new tree nodes from and by Algorithm 1, respectively. end if
|
3. Proposed Method
Evidential decision tree is introduced in this section. Motivated by the idea of building a decision tree based on Pearson’s correlation coefficient, the Deng Entropy is calculated as a measure in splitting rules processing the decision tree. The difference is that the relation between the probability distributions of attributes and the probability distribution of decision attributes can be measured by Pearson’s correlation coefficient, but BBAs can not in terms of uncertainty. Thus, the Deng Entropy is proposed in this paper, as a measure of splitting rules processing in the decision tree. In the end, the decision tree is built in the situation of uncertainty.
3.1. BBA Determination
It is an open issue to determine the BBAs of attributes. In this paper, one of them is chosen to determine the BBAs [
75]. The procedures are introduced in detail as follows.
Step 1: Normality test is carried out for each attribute column from each training set class. Consider a case where there are N samples in each class in the training set, and the attribute column (length N) are normality tested to get a Normality Index for the attribute j of class i, donated as (binary expression). If , it means the selected attribute obeys the experimental assumption. Otherwise, if , it represents that the attribute does not follow normal distribution. Transformation of the original data to an equivalent normal space will occur when condition is adopted.
Step 2: Calculate the value of the mean and the sample standard deviation of each sample for selected class and selected attribute.
is the sample value of the
attribute from the
sample in class
i. Thus, obtain the corresponding normal distribution function:
For each attribute, n normal distribution functions (or curves) can be obtained as models of different classes in the specific attribute.
Step 3: Determine the relationship between the test sample and the normal distribution models. Choose a sample from the test set, the n intersection of the selected sample is obtained by calculating the intersection of and the n normal distribution functions .
Step 4: For the
n intersections of the selected attribute
,
ranks them in decreasing order,
. For
, its corresponding class (i.e., the class the normal distribution curve belonged to) can be denoted as
. Assign
to a proposition by the following rule:
If
, then
. If
is a missing value, its corresponding BBA will be assigned as
, which means that the attribute is regarded as ignorance.
3.2. Deng Entropy Calculation
In this part, Deng Entropy is used to measure the degree of uncertainty of BBAs in each attribute. Deng Entropy will then be used as the measure of splitting rules. According to Equations (
5) and (
9), the Deng Entropy can be calculated as follows:
3.3. Evidential Decision Tree Construction
Based on the above equations, the decision tree based on Deng Entropy can be constructed in a top-down recursive way, which follows the traditional progress of decision trees. Firstly, the algorithm is proposed to find the best attribute for splitting rules shown in Algorithm 2.
| Algorithm 2 Splitting Rules based on Deng Entropy |
Require: A root node , where is the ith instance with n condition attributes and one decision attribute D; the stopping criterion: Until all conditional attributes are used up. Ensure: An Evidential Decision Tree. if the samples in X belong to some class then Mark X as a leaf node and assign the class as its label. return. end if for each attribute in X do Computer Deng Enropy according to Equation ( 10) represent a BBA for the instance i of attribute . The smaller the entropy value, the better the subsequent division. end for Get the best attribute and the splitting point .
|
Secondly, Algorithm 3 is proposed to classify samples by maximum value and minimum value of training set and find the child nodes of decision tree. In this section, the implementation of the algorithm is illustrated by taking the case of only three classes as an example. Similar to Algorithm 3, branches only need to be added when the number of classes increases.
| Algorithm 3 Construct an Evidential Decision Tree |
Require: Set attributes as Features. Set classes as A,B,C, etc. Ensure: An Evidential Decision Tree. for All samples do for All Feature do if Feature≥max() && Feature1≤min() then return A. end if if Feature≥max() && Feature1≤min() then return B. end if if Feature≥max() && Feature1≤min() then return C. end if end for end for
|
An Illustration For Evidential Decision Tree Construction
Assuming that there is a set of training instance , is a set of evidential test attributes, and each attribute is represented by a belief function on the set of possible terms. Let D be the decision attribute and the members of it compose the frame of discernment .
In order to better illustrate the implementation of the algorithm in the process of building a decision tree based on Deng entropy, a numerical example shown in
Table 1 is given to illustrate the meaning of each notations.
In this example, there are two test attributes and one decision attribute. According to proposed approach steps, the Deng entropy should be calculated under these circumstances.
In the implementation of Algorithm 2,
means each attribute,
represents the value of each focal element in the identification framework for the instance
of attribute
. In other words,
is the term
in Equation (
10).
For the two properties of
Table 1, there are some specific notation representations:
;
;
;
.
By comparing the calculation result of each attribute of Deng entropy, Algorithm 2 can find the father nodes of the decision tree, and Algorithm 3 is used to find the child of the decision tree.
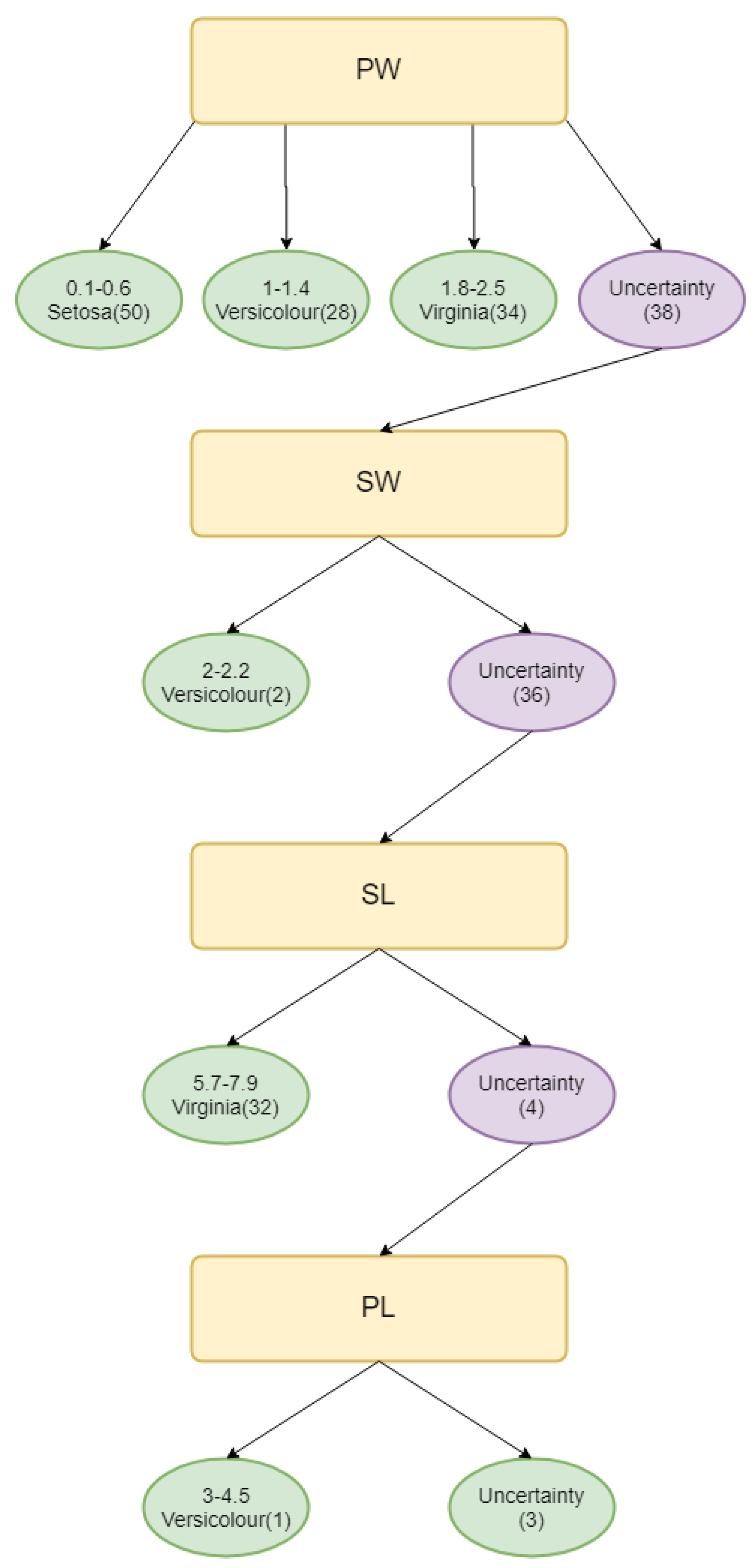
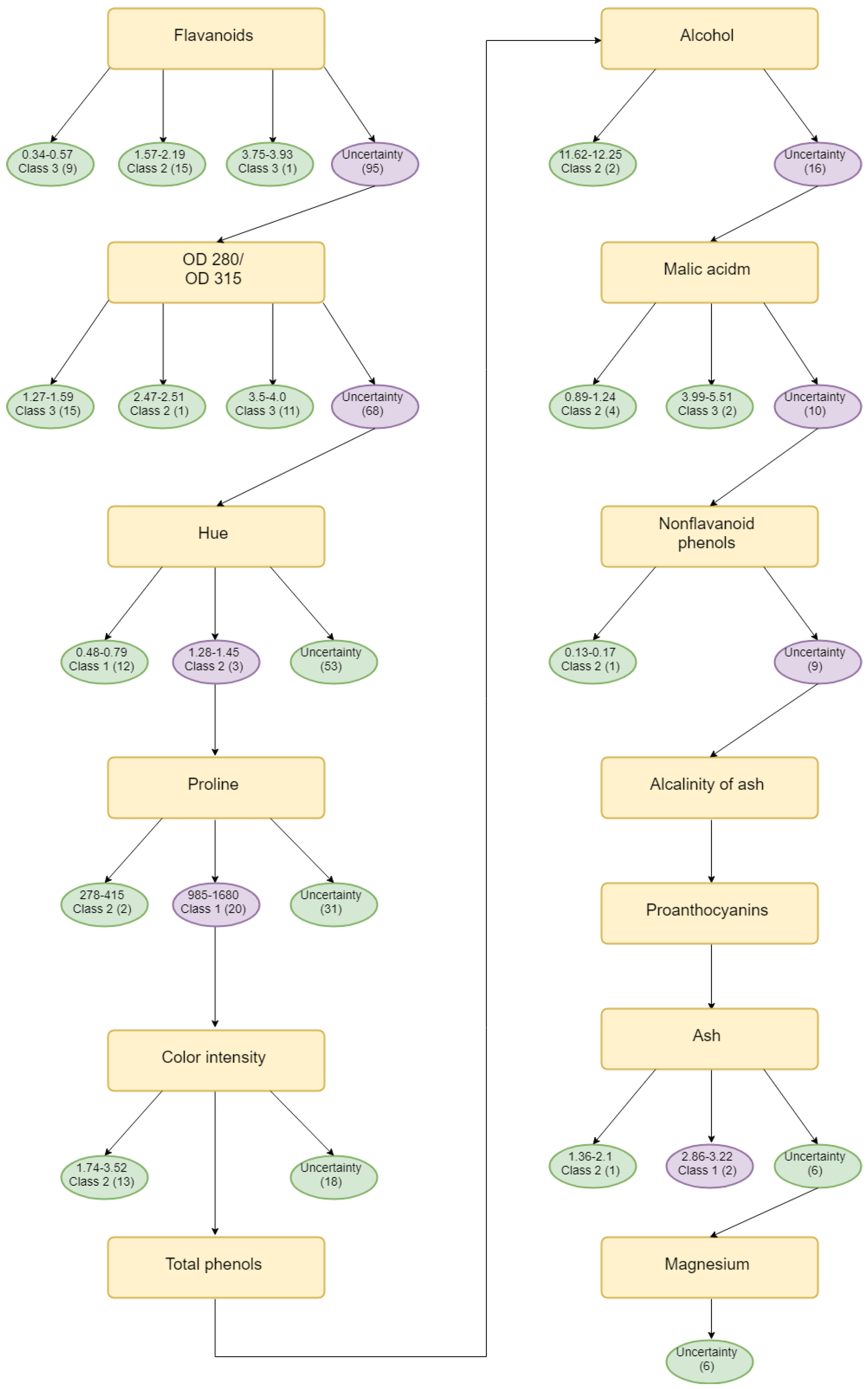
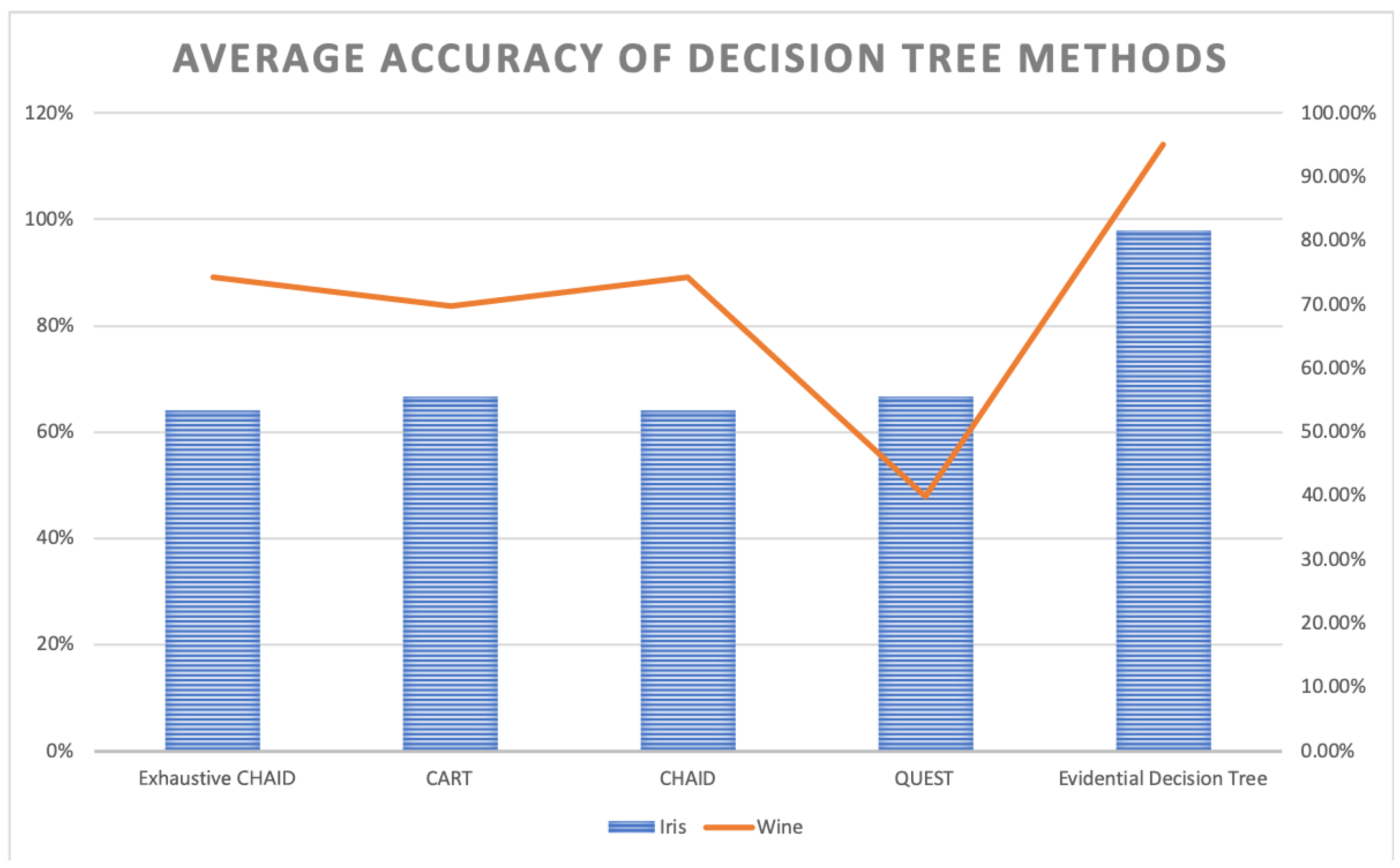
5. Conclusions
The existing methods have been based on Pearson’s correlation coefficient and information entropy to find the best splitting attribute in the process of building a decision tree. However, they are all impossible to handle with uncertain data classification, since Pearson’s correlation coefficient and the traditional information entropy both can only be used in the probability problem. When it comes to uncertain issues, the definition of BBA in D–S evidence theory can be seen as the probability in uncertain problems. Moreover, motivated by the idea of Deng entropy—which can measure the uncertain degree of BBAs—the evidential decision tree is proposed in this paper. The Deng entropy values of attributes’ BBAs are used as the measurement of the best splitting attribute. The lower the Deng entropy is, the more accurate the attribute can classify samples. Without using BBAs combination rules, 98% samples of iris and 95% samples of wine can be classified into certain decision attributes. In other words, the application of the evidential decision tree based on belief entropy efficiently reduces the complexity of algorithms for fuzzy data classification.