An Objective Non-Reference Metric Based on Arimoto Entropy for Assessing the Quality of Fused Images
Abstract
:1. Introduction
2. Preliminaries
3. Proposed Metric
- Concavity:
- Symmetry:
- Upper bound:
4. Experimental Section and Results
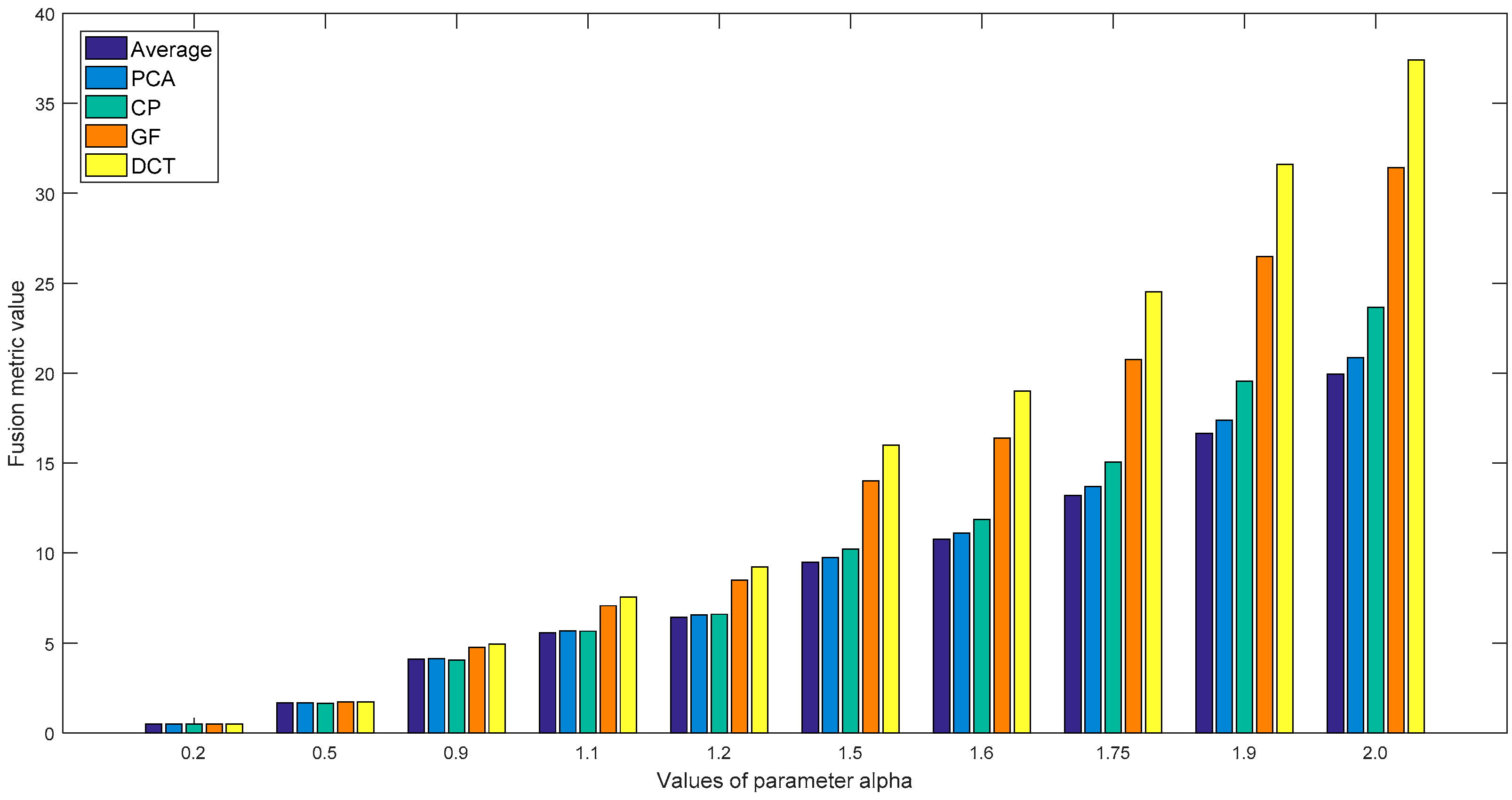
4.1. Test Data and Fusion Methods
4.2. Multi-Focus Image Fusion
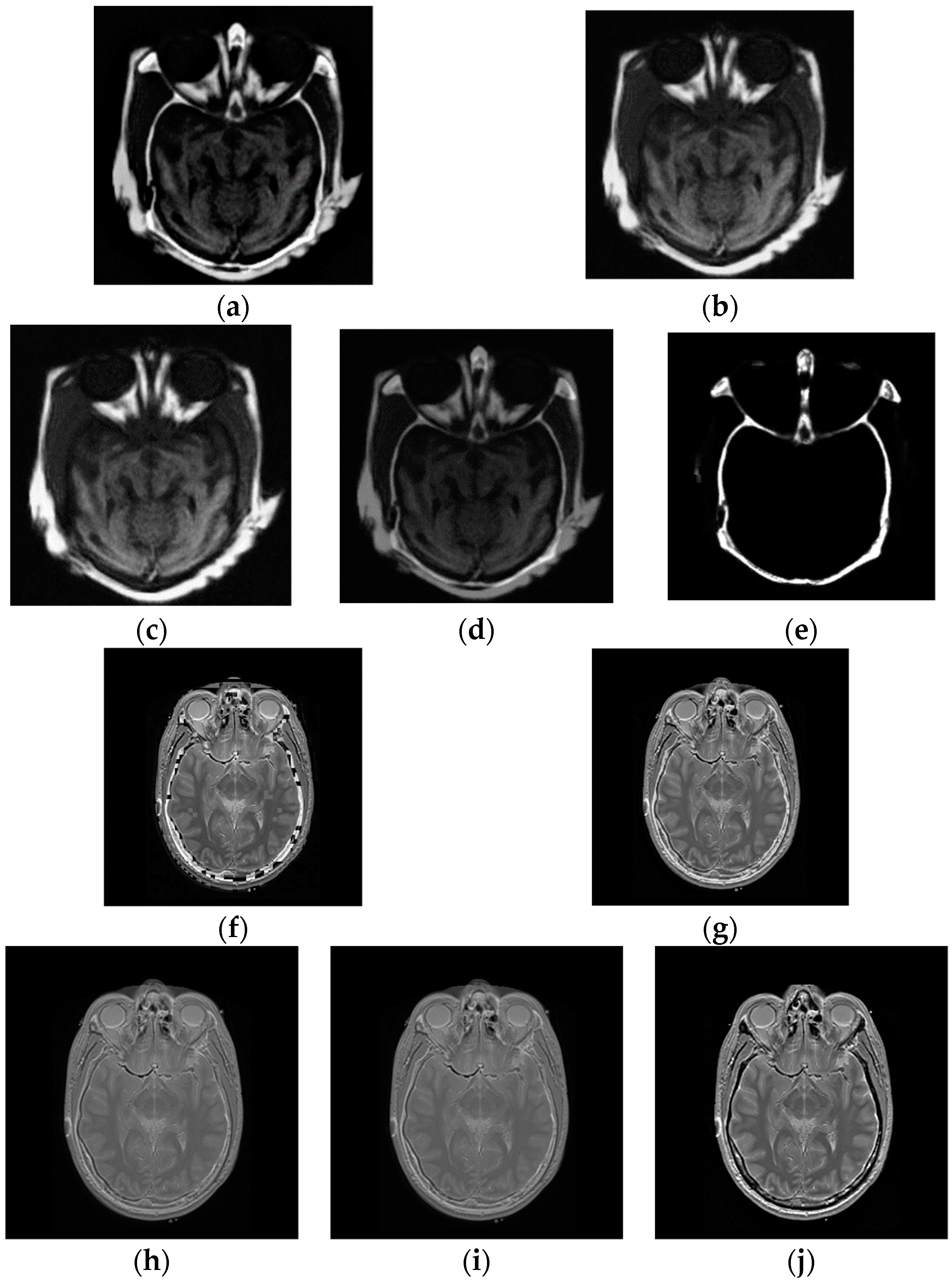
4.3. Multi-Modal Image Fusion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petrović, V. Subjective tests for image fusion evaluation and objective metric validation. Inform. Fusion 2007, 8, 208–216. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Quality assessment: From error measurement to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Proc. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Kavitha, S.; Thyagharajan, K.K. A survey on quantitative metrics for assessing the quality of fused medical images. Res. J. Appl. Sci. Eng. Technol. 2016, 12, 282–293. [Google Scholar] [CrossRef]
- Liu, Z.; Blasch, E.; Xue, Z.; Zhao, J.; Laganiere, R.; Wu, W. Objective assessment of multiresolution image fusion algorithms for context enhancement in night vision: A comparative study. IEEE T. Pattern. Anal. 2011, 34, 94–109. [Google Scholar] [CrossRef] [PubMed]
- Xydeas, C.A.; Petrovic, V. Objective image fusion performance measure. Electron. Lett. 2000, 36, 308–309. [Google Scholar] [CrossRef] [Green Version]
- Piella, G.; Heijmans, H. A new quality metric for image fusion. In Proceedings of the 9th International Conference on Image, Barcelona, Spain, 14–17 September 2003. [Google Scholar]
- Petrovic, V.; Xydeas, C. Objective image fusion performance characterisation. In Proceedings of the 10th IEEE International Conference on Computer Vision, Beijing, China, 17–20 October 2005. [Google Scholar]
- Chen, H.; Varshney, P.K. A human perception inspired quality metric for image fusion based on regional information. Inform. Fusion 2007, 8, 193–207. [Google Scholar] [CrossRef]
- Wang, X.; Pang, X.; Zhao, Z.; Xu, B. A Novel Image Fusion Metric based on Regional Information Similarity. J. Comput. Inf. Syst. 2013, 9, 1603–1613. [Google Scholar]
- Kotwal, K.; Chaudhuri, S. A novel approach to quantitative evaluation of hyperspectral image fusion techniques. Inform. Fusion 2013, 14, 5–18. [Google Scholar] [CrossRef]
- Han, Y.; Cai, Y.; Cao, Y.; Xu, X. A new image fusion performance metric based on visual information fidelity. Inform. Fusion 2013, 14, 127–135. [Google Scholar] [CrossRef]
- Li, S.; Hong, R.; Wu, X. A novel similarity based quality metric for image fusion. In Proceedings of the 2008 International Conference on Audio, Language and Image, Shanghai, China, 7–9 July 2008. [Google Scholar]
- Ferzli, R.; Karam, L.J. A no-reference objective image sharpness metric based on the notion of just noticeable blur (JNB). IEEE Trans. Image Process. 2009, 18, 717–728. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M. Elements of Information Theory; Wiley: New York, NY, USA, 2017. [Google Scholar]
- Qu, G.; Zhang, D.; Yan, P. Information measure for performance of image fusion. Electron. Lett. 2002, 38, 313–315. [Google Scholar] [CrossRef] [Green Version]
- Hossny, M.; Nahavandi, S.; Creighton, D. Comments on ‘Information measure for performance of image fusion’. Electron. Lett. 2008, 44, 1066–1067. [Google Scholar] [CrossRef]
- Cvejic, N.; Canagarajah, C.N.; Bull, D.R. Image fusion metric based on mutual information and Tsallis entropy. Electron. Lett. 2006, 42, 626–627. [Google Scholar] [CrossRef]
- Arimoto, S. Information-theoretical considerations on estimation problems. Inf. Control 1971, 19, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Boekee, D.E.; Van der Lubbe, J.C. The r-norm information measure. Inf. Control 1980, 45, 136–155. [Google Scholar] [CrossRef]
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inf. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Vila, M.; Bardera, A.; Feixas, M.; Sbert, M. Tsallis mutual information for document classification. Entropy 2011, 13, 1694–1707. [Google Scholar] [CrossRef]
- Jin, H.; Jiao, L.; Liu, F.; Qi, Y. Fusion of infrared and visual images based on contrast pyramid directional filter banks using clonal selection optimizing. Opt. Eng. 2008, 47, 027002. [Google Scholar] [CrossRef]
- Turhan-Sayan, G. Real time electromagnetic target classification using a novel feature extraction technique with PCA-based fusion. IEEE Trans. Antenn. Propag. 2005, 53, 766–776. [Google Scholar] [CrossRef]
- Haghighat, M.B.A.; Aghagolzadeh, A.; Seyedarabi, H. Multi-focus image fusion for visual sensor networks in DCT domain. Comput. Electr. Eng. 2011, 37, 789–797. [Google Scholar] [CrossRef]
- Burt, P.; Adelson, E. The Laplacian pyramid as a compact image code. IEEE Trans. Commun. 1983, 31, 532–540. [Google Scholar] [CrossRef]
- Li, S.; Kang, X.; Hu, J. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar] [PubMed]

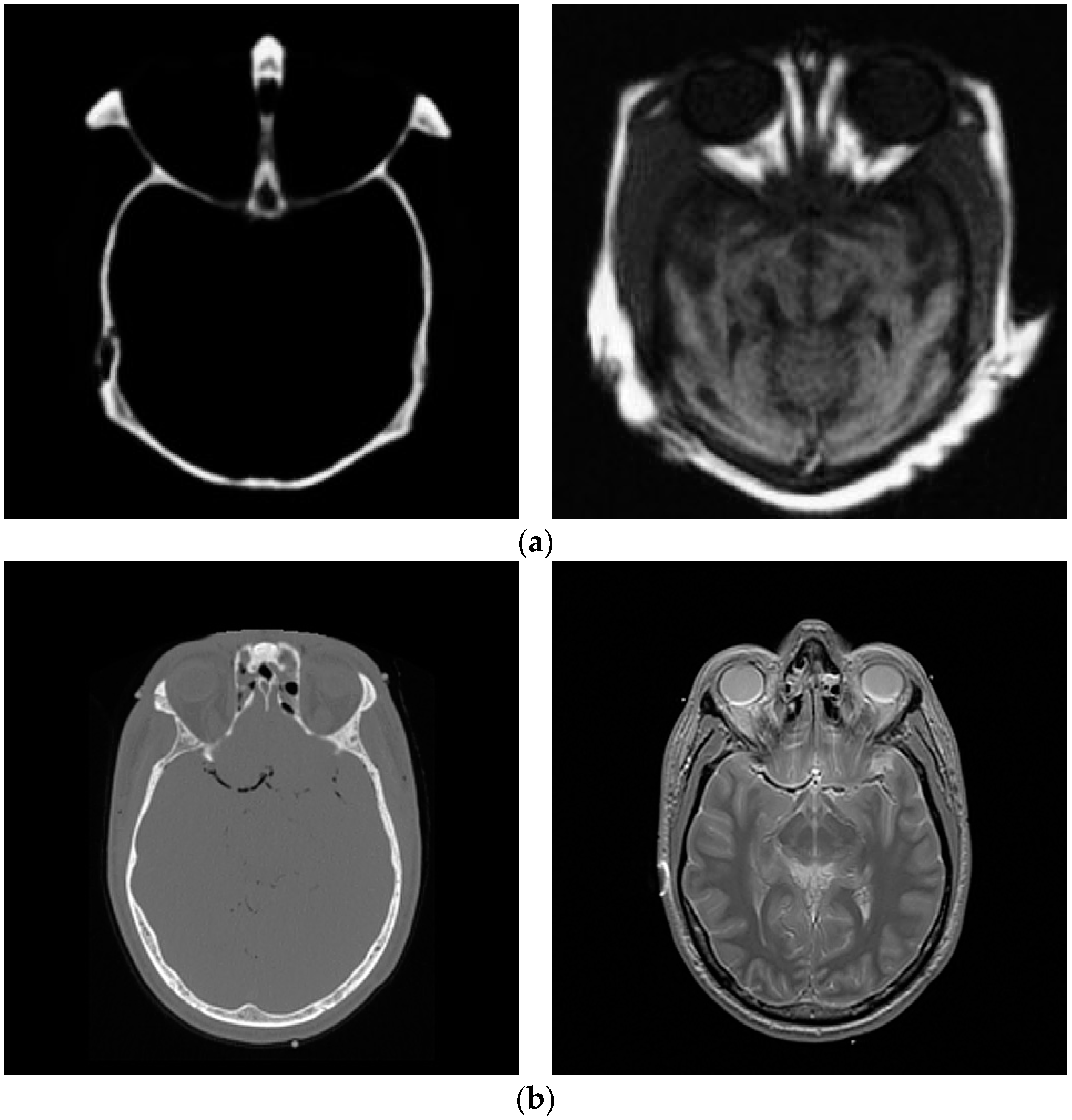


| Image | Dimension | Figure |
|---|---|---|
| Gear | 256 × 256 | Figure 1a |
| Laboratory | 480 × 640 | Figure 1b |
| CT & MR | 256 × 256 | Figure 2a |
| CT & MR | 464 × 464 | Figure 2b |
| “Gear” Images | Subjective Rank | |||||
|---|---|---|---|---|---|---|
| Method/Metric | MI | NMI | Petrovic | Tsallis | Proposed | |
| DCT | 8.796① | 1.319① | 0.852② | 24.96① | 15.99① | ① |
| GF | 8.347② | 1.252② | 0.854① | 20.97② | 14.005② | ② |
| CP | 6.846⑤ | 1.028⑤ | 0.842③ | 13.86③ | 10.228③ | ③ |
| PCA | 6.998③ | 1.061③ | 0.794④ | 13.04④ | 9.746④ | ④ |
| Average | 6.92④ | 1.05④ | 0.787⑤ | 12.57⑤ | 9.475⑤ | ⑤ |
| “Laboratory” Images | Subjective Rank | |||||
|---|---|---|---|---|---|---|
| Method/Metric | MI | NMI | Petrovic | Tsallis | Proposed | |
| GF | 7.911② | 1.133② | 0.751① | 30.66① | 19.31① | ① |
| DCT | 8.516① | 1.224① | 0.742② | 23.33② | 15.597② | ② |
| CP | 7.018⑤ | 1.003⑤ | 0.711③ | 15.47③ | 11.218③ | ③ |
| PCA | 7.122③ | 1.027③ | 0.59④ | 15.03④ | 10.974④ | ④ |
| Average | 7.08④ | 1.021④ | 0.589⑤ | 14.77⑤ | 10.812⑤ | ⑤ |
| CT-MR Images in Figure 2a | Subjective Rank | |||||
|---|---|---|---|---|---|---|
| Method/Metric | MI | NMI | Petrovic | Tsallis | Proposed | |
| LP | 2.564④ | 0.453⑤ | 0.729① | 31.652① | 19.101① | ① |
| PCA | 6.238② | 0.981② | 0.649③ | 24.408③ | 13.729② | ② |
| DCT | 7.028① | 1.092① | 0.667② | 23.221④ | 13.15③ | ③ |
| Average | 5.164③ | 0.879③ | 0.42④ | 27.369② | 12.631④ | ④ |
| CP | 1.635⑤ | 0.729④ | 0.253⑤ | 12.404⑤ | 9.0675⑤ | ⑤ |
| CT-MR Images in Figure 2b | Subjective Rank | |||||
|---|---|---|---|---|---|---|
| Method/Metric | MI | NMI | Petrovic | Tsallis | Proposed | |
| DCT | 5.911① | 1.12① | 0.673① | 27.732① | 17.858① | ① |
| LP | 3.236④ | 0.68⑤ | 0.609② | 13.800④ | 14.888② | ② |
| Average | 4.281② | 0.921② | 0.399④ | 21.573② | 14.403③ | ③ |
| PCA | 4.071③ | 0.90③ | 0.363⑤ | 15.990③ | 11.534④ | ④ |
| CP | 3.088⑤ | 0.698④ | 0.566③ | 12.738⑤ | 9.536⑤ | ⑤ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Li, R.; Liu, Z.; Li, C.; Wang, Z. An Objective Non-Reference Metric Based on Arimoto Entropy for Assessing the Quality of Fused Images. Entropy 2019, 21, 879. https://doi.org/10.3390/e21090879
Li B, Li R, Liu Z, Li C, Wang Z. An Objective Non-Reference Metric Based on Arimoto Entropy for Assessing the Quality of Fused Images. Entropy. 2019; 21(9):879. https://doi.org/10.3390/e21090879
Chicago/Turabian StyleLi, Bicao, Runchuan Li, Zhoufeng Liu, Chunlei Li, and Zongmin Wang. 2019. "An Objective Non-Reference Metric Based on Arimoto Entropy for Assessing the Quality of Fused Images" Entropy 21, no. 9: 879. https://doi.org/10.3390/e21090879
APA StyleLi, B., Li, R., Liu, Z., Li, C., & Wang, Z. (2019). An Objective Non-Reference Metric Based on Arimoto Entropy for Assessing the Quality of Fused Images. Entropy, 21(9), 879. https://doi.org/10.3390/e21090879





