Integrating Classical Preprocessing into an Optical Encryption Scheme
Abstract
1. Introduction
Our Contribution
2. Background and Tools
2.1. The AlphaEta Protocol
- ∘
- : average number of photons per pulse
- ∘
- : number of bases used
- ∘
- s: number of pulses sent in one round of the protocol
2.2. All-or-Nothing Transforms
- is a bijection.
- If any of the s output values are fixed, then any ℓ of the input values () are completely undetermined, in an information-theoretic sense.
- 1.
- ,
- 2.
- 3.
- For all with , and for all with , it holds that
3. Results
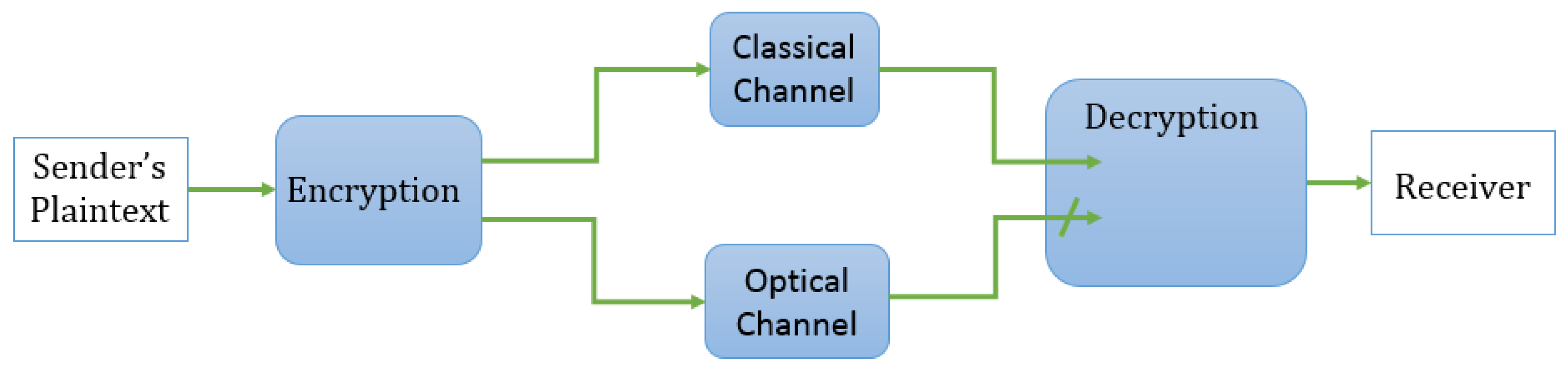
3.1. Symmetric-key Encryption Using Mesoscopic Coherent States
- KeyGen: Given a key length, outputs a corresponding secret key k.
- Enc: Given a plaintext m and secret key k, it outputs a ciphertext c, consisting of a sequence of coherent states and a bitstring:
- Dec: This process consists of two phases. Given a ciphertext c and a secret key k, the sequence of coherent states in c is measured in the first phase. Now c can be considered a classical bitstring when entering the second phase of the decryption. The final output of the algorithm is the plaintext m.
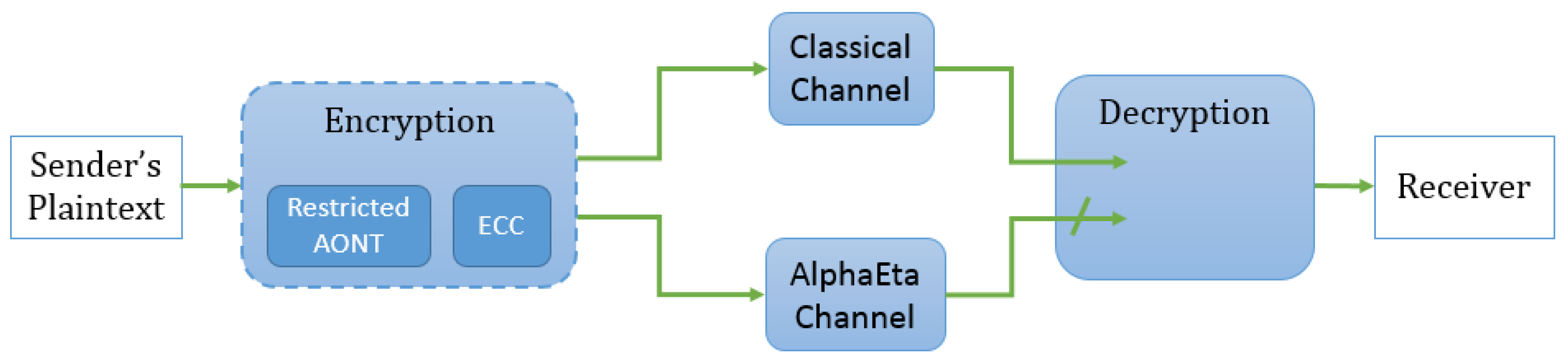
3.2. A Hybrid Construction
3.2.1. Description and Design Rationale
- For all i such that , .
- Let represent the collection of hidden bits. For all i such that , it holds that
3.2.2. Security Analysis
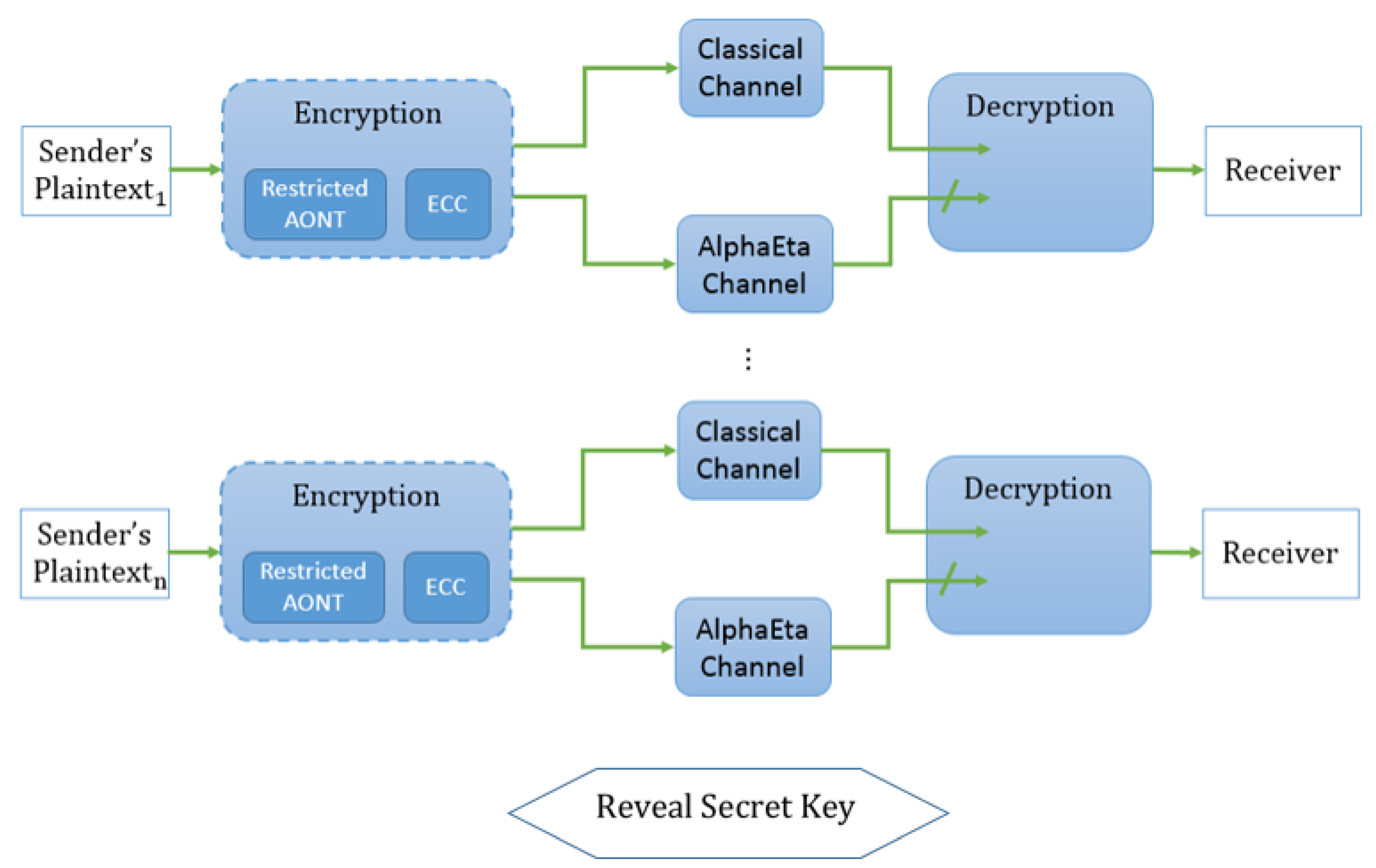
3.3. Forward Security
4. Discussion
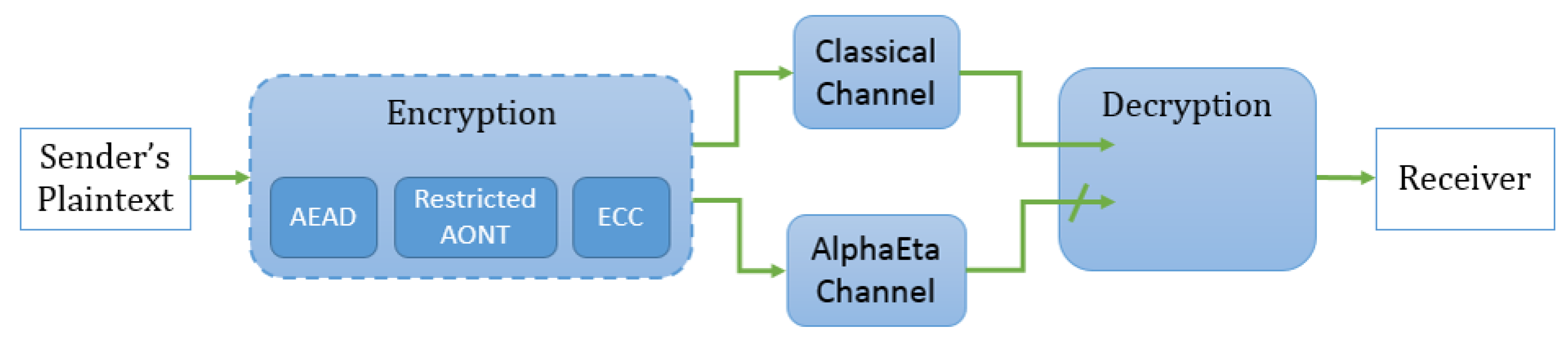
4.1. Integrating Classical Authenticated Encryption
4.2. Choosing Parameters
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FIPS PUB 197, Advanced Encryption Standard (AES); National Institute of Standards and Technology; U.S. Department of Commerce: Washington, DC, USA, 2011.
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; p. 175. [Google Scholar]
- Broadbent, A.; Schaffner, C. Quantum Cryptography Beyond Quantum Key Distribution. Des. Codes Cryptogr. 2016, 78, 351–382. [Google Scholar] [CrossRef]
- Shenoy-Hejamadi, A.; Pathak, A.; Radhakrishna, S. Quantum Cryptography: Key Distribution and Beyond. Quanta 2017, 6, 1–47. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, G.A.; Corndorf, E.; Kumar, P.; Yuen, H.P. Secure communication using mesoscopic coherent states. arXiv 2003, arXiv:quant-ph/0212018v2. [Google Scholar]
- Barbosa, G.A. Fast and secure key distribution using mesocopic coherent states of light. arXiv 2004, arXiv:quant-ph/0212033v4. [Google Scholar]
- Yuen, H.P.; Nair, R.; Corndorf, E.; Kanter, G.S.; Kumar, P. On the security of αη: Response to ‘some attacks on quantum-based cryptographic protocols’. Quantum Inf. Comput. 2006, 6, 561–582. [Google Scholar]
- Barbosa, G.A.; van de Graaf, J. Untappable communication channels over optical fibers from quantum-optical noise. IACR Cryptol. Eprint Arch. 2014, 2014, 146. [Google Scholar]
- Lo, H.K.; Ko, T.M. Some Attacks on Quantum-based Cryptographic Protocols. arXiv 2003, arXiv:quant-ph/0309127. Available online: https://arxiv.org/abs/quant-ph/0309127 (accessed on 4 September 2019).
- Nishioka, T.; Hasegawa, T.; Ishizuka, H.; Imafuku, K.; Imai, H. How much security does Y-00 protocol provide us? Phys. Lett. A 2004, 327, 28–32. [Google Scholar] [CrossRef]
- Yuen, H.P.; Kumar, P.; Corndorf, E.; Nair, R. Security of Y-00 and similar quantum cryptographic protocols. arXiv 2004, arXiv:quant-ph/0407067. Available online: https://arxiv.org/abs/quant-ph/0407067 (accessed on 4 September 2019).
- Hirota, O.; Kurosawa, K. An immunity against correlation attack on quantum stream cipher by Yuen 2000 protocol. arXiv 2006, arXiv:quant-ph/0604036. Available online: https://arxiv.org/abs/quant-ph/0604036 (accessed on 4 September 2019). [CrossRef]
- Lloyd, S. Quantum enigma machines. arXiv 2013, arXiv:quant-ph/1307.0380. Available online: https://arxiv.org/abs/1307.0380 (accessed on 4 September 2019).
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, A.; Barrera, J.F.; Vlez-Zea, A.; Torroba, R. Fractional optical cryptographic protocol for data containers in a noise-free multiuser environment. Opt. Lasers Eng. 2018, 102, 119–125. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J.; Liu, Z.; Du, X. Opto-digital spectrum encryption by using Baker mapping and gyrator transform. Opt. Lasers Eng. 2015, 66, 285–293. [Google Scholar] [CrossRef]
- Li, Y.B.; Song, T.T.; Huang, W.; Zhan, W.W. Fault-Tolerant Quantum Secure Direct Communication Protocol Based on Decoherence-Free States. Int. J. Theor. Phys. 2015, 54, 589–597. [Google Scholar] [CrossRef]
- Stinson, D.R. Something About All or Nothing (Transforms). Des. Codes Cryptogr. 2001, 22, 133–138. [Google Scholar] [CrossRef]
- D’Arco, P.; Esfahani, N.N.; Stinson, D.R. All or Nothing at All. Electr. J. Comb. 2016, 23, 4–10. [Google Scholar]
- Nir, Y.; Langley, A. ChaCha20 and Poly1305 for IETF Protocols. Internet Res. Task Force 2015. [Google Scholar] [CrossRef]
- Procter, G. A Security Analysis of the Composition of ChaCha20 and Poly1305. IACR Cryptol. Eprint Arch. 2014, 2014, 613. [Google Scholar]
- Bosma, W.; Cannon, J.; Playoust, C. The Magma algebra system. I. The user language. J. Symb. Comput. 1997, 24, 235–265. [Google Scholar] [CrossRef]


| r | |||
|---|---|---|---|
| 3 | 1 | ||
| 7 | 3 | ||
| 101 | 50 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, H.; Steinwandt, R.; Suárez Corona, A. Integrating Classical Preprocessing into an Optical Encryption Scheme. Entropy 2019, 21, 872. https://doi.org/10.3390/e21090872
Pham H, Steinwandt R, Suárez Corona A. Integrating Classical Preprocessing into an Optical Encryption Scheme. Entropy. 2019; 21(9):872. https://doi.org/10.3390/e21090872
Chicago/Turabian StylePham, Hai, Rainer Steinwandt, and Adriana Suárez Corona. 2019. "Integrating Classical Preprocessing into an Optical Encryption Scheme" Entropy 21, no. 9: 872. https://doi.org/10.3390/e21090872
APA StylePham, H., Steinwandt, R., & Suárez Corona, A. (2019). Integrating Classical Preprocessing into an Optical Encryption Scheme. Entropy, 21(9), 872. https://doi.org/10.3390/e21090872





