New Nonlinear Active Element Dedicated to Modeling Chaotic Dynamics with Complex Polynomial Vector Fields
Abstract
1. Introduction
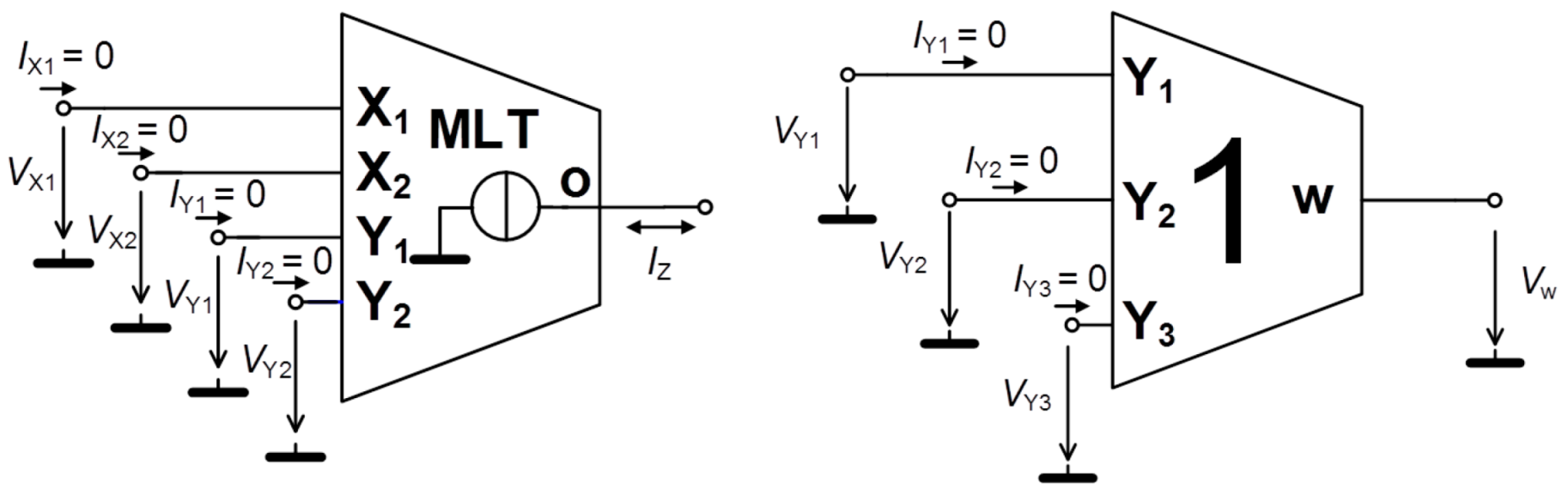
2. Evolution of Differential Voltage Trans-Conductance Multiplier (DV-TC-M)
3. Numerical Analysis of Chaotic Systems Dedicated for Circuit Synthesis
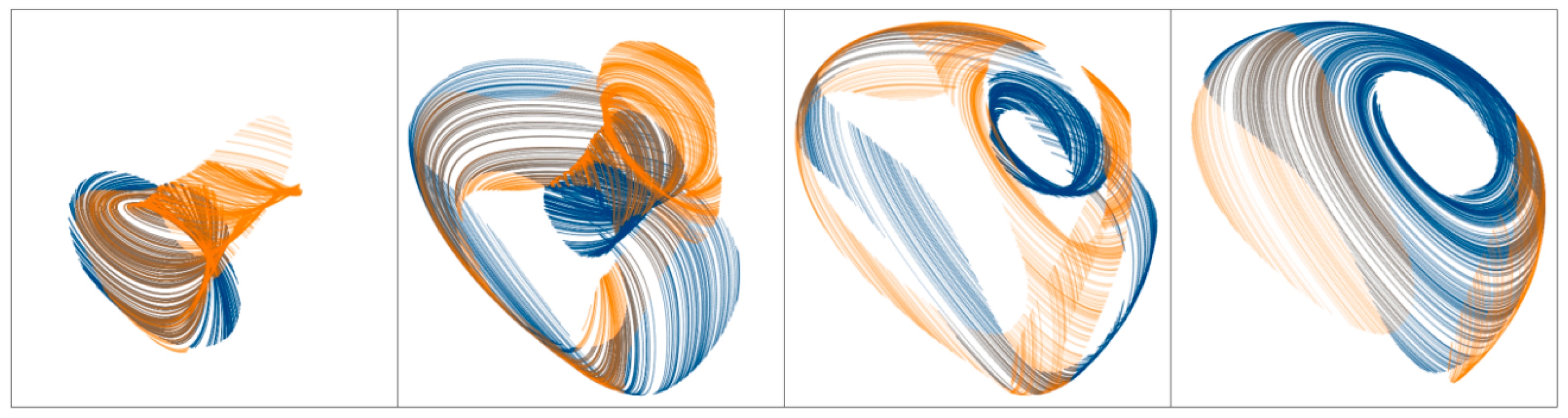
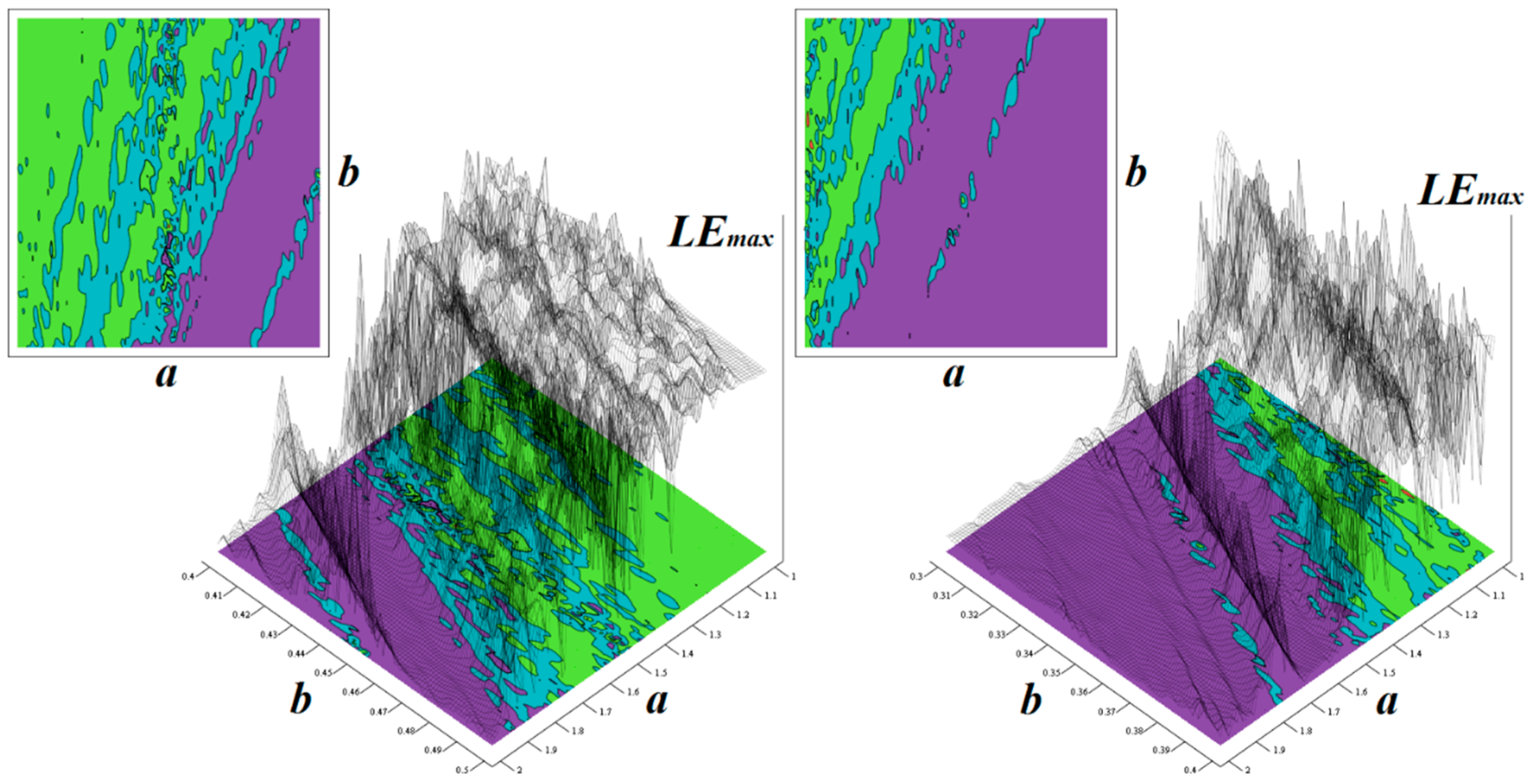
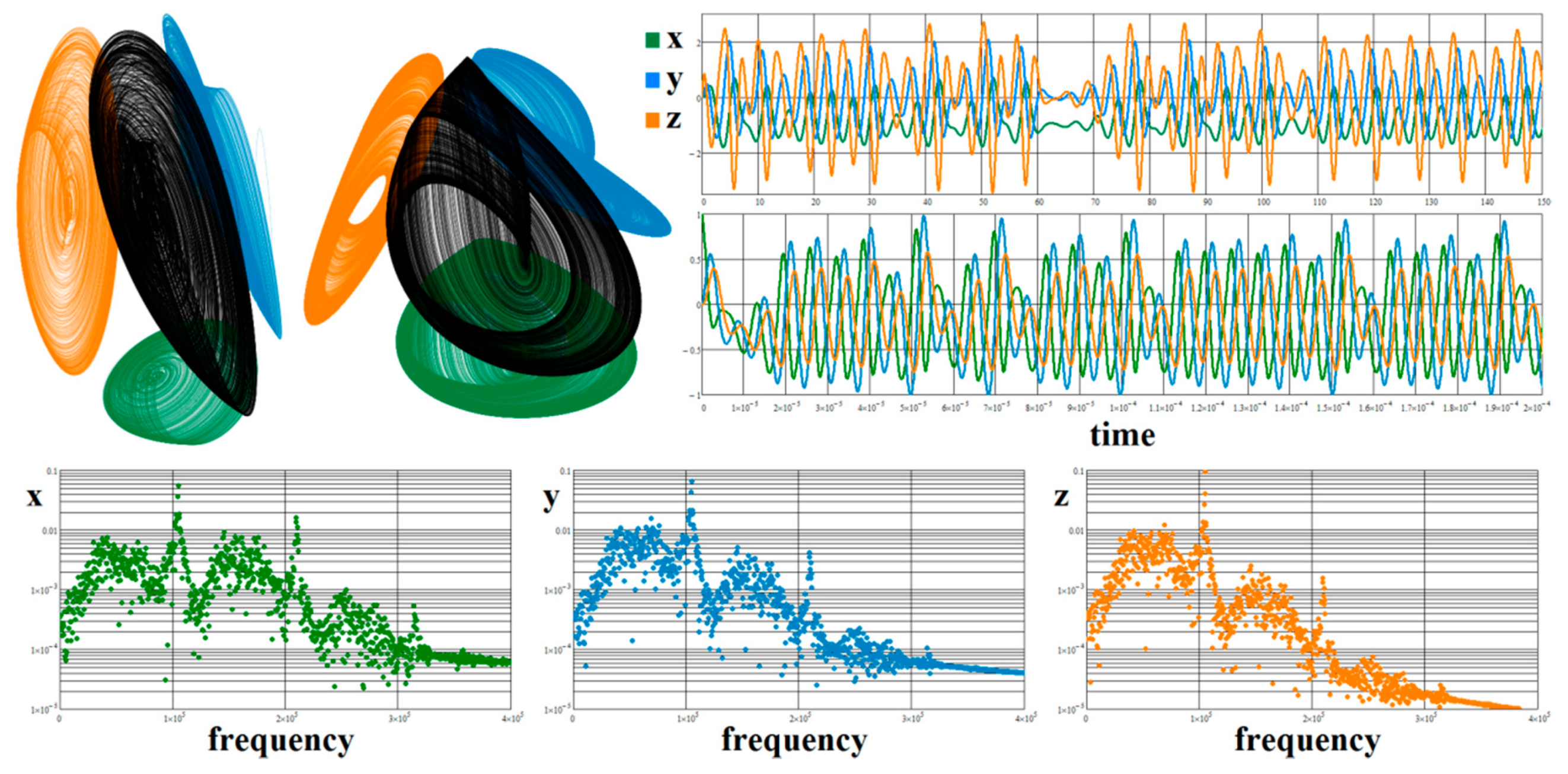
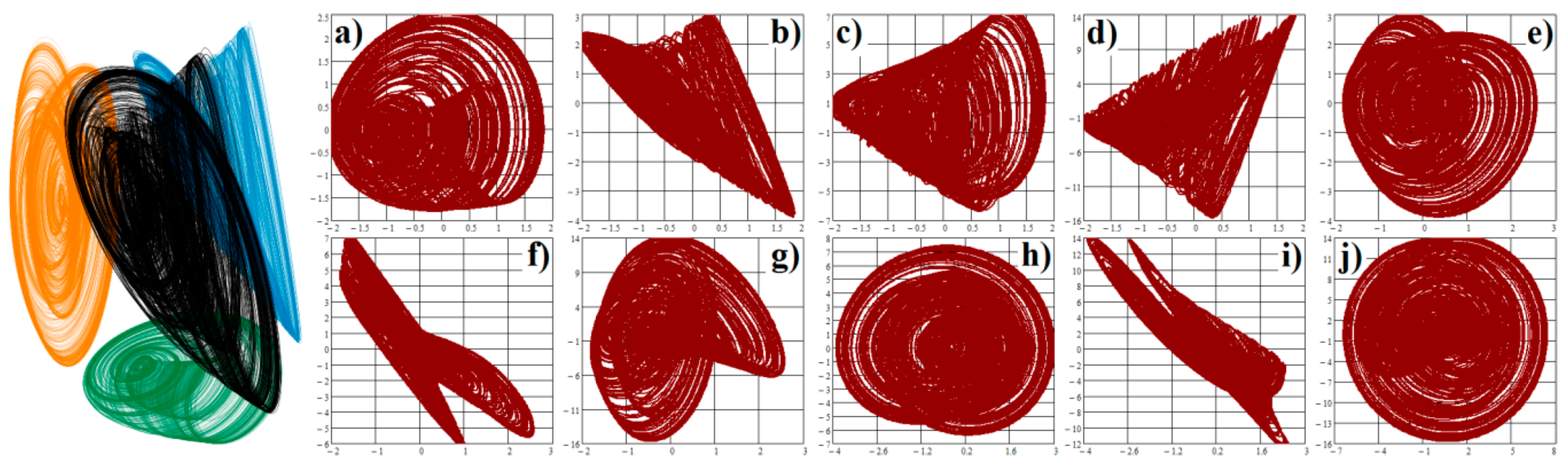
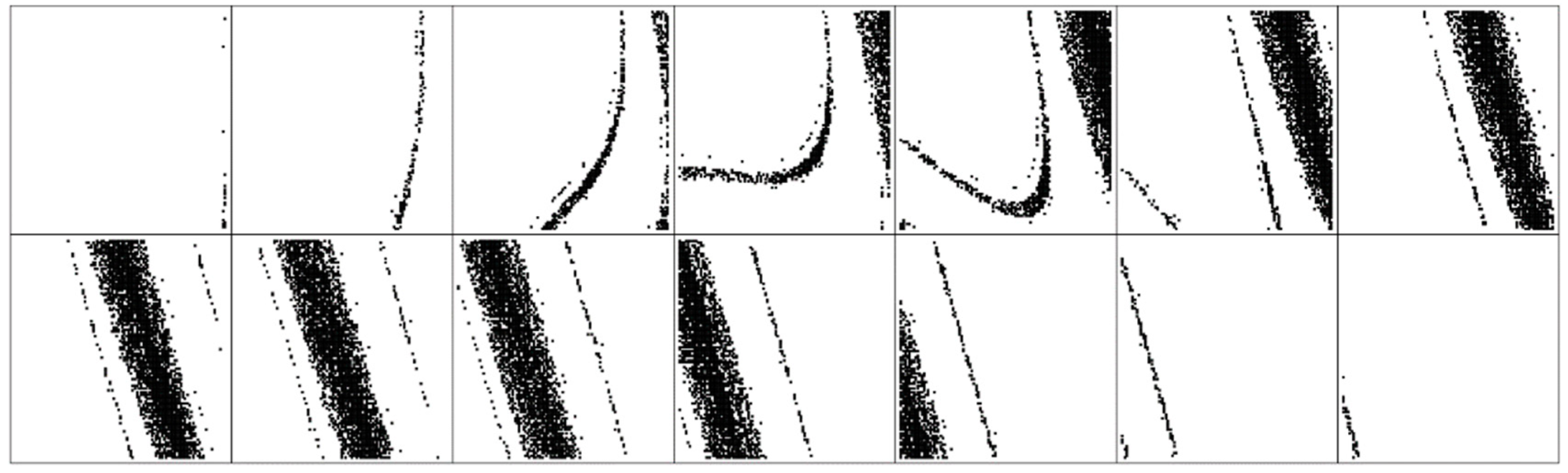
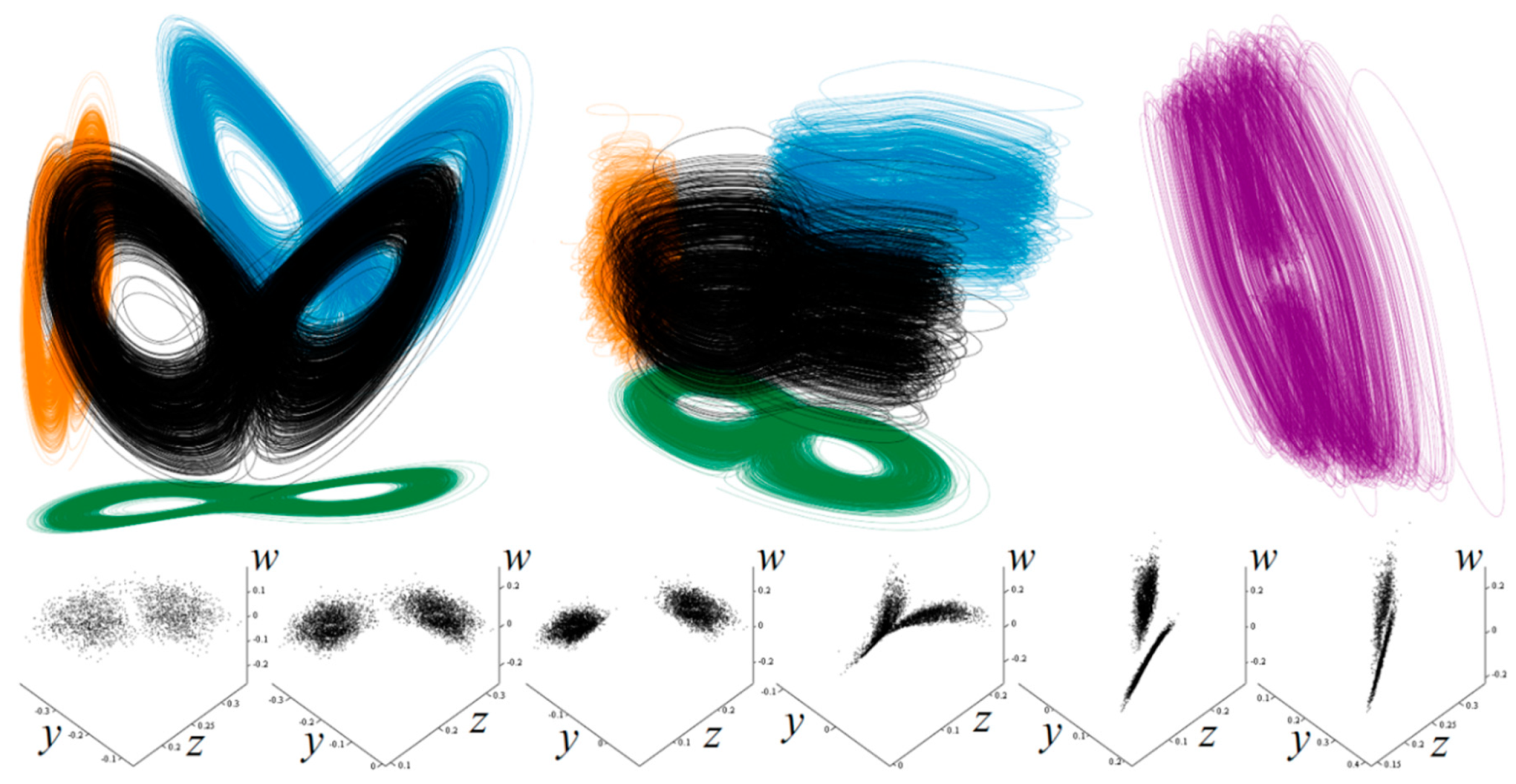
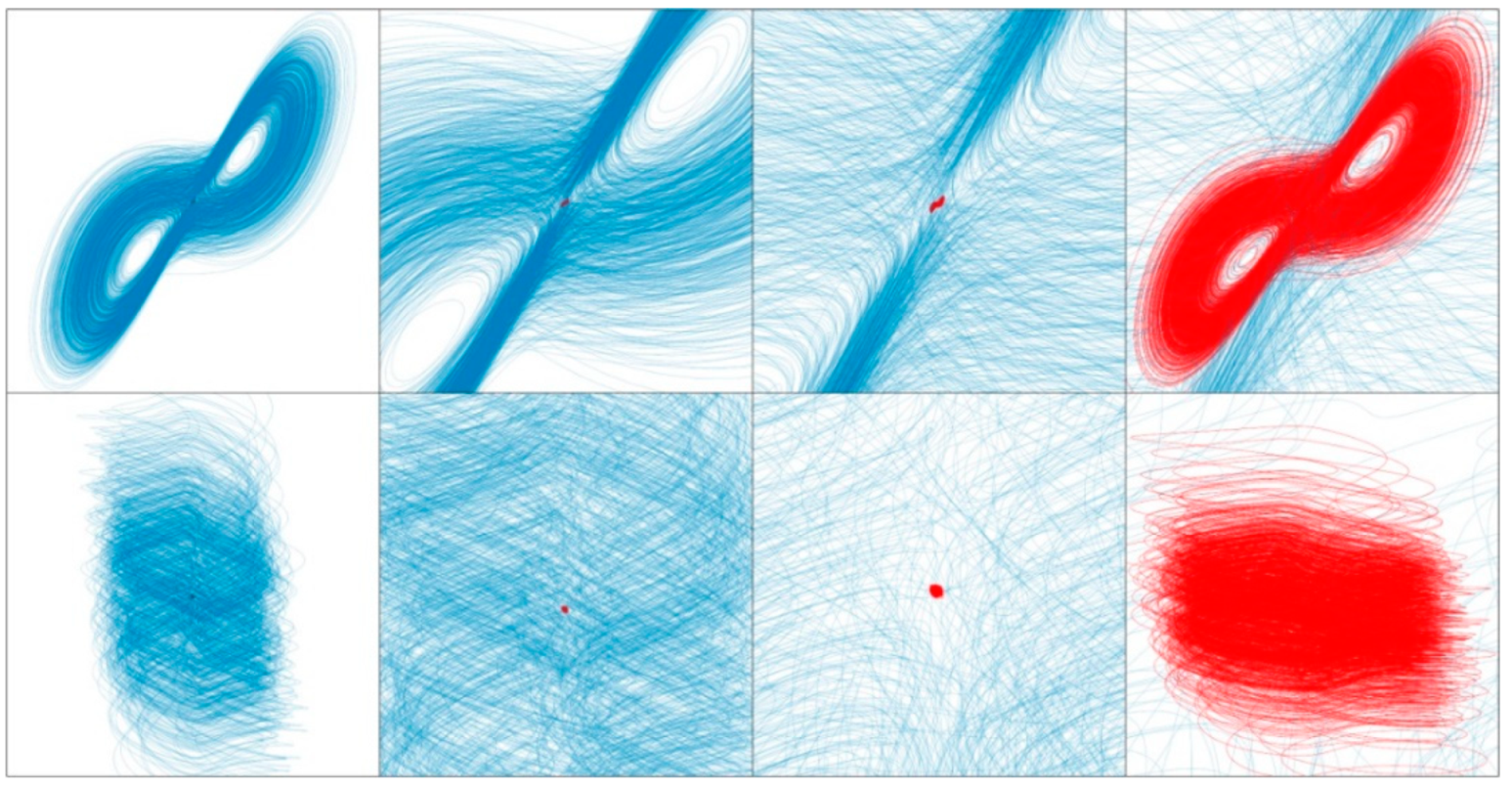
3.1. Numerical Investigation of Dynamical System with Cyclically Symmetrical Vector Field
3.2. Numerical Analysis of Fourth-Order and Fifth-Order Jerky Dynamics
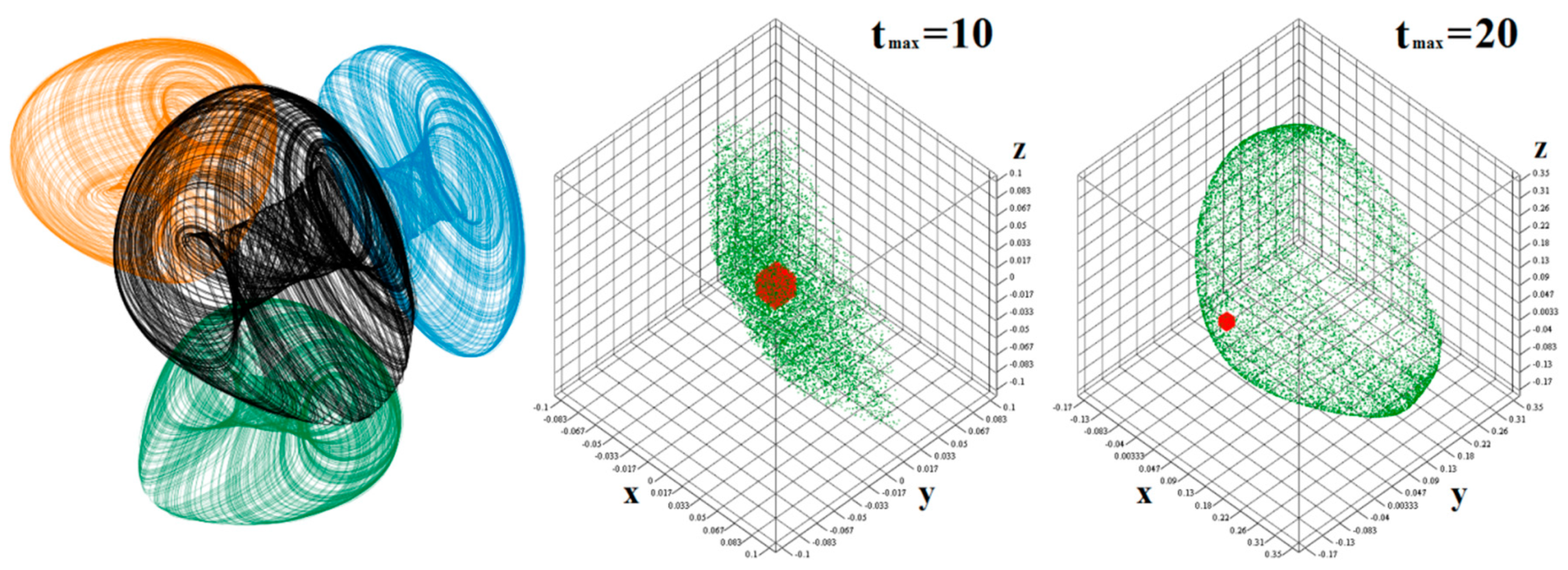
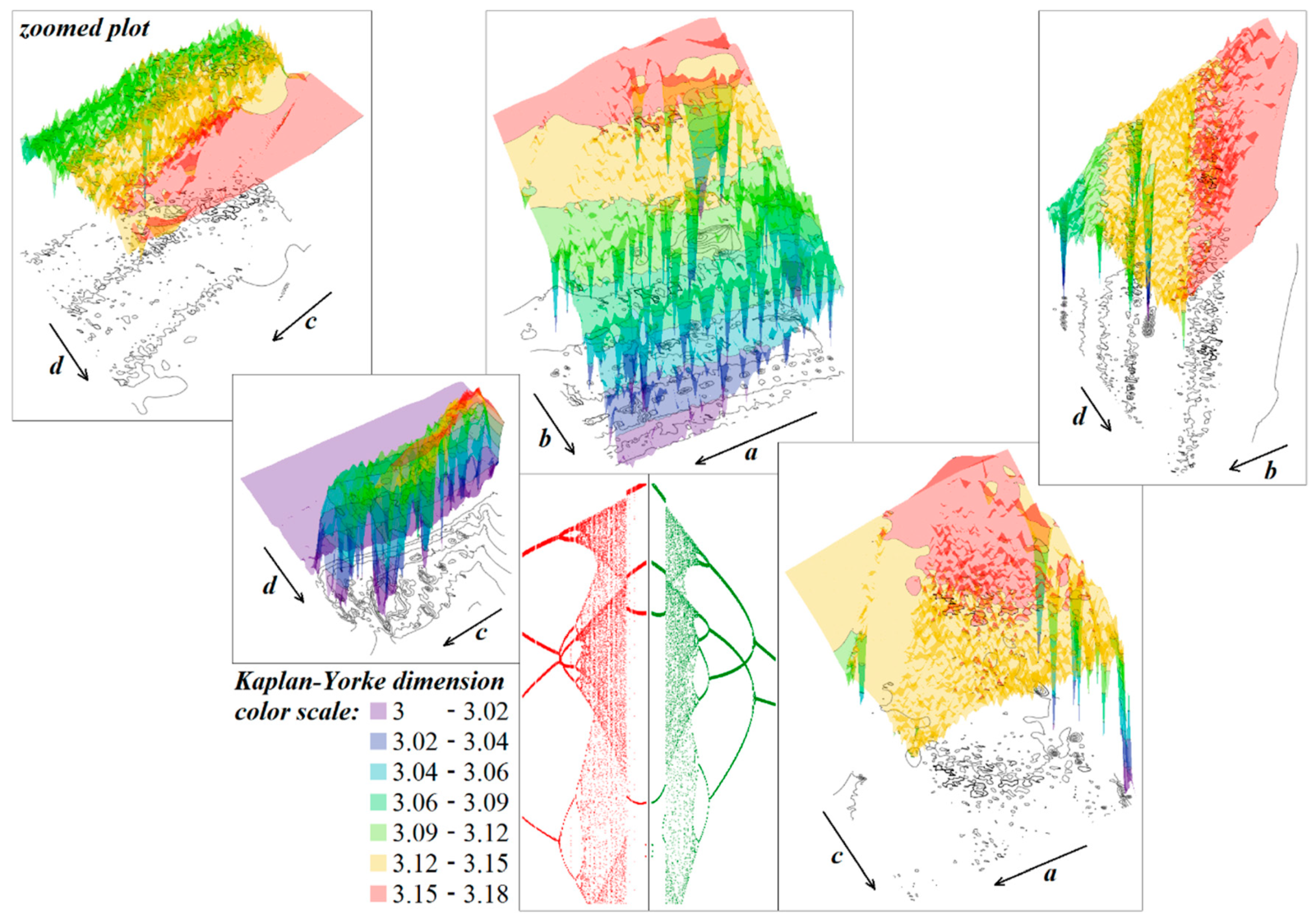
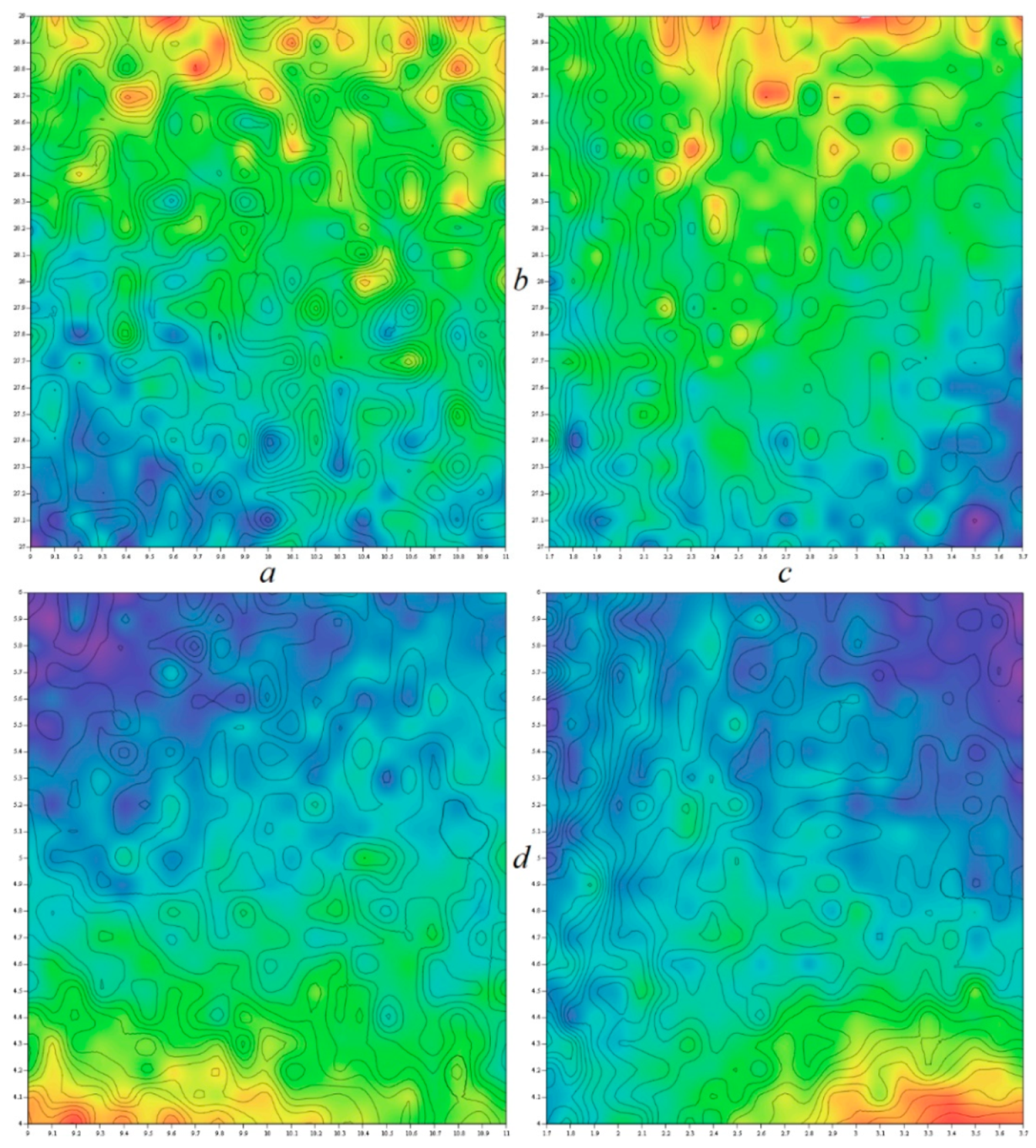
3.3. Numerical Analysis of Hyperchaotic Dynamics
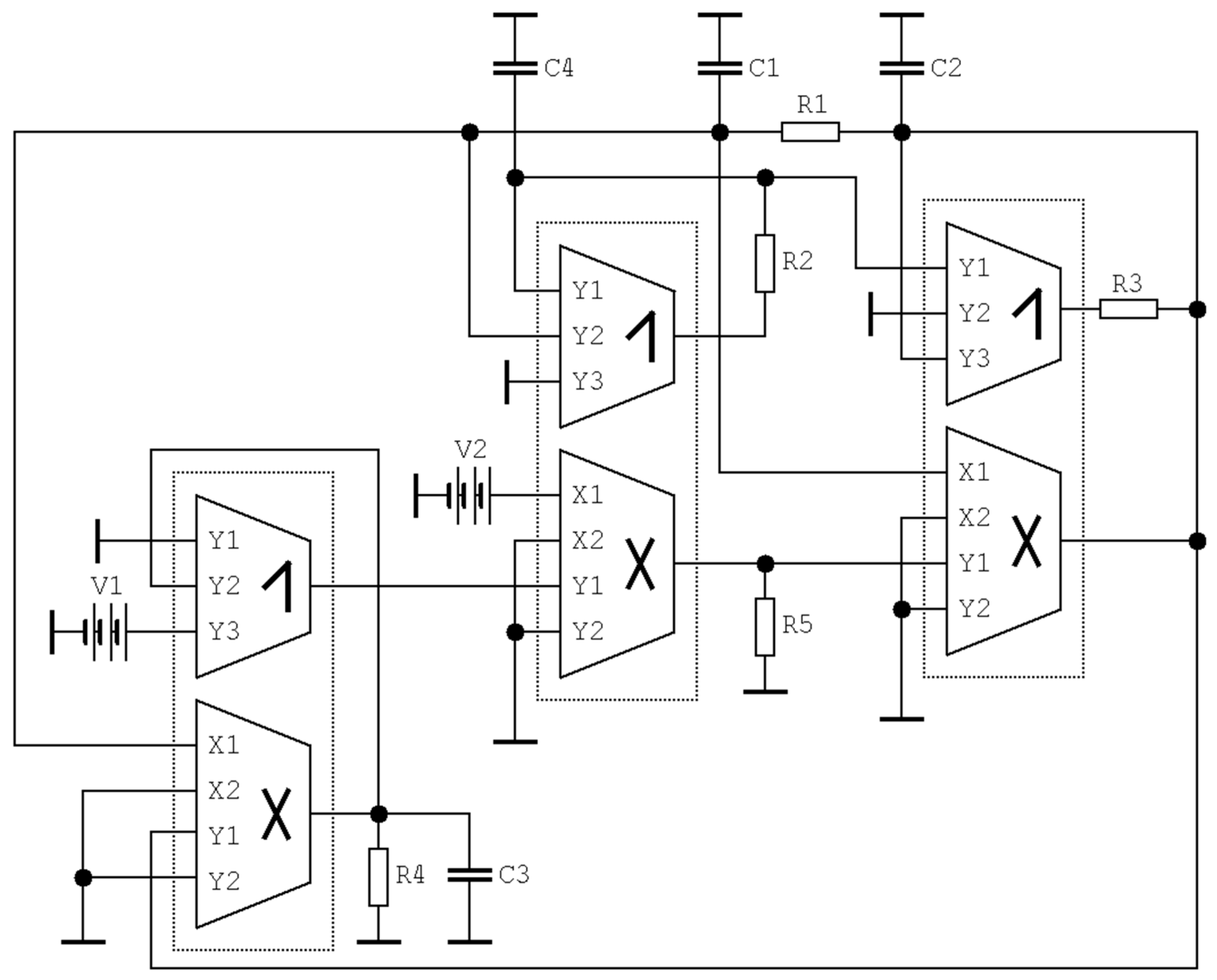
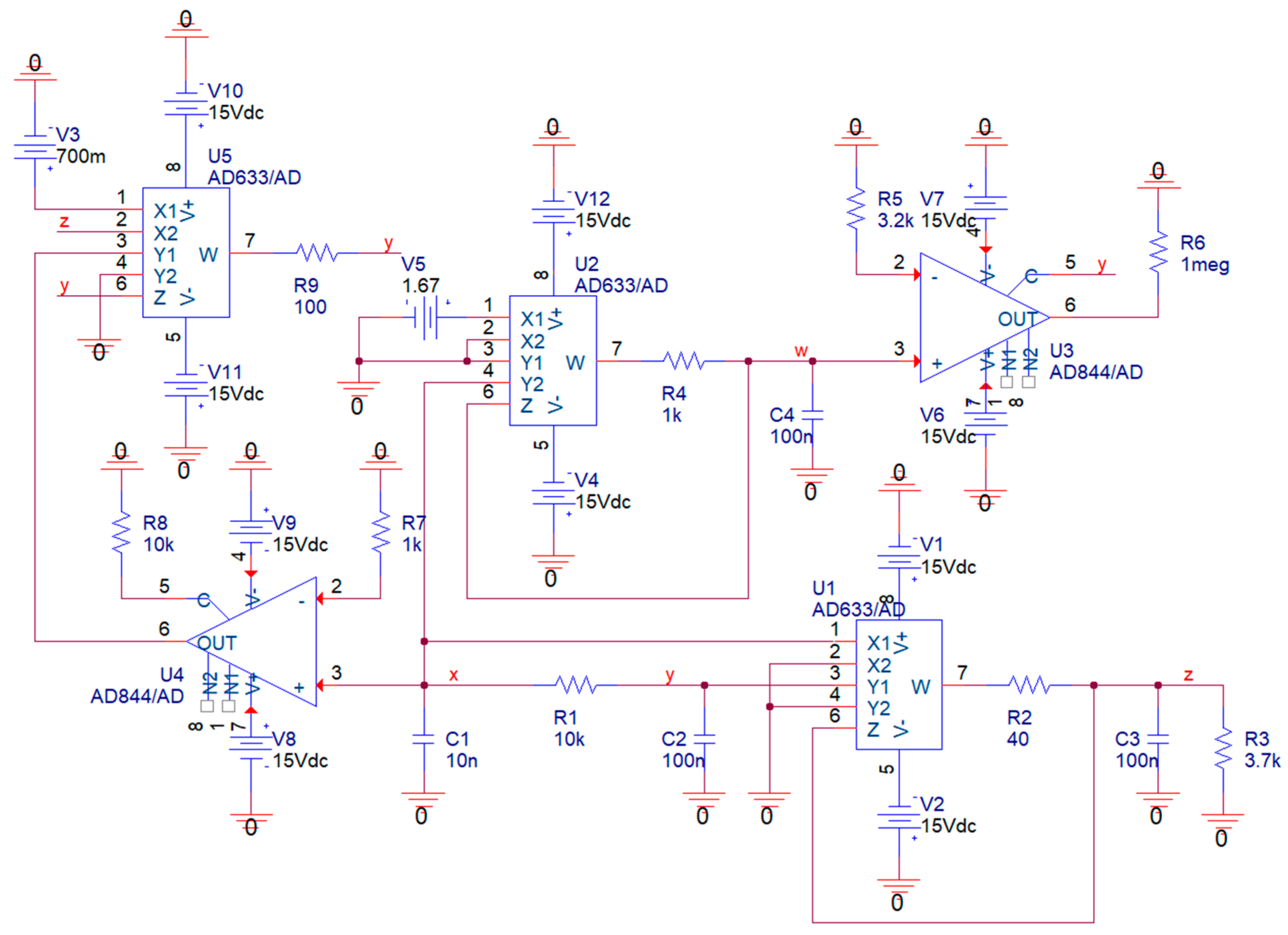
4. New Circuitry Realizations of Chaotic Dynamical Systems Employing DV-TC-M
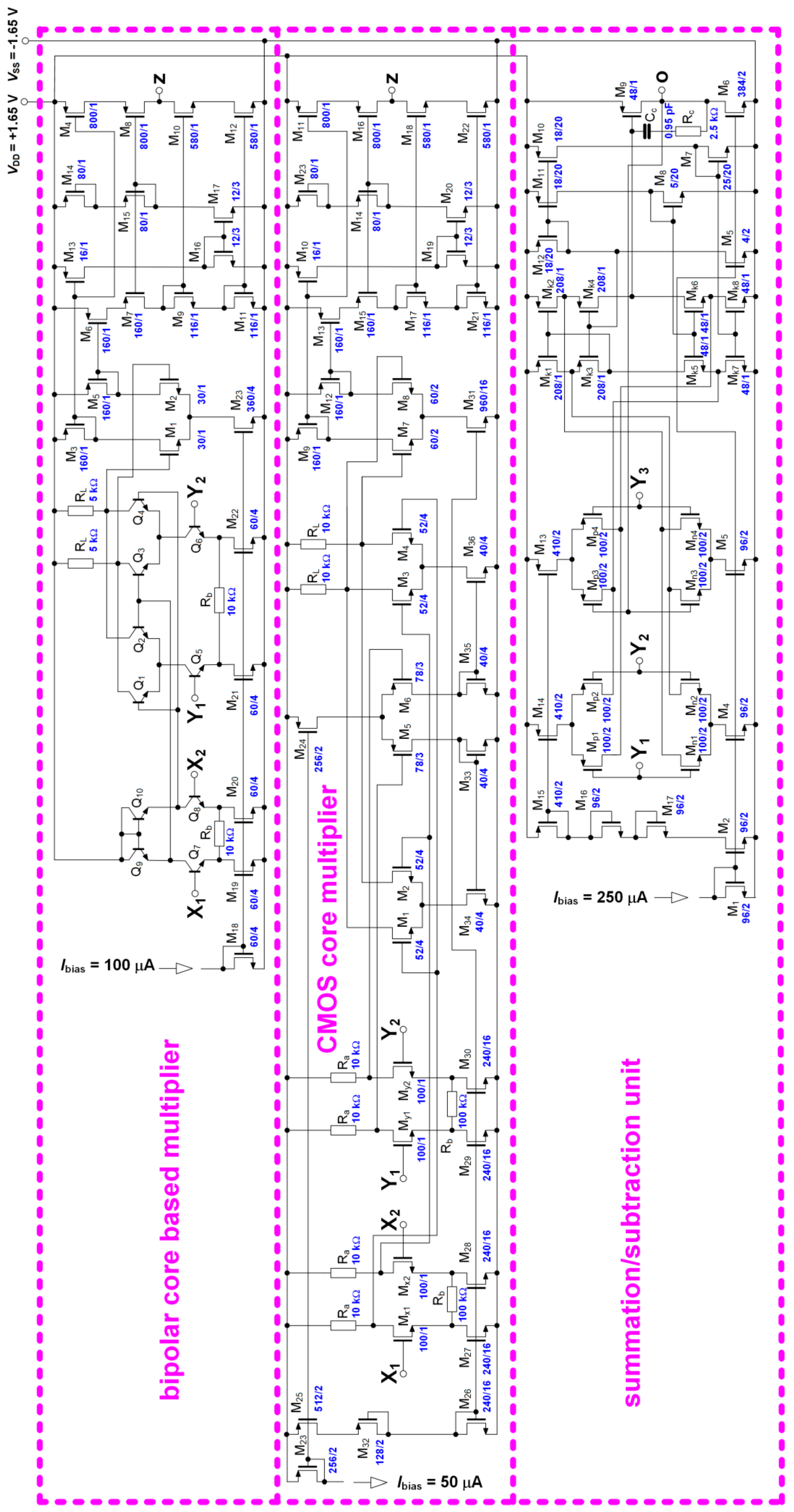
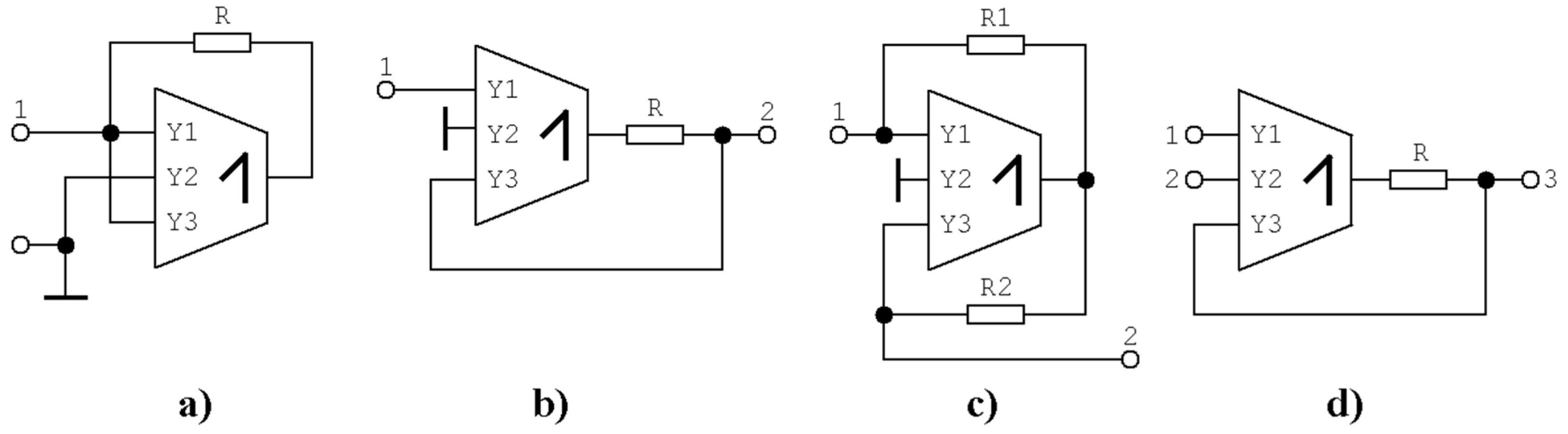
4.1. Analog Functional Blocks Based on DV-TC-M Active Element
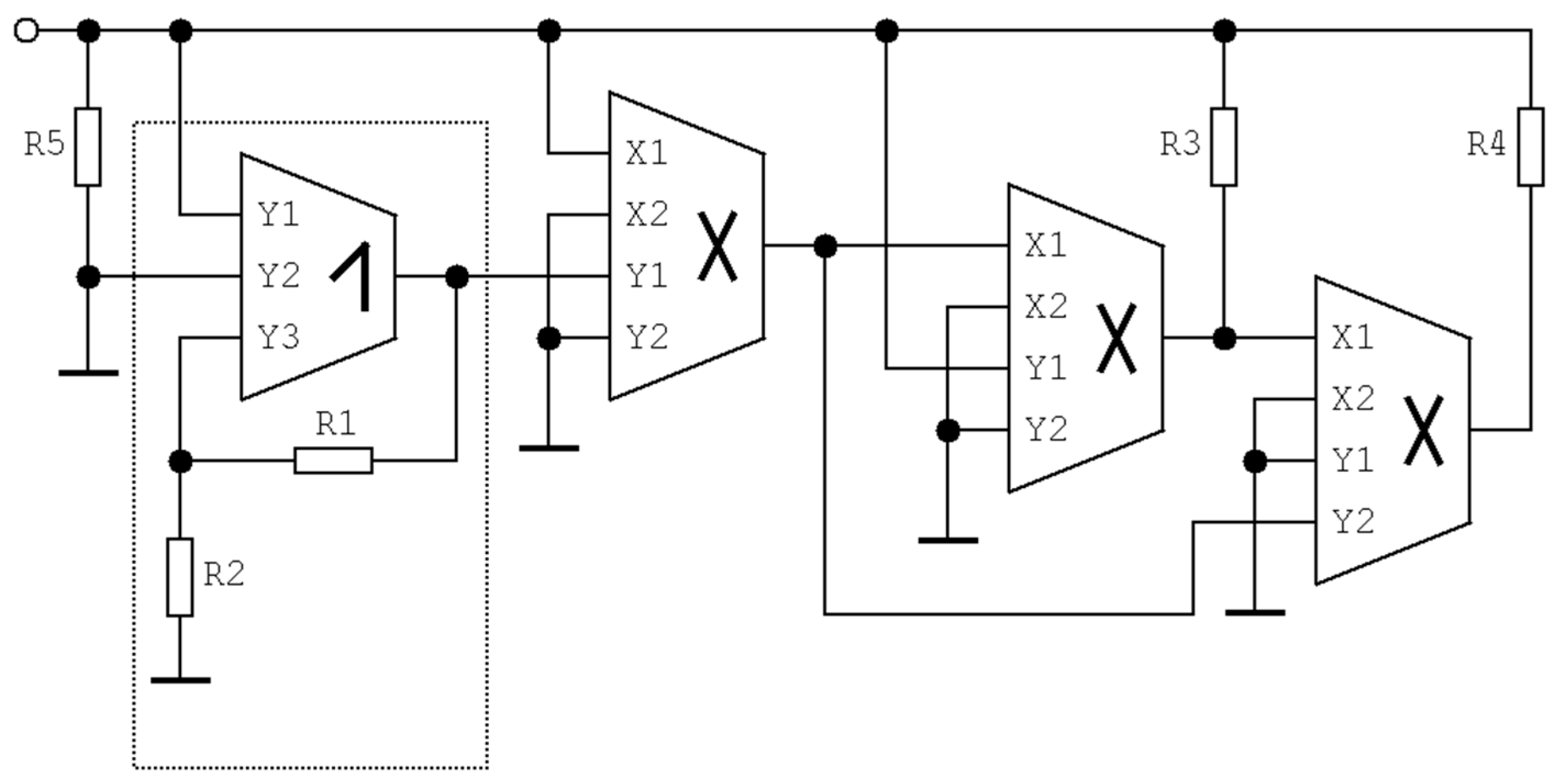
4.2. Chaotic Oscillator with Cyclically Symmetrical Vector Field
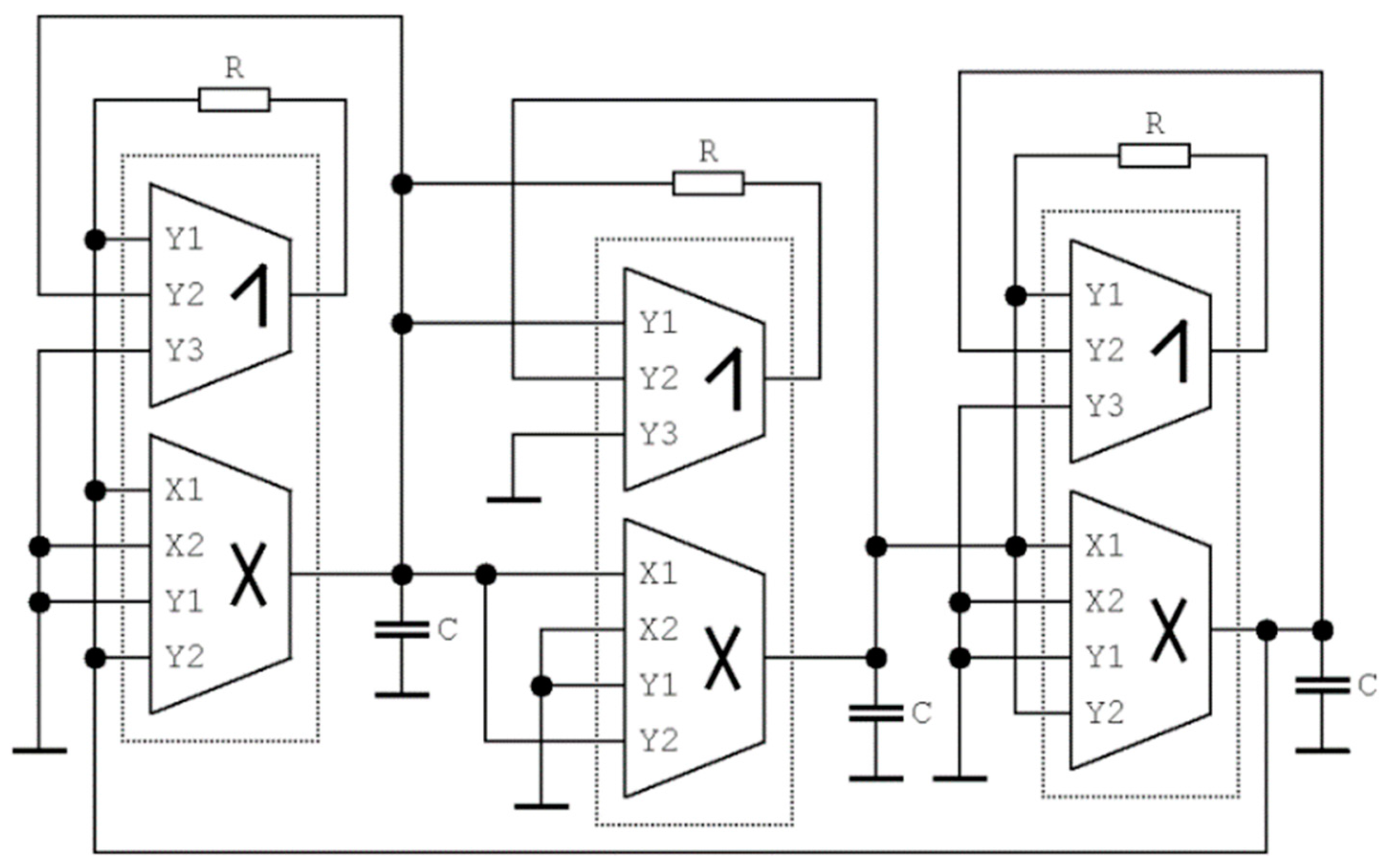
4.3. Circuitry Implementation of Fourth-Order Hyperjerk Function
4.4. Hyperchaotic System
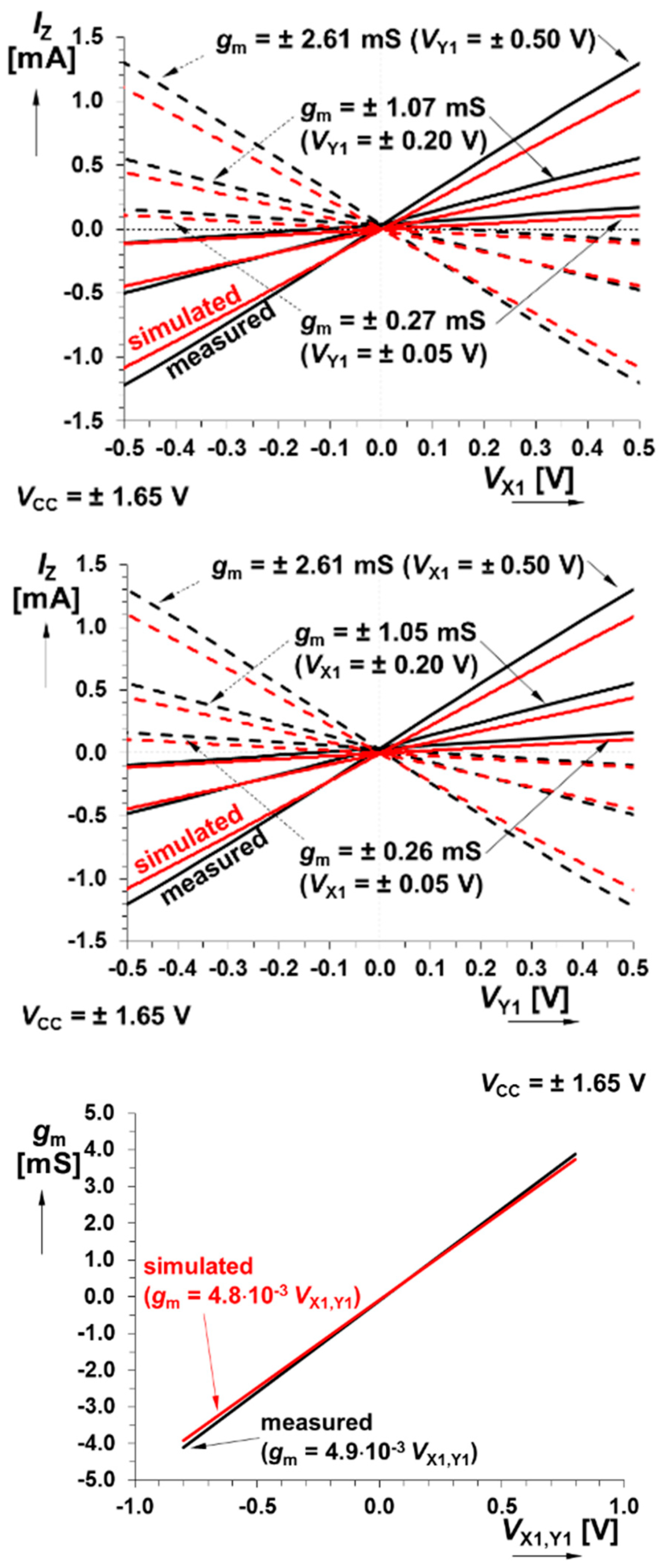
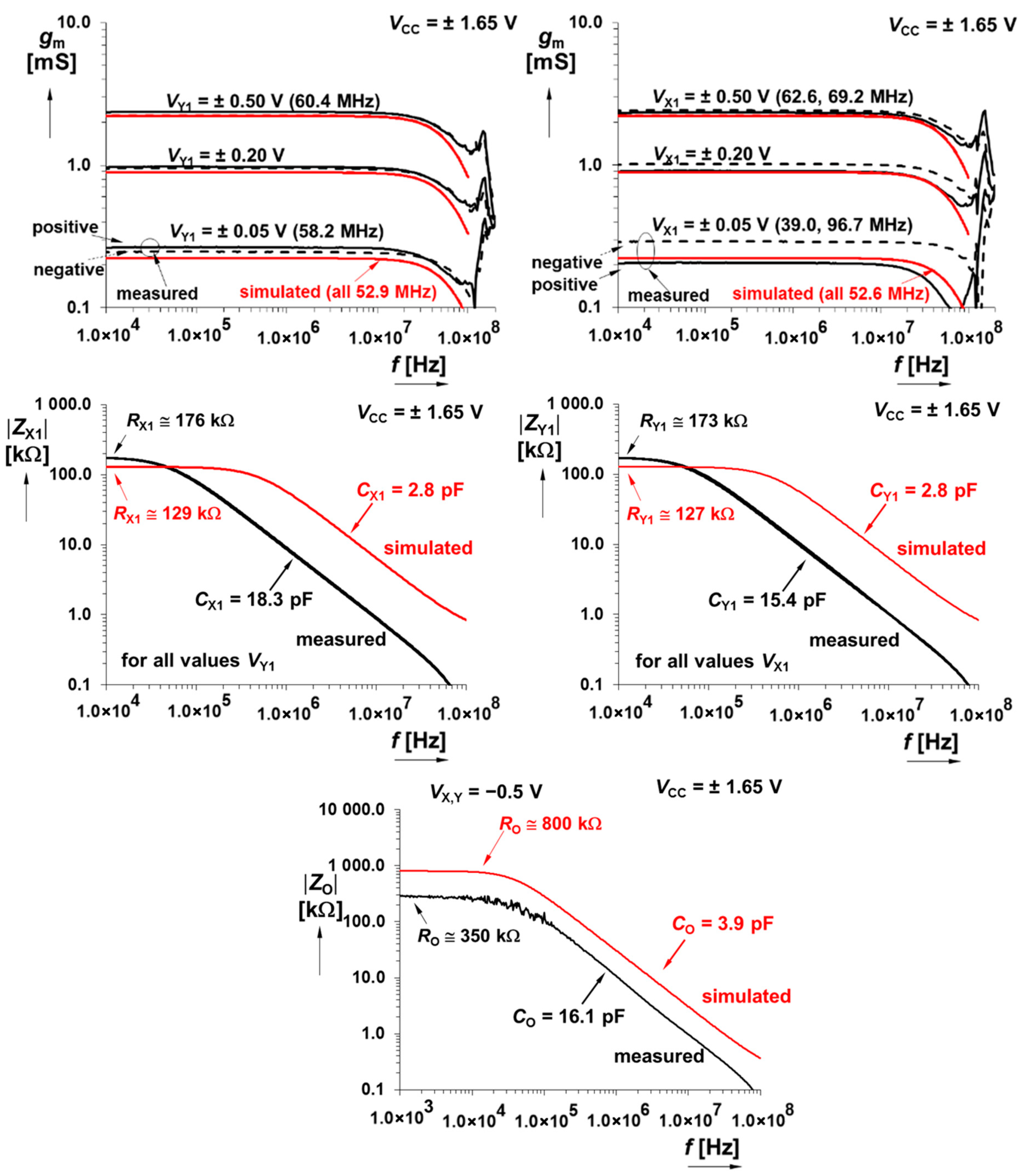
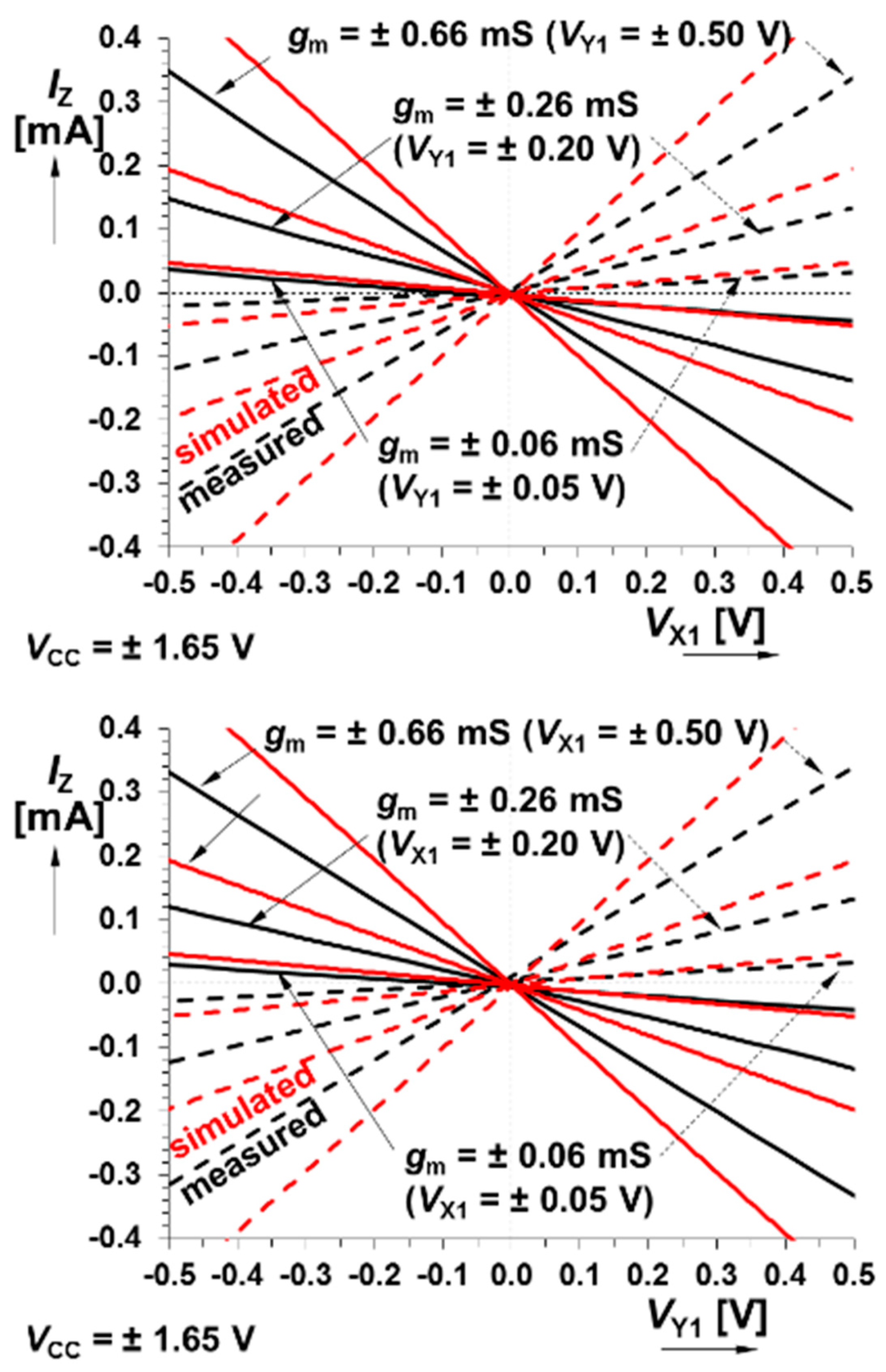
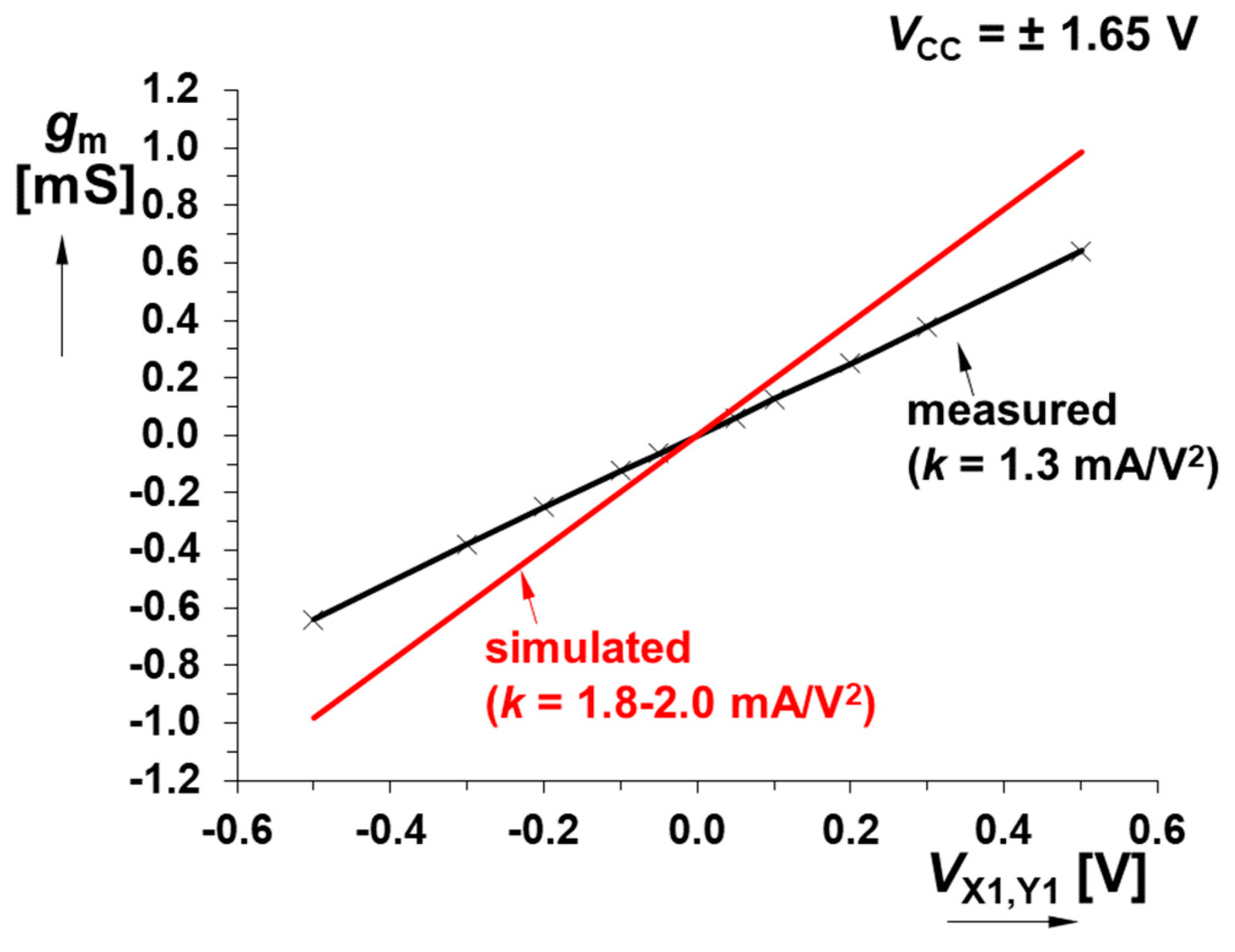
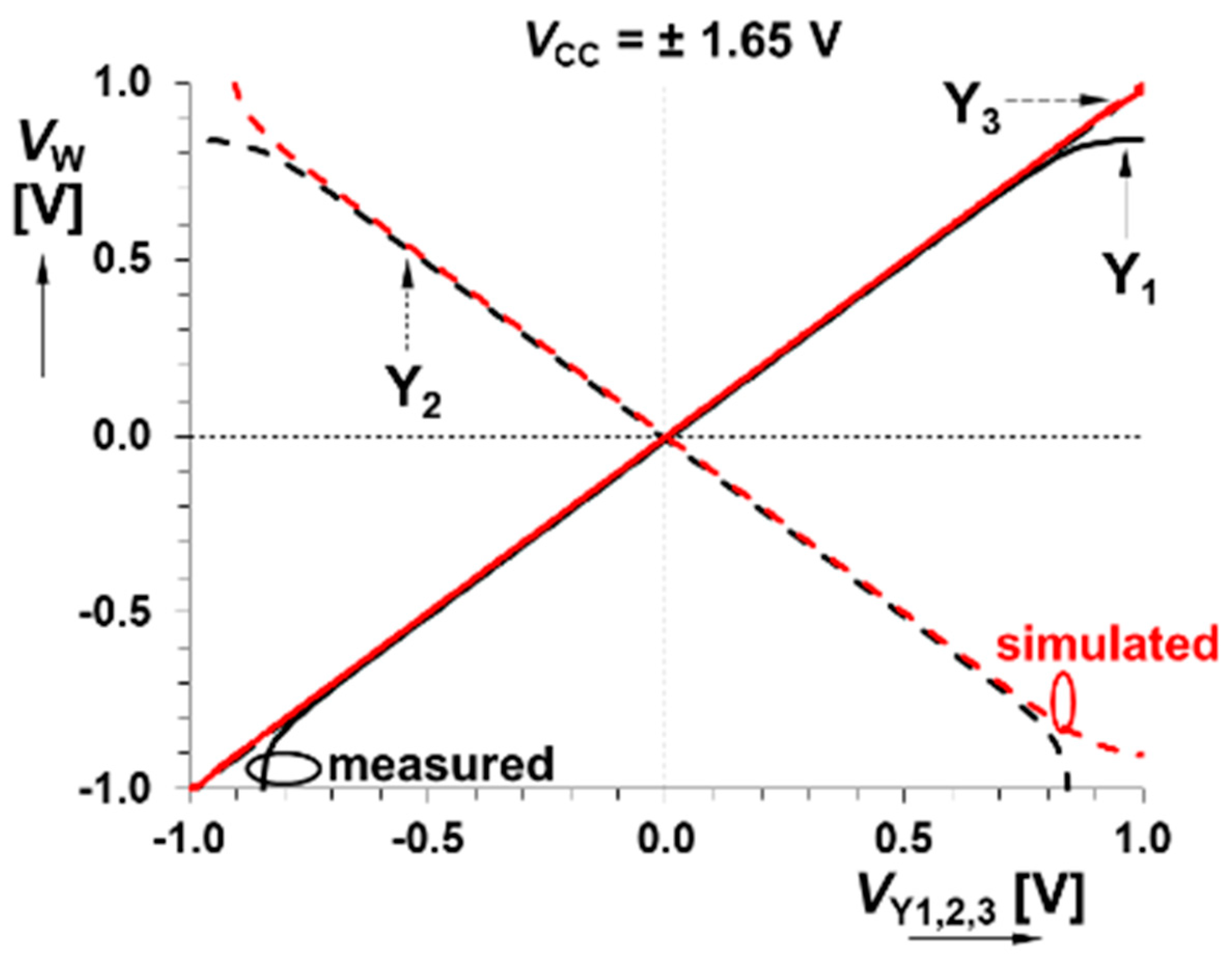
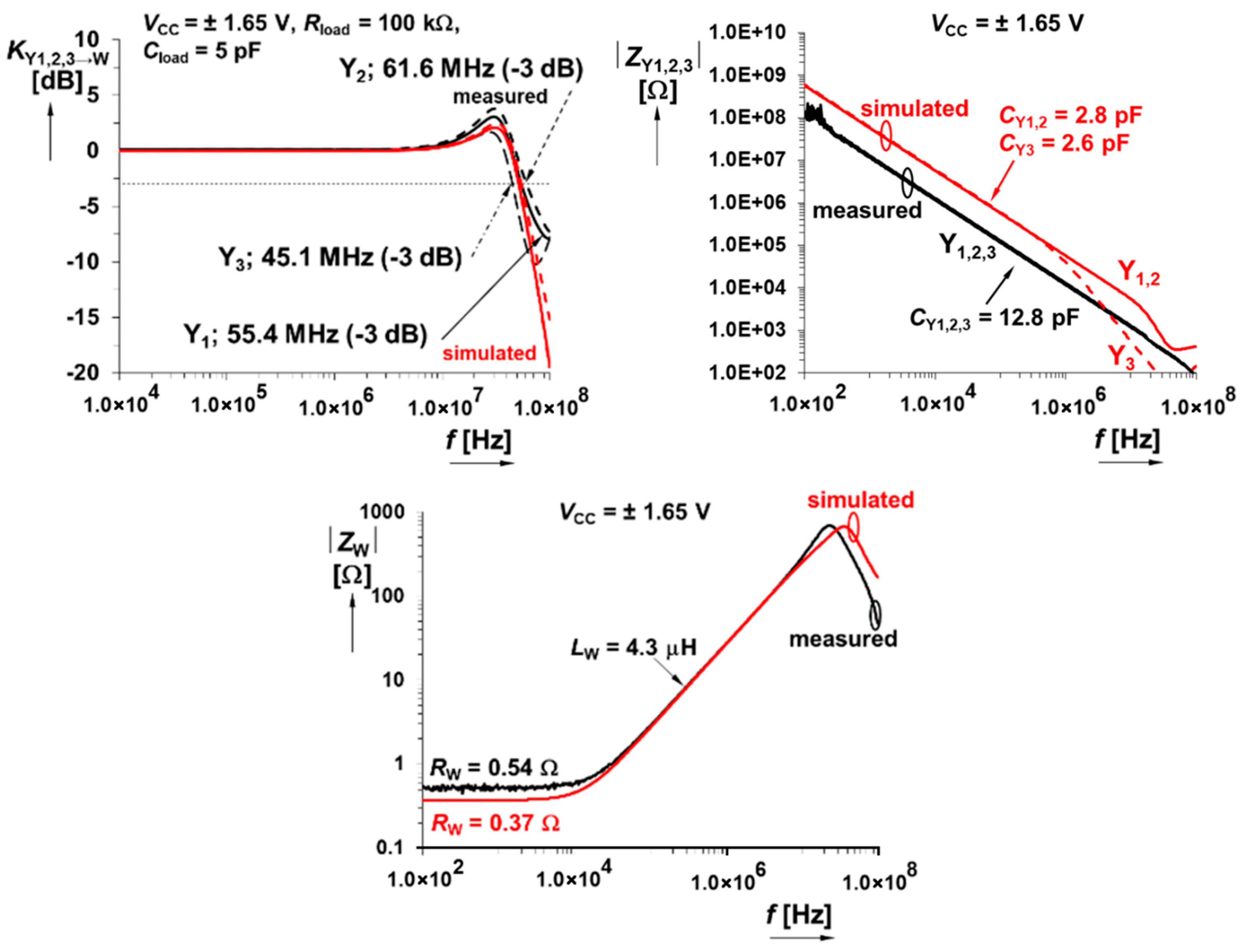
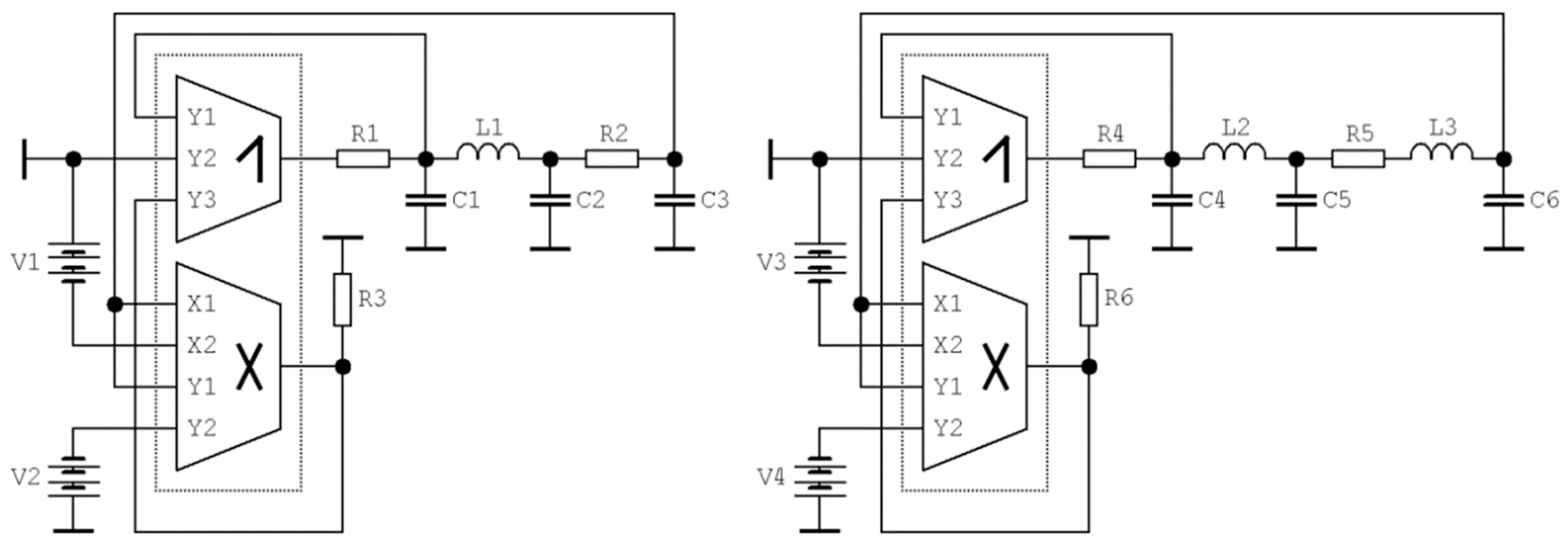
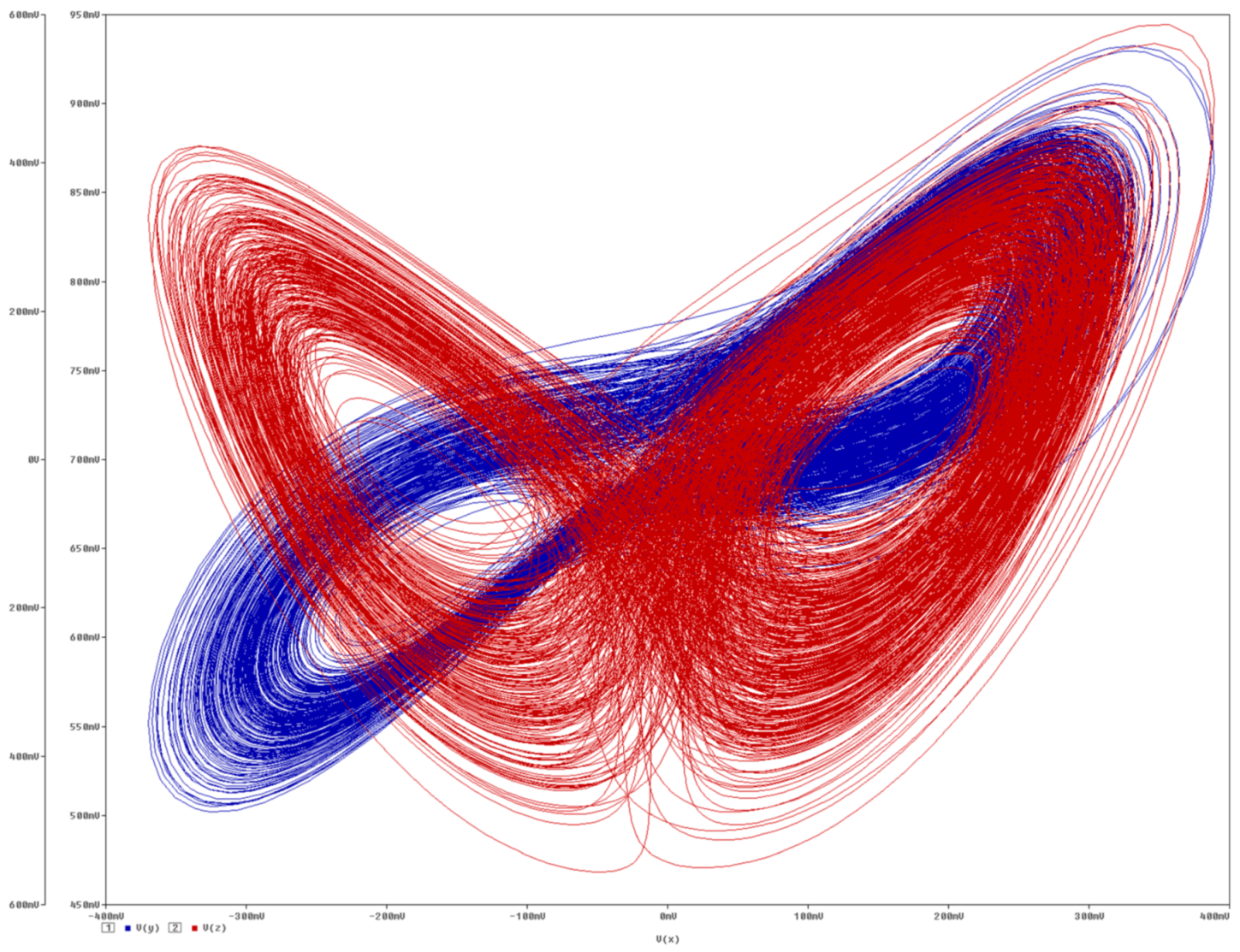
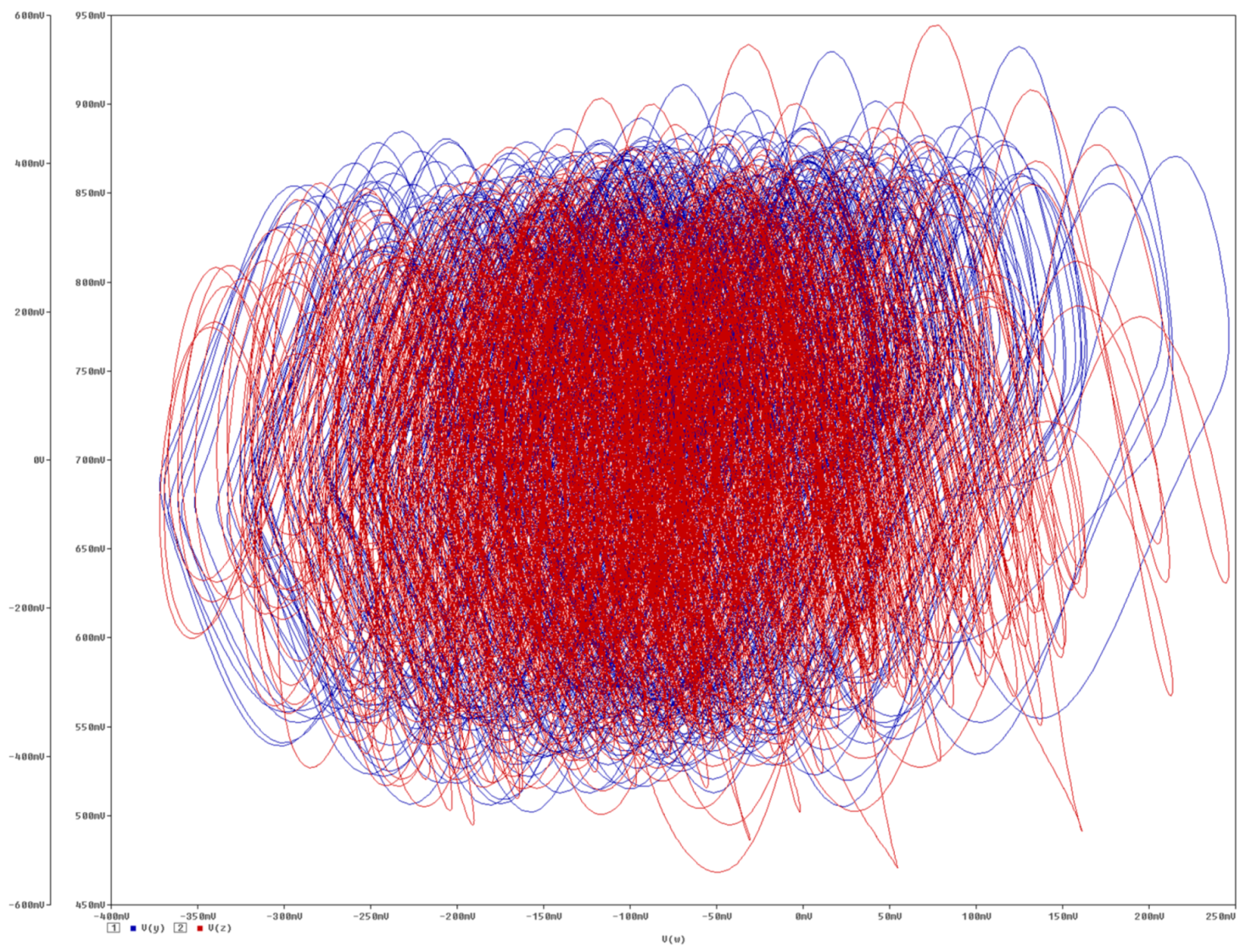
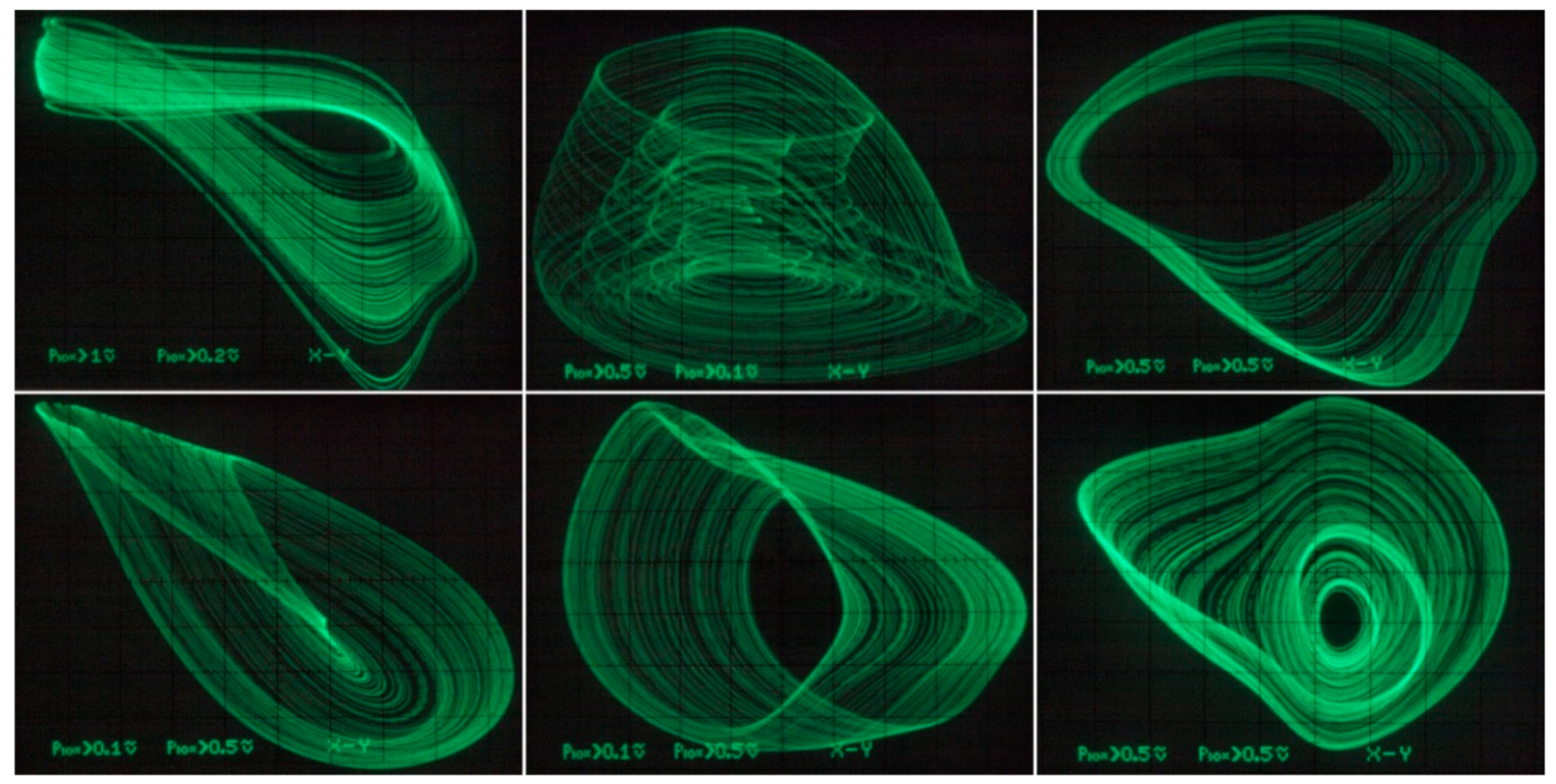
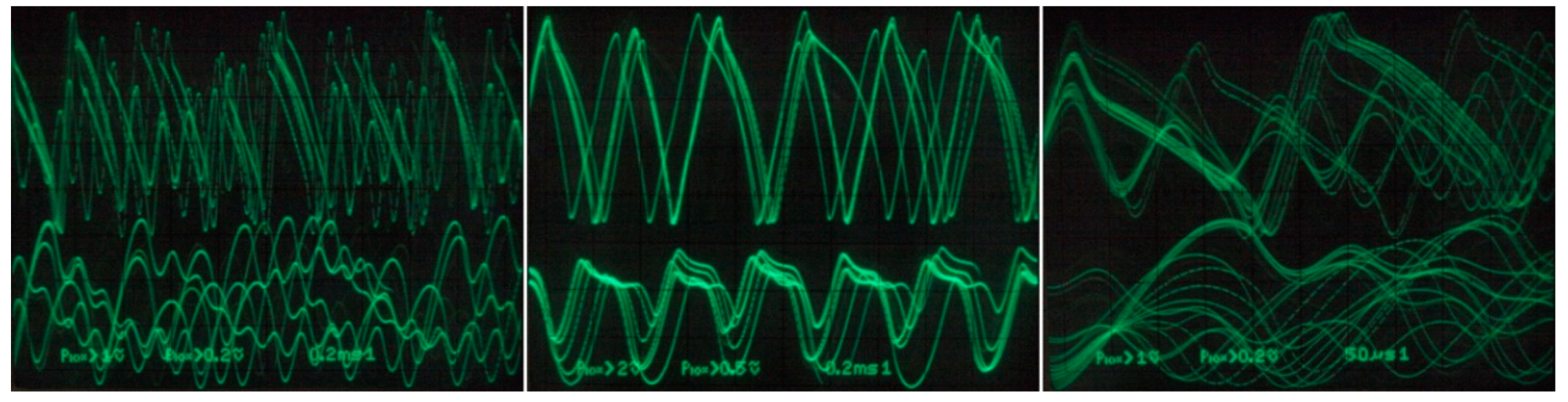
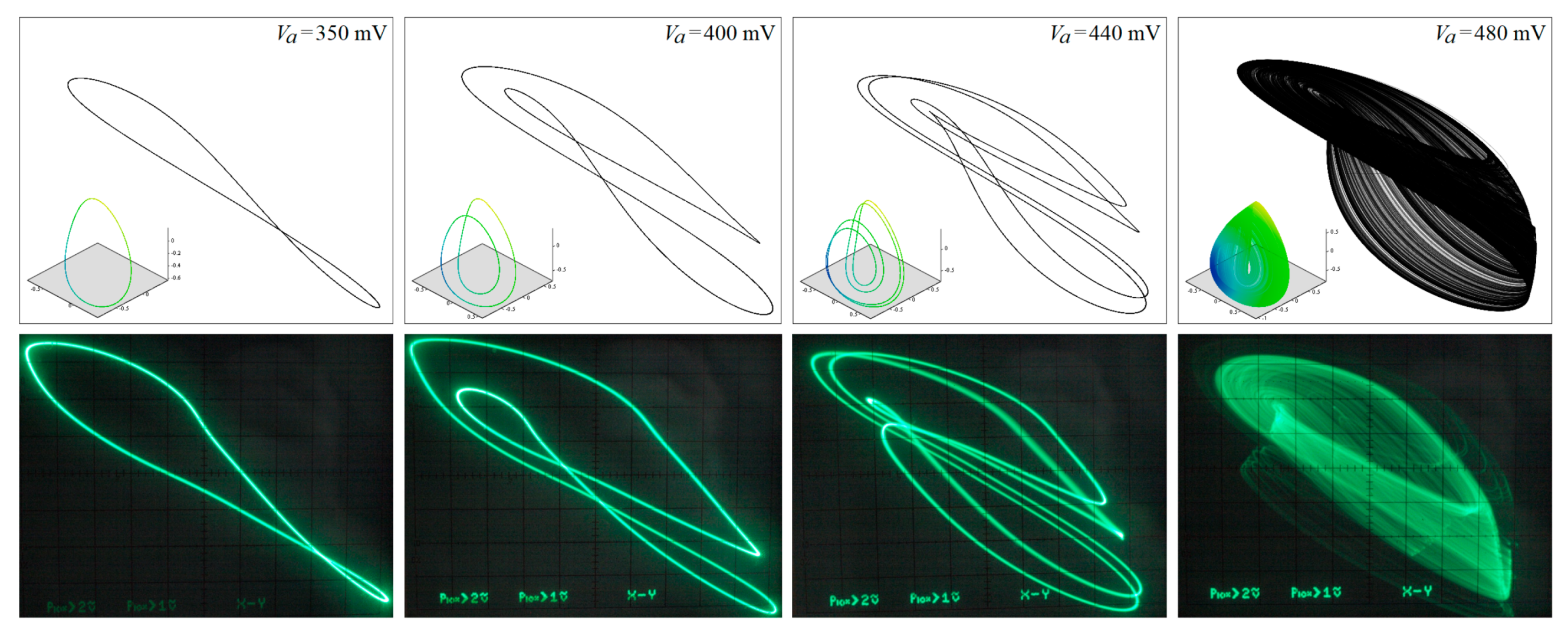
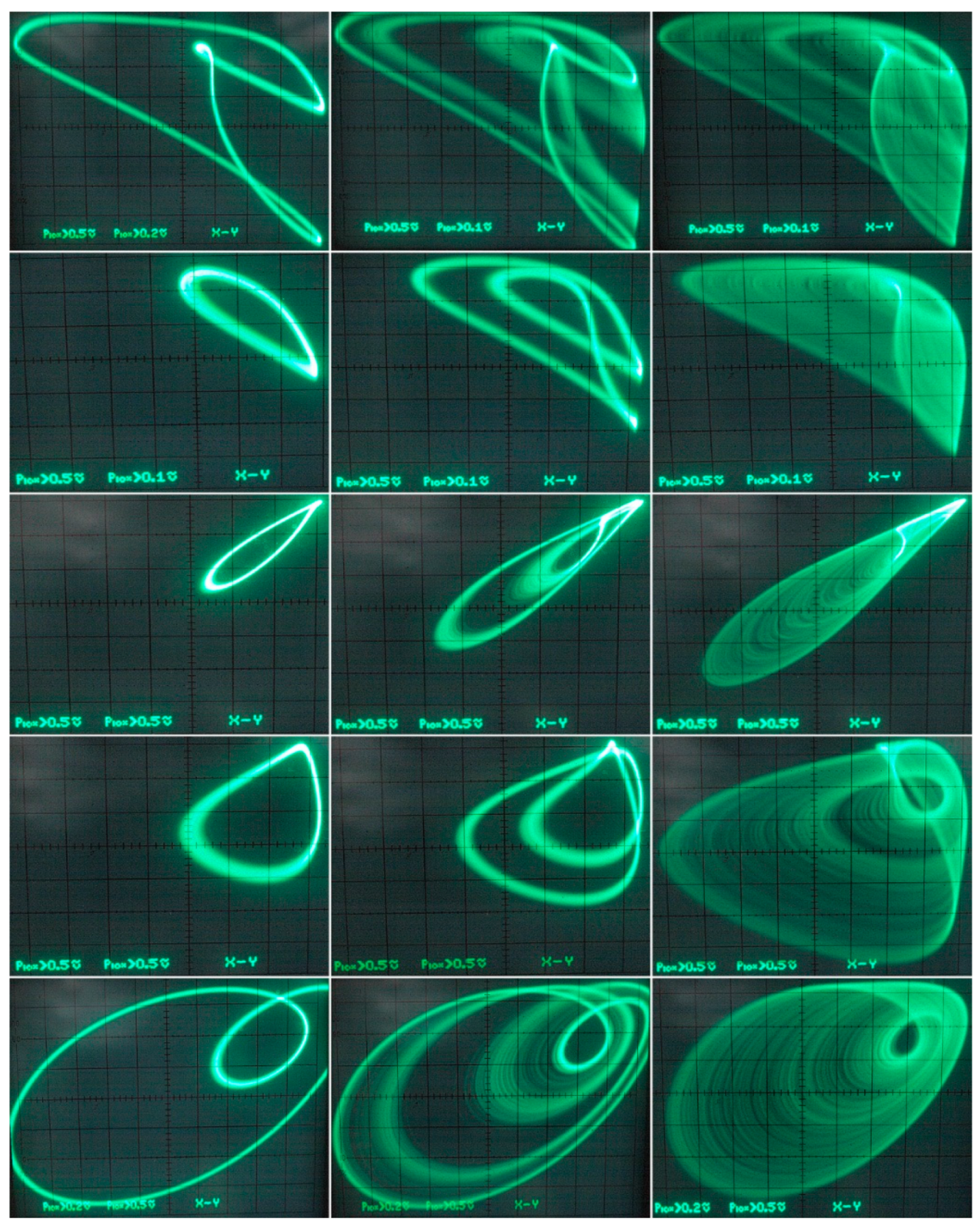
5. Experimental Verification
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
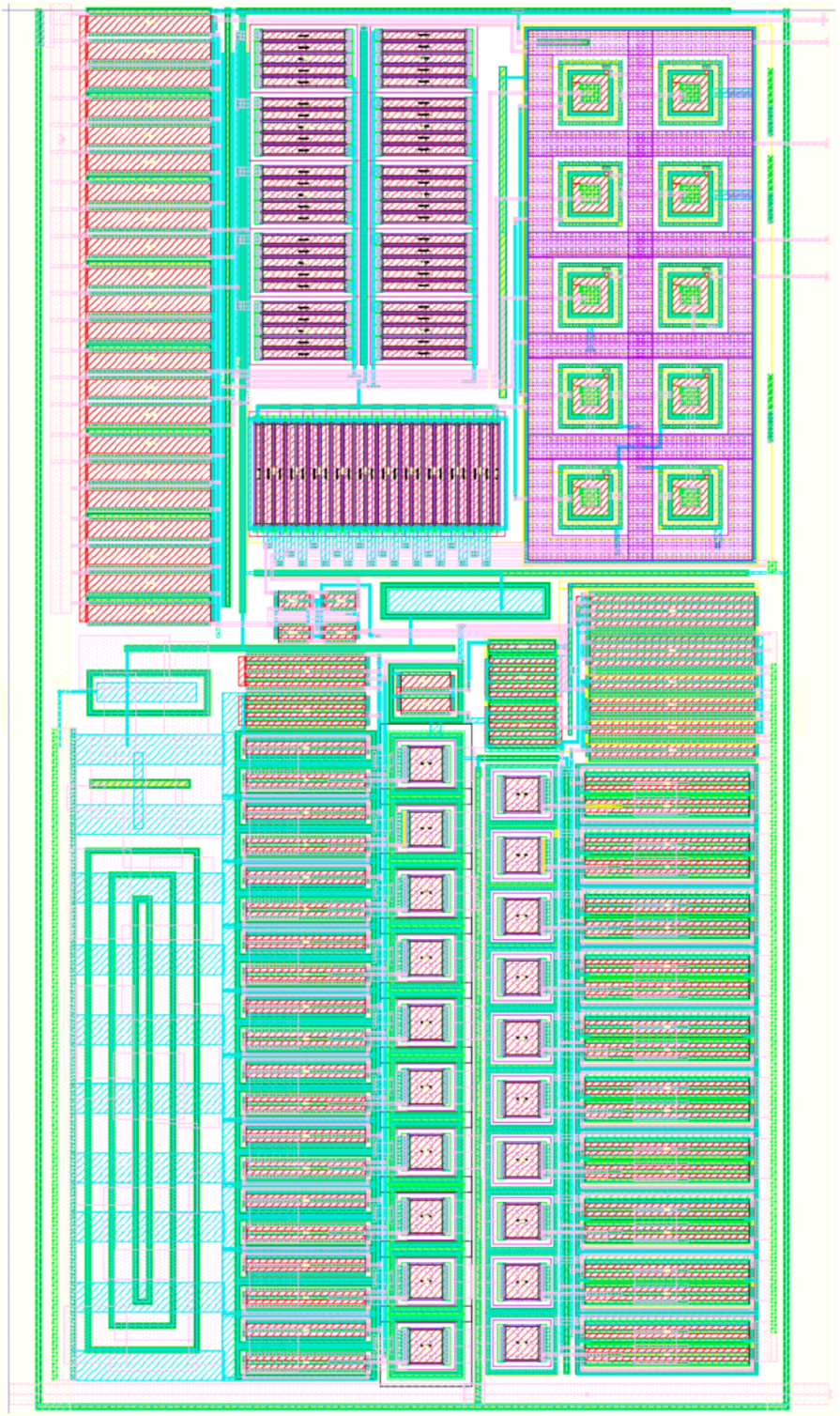
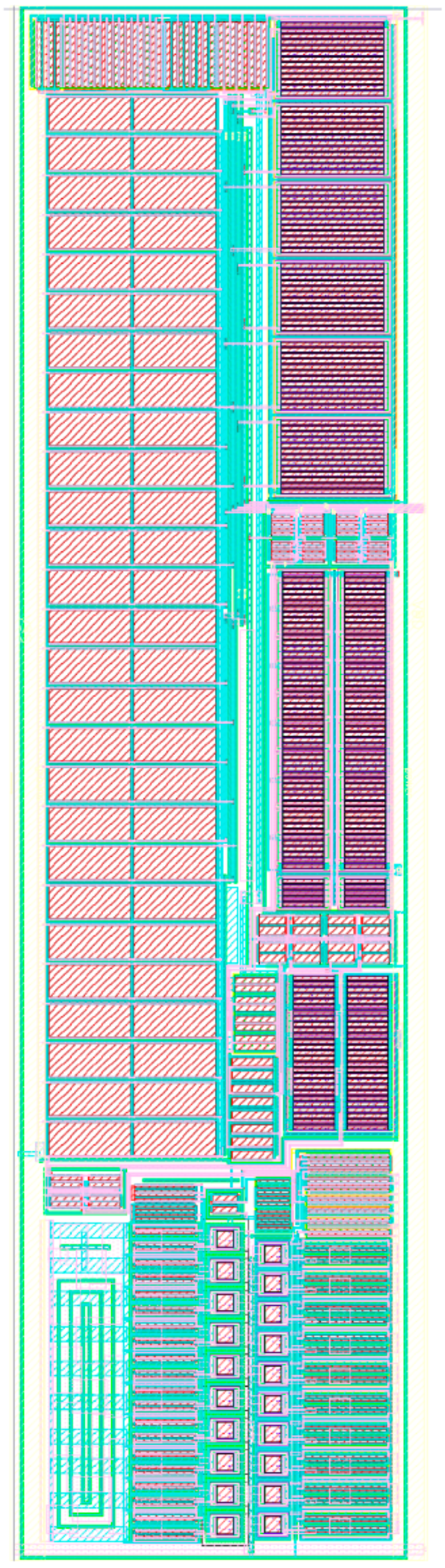

References
- Chua, L.O.; Lin, G.-N. Canonical realization of Chua’s circuit family. IEEE Trans. Circuits Syst. 1990, 37, 885–902. [Google Scholar] [CrossRef]
- Ogorzalek, M.J. Order and chaos in a third-order RC ladder network with nonlinear feedback. IEEE Trans. Circuits Syst. 1989, 36, 1221–1232. [Google Scholar] [CrossRef]
- Zhong, G.Q.; Ko, K.T.; Man, K.F.; Tang, K.S. A systematic procedure for synthesizing two-terminal devices with polynomial non-linearity. Int. J. Circuit Theory Appl. 2001, 29, 241–249. [Google Scholar] [CrossRef]
- Petrzela, J.; Pospisil, V. Nonlinear resistor with polynomial AV characteristics and its application in chaotic oscillator. Radioengineering 2004, 13, 20–25. [Google Scholar]
- Zhong, G.Q. Implementation of Chua’s circuit with a cubic non-linearity. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 934–941. [Google Scholar] [CrossRef]
- Tang, W.K.S.; Zhong, G.Q.; Chen, G.; Man, K.F. Generation of N-scroll attractors via sine function. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1369–1372. [Google Scholar] [CrossRef]
- Yalcin, M.E.; Suykens, J.A.K.; Vandewalle, J.; Ozoguz, S. Families of scroll grid attractors. Int. J. Bifurc. Chaos 2002, 12, 23–41. [Google Scholar] [CrossRef]
- Lu, J.; Chen, G. Generating multiscroll chaotic attractors: Theories, methods and applications. Int. J. Bifurc. Chaos 2006, 16, 775–858. [Google Scholar] [CrossRef]
- Chen, L.; Pan, W.; Wu, R.; Tenreiro Machado, J.A.; Lopes, A.M. Design and implementation of grid multi-scroll fractional-order chaotic oscillators. AIP Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 084303. [Google Scholar] [CrossRef]
- Gotthans, T.; Hrubos, Z. Multi grid chaotic attractors with discrete jumps. J. Electr. Eng. 2013, 64, 118–122. [Google Scholar] [CrossRef]
- Petrzela, J.; Polak, L. Minimal realizations of autonomous chaotic oscillators based on trans-immittance filters. IEEE Access 2019, 7, 17561–17577. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Munmuangsaen, B.; Srisuchinwong, B.; Sprott, J.C. Generalization of the simplest autonomous chaotic system. Phys. Lett. A 2011, 375, 1445–1450. [Google Scholar] [CrossRef]
- Sprott, J.C. Simplest dissipative chaotic flow. Phys. Lett. A 1997, 228, 271–274. [Google Scholar] [CrossRef]
- Sprott, J.C.; Linz, S.J. Algebraically simple chaotic flows. Int. J. Chaos Theory Appl. 2000, 5, 3–22. [Google Scholar]
- Elwakil, A.S.; Kennedy, M.P. A semi-systematic procedure for producing chaos from sinusoidal oscillators using diode-inductor and FET-capacitor composites. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 582–590. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Kennedy, M.P. Construction of classes of circuit-independent chaotic oscillators using passive-only nonlinear devices. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 289–307. [Google Scholar] [CrossRef]
- Petrzela, J.; Slezak, J. Conservative chaos generators with CCII+ based on mathematical model of nonlinear oscillator. Radioengineering 2008, 17, 19–24. [Google Scholar]
- Elwakil, A.S.; Kennedy, M.P. Chaotic oscillator configuration using a frequency dependent negative resistor. J. Circuits Syst. Comput. 1999, 9, 229–242. [Google Scholar] [CrossRef]
- Kilic, R.; Yildrim, F. A survey of Wien bridge-based chaotic oscillators: Design and experimental issues. Chaos Solitons Fractals 2008, 38, 1394–1410. [Google Scholar] [CrossRef]
- Kennedy, M.P. Chaos in the Colpitts oscillator. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Petrzela, J. Chaotic behavior of state variable filters with saturation-type integrators. Electron. Lett. 2015, 51, 1159–1161. [Google Scholar] [CrossRef]
- Petrzela, J. On the existence of chaos in the electronically adjustable structures of the state variable filters. Int. J. Circuit Theory Appl. 2016, 44, 1779–1797. [Google Scholar] [CrossRef]
- Gottlieb, H.P.W.; Sprott, J.C. Simplest driven conservative chaotic oscillator. Phys. Lett. A 2001, 291, 385–388. [Google Scholar] [CrossRef]
- Elwakil, A.S. Nonautonomous pulse-driven chaotic oscillator based on Chua’s circuit. Microelectron. J. 2002, 33, 479–486. [Google Scholar] [CrossRef]
- Hasler, M.J. Electrical circuits with chaotic behavior. Proc. IEEE 1987, 75, 1009–1021. [Google Scholar] [CrossRef]
- Petrzela, J. Chaotic admittance with analog multipliers. In Proceedings of the 41st International Conference on Telecommunications and Signal Processing, Athens, Greece, 4–6 July 2018; pp. 60–65, ISBN 978-1-5386-4695-3. [Google Scholar]
- Petrzela, J. Electronically tunable analog chaos converters. In Proceedings of the 41st International Conference on Telecommunications and Signal Processing, Prague, Czech Republic, 3–5 July 2012; pp. 100–106, ISBN 978-1-4673-1116-8. [Google Scholar]
- Ma, J.; Wang, L.; Duan, S.; Xu, Y. A multi-wing butterfly chaotic system and its implementation. Int. J. Circuit Theory Appl. 2017, 45, 1873–1884. [Google Scholar] [CrossRef]
- Tahir, F.R.; Jafari, S.; Pham, V.-T.; Volos, C. A novel no-equilibrium chaotic system with multiwing butterfly attractors. Int. J. Bifurc. Chaos 2015, 25, 1550056. [Google Scholar] [CrossRef]
- Petrzela, J.; Hrubos, Z.; Gotthans, T. Modeling deterministic chaos using electronic circuits. Radioengineering 2011, 20, 438–444. [Google Scholar]
- Yu, S.; Lu, J.; Leung, H.; Chen, G. Design and implementation of n-scroll chaotic attractors from a general jerk circuit. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1459–1476. [Google Scholar]
- Varrientos, J.E.; Sanchez-Sinencio, E. A 4-D chaotic oscillator based on a differential hysteresis comparator. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 3–10. [Google Scholar] [CrossRef]
- Itoh, M. Synthesis of electronic circuits for simulating nonlinear dynamics. Int. J. Bifurc. Chaos 2001, 11, 605–653. [Google Scholar] [CrossRef]
- Gotthans, T.; Petrzela, J. Experimental study of the sampled labyrinth chaos. Radioengineering 2011, 20, 873–879. [Google Scholar]
- Caponetto, R.; Di Mauro, A.; Fortuna, L.; Frasca, M. Field programmable analog array to implement a programmable Chua’s circuit. Int. J. Chaos Theory Appl. 2005, 15, 1829–1836. [Google Scholar] [CrossRef]
- Ozoguz, S.; Sengor, N.S. On the realization of NPN-only log-domain chaotic oscillators. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 291–294. [Google Scholar] [CrossRef]
- Trejo-Guerra, R.; Tlelo-Cuautle, E.; Cabajal-Gomez, V.H.; Rodriguez-Gomez, G. A survey on the integrated design of chaotic oscillators. Appl. Math. Comput. 2013, 219, 5113–5122. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Kennedy, M.P. Improved implementation of Chua’s oscillator using current feedback op amp. IEEE Trans. Circuits Syst. 2000, 47, 76–79. [Google Scholar] [CrossRef]
- Kushwaha, A.K.; Paul, S.K. Inductorless realization of Chua’s oscillator using DVCCTA. Analog Integr. Circuits Signal Process. 2016, 88, 137–150. [Google Scholar] [CrossRef]
- Rodriguez-Vazquez, A.; Delgado-Restituto, M. CMOS design of chaotic oscillators using state variables: A monolithic Chua’s circuit. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 596–613. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Soliman, A.M. Current conveyor chaos generators. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 393–398. [Google Scholar] [CrossRef]
- Petrzela, J. Multi-valued static memory with resonant tunneling diodes as natural source of chaos. Nonlinear Dyn. 2018, 94, 1867–1887. [Google Scholar] [CrossRef]
- Semenov, A. Mathematical simulation of the chaotic oscillator based on a field-effect transistor structure with negative resistance. In Proceedings of the 36th International Conference on Electronics and Nanotechnology, Kyiv, Ukraine, 12–19 April 2016; pp. 52–56, ISBN 978-1-5090-1431-6. [Google Scholar]
- Sotner, R.; Jerabek, J.; Prokop, R.; Kledrowetz, V.; Polak, J. A CMOS multiplied input differential difference amplifier: A new active device and its applications. Appl. Sci. 2017, 7, 106. [Google Scholar] [CrossRef]
- Polak, L.; Sotner, R.; Petrzela, J.; Jerabek, J. CMOS current feedback operational amplifier-based relaxation generator for capacity to voltage sensor interface. Sensors 2018, 18, 4488. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Tlelo-Cuautle, E.; Toxqui-Toxqui, I.; Sanchez-Lopez, C.; Trejo-Guerra, R. Frequency limitations in generating multi-scroll chaotic attractors using CFOAs. Int. J. Electron. 2014, 101, 1559–1569. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Brown, R. Calculating Lyapunov exponents for short and/or noisy data sets. Phys. Rev. E 1993, 47, 3962–3969. [Google Scholar] [CrossRef]
- Petrzela, J. Optimal piecewise-linear approximation of the quadratic chaotic dynamics. Radioengineering 2012, 21, 20–28. [Google Scholar]
- Nepomuceno, E.G.; Martins, S.A.M.; Silva, B.C.; Amaral, G.F.V.; Perc, M. Detecting unreliable computer simulations of recursive functions with interval extension. Appl. Math. Comput. 2018, 329, 408–419. [Google Scholar] [CrossRef]
- Corless, R.M. What good are numerical simulations of chaotic dynamical systems? Comput. Math. Appl. 1994, 28, 107–121. [Google Scholar] [CrossRef][Green Version]
- Galias, Z. The dangers of rounding errors for simulations and analysis of nonlinear circuits and systems? And how to avoid them. IEEE Circuits Syst. Mag. 2013, 13, 35–52. [Google Scholar] [CrossRef]
- Lozi, R. Can we trust in numerical computations of chaotic solutions of dynamical systems? World Sci. Ser. Nonlinear Sci. Ser. A Topol. Dyn. Chaos 2013, 63–98. [Google Scholar] [CrossRef]
- Thomas, R. Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, labyrinth chaos. Int. J. Bifurc. Chaos 1999, 9, 1889–1905. [Google Scholar] [CrossRef]
- Sprott, J.C.; Chlouverakis, K.E. Labyrinth chaos. Int. J. Bifurc. Chaos 2007, 17, 2097–2108. [Google Scholar] [CrossRef]
- Chlouverakis, K.E.; Sprott, J.C. Chaotic hyperjerk systems. Int. J. Bifurc. Chaos 2007, 17, 2097–2108. [Google Scholar] [CrossRef]
- Dalkiran, F.Y.; Sprott, J.C. Simple chaotic hyperjerk system. Int. J. Bifurc. Chaos 2016, 26, 1650189. [Google Scholar] [CrossRef]
- Barboza, R. Dynamics of a hyperchaotic Lorenz system. Int. J. Bifurc. Chaos 2007, 17, 4285–4294. [Google Scholar] [CrossRef]
- Jia, Q. Hyperchaos generated from the Lorenz chaotic system and its control. Phys. Lett. A 2007, 366, 217–222. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Q. Dynamics of a hyperchaotic Lorenz-type system. Nonlinear Dyn. 2014, 77, 569–581. [Google Scholar] [CrossRef]
- Piper, J.R.; Sprott, J.C. Simple autonomous chaotic circuits. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 730–734. [Google Scholar] [CrossRef]
- Kilic, R. Universal programmable chaos generator: Design and implementation issues. Int. J. Bifurc. Chaos 2010, 20, 419–435. [Google Scholar] [CrossRef]
- Kilic, R.; Yildrim Dalkiran, F. FPAA-based programmable implementation of a chaotic system characterized with different nonlinear functions. In Proceedings of the International Symposium on Nonlinear Theory and its Applications, Budapest, Hungary, 7–10 September 2008; pp. 132–135. [Google Scholar] [CrossRef]
- Hulub, M.; Frasca, M.; Fortuna, L.; Arena, P. Implementation and synchronization of 3x3 grid scroll chaotic circuits with analog programmable devices. Chaos 2006, 16, 013121. [Google Scholar] [CrossRef]
- Prebianca, F.; Marcondes, D.W.C.; Albuquerque, H.A.; Beims, M.W. Exploring an experimental analog Chua’s circuit. Eur. Phys. J. B 2019, 92, 134. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Volos, C.; Jafari, S.; Kengne, J.; Rajagopal, K. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef]
- Dar, M.R.; Kant, N.A.; Khanday, F.A. Realization of fractional-order double-scroll chaotic system using operational transconductance amplifier (OTA). J. Circuits Syst. Comput. 2018, 27, 1850006. [Google Scholar] [CrossRef]
- Kathikeyan, R.; Akif, A.; Jafari, S.; Anitha, K.; Ismail, K. Chaotic chameleon: Dynamic analysis, circuit implementation, FPGA design and fractional-order form with basic analysis. Chaos Solitons Fractals 2017, 103, 476–487. [Google Scholar] [CrossRef]
- Rajagopal, K.; Li, C.; Nazarimehr, F.; Karthikeyan, A.; Duraisamy, P.; Jafari, S. Chaotic dynamics of modified wien bridge oscillator with fractional order memristor. Radioengineering 2019, 28, 165–174. [Google Scholar] [CrossRef]
- Valsa, J.; Dvorak, P.; Friedl, M. Network model of the CPE. Radioengineering 2011, 20, 619–626. [Google Scholar]
- Jin, J. Programmable multi-direction fully integrated chaotic oscillator. Microelectron. J. 2018, 75, 27–34. [Google Scholar] [CrossRef]
- Wu, Y.-L.; Yang, C.-H.; Wu, C.-H. Chip implementation of a new hyperchaotic oscillator. Electron. Lett. 2017, 53, 226–228. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.H. A novel multi-attractor period multi-scroll chaotic integrated circuit based on CMOS wide adjustable CCCII. IEEE Access 2019, 7, 16336–16350. [Google Scholar] [CrossRef]
- Trejo-Guerra, R.; Tlelo-Cuautle, E.; Jimenez-Fuentes, J.M.; Sanchez-Lopez, C.; Munoz-Pacheco, J.M.; Espinosa-Flores-Verdad, G.; Rocha-Perez, J.M. Integrated circuit generating 3- and 5-scroll attractors. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4328–4335. [Google Scholar] [CrossRef]
- Carbajal-Gomez, V.H.; Tlelo-Cuautle, E.; Munoz-Pacheco, J.M.; Gerardo de la Fraga, L.; Sanchez-Lopez, F.V. Optimization and CMOS design of chaotic oscillators robust to PVT variations. Integration 2019, 65, 32–42. [Google Scholar] [CrossRef]
- Carbajal-Gomez, V.H.; Tlelo-Cuautle, E.; Sanchez-Lopez, C.; Fernandez-Fernandez, F.V. PVT-robust CMOS programmable chaotic oscillator: Synchronization of two 7-scroll attractors. Electronics 2018, 7, 252. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrzela, J.; Sotner, R. New Nonlinear Active Element Dedicated to Modeling Chaotic Dynamics with Complex Polynomial Vector Fields. Entropy 2019, 21, 871. https://doi.org/10.3390/e21090871
Petrzela J, Sotner R. New Nonlinear Active Element Dedicated to Modeling Chaotic Dynamics with Complex Polynomial Vector Fields. Entropy. 2019; 21(9):871. https://doi.org/10.3390/e21090871
Chicago/Turabian StylePetrzela, Jiri, and Roman Sotner. 2019. "New Nonlinear Active Element Dedicated to Modeling Chaotic Dynamics with Complex Polynomial Vector Fields" Entropy 21, no. 9: 871. https://doi.org/10.3390/e21090871
APA StylePetrzela, J., & Sotner, R. (2019). New Nonlinear Active Element Dedicated to Modeling Chaotic Dynamics with Complex Polynomial Vector Fields. Entropy, 21(9), 871. https://doi.org/10.3390/e21090871





