A New Model for Complex Dynamical Networks Considering Random Data Loss
Abstract
1. Introduction
2. Network Modeling and Preliminaries
3. Model Analysis
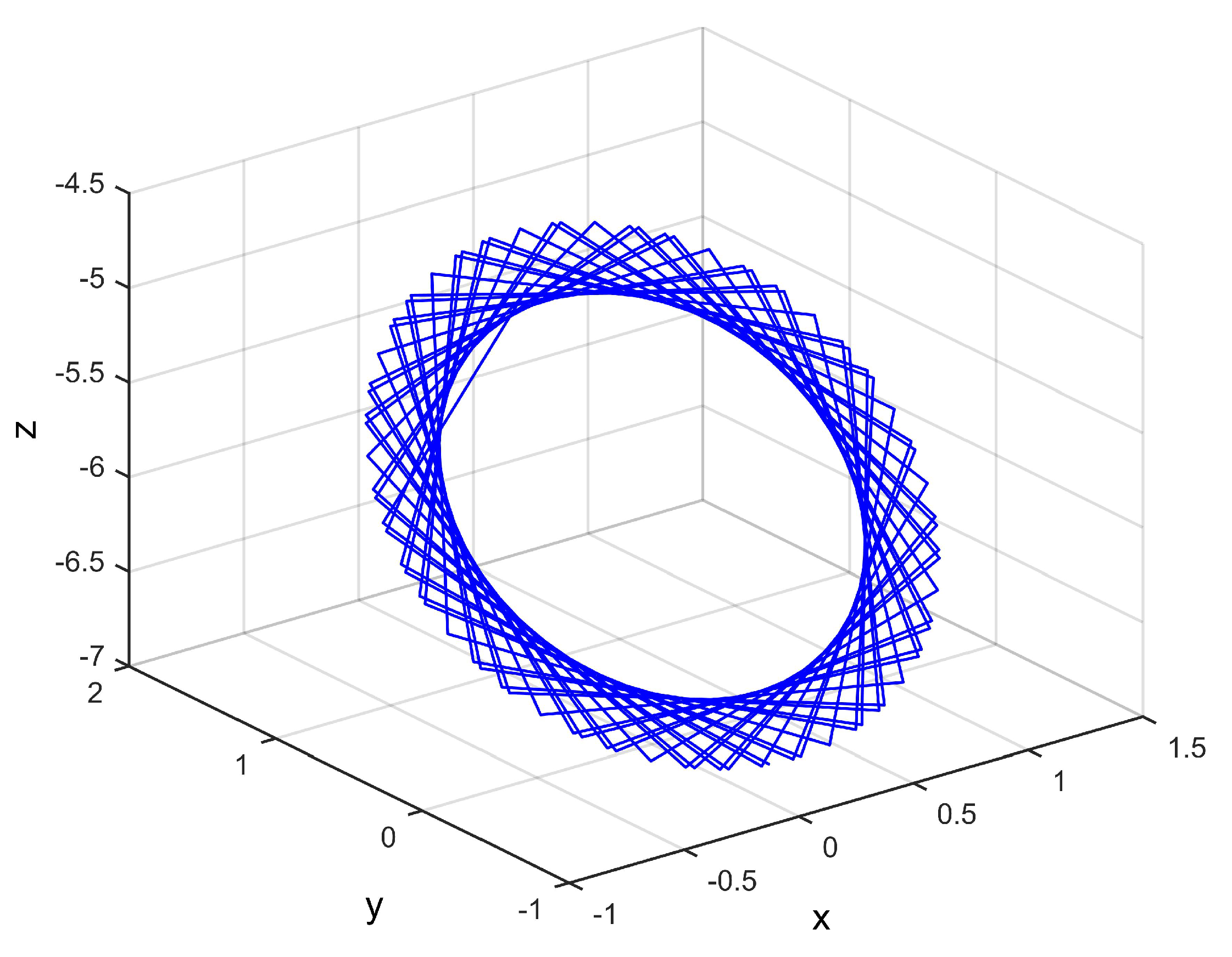
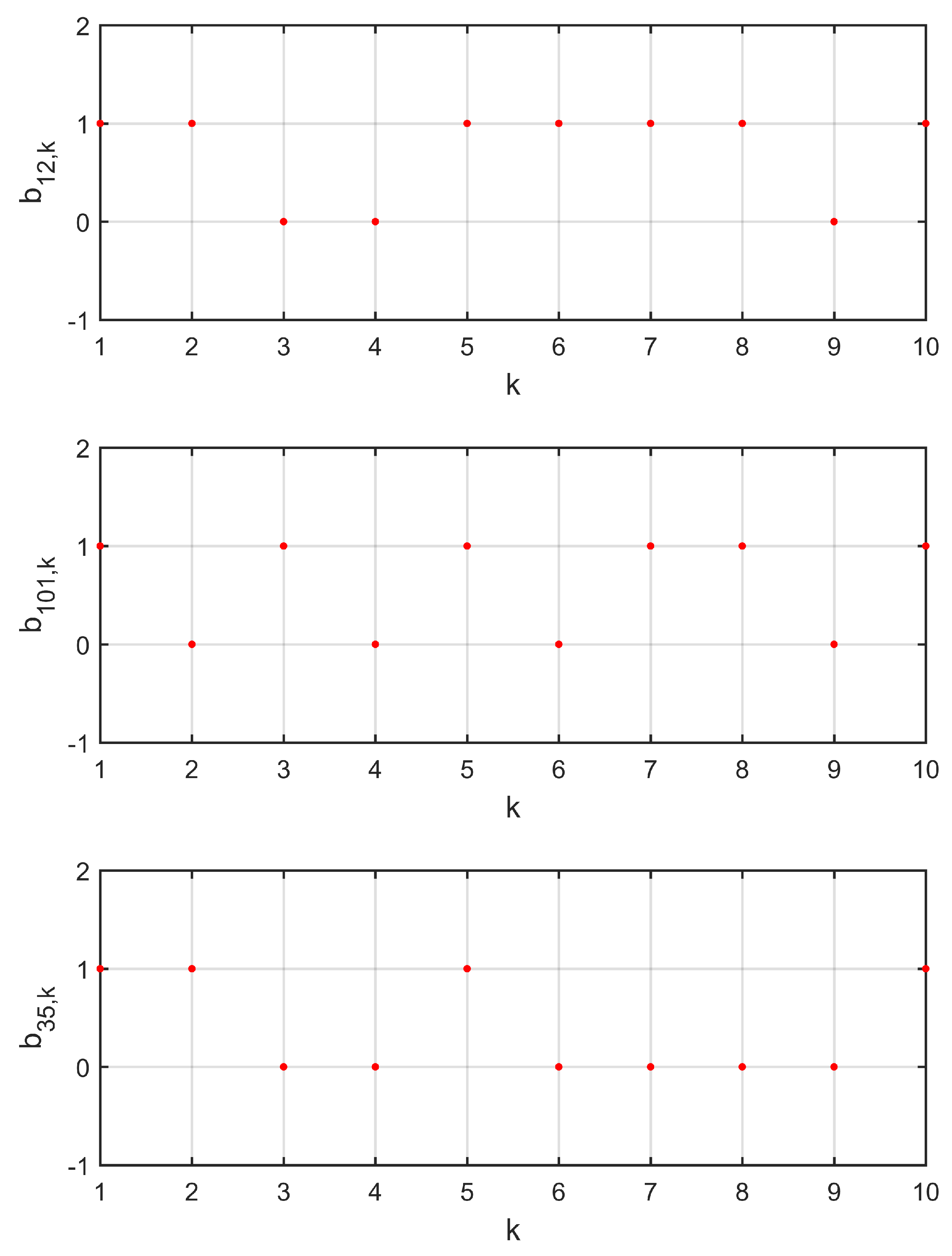
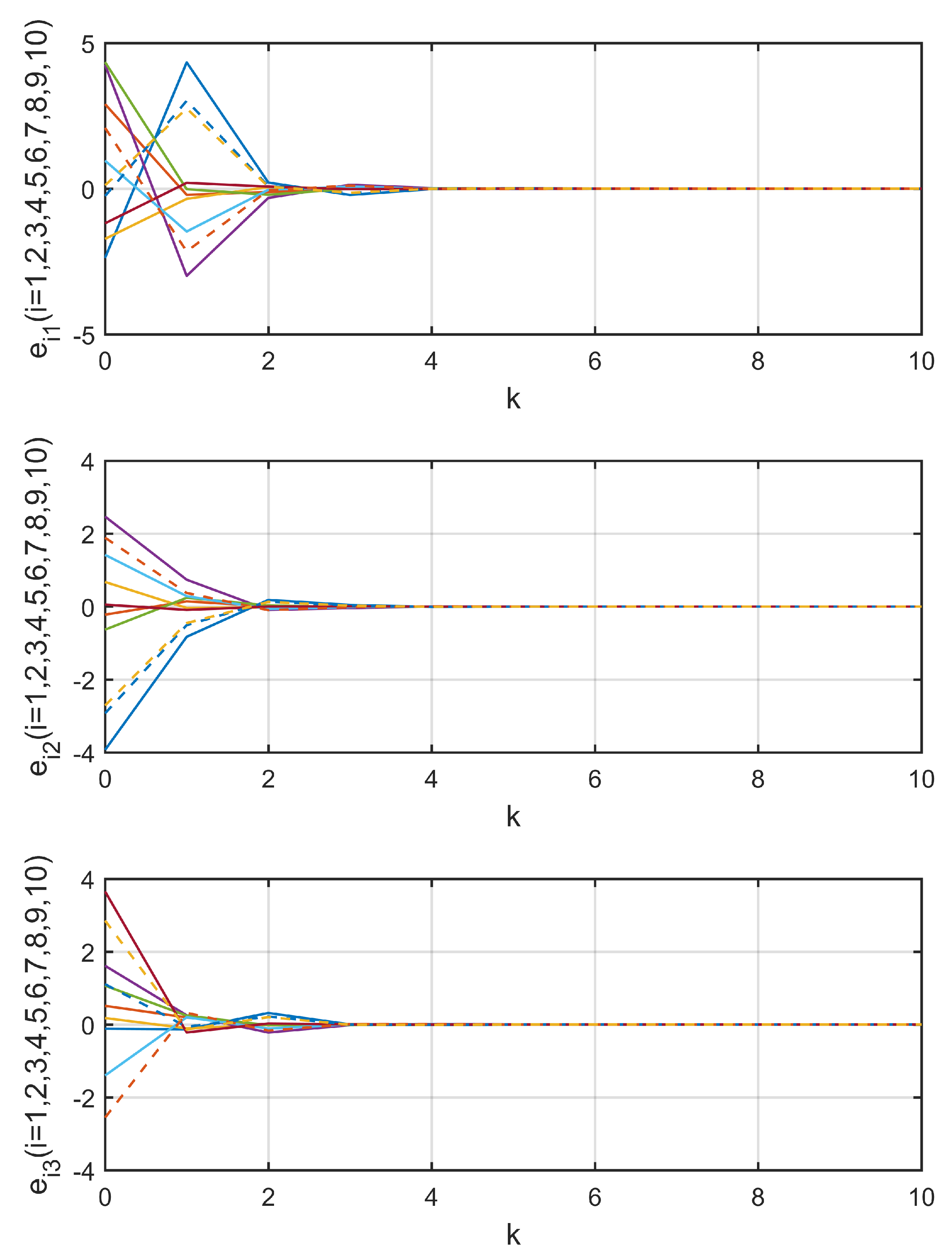
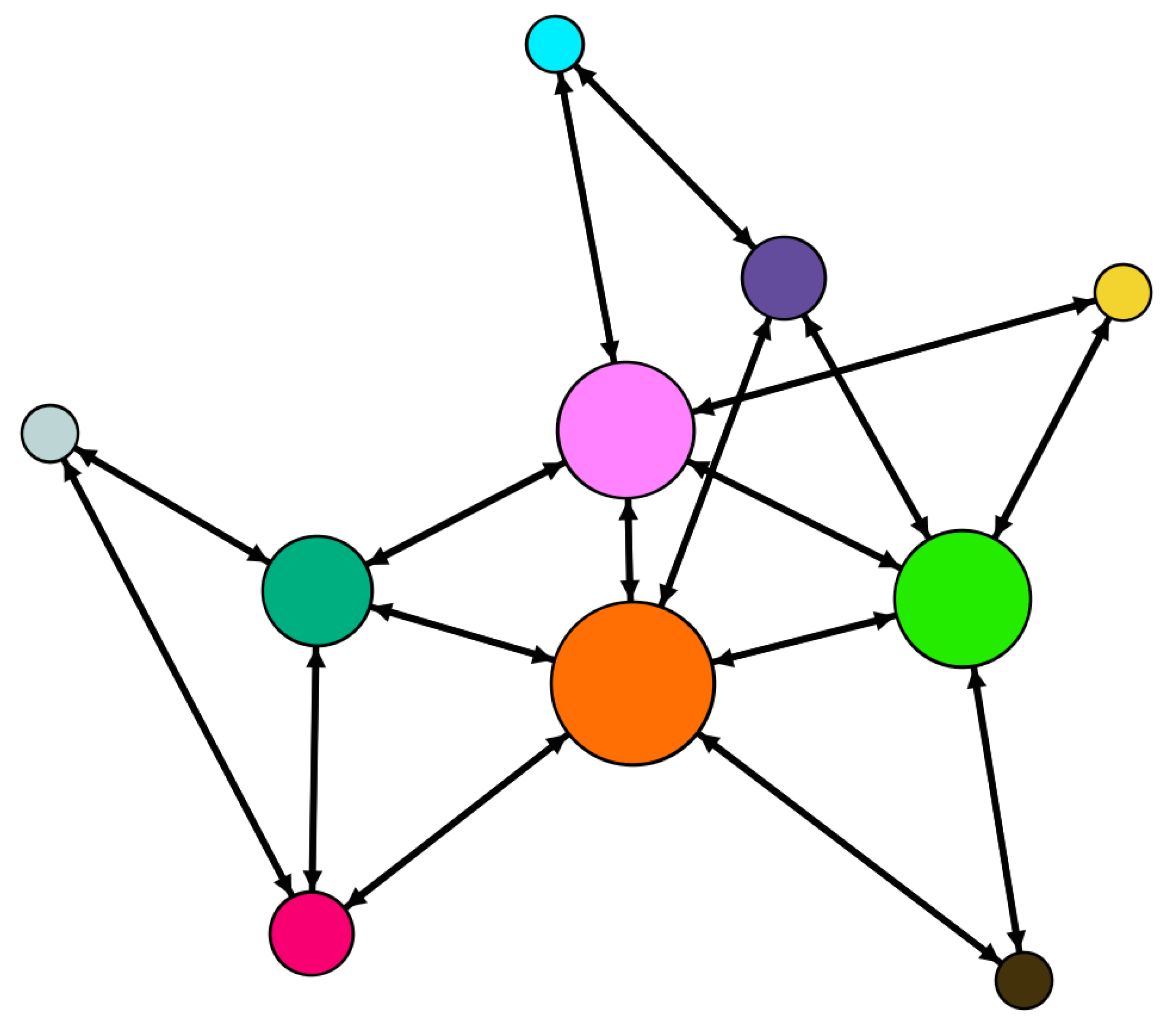
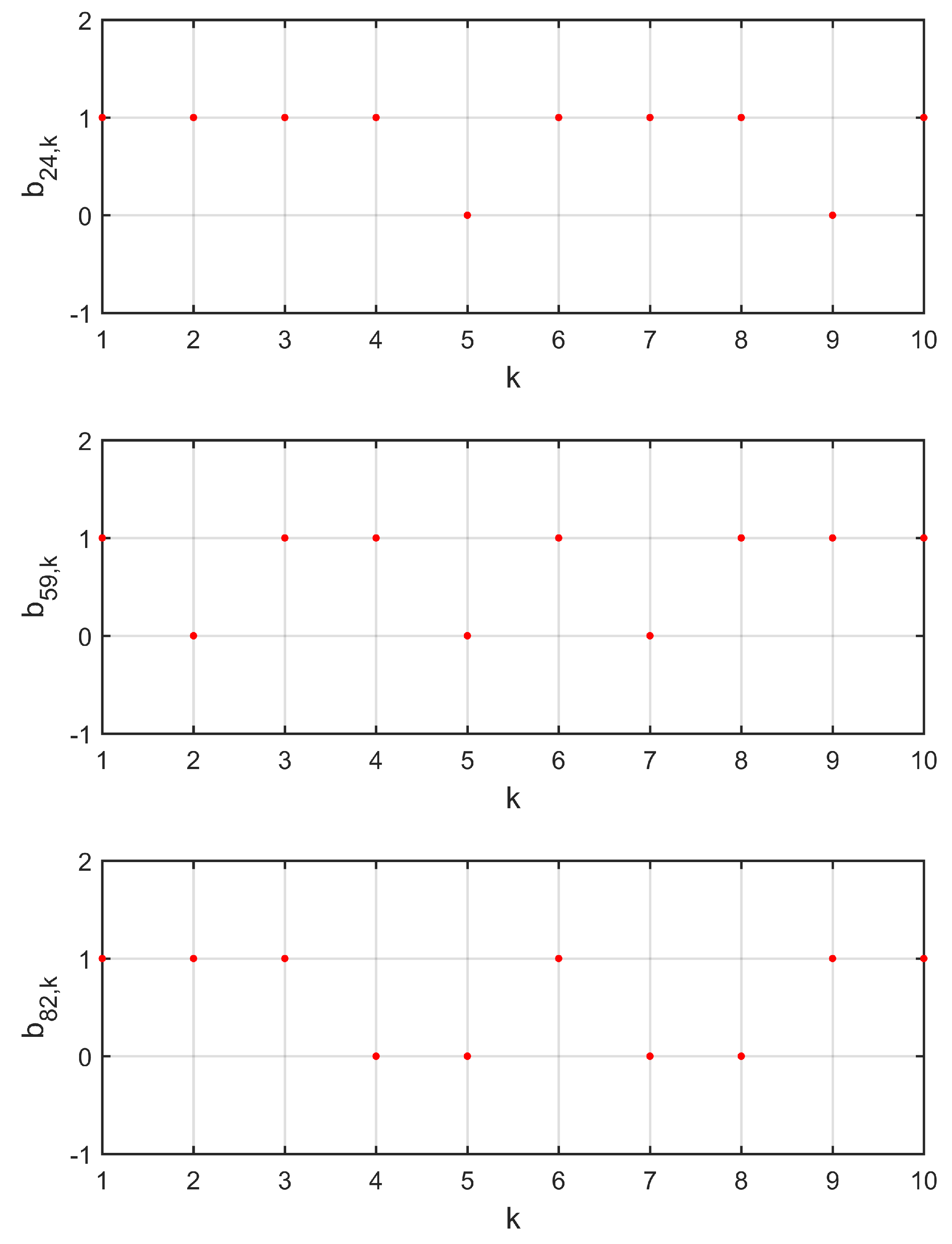
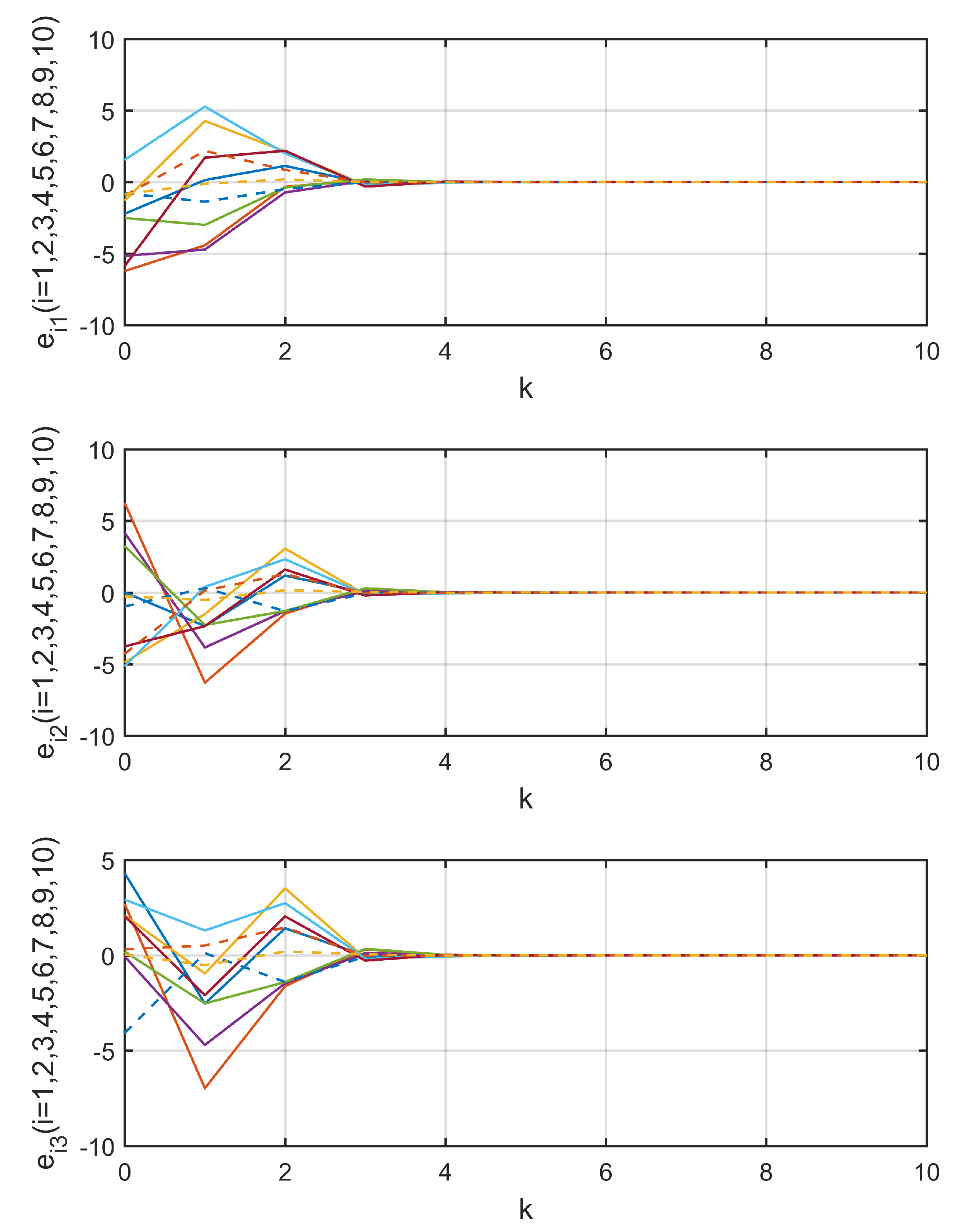
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Erdös, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–60. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Carroll, T.L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 1998, 80, 2109–2112. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G.R. Synchronization in Scale-Free Dynamical Networks: Robustness and Fragility. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 54–62. [Google Scholar] [CrossRef]
- Lü, J.H.; Yu, X.H.; Chen, G.R. Chaos synchronization of general complex dynamical networks. Phys. A Stat. Mech. Appl. 2004, 334, 281–302. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.R. Synchronization and Desynchronization of Complex Dynamical Networks: An Engineering Viewpoint. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 1381–1390. [Google Scholar]
- Wang, Q.; Zeng, G.; Tu, X. Information Technology Project Portfolio Implementation Process Optimization Based on Complex Network Theory and Entropy. Entropy 2017, 19, 287. [Google Scholar] [CrossRef]
- Almgren, K.; Kim, M.; Lee, J. Extracting Knowledge from the Geometric Shape of Social Network Data Using Topological Data Analysis. Entropy 2017, 19, 360. [Google Scholar] [CrossRef]
- Baglietto, G.; Albano, E.V.; Candia, J. Complex network structure of flocks in the Vicsek Model with Vectorial Noise. Int. J. Mod. Phys. C 2014, 25, 1350095. [Google Scholar] [CrossRef]
- Buscarino, A.; Gambuzza, L.V.; Porfiri, M.; Fortuna, L.; Frasca, M. Robustness to noise in synchronization of complex networks. Sci. Rep. 2013, 3, 2026. [Google Scholar] [CrossRef] [PubMed]
- Conti, G.; Navarra, A.; Tribbia, J. The ENSO Transition Probabilities. J. Clim. 2017, 30, 4951–4964. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Park, J.H.; Lee, S.M.; Cha, E.J. Synchronization of discrete-time complex dynamical networks with interval time-varying delays via non-fragile controller with randomly occurring perturbation. J. Frankl. Inst. 2014, 351, 4850–4871. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, J.; Chen, D.; Alsaadi, F.E. Synchronization in Fractional-Order Complex-Valued Delayed Neural Networks. Entropy 2018, 20, 54. [Google Scholar] [CrossRef]
- Banu, L.J.; Balasubramaniam, P. Synchronisation of discrete-time complex networks with randomly occurring uncertainties, nonlinearities and time-delays. Int. J. Syst. Sci. 2014, 45, 1427–1450. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, J.; Li, T.; Zhang, A.; Chen, X. Projective Exponential Synchronization for a Class of Complex PDDE Networks with Multiple Time Delays. Entropy 2015, 17, 7298–7309. [Google Scholar] [CrossRef]
- Li, H.Y.; Wu, C.W.; Shi, P.; Gao, Y.B. Control of nonlinear networked systems with packet dropouts: Interval type-2 fuzzy model-based approach. IEEE Trans. Cybern. 2015, 45, 2378–2389. [Google Scholar] [CrossRef]
- Kalidass, M.; Su, H.Y.; Wu, Y.Q.; Rathinasamy, S. H∞ filtering for impulsive networked control systems with random packet dropouts and randomly occurring nonlinearities. Int. J. Robust Nonlinear Control 2015, 25, 1767–1782. [Google Scholar] [CrossRef]
- Bai, J.J.; Lu, R.Q.; Su, H.Y.; Xue, A.K. Modeling and H∞ control of wireless networked control system with both delay and packet loss. J. Frankl. Inst. 2015, 352, 3915–3928. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Jin, Z.W.; Qi, S.; Sun, C.Y. Estimation fusion for networked systems with multiple asynchronous sensors and stochastic packet dropouts. J. Frankl. Inst. 2017, 354, 145–159. [Google Scholar] [CrossRef]
- Persis, C.D.; Tesi, P. A Comparison Among Deterministic Packet-Dropouts Models in Networked Control Systems. IEEE Control Syst. Lett. 2018, 2, 109–114. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Sakthivel, N.; Cao, J.D. Stochastic sampled-data control for synchronization of complex dynamical networks with control packet loss and additive time-varying delays. Neural Netw. 2015, 66, 46–63. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Wang, Y.W.; Yi, J.W.; Huang, Y. Stability and synchronization of directed complex dynamical networks with random packet loss: The continuous-time case and the discrete-time case. Int. J. Circuit Theory Appl. 2013, 41, 1272–1289. [Google Scholar] [CrossRef]
- Zhang, W.A.; Yu, L. Output Feedback Stabilization of Networked Control Systems With Packet Dropouts. IEEE Trans. Autom. Control 2007, 52, 1705–1710. [Google Scholar] [CrossRef]
- Moayedi, M.; Foo, Y.K.; Soh, Y.C. Adaptive Kalman Filtering in Networked Systems With Random Sensor Delays, Multiple Packet Dropouts and Missing Measurements. IEEE Trans. Signal Process 2010, 58, 1577–1588. [Google Scholar] [CrossRef]
- Ishido, Y.; Takaba, K.; Quevedo, D.E. Stability analysis of networked control systems subject to packet-dropouts and finite-level quantization. Syst. Control Lett. 2011, 60, 325–332. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Jin, Z.W.; Wang, Y.Q. State Fusion Estimation for Networked Stochastic Hybrid Systems With Asynchronous Sensors and Multiple Packet Dropouts. IEEE Access 2018, 6, 10402–10409. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z.D.; Liu, S.; Gao, H.J. A variance-constrained approach to recursive state estimation for time-varying complex networks with missing measurements. Automatica 2016, 64, 155–162. [Google Scholar] [CrossRef]
- Shen, B.; Wang, Z.D.; Ding, D.R.; Shu, H.S. H∞ State Estimation for Complex Networks With Uncertain Inner Coupling and Incomplete Measurements. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 2027–2037. [Google Scholar] [CrossRef]
- Jiang, G.P.; Tang, W.K.S.; Chen, G.R. A State-Observer-Based Approach for Synchronization in Complex Dynamical Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 2739–2745. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Joint Entropy and Conditional Entropy. In Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 16. [Google Scholar]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory. In Studies in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Zhang, C.; Wang, X.Y.; Wang, S.B.; Zhou, W.J.; Xia, Z.Q. Finite-Time Synchronization for a Class of Fully Complex-Valued Networks With Coupling Delay. IEEE Access 2018, 6, 17923–17932. [Google Scholar] [CrossRef]
- Sivaranjani, K.; Rakkiyappan, R.; Joo, Y.H. Event triggered reliable synchronization of semi-Markovian jumping complex dynamical networks via generalized integral inequalities. J. Frankl. Inst. 2018, 355, 3691–3716. [Google Scholar] [CrossRef]
- Lü, J.H.; Yu, X.H.; Chen, G.R.; Cheng, D.Z. Characterizing the synchronizability of small-world dynamical networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 787–796. [Google Scholar] [CrossRef]
- Kaviarasan, B.; Sakthivel, R.; Lim, Y. Synchronization of complex dynamical networks with uncertain inner coupling and successive delays based on passivity theory. Neurocomputing 2016, 186, 127–138. [Google Scholar] [CrossRef]
- Lee, T.H.; Wu, Z.G.; Park, J.H. Synchronization of a complex dynamical network with coupling time-varying delays via sampled-data control. Appl. Math. Comput. 2012, 219, 1354–1366. [Google Scholar] [CrossRef]
- Badin, G.; Domeisen, D.I.V. A Search for Chaotic Behavior in Northern Hemisphere Stratospheric Variability. J. Atmos. Sci. 2014, 71, 1494–1507. [Google Scholar] [CrossRef]
- Gupta, K.; Ambika, G. Role of time scales and topology on the dynamics of complex networks. Chaos 2019, 29, 033119. [Google Scholar] [CrossRef]
- Chen, W.H.; Liu, Y.; Zheng, W.X. Synchronization Analysis of Two-Time-Scale Nonlinear Complex Networks With Time-Scale-Dependent Coupling. IEEE Trans. Cybern. 2018, 49, 1–13. [Google Scholar] [CrossRef]
- Badin, G.; Domeisen, D.I.V. Nonlinear stratospheric variability: Multifractal de-trended fluctuation analysis and singularity spectra. Proc. Royal Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150864. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Jiang, G.-P.; Wang, X. A New Model for Complex Dynamical Networks Considering Random Data Loss. Entropy 2019, 21, 797. https://doi.org/10.3390/e21080797
Wu X, Jiang G-P, Wang X. A New Model for Complex Dynamical Networks Considering Random Data Loss. Entropy. 2019; 21(8):797. https://doi.org/10.3390/e21080797
Chicago/Turabian StyleWu, Xu, Guo-Ping Jiang, and Xinwei Wang. 2019. "A New Model for Complex Dynamical Networks Considering Random Data Loss" Entropy 21, no. 8: 797. https://doi.org/10.3390/e21080797
APA StyleWu, X., Jiang, G.-P., & Wang, X. (2019). A New Model for Complex Dynamical Networks Considering Random Data Loss. Entropy, 21(8), 797. https://doi.org/10.3390/e21080797




