Twenty Years of Quantum State Teleportation at the Sapienza University in Rome
Abstract
:1. Introduction
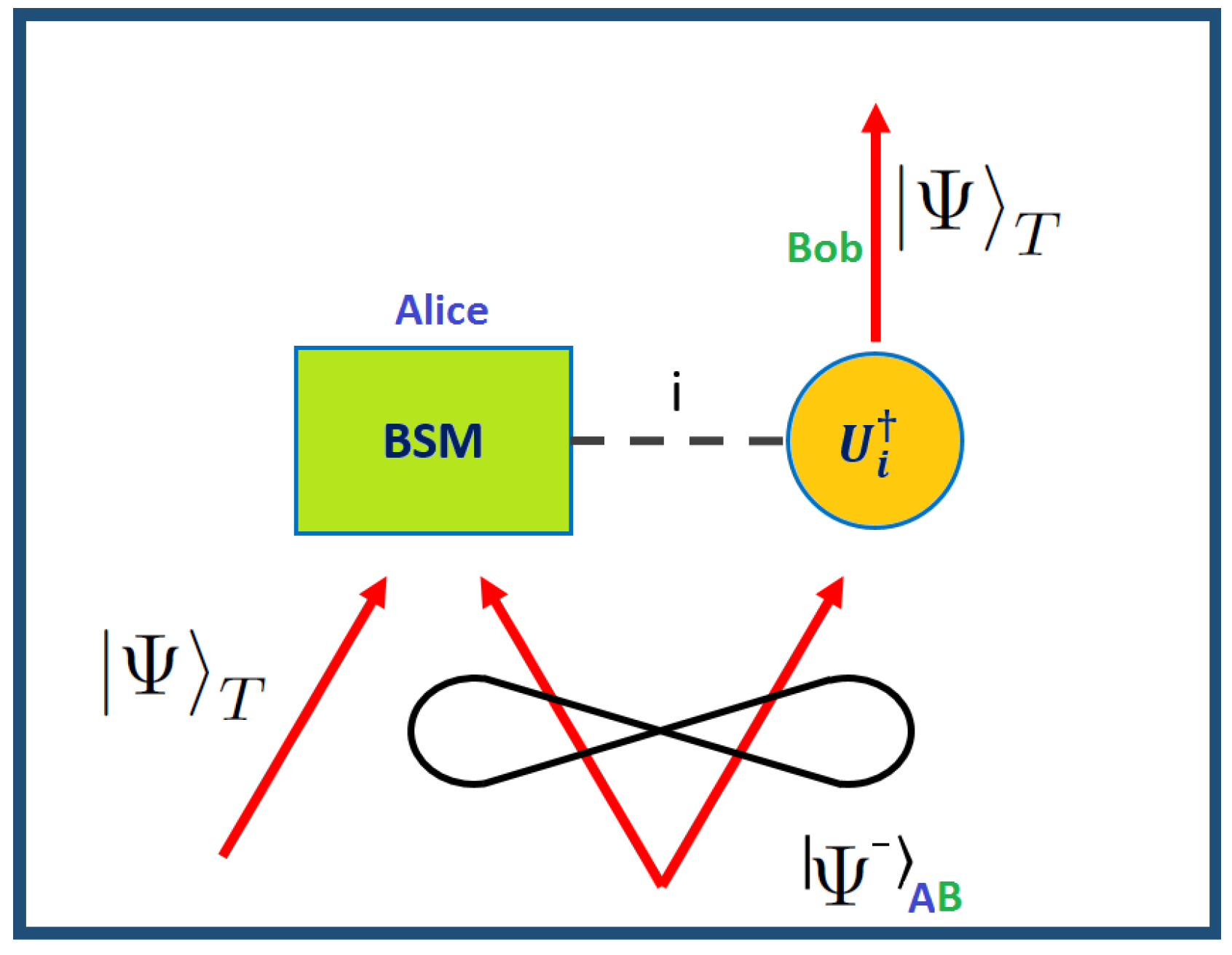
2. Teleportation and Entanglement Swapping
2.1. Quantum Teleportation Protocol
2.2. Entanglement-Swapping Protocol
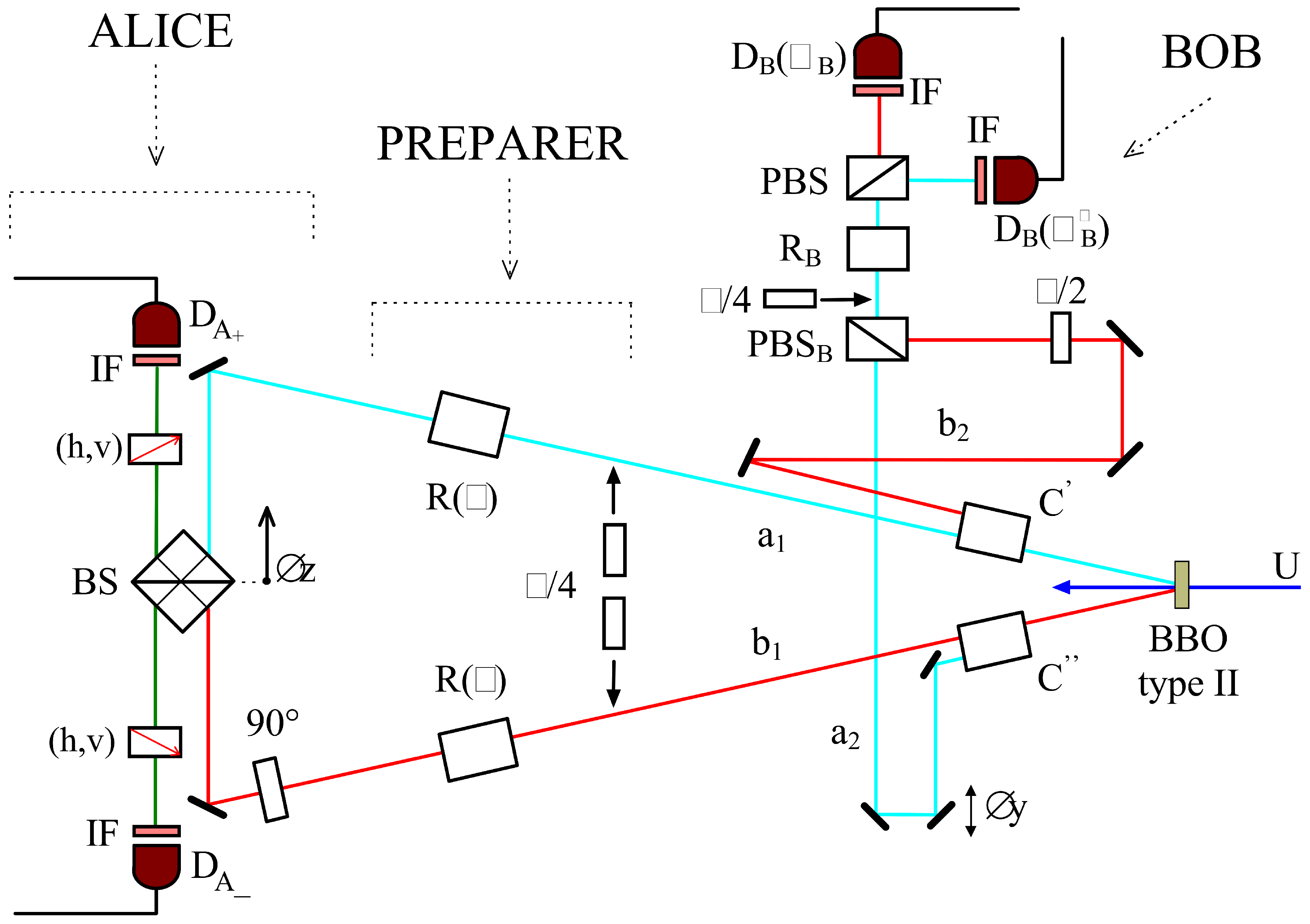
3. The First Teleportation
"Two groups achieved the feat of quantum teleportation in 1997—just four years after the theoretical breakthrough. First, it was the team of Boschi et al. based in Italy, followed only a few months later by the team of Bouwmeester et al. in Austria."
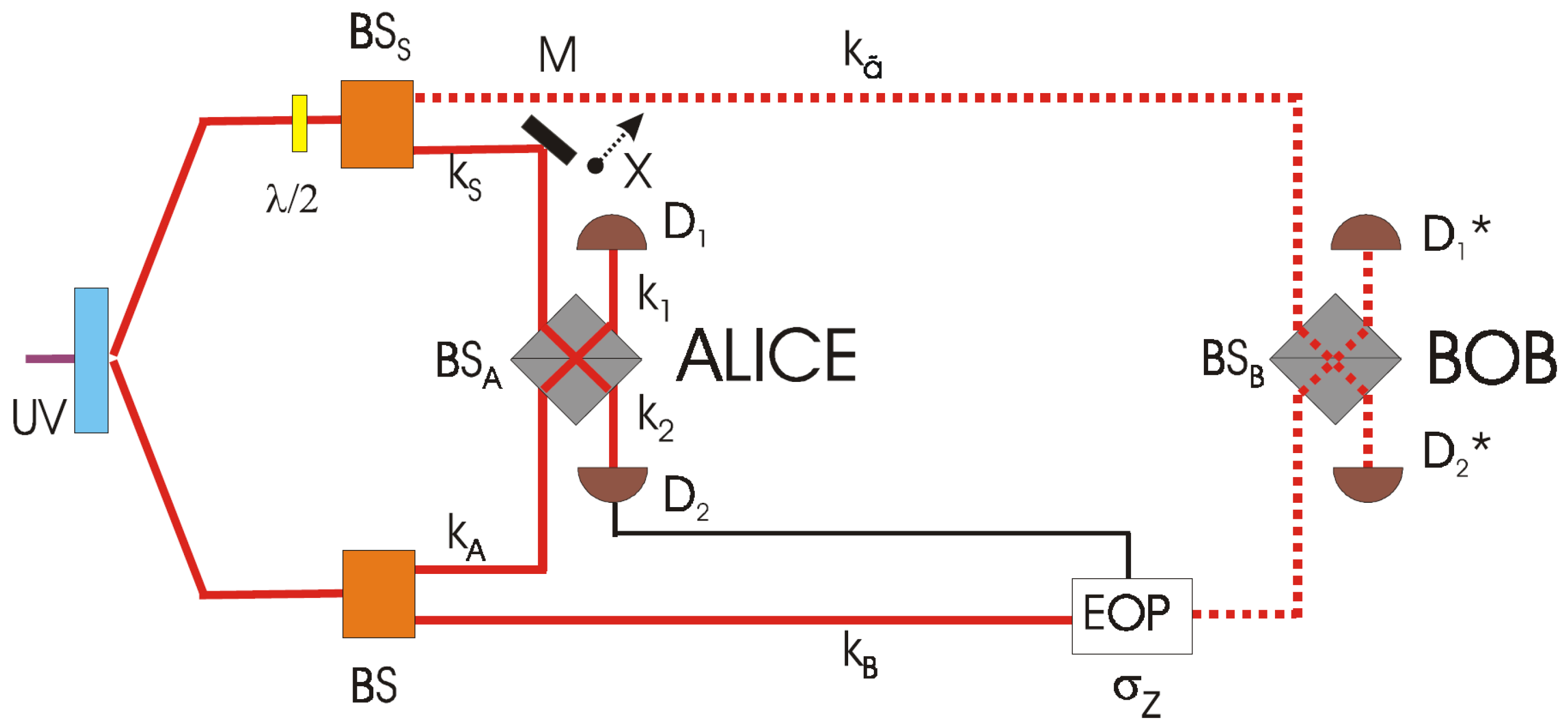
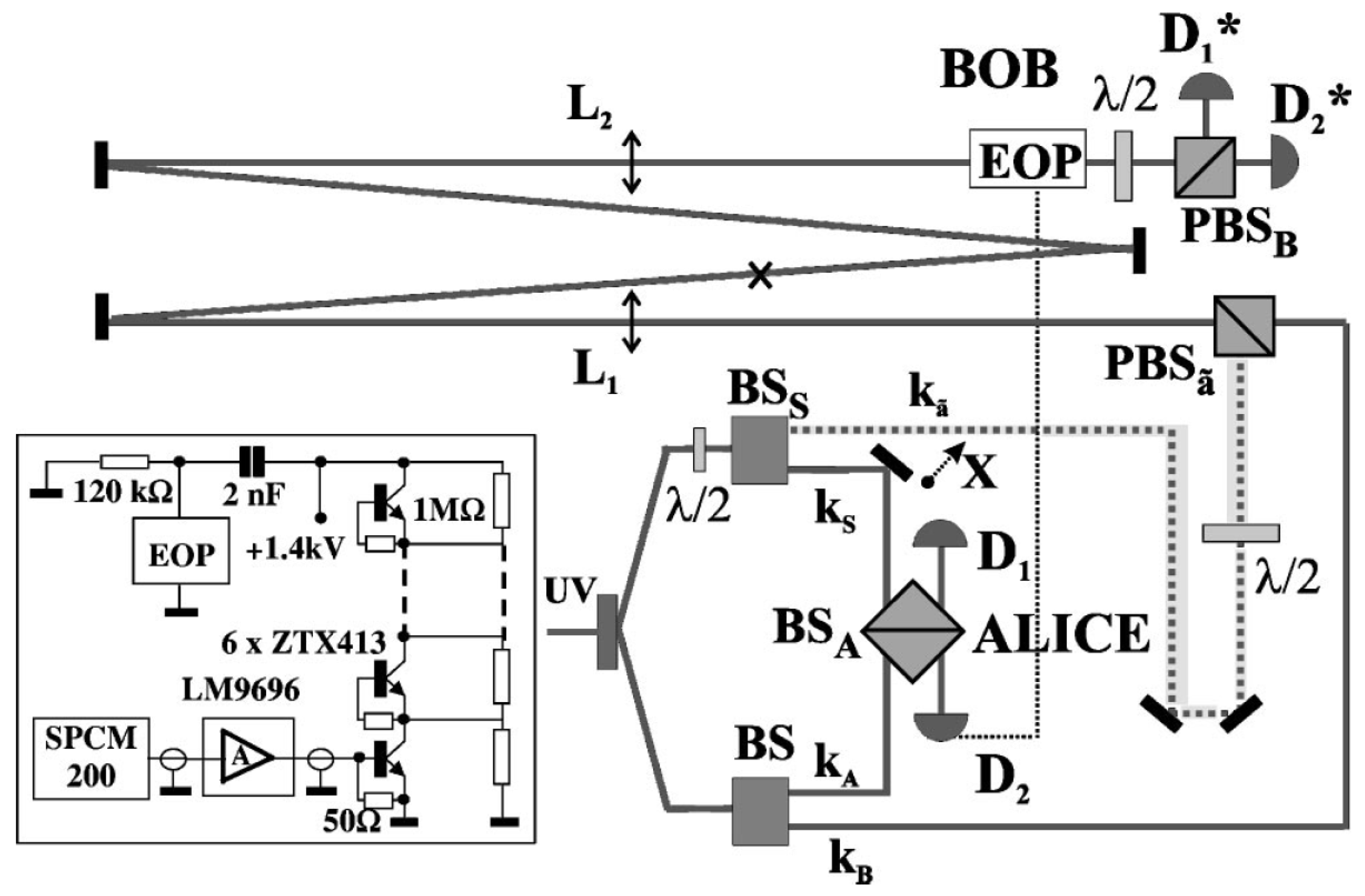
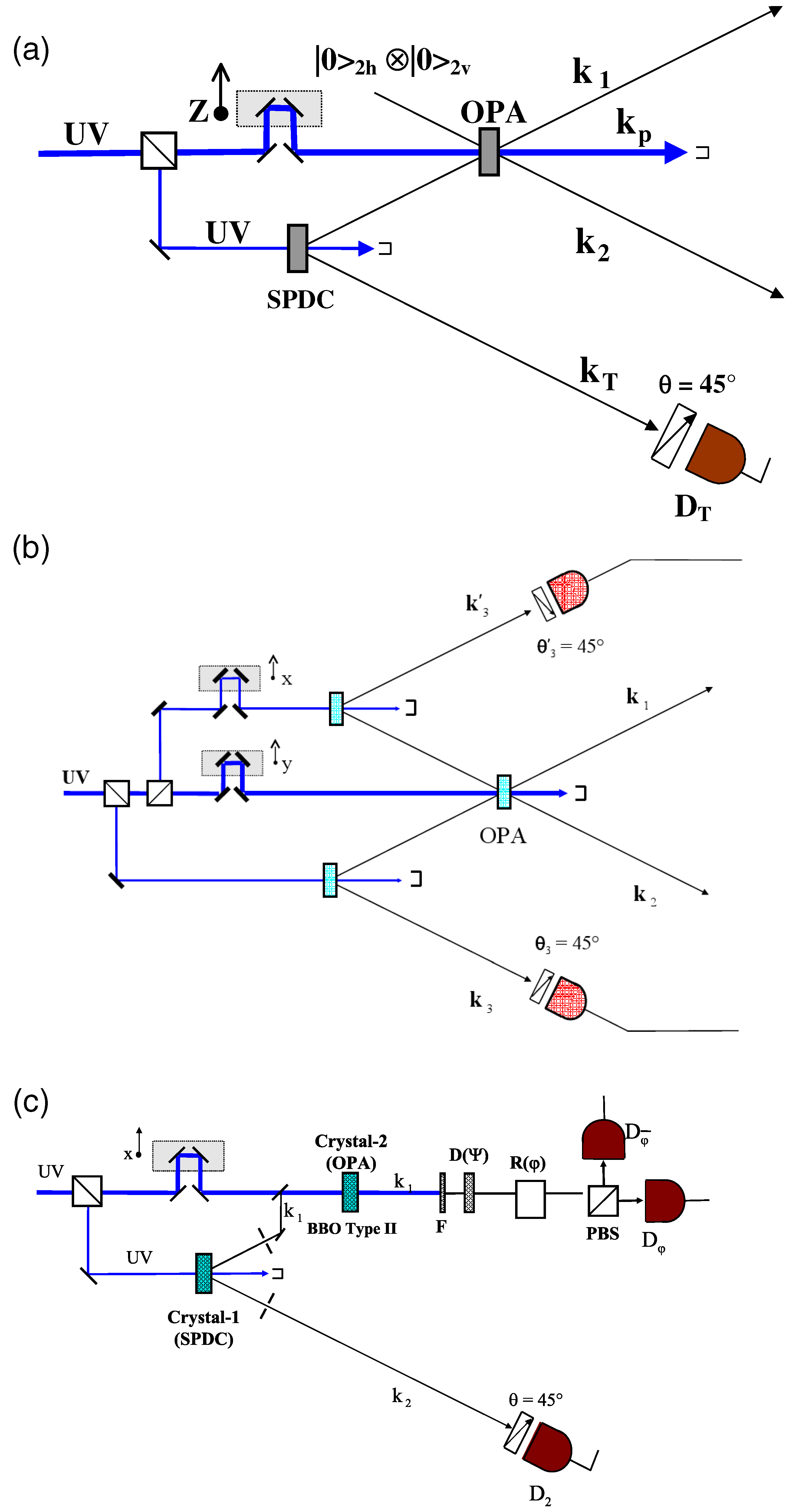
4. Teleportation of Vacuum-One Photon
5. Active Teleportation
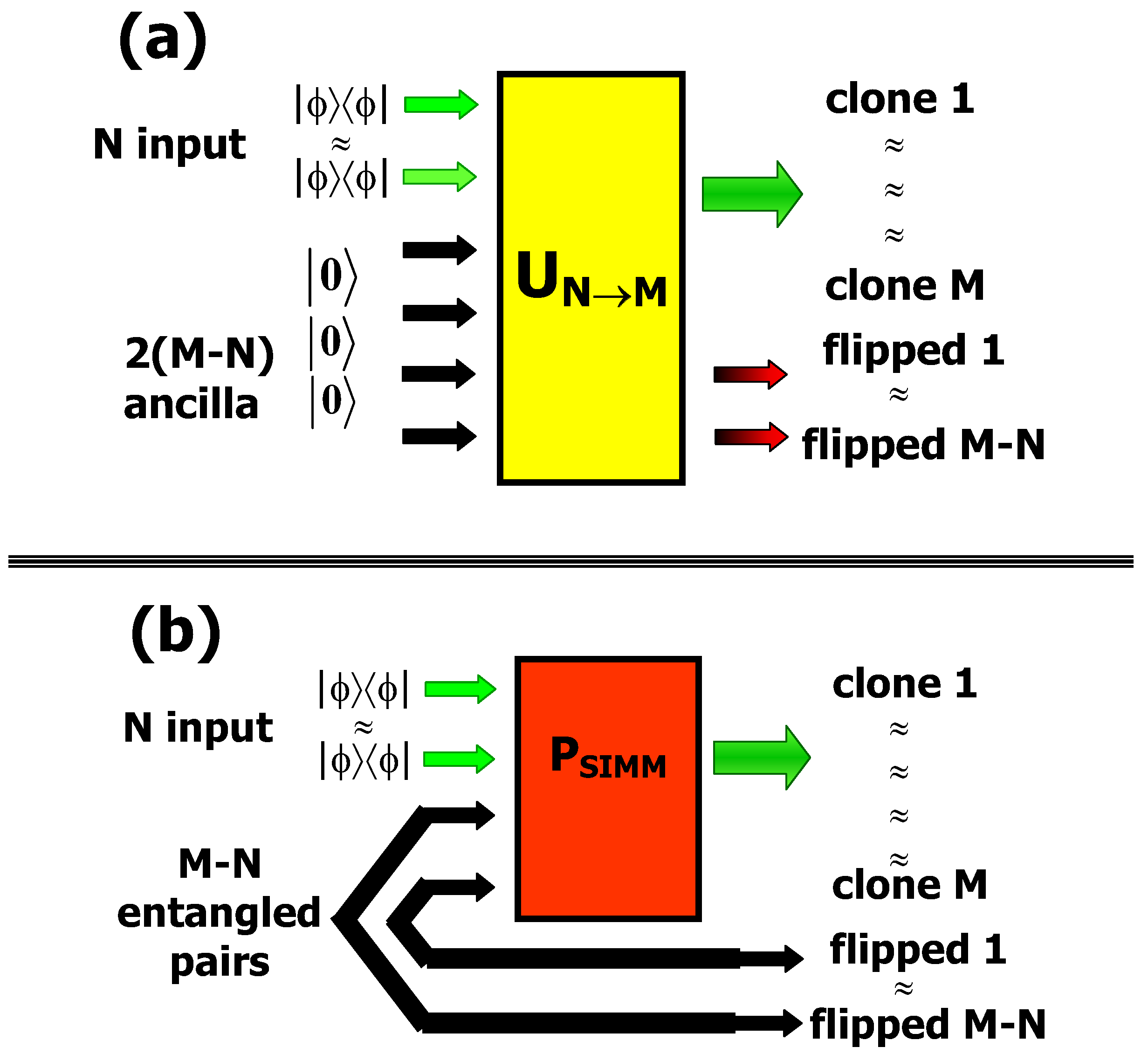
6. Optimal Quantum Machines Based on Teleportation
- (i)
- The first one has been based on finding a suitable unitary operator , acting on N input qubits and on ancillary qubits: Figure 5a. At the output of this device we obtain M and qubits which are, respectively, the optimal clones and the best flipped qubits of the input ones. The transformation can be deterministically realized by means of a quantum network, as proposed by Buzek et al. [65].
- (ii)
- The second approach to implement the cloning and the flipping is a probabilistic method that exploits a symmetrization process: Figure 5b. The initial state of the overall system consists of the N input qubits and of pairs of entangled qubits. The two optimal quantum machines are performed by applying a projective operation on the symmetric subspace to the N input qubits and to ancilla qubits, each one belonging to a different entangled pair. This scheme corresponds to a modified QST scheme: Instead of performing a Bell state measurement a project over the symmetric subspace is performed. This transformation assures the uniform distribution of the initial information into the overall system and guarantees that all output clone qubits are indistinguishable. The success probability is equal to . The optimal flipped qubits are teleported in a different location since there is no interaction between the N input qubits and the flipped ones.
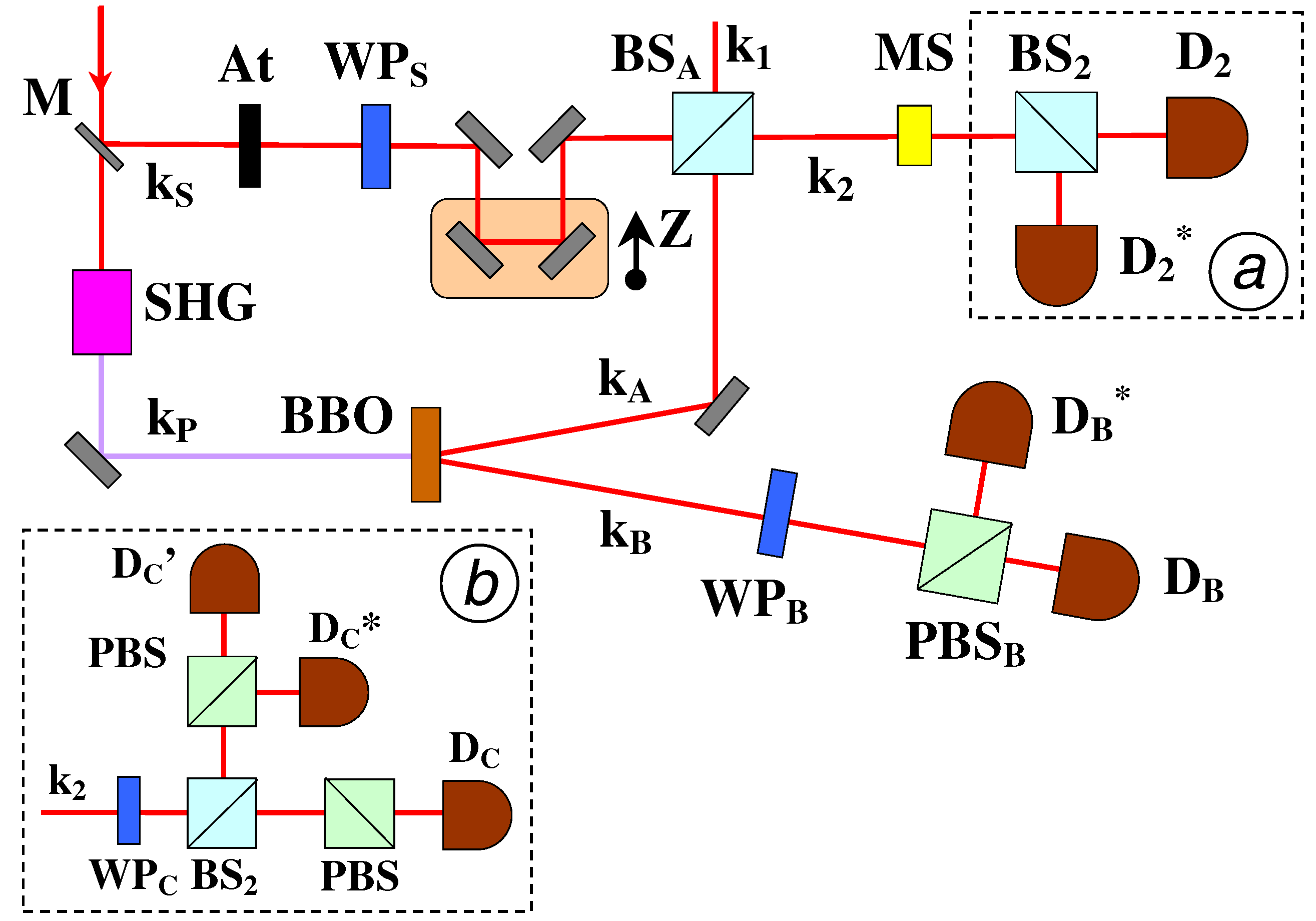
Qubits Symmetrization: Linear Optics Implementation
7. Micro and Macro Entanglement
8. Summary and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef] [Green Version]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar] [CrossRef]
- Steane, A.M. Error correcting codes in quantum theory. Phys. Rev. Lett. 1996, 77, 793–797. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Jennewein, T.; Simon, C.; Weihs, G.; Weinfurter, H.; Zeilinger, A. Quantum cryptography with entangled photons. Phys. Rev. Lett. 2000, 84, 4729–4732. [Google Scholar] [CrossRef]
- Acin, A.; Brunner, N.; Gisin, N.; Massar, S.; Pironio, S.; Scarani, V. Device-Independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 2007, 98, 230501. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian Quantum Information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Pirandola, S.; Eisert, J.; Weedbrook, C.; Furusawa, A.; Braunstein, S.L. Advances in quantum teleportation. Nat. Photon. 2015, 9, 641–652. [Google Scholar] [CrossRef]
- Briegel, H.-J.; Dur, W.; Cirac, J.I.; Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 1998, 81, 5932. [Google Scholar] [CrossRef]
- Dur, W.; Briegel, H.-J.; Cirac, J.I.; Zoller, P. Quantum repeaters based on entanglement purification. Phys. Rev. A 1999, 60, 725. [Google Scholar] [CrossRef]
- Gottesman, D.; Chuang, I.L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 1999, 402, 6390–6393. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef] [Green Version]
- Boschi, D.; Branca, S.; De Martini, F.; Hardy, L.; Popescu, S. Experimental realisation of teleporting an unknown pure quantum state via dual classical and Einstein–Podolski–Rosen channels. Phys. Rev. Lett. 1998, 80, 1121–1125. [Google Scholar] [CrossRef]
- Lombardi, E.; Sciarrino, F.; Popescu, S.; De Martini, F. Teleportation of a Vacuum–One-Photon Qubit. Phys. Rev. Lett. 2002, 88, 070402. [Google Scholar] [CrossRef]
- Giacomini, S.; Sciarrino, F.; Lombardi, E.; De Martini, F. Active teleportation of a quantum bit. Phys. Rev. A 2002, 66, 030302. [Google Scholar] [CrossRef] [Green Version]
- Ursin, R.; Jennewein, T.; Aspelmeyer, M.; Kaltenbaek, R.; Lindenthal, M.; Walther, P.; Zeilinger, A. Quantum teleportation across the Danube. Nature 2004, 430, 849. [Google Scholar] [CrossRef]
- Marcikic, I.; de Riedmatten, H.; Tittel, W.; Zbinden, H.; Gisin, N. Long-distance teleportation of qubits at telecommunication wavelengths. Nature 2003, 421, 509–513. [Google Scholar] [CrossRef]
- De Riedmatten, H.; Marcikic, I.; Tittel, W.; Zbinden, H.; Collins, D.; Gisin, N. Long-distance quantum teleportation in a quantum relay configuration. Phys. Rev. Lett. 2004, 92, 047904. [Google Scholar] [CrossRef]
- Yin, J.; Ren, J.G.; Lu, H.; Cao, Y.; Yong, H.L.; Wu, Y.P.; Liu, C.; Liao, S.K.; Zhou, F.; Jiang, Y.; et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature 2012, 488, 185–188. [Google Scholar] [CrossRef]
- Ma, X.S.; Herbst, T.; Scheidl, T.; Wang, D.; Kropatschek, S.; Naylor, W.; Wittmann, B.; Mech, A.; Kofler, J.; Anisimova, E.; et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 2012, 489, 269–273. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.G.; Xu, P.; Yong, H.L.; Zhang, L.; Liao, S.K.; Yin, J.; Liu, W.Y.; Cai, W.Q.; Yang, M.; Li, L.; et al. Ground-to-satellite quantum teleportation. Nature 2017, 549, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706. [Google Scholar] [CrossRef]
- Wang, X.L.; Cai, X.D.; Su, Z.E.; Chen, M.C.; Wu, D.; Li, L.; Liu, N.L.; Lu, C.Y.; Pan, J.W. Quantum teleportation of multiple degrees of freedom in a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Knill, E.; Laflamme, R. Complete quantum teleportation using nuclear magnetic resonance. Nature 1998, 396, 52. [Google Scholar] [CrossRef]
- Sherson, J.F.; Krauter, H.; Olsson, R.K.; Julsgaard, B.; Hammerer, K.; Cirac, I.; Polzik, E.S. Quantum teleportation between light and matter. Nature 2006, 443, 557–560. [Google Scholar] [CrossRef]
- Krauter, H.; Salart, D.; Muschik, C.A.; Petersen, J.M.; Shen, H.; Fernholz, T.; Polzik, E.S. Deterministic quantum teleportation between distant atomic objects. Nat. Phys. 2013, 9, 400–404. [Google Scholar] [CrossRef]
- Barrett, M.D.; Chiaverini, J.; Schaetz, T.; Britton, J.; Itano, W.M.; Jost, J.D.; Knill, E.; Langer, C.; Leibfried, D.; Ozeri, R.; et al. Deterministic quantum teleportation of atomic qubits. Nature 2004, 429, 737–739. [Google Scholar] [CrossRef]
- Riebe, M.; Häffner, H.; Roos, C.F.; Hänsel, W.; Benhelm, J.; Lancaster, G.P.T.; Körber, T.W.; Becher, C.; Schmidt-Kaler, F.; James, D.F.V.; et al. Deterministic quantum teleportation with atoms. Nature 2004, 429, 734–737. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.B.; Fallahi, P.; Togan, E.; Delteil, A.; Chin, Y.S.; Miguel-Sanchez, J.; Imamoğlu, A. Quantum teleportation from a propagating photon to a solid-state spin qubit. Nat. Commun. 2013, 4, 2744. [Google Scholar] [CrossRef] [Green Version]
- Steffen, L.; Salathe, Y.; Oppliger, M.; Kurpiers, P.; Baur, M.; Lang, C.; Eichler, C.; Puebla-Hellmann, G.; Fedorov, A.; Wallraff, A. Deterministic quantum teleportation with feed-forward in a solid state system. Nature 2013, 500, 319–322. [Google Scholar] [CrossRef] [Green Version]
- Pfaff, W.; Hensen, B.J.; Bernien, H.; van Dam, S.B.; Blok, M.S.; Taminiau, T.H.; Tiggelman, M.J.; Schouten, R.N.; Markham, M.; Twitchen, D.J.; et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 2014, 345, 532–535. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 6343. [Google Scholar] [CrossRef]
- Valivarthi, R.; Zhou, Q.; Aguilar, G.H.; Verma, V.B.; Marsili, F.; Shaw, M.D.; Nam, S.W.; Oblak, D.; Tittel, W. Quantum teleportation across a metropolitan fibre network. Nat. Photonics 2016, 10, 677. [Google Scholar] [CrossRef]
- Simon, C. Towards a global quantum network. Nat. Photonics 2017, 11, 678. [Google Scholar] [CrossRef]
- Xia, X.-X.; Sun, Q.-C.; Zhang, Q.; Pan, J.-W. Long distance quantum teleportation. Quantum Sci. Technol. 2018, 3, 014012. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682. [Google Scholar] [CrossRef]
- Zukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. Event-ready detectors Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef]
- Schmid, C.; Kiesel, N.; Weber, U.K.; Ursin, R.; Zeilinger, A.; Weinfurter, H. Quantum teleportation and entanglement swapping with linear optics logic gates. New J. Phys. 2009, 11, 033008. [Google Scholar] [CrossRef]
- Sangouard, N.; Simon, C.; de Riedmatten, H.; Gisin, N. Quantum repeaters based on entanglement purification. Rev. Mod. Phys. 2011, 83, 33. [Google Scholar] [CrossRef]
- Bose, S.; Vedral, V.; Knight, P.L. Multiparticle generalization of entanglement swapping. Phys. Rev. A 1998, 57, 822. [Google Scholar] [CrossRef]
- Gisin, N. Quantum-teleportation experiments turn 20. Nature 2017, 552, 42–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popescu, S. An optical method for teleportation. arXiv 1995, arXiv:quant-ph/9501020. [Google Scholar]
- Vitelli, C.; Spagnolo, N.; Aparo, L.; Sciarrino, F.; Santamato, E.; Marrucci, L. Joining the quantum state of two photons into one. Nat. Photonics 2013, 7, 521. [Google Scholar] [CrossRef]
- Passaro, E.; Vitelli, C.; Spagnolo, N.; Sciarrino, F.; Santamato, E.; Marrucci, L. Joining and splitting the quantum states of photons. Phys. Rev. A 2013, 88, 062321. [Google Scholar] [CrossRef]
- Peyronel, T.; Firstenberg, O.; Liang, Q.-Y.; Hofferberth, S.; Gorshkov, A.V.; Pohl, T.; Lukin, M.D.; Vuletic, V. Attractive photons in a quantum nonlinear medium. Nature 2012, 488, 57. [Google Scholar] [CrossRef]
- Sudbery, T. The fastest way from A to B. Nature 1997, 390, 551–552. [Google Scholar] [CrossRef]
- Pirandola, S.; and Mancini, S. Quantum Teleportation with Continuous Variables: a survey. Laser Phys. 2006, 16, 418. [Google Scholar] [CrossRef]
- Pan, J.-W.; Chen, Z.B.; Lu, C.-Y.; Weinfurter, H.; Zeilinger, A.; Zukowski, M. Multi-photon entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777. [Google Scholar] [CrossRef]
- Sciarrino, F.; Lombardi, E.; Giacomini, S.; De Martini, F. Active teleportation and entanglement swapping of a vacuum-one photon qubit. Fortschr. Phys. 2003, 51, 331–341. [Google Scholar] [CrossRef]
- Bohr, N. Albert Einstein: Philosopher-Scientist; Schlipp, P.A., Ed.; Northwestern University Press: Evanston, IL, USA, 1949. [Google Scholar]
- Tan, S.; Walls, D.; Collet, M. Nonlocality of a single photon. Phys. Rev. Lett. 1991, 66, 252. [Google Scholar] [CrossRef] [PubMed]
- Hardy, L. Nonlocality of a Single Photon Revisited. Phys. Rev. Lett. 1994, 73, 2279. [Google Scholar] [CrossRef] [PubMed]
- Knill, E.; Laflamme, R.; Milburn, G. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46. [Google Scholar] [CrossRef] [PubMed]
- Wooters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802. [Google Scholar] [CrossRef]
- Bechmann-Pasquinucci, H.; Gisin, N. Incoherent and coherent eavesdropping in the six-state protocol of quantum cryptography. Phys. Rev. A 1999, 59, 4238. [Google Scholar] [CrossRef]
- Buzek, V.; Hillery, M.; Werner, R.F. Optimal manipulations with qubits: Universal-NOT gate. Phys. Rev. A 1999, 60, 2626. [Google Scholar] [CrossRef]
- Massar, S.; Popescu, S. Optimal Extraction of Information from Finite Quantum Ensembles. Phys. Rev. Lett. 1995, 74, 1259. [Google Scholar] [CrossRef]
- Buzek, V.; Hillery, M. Quantum copying: Beyond the no-cloning theorem. Phys. Rev. A 1996, 54, 1844. [Google Scholar] [CrossRef]
- Gisin, N.; Massar, S. Optimal Quantum Cloning Machines. Phys. Rev. Lett. 1997, 79, 2153. [Google Scholar] [CrossRef]
- Buzek, V.; Hillery, M. Universal Optimal Cloning of Arbitrary Quantum States: From Qubits to Quantum Registers. Phys. Rev. Lett. 1998, 81, 5003. [Google Scholar] [CrossRef]
- Buzek, V.; Braunstein, S.L.; Hillery, M.; Bruß, D. Quantum copying: A network. Phys. Rev. A 1997, 56, 3446. [Google Scholar] [CrossRef]
- Werner, R.F. Optimal cloning of pure states. Phys. Rev. A 1998, 58, 1827. [Google Scholar] [CrossRef]
- Sciarrino, F.; Sias, C.; Ricci, M.; De Martini, F. Realization of universal optimal quantum machines by projective operators and stochastic maps. Phys. Rev. A 2004, 70, 052305. [Google Scholar] [CrossRef] [Green Version]
- Ricci, M.; Sciarrino, F.; Sias, C.; De Martini, F. Teleportation Scheme Implementing the Universal Optimal Quantum Cloning Machine and the Universal NOT Gate. Phys. Rev. Lett. 2004, 92, 047901. [Google Scholar] [CrossRef] [Green Version]
- De Martini, F.; Sciarrino, F. Colloquium: Multiparticle quantum superpositions and the quantum-to-classical transition. Rev. Mod. Phys. 2012, 84, 1766. [Google Scholar] [CrossRef]
- Ishizaka, S.; Hiroshima, T. Asymptotic Teleportation Scheme as a Universal Programmable Quantum Processor. Phys. Rev. Lett. 2008, 101, 240501. [Google Scholar] [CrossRef] [Green Version]
- Raussendorf, R.; Briegel, H.J. A One-Way Quantum Computer. Phys. Rev. Lett. 2001, 86, 5188. [Google Scholar] [CrossRef]
- Jennewein, T.; Weihs, G.; Pan, J.-W.; Zeilinger, A. Experimental nonlocality proof of quantum teleportation and entanglement swapping. Phys. Rev. Lett. 2001, 88, 017903. [Google Scholar] [CrossRef]
- Fattal, D.; Diamanti, E.; Inoue, K.; Yamamoto, Y. Quantum Teleportation with a Quantum Dot Single Photon Source. Phys. Rev. Lett. 2004, 92, 037904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takeda, S.; Mizuta, T.; Fuwa, M.; van Loock, P.; Furusawa, A. Deterministic quantum teleportation of photonic quantum bits by a hybrid technique. Nature 2013, 500, 315. [Google Scholar] [CrossRef] [PubMed]
- Metcalf, B.J.; Spring, J.B.; Humphreys, P.C.; Thomas-Peter, N.; Barbieri, M.; Kolthammer, W.S.; Jin, X.M.; Langford, N.K.; Kundys, D.; Gates, J.C.; et al. Quantum teleportation on a photonic chip. Nat. Photon. 2014, 8, 770. [Google Scholar] [CrossRef]
- Goyal, S.K.; Boukama-Dzoussi, P.E.; Ghosh, S.; Roux, F.S.; Konrad, T. Qudit-teleportation for photons with linear optics. Sci. Rep. 2014, 4, 4543. [Google Scholar] [CrossRef] [PubMed]
- Carvacho, G.; Chaves, R.; Sciarrino, F. Perspectives on experimental quantum causality. Europhys. Lett. 2019, 125, 3. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martini, F.; Sciarrino, F. Twenty Years of Quantum State Teleportation at the Sapienza University in Rome. Entropy 2019, 21, 768. https://doi.org/10.3390/e21080768
De Martini F, Sciarrino F. Twenty Years of Quantum State Teleportation at the Sapienza University in Rome. Entropy. 2019; 21(8):768. https://doi.org/10.3390/e21080768
Chicago/Turabian StyleDe Martini, Francesco, and Fabio Sciarrino. 2019. "Twenty Years of Quantum State Teleportation at the Sapienza University in Rome" Entropy 21, no. 8: 768. https://doi.org/10.3390/e21080768
APA StyleDe Martini, F., & Sciarrino, F. (2019). Twenty Years of Quantum State Teleportation at the Sapienza University in Rome. Entropy, 21(8), 768. https://doi.org/10.3390/e21080768





