Quantum Thermodynamics in the Refined Weak Coupling Limit
Abstract
1. Introduction
2. Weak Coupling and Refined Weak Coupling Limit
2.1. Weak Coupling Limit
2.2. Refined Weak Coupling Limit
2.3. Refined Weak Coupling Limit under Slowly-Varying Time-Dependent Hamiltonians
3. Standard Thermodynamics of Open Quantum Systems
3.1. The First Law
3.2. The Second Law
3.3. Difficulties Beyond the Weak Coupling Limit
4. Thermodynamics in the Refined Weak Coupling Limit
4.1. Time-Independent System Hamiltonian
- . Thus, the deviation of from at finite times is unambiguously caused by the interaction term in the Hamiltonian.
- approaches for t large. In such a case approaches Davies’ semigroup (16), and then, approaches .
4.2. Time-Dependent System Hamiltonian
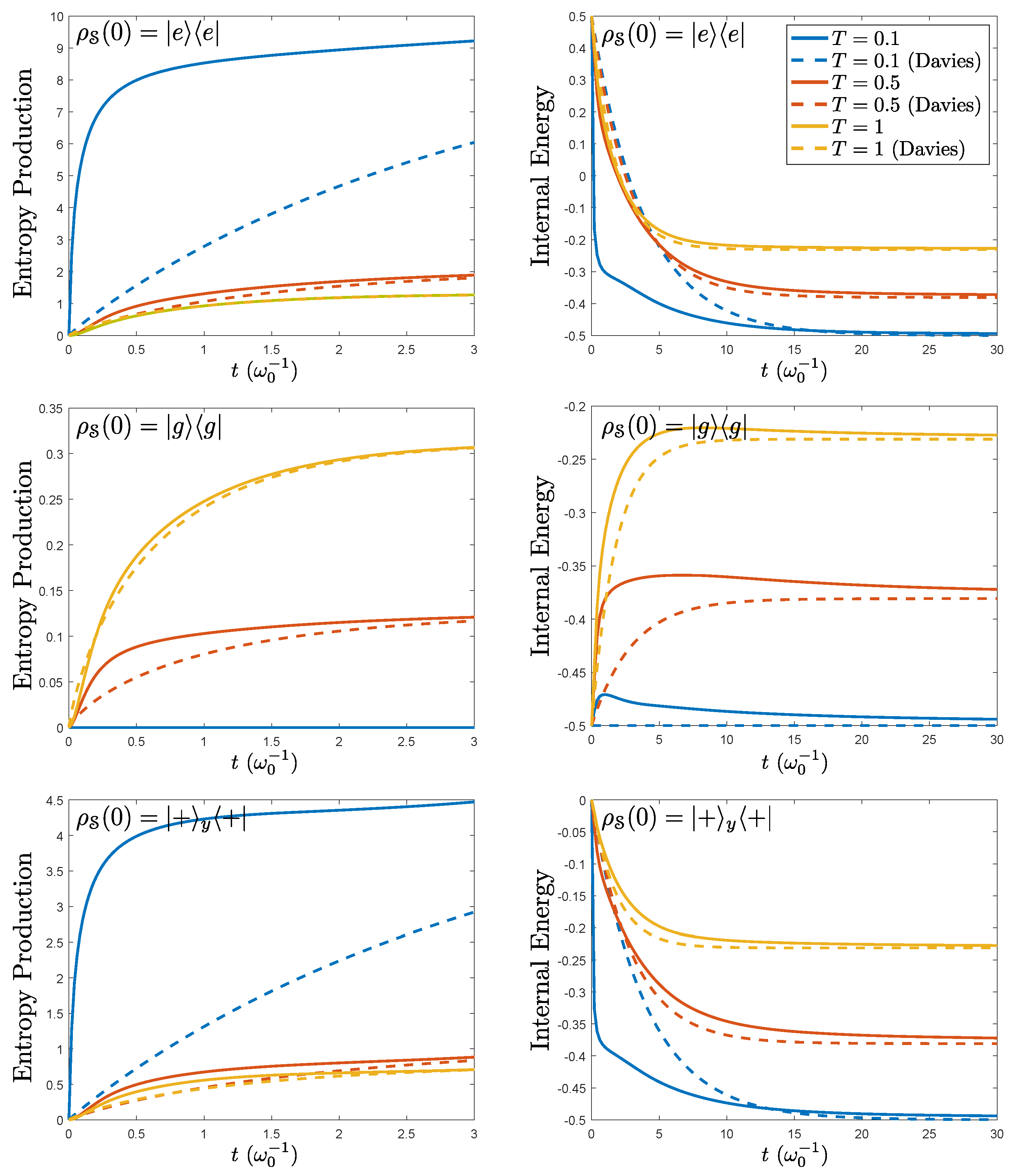
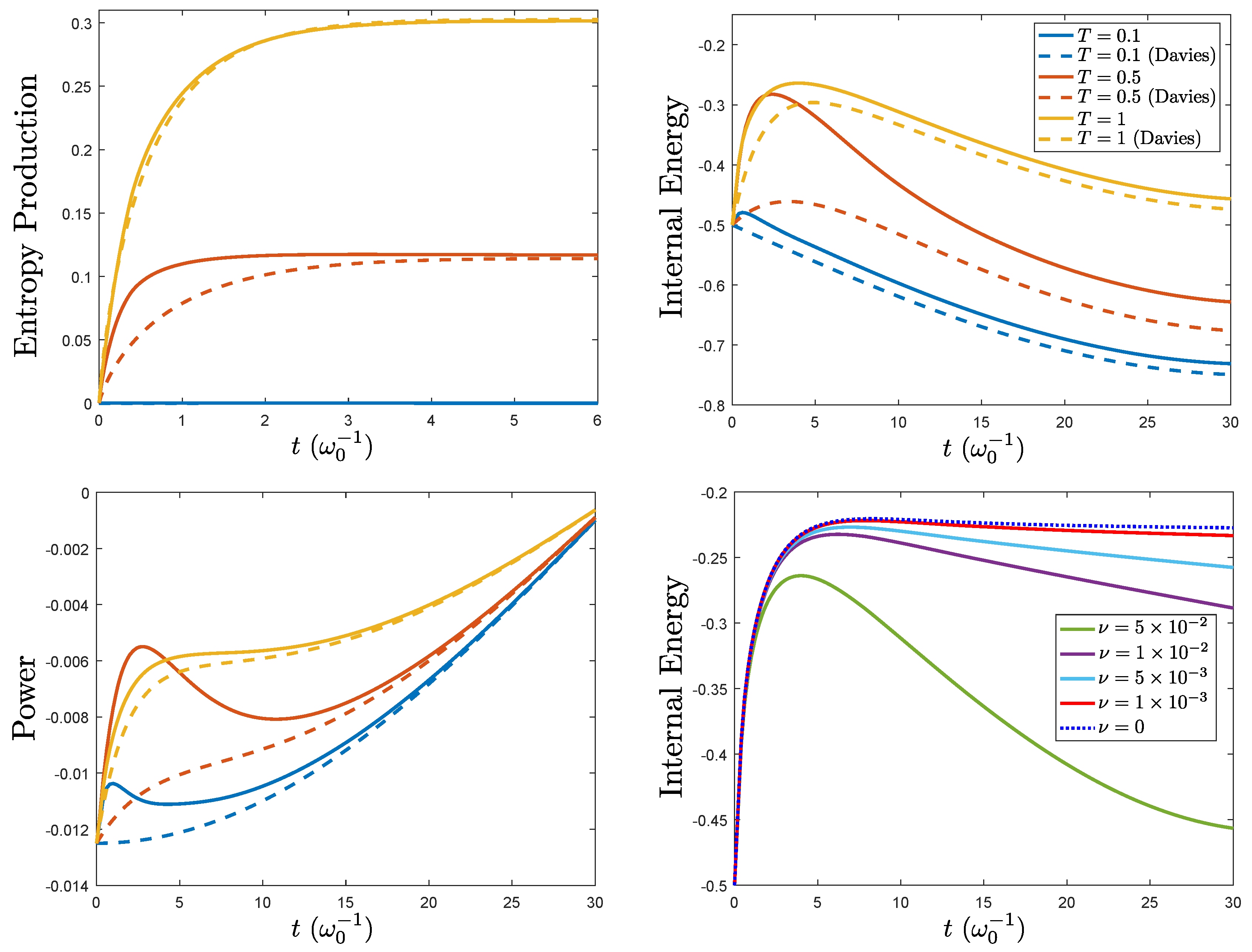
5. Example: Spin-Boson Model in the Refined Weak Coupling Limit
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Internal Energy in the Weak Coupling Limit
Appendix B. Calculation of the Time-Ordered Exponential for the Driven Spin-Boson Model in the Refined Weak Coupling
References
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Gardiner, C.W.; Zoller, P. Quantum Noise; Springer: Berlin, Germany, 2004. [Google Scholar]
- Rivas, A.; Huelga, S.F. Open Quantum Systems. An Introduction; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Gemmer, J.; Michel, M.; Mahler, G. Quantum Thermodynamics: Emergence of Thermodynamic Behavior within Composite Quantum Systems; Springer: Berlin, Germany, 2004. [Google Scholar]
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Binder, F.; Correa, L.A.; Gogolin, C.; Anders, J.; Adesso, G. (Eds.) Thermodynamics in the Quantum Regime; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Davies, E.B. Markovian Master Equations. Commun. Math. Phys. 1974, 39, 91–110. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Chruściński, D.; Pascazio, S. A Brief History of the GKLS Equation. Open Syst. Inf. Dyn. 2017, 24, 1740001. [Google Scholar] [CrossRef]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Springer: Berlin, Germany, 1987. [Google Scholar]
- Spohn, H. Entropy production for quantum dynamical semigroups. J. Math. Phys. 1978, 19, 1227–1230. [Google Scholar] [CrossRef]
- Spohn, H.; Lebowitz, J. Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 1979, 38, 109–142. [Google Scholar]
- Alicki, R. Quantum open systems as a model of a heat engine. J. Phys A Math. Gen. 1979, 12, L103–L107. [Google Scholar] [CrossRef]
- Alicki, R.; Gelbwaser-Klimovsky, D.; Kurizki, G. Periodically driven quantum open systems: Tutorial. arXiv 2012, arXiv:1205.4552. [Google Scholar]
- Esposito, M.; Lindberg, K.; van den Broek, C. Entropy production as correlation between system and reservoir. New J. Phys. 2010, 12, 013013. [Google Scholar] [CrossRef]
- Binder, F.C.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantum thermodynamics of general quantum processes. Phys. Rev. E 2015, 91, 032119. [Google Scholar] [CrossRef] [PubMed]
- Kato, A.; Tanimura, Y. Quantum heat current under non-perturbative and non-Markovian conditions: Applications to heat machines. J. Chem. Phys. 2016, 145, 224105. [Google Scholar] [CrossRef] [PubMed]
- Alipour, S.; Benatti, F.; Bakhshinezhad, F.; Afsary, M.; Marcantoni, S.; Rezakhani, A.T. Correlations in quantum thermodynamics. Sci. Rep. 2016, 6, 35568. [Google Scholar] [CrossRef] [PubMed]
- Marcantoni, S.; Alipour, S.; Benatti, F.; Floreanini, R.; Rezakhani, A.T. Entropy production and non-Markovian dynamical maps. Sci. Rep. 2017, 7, 12447. [Google Scholar] [CrossRef] [PubMed]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A Unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Misra, A.; Mukhopadhyay, C.; Pati, A.K. Exact master equation for a spin interacting with a spin bath: Non-Markovianity and negative entropy production rate. Phys. Rev. A 2017, 95, 012122. [Google Scholar] [CrossRef]
- Thomas, G.; Siddharth, H.; Banerjee, S.; Ghosh, S. Thermodynamics of non-Markovian reservoirs and heat engines. Phys. Rev. E 2018, 97, 062108. [Google Scholar] [CrossRef] [PubMed]
- Strasberg, P.; Esposito, M. Non-Markovianity and negative entropy production rates. Phys. Rev. E 2019, 99, 012120. [Google Scholar] [CrossRef]
- Gelin, M.F.; Thoss, M. Thermodynamics of a subensemble of a canonical ensemble. Phys. Rev. E 2009, 79, 051121. [Google Scholar] [CrossRef]
- Seifert, U. First and second law of thermodynamics at strong coupling. Phys. Rev. Lett. 2016, 116, 020601. [Google Scholar] [CrossRef]
- Hsiang, J.-T.; Hu, B.-L. Quantum Thermodynamics at Strong Coupling: Operator Thermodynamic Functions and Relations. Entropy 2018, 20, 423. [Google Scholar] [CrossRef]
- Alicki, R. Master equations for a damped nonlinear oscillator and the validity of the Markovian approximation. Phys. Rev. A 1989, 40, 4077. [Google Scholar] [CrossRef]
- Schaller, G.; Brandes, T. Preservation of positivity by dynamical coarse graining. Phys. Rev. A 2008, 78, 022106. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Marzolino, U. Environment induced entanglement in a refined weak-coupling limit. EPL 2009, 88, 20011. [Google Scholar] [CrossRef]
- Rivas, A. Refined weak-coupling limit: Coherence, entanglement, and non-Markovianity. Phys. Rev. A 2017, 95, 042104. [Google Scholar] [CrossRef]
- Merkli, M.; Könenberg, M. Completely positive dynamical semigroups and quantum resonance theory. Lett. Math. Phys. 2017, 107, 1215–1233. [Google Scholar]
- Davies, E.B.; Spohn, H. Open quantum systems with time-dependent Hamiltonians and their linear response. J. Stat. Phys. 1978, 19, 511–523. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Piani, M. Nonpositive evolutions in open system dynamics. Phys. Rev. A 2003, 67, 042110. [Google Scholar] [CrossRef]
- Benatti, F.; Floreanini, R.; Breteaux, S. Slipped nonpositive reduced dynamics and entanglement. Laser Phys. 2006, 16, 1395. [Google Scholar] [CrossRef]
- Anderloni, S.; Benatti, F.; Floreanini, R. Redfield reduced dynamics and entanglement. J. Phys. A Math. Theor. 2007, 40, 1625. [Google Scholar] [CrossRef]
- Schaller, G.; Zedler, P.; Brandes, T. Systematic perturbation theory for dynamical coarse-graining. Phys. Rev. A 2009, 79, 032110. [Google Scholar] [CrossRef]
- Snider, R.F. Perturbation Variation Methods for a Quantum Boltzmann Equation. J. Math. Phys. 1964, 5, 1580–1587. [Google Scholar] [CrossRef]
- Wilcox, R.M. Exponential Operators and Parameter Differentiation in Quantum Physics. J. Math. Phys. 1967, 8, 962–982. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Spohn, H. An algebraic condition for the approach to equilibrium of an open N-level system. Lett. Math. Phys. 1977, 2, 33–38. [Google Scholar] [CrossRef]
- Wolf, M. Quantum Channels & Operations: Guided Tour. 2012. Available online: https://www-m5.ma.tum.de/foswiki/pub/M5/Allgemeines/MichaelWolf/QChannelLecture.pdf (accessed on 25 July 2019).
- Lindblad, G. Completely positive maps and entropy inequalities. Commun. Math. Phys. 1975, 40, 147–151. [Google Scholar] [CrossRef]
- Uhlmann, A. Relative entropy and the Wigner-Yanase-Dyson-Lieb concavity in an interpolation theory. Commun. Math. Phys. 1977, 54, 21–32. [Google Scholar] [CrossRef]
- Müller-Hermes, A.; Reeb, D. Monotonicity of the Quantum Relative Entropy Under Positive Maps. Ann. Henri Poincaré 2017, 18, 1777–1788. [Google Scholar] [CrossRef]
- Das, S.; Khatri, S.; Siopsis, G.; Wilde, M.M. Fundamental limits on quantum dynamics based on entropy change. J. Math. Phys. 2018, 59, 012205. [Google Scholar] [CrossRef]
- Rivas, A.; Plato, A.D.K.; Huelga, S.F.; Plenio, M.B. Markovian master equations: A critical study. New J. Phys. 2010, 12, 113032. [Google Scholar] [CrossRef]
- Puri, R.R. Mathematical Methods of Quantum Optics; Springer: Berlin, Germany, 2001. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivas, Á. Quantum Thermodynamics in the Refined Weak Coupling Limit. Entropy 2019, 21, 725. https://doi.org/10.3390/e21080725
Rivas Á. Quantum Thermodynamics in the Refined Weak Coupling Limit. Entropy. 2019; 21(8):725. https://doi.org/10.3390/e21080725
Chicago/Turabian StyleRivas, Ángel. 2019. "Quantum Thermodynamics in the Refined Weak Coupling Limit" Entropy 21, no. 8: 725. https://doi.org/10.3390/e21080725
APA StyleRivas, Á. (2019). Quantum Thermodynamics in the Refined Weak Coupling Limit. Entropy, 21(8), 725. https://doi.org/10.3390/e21080725




