Empirical Estimation of Information Measures: A Literature Guide
Abstract
1. Introduction
- Entropy: of a probability mass function P on a discrete set :
- Relative Entropy: of a pair of probability measures defined on the same measurable space (P and Q are known as the dominated and reference probability measures, respectively; indicates , for any event B):
- Mutual Information: of a joint probability measure :which specializes to in the discrete case.
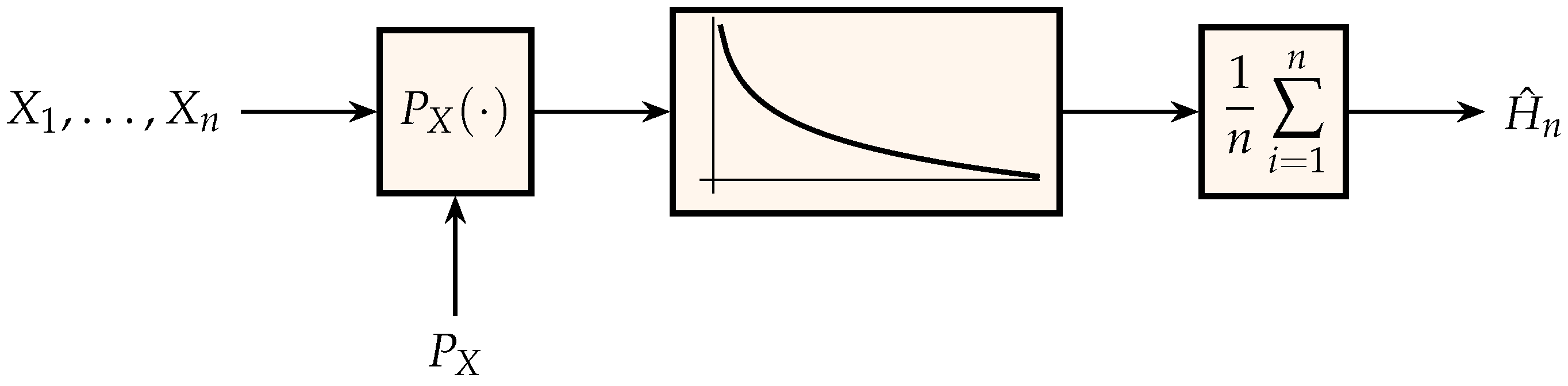
2. Entropy: Memoryless Sources
3. Entropy: Sources with Memory
4. Differential Entropy: Memoryless Sources
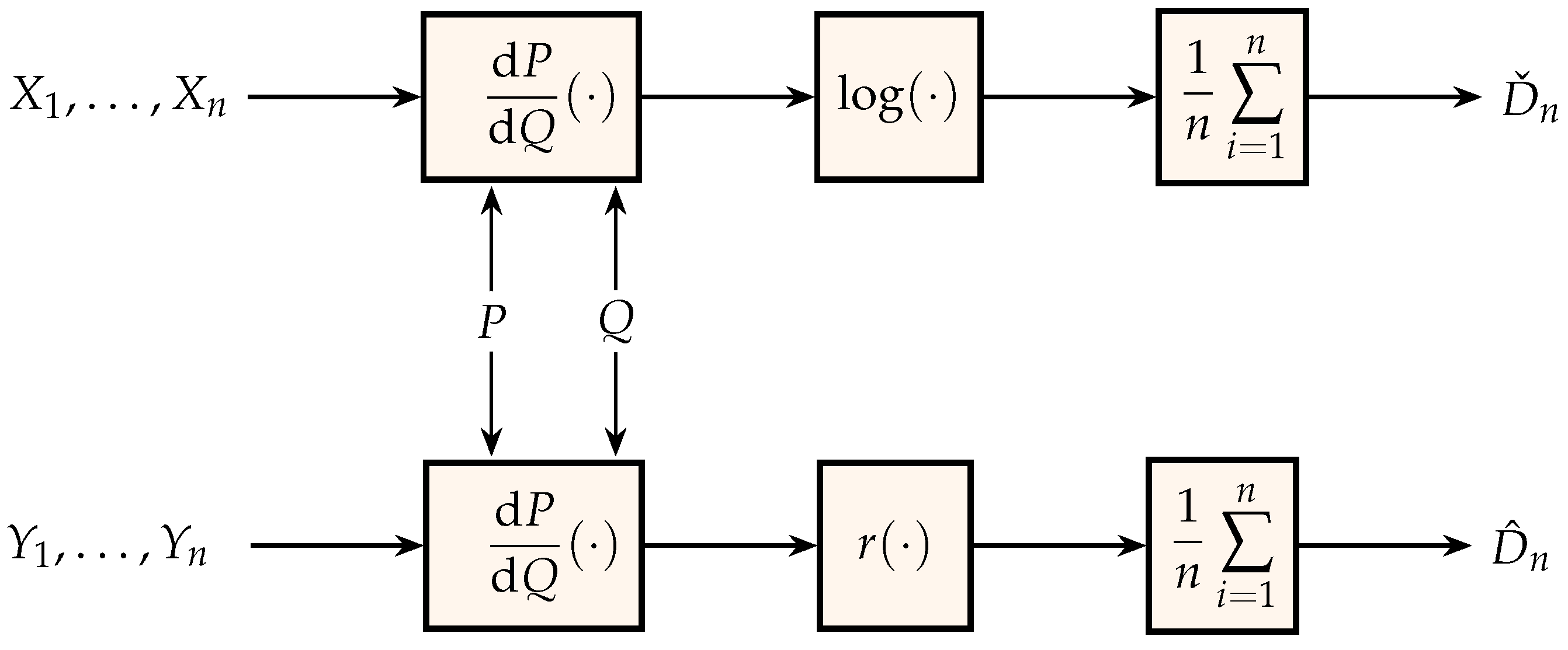
5. Relative Entropy: Memoryless Sources
- Finite alphabet. In the discrete case, we can base a relative entropy estimator on the decompositionwith . Therefore, once an empirical estimator of entropy is available, the task is to design an algorithm for estimating the cross term. To that end, it is beneficial to regularize the probability estimate for those symbols that are infrequent under the reference measure. Various regularization and bias-reduction strategies are proposed in [99,100], leading to consistent estimators.In the memoryless case, several of the algorithms reviewed in Section 2 for entropy estimation (e.g., [40,47]) find natural generalizations for the estimation of relative entropy. As for entropy estimation, the straightforward ratio of empirical counts can be used in the plug-in approach if is negligible with respect to the number of observations. Otherwise, sample complexity can be lowered by a logarithmic factor by distorting the plug-in function; an estimator is proposed in [101], which is optimal in the minimax mean-square sense when the likelihood ratio is upper bounded by a constant that may depend on , although the algorithm can operate without prior knowledge of either the upper bound or . Another nice feature of that algorithm is that it can be modified to estimate other distance measures such as -divergence and Hellinger distance. The asymptotic (in the alphabet size) minimax mean-square error is analyzed in [102] (see also [101]) when the likelihood ratio is bounded by a function of the alphabet size, and the number of observations is also allowed to grow with .
- Continuous alphabet. By the relative entropy data processing theorem,where , and is arbitrary. If is injective, then the equality in Equation (18) holds. If we choose to be a finite set, then an empirical estimate of the lower bound in Equation (18) can be obtained using one of the methods to estimate the relative entropy for finite alphabets. It is to be expected that keeping the number of bins small results in lower complexity and coarser bounds; on the other hand, allowing to grow too large incurs in unreliable estimates for the probabilities of infrequent values of . Of course, for a given , the slackness in Equation (18) will depend on the choice of . An interesting option propounded in [103] is to let be such that is independent of , in which caseNaturally, we cannot instrument such a function since we do not know , but we can get a fairly good approximation by letting depend on the observations obtained under the reference measure, such that each bin contains the same number of samples. Various strongly consistent algorithms based on data-dependent partitions are proposed in [79,103].For multidimensional densities, relative entropy estimation via k-nearest-neighbor distances [104] is more attractive than the data-dependent partition methods. This has been extended to the estimation of Rényi divergence in [105]. Earlier, Hero et al. [106] considered the estimation of Rényi divergence when one of the measures is known, using minimum spanning trees.As shown in [107], it is possible to design consistent empirical relative entropy estimators based on non-consistent density estimates.The empirical estimation of the minimum relative entropy between the unknown probability measure that generates an observed independent sequence and a given exponential family is considered in [108] with a local likelihood modeling algorithm.M-estimators for the empirical estimation of f-divergence (according to Equation (16), r-divergence with in Equation (15) is the relative entropy)where f is a convex function with are proposed in [109] using the Fenchel–Lagrange dual variational representation of [110]. A k-nearest neighbor estimator of is proposed and analyzed in [111].A recent open-source toolbox for the empirical estimation of relative entropy (as well as many other information measures) for analog random variables can be found in [112]. Software estimating mutual information in independent component analysis can be found in [113]. Experimental results contrasting various methods can be found in [114].
6. Relative Entropy: Discrete Sources with Memory
7. Mutual Information: Memoryless Sources
Funding
Acknowledgments
Conflicts of Interest
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Johnson, J.B.; Omland, K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Maasoumi, E. A compendium to information theory in economics and econometrics. Econom. Rev. 1993, 12, 137–181. [Google Scholar] [CrossRef]
- Sims, C.A. Implications of rational inattention. J. Monet. Econ. 2003, 50, 665–690. [Google Scholar] [CrossRef]
- MacLean, L.C.; Thorp, E.O.; Ziemba, W.T. The Kelly Capital Growth Investment Criterion: Theory and Practice; World Scientific: Singapore, 2011; Volume 3. [Google Scholar]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 47–51. [Google Scholar] [CrossRef]
- Chomsky, N. Three models for the description of language. IEEE Trans. Inf. Theory 1956, 2, 113–124. [Google Scholar] [CrossRef]
- Nowak, M.A.; Komarova, N.L. Towards an evolutionary theory of language. Trends Cognit. Sci. 2001, 5, 288–295. [Google Scholar] [CrossRef]
- Benedetto, D.; Caglioti, E.; Loreto, V. Language trees and zipping. Phys. Rev. Lett. 2002, 88, 048702. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, S.R.; Lugosi, G.; Venkatesh, S. A Survey of Statistical Pattern Recognition and Learning Theory. IEEE Trans. Inf. Theory 1998, 44, 2178–2206. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Andrzejak, R.G.; Grassberger, P. Hierarchical clustering using mutual information. Europhys. Lett. 2005, 70, 278. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Yockey, H.P. Information Theory and Molecular Biology; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Frieden, B.R. Information theory in living systems, methods, applications, and challenges. Bull. Math. Biol. 2007, 69, 635–657. [Google Scholar] [CrossRef] [PubMed]
- Rieke, F.; Warland, D.; de Ruyter van Steveninck, R.; Bialek, W. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Bialek, W. Biophysics: Searching for Principles; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Borst, A.; Theunissen, F.E. Information theory and neural coding. Nat. Neurosci. 1999, 2, 947. [Google Scholar] [CrossRef] [PubMed]
- Nemenman, I.; Bialek, W.; van Steveninck, R.d.R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef] [PubMed]
- LaBerge, D. Attentional Processing: The Brain’s Art of Mindfulness; Harvard University Press: Cambridge, MA, USA, 1995; Volume 2. [Google Scholar]
- Laming, D. Statistical information, uncertainty, and Bayes’ theorem: Some applications in experimental psychology. In European Conference on Symbolic and Quantitative Approaches to Reasoning and Uncertainty; Benferhat, S., Besnard, P., Eds.; Springer: Berlin, Germany, 2001; pp. 635–646. [Google Scholar]
- Basseville, M. Distance measures for signal processing and pattern recognition. Signal Process. 1989, 18, 349–369. [Google Scholar] [CrossRef]
- Kullback, S. An application of information theory to multivariate analysis. Ann. Math. Stat. 1952, 23, 88–102. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover: New York, NY, USA, 1968; Originally published in 1959 by John Wiley. [Google Scholar]
- Barron, A.R.; Rissanen, J.; Yu, B. The minimum description length principle in coding and modeling. IEEE Trans. Inf. Theory 1998, 44, 2743–2760. [Google Scholar] [CrossRef]
- Csiszár, I.; Shields, P.C. Information Theory and Statistics: A Tutorial. Found. Trends Commun. Inf. Theory 2004, 1, 417–528. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Verdú, S.; Weissman, T. The information lost in erasures. IEEE Trans. Inf. Theory 2008, 54, 5030–5058. [Google Scholar] [CrossRef]
- Vajda, I. Theory of Statistical Inference and Information; Kluwer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Massey, J.L. Causality, feedback and directed information. In Proceedings of the 1990 International Symposium Information Theory and Applications, Waikiki, HI, USA, 27–30 November 1990; pp. 303–305. [Google Scholar]
- Palomar, D.P.; Verdú, S. Lautum Information. IEEE Trans. Inf. Theory 2008, 54, 964–975. [Google Scholar] [CrossRef]
- Miller, G.; Madow, W. On the Maximum Likelihood Estimate of the Shannon-Wiener Measure of Information; Operational Applications Laboratory, Air Force Cambridge Research Center, Air Research and Development Command, Bolling Air Force Base: Montgomery County, OH, USA, 1954. [Google Scholar]
- Miller, G. Note on the bias of information estimates. Inf. Theory Psychol. II. B Probl. Methods 1955, 95–100. [Google Scholar]
- Carlton, A. On the bias of information estimates. Psychol. Bull. 1969, 71, 108. [Google Scholar] [CrossRef]
- Grassberger, P. Finite sample corrections to entropy and dimension estimates. Phys. Lett. A 1988, 128, 369–373. [Google Scholar] [CrossRef]
- Strong, S.P.; Koberle, R.; van Steveninck, R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197. [Google Scholar] [CrossRef]
- Hausser, J.; Strimmer, K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Minimax estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2015, 61, 2835–2885. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, P. Minimax rates of entropy estimation on large alphabets via best polynomial approximation. IEEE Trans. Inf. Theory 2016, 62, 3702–3719. [Google Scholar] [CrossRef]
- Han, Y.; Jiao, J.; Weissman, T. Adaptive estimation of Shannon entropy. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 1372–1376. [Google Scholar]
- Dobrushin, R.L. A simplified method of experimentally evaluating the entropy of a stationary sequence. Theory Probab. Appl. 1958, 3, 428–430. [Google Scholar] [CrossRef]
- Yi, H.; Orlitsky, A.; Suresh, A.T.; Wu, Y. Data Amplification: A Unified and Competitive Approach to Property Estimation. Adv. Neural Inf. Process. Syst. 2018, 8834–8843. [Google Scholar]
- Hao, Y.; Orlitsky, A. Data Amplification: Instance-Optimal Property Estimation. arXiv 2019, arXiv:1903.01432. [Google Scholar]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Maximum likelihood estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2017, 63, 6774–6798. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. The power of linear estimators. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science (FOCS), Palm Springs, CA, USA, 22–25 October 2011; pp. 403–412. [Google Scholar]
- Valiant, P.; Valiant, G. Estimating the unseen: Improved estimators for entropy and other properties. Adv. Neural Inf. Process. Syst. 2013, 2157–2165. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. A CLT and tight lower bounds for estimating entropy. Electron. Colloq. Computat. Complex. (ECCC) 2010, 17, 9. [Google Scholar]
- Han, Y.; Jiao, J.; Weissman, T. Local moment matching: A unified methodology for symmetric functional estimation and distribution estimation under Wasserstein distance. arXiv 2018, arXiv:1802.08405. [Google Scholar]
- Acharya, J.; Das, H.; Orlitsky, A.; Suresh, A.T. A unified maximum likelihood approach for estimating symmetric properties of discrete distributions. Int. Conf. Mach. Learn. 2017, 70, 11–21. [Google Scholar]
- Pavlichin, D.S.; Jiao, J.; Weissman, T. Approximate profile maximum likelihood. arXiv 2017, arXiv:1712.07177. [Google Scholar]
- Vatedka, S.; Vontobel, P.O. Pattern maximum likelihood estimation of finite-state discrete-time Markov chains. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 2094–2098. [Google Scholar]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841. [Google Scholar] [CrossRef]
- Keziou, A. Sur l’estimation de l’entropie des lois ą support dénombrable. Comptes Rendus Math. 2002, 335, 763–766. [Google Scholar] [CrossRef]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Cover, T.M.; King, R.C. A Convergent gambling estimate of the entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Jiao, J.; Han, Y.; Fischer-Hwang, I.; Weissman, T. Estimating the fundamental limits is easier than achieving the fundamental limits. arXiv 2017, arXiv:1707.01203. [Google Scholar] [CrossRef]
- Tatwawadi, K.S.; Jiao, J.; Weissman, T. Minimax redundancy for Markov chains with large state space. arXiv 2018, arXiv:1805.01355. [Google Scholar]
- Han, Y.; Jiao, J.; Lee, C.Z.; Weissman, T.; Wu, Y.; Yu, T. Entropy Rate Estimation for Markov Chains with Large State Space. arXiv 2018, arXiv:1802.07889. [Google Scholar]
- Kamath, S.; Verdú, S. Estimation of Entropy rate and Rényi entropy rate for Markov chains. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 685–689. [Google Scholar]
- Kaltchenko, A.; Timofeeva, N. Entropy estimators with almost sure convergence and an o(n−1) variance. Adv. Math. Commun. 2008, 2, 1–13. [Google Scholar]
- Kaltchenko, A.; Timofeeva, N. Rate of convergence of the nearest neighbor entropy estimator. AEU-Int. J. Electron. Commun. 2010, 64, 75–79. [Google Scholar] [CrossRef]
- Timofeev, E.A.; Kaltchenko, A. Fast algorithm for entropy estimation. In Proceedings of the SPIE 8750, Independent Component Analyses, Compressive Sampling, Wavelets, Neural Net, Biosystems, and Nanoengineering XI, Baltimore, MA, USA, 28 April–3 May 2013. [Google Scholar]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Grassberger, P. Estimating the information content of symbol sequences and efficient codes. IEEE Trans. Inf. Theory 1989, 35, 669–675. [Google Scholar] [CrossRef]
- Wyner, A.D.; Ziv, J. Some asymptotic properties of the entropy of a stationary ergodic data source with applications to data compression. IEEE Trans. Inf. Theory 1989, 35, 1250–1258. [Google Scholar] [CrossRef]
- Ornstein, D.S.; Weiss, B. Entropy and data compression schemes. IEEE Trans. Inf. Theory 1993, 39, 78–83. [Google Scholar] [CrossRef]
- Shields, P.C. Entropy and prefixes. Ann. Probab. 1992, 20, 403–409. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Suhov, Y.M. Prefixes and the entropy rate for long-range sources. In Probability Statistics and Optimization: A Tribute to Peter Whittle; Kelly, F.P., Ed.; Wiley: New York, NY, USA, 1994; pp. 89–98. [Google Scholar]
- Kontoyiannis, I.; Algoet, P.; Suhov, Y.; Wyner, A.J. Nonparametric entropy estimation for stationary processes and random fields, with applications to English text. IEEE Trans. Inf. Theory 1998, 44, 1319–1327. [Google Scholar] [CrossRef]
- Gao, Y.; Kontoyiannis, I.; Bienenstock, E. Estimating the entropy of binary time series: Methodology, some theory and a simulation study. Entropy 2008, 10, 71–99. [Google Scholar] [CrossRef]
- Cai, H.; Kulkarni, S.R.; Verdú, S. Universal entropy estimation via block sorting. IEEE Trans. Inf. Theory 2004, 50, 1551–1561. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.M.; Tjalkens, T.J. The context-tree weighting method: Basic properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef]
- Cleary, J.G.; Witten, I.H. Data compression using adaptive coding and partial string matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]
- Yu, J.; Verdú, S. Universal estimation of erasure entropy. IEEE Trans. Inf. Theory 2009, 55, 350–357. [Google Scholar] [CrossRef][Green Version]
- Wiener, N. Cybernetics, Chapter III: Time Series, Information and Communication; Wiley: New York, NY, USA, 1948. [Google Scholar]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Universal estimation of information measures for analog sources. Found. Trends Commun. Inf. Theory 2009, 5, 265–353. [Google Scholar] [CrossRef]
- Ahmad, I.; Lin, P.E. A nonparametric estimation of the entropy for absolutely continuous distributions. IEEE Trans. Inf. Theory 1976, 22, 372–375. [Google Scholar] [CrossRef]
- Györfi, L.; Van der Meulen, E.C. Density-free convergence properties of various estimators of entropy. Comput. Stat. Data Anal. 1987, 5, 425–436. [Google Scholar] [CrossRef]
- Joe, H. Estimation of entropy and other functionals of a multivariate density. Ann. Inst. Stat. Math. 1989, 41, 683–697. [Google Scholar] [CrossRef]
- Hall, P.; Morton, S. On the estimation of entropy. Ann. Inst. Stat. Math. Mar. 1993, 45, 69–88. [Google Scholar] [CrossRef]
- Godavarti, M.; Hero, A. Convergence of differential entropies. IEEE Trans. Inf. Theory 2004, 50, 171–176. [Google Scholar] [CrossRef]
- Kozachenko, L.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Pereda. Inf. 1987, 23, 9–16. [Google Scholar]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; Van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stat. Sci. 1997, 6, 17–39. [Google Scholar]
- Han, Y.; Jiao, J.; Weissman, T.; Wu, Y. Optimal rates of entropy estimation over Lipschitz balls. arXiv 2017, arXiv:1711.02141. [Google Scholar]
- Tsybakov, A.B.; Van der Meulen, E. Root-n consistent estimators of entropy for densities with unbounded support. Scand. J. Stat. 1996, 23, 75–83. [Google Scholar]
- Hall, P. On powerful distributional tests based on sample spacings. J. Multivar. Anal. 1986, 19, 201–224. [Google Scholar] [CrossRef]
- El Haje Hussein, F.; Golubev, Y. On entropy estimation by m-spacing method. J. Math. Sci. 2009, 163, 290–309. [Google Scholar] [CrossRef]
- Sricharan, K.; Wei, D.; Hero, A.O., III. Ensemble estimators for multivariate entropy estimation. IEEE Trans. Inf. Theory 2013, 59, 4374–4388. [Google Scholar] [CrossRef] [PubMed]
- Berrett, T.B. Modern k-Nearest Neighbour Methods in Entropy Estimation, Independence Testing and Classification. PhD Thesis, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Berrett, T.B.; Samworth, R.J.; Yuan, M. Efficient multivariate entropy estimation via k-nearest neighbour distances. arXiv 2016, arXiv:1606.00304. [Google Scholar] [CrossRef]
- Delattre, S.; Fournier, N. On the Kozachenko–Leonenko entropy estimator. J. Stat. Plan. Inference 2017, 185, 69–93. [Google Scholar] [CrossRef][Green Version]
- Jiao, J.; Gao, W.; Han, Y. The nearest neighbor information estimator is adaptively near minimax rate-optimal. arXiv 2017, arXiv:1711.08824. [Google Scholar]
- Birgé, L.; Massart, P. Estimation of integral functionals of a density. Ann. Stat. 1995, 23, 11–29. [Google Scholar] [CrossRef]
- Adams, T.M.; Nobel, A.B. On density estimation from ergodic processes. Ann. Probab. 1998, 26, 794–804. [Google Scholar]
- Sugiyama, M.; Suzuki, T.; Kanamori, T. Density Ratio Estimation in Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Cai, H.; Kulkarni, S.R.; Verdú, S. Universal divergence estimation for finite-alphabet sources. IEEE Trans. Inf. Theory 2006, 52, 3456–3475. [Google Scholar] [CrossRef]
- Zhang, Z.; Grabchak, M. Nonparametric estimation of Kullback-Leibler divergence. Neural Comput. 2014, 26, 2570–2593. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Jiao, J.; Weissman, T. Minimax Rate-Optimal Estimation of Divergences between Discrete Distributions. arXiv 2016, arXiv:1605.09124. [Google Scholar]
- Bu, Y.; Zou, S.; Liang, Y.; Veeravalli, V.V. Estimation of KL divergence: Optimal minimax rate. IEEE Trans. Inf. Theory 2018, 64, 2648–2674. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation of continuous distributions based on data-dependent partitions. IEEE Trans. Inf. Theory 2005, 51, 3064–3074. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k-nearest-neighbor distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Póczos, B.; Schneider, J. On the estimation of alpha-divergences. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Lauderdale, FL, USA, 11–13 April 2011; pp. 609–617. [Google Scholar]
- Hero, A.O.; Ma, B.; Michel, O.J.; Gorman, J. Applications of entropic spanning graphs. IEEE Signal Process. Mag. 2002, 19, 85–95. [Google Scholar] [CrossRef]
- Pérez-Cruz, F. Kullback-Leibler divergence estimation of continuous distributions. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1666–1670. [Google Scholar]
- Lee, Y.K.; Park, B.U. Estimation of Kullback–Leibler divergence by local likelihood. Ann. Inst. Stat. Math. 2006, 58, 327–340. [Google Scholar] [CrossRef]
- Nguyen, X.; Wainwright, M.J.; Jordan, M.I. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Trans. Inf. Theory 2010, 56, 5847–5861. [Google Scholar] [CrossRef]
- Keziou, A. Dual representation of φ-divergences and applications. Comptes Rendus Math. 2003, 336, 857–862. [Google Scholar] [CrossRef]
- Moon, K.; Hero, A. Multivariate f-divergence estimation with confidence. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2420–2428. [Google Scholar]
- Szabó, Z. Information theoretical estimators toolbox. J. Mach. Learn. Res. 2014, 15, 283–287. [Google Scholar]
- Stoegbauer, H. MILCA and SNICA. Available online: http://bsp.teithe.gr/members/downloads/Milca.html (accessed on 16 May 2019).
- Budka, M.; Gabrys, B.; Musial, K. On accuracy of PDF divergence estimators and their applicability to representative data sampling. Entropy 2011, 13, 1229–1266. [Google Scholar] [CrossRef]
- Pereira Coutinho, D.; Figueiredo, M.A.T. Information Theoretic Text Classification Using the Ziv-Merhav Method. In Pattern Recognition and Image Analysis; Marques, J.S., Pérez de la Blanca, N., Pina, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 355–362. [Google Scholar]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitányi, P.M. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Vitányi, P.M.; Balbach, F.J.; Cilibrasi, R.L.; Li, M. Normalized information distance. In Information Theory and Statistical Learning; Springer: Berlin, Germay, 2009; pp. 45–82. [Google Scholar]
- Kaltchenko, A. Algorithms for estimating information distance with application to bioinformatics and linguistics. In Proceedings of the 2004 IEEE Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 2–5 May 2004; Volume 4, pp. 2255–2258. [Google Scholar]
- Brillinger, D.R. Some data analyses using mutual information. Braz. J. Probab. Stat. 2004, 18, 163–182. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Kannan, S.; Oh, S.; Viswanath, P. Estimating mutual information for discrete-continuous mixtures. In Proceedings of the Thirty-first Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 14–17 December 2017; pp. 5986–5997. [Google Scholar]
- Bulinski, A.; Kozhevin, A. Statistical Estimation of Conditional Shannon Entropy. arXiv 2018, arXiv:1804.08741. [Google Scholar] [CrossRef]
- Joe, H. Relative entropy measures of multivariate dependence. J. Am. Stat. Assoc. 1989, 84, 171–176. [Google Scholar] [CrossRef]
- Moon, Y.I.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318. [Google Scholar] [CrossRef]
- Moddemeijer, R. On estimation of entropy and mutual information of continuous distributions. Signal Process. 1989, 16, 233–248. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Vajda, I. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 1315–1321. [Google Scholar] [CrossRef]
- Slonim, N.; Atwal, G.S.; Tkačik, G.; Bialek, W. Information-based clustering. Proc. Natl. Acad. Sci. USA 2005, 102, 18297–18302. [Google Scholar] [CrossRef]
- Victor, J.D. Binless strategies for estimation of information from neural data. Phys. Rev. E 2002, 66, 051903. [Google Scholar] [CrossRef]
- Jiao, J.; Permuter, H.H.; Zhao, L.; Kim, Y.H.; Weissman, T. Universal estimation of directed information. IEEE Trans. Inf. Theory 2013, 59, 6220–6242. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Skoularidou, M. Estimating the directed information and testing for causality. IEEE Trans. Inf. Theory 2016, 62, 6053–6067. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verdú, S. Empirical Estimation of Information Measures: A Literature Guide. Entropy 2019, 21, 720. https://doi.org/10.3390/e21080720
Verdú S. Empirical Estimation of Information Measures: A Literature Guide. Entropy. 2019; 21(8):720. https://doi.org/10.3390/e21080720
Chicago/Turabian StyleVerdú, Sergio. 2019. "Empirical Estimation of Information Measures: A Literature Guide" Entropy 21, no. 8: 720. https://doi.org/10.3390/e21080720
APA StyleVerdú, S. (2019). Empirical Estimation of Information Measures: A Literature Guide. Entropy, 21(8), 720. https://doi.org/10.3390/e21080720



