Abstract
We give a brief survey of the literature on the empirical estimation of entropy, differential entropy, relative entropy, mutual information and related information measures. While those quantities are of central importance in information theory, universal algorithms for their estimation are increasingly important in data science, machine learning, biology, neuroscience, economics, language, and other experimental sciences.
1. Introduction
The edifice of information theory is built upon the foundation of three major information measures (e.g., [1]):
- Entropy: of a probability mass function P on a discrete set :
- Relative Entropy: of a pair of probability measures defined on the same measurable space (P and Q are known as the dominated and reference probability measures, respectively; indicates , for any event B):
- Mutual Information: of a joint probability measure :which specializes to in the discrete case.
Using bits, or other information units, those nonnegative measures gauge the randomness of P (entropy); the dissimilarity between P and Q (relative entropy); and the statistical dependence of X and Y (mutual information). They attain their minimum value, zero, if and only if P is deterministic, , and X and Y are independent, respectively.
We would not be far off the mark if we were to define information theory as the study of the properties of those information measures, in particular, as they pertain to their role in the fundamental limits of various operational engineering problems such as the compression and transmission of data.
Often, when dealing with random processes with memory, the role of those information measures is supplanted by their asymptotic counterparts: entropy rate, relative entropy rate, and mutual information rate, defined as the asymptotic linear growth in m of the corresponding measure for a block of m random variables, e.g.,
The importance of information measures transcends information theory. Indeed, since shortly after their inception, a wide variety of experimental sciences have found significant applications for entropy, mutual information and relative entropy. For example,
- Ecology [2];
- Economics [3,4];
- Finance [5];
- Language [6,7,8,9];
- Machine learning [10,11,12];
- Molecular biology and genomics [13,14,15];
- Neuroscience [16,17,18,19];
- Psychology [20,21];
- Signal processing [22]; and
- Statistics [23,24,25,26].
Frequently, in those applications, the need arises to estimate information measures empirically: data are generated under an unknown probability law, and we would like to design a machine learning algorithm that estimates the information measure, assuming that the random data are stationary and ergodic, so that time averages converge to statistical averages. In fact, much more is usually assumed, and, at this point in time, the state-of-the-art in the design and analysis of empirical estimators is much more advanced in the ideal case of independent identically distributed data.
Another application of such universal empirical estimators is to approximate (4) (or relative entropy rate or mutual information rate) when the distribution is known but the analytical computation of the limit is not feasible.
Although we limit this survey to entropy, relative entropy and mutual information, there are other information measures, distances between probability distributions, and statistical dependence measures whose empirical estimation has received considerable interest, such as Rényi entropy (including support size) and Rényi divergence [27], f-divergence [28], erasure entropy [29], total variation distance, Hellinger distance, distance (e.g., [30]), directed information [31], and lautum information [32].
2. Entropy: Memoryless Sources
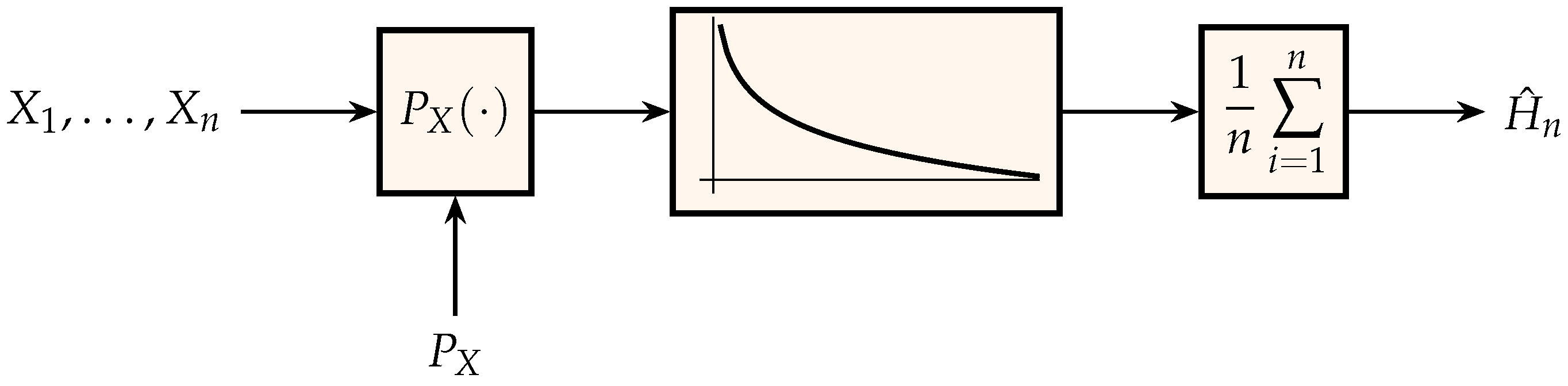
The output estimate, , of the scheme in Figure 1 is consistent, i.e., it converges to the entropy, because of the law of large numbers. Unfortunately, it has no practical utility as an empirical estimator of entropy since it requires knowledge of . Nevertheless, the scheme in Figure 1 suggests a two-pass algorithm for estimating the entropy of samples drawn independently from an unknown distribution by replacing the unknown in the left block with its empirical estimate computed from the n observations :
Figure 1.
Generation of an estimate for entropy where the middle block is the function , .
The plug-in universal estimator of entropy in Equation (6) is a maximum-likelihood estimator, which converges almost surely, as , to .
Because of the strict concavity of Equation (7) and , for any n the estimate in Equation (6) is underbiased,
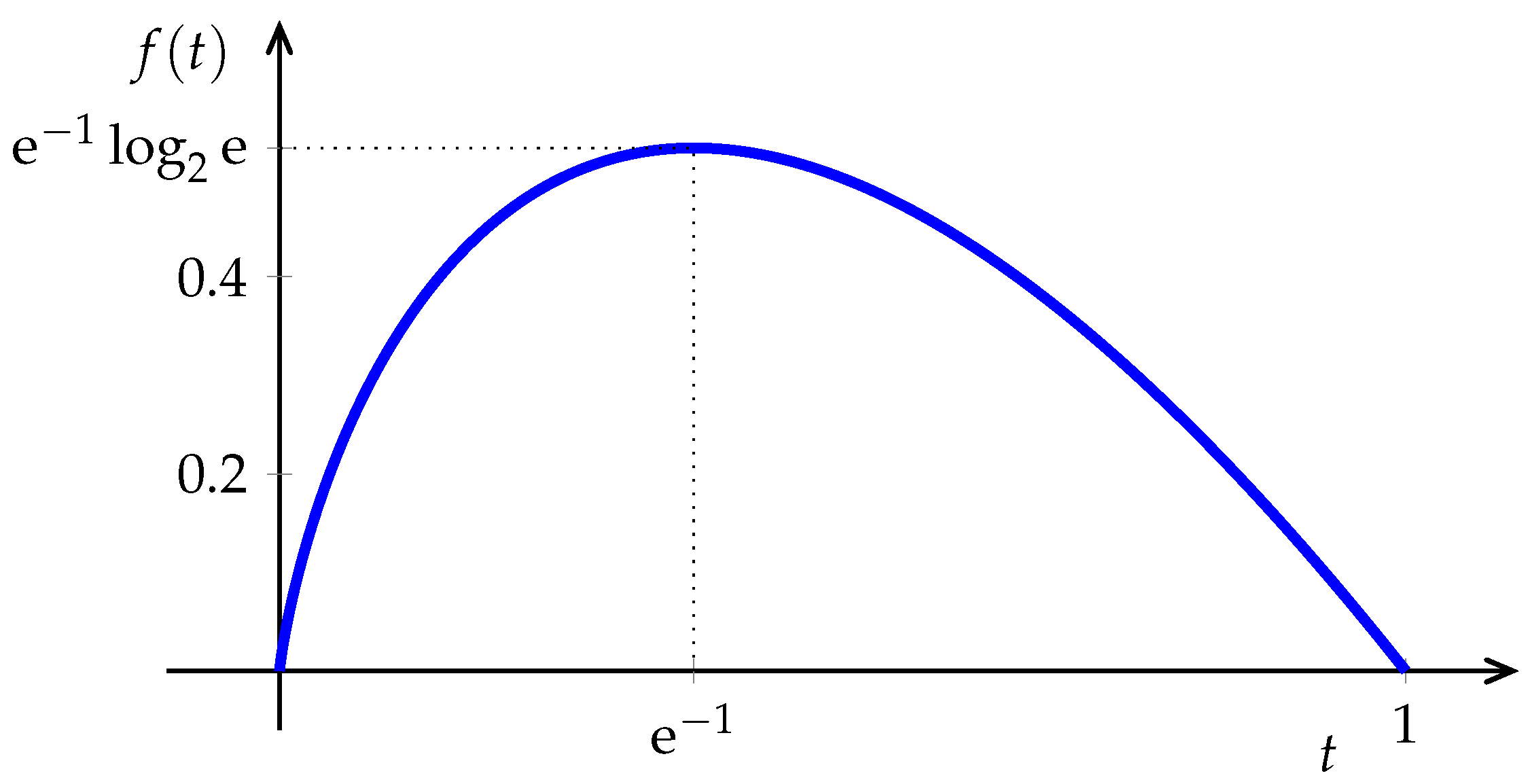
except in the trivial deterministic case. Although, as , the bias (which is equal to the relative entropy between the empirical distribution and the unknown ) vanishes, in applications with large alphabets the bias may be appreciable unless n is exceedingly large. The reason is that the innocuous looking function in Figure 2 has an infinite right-derivative at 0, thus, for distributions with many infrequent symbols, errors in the empirical estimates of their probabilities translate into large errors in their contributions to the sum in Equation (6). This challenge has received considerable attention, particularly in recent years. In addition to standard statistical bias-reduction techniques (e.g., [33,34,35,36,37]) and shrinkage techniques [38], one way to ameliorate this issue is to distort the function in Equation (6) by replacing the initial portion with a polynomial (see, e.g., [39,40,41,42]). Incidentally, we note that the idea of classifying the symbols in the alphabet into two categories (those with large enough probability whose frequency is plugged in Equation (6) directly, and those trouble-making infrequent ones that need to be dealt with separately) goes back to the work of Dobrushin [43] in 1958, which deals with the infrequent symbols by averaging the logarithms of their interoccurrence times. This approach is applied in [44] (see also [45]) to obtain, with observations, the same performance that the plug-in estimator would obtain with observations, not only for the estimation of entropy, but a large class of information measures.
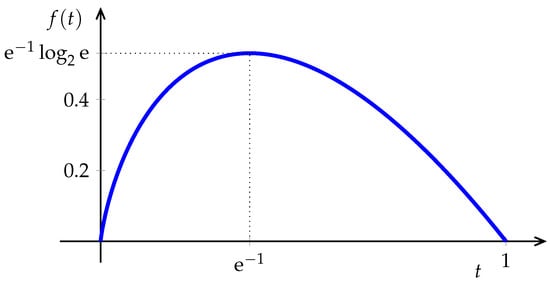
Figure 2.
The function .
Demanding consistency and low bias from the empirical estimator is desirable but not enough to obtain a useful estimator. How can we estimate the sample size n that a given algorithm will require in order to output a reliable estimate? The quality of the empirical estimator is usually judged by its worst case mean-square error over all possible (or a subset if some prior knowledge is available). A lower bound on the worst case mean-square error incurred by the plug-in estimator is obtained in [41,46], which also shows (see also [47]) that the plug-in method requires samples to achieve the same performance that a minimax estimator can achieve with n samples, so there is plenty of motivation to search for optimal or near-optimal computationally feasible solutions instead of using the plug-in method.
Paninski [39] gave a non-constructive proof of the existence of consistent estimators of entropy when the number of observations is less than the order of the alphabet size. Applications where the number of observations is much smaller than the alphabet size are increasingly common in modern machine learning; in that domain, it is futile to try to have an accurate empirical distribution. However, even if the number of observations grows only as , with a “constant” that, naturally, depends on the sought-after estimation accuracy, Valiant and Valiant [48] proposed a computationally intensive linear-programming based algorithm that estimates entropy accurately. Moreover, Valiant and Valiant [49] showed a converse result stating the impossibility of lower sample complexity in the regime in which the number of observations is not too large and the bias, rather than stochastic fluctuations, is responsible for most of the inaccuracy. The bias of the absolute error incurred by the linear programming algorithm of Valiant and Valiant [48] is upper bounded as the square root of the bias achieved both by a plug-in to a distorted target function [40,41] and by the linear programming type algorithm proposed in [50].
Entropy estimators that are linear on the fingerprint or profile (histogram of the histogram) of the observed sample were studied, among others, by Valiant and Valiant [47], Jiao et al. [40], Wu and Yang [41]. Nonlinear processing of the fingerprint may be more efficient, as pointed out in [51], which shows the optimality (even beyond entropy estimation) of algorithms based on finding the distribution that maximizes the likelihood of the observed fingerprint, also known as the profile maximum likelihood method. Efficient algorithms for such nontrivial optimization are proposed in [52,53], the latter of which also considers the more general setting of Markov sources.
Less studied is the Bayesian approach to empirical entropy estimation, which improves accuracy by incorporating prior information about the unknown probability mass function (see, e.g., the work of Wolpert and Wolf [54] and Jiao et al. [40], who showed essentially the same nonasymptotic worst-case performance as the maximum likelihood estimate).
The behavior of the plug-in estimator of entropy when the discrete distribution has infinite support (e.g., in applications where unbounded waiting times are observed) is studied in [55,56]. Unless some restriction is placed on the possible set of probability mass functions, Antos and Kontoyiannis [56] showed that for any sequence of estimators, the worst-case convergence rate can be arbitrarily slow. A universal non-asymptotic upper bound on the variance of the plug-in estimator is also found in [56].
3. Entropy: Sources with Memory
We turn to the empirical estimation of the entropy rate in Equation (4) from a sample path of the finite alphabet stationary ergodic process . In principle, for any integer m, we can estimate the empirical joint distribution
and then apply a plug-in approach or any of the methods surveyed in Section 2 to estimate . We can then increment m until the estimate stabilizes to near its limit. However, except for toy examples, this approach is not computationally feasible because of the exponential dependence of the effective alphabet size on m, which dictates astronomical values of n to get reliable empirical estimates of the joint distribution.
Claude Shannon [6,57] made the first forays in the empirical estimation of the entropy rate of an English text, not by a machine learning algorithm but also by a human, who arrived at an estimate based not only on the text itself but on the knowledge of the syntax and lexicon of the language, in addition to any information useful in guessing the next letter based on the previous text. This is based on the fact that, if the entropy is finite, then the entropy rate can be expressed as the limit of the conditional entropy of the next symbol given the past:
This line of research was continued by Cover and King [58], who came up with a convergent estimate based on sequential gambling on the next letter of the text.
Any optimal (i.e., achieving the entropy rate) universal data compression algorithm can be used as an estimator of the entropy rate by simply measuring the length of the output of the compressor. However, Jiao et al. [59] (see also [60]) gave evidence that insisting on compression incurs in higher sample complexity than entropy estimation: optimal universal compression (of memoryless sources) cannot be accomplished with samples, while suffices for entropy estimation. Under mixing conditions, Han et al. [61] showed that the sample complexity for Markov chains scales with the state space cardinality as . The finite sample-size behavior of plug-in estimators for the entropy rate of unknown Markov chains is analyzed in [62] along with a corresponding algorithm for the estimation of Rényi entropy rate.
Even though empirical estimation of entropy rate has smaller sample complexity than universal compression at the Shannon limit, most successful algorithms for empirical estimation of entropy rate are inspired by universal data compressors. Notable exceptions include Kaltchenko’s nearest-neighbor entropy rate estimators [63,64,65].
In the general context of stationary ergodic sources, Ziv and Merhav [66] proposed using the number of Lempel–Ziv (LZ) parsing phrases times its logarithm, normalized by sequence length, as an estimate of the entropy rate. Grassberger [67] proposed an alternative family of consistent estimators for the entropy rate of stationary ergodic sources, which is suggested by a result of Wyner and Ziv [68], Ornstein and Weiss [69] that states that, for an arbitrarily chosen time , the length of the shortest string occurring after that has no match as a substring occurring in behaves as
Consistency was shown in increasing generality by Shields [70], Kontoyiannis and Suhov [71] and Kontoyiannis et al. [72]. Improved versions of matching-based estimators are proposed in [73].
An efficient method for universal entropy estimation based on block sorting (Burrows–Wheeler transform, BWT) is proposed in [74], and shown to achieve almost sure convergence to entropy rate, along with an analysis of its convergence rate for finite-alphabet finite-memory sources. The principle followed in [74] is to revert to the estimation of the entropy of memoryless sources, and therefore the quality of its estimates can be improved by importing the recent advances outlined in Section 2.
At the expense of increased software complexity over LZ compression, universal compressors based on arithmetic coding and sequential modeling algorithms such as context-tree-weighting (CTW) [75] and prediction by partial match (PPM) [76] achieve faster convergence to the entropy rate. These modeling algorithms compute an estimate of the probability of the next symbol given the past. Therefore, they can be readily adopted to estimate the conditional entropies in Equation (10). A comparison of empirical entropy estimators based on CTW and on matching [73] shows the practical superiority of CTW-based empirical entropy estimation. The related problem of empirical estimation of erasure entropy [29] is studied in [77] where a bilateral version of CTW is proposed.
4. Differential Entropy: Memoryless Sources
The differential entropy of a probability density function on the real line (or ) was introduced by Shannon [57] (and independently by Wiener [78]):
Although not as fundamental as entropy, mutual information and relative entropy, the empirical estimation of differential entropy has also received considerable attention for memoryless sources. For example, a normality test can be based on whether the empirical differential entropy attains a value close to . A survey of the state of the art in 2009 of empirical estimation of the differential entropy of continuous random variables and vectors can be found in [79].
The scheme in Figure 1 can be readily adapted to estimate differential entropy by letting the left-block use an estimate of the probability density function. This approach is followed in [80,81,82,83,84]. In particular, Györfi and Van der Meulen [81] advocated using half of the samples as inputs to the scheme in Figure 1, and the other half to estimate the probability density function; input samples which correspond to very small values of the estimated probability density function are discarded.
Naturally, the most popular approach is to use a plug-in method where the density in Equation (12) is replaced by an estimate based on a histogram, or a kernel approximation (e.g., [80,85,86]). Note that the integrand in Equation (12) is also the function in Figure 2, except that now its domain extends to the whole positive real line. As argued in Section 2, in view of the infinite derivative at zero, it is to be expected that estimation inaccuracies will arise from improbable intervals. Restricting the possible density governing the data to satisfy a sufficiently large Lipschitz constraint enabled Han et al. [87] to show matching achievability and converse results showing that the square root of the minimax mean square error behaves as
where is a smoothness parameter that governs the Lipschitz constraint, and d is the dimension of the observation vectors. As in the case of (discrete) entropy, Han et al. [87] showed that, without distorting the function in Figure 2 near the origin, plug-in methods are doomed to be strictly suboptimal.
Kozachenko and Leonenko [85] proposed the nearest neighbor estimator
where c is a constant. A truncated version of this estimate is shown in [88] to achieve a mean-square error of . More generally, k-nearest-neighbor methods for the empirical estimation of differential entropy have received considerable attention. A simple k-nearest-neighbor estimate is given by
where denote the sorted version of . If in addition to , k is allowed to grow, is shown in [89] to be asymptotically normal with zero mean and variance under the assumption that is bounded and bounded away from zero on its support. Other nearest-neighbor methods for the empirical estimation of differential entropy are proposed and analyzed in [90,91,92,93,94]. An upper bound on the minimax mean-square error attained by nearest-neighbor estimators of differential entropy is established in [95].
Estimation of other nonlinear functionals of probability density functions, beyond differential entropy, has received considerable attention in the statistics literature (see, e.g, [96]).
5. Relative Entropy: Memoryless Sources
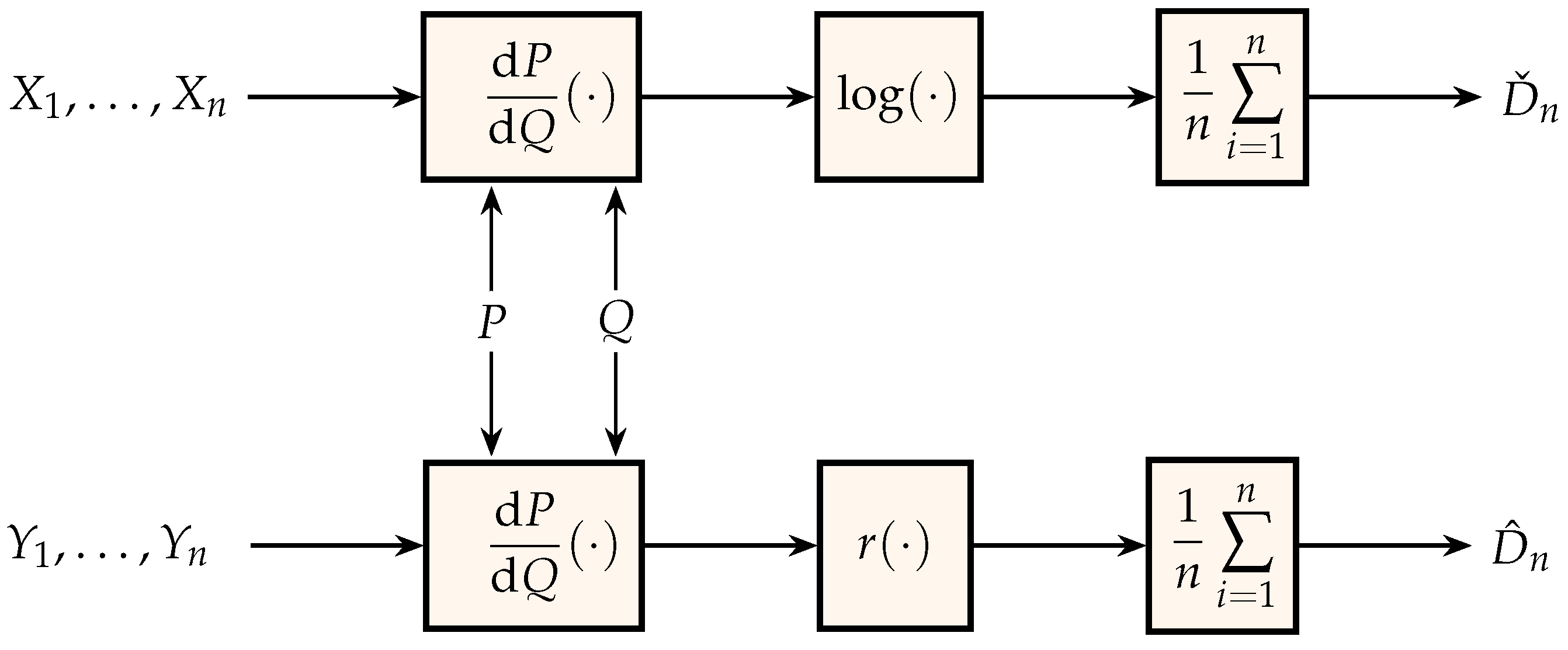
In the same spirit as Figure 1, Figure 3 shows two estimators of the relative entropy between the probability measures that generate the independent identically distributed sequences and . The middle block in the bottom estimator is the nonnegative function
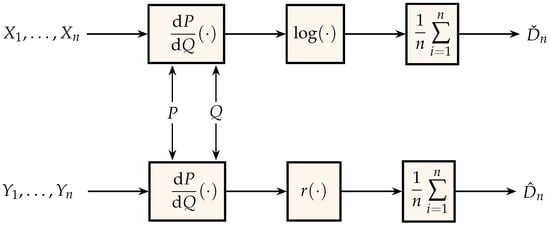
Figure 3.
Generation of estimates for relative entropy.
To see the rationale for this, note that, in addition to Equation (2), we can express relative entropy as
Empirical estimation requires a two-pass algorithm in which the first pass estimates the unknown density (see, e.g., [97,98]).
- Finite alphabet. In the discrete case, we can base a relative entropy estimator on the decompositionwith . Therefore, once an empirical estimator of entropy is available, the task is to design an algorithm for estimating the cross term. To that end, it is beneficial to regularize the probability estimate for those symbols that are infrequent under the reference measure. Various regularization and bias-reduction strategies are proposed in [99,100], leading to consistent estimators.In the memoryless case, several of the algorithms reviewed in Section 2 for entropy estimation (e.g., [40,47]) find natural generalizations for the estimation of relative entropy. As for entropy estimation, the straightforward ratio of empirical counts can be used in the plug-in approach if is negligible with respect to the number of observations. Otherwise, sample complexity can be lowered by a logarithmic factor by distorting the plug-in function; an estimator is proposed in [101], which is optimal in the minimax mean-square sense when the likelihood ratio is upper bounded by a constant that may depend on , although the algorithm can operate without prior knowledge of either the upper bound or . Another nice feature of that algorithm is that it can be modified to estimate other distance measures such as -divergence and Hellinger distance. The asymptotic (in the alphabet size) minimax mean-square error is analyzed in [102] (see also [101]) when the likelihood ratio is bounded by a function of the alphabet size, and the number of observations is also allowed to grow with .
- Continuous alphabet. By the relative entropy data processing theorem,where , and is arbitrary. If is injective, then the equality in Equation (18) holds. If we choose to be a finite set, then an empirical estimate of the lower bound in Equation (18) can be obtained using one of the methods to estimate the relative entropy for finite alphabets. It is to be expected that keeping the number of bins small results in lower complexity and coarser bounds; on the other hand, allowing to grow too large incurs in unreliable estimates for the probabilities of infrequent values of . Of course, for a given , the slackness in Equation (18) will depend on the choice of . An interesting option propounded in [103] is to let be such that is independent of , in which caseNaturally, we cannot instrument such a function since we do not know , but we can get a fairly good approximation by letting depend on the observations obtained under the reference measure, such that each bin contains the same number of samples. Various strongly consistent algorithms based on data-dependent partitions are proposed in [79,103].For multidimensional densities, relative entropy estimation via k-nearest-neighbor distances [104] is more attractive than the data-dependent partition methods. This has been extended to the estimation of Rényi divergence in [105]. Earlier, Hero et al. [106] considered the estimation of Rényi divergence when one of the measures is known, using minimum spanning trees.As shown in [107], it is possible to design consistent empirical relative entropy estimators based on non-consistent density estimates.The empirical estimation of the minimum relative entropy between the unknown probability measure that generates an observed independent sequence and a given exponential family is considered in [108] with a local likelihood modeling algorithm.M-estimators for the empirical estimation of f-divergence (according to Equation (16), r-divergence with in Equation (15) is the relative entropy)where f is a convex function with are proposed in [109] using the Fenchel–Lagrange dual variational representation of [110]. A k-nearest neighbor estimator of is proposed and analyzed in [111].A recent open-source toolbox for the empirical estimation of relative entropy (as well as many other information measures) for analog random variables can be found in [112]. Software estimating mutual information in independent component analysis can be found in [113]. Experimental results contrasting various methods can be found in [114].
6. Relative Entropy: Discrete Sources with Memory
Dropping the assumption that the unknown sources are independent presents considerable new challenges for the empirical estimation of relative entropy rate, which have not yet been addressed in the realm of analog data. In the finite-alphabet case, a paradigmatic application is the quantitative measure of the “statistical similarity” between long texts.
A useful starting point is to leverage Equation (17) and separate the task into entropy estimation and the estimation of the cross term (average of information under the reference measure with respect to the other measure). Universal data compression techniques have inspired a variety of algorithms for the empirical estimation of the cross term starting with [66], which is proposed using a cross Lempel–Ziv-like parsing of a sequence with respect to another. Consistency is shown in [66] under the assumption that both sources are Markov and independent. Text classification using the algorithm in [66] was studied by Pereira Coutinho and Figueiredo [115]. A heuristic application of Lempel–Ziv compression is proposed in [9] motivated by the fact that, according to Equation (17) and basic results in data compression, the relative entropy rate is, approximately, the penalty in length when instead of using an optimum compressor tuned to , we use a compressor tuned to . This suggests training a universal compression algorithm with the text generated under and measure its compression length under the other text. Instead of relying on Lempel–Ziv compression, Cai et al. [99] used the Burrows–Wheeler transform (BWT), which transfers the redundancy in the data due to memory into redundancy due to non-uniformity of the marginals of the piecewise stationary asymptotically independent outputs. The main algorithmic challenge is to segment the outputs adaptively in order to determine the points at which the statistics switch. In the algorithm in [99], the Burrows–Wheeler transform is applied to the concatenated texts, and the segmentation is done with respect to the reference text, so as to produce an estimate of the cross term in Equation (17). Consistency of the estimator is shown in [99] along with an analysis of its convergence rate for finite-alphabet finite-memory sources, and an experimental application to texts: the Bible written in various languages and novels of various authors. Further experimentation with the Universal Declaration of Human Rights written in various languages and a mammalian DNA evolutionary tree are reported in [116] (see also [117]) using data compression algorithms. These and other experimental results led Kaltchenko [118] to conjecture that relative entropy is a more powerful discriminator than other measures of statistical distance.
7. Mutual Information: Memoryless Sources
Discussing specific data in soccer (influence of home/away in scoring goals), the spread of wildfires, and neuroscience, Brillinger [119] made a case for the benefit of empirical estimates of mutual information in various data science applications over other more established statistical dependence-testing tools. In particular, a natural application is testing the independence of the components in independent component analysis (e.g., [113,120]).
If both random variables are discrete, then we can leverage empirical estimators of entropy in order to estimate mutual information since, in that case,
A similar approach can be followed when both random variables are analog by using algorithms to estimate the differential entropy (Section 4). A word of caution is that, in some applications with weakly dependent random variables, the error in the entropy estimator may be non-negligible with respect to the mutual information. Although the plug-in estimator of entropy is underbiased, using it in conjunction with Equation (21) yields estimates of mutual information that may be positively or negatively biased depending on the joint distribution [39]. Although largely unexplored (see [121,122] for recent work), the empirical estimation of mutual information between discrete X and analog Y is also of interest in a number of applications; for example, suppose that and Y is an intracellular voltage trace from visual cortex neurons.
In the domain of memoryless analog sources, generally preferable to differential-entropy based methods are estimation algorithms that exploit the definition of mutual information as a relative entropy between the joint probability measure and the product of its marginals (Equation (3)), thereby opening the possibility of using the approaches taken in Section 5. The upper scheme in Figure 3 has been used for the estimation of the mutual information of analog random variables in [82,123,124]. Note that those algorithms have not yet been extended to deal with sources with memory. For those cases, a pragmatic approach is advocated in [79] where multimedia data are pre-processed by a standard lossy compression front-end (such as JPEG or MPEG), which projects on a multiresolution basis producing essentially memoryless streams of analog data. Then, the algorithms for mutual information estimation of memoryless sources can be applied to those streams. Naturally, the projections in off-the-shelf standard software have very low complexity and they leave residual correlations among the streams, which result in both data rate inefficiencies and estimation inaccuracies.
A widely used empirical estimator of for real-valued random variables is proposed in [125] by simply quantizing the real-line and using a plug-in estimator for relative entropy. The variance of the estimate is closely approximated by the variance of the information density, , normalized by the number of observations. The highly influential estimator proposed by Fraser and Swinney [126] goes one step further by adapting the quantization size to the data, leading to a more systematic treatment of data-dependent partitions (not necessarily products of scalar quantizers) in [127]. Even greater adaptivity is beneficial by having equally-populated partitions (see [128] and its supplemental material). Those approaches are studied more systematically in the more general context of relative entropy estimation [79,103].
k-Nearest-neighbor estimators of mutual information are studied in [79,104,120,129].
Directed (mutual) information [31] defined for two time series as
is important in the fundamental limits of channels with memory with feedback, and has been proposed for quantifying the elusive notion of causality. Empirical estimators of directed information for finite alphabet processes are proposed in [130,131], the latter of which shows an optimal rate of convergence of and adapts the estimator to testing for causality.
Funding
This work was supported by the US National Science Foundation under Grant CCF-1016625, and in part by the Center for Science of Information, an NSF Science and Technology Center under Grant CCF-0939370.
Acknowledgments
Suggestions from Jiantao Jiao, Yiannis Kontoyiannis, and Yihong Wu are gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Johnson, J.B.; Omland, K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Maasoumi, E. A compendium to information theory in economics and econometrics. Econom. Rev. 1993, 12, 137–181. [Google Scholar] [CrossRef]
- Sims, C.A. Implications of rational inattention. J. Monet. Econ. 2003, 50, 665–690. [Google Scholar] [CrossRef]
- MacLean, L.C.; Thorp, E.O.; Ziemba, W.T. The Kelly Capital Growth Investment Criterion: Theory and Practice; World Scientific: Singapore, 2011; Volume 3. [Google Scholar]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 47–51. [Google Scholar] [CrossRef]
- Chomsky, N. Three models for the description of language. IEEE Trans. Inf. Theory 1956, 2, 113–124. [Google Scholar] [CrossRef]
- Nowak, M.A.; Komarova, N.L. Towards an evolutionary theory of language. Trends Cognit. Sci. 2001, 5, 288–295. [Google Scholar] [CrossRef]
- Benedetto, D.; Caglioti, E.; Loreto, V. Language trees and zipping. Phys. Rev. Lett. 2002, 88, 048702. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, S.R.; Lugosi, G.; Venkatesh, S. A Survey of Statistical Pattern Recognition and Learning Theory. IEEE Trans. Inf. Theory 1998, 44, 2178–2206. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Andrzejak, R.G.; Grassberger, P. Hierarchical clustering using mutual information. Europhys. Lett. 2005, 70, 278. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Yockey, H.P. Information Theory and Molecular Biology; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Frieden, B.R. Information theory in living systems, methods, applications, and challenges. Bull. Math. Biol. 2007, 69, 635–657. [Google Scholar] [CrossRef] [PubMed]
- Rieke, F.; Warland, D.; de Ruyter van Steveninck, R.; Bialek, W. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Bialek, W. Biophysics: Searching for Principles; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Borst, A.; Theunissen, F.E. Information theory and neural coding. Nat. Neurosci. 1999, 2, 947. [Google Scholar] [CrossRef] [PubMed]
- Nemenman, I.; Bialek, W.; van Steveninck, R.d.R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef] [PubMed]
- LaBerge, D. Attentional Processing: The Brain’s Art of Mindfulness; Harvard University Press: Cambridge, MA, USA, 1995; Volume 2. [Google Scholar]
- Laming, D. Statistical information, uncertainty, and Bayes’ theorem: Some applications in experimental psychology. In European Conference on Symbolic and Quantitative Approaches to Reasoning and Uncertainty; Benferhat, S., Besnard, P., Eds.; Springer: Berlin, Germany, 2001; pp. 635–646. [Google Scholar]
- Basseville, M. Distance measures for signal processing and pattern recognition. Signal Process. 1989, 18, 349–369. [Google Scholar] [CrossRef]
- Kullback, S. An application of information theory to multivariate analysis. Ann. Math. Stat. 1952, 23, 88–102. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover: New York, NY, USA, 1968; Originally published in 1959 by John Wiley. [Google Scholar]
- Barron, A.R.; Rissanen, J.; Yu, B. The minimum description length principle in coding and modeling. IEEE Trans. Inf. Theory 1998, 44, 2743–2760. [Google Scholar] [CrossRef]
- Csiszár, I.; Shields, P.C. Information Theory and Statistics: A Tutorial. Found. Trends Commun. Inf. Theory 2004, 1, 417–528. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Neyman, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Verdú, S.; Weissman, T. The information lost in erasures. IEEE Trans. Inf. Theory 2008, 54, 5030–5058. [Google Scholar] [CrossRef]
- Vajda, I. Theory of Statistical Inference and Information; Kluwer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Massey, J.L. Causality, feedback and directed information. In Proceedings of the 1990 International Symposium Information Theory and Applications, Waikiki, HI, USA, 27–30 November 1990; pp. 303–305. [Google Scholar]
- Palomar, D.P.; Verdú, S. Lautum Information. IEEE Trans. Inf. Theory 2008, 54, 964–975. [Google Scholar] [CrossRef]
- Miller, G.; Madow, W. On the Maximum Likelihood Estimate of the Shannon-Wiener Measure of Information; Operational Applications Laboratory, Air Force Cambridge Research Center, Air Research and Development Command, Bolling Air Force Base: Montgomery County, OH, USA, 1954. [Google Scholar]
- Miller, G. Note on the bias of information estimates. Inf. Theory Psychol. II. B Probl. Methods 1955, 95–100. [Google Scholar]
- Carlton, A. On the bias of information estimates. Psychol. Bull. 1969, 71, 108. [Google Scholar] [CrossRef]
- Grassberger, P. Finite sample corrections to entropy and dimension estimates. Phys. Lett. A 1988, 128, 369–373. [Google Scholar] [CrossRef]
- Strong, S.P.; Koberle, R.; van Steveninck, R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197. [Google Scholar] [CrossRef]
- Hausser, J.; Strimmer, K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. J. Mach. Learn. Res. 2009, 10, 1469–1484. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Minimax estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2015, 61, 2835–2885. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, P. Minimax rates of entropy estimation on large alphabets via best polynomial approximation. IEEE Trans. Inf. Theory 2016, 62, 3702–3719. [Google Scholar] [CrossRef]
- Han, Y.; Jiao, J.; Weissman, T. Adaptive estimation of Shannon entropy. In Proceedings of the 2015 IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 1372–1376. [Google Scholar]
- Dobrushin, R.L. A simplified method of experimentally evaluating the entropy of a stationary sequence. Theory Probab. Appl. 1958, 3, 428–430. [Google Scholar] [CrossRef]
- Yi, H.; Orlitsky, A.; Suresh, A.T.; Wu, Y. Data Amplification: A Unified and Competitive Approach to Property Estimation. Adv. Neural Inf. Process. Syst. 2018, 8834–8843. [Google Scholar]
- Hao, Y.; Orlitsky, A. Data Amplification: Instance-Optimal Property Estimation. arXiv 2019, arXiv:1903.01432. [Google Scholar]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Maximum likelihood estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2017, 63, 6774–6798. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. The power of linear estimators. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science (FOCS), Palm Springs, CA, USA, 22–25 October 2011; pp. 403–412. [Google Scholar]
- Valiant, P.; Valiant, G. Estimating the unseen: Improved estimators for entropy and other properties. Adv. Neural Inf. Process. Syst. 2013, 2157–2165. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. A CLT and tight lower bounds for estimating entropy. Electron. Colloq. Computat. Complex. (ECCC) 2010, 17, 9. [Google Scholar]
- Han, Y.; Jiao, J.; Weissman, T. Local moment matching: A unified methodology for symmetric functional estimation and distribution estimation under Wasserstein distance. arXiv 2018, arXiv:1802.08405. [Google Scholar]
- Acharya, J.; Das, H.; Orlitsky, A.; Suresh, A.T. A unified maximum likelihood approach for estimating symmetric properties of discrete distributions. Int. Conf. Mach. Learn. 2017, 70, 11–21. [Google Scholar]
- Pavlichin, D.S.; Jiao, J.; Weissman, T. Approximate profile maximum likelihood. arXiv 2017, arXiv:1712.07177. [Google Scholar]
- Vatedka, S.; Vontobel, P.O. Pattern maximum likelihood estimation of finite-state discrete-time Markov chains. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 2094–2098. [Google Scholar]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841. [Google Scholar] [CrossRef]
- Keziou, A. Sur l’estimation de l’entropie des lois ą support dénombrable. Comptes Rendus Math. 2002, 335, 763–766. [Google Scholar] [CrossRef]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Cover, T.M.; King, R.C. A Convergent gambling estimate of the entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Jiao, J.; Han, Y.; Fischer-Hwang, I.; Weissman, T. Estimating the fundamental limits is easier than achieving the fundamental limits. arXiv 2017, arXiv:1707.01203. [Google Scholar] [CrossRef]
- Tatwawadi, K.S.; Jiao, J.; Weissman, T. Minimax redundancy for Markov chains with large state space. arXiv 2018, arXiv:1805.01355. [Google Scholar]
- Han, Y.; Jiao, J.; Lee, C.Z.; Weissman, T.; Wu, Y.; Yu, T. Entropy Rate Estimation for Markov Chains with Large State Space. arXiv 2018, arXiv:1802.07889. [Google Scholar]
- Kamath, S.; Verdú, S. Estimation of Entropy rate and Rényi entropy rate for Markov chains. In Proceedings of the 2016 IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 685–689. [Google Scholar]
- Kaltchenko, A.; Timofeeva, N. Entropy estimators with almost sure convergence and an o(n−1) variance. Adv. Math. Commun. 2008, 2, 1–13. [Google Scholar]
- Kaltchenko, A.; Timofeeva, N. Rate of convergence of the nearest neighbor entropy estimator. AEU-Int. J. Electron. Commun. 2010, 64, 75–79. [Google Scholar] [CrossRef]
- Timofeev, E.A.; Kaltchenko, A. Fast algorithm for entropy estimation. In Proceedings of the SPIE 8750, Independent Component Analyses, Compressive Sampling, Wavelets, Neural Net, Biosystems, and Nanoengineering XI, Baltimore, MA, USA, 28 April–3 May 2013. [Google Scholar]
- Ziv, J.; Merhav, N. A measure of relative entropy between individual sequences with application to universal classification. IEEE Trans. Inf. Theory 1993, 39, 1270–1279. [Google Scholar] [CrossRef]
- Grassberger, P. Estimating the information content of symbol sequences and efficient codes. IEEE Trans. Inf. Theory 1989, 35, 669–675. [Google Scholar] [CrossRef]
- Wyner, A.D.; Ziv, J. Some asymptotic properties of the entropy of a stationary ergodic data source with applications to data compression. IEEE Trans. Inf. Theory 1989, 35, 1250–1258. [Google Scholar] [CrossRef]
- Ornstein, D.S.; Weiss, B. Entropy and data compression schemes. IEEE Trans. Inf. Theory 1993, 39, 78–83. [Google Scholar] [CrossRef]
- Shields, P.C. Entropy and prefixes. Ann. Probab. 1992, 20, 403–409. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Suhov, Y.M. Prefixes and the entropy rate for long-range sources. In Probability Statistics and Optimization: A Tribute to Peter Whittle; Kelly, F.P., Ed.; Wiley: New York, NY, USA, 1994; pp. 89–98. [Google Scholar]
- Kontoyiannis, I.; Algoet, P.; Suhov, Y.; Wyner, A.J. Nonparametric entropy estimation for stationary processes and random fields, with applications to English text. IEEE Trans. Inf. Theory 1998, 44, 1319–1327. [Google Scholar] [CrossRef]
- Gao, Y.; Kontoyiannis, I.; Bienenstock, E. Estimating the entropy of binary time series: Methodology, some theory and a simulation study. Entropy 2008, 10, 71–99. [Google Scholar] [CrossRef]
- Cai, H.; Kulkarni, S.R.; Verdú, S. Universal entropy estimation via block sorting. IEEE Trans. Inf. Theory 2004, 50, 1551–1561. [Google Scholar] [CrossRef]
- Willems, F.M.J.; Shtarkov, Y.M.; Tjalkens, T.J. The context-tree weighting method: Basic properties. IEEE Trans. Inf. Theory 1995, 41, 653–664. [Google Scholar] [CrossRef]
- Cleary, J.G.; Witten, I.H. Data compression using adaptive coding and partial string matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]
- Yu, J.; Verdú, S. Universal estimation of erasure entropy. IEEE Trans. Inf. Theory 2009, 55, 350–357. [Google Scholar] [CrossRef][Green Version]
- Wiener, N. Cybernetics, Chapter III: Time Series, Information and Communication; Wiley: New York, NY, USA, 1948. [Google Scholar]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Universal estimation of information measures for analog sources. Found. Trends Commun. Inf. Theory 2009, 5, 265–353. [Google Scholar] [CrossRef]
- Ahmad, I.; Lin, P.E. A nonparametric estimation of the entropy for absolutely continuous distributions. IEEE Trans. Inf. Theory 1976, 22, 372–375. [Google Scholar] [CrossRef]
- Györfi, L.; Van der Meulen, E.C. Density-free convergence properties of various estimators of entropy. Comput. Stat. Data Anal. 1987, 5, 425–436. [Google Scholar] [CrossRef]
- Joe, H. Estimation of entropy and other functionals of a multivariate density. Ann. Inst. Stat. Math. 1989, 41, 683–697. [Google Scholar] [CrossRef]
- Hall, P.; Morton, S. On the estimation of entropy. Ann. Inst. Stat. Math. Mar. 1993, 45, 69–88. [Google Scholar] [CrossRef]
- Godavarti, M.; Hero, A. Convergence of differential entropies. IEEE Trans. Inf. Theory 2004, 50, 171–176. [Google Scholar] [CrossRef]
- Kozachenko, L.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Pereda. Inf. 1987, 23, 9–16. [Google Scholar]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; Van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stat. Sci. 1997, 6, 17–39. [Google Scholar]
- Han, Y.; Jiao, J.; Weissman, T.; Wu, Y. Optimal rates of entropy estimation over Lipschitz balls. arXiv 2017, arXiv:1711.02141. [Google Scholar]
- Tsybakov, A.B.; Van der Meulen, E. Root-n consistent estimators of entropy for densities with unbounded support. Scand. J. Stat. 1996, 23, 75–83. [Google Scholar]
- Hall, P. On powerful distributional tests based on sample spacings. J. Multivar. Anal. 1986, 19, 201–224. [Google Scholar] [CrossRef]
- El Haje Hussein, F.; Golubev, Y. On entropy estimation by m-spacing method. J. Math. Sci. 2009, 163, 290–309. [Google Scholar] [CrossRef]
- Sricharan, K.; Wei, D.; Hero, A.O., III. Ensemble estimators for multivariate entropy estimation. IEEE Trans. Inf. Theory 2013, 59, 4374–4388. [Google Scholar] [CrossRef] [PubMed]
- Berrett, T.B. Modern k-Nearest Neighbour Methods in Entropy Estimation, Independence Testing and Classification. PhD Thesis, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Berrett, T.B.; Samworth, R.J.; Yuan, M. Efficient multivariate entropy estimation via k-nearest neighbour distances. arXiv 2016, arXiv:1606.00304. [Google Scholar] [CrossRef]
- Delattre, S.; Fournier, N. On the Kozachenko–Leonenko entropy estimator. J. Stat. Plan. Inference 2017, 185, 69–93. [Google Scholar] [CrossRef][Green Version]
- Jiao, J.; Gao, W.; Han, Y. The nearest neighbor information estimator is adaptively near minimax rate-optimal. arXiv 2017, arXiv:1711.08824. [Google Scholar]
- Birgé, L.; Massart, P. Estimation of integral functionals of a density. Ann. Stat. 1995, 23, 11–29. [Google Scholar] [CrossRef]
- Adams, T.M.; Nobel, A.B. On density estimation from ergodic processes. Ann. Probab. 1998, 26, 794–804. [Google Scholar]
- Sugiyama, M.; Suzuki, T.; Kanamori, T. Density Ratio Estimation in Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Cai, H.; Kulkarni, S.R.; Verdú, S. Universal divergence estimation for finite-alphabet sources. IEEE Trans. Inf. Theory 2006, 52, 3456–3475. [Google Scholar] [CrossRef]
- Zhang, Z.; Grabchak, M. Nonparametric estimation of Kullback-Leibler divergence. Neural Comput. 2014, 26, 2570–2593. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Jiao, J.; Weissman, T. Minimax Rate-Optimal Estimation of Divergences between Discrete Distributions. arXiv 2016, arXiv:1605.09124. [Google Scholar]
- Bu, Y.; Zou, S.; Liang, Y.; Veeravalli, V.V. Estimation of KL divergence: Optimal minimax rate. IEEE Trans. Inf. Theory 2018, 64, 2648–2674. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation of continuous distributions based on data-dependent partitions. IEEE Trans. Inf. Theory 2005, 51, 3064–3074. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k-nearest-neighbor distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Póczos, B.; Schneider, J. On the estimation of alpha-divergences. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Lauderdale, FL, USA, 11–13 April 2011; pp. 609–617. [Google Scholar]
- Hero, A.O.; Ma, B.; Michel, O.J.; Gorman, J. Applications of entropic spanning graphs. IEEE Signal Process. Mag. 2002, 19, 85–95. [Google Scholar] [CrossRef]
- Pérez-Cruz, F. Kullback-Leibler divergence estimation of continuous distributions. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1666–1670. [Google Scholar]
- Lee, Y.K.; Park, B.U. Estimation of Kullback–Leibler divergence by local likelihood. Ann. Inst. Stat. Math. 2006, 58, 327–340. [Google Scholar] [CrossRef]
- Nguyen, X.; Wainwright, M.J.; Jordan, M.I. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Trans. Inf. Theory 2010, 56, 5847–5861. [Google Scholar] [CrossRef]
- Keziou, A. Dual representation of φ-divergences and applications. Comptes Rendus Math. 2003, 336, 857–862. [Google Scholar] [CrossRef]
- Moon, K.; Hero, A. Multivariate f-divergence estimation with confidence. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2420–2428. [Google Scholar]
- Szabó, Z. Information theoretical estimators toolbox. J. Mach. Learn. Res. 2014, 15, 283–287. [Google Scholar]
- Stoegbauer, H. MILCA and SNICA. Available online: http://bsp.teithe.gr/members/downloads/Milca.html (accessed on 16 May 2019).
- Budka, M.; Gabrys, B.; Musial, K. On accuracy of PDF divergence estimators and their applicability to representative data sampling. Entropy 2011, 13, 1229–1266. [Google Scholar] [CrossRef]
- Pereira Coutinho, D.; Figueiredo, M.A.T. Information Theoretic Text Classification Using the Ziv-Merhav Method. In Pattern Recognition and Image Analysis; Marques, J.S., Pérez de la Blanca, N., Pina, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 355–362. [Google Scholar]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitányi, P.M. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Vitányi, P.M.; Balbach, F.J.; Cilibrasi, R.L.; Li, M. Normalized information distance. In Information Theory and Statistical Learning; Springer: Berlin, Germay, 2009; pp. 45–82. [Google Scholar]
- Kaltchenko, A. Algorithms for estimating information distance with application to bioinformatics and linguistics. In Proceedings of the 2004 IEEE Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 2–5 May 2004; Volume 4, pp. 2255–2258. [Google Scholar]
- Brillinger, D.R. Some data analyses using mutual information. Braz. J. Probab. Stat. 2004, 18, 163–182. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Kannan, S.; Oh, S.; Viswanath, P. Estimating mutual information for discrete-continuous mixtures. In Proceedings of the Thirty-first Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 14–17 December 2017; pp. 5986–5997. [Google Scholar]
- Bulinski, A.; Kozhevin, A. Statistical Estimation of Conditional Shannon Entropy. arXiv 2018, arXiv:1804.08741. [Google Scholar] [CrossRef]
- Joe, H. Relative entropy measures of multivariate dependence. J. Am. Stat. Assoc. 1989, 84, 171–176. [Google Scholar] [CrossRef]
- Moon, Y.I.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318. [Google Scholar] [CrossRef]
- Moddemeijer, R. On estimation of entropy and mutual information of continuous distributions. Signal Process. 1989, 16, 233–248. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Vajda, I. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 1315–1321. [Google Scholar] [CrossRef]
- Slonim, N.; Atwal, G.S.; Tkačik, G.; Bialek, W. Information-based clustering. Proc. Natl. Acad. Sci. USA 2005, 102, 18297–18302. [Google Scholar] [CrossRef]
- Victor, J.D. Binless strategies for estimation of information from neural data. Phys. Rev. E 2002, 66, 051903. [Google Scholar] [CrossRef]
- Jiao, J.; Permuter, H.H.; Zhao, L.; Kim, Y.H.; Weissman, T. Universal estimation of directed information. IEEE Trans. Inf. Theory 2013, 59, 6220–6242. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Skoularidou, M. Estimating the directed information and testing for causality. IEEE Trans. Inf. Theory 2016, 62, 6053–6067. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).