Gaussian Belief Propagation for Solving Network Utility Maximization with Delivery Contracts
Abstract
1. Introduction
2. Background and Related Work
2.1. Basic Primary-Dual Algorithm
2.2. Related Work
3. Our Method
3.1. Optimality Conditions
3.2. Inference Problem
3.3. Parameter Evaluation Based on GaBP
| Algorithm 1: GaBP Algorithm |
|
4. Experiments and Analysis
4.1. Experimental Settings
4.2. Experimental Results
4.3. Experiment Analysis
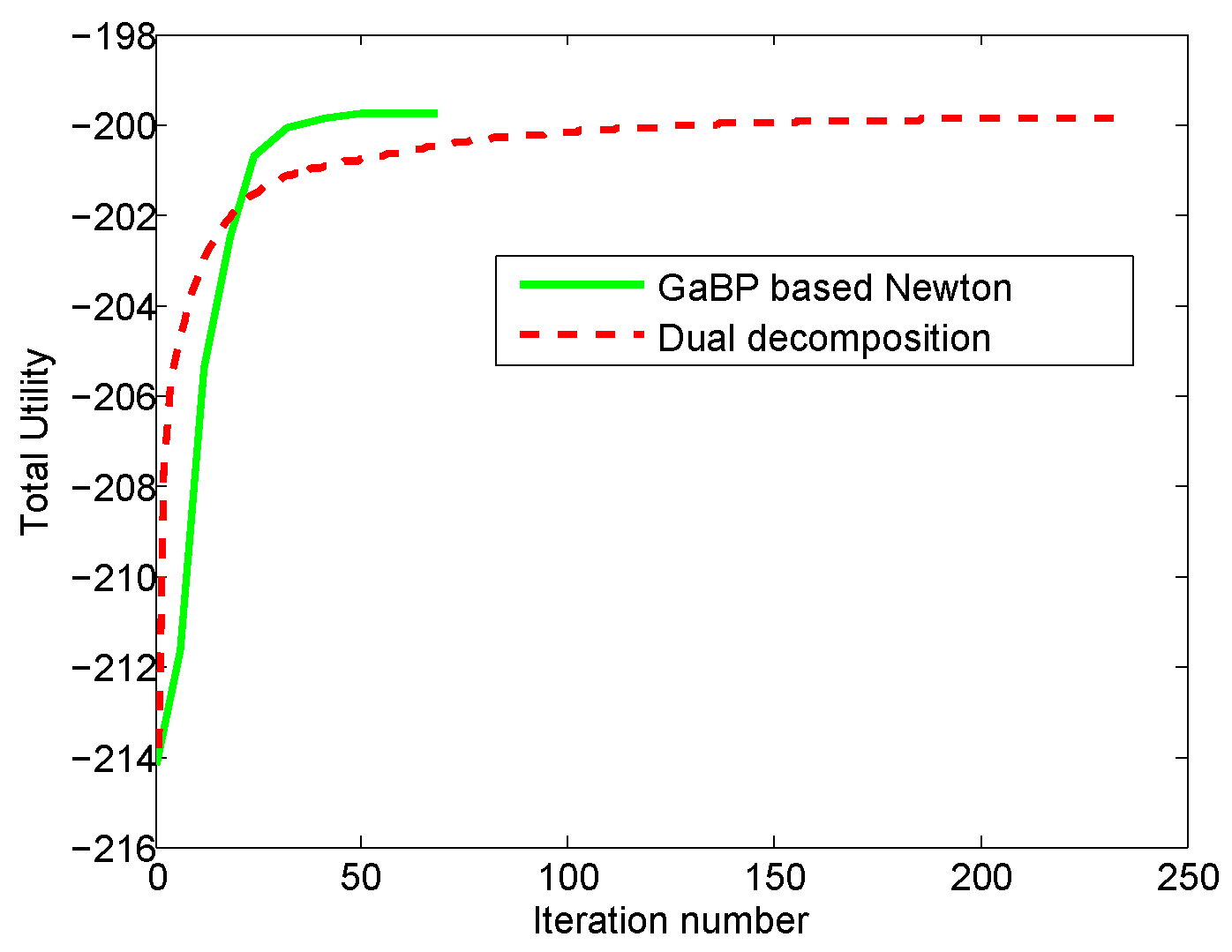
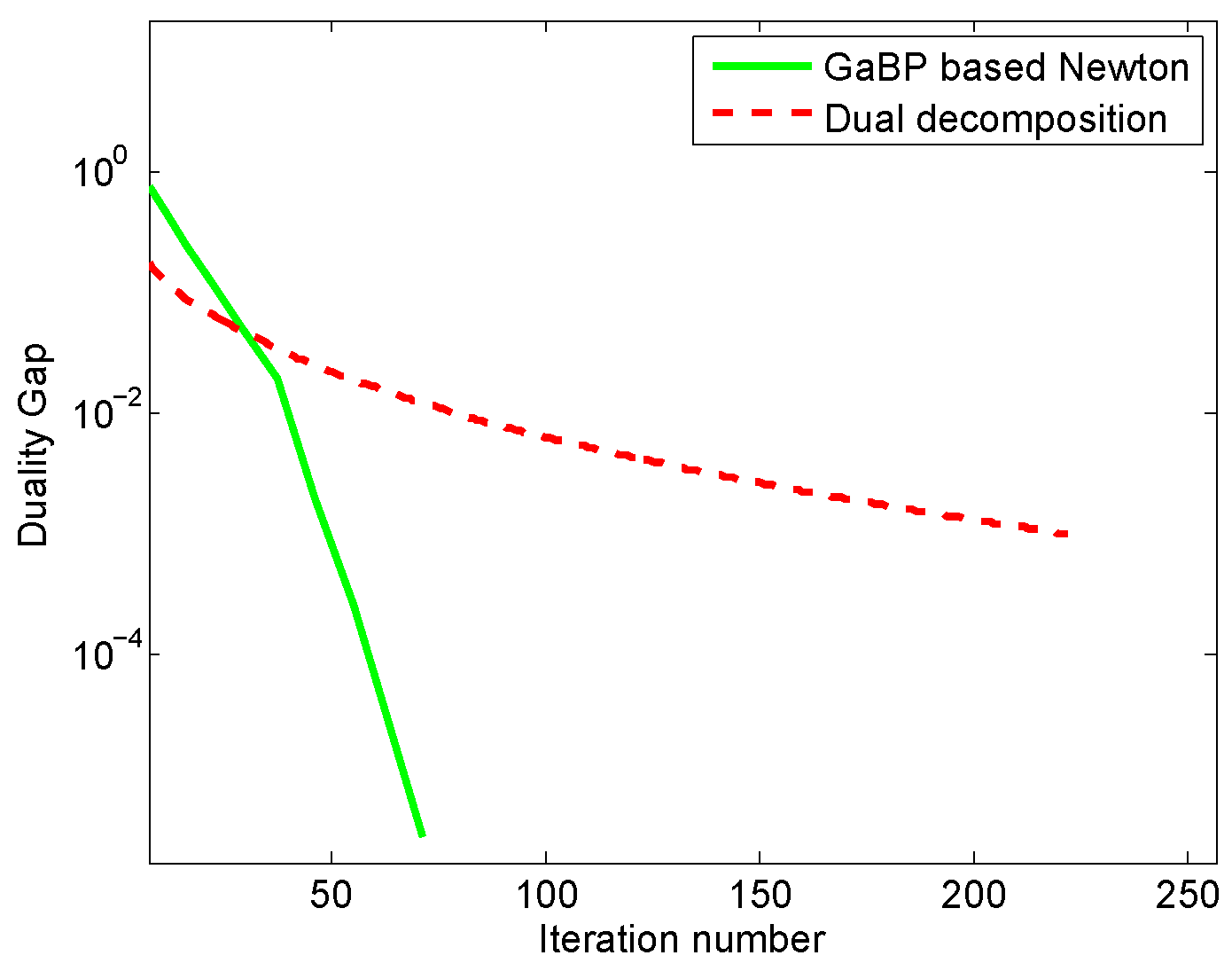
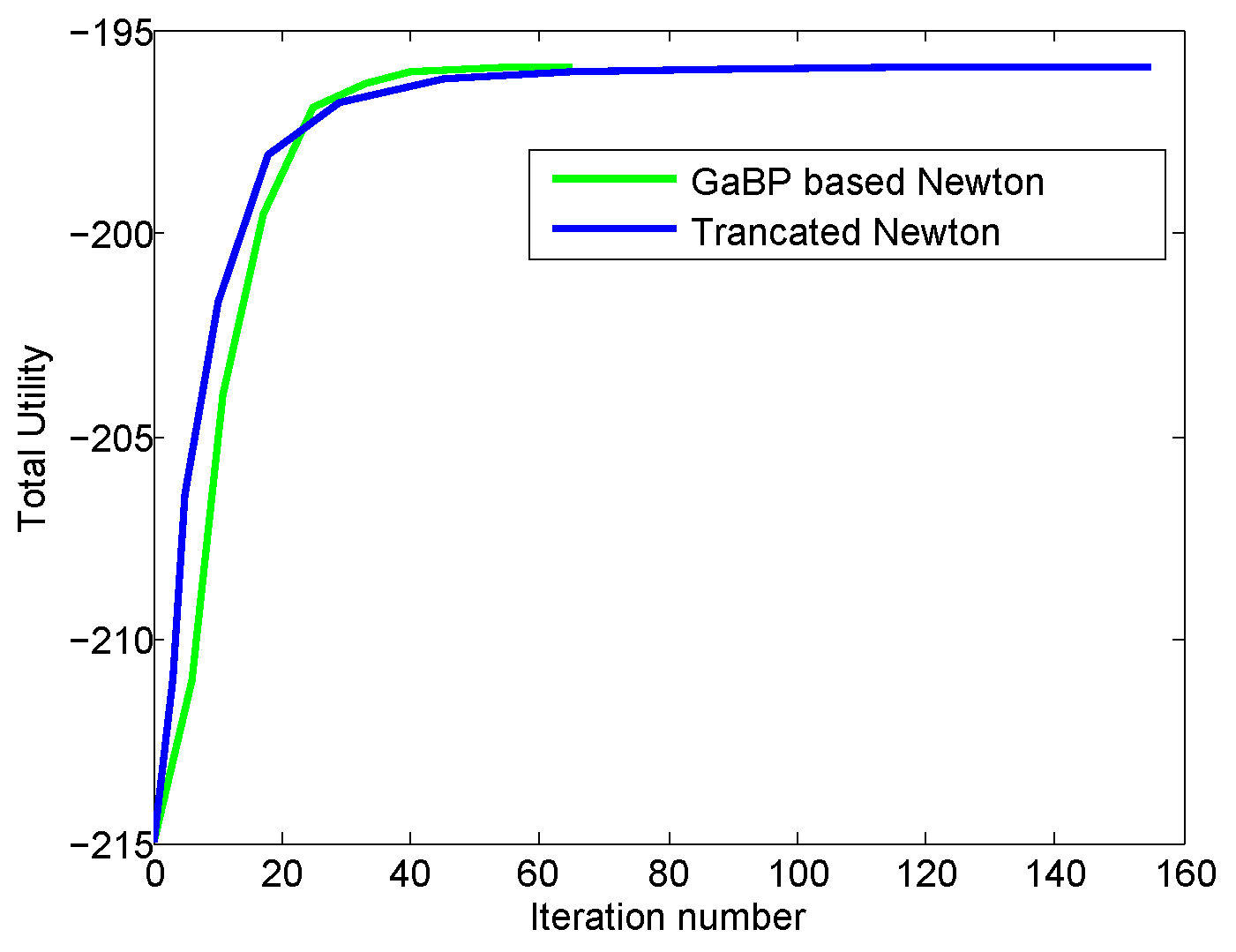
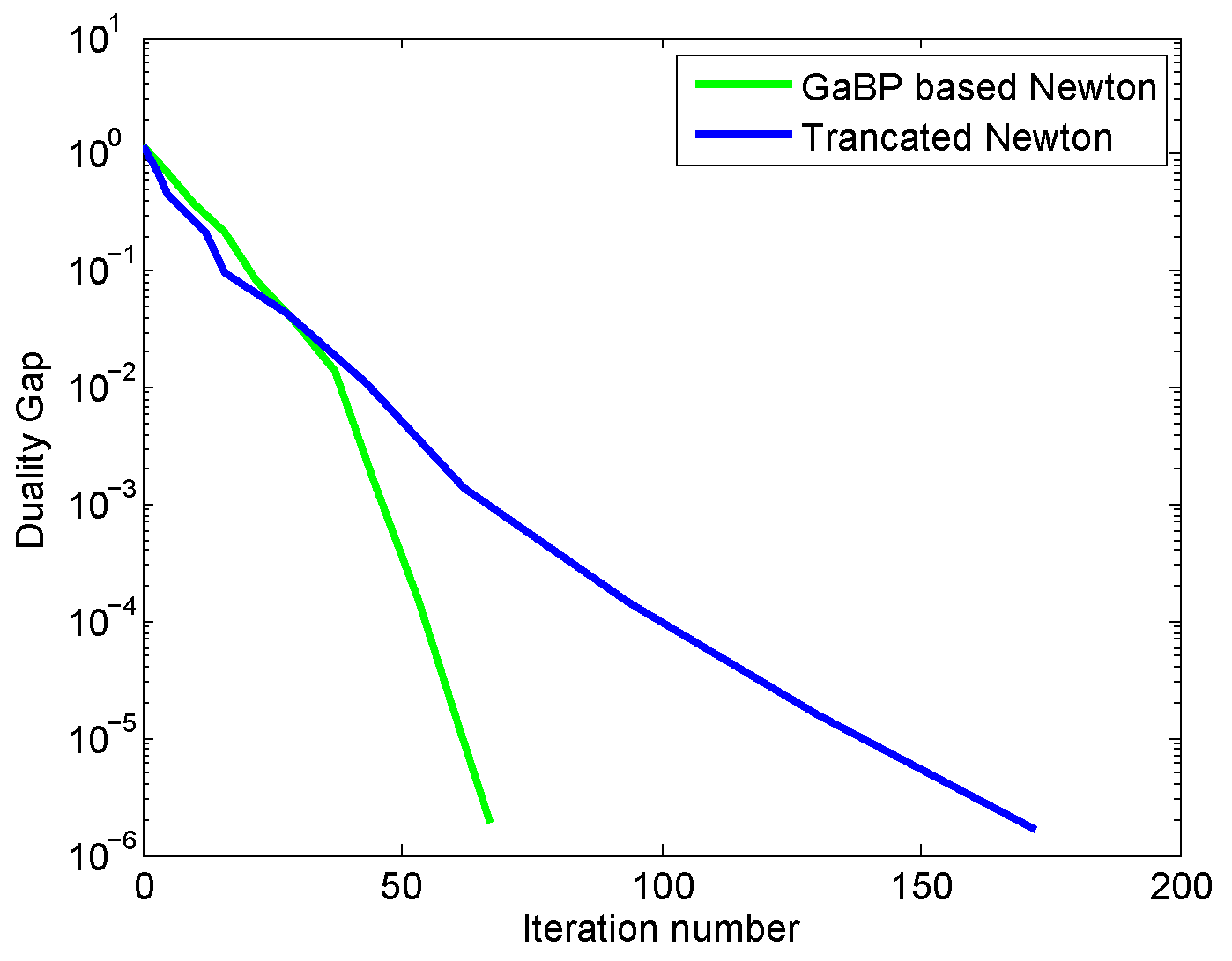
4.3.1. Analysis and Comparison with a Distributed Method
4.3.2. Analysis and Comparison with a Centralized Approach
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NUM | Network utility maximization |
| GaBP | Gaussian belief propagation |
| QoS | Quality of service |
| KKT | Karush-Kuhn-Tucker |
| PCG | preconditioned conjugate gradient |
| The transpose of a matrix or a vector |
Appendix A
References
- Kelly, F.P.; Maulloo, A.; Tan, D. Rate control for communication networks: Shadow prices, proportional fairness and stability. J. Oper. Res. Soc. Am. 1998, 49, 237–252. [Google Scholar] [CrossRef]
- Chiang, M.; Low, S.H.; Calderbank, A.R.; Doyle, J.C. Layering as optimization decomposition: A mathematical theory of network architectures. Proc. IEEE 2007, 95, 255–312. [Google Scholar] [CrossRef]
- Low, S.H.; Lapsley, D.E. Optimal flow control, I: Basic algorithm and convergence. IEEE/ACM Trans. Netw. 1999, 7, 861–874. [Google Scholar] [CrossRef]
- Trichakis, N.; Zymnis, A.; Boyd, S. Dynamic Network Utility Maximization with delivery contracts. In Proceedings of the IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 2907–2912. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Bertsekas, D.P. Nonlinear Programming, 2nd ed.; Athena Scientific: Nashua, NH, USA, 1999. [Google Scholar]
- Weiy, E.; Ozdaglary, A.; Eryilmazz, A.; Jadbabaie, A. A Distributed Newton Method for Dynamic Network Utility Maximization with Delivery Contracts. In Proceedings of the 46th Annual Conference on Information Sciences and Systems (CISS 2012), Princeton, NJ, USA, 21–23 March 2012; pp. 1–6. [Google Scholar]
- Weiss, Y.; Freeman, W.T. Correctness of Belief Propagation in Gaussian Graphical Models of Arbitrary Topology. Neural Comput. 2001, 13, 2173–2200. [Google Scholar] [CrossRef] [PubMed]
- Danny, B. Gaussian Belief Propagation: Theory and Application. Ph.D. Thesis, The Hebrew University of Jerusalem, Jerusalem, Israel, 2009. [Google Scholar]
- Wright, S.J. Primal-Dual Interior-Point Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Bickson, D.; Tock, Y.; Zymnis, A.; Boyd, S.P.; Dolev, D. Distributed large scale network utility maximization. In Proceedings of the IEEE International Symposium on Information Theory (ISIT 2009), Seoul, Korea, 28 June–3 July 2009; pp. 829–833. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Pham, Q.V.; Hwang, W.J. Network utility maximization-based congestion control over Wireless Networks: A survey and potential directives. IEEE Commun. Surv. Tutor. 2017, 9, 1173–1200. [Google Scholar] [CrossRef]
- Shengbin, L.; Jianhua, H. Design and analysis of distributed utility maximization algorithm for multihop wireless network with inaccurate feedback. Int. J. Commun. Syst. 2014, 27, 4280–4299. [Google Scholar]
- Jan, V. Dynamic Scoring: Probabilistic Model Selection Based on Utility Maximization. Entropy 2019, 21, 36. [Google Scholar] [CrossRef]
- Im, Y.; Joe-Wong, C.; Ha, S.; Sen, S.; Kwon, T.; Chiang, M. AMUSE: Empowering users for cost-aware offloading with throughput-delay tradeoff. IEEE Trans. Mob. Comput. 2016, 15, 1062–1076. [Google Scholar] [CrossRef]
- Merayo, N.; Pavon-Marino, P.; Aguado, J.C.; Duran, R.J.; Burrull, F.; Bueno-Delgaado, V. Fair bandwidth allocation algorithm for PONS based on network utility maximization. J. Opt. Commun. Netw. 2017, 9, 75–86. [Google Scholar] [CrossRef]
- Abhishek, S.; Eytan, M. Network utility maximization with heterogeneous traffic flows. In Proceedings of the 16th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt 2018), Shanghai, China, 7–11 May 2018; pp. 1–10. [Google Scholar]
- Shengbin, L.; Qingfu, Z. A multiutility framework with application for studying tradeoff between utility and lifetime in wireless sensor networks. IEEE Trans. Veh. Technol. 2011, 64, 4701–4711. [Google Scholar]
- Wang, W.; Palaniswami, M.; Low, S.H. Optimal flow control and routing in multi-path net-works. Perform. Eval. 2003, 52, 119–132. [Google Scholar] [CrossRef]
- Lin, X.; Shroff, N.B. Utility maximization for communication networks withmultipath routing. IEEE Trans. Autom. Contr. 2006, 51, 766–781. [Google Scholar] [CrossRef]
- Pal, A.; Kant, K. On the Feasibility of Distributed Sampling Rate Adaptation in Heterogeneous and Collaborative Wireless Sensor Networks. In Proceedings of the 25th International Conference on Computer Communication and Networks (ICCCN 2016), Waikoloa, HI, USA, 1–4 August 2016; pp. 1–9. [Google Scholar]
- Liao, S.; Sun, J.; Chen, Y.; Wang, Y.; Zhang, P. Distributed power control for wireless networks via the alternating direction method of multipliers. J. Netw. Comput. Appl. 2015, 55, 81–88. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M. Extended duality for nonlinear programming. Comput. Optim. Appl. 2010, 47, 33–59. [Google Scholar] [CrossRef]
- Liu, R.; Sinha, P.; Koksal, C.E. Joint energy management and resource allocation inrechargeable sensor networks. In Proceedings of the 29th Conference on Computer Communications (INFOCOM 2010), San Diego, CA, USA, 15–19 March 2010; pp. 902–910. [Google Scholar]
- Pal, A.; Kant, K. Water flow driven sensor networks for leakage and contamination monitoring. In Proceedings of the IEEE 16th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM 2015), Boston, MA, USA, 14–17 June 2015; pp. 1–9. [Google Scholar]
- Sadagopan, N.; Singh, M.; Krishnamachari, B. Decentralized utility-based sensor network design. Mob. Netw. Appl. 2006, 11, 341–350. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Mao, S.; Neel, J.; Reed, J. Performance evaluation of cognitive radios: Metrics, utility functions, and methodology. Proc. IEEE 2009, 97, 642–659. [Google Scholar] [CrossRef]
- Qingkai, L.; Eytan, M. Network Utility Maximization in Adversarial Environments. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM 2018), Honolulu, HI, USA, 15–19 April 2018; pp. 1–10. [Google Scholar]
- Junting, C.; Vincent, K.N.L.; Yong, C. Distributive network utility maximization over time-varying fading channels. IEEE Trans. Signal Process. 2011, 59, 2395–2404. [Google Scholar]
- Lutbat, Y.; Enkhbat, R.; Suk-Hwan, L.; Won-Joo, H. Parametric network utility maximization problem. Optim. Lett. 2014, 8, 889–901. [Google Scholar]
- Guddat, J.; Guerra, V.F. Parametric Optimization: Singularities, Pathfollowing and Jumps; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Ehsan, N.; Tansu, A.; Girish, N.N.; Robin, J.E. Convergence analysis of quantized primal-dual algorithms in network utility maximization problems. IEEE Trans. Control Netw. Syst. 2018, 5, 284–297. [Google Scholar]
- Michael, Z.; Alejandro, R.; Asuman, O.; Ali, J. Accelerated dual descent for network flow optimization. IEEE Trans. Autom. Control 2014, 59, 905–920. [Google Scholar]
- Zymnis, A.; Trichakis, N.; Boyd, S.; O’Neill, D. An interior-point method for large scale network utility maximization. In Proceedings of the Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 26–28 September 2007; pp. 877–882. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Francisco, CA, USA, 1988. [Google Scholar]
- Kelley, C.T. Iterative Methods for Linear and Nonlinear Equations; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1995; ISBN 9780898713527. [Google Scholar]
- Avriel, M. Nonlinear Programming: Analysis and Methods; Dover Publishing: Mineola, NY, USA, 2003; ISBN 0-486-43227-0. [Google Scholar]
- Bonnans, J.F.; Gilbert, J.C.; Lemaréchal, C.; Sagastizábal, C.A. Numerical Optimization: Theoretical and Practical Aspects; Springer: Berlin, Germany, 2006; ISBN 3-540-35445-X. [Google Scholar]
| Newton Step Number | GaBP | PCG |
|---|---|---|
| 1 | 6 | 3 |
| 2 | 6 | 2 |
| 3 | 6 | 2 |
| 4 | 7 | 5 |
| 5 | 9 | 9 |
| 6 | 10 | 12 |
| 7 | 12 | 13 |
| 8 | 15 | 22 |
| 9 | 14 | 29 |
| 10 | 13 | 34 |
| 11 | 43 | |
| total | 98 | 174 |
| Newton Step Number | GaBP | PCG |
|---|---|---|
| 1 | 6 | 2 |
| 2 | 5 | 4 |
| 3 | 5 | 8 |
| 4 | 6 | 3 |
| 5 | 7 | 16 |
| 6 | 7 | 20 |
| 7 | 7 | 36 |
| 8 | 7 | 64 |
| 9 | 101 | |
| total | 50 | 253 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, S.; Sun, J. Gaussian Belief Propagation for Solving Network Utility Maximization with Delivery Contracts. Entropy 2019, 21, 708. https://doi.org/10.3390/e21070708
Liao S, Sun J. Gaussian Belief Propagation for Solving Network Utility Maximization with Delivery Contracts. Entropy. 2019; 21(7):708. https://doi.org/10.3390/e21070708
Chicago/Turabian StyleLiao, Shengbin, and Jianyong Sun. 2019. "Gaussian Belief Propagation for Solving Network Utility Maximization with Delivery Contracts" Entropy 21, no. 7: 708. https://doi.org/10.3390/e21070708
APA StyleLiao, S., & Sun, J. (2019). Gaussian Belief Propagation for Solving Network Utility Maximization with Delivery Contracts. Entropy, 21(7), 708. https://doi.org/10.3390/e21070708




