Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis
Abstract
1. Introduction
Thermodynamics-Based Fatigue Models
- Section 2 introduces and reviews the DEG theorem and procedure.
- Section 3 reviews thermodynamics and introduces phenomenological entropy, consisting of a boundary work component and an internal fluctuation component.
- Section 4 couples fatigue analysis to thermodynamics.
- Section 5 uses published experimental data to validate and visualize the model.
- Section 6 discusses results and the models.
- Section 7 summarizes and concludes.
2. Degradation-Entropy Generation Theorem Review
2.1. Statement
2.2. Generalized Degradation Analysis Procedure
- (1)
- identifies the degradation measure w, dissipative process energies and phenomenological variables ,
- (2)
- finds entropy generation caused by the ,
- (3)
- evaluates coefficients by measuring increments/accumulation or rates of degradation versus increments/accumulation or rates of entropy generation, with process active.
3. Thermodynamic Formulations
3.1. First Law—Energy Conservation
3.2. Second Law and Entropy Balance—Irreversible Entropy Generation
3.3. Combining First and Second Laws with Helmholtz Potential
3.4. Entropy Content S and Internal Free Energy Dissipation ““
4. Differential/Elemental Fatigue Analysis
4.1. Local Equilibrium
4.2. Helmholtz Energy Dissipation and Entropy Generation
4.3. Stress and Strain as Thermodynamic Variables
4.3.1. Cyclic Loading—High-and Low-Cycle Fatigue
4.3.2. Infinite Life Design
4.4. Degradation-Entropy Generation (DEG) Analysis
4.4.1. Applying the Degradation-Entropy Generation Theorem to Cumulative Strain (or Stress)
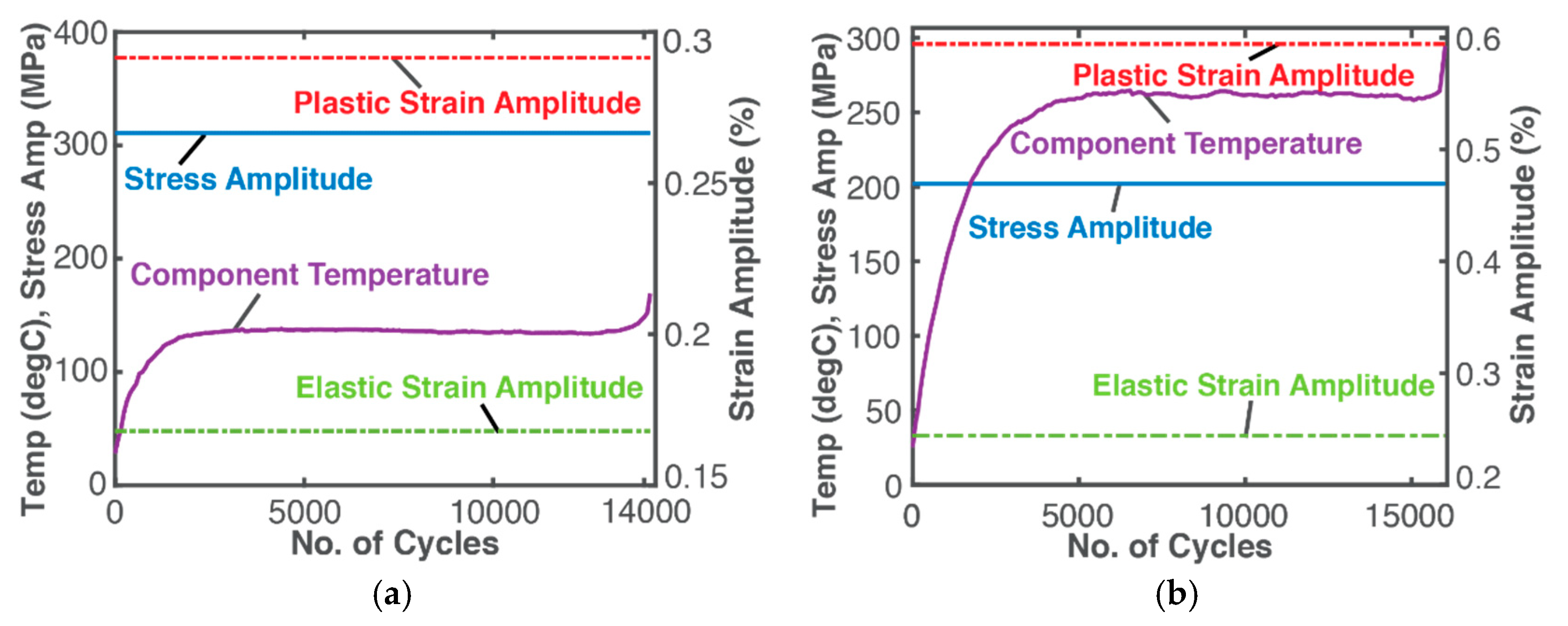
5. Fatigue Experiments and Data Analysis—Instantaneous Characterization
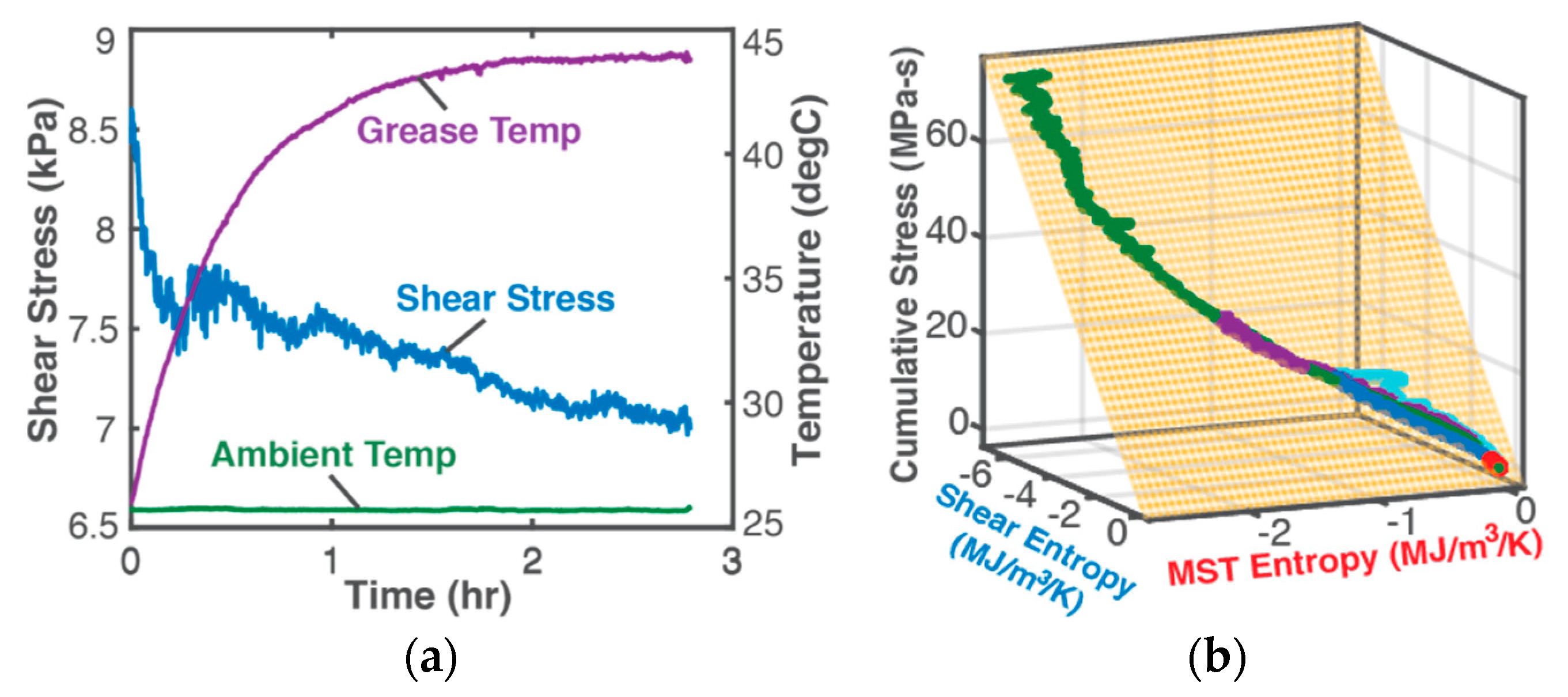
5.1. Instantaneous Evolution of Helmholtz Energy Density (Toughness) and Entropy Density
5.2. DEG Analysis—Strain Versus Entropy (Linear Transformation)
5.3. Phenomenological Transformation Versus Measured/Estimated Fatigue Parameter
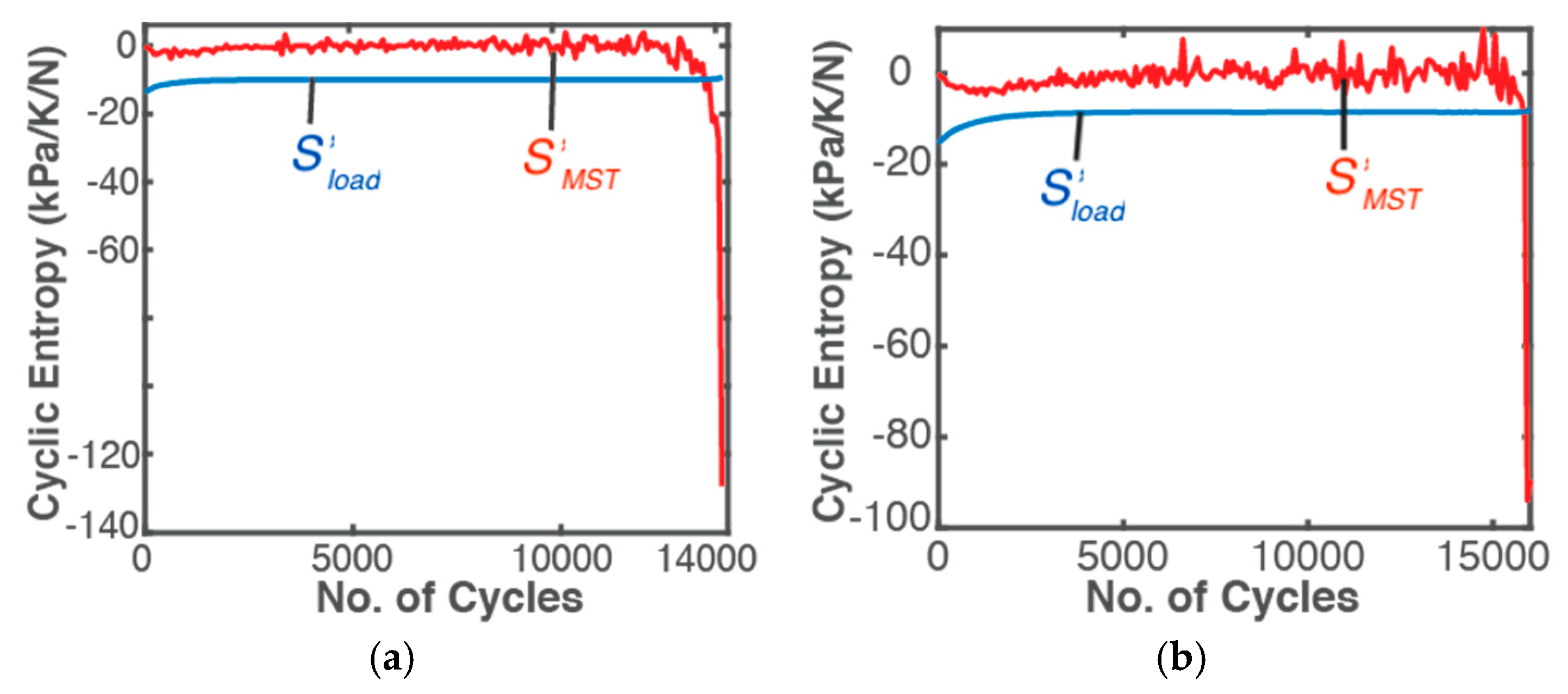
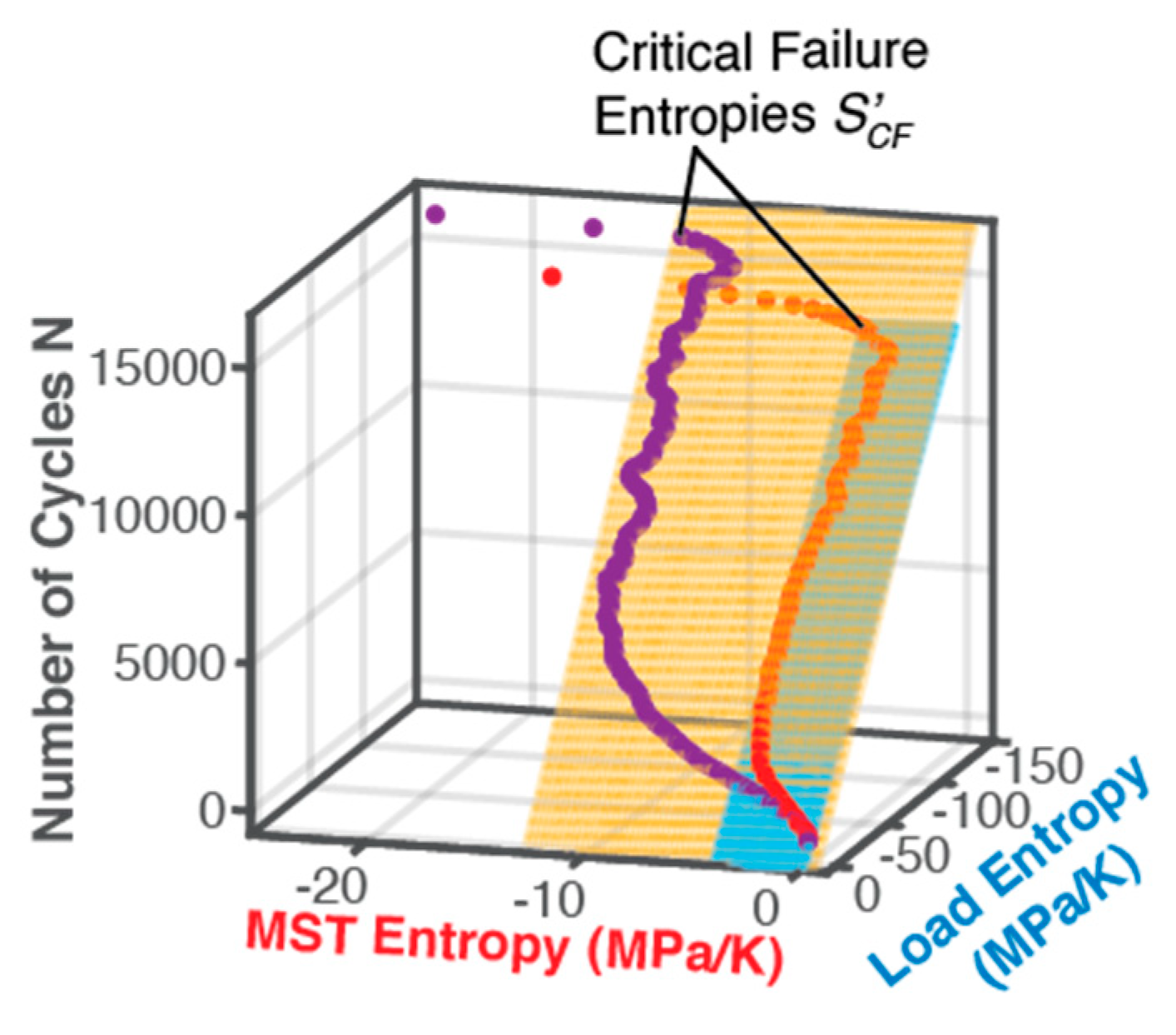
Critical Failure Entropy —MST Entropy and Fatigue Failure
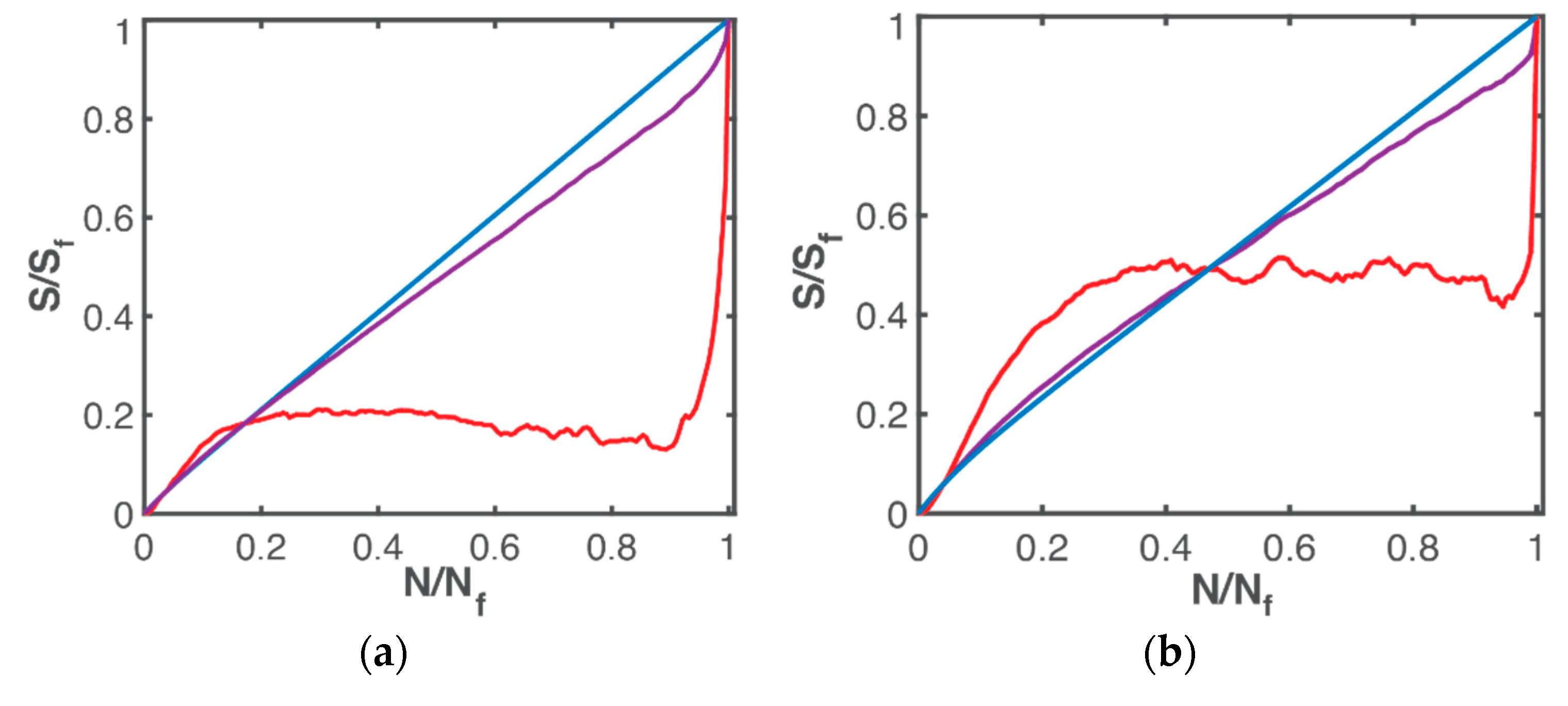
5.4. Nonlinear Response
6. Discussion and Contributions
- phenomenological entropy generation is the sum of boundary work/load entropy and microstructurothermal MST entropy ;
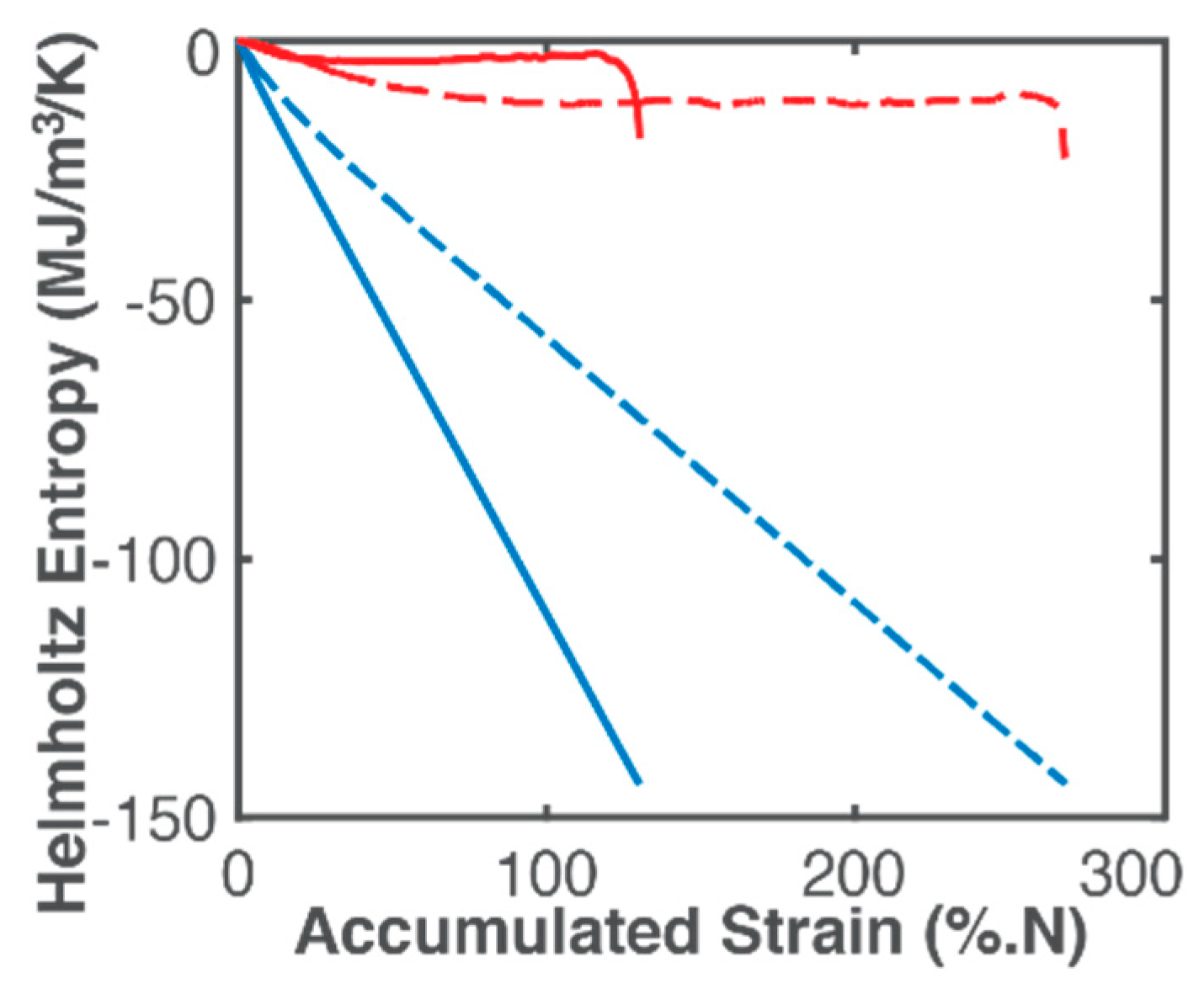
- entropy generation is the difference between phenomenological and reversible Helmholtz entropies at every instant;
- entropy generation is always non-negative in accordance with the second law, whereas components and are directional, negative for a loaded system. This implies during load application in accordance with experience and thermodynamic laws. The actual work obtained from the system is always less than the maximum/reversible work.
6.1. Features of the DEG Methodology
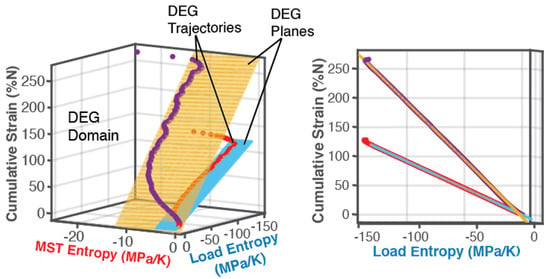
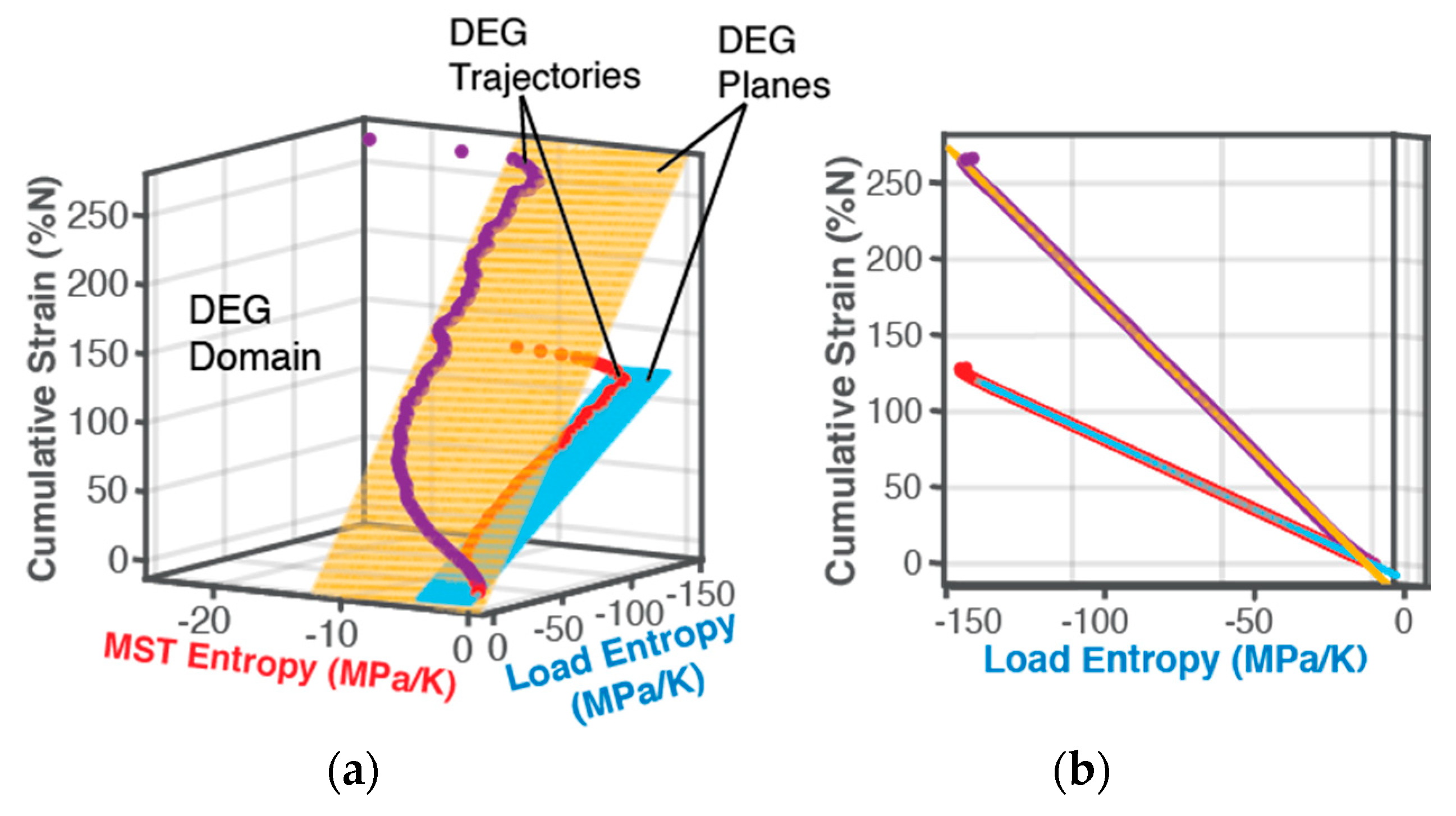
6.1.1. DEG Trajectories, Surfaces and Domains
6.1.2. DEG Coefficients
6.2. Entropy Generation vs Number of Cycles—A Linear Arrow of Time
7. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | Name | Unit |
| A | Helmholtz free energy density | J/m3 |
| B | DEG coefficient | %NK/MPa |
| C | heat capacity | J/K |
| N | number of cycles | |
| N, Nk | number of moles of substance | mol |
| P | dissipative process energy | J |
| P | pressure | Pa |
| Q | heat | J |
| S | entropy density or entropy content | J/m3K or MPa/K |
| S’ | entropy generation or production | J/m3K or MPa/K |
| t | time | s |
| T | temperature | degC or K |
| U | internal energy | J |
| volume | m3 | |
| w | degradation measure | |
| W | work, strain energy density | J, J/m3 |
| Symbols | ||
| α | thermal expansion coefficient | /K |
| κT | isothermal loadability | |
| μ | chemical potential | |
| ρ | density | Kg/m3 |
| stress | MPa | |
| strain | % | |
| ζ | phenomenological variable | |
| Subscripts & acronyms | ||
| 0 | initial | |
| e | elastic | |
| MST, μT | Micro-Structuro-Thermal | |
| p | plastic | |
| rev | reversible | |
| irr | irreversible | |
| phen | phenomenological | |
| DEG | Degradation-Entropy Generation |
References
- Vasudevan, A.K.; Sadananda, K.; Glinka, G. Critical parameters for fatigue damage. Int. J. Fatigue 2001, 23, 39–53. [Google Scholar] [CrossRef]
- Callister, W.D., Jr. Fundamentals of Materials Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Timoshenko, S. Strength of Materials (Part I), 2nd ed.; D. Van Nostrand Company Inc.: New York, NY, USA, 1940. [Google Scholar]
- Goodno, B.J.; Gere, J.M. Mechanics of Materials, 9th ed.; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Hibbeler, R.C. Mechanics of Materials, 10th ed.; Pearson: London, UK, 2017. [Google Scholar]
- Shigley, J.E.; Mischke, C.R. (Eds.) Standard Handbook of Machine Design, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Vasudevan, A.K.; Sadananda, K.; Iyyer, N. Fatigue damage analysis: Issues and challenges. Int. J. Fatigue 2015, 82, 120–133. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. A thermodynamics based damage mechanics constitutive model for low cycle fatigue analysis of microelectronics solder joints incorporating size effects. Int. J. Solids Struct. 2005, 42, 3744–3772. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. Damage mechanics constitutive model for Pb/Sn solder joints incorporating nonlinear kinematic hardening and rate dependent effects using a return mapping integration algorithm. Mech. Mater. 2006, 38, 585–598. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M.; Ye, H. A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 2003, 40, 7315–7327. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An Irreversible Thermodynamics Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
- Basaran, C.; Gomez, J.; Gunel, E.; Li, S. Thermodynamic Theory for Damage Evolution in Solids. In Handbook of Damage Mechanics; Voyiadjis, G., Ed.; Springer: New York, NY, USA, 2014; pp. 721–762. [Google Scholar]
- Amiri, M.; Khonsari, M.M. Life prediction of metals undergoing fatigue load based on temperature evolution. Mater. Sci. Eng. A 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. A thermodynamic approach to fatigue damage accumulation under variable loading. Mater. Sci. Eng. A 2010, 527, 6133–6139. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M. Real-time fatigue life monitoring based on thermodynamic entropy. Struct. Health Monit. 2011, 10, 189–197. [Google Scholar] [CrossRef]
- Amiri, M.; Naderi, M.; Khonsari, M.M. An Experimental Approach to Evaluate the Critical Damage. Int. J. Damage Mech. 2011, 20, 89–112. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. A comprehensive fatigue failure criterion based on thermodynamic approach. J. Compos. Mater. 2012, 46, 437–447. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. Thermodynamic analysis of fatigue failure in a composite laminate. Mech. Mater. 2012, 46, 113–122. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. On the role of damage energy in the fatigue degradation characterization of a composite laminate. Compos. Part B Eng. 2013, 45, 528–537. [Google Scholar] [CrossRef]
- Amiri, M.; Modarres, M. An entropy-based damage characterization. Entropy 2014, 16, 6434–6463. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Chaboche, J.L. Constitutive Equations for Cyclic Plasticity and Cyclic Viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 1985. [Google Scholar]
- Doelling, B.P.; Ling, K.L.; Bryant, F.F.; Heilman, M.D. An experimental study of the correlation between wear and entropy flow in machinery components. J. Appl. Phys. 2000, 88, 2999–3003. [Google Scholar] [CrossRef]
- Duyi, Y.; Zhenlin, W. A new approach to low-cycle fatigue damage based on exhaustion of static toughness and dissipation of cyclic plastic strain energy during fatigue. Int. J. Fatigue 2001, 23, 679–687. [Google Scholar] [CrossRef]
- Sosnovskiy, L.; Sherbakov, S. Surprises of Tribo-Fatigue; Magic Book: Minsk, Belarus, 2009. [Google Scholar]
- Sosnovskiy, L.; Sherbakov, S. Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Osara, J.A.; Bryant, M.D. Thermodynamics of Grease Degradation. Tribol. Int. 2019, 137, 433–445. [Google Scholar] [CrossRef]
- Strutt, J.W.; Rayleigh, B. The Theory of Sound; Macmillan & Co.: London, UK, 1877; Volume 2. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible processes 1. Am. Phys. Soc. 1931, 37, 405. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; John Wiley & Sons: Hoboken, NJ, USA, 1977. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Bryant, M.D. On Constitutive Relations for Friction From Thermodynamics and Dynamics. J. Tribol. 2016, 138, 041603. [Google Scholar] [CrossRef]
- Bryant, M.D. Entropy and Dissipative Processes of Friction and Wear. FME Trans. 2009, 37, 55–60. [Google Scholar]
- Osara, J.A. Thermodynamics of Degradation; The University of Texas at Austin: Austin, TX, USA, 2017. [Google Scholar]
- Osara, J.A.; Bryant, M.D. A Thermodynamic Model for Lithium-Ion Battery Degradation: Application of the Degradation-Entropy Generation Theorem. Inventions 2019, 4, 23. [Google Scholar] [CrossRef]
- DeHoff, R.T. Thermodynamics in Material Science, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- de Groot, S.R. Thermodynamics of Irreversible Processes; North-Holland Publishing Company: Amsterdam, The Netherlands, 1951. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Charles C Thomas: Springfield, IL, USA, 1955. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1997; Volume 70. [Google Scholar]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 5th ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Burghardt, M.D.; Harbach, J.A. Engineering Thermodynamics, 4th ed.; HarperCollins College Publishers: New York, NY, USA, 1993. [Google Scholar]
- Karnopp, D. Bond Graph Models for Electrochemical Energy Storage: Electrical, Chemical and Thermal Effects. J. Frankl. Inst. 1990, 327, 983–992. [Google Scholar] [CrossRef]
- Bejan, A. The Method of Entropy Generation Minimization. In Energy and the Environment; Springer: Dordrecht, The Netherlands, 1990; pp. 11–22. [Google Scholar]
- Pal, R. Demystification of the Gouy-Stodola theorem of thermodynamics for closed systems. Int. J. Mech. Eng. Educ. 2017, 45, 142–153. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: London, UK; New York, NY, USA, 1971. [Google Scholar]
- Morris, J.W. Notes on the Thermodynamics of Solids, Chapter 16: Elastic Solids. 2007, pp. 366–411. Available online: http://www.mse.berkeley.edu/groups/morris/MSE205/Extras/Elastic.pdf (accessed on 10 July 2019).
- Ramberg, W.; Osgood, W. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals. In Internal Friction, Damping, and Cyclic Plasticit; ASTM International: West Conshohocken, PA, USA, 1965. [Google Scholar]
- Kim, K.; Chen, X.; Kim, K.S. Estimation methods for fatigue properties of steels under axial and torsional loading Estimation methods for fatigue properties of steels under axial and torsional loading. Int. J. Fatigue 2002, 24, 783–793. [Google Scholar] [CrossRef]
- Socie, D. Multiaxial Fatigue Damage Models. ASME Trans. 1987, 324–325, 747–750. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Meneghetti, G. Analysis of the fatigue strength of a stainless steel based on the energy dissipation. Int. J. Fatigue 2007, 29, 81–94. [Google Scholar] [CrossRef]
- Osara, J.A. Thermodynamics of Manufacturing Processes—The Workpiece and the Machinery. Inventions 2019, 4, 28. [Google Scholar] [CrossRef]
- Barsom, J.; Rolfe, S. Fracture and Fatigue Control. In Structures: Applications of Fracture Mechanics; ASTM International: West Conshohocken, PA, USA, 1999. [Google Scholar]
- Bryant, M. Unification of friction and wear. Recent Dev. Wear Prev. Frict. Lubr. 2010, 248, 159–196. [Google Scholar]
- Rice, J.R. Thermodynamics of the quasi-static growth of Griffith cracks. J. Mech. Phys. Solids 1978, 26, 61–78. [Google Scholar] [CrossRef]


| Property | Bending | Torsion |
|---|---|---|
| Modulus, GPa | E = 195 | G = 82.8 |
| Fatigue strength coefficient, MPa | = 1000 | = 709 |
| Fatigue strength exponent b | −0.114 | −0.121 |
| Fatigue ductility coefficient | = 0.171 | = 0.413 |
| Fatigue ductility exponent c | −0.402 | −0.353 |
| Cyclic strain hardening exponent n’ | 0.287 | 0.296 |
| Specific heat capacity , J/kg K | 500 | |
| Density , kg/m3 | 7900 | |
| Coefficient of linear thermal expansion | 17.3 × 10−6 | |
| Load | %N | GJ/m3 | GJ/m3 | MPa/K | MPa/K | %NK/MPa | %NK/MPa |
|---|---|---|---|---|---|---|---|
| Bending | 130.1 | −58.0 | −7.8 | −143.5 | −18.8 | −0.92 | 0.22 |
| Torsion | 268.5 | −73.4 | −12.3 | −143.5 | −24.1 | −1.96 | 0.42 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osara, J.A.; Bryant, M.D. Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis. Entropy 2019, 21, 685. https://doi.org/10.3390/e21070685
Osara JA, Bryant MD. Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis. Entropy. 2019; 21(7):685. https://doi.org/10.3390/e21070685
Chicago/Turabian StyleOsara, Jude A., and Michael D. Bryant. 2019. "Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis" Entropy 21, no. 7: 685. https://doi.org/10.3390/e21070685
APA StyleOsara, J. A., & Bryant, M. D. (2019). Thermodynamics of Fatigue: Degradation-Entropy Generation Methodology for System and Process Characterization and Failure Analysis. Entropy, 21(7), 685. https://doi.org/10.3390/e21070685