An Entropy Regularization k-Means Algorithm with a New Measure of between-Cluster Distance in Subspace Clustering
Abstract
1. Introduction
- The study on subspace clustering mentioned in previous papers is summarized.
- By optimization, the update rules of ERKM algorithm are obtained, and the convergence and robustness analysis of the algorithm are given.
- The hyperparameters are studied on synthetic and real-life datasets. Finally, through experimental comparison, the results show that the ERKM algorithm outperforms most existing state-of-the-art k-means-type clustering algorithms.
2. Related Work
2.1. Sparseness-Based Methods
2.2. Entropy-Based Methods
2.3. Between-Cluster Measure-Based Methods
2.3.1. Liang Bai’s Methods
2.3.2. Huang’s Methods
2.4. Others
3. Entropy Regularization Clustering
3.1. ERKM Algorithm
| Algorithm 1 ERKM. |
| Input: The number of clusters k and parameters ; Randomly choose k cluster centers, and set all initial weights with a normalized uniform distribution; repeat Fixed , update the partition matrix U by (29) Fixed , update the cluster centers Z by (23) Fixed , update the dimension weights W by (14) until Convergence return |
- For others, according to (14) and (15), is proportional to . The larger , the larger . This violates the basic idea that the more important the corresponding dimension, the smaller the sum of the distance on this dimension. Under this circumstance, it will cause the value of , so that the objective function diverges.
3.2. Convergency and Complexity Analysis
4. Experiments and Discussion
4.1. Experimental Setup
4.2. Evaluation Method
4.3. Parameter Setting
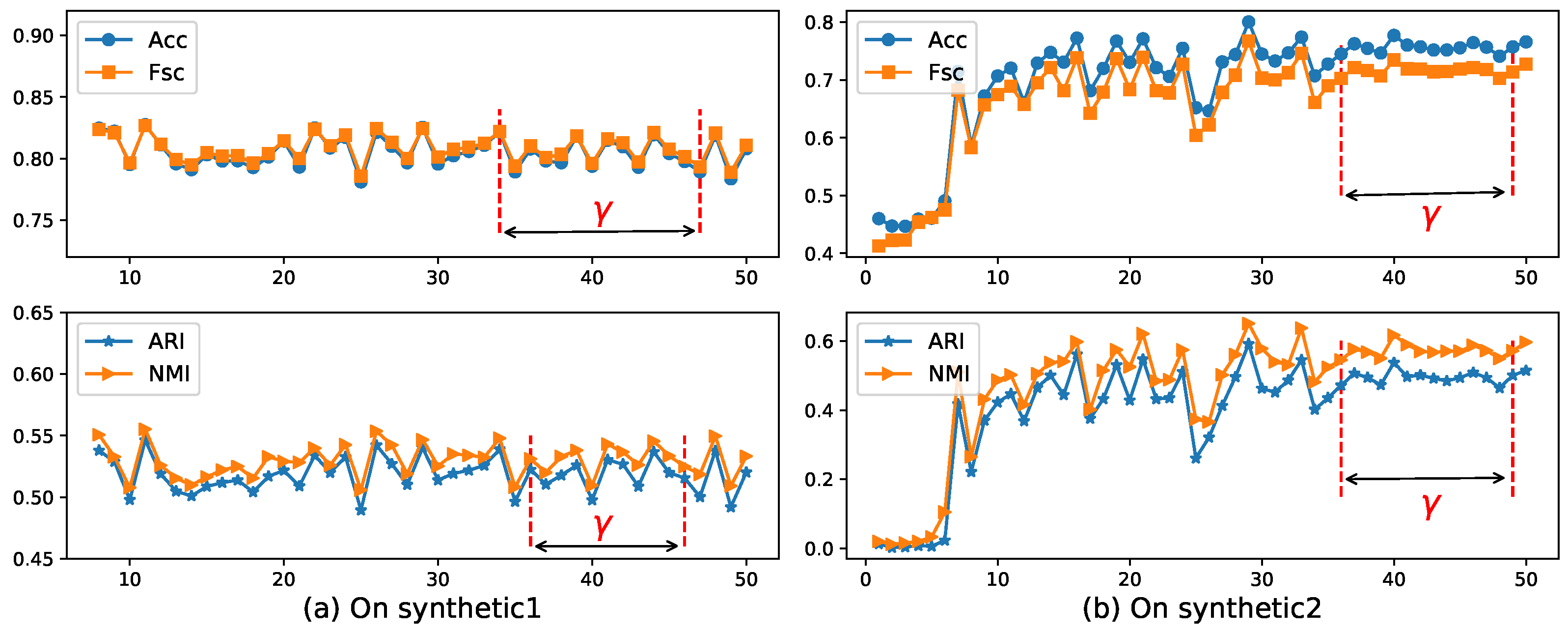
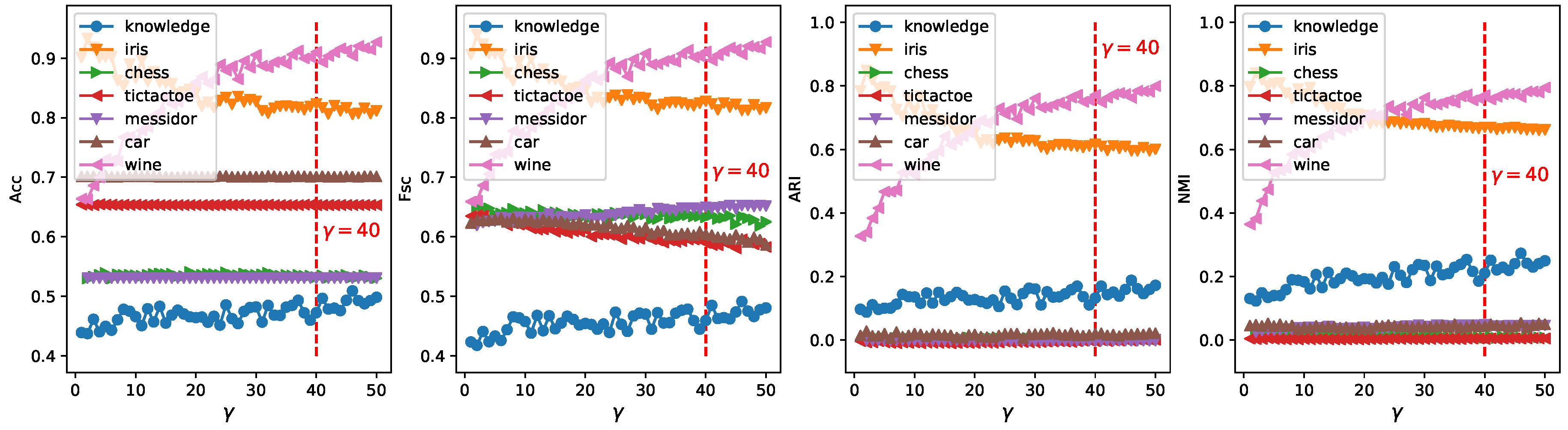
- Parameter :Hyperparameter appears in the EWKM, ESSC, and ERKM algorithms. ESSC and ERKM algorithms were directly extended from the EWKM algorithm, and only a between-cluster distance constraint was added to the objective function of the EWKM algorithm. At the same time, since the EWKM only contained one parameter , the value of can be studied by the performance of EWKM on two synthetic and seven real-life datasets, respectively. We fixed the range of in [1, 50] and set the step to 1.
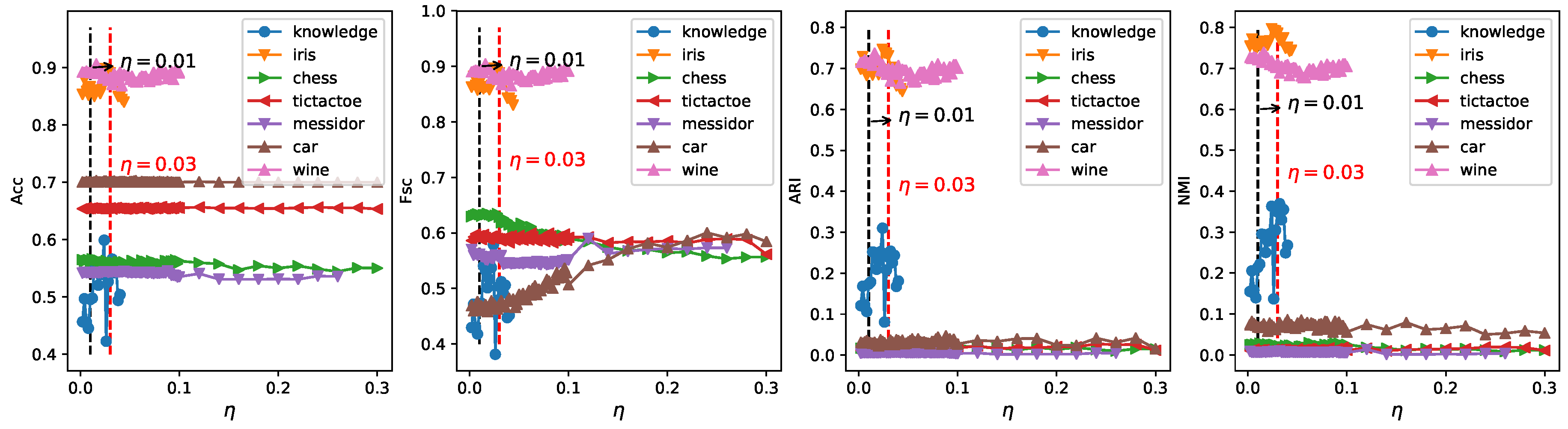
- Parameter :In the algorithm ERKM, has a similar effect as in the ESSC algorithm. However, since the two algorithms adopted different feature weighting methods and between-cluster distance measures, a reasonable value will be selected by the results of the ERKM algorithm on two synthetic and seven real-life datasets, respectively. Since the within-cluster distance and the between-cluster distance have different contributions to the whole clustering process, the value of should satisfy the condition (33), so as to avoid the divergence of the objective function. In the section below, we fixed the range of in [0.002, 0.2] and set the step to 0.002 in [0, 0.05] and 0.02 in (0.05, 0.2] to search for a proper value.
4.4. Experiment on Synthetic Data
4.4.1. Parameter Study
4.4.2. Results and Analysis
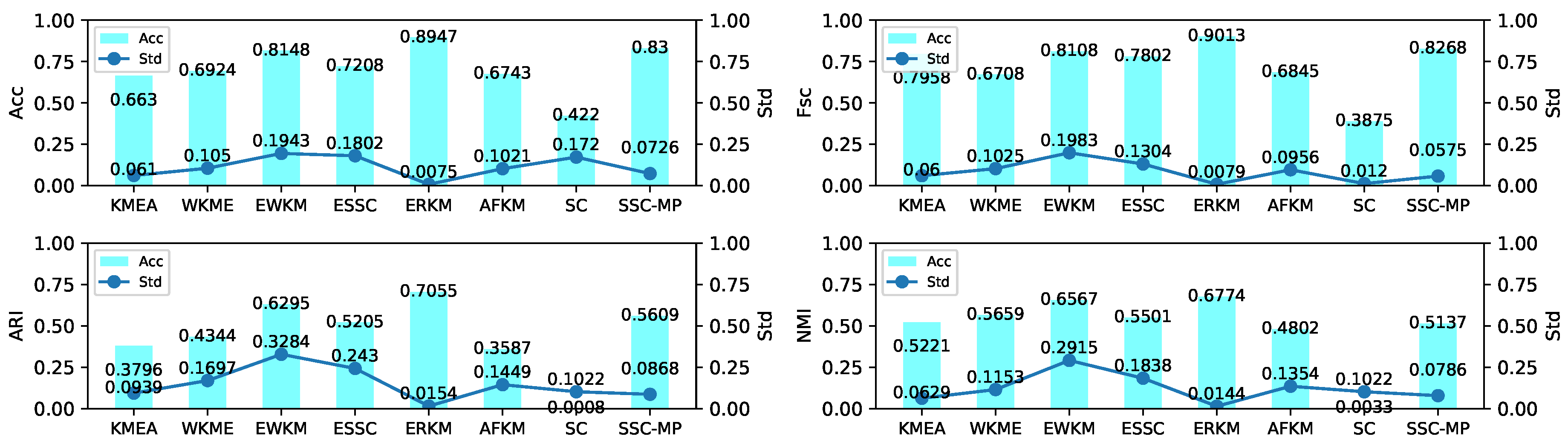
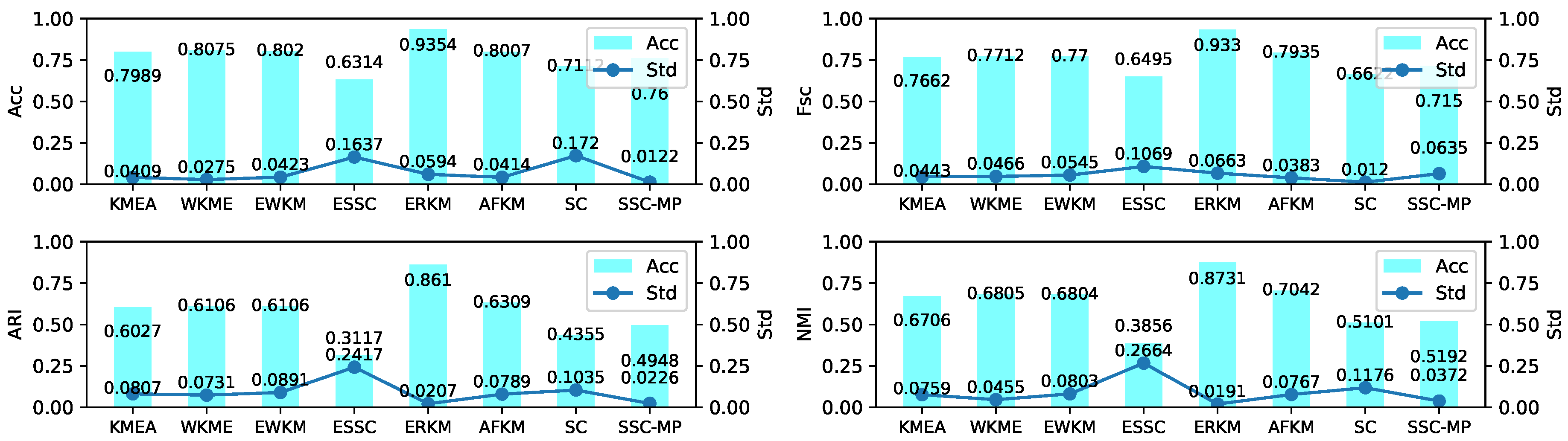
4.5. Experiment on Real-Life Data
4.5.1. Parameter Study
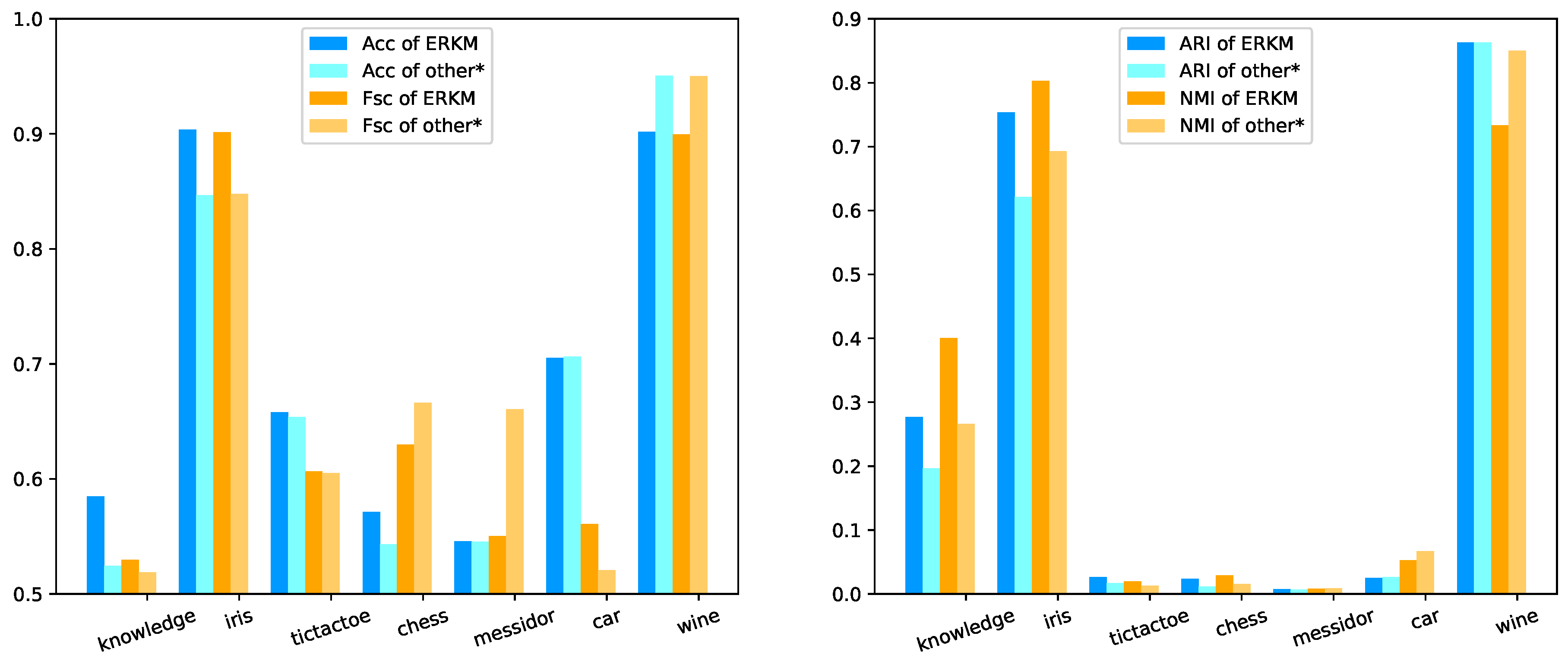
4.5.2. Results and Analysis
4.6. Convergence Speed
4.7. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ERKM | Entropy Regularization k-means |
| KMEA | k-Means |
| WKME | Weighted k-Means |
| EWKM | Entropy Weighted k-Means |
| ESSC | Enhanced Soft-Subspace Clustering |
| AFKM | Assumption-Free k-Means |
| SC | Sampling-Clustering |
| SSC-MP | Subspace Sparse Clustering by the greedy orthogonal Matching Pursuit |
| Acc | Accuracy |
| ARI | Adjusted Rand Index |
| Fsc | F-score |
| NMI | Normal Mutual Information |
References
- Huang, Z. Extensions to the k-means algorithm for clustering large datasets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1967; Volume 1, pp. 281–297. [Google Scholar]
- Green, P.E.; Kim, J.; Carmone, F.J. A preliminary study of optimal variable weighting in k-means clustering. J. Classif. 1990, 7, 271–285. [Google Scholar] [CrossRef]
- ElSherbiny, A.; Moreno-Hagelsieb, G.; Walsh, S.; Wang, Z. Phylogenomic clustering for selecting non-redundant genomes for comparative genomics. Bioinformatics 2013, 29, 947–949. [Google Scholar]
- Deng, Z.; Choi, K.S.; Chung, F.L.; Wang, S. Enhanced soft subspace clustering integrating within-cluster and between-cluster information. Pattern Recognit. 2010, 43, 767–781. [Google Scholar] [CrossRef]
- Sardana, M.; Agrawal, R. A comparative study of clustering methods for relevant gene selection in microarray data. In Advances in Computer Science, Engineering & Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 789–797. [Google Scholar]
- Tang, L.; Liu, H.; Zhang, J. Identifying evolving groups in dynamic multimode networks. IEEE Trans. Knowl. Data Eng. 2012, 24, 72–85. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, J. Projective ART for clustering datasets in high dimensional spaces. Neural Netw. 2002, 15, 105–120. [Google Scholar] [CrossRef]
- Huang, J.Z.; Ng, M.K.; Rong, H.; Li, Z. Automated variable weighting in k-means type clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 657–668. [Google Scholar] [CrossRef]
- DeSarbo, W.S.; Carroll, J.D.; Clark, L.A.; Green, P.E. Synthesized clustering: A method for amalgamating alternative clustering bases with differential weighting of variables. Psychometrika 1984, 49, 57–78. [Google Scholar] [CrossRef]
- De Soete, G. Optimal variable weighting for ultrametric and additive tree clustering. Qual. Quant. 1986, 20, 169–180. [Google Scholar] [CrossRef]
- De Soete, G. OVWTRE: A program for optimal variable weighting for ultrametric and additive tree fitting. J. Classif. 1988, 5, 101–104. [Google Scholar] [CrossRef]
- Makarenkov, V.; Legendre, P. Optimal variable weighting for ultrametric and additive trees and k-means partitioning: Methods and software. J. Classif. 2001, 18, 245–271. [Google Scholar]
- Wang, Y.X.; Xu, H. Noisy sparse subspace clustering. J. Mach. Learn. Res. 2016, 17, 320–360. [Google Scholar]
- Jing, L.; Ng, M.K.; Huang, J.Z. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data. IEEE Trans. Knowl. Data Eng. 2007, 19, 1026–1041. [Google Scholar] [CrossRef]
- Wu, K.L.; Yu, J.; Yang, M.S. A novel fuzzy clustering algorithm based on a fuzzy scatter matrix with optimality tests. Pattern Recognit. Lett. 2005, 26, 639–652. [Google Scholar] [CrossRef]
- Huang, X.; Ye, Y.; Zhang, H. Extensions of kmeans-type algorithms: A new clustering framework by integrating intracluster compactness and intercluster separation. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1433–1446. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Ye, Y.; Guo, H.; Cai, Y.; Zhang, H.; Li, Y. DSKmeans: A new kmeans-type approach to discriminative subspace clustering. Knowl.-Based Syst. 2014, 70, 293–300. [Google Scholar] [CrossRef]
- Han, K.J.; Narayanan, S.S. Novel inter-cluster distance measure combining GLR and ICR for improved agglomerative hierarchical speaker clustering. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 4373–4376. [Google Scholar]
- Bai, L.; Liang, J.; Dang, C.; Cao, F. A novel fuzzy clustering algorithm with between-cluster information for categorical data. Fuzzy Sets Syst. 2013, 215, 55–73. [Google Scholar] [CrossRef]
- Bai, L.; Liang, J. The k-modes type clustering plus between-cluster information for categorical data. Neurocomputing 2014, 133, 111–121. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, L.; Chen, C.P.; Zhang, Y.; Li, H.X. Fuzzy clustering with the entropy of attribute weights. Neurocomputing 2016, 198, 125–134. [Google Scholar] [CrossRef]
- Deng, Z.; Choi, K.S.; Jiang, Y.; Wang, J.; Wang, S. A survey on soft subspace clustering. Inf. Sci. 2016, 348, 84–106. [Google Scholar] [CrossRef]
- Chang, X.; Wang, Y.; Li, R.; Xu, Z. Sparse k-means with ℓ∞/ℓ0 penalty for high-dimensional data clustering. Stat. Sin. 2018, 28, 1265–1284. [Google Scholar]
- Witten, D.M.; Tibshirani, R. A framework for feature selection in clustering. J. Am. Stat. Assoc. 2010, 105, 713–726. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Shen, X. Penalized model-based clustering with application to variable selection. J. Mach. Learn. Res. 2007, 8, 1145–1164. [Google Scholar]
- Zhou, J.; Chen, C.P. Attribute weight entropy regularization in fuzzy c-means algorithm for feature selection. In Proceedings of the 2011 International Conference on System Science and Engineering, Macao, China, 8–10 June 2011; pp. 59–64. [Google Scholar]
- Sri Lalitha, Y.; Govardhan, A. Improved Text Clustering with Neighbours. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 23–37. [Google Scholar]
- Forghani, Y. Comment on “Enhanced soft subspace clustering integrating within-cluster and between-cluster information” by Z. Deng et al. (Pattern Recognition, vol. 43, pp. 767–781, 2010). Pattern Recognit. 2018, 77, 456–457. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Konar, A. Automatic clustering using an improved differential evolution algorithm. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2008, 38, 218–237. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Peel, D.; Bean, R. Modelling high-dimensional data by mixtures of factor analyzers. Comput. Stat. Data Anal. 2003, 41, 379–388. [Google Scholar] [CrossRef]
- Chang, X.; Wang, Q.; Liu, Y.; Wang, Y. Sparse Regularization in Fuzzy c-Means for High-Dimensional Data Clustering. IEEE Trans. Cybern. 2017, 47, 2616–2627. [Google Scholar] [CrossRef]
- Bezdek, J.C. A convergence theorem for the fuzzy ISODATA clustering algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 1–8. [Google Scholar] [CrossRef]
- Selim, S.Z.; Ismail, M.A. K-means-type algorithms: A generalized convergence theorem and characterization of local optimality. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 81–87. [Google Scholar] [CrossRef]
- Bachem, O.; Lucic, M.; Hassani, H.; Krause, A. Fast and provably good seedings for k-means. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 55–63. [Google Scholar]
- Tarn, C.; Zhang, Y.; Feng, Y. Sampling Clustering. arXiv 2018, arXiv:1806.08245. [Google Scholar]
- Tschannen, M.; Bölcskei, H. Noisy subspace clustering via matching pursuits. IEEE Trans. Inf. Theory 2018, 64, 4081–4104. [Google Scholar] [CrossRef]
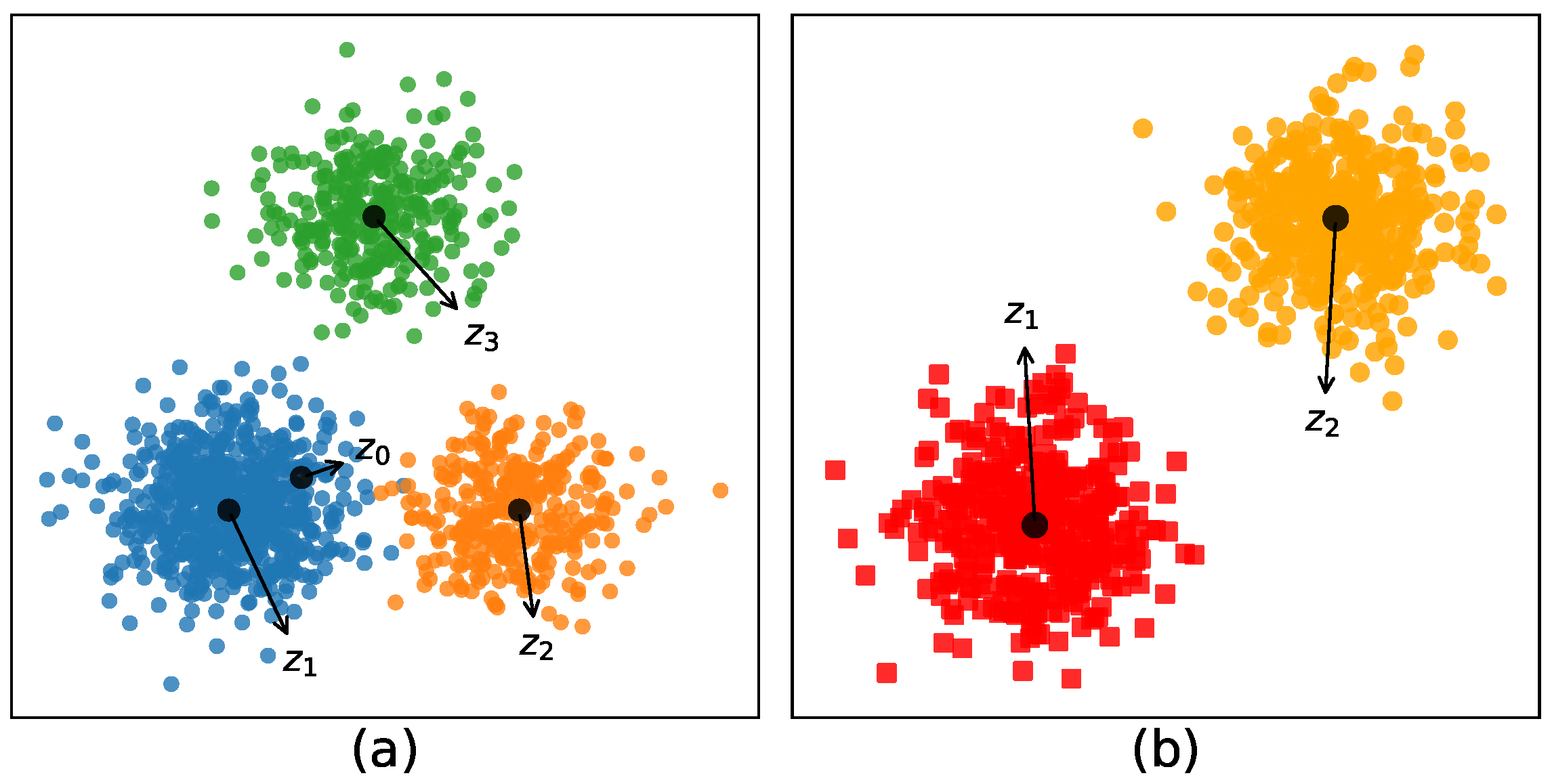
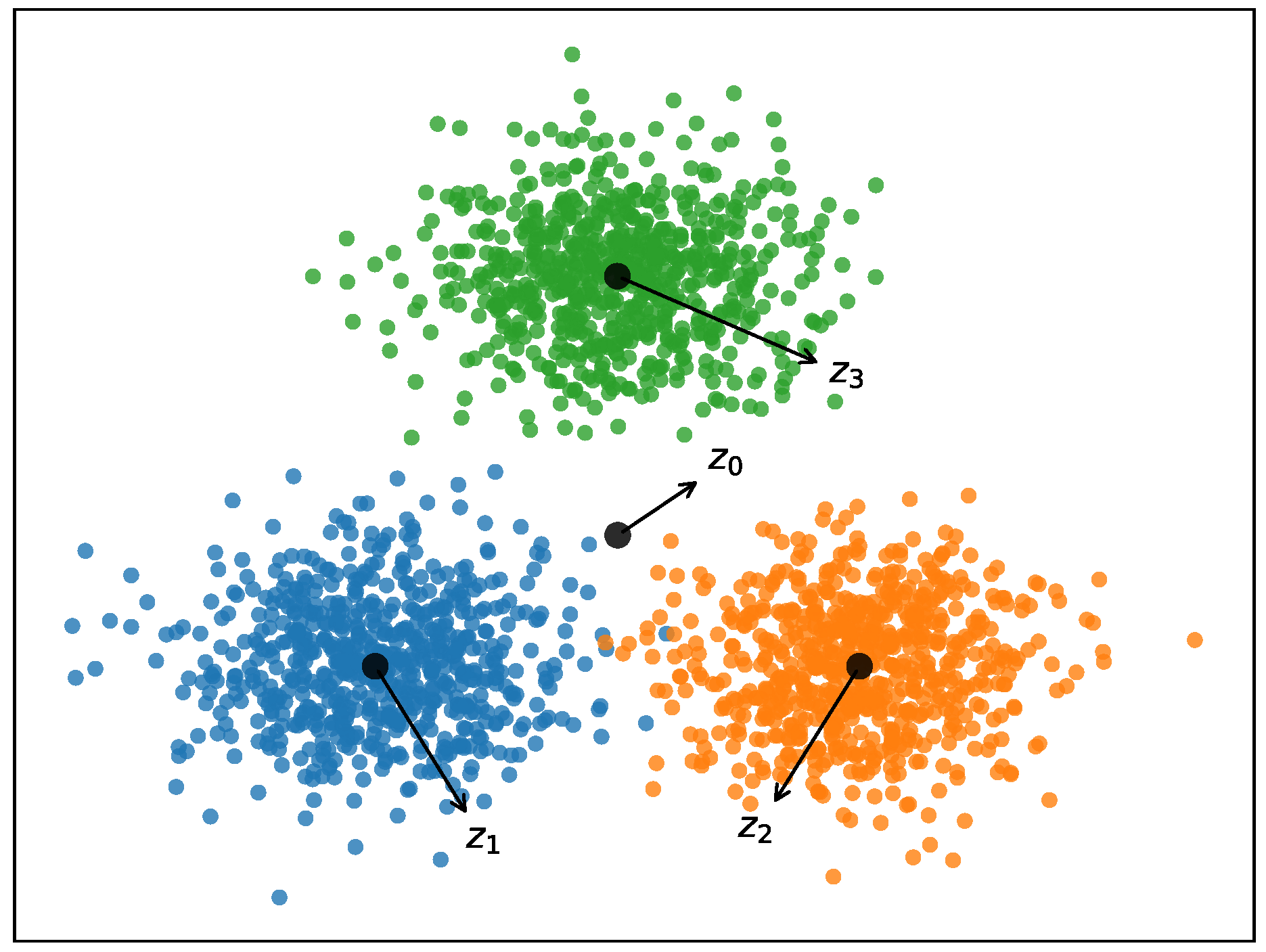
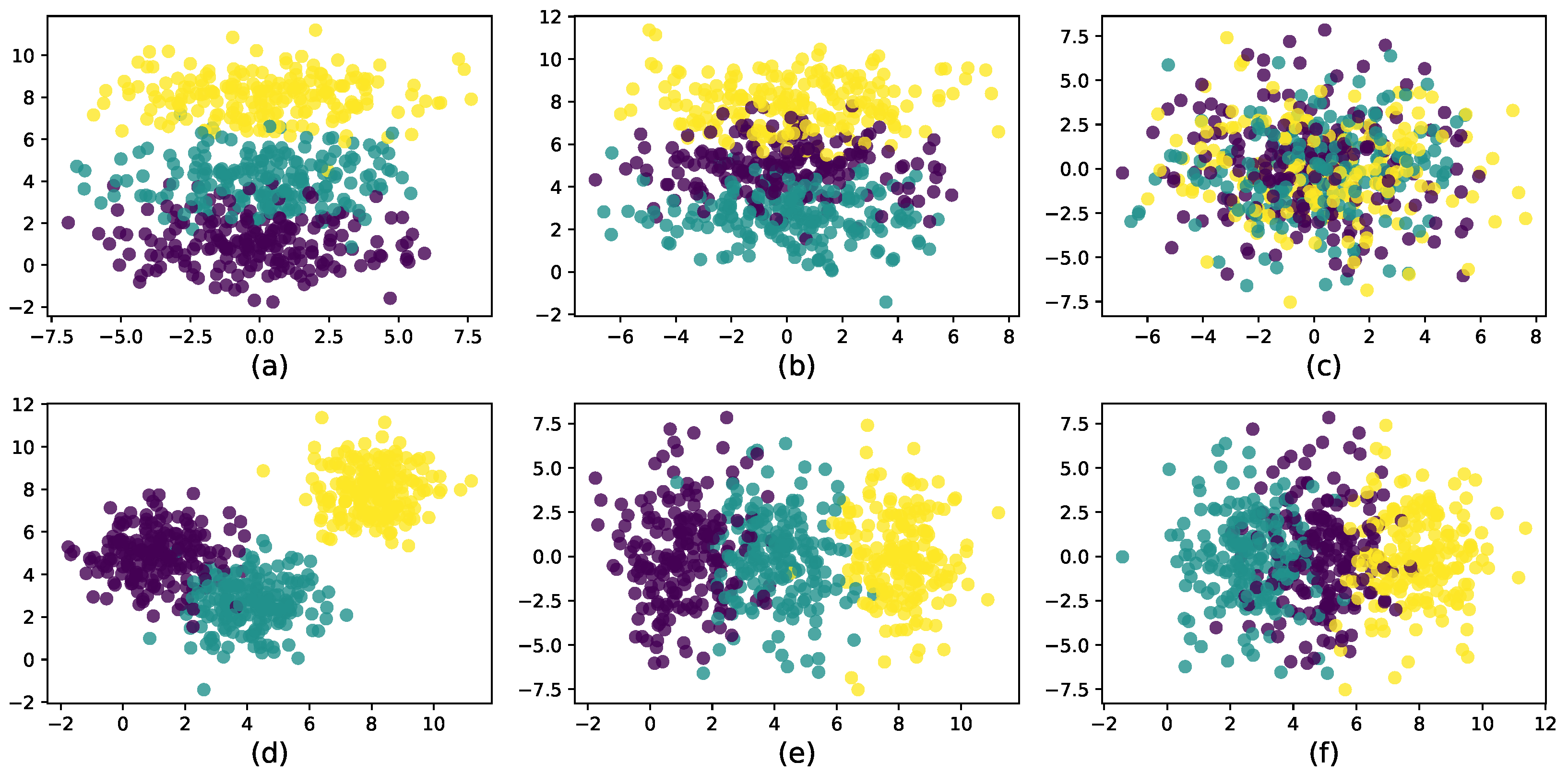

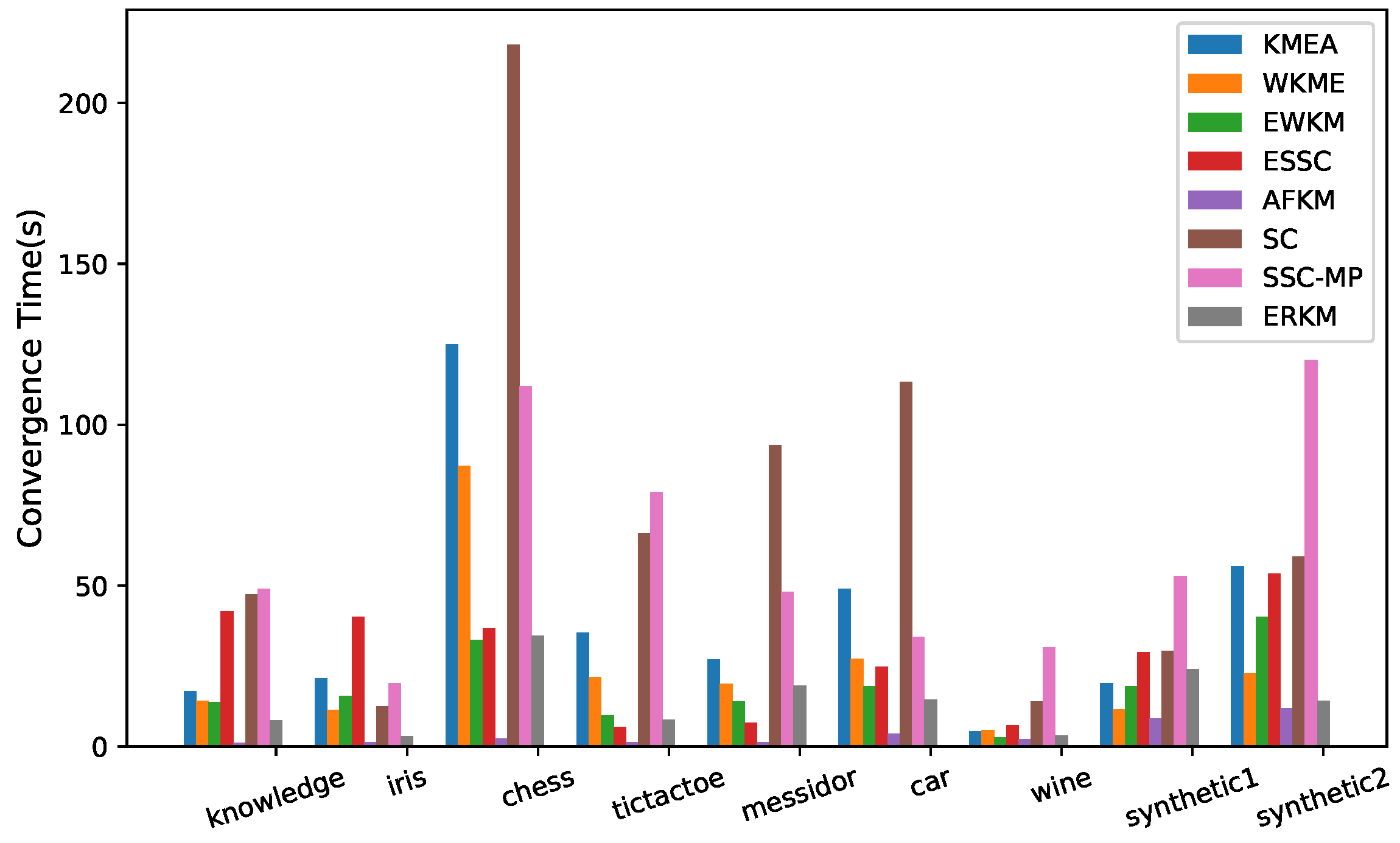
| Datasets | Points | Dimensions | Clusters |
|---|---|---|---|
| Synthetic1 | 500 | 4 | 3 |
| Synthetic2 | 250 | 1000 | 3 |
| Knowledge | 403 | 5 | 4 |
| Iris | 150 | 4 | 3 |
| Chess | 3196 | 36 | 2 |
| Tictactoe | 958 | 9 | 2 |
| Messidor | 1151 | 19 | 2 |
| Car | 1728 | 6 | 4 |
| Wine | 178 | 13 | 3 |
| Algorithms | Parameters |
|---|---|
| KMEA | - |
| WKME [10] | |
| EWKM [16] | |
| ESSC [5] | = 0.01 |
| AFKM [36] | - |
| SC [37] | r = 0.2, size = 16 |
| SSC-MP [38] |
| Metric | Model | Knowledge | Iris | Tictactoe | Chess | Messidor | Car | Wine |
|---|---|---|---|---|---|---|---|---|
| KMEA | 0.4600(0.02) | 0.8054(0.06) | 0.6535(0.01) | 0.5359(0.02) | 0.5452(0.01) | 0.7057(0.02) | 0.9443(0.07) | |
| WKME | 0.4897(0.06) | 0.7847(0.08) | 0.6534(0.00) | 0.5432(0.03) | 0.5382(0.01) | 0.7063(0.016) | 0.9471(0.07) | |
| EWKM | 0.4789(0.09) | 0.8209(0.06) | 0.6534(0.00) | 0.5334(0.02) | 0.5329(0.00) | 0.7011(0.01) | 0.9024(0.08) | |
| Acc | ESSC | 0.5244(0.02) | 0.8466(0.00) | 0.6539(0.00) | 0.5288(0.00) | 0.5308(0.00) | 0.7004(0.00) | 0.9506(0.00) |
| AFKM | 0.4780(0.04) | 0.8127(0.06) | 0.6534(0.00) | 0.5354(0.00) | 0.5416(0.01) | 0.7002(0.00) | 0.9399(0.08) | |
| SC | 0.4987(0.00) | 0.8066(0.00) | 0.6535(0.00) | 0.5222(0.00) | 0.5308(0.00) | 0.7002(0.01 | 0.8707(0.00) | |
| SSC-MP | 0.5012(0.00) | 0.7120(0.01) | 0.6513(0.00) | 0.5222(0.00) | 0.5311(0.00) | 0.7002(0.00) | 0.5865(0.00) | |
| ERKM | 0.5848(0.08) | 0.9036(0.01) | 0.6580(0.01) | 0.5714(0.03) | 0.5456(0.01) | 0.7051(0.02) | 0.9016(0.04) | |
| KMEA | 0.1945(0.02) | 0.8115(0.04) | 0.5672(0.03) | 0.5270(0.02) | 0.5533(0.03) | 0.4613(0.06) | 0.9469(0.06) | |
| WKME | 0.4769(0.05) | 0.7979(0.07) | 0.5643(0.03) | 0.5350(0.03) | 0.6029(0.06) | 0.4551(0.05) | 0.9482(0.06) | |
| EWKM | 0.4652(0.09) | 0.8264(0.05) | 0.6051(0.03) | 0.6210(0.05) | 0.6601(0.01) | 0.5206(0.06) | 0.9046(0.07) | |
| Fsc | ESSC | 0.5151(0.03) | 0.8477(0.00) | 0.6004(0.04) | 0.6642(0.00) | 0.6604(0.01) | 0.5156(0.05) | 0.9503(0.00) |
| AFKM | 0.4689(0.03) | 0.8158(0.05) | 0.5699(0.03) | 0.5895(0.00) | 0.5814(0.05) | 0.3864(0.04) | 0.9431(0.06) | |
| SC | 0.4355(0.21) | 0.4719(0.00) | 0.5709(0.01) | 0.543(0.00) | 0.5349(0.00) | 0.3818(0.04) | 0.8694(0.00) | |
| SSC-MP | 0.5189(0.01) | 0.7672(0.00) | 0.5207(0.00) | 0.6662(0.00) | 0.5629(0.00) | 0.5176(0.00) | 0.5842(0.00) | |
| ERKM | 0.5295(0.08) | 0.9015(0.01) | 0.6065(0.04) | 0.6297(0.02) | 0.5503(0.02) | 0.5606(0.06) | 0.8997(0.04) | |
| KMEA | 0.1318(0.02) | 0.5890(0.06) | 0.0140(0.02) | 0.0068(0.01) | 0.0070(0.00) | 0.0526(0.05) | 0.8580(0.11) | |
| WKME | 0.1588(0.06) | 0.5719(0.10) | 0.0128(0.02) | 0.0113(0.01) | 0.0024(0.00) | 0.0474(0.04) | 0.8632(0.11) | |
| EWKM | 0.1425(0.14) | 0.6144(0.07) | −0.0028(0.02) | 0.0047(0.01) | 0.0000(0.00) | 0.0152(0.05) | 0.7545(0.12) | |
| ARI | ESSC | 0.1965(0.03) | 0.6210(0.00) | 0.0023(0.02) | 0.0015(0.00) | −0.0008(0.00) | 0.0259(0.05) | 0.8520(0.00) |
| AFKM | 0.1412(0.04) | 0.5987(0.07) | 0.0171(0.02) | 0.0053(0.00) | 0.0046(0.00) | 0.0162(0.02) | 0.8496(0.12) | |
| SC | 0.1062(0.00) | 0.1851(0.00) | 0.0123(0.00) | 0.0004(0.00) | 0.0013(0.00) | −0.0070(0.02) | 0.6458(0.00) | |
| SSC-MP | 0.1453(0.00) | 0.5520(0.00) | 0.0055(0.00) | 0.0013(0.00) | 0.0020(0.00) | 0.0266(0.00) | 0.2135(0.00) | |
| ERKM | 0.277(0.10) | 0.7535(0.01) | 0.0263(0.05) | 0.0234(0.02) | 0.0072(0.00) | 0.0247(0.01) | 0.8632(0.11) | |
| KMEA | 0.1945(0.02) | 0.6472(0.02) | 0.0100(0.01) | 0.0054(0.01) | 0.0088(0.01) | 0.1187(0.06) | 0.8474(0.08) | |
| WKME | 0.2323(0.08) | 0.6511(0.04) | 0.0084(0.01) | 0.0091(0.01) | 0.0184(0.01) | 0.0962(0.06) | 0.8503(0.08) | |
| EWKM | 0.2197(0.15) | 0.6691(0.02) | 0.0038(0.00) | 0.0074(0.01) | 0.0261(0.01) | 0.0396(0.03) | 0.7620(0.09) | |
| NMI | ESSC | 0.2662(0.03) | 0.6321(0.00) | 0.0060(0.011) | 0.0153(0.01) | 0.0089(0.01) | 0.0458(0.04) | 0.8197(0.00) |
| AFKM | 0.2102(0.05) | 0.6560(0.03) | 0.0127(0.01) | 0.0125(0.00) | 0.0164(0.01) | 0.0431(0.03) | 0.8414(0.09) | |
| SC | 0.1819(0.00) | 0.4667(0.00) | 0.0045(0.01) | 0.0003(0.00) | 0.0011(0.00) | 0.0159(0.04) | 0.649(0.00) | |
| SSC-MP | 0.1684(0.00) | 0.6930(0.01) | 0.0032(0.00) | 0.0006(0.00) | 0.0087(0.00) | 0.0671(0.00) | 0.2289(0.00) | |
| ERKM | 0.4003(0.14) | 0.8026(0.01) | 0.0193(0.03) | 0.0291(0.03) | 0.0079(0.00) | 0.0526(0.06) | 0.7333(0.05) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, L.; Wang, C.; Huang, X.; Zeng, H. An Entropy Regularization k-Means Algorithm with a New Measure of between-Cluster Distance in Subspace Clustering. Entropy 2019, 21, 683. https://doi.org/10.3390/e21070683
Xiong L, Wang C, Huang X, Zeng H. An Entropy Regularization k-Means Algorithm with a New Measure of between-Cluster Distance in Subspace Clustering. Entropy. 2019; 21(7):683. https://doi.org/10.3390/e21070683
Chicago/Turabian StyleXiong, Liyan, Cheng Wang, Xiaohui Huang, and Hui Zeng. 2019. "An Entropy Regularization k-Means Algorithm with a New Measure of between-Cluster Distance in Subspace Clustering" Entropy 21, no. 7: 683. https://doi.org/10.3390/e21070683
APA StyleXiong, L., Wang, C., Huang, X., & Zeng, H. (2019). An Entropy Regularization k-Means Algorithm with a New Measure of between-Cluster Distance in Subspace Clustering. Entropy, 21(7), 683. https://doi.org/10.3390/e21070683




