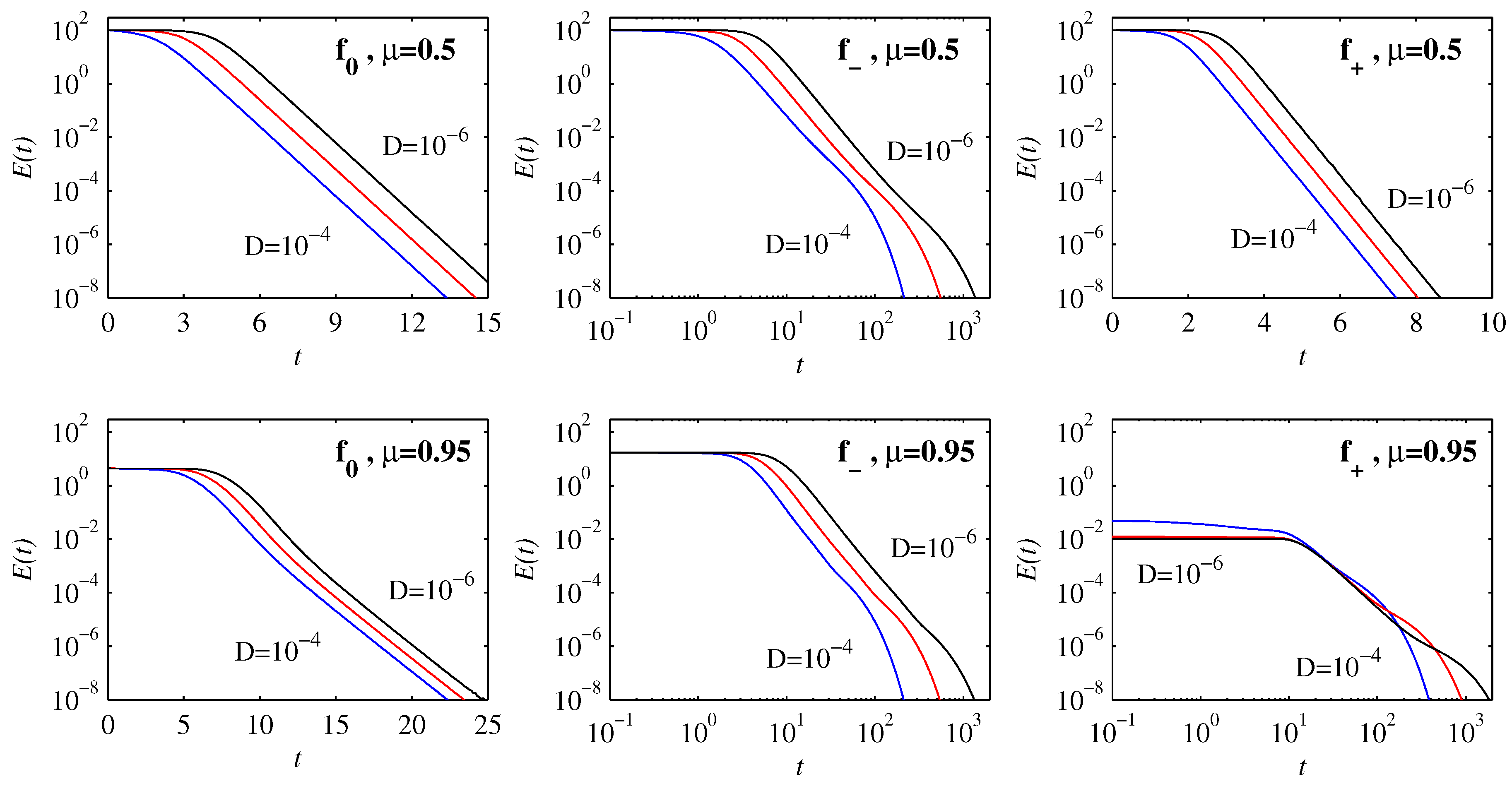1. Introduction
It is of interest to apply the idea of a metric to problems involving stochastic processes, e.g., [
1,
2,
3,
4,
5,
6]. Given a metric, the differences between different Probability Density Functions (PDFs) can be quantified, with different metrics focusing on a range of aspects, and hence most suitable for various applications. Fisher information [
7] yields a metric where distance is measured in units of the PDF’s width. The distance in the Fisher metric is thus dimensionless, and represents the number of statistically different states [
8].
By extending the statistical distance in [
8] to time-dependent situations, we recently introduced a way of quantifying information changes associated with time-varying PDFs [
9,
10,
11,
12,
13,
14,
15,
16]. We first compare two PDFs separated by an infinitesimal increment in time, and consider the corresponding infinitesimal distance. Integrating in time gives the total number of statistically distinguishable states that the system passes through, called the
information length , e.g., [
6,
7,
8,
14]. Another interpretation of
that can be useful is as a measure of the total elapsed time in units of an ‘information-change’ dynamical timescale.
We start by defining the dynamical time
as
That is,
is the characteristic timescale over which the information changes, and quantifies the PDF’s correlation time. Alternatively,
quantifies the (average) rate of change of information in time. A PDF that evolves such that
is constant in time is referred to as a geodesic, along which the information propagates at a uniform rate [
6]. The information length
is then defined by
which can be interpreted as measuring time in units of
. It is important to note that
has no dimension (unlike entropy) and represents the total number of statistically different states that a system passes through in time between 0 and
t. If we know the parameters that determine the PDF
,
and
in Equations (
1) and (
2) can be written in terms of the Fisher metric tensor defined in the statistical space spanned by those parameters. However, it is not always possible to have access to the parameters that govern PDFs, for instance, in the case of PDFs calculated from data. The merit of Equations (
1) and (
2) is thus that
and
can be directly calculated from PDFs even without knowing the parameters governing the PDFs, nor the Fisher metric. For instance,
was calculated from PDFs of music data in [
10]. In the work here, we first compute time-dependent PDFs by solving the Fokker–Planck equation numerically, and then calculate
and
from these PDFs as additional diagnostics.
Unlike quantities such as entropy, relative entropy, Kullback–Leibler divergence, or Jensen divergence, information length is a Lagrangian measure, that is, it includes the full details of the PDF’s evolution, and not just the initial and final states.
, the total information length over the entire evolution, is then particularly useful to quantify the proximity of any initial PDF to a final attractor of a dynamical system. In previous work [
12,
15] we explored these aspects of
for restoring forces that were power-laws in the distance to the attractor. For instance, for the Ornstein–Uhlenbeck process, which is a linear relaxation process, we showed that
consists of two parts: the first is due to the movement of the mean position measured in units of the width of the PDF, and the second is due to the entropy change. Thus, the total entropy change that is often discussed in previous works (e.g., [
17]) contributes only partially to
. Importantly, for the Ornstein–Uhlenbeck process,
increases linearly from the stable equilibrium point (with its minimum value at the stable equilibrium point) with the mean position of the initial PDFs regardless of the strength of the stochastic noise and the width of the initial PDFs. The linear relation indicates that a linear process preserves a linearity of the underlying process. Heseltine & Kim [
18] shows that this linear relation is lost for other metrics (e.g., Kullback–Leibler divergence, Jensen divergence). Note that
is related to the integral of the square root of the infinitesimal relative entropy (see
Appendix A). In comparison, for a chaotic attractor,
varies sensitively with the mean position of a narrow initial PDF, taking its minimum value at the most unstable point [
9]. This sensitive dependence of
on the initial PDF is similar to a Lyapunov exponent.
These results highlight
as an alternative diagnostic to understand attractor structures of dynamical systems. It is this attractor structure that we are interested in in this paper. We thus focus on the relaxation problem as in [
9,
12,
15,
18] by considering periodic deterministic forces and elucidate the importance of the initial condition and its interplay with the deterministic forces in the relaxation and thus attractor structure.
2. Model
We consider the following nonlinear Langevin equation:
Here
x is a random variable;
is a deterministic force;
is a stochastic forcing, which for simplicity can be taken as a short-correlated Gaussian random forcing as follows:
where the angular brackets represent the average over
,
, and
D is the strength of the forcing.
In [
15] we considered the choice
and investigated how varying the degree of nonlinearity
affects the system. In this work we take
to be periodic in
x, and explore some of the new effects this can create. The three choices of
we consider are
Figure 1 shows these profiles, which are all anti-symmetric in
x, and periodic on the interval
. All three choices have
as an attractor, and
as an unstable fixed point. The particular combinations of harmonics for
were chosen so that they are locally cubic rather than linear at either
(for
) or
(for
). In applications such a Brownian motors many specific choices of
are considered to model particular physics. However, as noted in the introduction, we are here more interested in attractor structures in the relaxation problem, in particular, how initial conditions and stochastic noise interact with deterministic forces and the role of the asymmetry of the deterministic force and the stable and unstable fixed points on the local dynamics.
Comparing these three periodic functions with the previous choices, two significant differences stand out. First, for with , all initial conditions are pushed directly toward the origin, and there are no unstable fixed points. It is therefore of particular interest to see how the choices here behave for initial conditions near . Second, all curve upward (that is, have for all ), whereas the choices here have different combinations of curvatures, which will turn out to have clearly identifiable effects.
The Fokker–Planck equation [
19,
20] corresponding to Equation (
3) is
In [
15] we solved the corresponding equation by finite-differencing in
x. For the periodic systems considered here, it is more convenient to start with the Fourier expansion
The coefficients
and
are then time-stepped using second-order Runge-Kutta. The term
is separated out into the relevant Fourier components using a fast Fourier transform. (For the very simple choices of
considered here, consisting of at most two Fourier modes, it would be straightforward to do this separation analytically, and thereby do the entire calculation purely in Fourier space, but the code was developed with more general choices for
in mind, where this approach becomes increasingly cumbersome as the number of harmonics in
increases. For such more general choices of
the FFT approach is most convenient).
Resolutions in the range are used, and carefully checked to ensure fully resolved solutions. Time-steps were in the range –, and were again varied to ensure proper accuracy. Another useful test of the numerical implementation is to monitor the coefficient : this is time-stepped along with the others, but must in fact remain constant if the total probability is to remain constant. It was found that if the initial condition is correctly set to have , then this was maintained throughout the entire subsequent evolution.
The initial conditions are of the form
that is, Gaussians centred at
and having half-width scaling as
. We are interested in the range
; by symmetry the range
would behave the same, simply approaching
from the other direction.
This initial condition is also periodic, on the same
interval as the entire problem. For the purposes of actually implementing Equation (
8), it was most convenient to consider the range as being
. In particular, for
and the values of
considered here, Equation (
8) yields results at
and
that are different, but both are so vanishingly small that the discrepancy does not need to be smoothed out in defining the initial condition. If instead Equation (
8) were implemented on either
or
, then
near either 0 or 1 would be more awkward to handle correctly.
In [
15] we also used a Gaussian initial condition, with
, and then explored the regime
to
. Here we are again interested in the regime
, which allows at least the initial parts of the evolution to be nondiffusive. Having the initial peak be so narrow that
can also be interesting in other contexts (e.g., [
21]), but diffusive effects are then necessarily important from the outset, which would obscure some of the dynamics of interest here. We therefore focus on the range
to
, and
to
.
3. Results
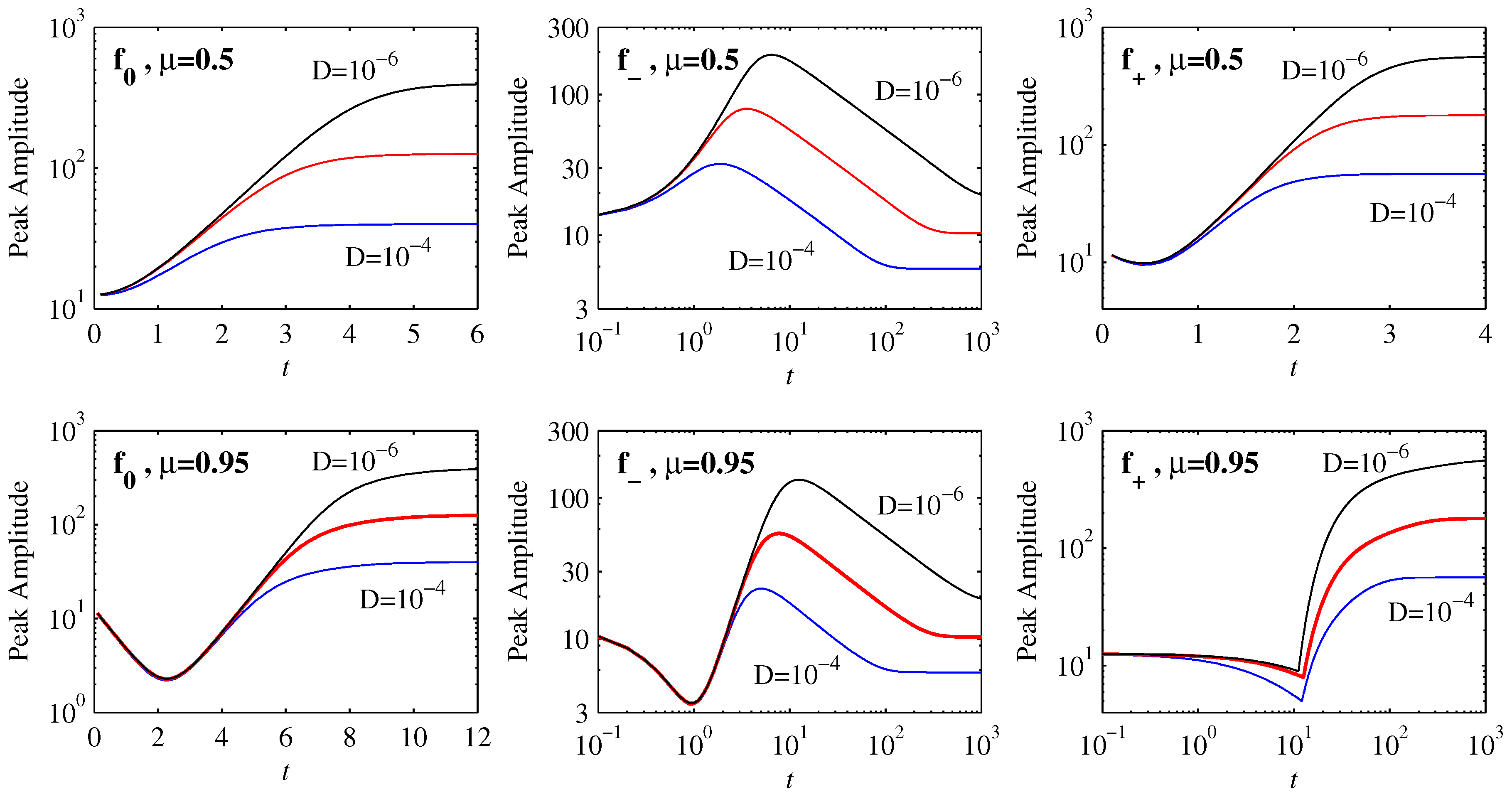
Figure 2 shows how the peak amplitudes evolve in time for the three choices
,
and
. Starting with the initial position
in the top row, we see that the solutions for
and
equilibrate to their final values on very rapid timescales, involving relatively little variation with
D. In contrast, the timescales for
are much longer, and vary substantially with
D. Comparing the
results here with
Figure 1 in [
15], we see that
is exactly analogous to the previous
. This is because for
the shape of
is very close to a cubic. Similarly, for
the shape of
is still reasonably close to linear, and the evolution is therefore essentially like the linear Ornstein–Uhlenbeck process
, for which an exact analytic solution exists [
21].
It is only
whose shape is already substantially different from either linear or cubic even on the interval
, being close to linear for
but strongly curved for
. Correspondingly
also shows a new effect, namely an initial reduction in the peak amplitudes. This effect becomes even more pronounced for
and
and the initial position
, in the bottom row of
Figure 2. This reduction in the peak amplitudes is
not caused by diffusive spreading but is a consequence of the non-diffusive (
) evolution resulting from the interplay between an initial PDF and the deterministic force. We note in particular how
to
yield identical reductions in amplitudes here. It is worth comparing this with the non-diffusive evolution in [
15] where the opposite behavior—an initial increase in peak amplitudes (the same effect as seen here for
,
)—was observed. The interplay between the initial PDF and the deterministic force is elaborated below.
If is such that it increases more rapidly than linearly, i.e., curves upward, then those parts of any initial condition furthest from the origin are pushed toward it fastest, whereas those parts closest move more slowly. The result is that an initial Gaussian peak bunches up on itself, causing the amplitude to increase. In contrast, if curves downward the opposite effect occurs, and an initial Gaussian peak is spread out, even before diffusion starts to play a role. Eventually of course the peak moves sufficiently close to the origin that the behaviour is as before, explaining why the behaviour at later times is similar to the previous results.
Finally, the behaviour for with is yet again different, namely an initial reduction in amplitude up to , followed by an abrupt increase. This is caused by a fundamentally new peak forming at the origin, rather than the initial peak moving toward it. Note also that time here is on a logarithmic scale, corresponding to a very slow equilibration process, unlike the previous case with .
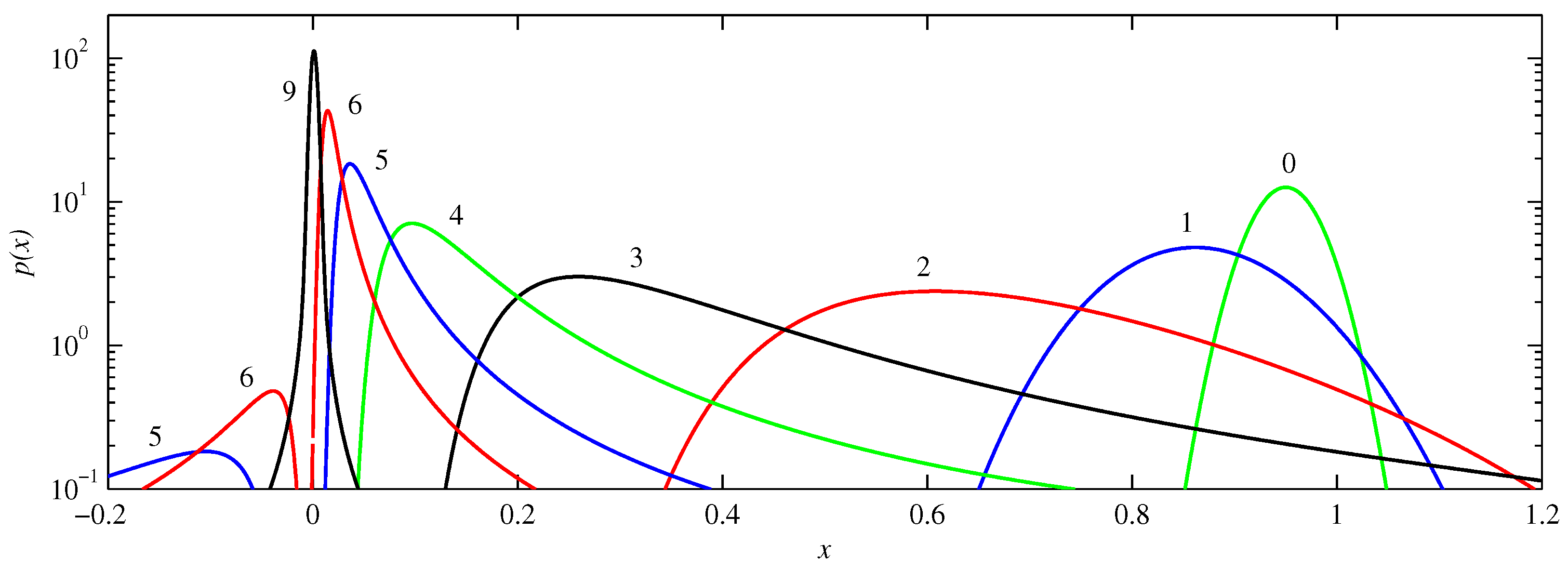
Figure 3,
Figure 4 and
Figure 5 illustrate these various behaviours in more detail, showing the actual PDFs at different times for
,
and
, respectively. Starting with
, we see how the peak initially located at
becomes broader as it moves toward the origin, an effect again not caused by diffusion, but rather by the curvature of
at these values of
x. Note for example how the solutions at
or 4 have much steeper leading edges (nearer to the origin) than trailing edges, caused by the trailing edges moving so much slower. Another feature to note is how parts of the solution reach the origin coming from the ‘other’ direction. That is, if the initial condition is a peak centred at
, and having half-width 0.07 (corresponding to
), then a small but non-negligible portion of the initial condition is in the range
, as seen also in
Figure 3. For this part of the initial condition the nearest attractor is
rather than
. Viewed on the interval
, this part therefore approaches from negative
x values, as seen at times
and 6. (The interval
or equivalently
is not shown in these figures because the amplitudes are rather small there, due to the PDFs being very spread out as they traverse this range). Finally, between
and 9 we see how the two peaks coming from negative and positive
x values combine to form the single final equilibrium consisting of a Gaussian centred at the origin.
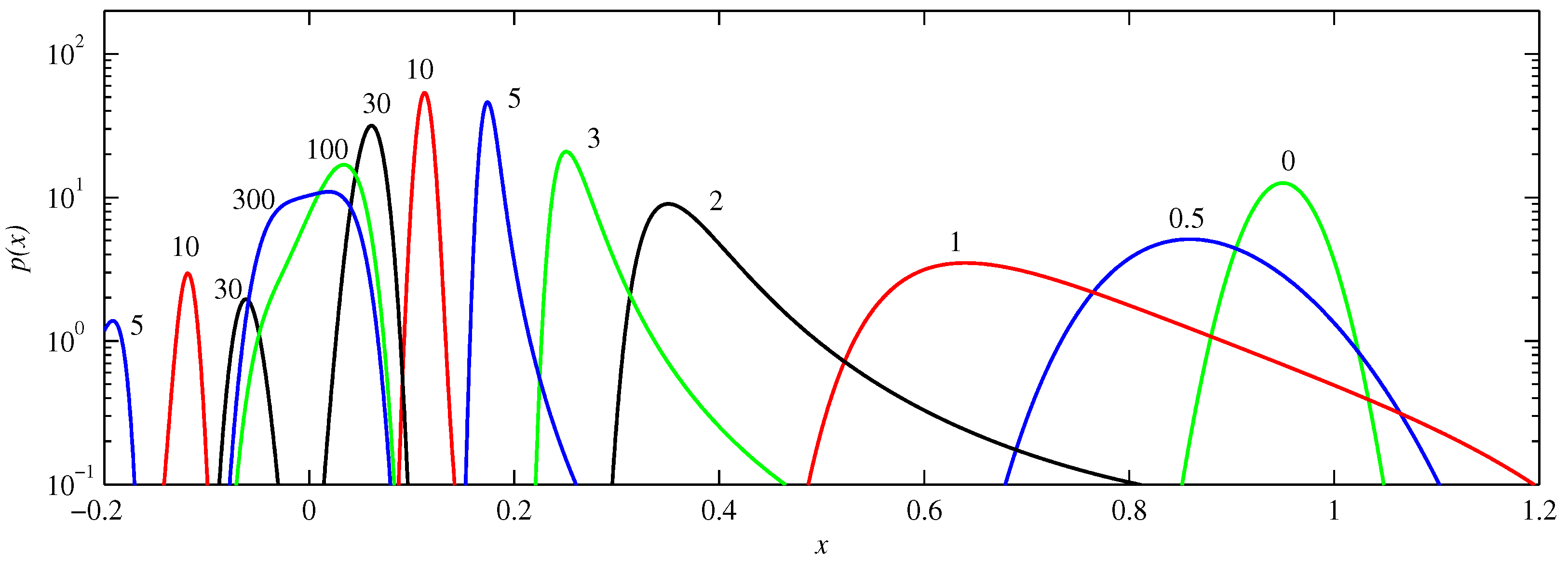
Figure 4 shows the corresponding solutions for
. For small durations the behaviour is very similar to that seen in
Figure 3, except that it happens roughly twice faster (e.g., compare
in
Figure 4 with
in
Figure 3). This is readily understandable by noting that the slope of
near
is roughly twice that of
, yielding faster evolution. The later evolution is much slower though, with the merging of the two peaks only occurring between
and 100, and even
still displaying some asymmetry, and hence not yet the final quartic profile. This is the same very slow final adjustment process previously analysed in detail in [
15], and is caused by
being cubic rather than linear near the origin.
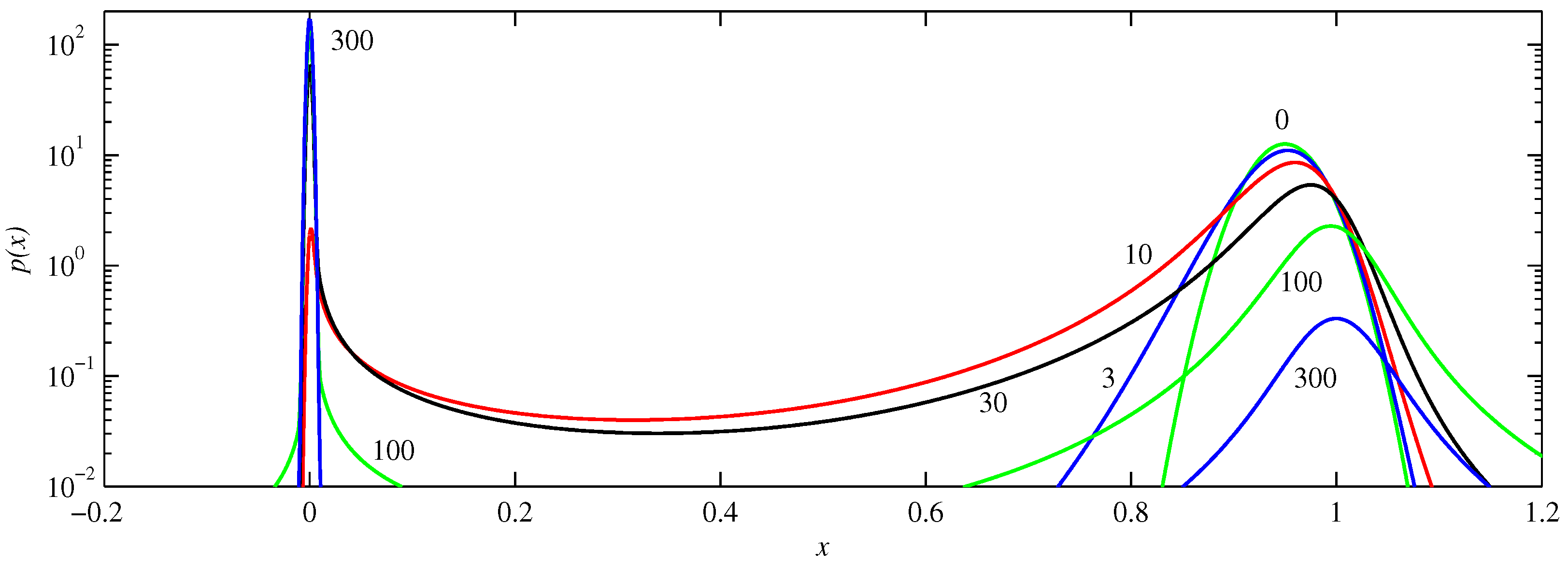
Figure 5 shows the solutions for
. We see the behaviour alluded to above, of an abrupt transition from one peak to another. Because
is so flat near
, there is hardly any tendency to push the initial peak away. Instead, it simply broadens out, slumping as it spreads. A new peak then forms at the origin, overtaking the original one in amplitude around
, as previously noted in
Figure 2. Note though that long after this time a significant portion of the original peak still remains near
, and this portion only fades away on very long timescales;
is an unstable fixed point, but
is so small everywhere near
that there is very little tendency to push the solutions away from there.
As noted in the introduction, we are particularly interested in the effects that these various different types of behaviour have on the information length quantities
and
.
Figure 6 shows
for the same solutions as before in
Figure 2. We see that
is initially uniform, and independent of
D (provided
D is sufficiently small in comparison with
), corresponding to the ‘geodesic’ behaviour first identified by [
6]. For some configurations,
then immediately transitions to an exponential decay, whereas for others it first has a power-law decay before ultimately decaying exponentially. Correspondingly, the timescales to achieve
also vary dramatically, as seen by the various linear and logarithmic scales for
t. Different scaling regimes signify fundamentally different dynamics.
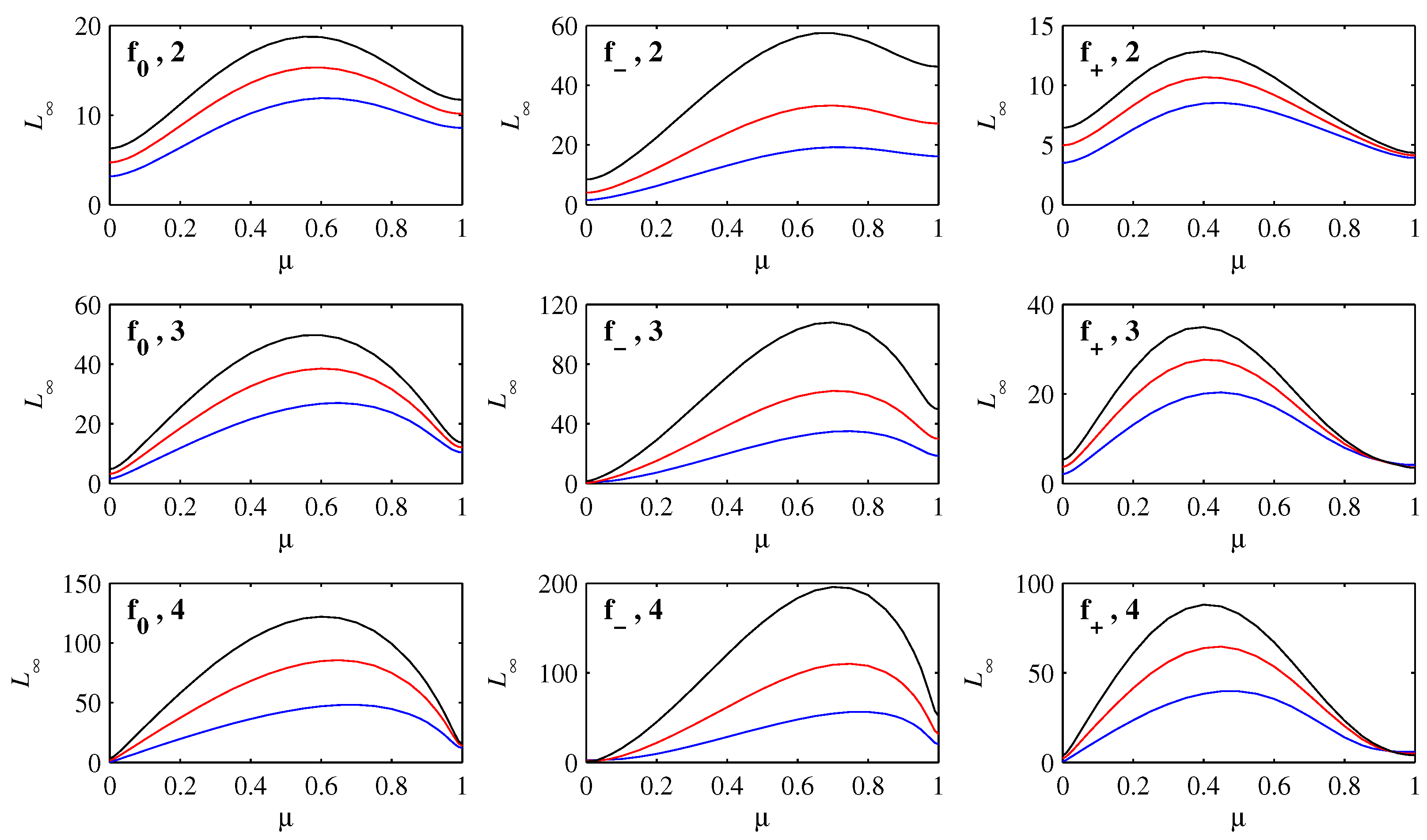
Figure 7 shows how
varies with
, for
to
, and
to
within each panel. It is interesting to note how the shapes generally mimic the corresponding functions
,
and
. The largest values always occur for intermediate values of
, even though larger values correspond to initial conditions that have farther to travel to reach the origin. Such initial conditions also spread out much more though, as seen above, and according to the interpretation of information length, this should indeed reduce
. Very close to
the
values are particularly small, because having peaks collapse in place and reform at the new location is an informationally very efficient way to move, as seen also in other contexts [
13,
22,
23].
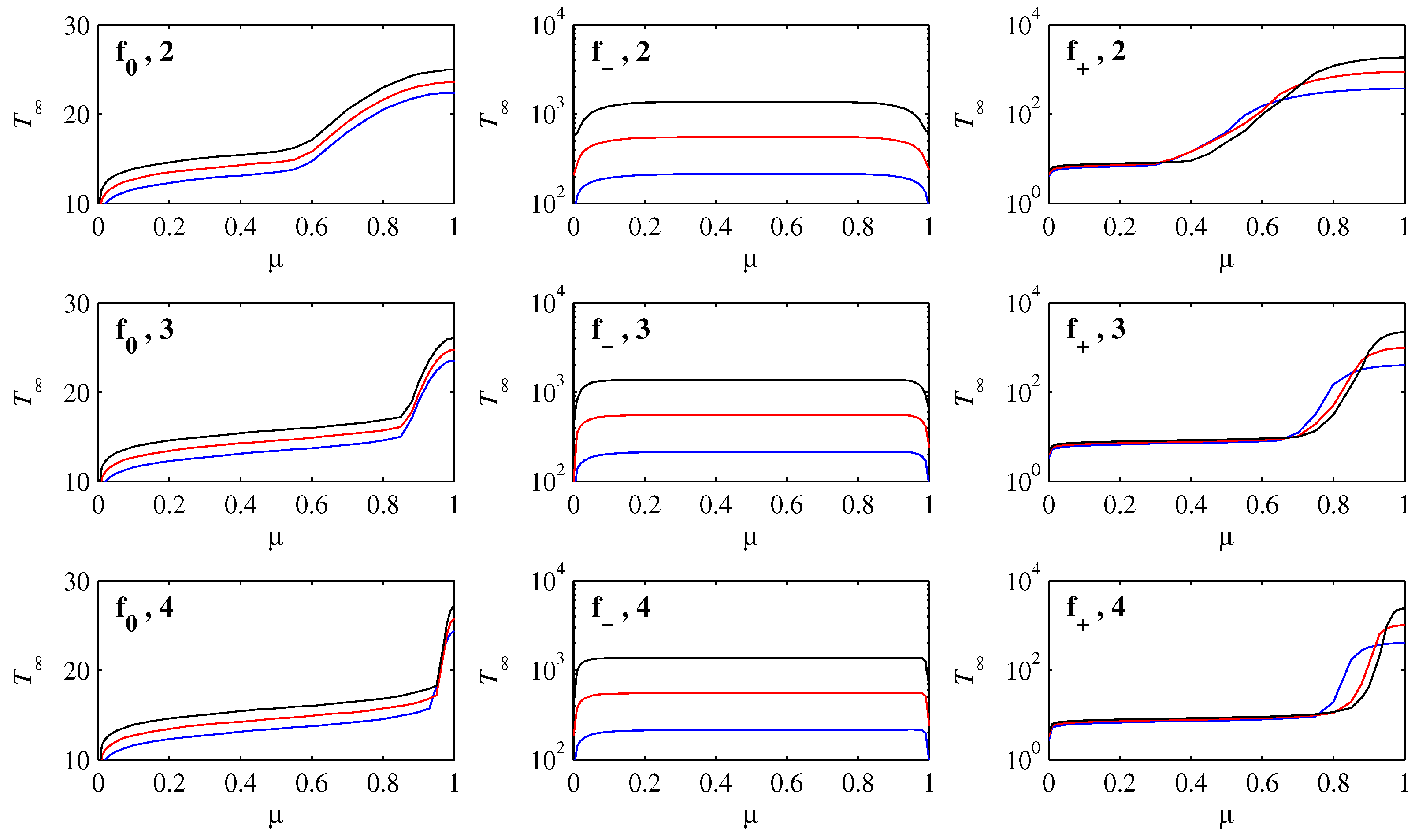
Finally,
Figure 8 shows the time, call it
, needed for
to drop to
. The precise cutoff
is of course somewhat arbitrary, but as seen in
Figure 6 is sufficiently small to be in the exponential decay regime in all cases. This is therefore a convenient measure of the time taken to reach
, and any even smaller cutoff would only add small increments to
(and essentially nothing to
).
Starting with
, we note first that
is on a linear scale, meaning that each reduction of
D by a factor of 10 only adds a constant amount to
. This is the same effect already seen in
Figure 2, where smaller
D requires slightly longer to settle in to the final states. Equivalently, smaller
D in
Figure 6 remains in the flat, geodesic regime for slightly longer times. The other feature to note for
is the behaviour near
, where
increases strongly, and increasingly abruptly for smaller
. This can be understood by noting that if
, the initial condition Equation (
8) is essentially zero at
, whereas if
is within
of 1, Equation (
8) does have a non-negligible component at
. Therefore, if
the initial peak will simply move monotonically toward the origin, which occurs on a rapid timescale, whereas if
the evolution will include a significant component of the slumping-in-place behaviour, which we saw only happens on slower timescales.
For
, the scale for
is logarithmic, so that each reduction of
D by a factor of 10 increases
by a factor of
. For intermediate values of
,
is also essentially independent of
. The equilibration time is completely dominated by the final settling-in time, just as in the cubic case in [
15], and the initial motion of the peak toward the origin is negligible in comparison. For very small values of
the behaviour is different, with much smaller values of
. If
, the peak is essentially at the origin already, making the adjustment quicker. Finally, there is a similar end-effect for
sufficiently close to 1; if
, the initial peak is essentially at the unstable fixed point, and the evolution is the slumping-in-place behaviour, which has a faster final adjustment than if the peak moves toward the origin and then adjusts its shape there (but still scaling as
).
Finally,
is qualitatively similar to
, in the sense that
is a monotonically increasing function of
. Indeed, for intermediate values of
the behaviour is virtually identical to
, with
increasing by a constant amount every time
D is decreased by a constant factor. (This is simply not visible because
is on a logarithmic rather than linear scale here). Because
and
are both linear near the origin, the extremely slow final adjustment that happens for
does not apply to either of them, leaving only this much weaker dependence on
D. The behaviour near
, with the very strong increase in
, and again more abruptly for smaller
, is again because this is the regime where the slumping-in-place behaviour occurs. Also, because
is so much flatter near
than either of
of
, this slumping-in-place behaviour is much slower for
than for the other choices (recall again how long the peak at
lasts in
Figure 5). This explains why
is on a logarithmic scale for
but on a linear scale for
, even though for intermediate values of
they exhibit the same (weak) scaling with
D.