1. Introduction
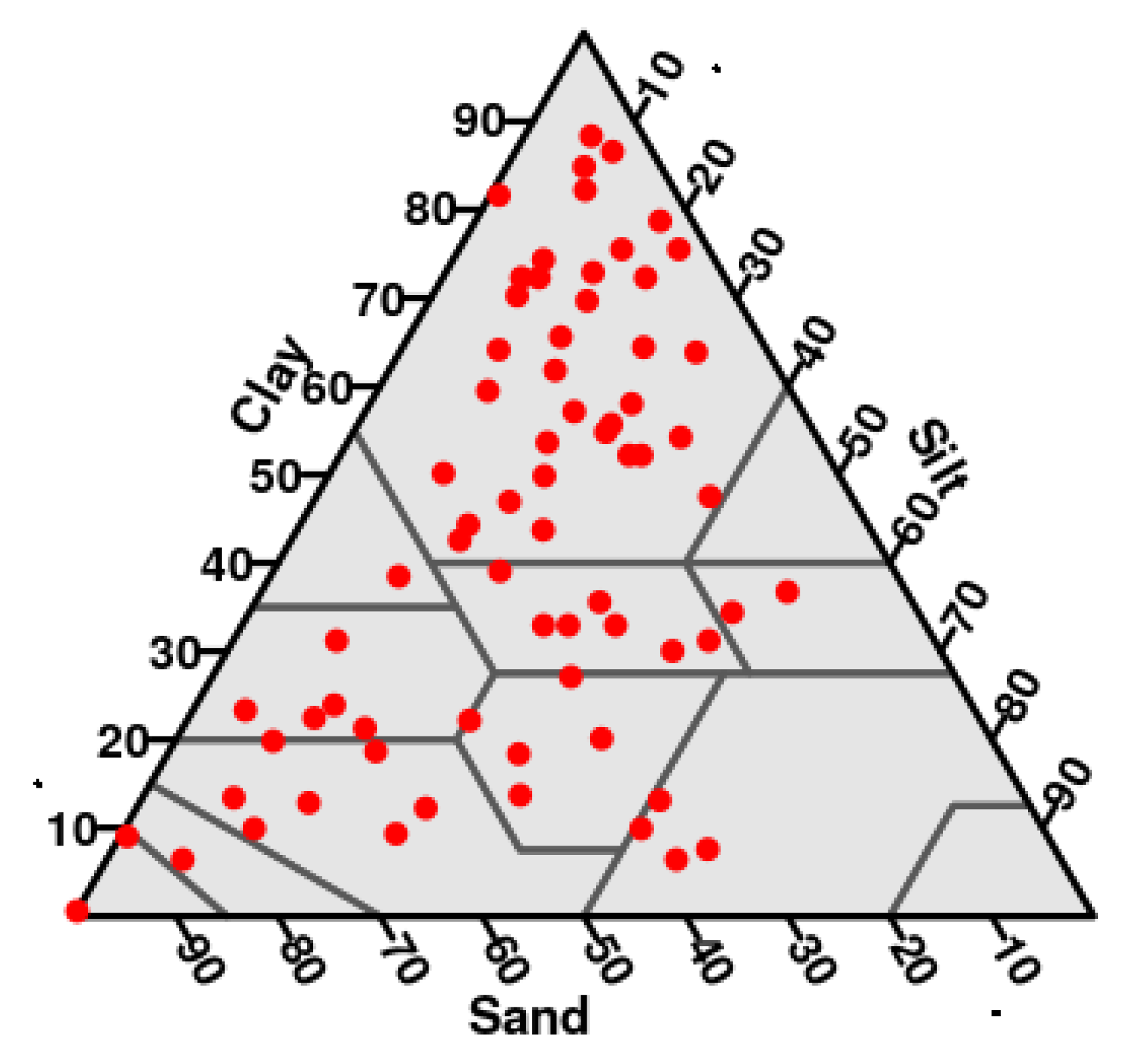
Granular media resulting from sedimentation and/or fragmentation processes are of great interest in different fields of science, technology and industry. The particle size distribution (PSD) is a main characteristic of these granular media since it has a crucial influence on their physical properties. These media are formed by an enormous amount of particles and, in fact, any particle size within the size interval might potentially be represented in a sample, so that, the PSD may be considered as a continuous distribution. In spite of this, experimental data on this distribution is usually very limited. In the case of soil, a paradigmatic natural granular media, the distribution information is commonly reduced to three classical size fractions, clay, silt and sand [
1]. A first natural question arising at this point is if there is a theoretical framework supporting the supposed information value of so limited experimental data. While several mathematical distributions have been used as PSD models [
2], the PSD reconstruction from this extremely poor information needs a rationale based in some driving idea different from empirical fitting procedures.
To address this challenge, this work is focused on characterizing the PSD by a specific property which could satisfy a simple equation (differential, difference or dynamical). An outstanding example of this kind of approach is the pioneering work [
3] in which a differential equation is proposed as a semiempirical model for the cumulative mass-size distribution
of certain granular media with grain size below a given limit
x.
The differential equation is formulated for granular materials whose grain distribution is arranged in the same statistical manner for both the smaller and for the greater sizes and conformed in such a way that adding a portion of greater grains, the resulting distribution is geometrically similar to the previous one; using the terminology of the authors, they have the same granulography.
Interestingly, behind this
old model swarm features nowadays recognized in many complex dissipative systems. Indeed the formation processes of some granular media have certain aspects that are present in the dynamics of dissipative systems. Fragmentation of particles together with other coupled processes, suggest that the use of energy and its storage takes place in the form of “information” or disorder in the particle sizes. There are two constrains: the available energy for fragmentation is limited and also the energy needed to fragment a particle has a power law dependence of the size of the particle [
4]. The maximum entropy principle [
5] states that, under certain rules of optimality and randomness, the system thus would reach the maximum level of disorder conditional to the constrains imposed on the process. Entropy maximization methods have already been used to explain the power-scaling nature of size distributions caused by sudden breakage [
6]. According to Prigogine [
7], the balance of entropy production in dissipative systems should produce a characteristic organization level in a stationary state. In the context of this paper, this corresponds with a characteristic PSD heterogeneity. Notably the term
granulography used in [
3] may be interpreted in a very similar way. These features suggest the use certain elements of Information and Complex Systems Theories in the study of complex granular media, with the goal of establishing a rational basis under which one can evaluate and test the information content of a small number of wide ranges from the distribution.
The paper is organized as follows: in
Section 2 a differential information equation is proposed as a conceptual approach for the PSD of complex granular media. Under this approach, experimental data may be seen as initial conditions of the above differential information equation. In
Section 3 the use of detailed soil PSD data, together with methods based in the above mathematical approach are used to test the ability of limited experimental data to generate a full reconstruction of the PSD.
2. The Differential Information Equation for the PSD
Instead of the differential equation for the cumulative distribution proposed in [
3], we present a rather different type of differential equation framed in a typical quantity used in the description of complex systems: the information entropy (IE).
In mathematical terms, the PSD of granular media may be seen as a mass particle-size distribution supported in the interval I of grain sizes.
Limited information on PSD is usually provided as a list of size ranges that cover
I. Grains sorted according to their size thus appear distributed in a partition of size classes
defined by those ranges on the list. If the corresponding mass fractions are
, respectively, the IE of the partition
P is defined by [
8]
provided
if
.
The number is expressed in information units (bits) and its extreme values are , which corresponds to the most even case, when all the intervals have the same cumulative mass; and 0, which corresponds to the most uneven case, when the whole mass is concentrated in a single interval.
The number
can be interpreted as a measure of heterogeneity. In fact, in [
9] it is shown that any measure of heterogeneity having the natural properties for this purpose, must be a multiple of
. Both, the physical hypothesis and the differential equation in [
3] have an implicit recognition of scale invariant features. Also the term
granulography used there agrees with the concept of heterogeneity, which has a precise formulation in mathematical terms, as it was said above. Thus, instead of the differential equation proposed in [
3] for the cumulative distribution, we propose a different type of differential equation involving the IE.
If we consider all the partitions
of the size interval
I that support the mass particle-size distribution
, we define
where
and
is the diameter of
P, this is, the length of the greater subinterval of
P.
The use of IE allows to formulate a natural property of many multiparticular granular media similar to the master property proposed in [
3]: after an arbitrary sieving at a characteristic size scale
r, the amount of information received is related to that received at an “inmediately previous” sieving. This relation can be encapsulated in the following initial value problem
where
D is constant and
is the information received at an initial sieving of characteristic size
. This is the model we propose for the quantitative description of the PSD.
Although formally this differential equation resembles the proposed in [
3], it involves different variables and has a complete different meaning. The physical hypothesis stated by [
3], in these new terms, signify that when one travels through the scales using the logarithmic transformation, i.e., changes the size scale, the information content increases on the multiplicative scale. In particular, the equation implies that the information is conserved through the scales.
Under the theoretical point of view, for any partition
, the coarse information content of the corresponding empiric data
may be used to provide the initial condition
A first issue is to find out if there is a solution of the Equation (
3) corresponding to these initial conditions. Theoretical results from Fractal Geometry [
10,
11] assure that for each set of empiric data there exists a unique selfsimilar measure, which is a particular solution of (
3) using those measured data as initial condition.
Initial data has an static information content that can be calculated with Shannon’s entropy. But the information potential of initial data is to suppose that this static information content is mantained, at least statistically, across the scales, which is exactly what the model (
3) implies. Also, there is a scaling behaviour in every natural granular media.
Moreover, it turns out, that in the general case (
,
, …,
) this measure agrees with the proposed as a model for soil mass size particle-size soil distribution in [
12]. The latter now appears founded under this approach, and also gives the possibility of simulation. Furthermore, this result links the fractal PSD model proposed in [
12] with the model given more than seventy five years earlier in [
3].
Nevertheless, the multiplicative cascade associated to each set of experimental data is unique, so a second issue is to study for which initial conditions the corresponding solution better reconstructs the real PSD of a certain granular media. This study will take account of which experimental initial conditions (fraction contents) storage greater information content and are most useful to retrieve the actual PSD. There rest of this work is devoted to the study of this problem in the particular case of soil.
4. Results and Discussion
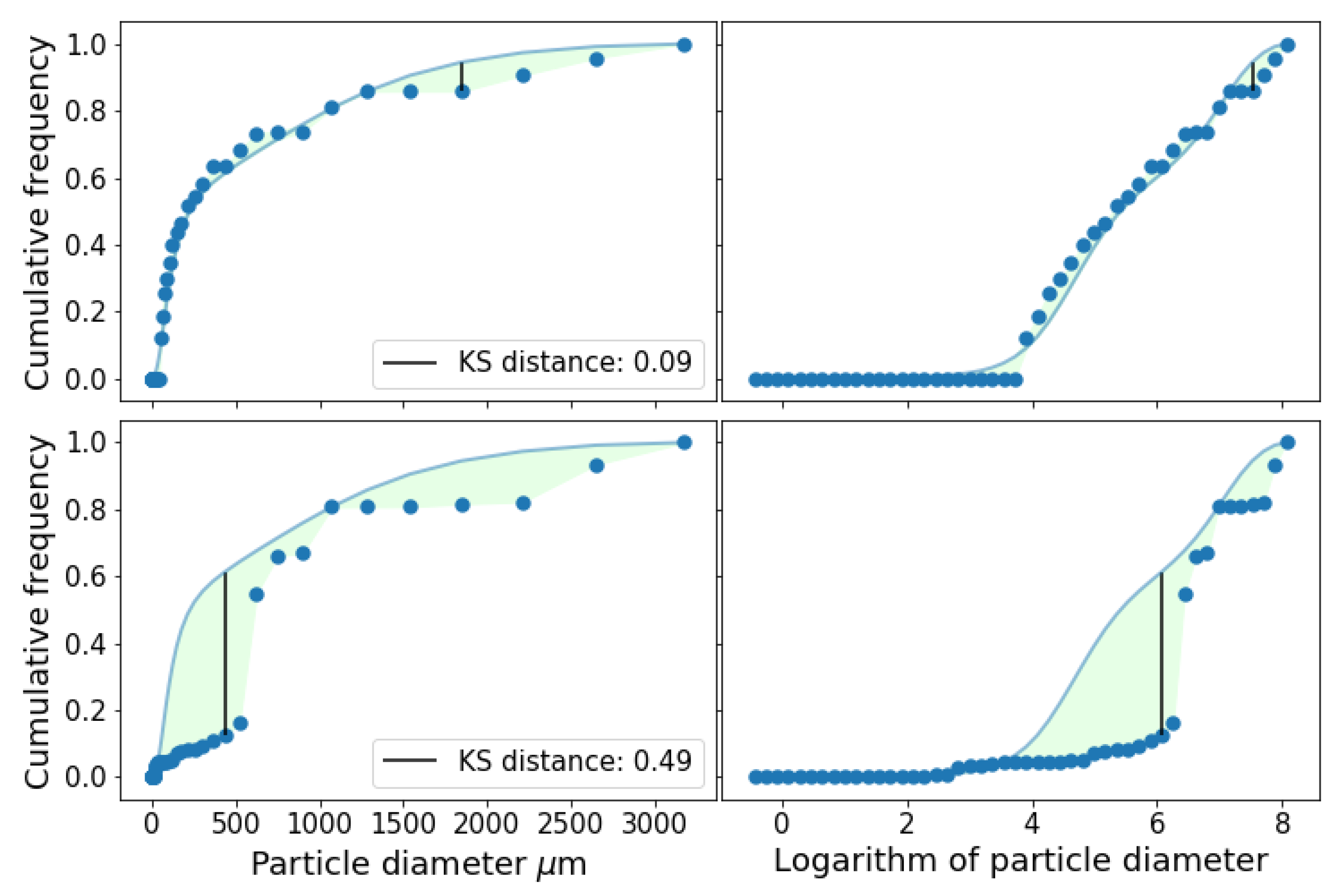
There was total of 1081 possible input triplets to simulate the whole PSD. At least 28 triplets (2.6%) passed the KS test for all soils in the database. On average 16.9% (∼182) of the available triplets passed the test for each soil. The number of triplets that passed the test was above 400 (>37%) for soils labeled 6 and 44. Example of simulation results is shown in
Figure 2. Simulation with two different triplets is shown. The first one with input intervals
,
and
in
m. The values of
and
for this triplet were 0.0003 and 0.4049.
The other triplet was , and m, with and .
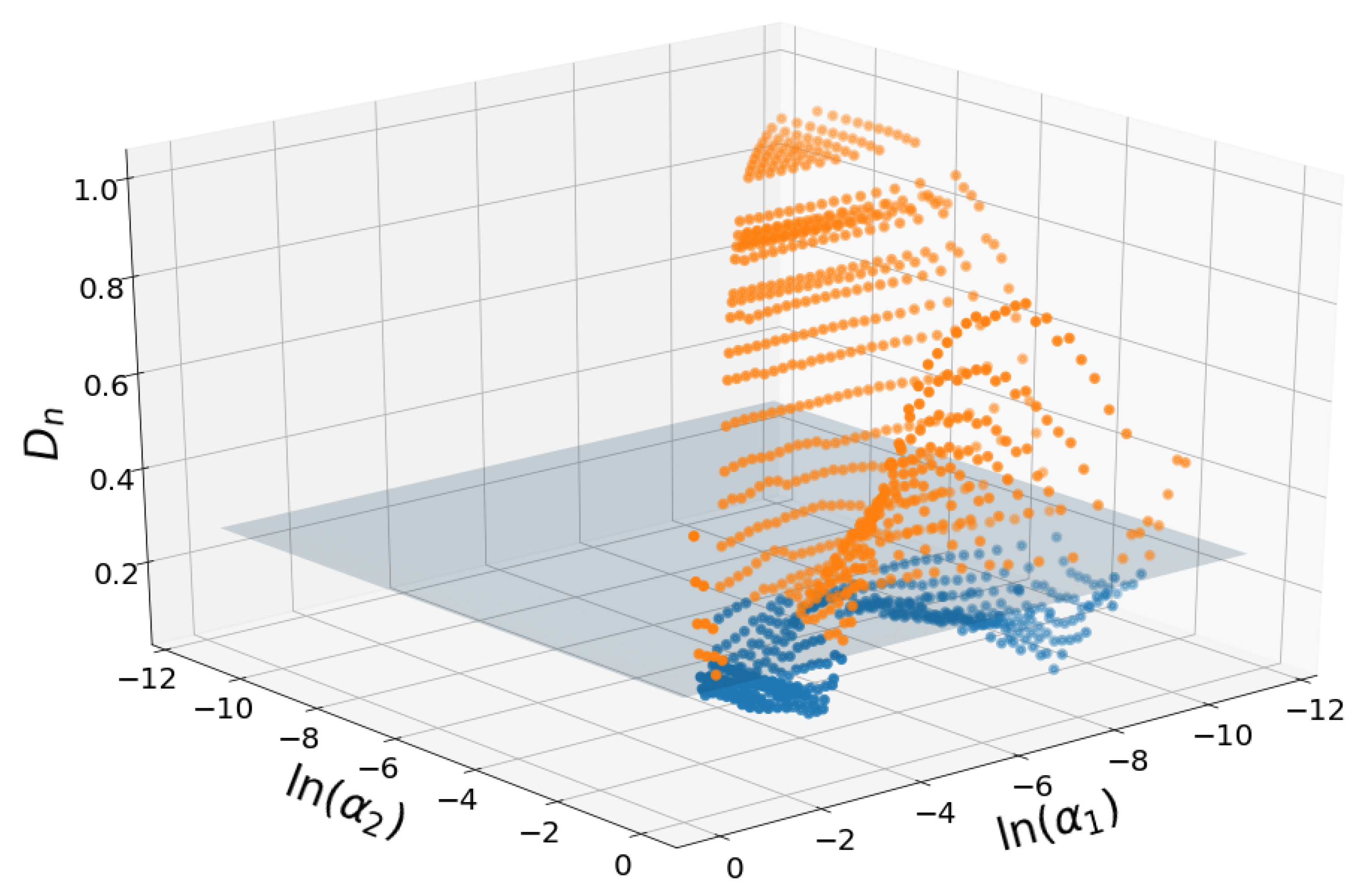
Figure 3 shows the Kolmogorov-Smirnov statistics for all triplets represented in the
plane. The horizontal plane at the height of acceptance of the null hypothesis is shown.
The surface has butterfly-like shape with maximum values found at the extremes of the values and intermediate values. Either fine fraction (small ) or coarse fraction (large ) have to dominate to provide better modeling results.
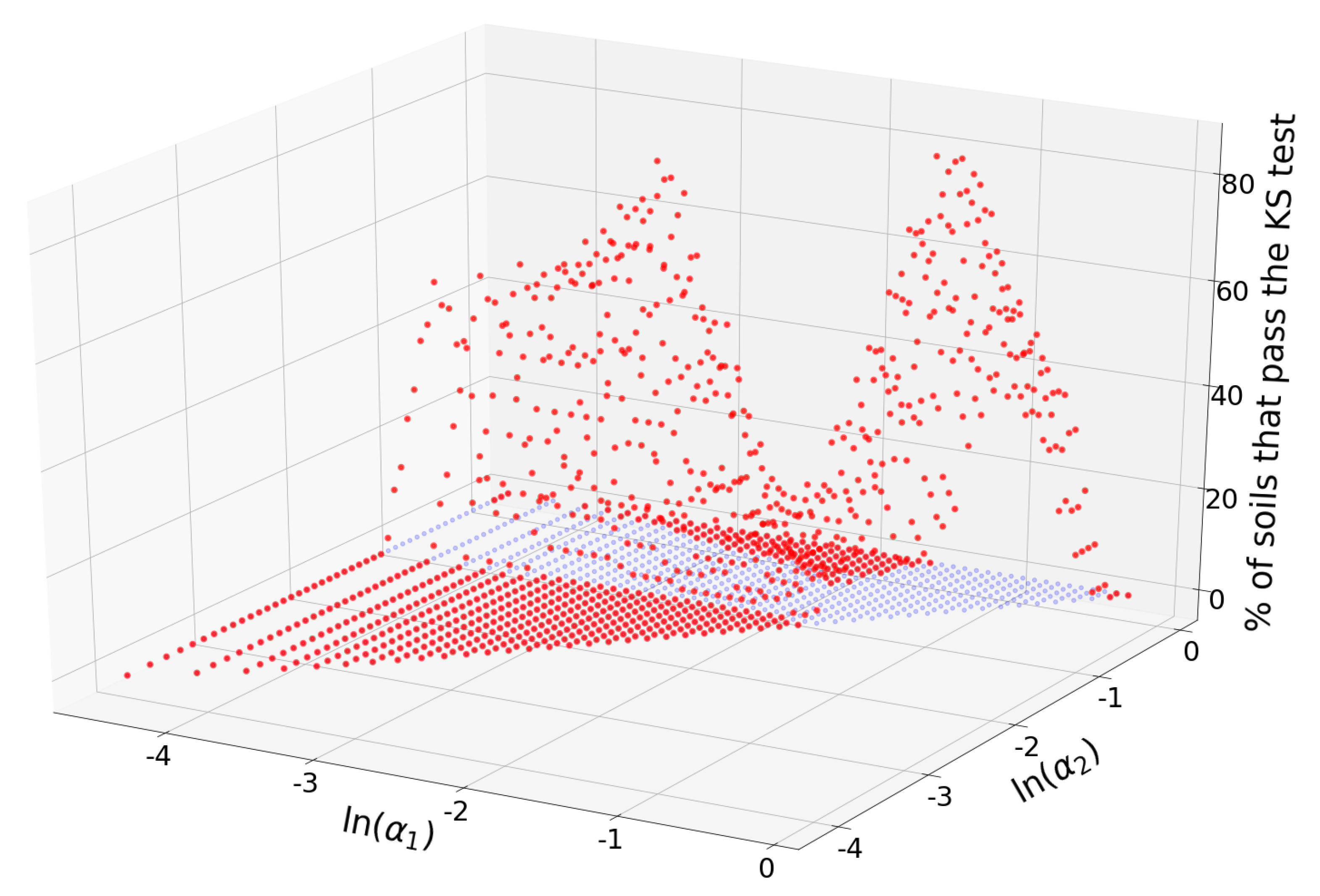
Total of 536 (49.6%) of all the 1,081 available input triplets passed the KS test for at least one of the soils. The triplet that passed the KS test for most soils was
,
,
m, with
and
. The number of soils for which this triplet passed the KS test was 65 (93%). In terms of the USDA textural classification, this triplet consists of “clay + silt + fine sand”, “medium sand + coarse sand”, and “very coarse sand + gravel”. Total of 22 triplets passed the KS test for 55 soils (79%) or more. The percentage of soils for which each triplet
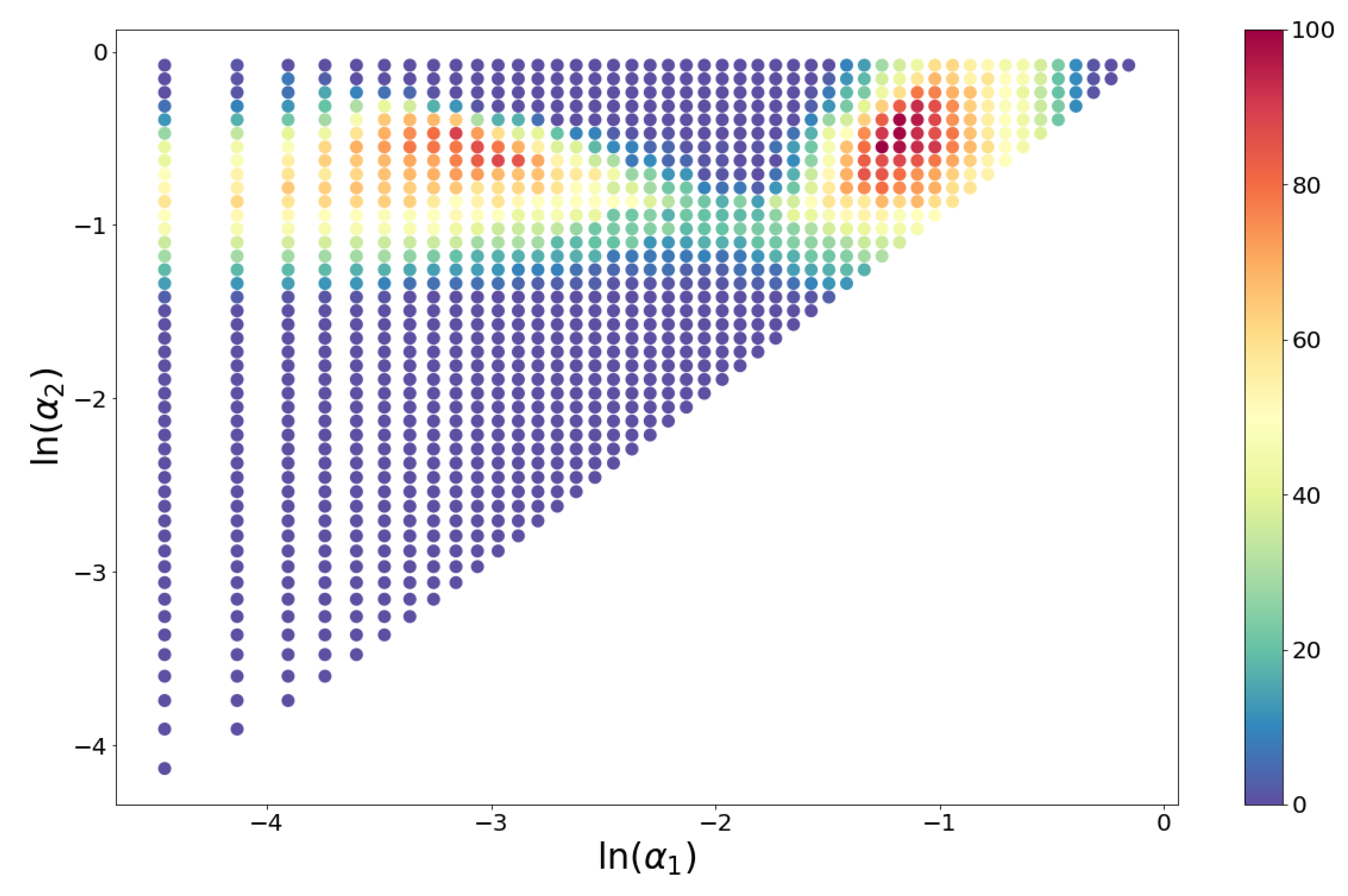
passes the KS test is shown in
Figure 4.
Triplets with maximum acceptance rates are concentrated in the neighborhood of the point
, but there are other combinations of alpha values with relatively large acceptances.
Figure 5 shows a heatmap of the acceptance percentage for the
plane.
Whether these points attractors have a general significance, are soil database specific or have relations with conditions of soil formation presents an interesting avenue for further research.