Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics
Abstract
1. Introduction
2. Data and Models in Spherical Harmonics
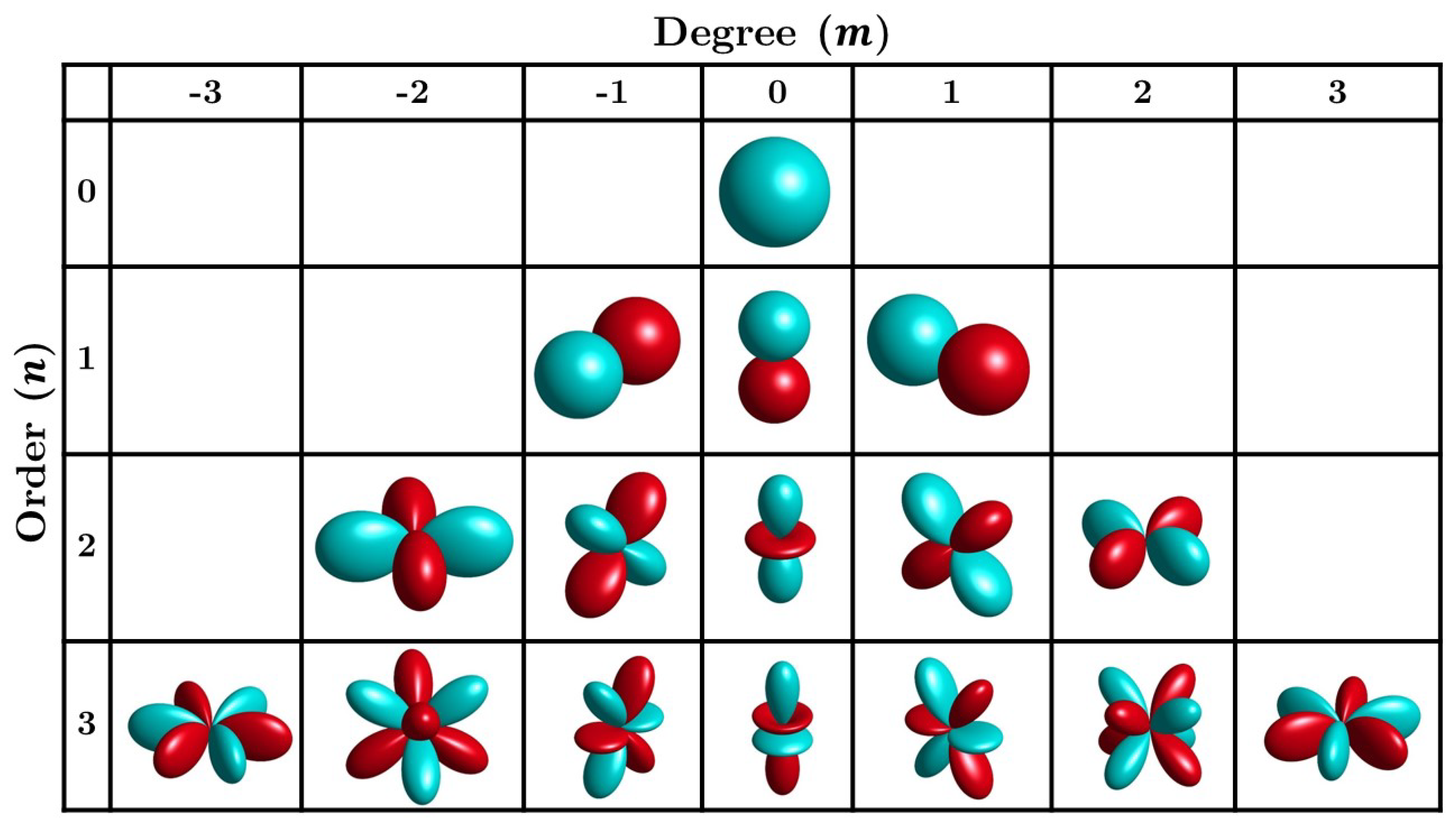
2.1. Spherical Harmonics
2.2. Spherical Array Data Processing
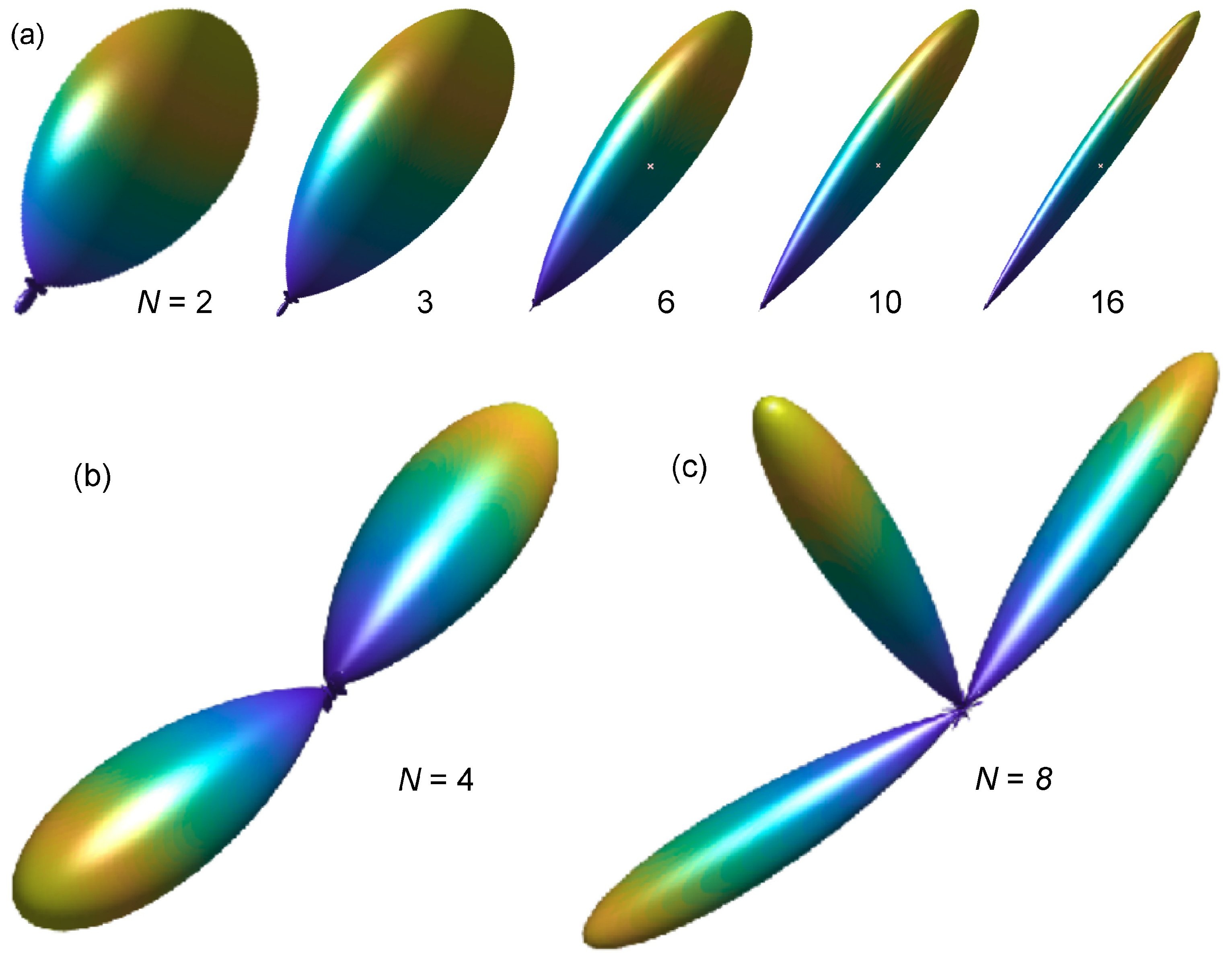
2.3. Analytical Beamforming Models
3. Model-Based Bayesian Inference
3.1. Bayesian Model Selection
3.2. Bayesian Parameter Estimation
3.3. Unified Bayesian Framework
4. Maximum Entropy Priors
4.1. Likelihood Assignment
4.2. Prior Probability Assignment
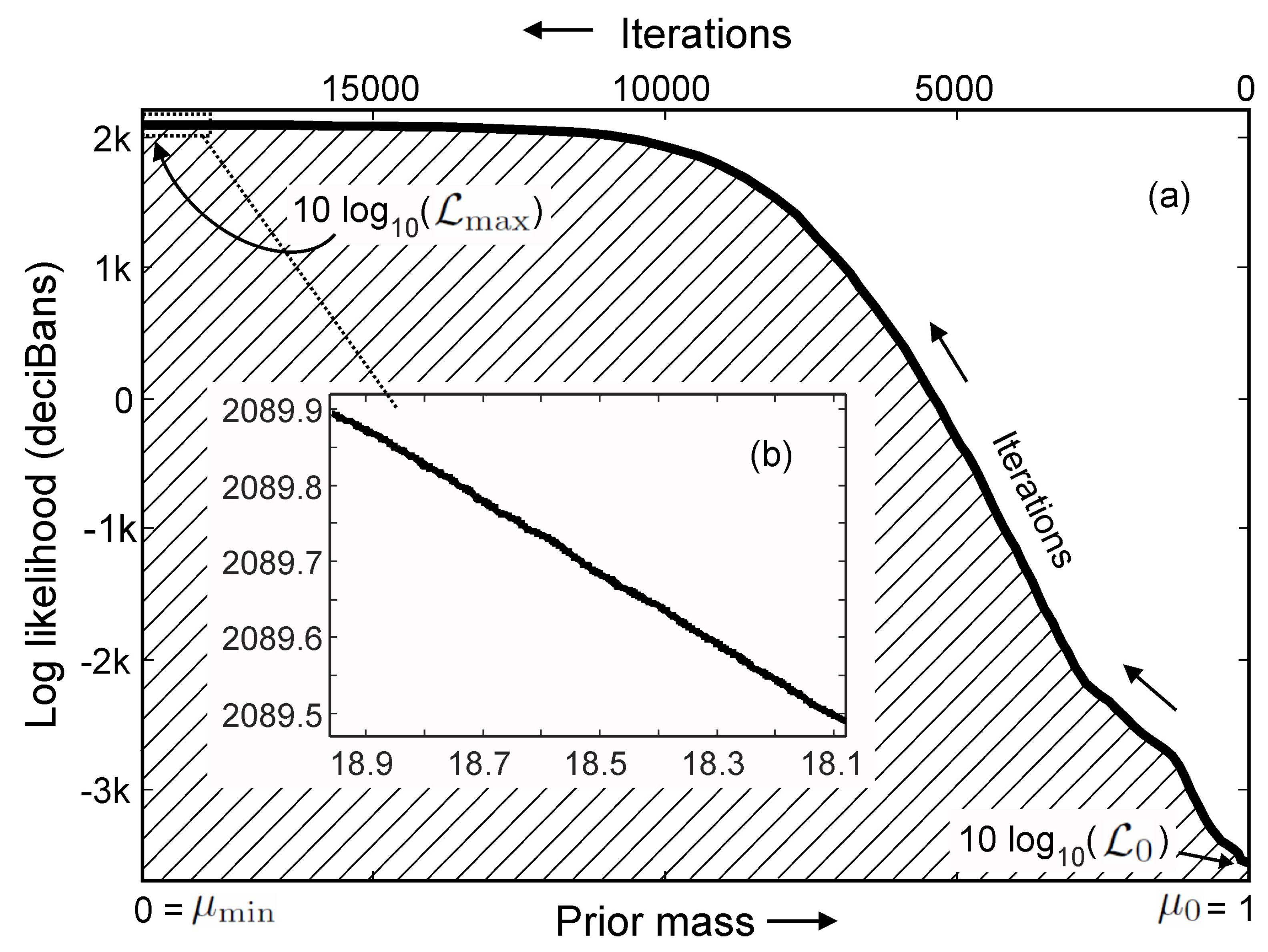
5. Nested Sampling
5.1. Lebesgue Integration as Foundation
5.2. Major Implementation Steps
- Draw a sufficient initial population, P, uniformly distributed samples, containing randomly generated values of all parameters, based on the maximum entropy prior probability (Section 4.2). In this case, .
- Identify the sample with the lowest likelihood value, within the population.
- Store this lowest likelihood value along with associated sample in a list outside the initial population. The list is referred to as the sample list below.
- For the following step , perturb the parameters associated with this least-likely sample in a random fashion and re-evaluate the likelihood value, with constraint, .
- (a)
- If the perturbed sample now meets the constraint, replace by this new sample, , into the initial population, then move on to the next step.
- (b)
- If not, keep perturbing in a way of randomly walking around in the parameter space, until the above constraint is fulfilled.
- Repeat steps 3–5 until the sample population has satisfied some predefined convergence criteria [44], or until some maximum number of iterations is met.
- The sample list storing all the likelihood values along with their samples, are already in the sequence in Equation (32) which is the ordered partition. The summation in Equation (34) along with Equations (35) and (36) using this likelihood sequence approximates the evidence estimate for the model under consideration.
- Use the evidence estimates from step 8 to evaluate Bayes factor distribution using Equation (18) over all the models, this facilitates the model selection.
5.3. Evidence Via Likelihood Range Partitions
5.4. Posterior Estimates as Byproducts
6. Experimental Results
7. Discussions
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meyer, J.; Elko, G. A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 6 August 2002; pp. 1781–1784. [Google Scholar] [CrossRef]
- Rafaely, B. Fundamentals of Spherical Array Processing; Springer: Berlin/Heidelberg, Germany, 2015; Volume 8. [Google Scholar]
- Williams, E. Fourier Acoustics: Sound Radiation and Near Field Acoustical Holography; Academic Press: London, UK, 1999; Volume 2, pp. 185–232. [Google Scholar] [CrossRef]
- Xiang, N.; Fackler, C. Objective Bayesian analysis in acoustics. Acoust. Today 2015, 11, 54–61. [Google Scholar]
- Knuth, K.H.; Habeck, M.; Malakare, N.K.; Mubeen, A.M.; Placek, B. Bayesian evidence and model selection. Digit. Signal Process. 2015, 47, 50–67. [Google Scholar] [CrossRef]
- Blandin, C.; Ozerov, A.; Vincent, E. Multi-source TDOA estimation in reverberant audio using angular spectra and clustering. Signal Process. 2012, 92, 1950–1960. [Google Scholar] [CrossRef]
- Bush, D.; Xiang, N. A model-based Bayesian framework for sound source enumeration and direction of arrival estimation using a coprime microphone array. J. Acoust. Soc. Am. 2018, 143, 3934–3945. [Google Scholar] [CrossRef] [PubMed]
- Escolano, J.; Xiang, N.; Perez-Lorenzo, J.M.; Cobos, M.; Lopez, J.J. A Bayesian direction-of-arrival model for an undetermined number of sources using a two-microphone array. J. Acoust. Soc. Am. 2014, 135, 742–753. [Google Scholar] [CrossRef] [PubMed]
- Mohan, S.; Lockwood, M.E.; Kramer, M.L.; Jones, D.L. Localization of multiple acoustic sources with small arrays using a coherence test. J. Acoust. Soc. Am. 2008, 123, 2136–2147. [Google Scholar] [CrossRef] [PubMed]
- Strutt, J.W. Investigation of the disturbance produced by a spherical obstacle on the waves of sound. Proc. Lond. Math. Soc. 1871, s1-4, 253–283. [Google Scholar] [CrossRef]
- Lowan, A.N. Spheroidal Wave Functions. In Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables; Abramowitz, M., Stegun, I.A., Eds.; NIST: Washington, DC, USA, 1972; pp. 751–759. [Google Scholar]
- MacRobert, T.M. Spherical Harmonics: An Elementary Treatise on Harmonic Functions, with Applications; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Madhu, N.; Martin, R. Acoustic Source Localization with Microphone Arrays; John Willey & Sons Inc.: Hoboken, NJ, USA, 2008; pp. 135–166. [Google Scholar]
- Nannuru, S.; Koochakzadeh, A.; Gemba, K.L.; Pal, P.; Gerstoft, P. Sparse Bayesian learning for beamforming using sparse linear arrays. J. Acoust. Soc. Am. 2018, 144, 2719–2729. [Google Scholar] [CrossRef] [PubMed]
- Khaykin, D.; Rafaely, B. Acoustic analysis by spherical microphone array processing of room impulse responses. J. Acoust. Soc. Am. 2012, 132, 261–270. [Google Scholar] [CrossRef] [PubMed]
- Morgenstern, H.; Rafaely, B. Modal smoothing for analysis of room reflections measured with spherical microphone and loudspeaker arrays. J. Acoust. Soc. Am. 2018, 143, 1008–1018. [Google Scholar] [CrossRef]
- Nadiri, O.; Rafaely, B. Localization of Multiple Speakers under High Reverberation using a Spherical Microphone Array and the Direct-Path Dominance Test. IEEE ACM Trans. Audio Speech Lang. Process. 2014, 22, 1494–1505. [Google Scholar] [CrossRef]
- Sun, H.; Mabande, E.; Kowalczyk, K.; Kellermann, W. Localization of distinct reflections in rooms using spherical microphone array eigenbeam processing. J. Acoust. Soc. Am. 2012, 131, 2828–2840. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Duraiswami, R. Hemispherical Microphone Arrays for Sound Capture and Beamforming. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 16 October 2005; pp. 106–109. [Google Scholar]
- Shabtai, N.R.; Vorländer, M. Acoustic centering of sources with high-order radiation patterns. J. Acoust. Soc. Am. 2015, 137, 1947–1961. [Google Scholar] [CrossRef] [PubMed]
- Fernandez Grande, E. Sound field reconstruction using a spherical microphone array. J. Acoust. Soc. Am. 2016, 139, 1168–1178. [Google Scholar] [CrossRef] [PubMed]
- Richard, A.; Fernandez Grande, E.; Brunskog, J.; Jeong, C.H. Estimation of surface impedance at oblique incidence based on sparse array processing. J. Acoust. Soc. Am. 2017, 141, 4115–4125. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Dabin, M.; Cheng, E.; Qiu, X.; Burnett, I.; Liu, J.C. Mitigating wind noise with a spherical microphone array. J. Acoust. Soc. Am. 2018, 144, 3211–3220. [Google Scholar] [CrossRef] [PubMed]
- Zuo, H.; Samarasinghe, P.N.; Abhayapala, T.D. Spatial sound intensity vectors in spherical harmonic domain. J. Acoust. Soc. Am. Express Lett. 2019, 145, EL149–EL155. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.T.; Morris, Z.N.; Nnonyelu, C.J. Rules-of-thumb to design a uniform spherical array for direction finding – Its Cramér-Rao bounds’ nonlinear dependence on the number of sensors. J. Acoust. Soc. Am. 2019, 145, 714–723. [Google Scholar] [CrossRef] [PubMed]
- Jo, B.; Choi, J.W. Direction of arrival estimation using nonsingular spherical ESPRIT. J. Acoust. Soc. Am. Express Lett. 2018, 143, EL181–EL187. [Google Scholar] [CrossRef]
- Xenaki, A.; Fernandez-Grande, E.; Gerstoft, P. Block-sparse beamforming for spatially extended sources in a Bayesian formulation. J. Acoust. Soc. Am. 2016, 140, 1828–1838. [Google Scholar] [CrossRef] [PubMed]
- Xiang, N.; Goggans, P.M. Evaluation of decay times in coupled spaces: Bayesian decay model selection. J. Acoust. Soc. Am. 2003, 113, 2685–2697. [Google Scholar] [CrossRef] [PubMed]
- Beaton, D.; Xiang, N. Room acoustic modal analysis using Bayesian inference. J. Acoust. Soc. Am. 2017, 141, 4480–4493. [Google Scholar] [CrossRef] [PubMed]
- Blauert, J.; Xiang, N. Acoustics for Engineers—Troy Lectures; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Rafaely, B. Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process. 2005, 13, 135–143. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Oxford University Press: Oxford, UK, 1965; pp. 193–244. [Google Scholar]
- Sivia, D.; Skilling, J. Data Analysis: A Bayesian Tutorial, 2nd ed.; Oxford University Press: New York, NY, USA, 2006; Chapter 9. [Google Scholar]
- Skilling, J. Nested sampling. AIP Conf. Proc. 2004, 735, 395–405. [Google Scholar] [CrossRef]
- Jaynes, E. Prior probabilities. IEEE Trans. Inf. Theory 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Shannon, C.E. The Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gregory, P.C. Bayesian Logical Data Analysis for the Physical Sciences; Cambridge University Press: Cambridge, UK, 2005; pp. 184–242. [Google Scholar]
- Candy, J. Bayesian Signal Processing—Classical, Modern, and Particle Filtering Methods, 2nd ed.; John Willey & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Woodward, P.M. Probability and Information Theory, with Applications to Radar, 2nd ed.; Pergamon Press, Ltd.: London, UK, 1953. [Google Scholar]
- Jeffreys, H. An Invariant Form for the Prior Probability in Estimation Problems. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Bretthorst, G.L. Bayesian Analysis. I. Parameter Estimation Using Quadrature NMR Models. J. Mag. Res. 1990, 88, 533–551. [Google Scholar] [CrossRef]
- Xiang, N.; Goggans, P.M. Evaluation of decay times in coupled spaces: Bayesian parameter estimation. J. Acoust. Soc. Am. 2001, 110, 1415–1424. [Google Scholar] [CrossRef]
- Skilling, J. Nested Sampling for General Bayesian Computation. Bayesian Anal. 2006, 1, 833–860. [Google Scholar] [CrossRef]
- Jasa, T.; Xiang, N. Using Nested Sampling in the Analysis of Multi-rate Sound Energy Decay in Acoustically Coupled Spaces. In AIP Conference Proceedings; AIP: Melville, NY, USA, 2005; pp. 189–196. [Google Scholar]
- Jasa, T.; Xiang, N. Nested sampling applied in Bayesian room-acoustics decay analysis. J. Acoust. Soc. Am. 2012, 132, 3251–3262. [Google Scholar] [CrossRef] [PubMed]
- Fackler, C.J.; Xiang, N.; Horoshenkov, K. Bayesian acoustic analysis of multilayer porous media. J. Acoust. Soc. Am. 2018, 144, 3582–3592. [Google Scholar] [CrossRef] [PubMed]
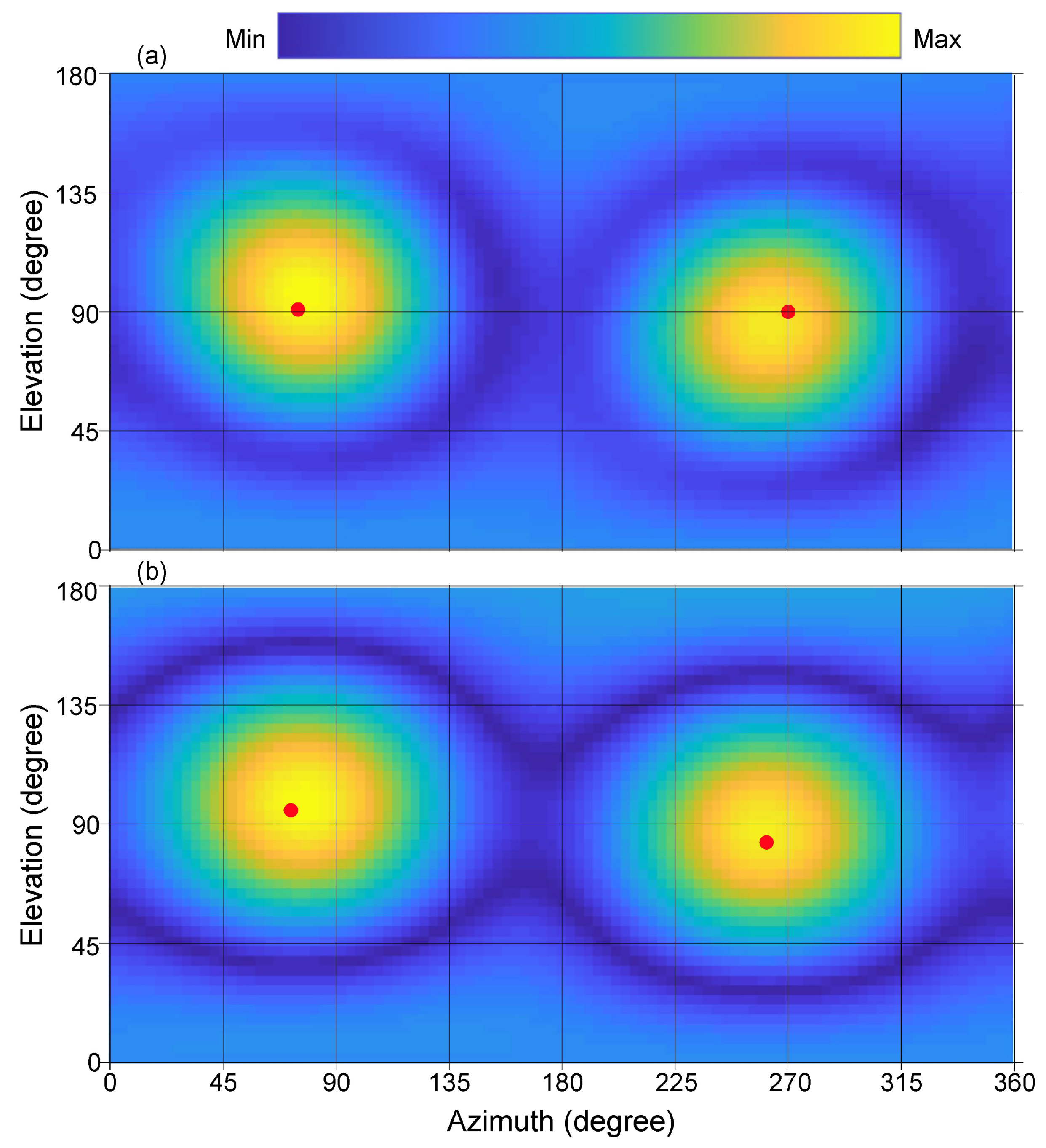
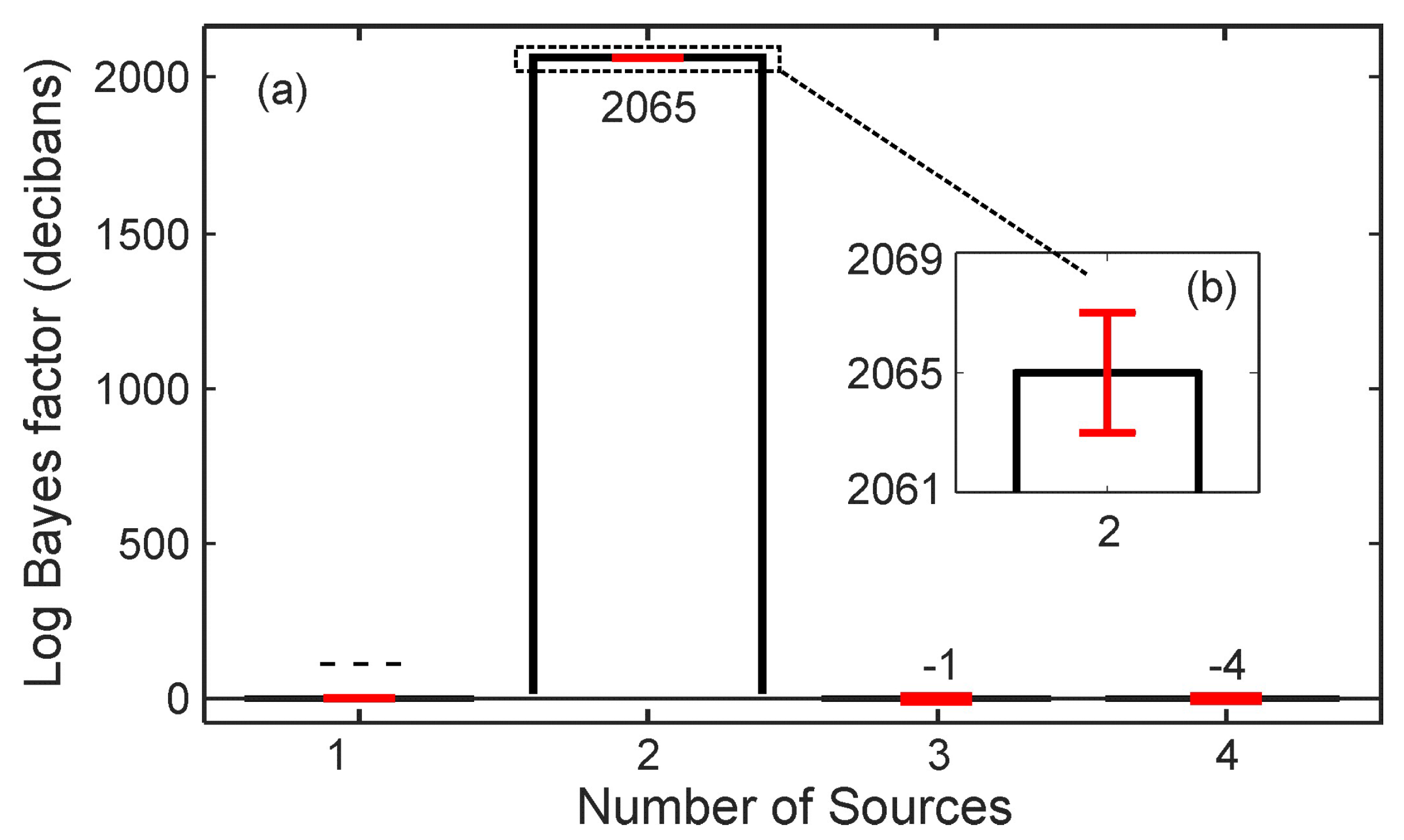

| Comparison | Direction of Arrival | |
|---|---|---|
| Experiment | ||
| Estimates | ||
| Deviation | ||
| Error | ||
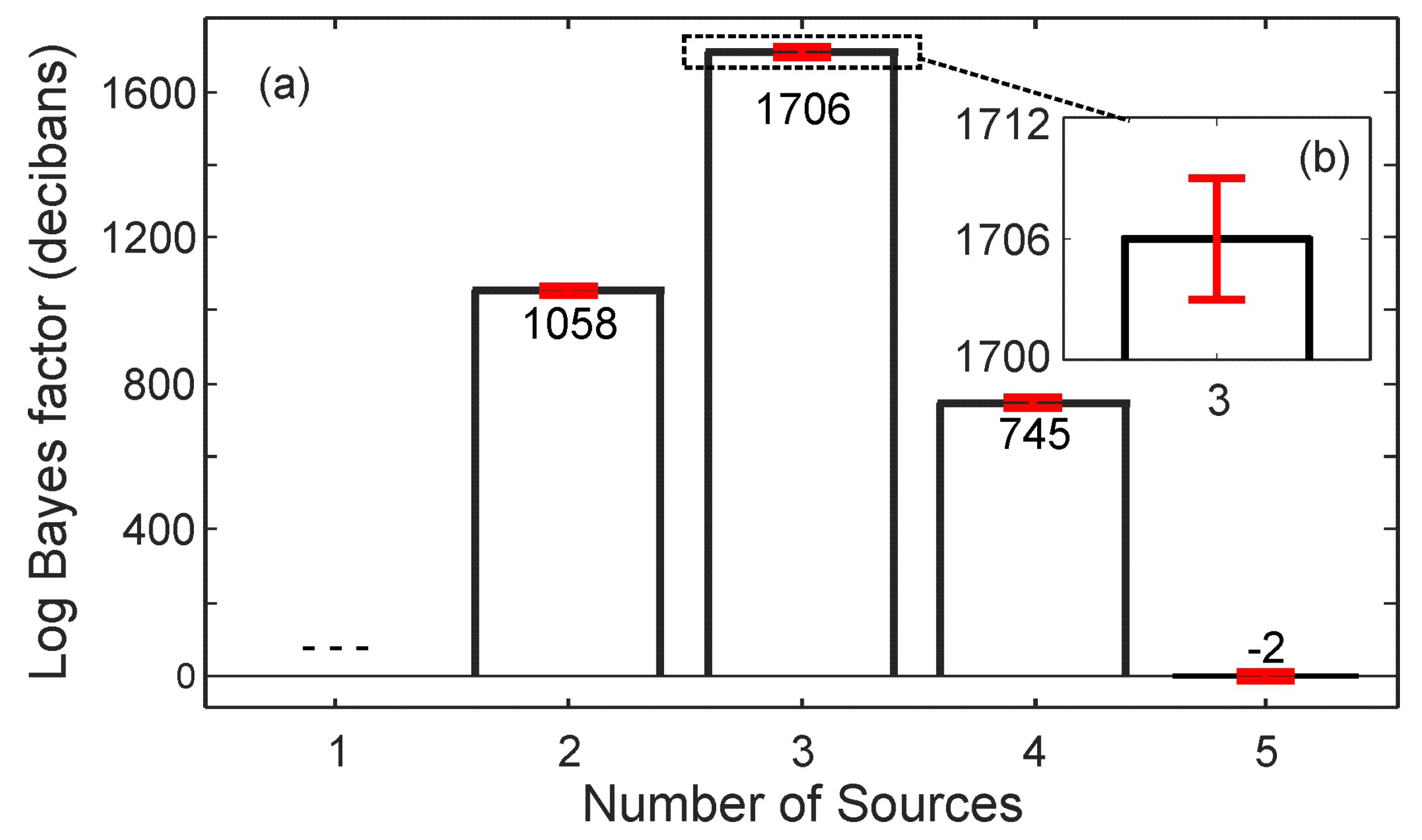
| Comparison | Direction of Arrival | ||
|---|---|---|---|
| Experiment | |||
| Estimates | |||
| Deviation | |||
| Error | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, N.; Landschoot, C. Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics. Entropy 2019, 21, 579. https://doi.org/10.3390/e21060579
Xiang N, Landschoot C. Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics. Entropy. 2019; 21(6):579. https://doi.org/10.3390/e21060579
Chicago/Turabian StyleXiang, Ning, and Christopher Landschoot. 2019. "Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics" Entropy 21, no. 6: 579. https://doi.org/10.3390/e21060579
APA StyleXiang, N., & Landschoot, C. (2019). Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics. Entropy, 21(6), 579. https://doi.org/10.3390/e21060579





