Seasonal Entropy, Diversity and Inequality Measures of Submitted and Accepted Papers Distributions in Peer-Reviewed Journals
Abstract
1. Introduction
2. Definitions
- the number of monthly submissions in a given month () in year (y) is called
- the percentage of this set is the probability of submission in a given month for a specific year
- similarly, one can define , as being the number of accepted papers when submitted in year (y) in a specific month (m),
- and for the related percentage, one has ;
- more importantly, for authors, the (conditional) probability of a paper acceptance when submitted in a given month may be considered and estimated before submission
- , from which one deduces
- and similarly for the accepted papers , and
- leading to the ratio between cumulated monthly data
- and to the corresponding “monthly cumulated entropy”, ,
- finally to
3. Data Analysis
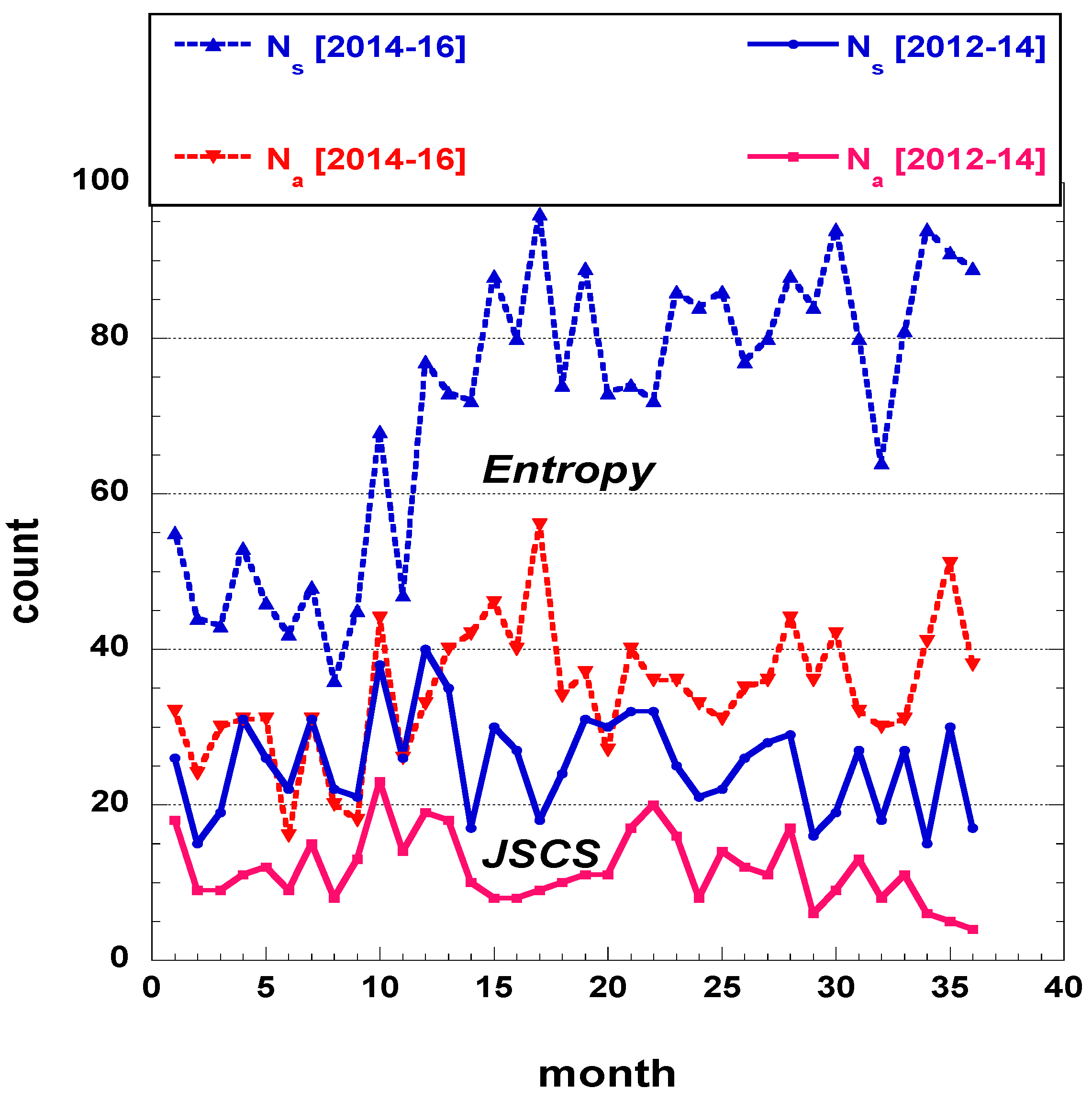
3.1. Data
3.2. Analysis
3.2.1. A posteriori features findings
3.2.2. Non-Linear Entropy Indices
3.2.3. Forecasting Aspects
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Series Data
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| f | ||||||||
| 1 | 125.42 | 0.3333 (3) | 66.83 | 0.0833 (12) | 720.23 | 0.0278 (36) | 169.36 | 0.0556 (18) |
| 2 | 94.94 | 0.3889 (2.57) | 51.11 | 0.3333 (3) | 378.38 | 0.0833 (12) | 164.15 | 0.0833 (12) |
References
- Boja, C.E.; Herţeliu, C.; Dârdală, M.; Ileanu, B.V. Day of the week submission effect for accepted papers in Physica A, PLOS ONE, Nature and Cell. Scientometrics 2018, 117, 887–918. [Google Scholar] [CrossRef]
- Mrowinski, M.J.; Fronczak, A.; Fronczak, P.; Nedic, O.; Ausloos, M. Review times in peer review: Quantitative analysis and modelling of editorial work flows. Scientometrics 2016, 107, 271–286. [Google Scholar] [CrossRef] [PubMed]
- Mrowinski, M.J.; Fronczak, P.; Fronczak, A.; Ausloos, M.; Nedic, O. Artificial intelligence in peer review: How can evolutionary computation support journal editors? PLoS ONE 2017, 12, e0184711. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, M. Seasonal bias in editorial decisions for a physics journal: You should write when you like, but submit in July. Learn. Publ. 2012, 25, 145–151. [Google Scholar] [CrossRef]
- Shalvi, S.; Baas, M.; Handgraaf, M.J.J.; De Dreu, C.K.W. Write when hot—Submit when not: Seasonal bias in peer review or acceptance? Learn. Publ. 2010, 23, 117–123. [Google Scholar] [CrossRef]
- Ausloos, M.; Nedič, O.; Dekanski, A. Correlations between submission and acceptance of papers in peer review journals. Scientometrics 2019, 119, 279–302. [Google Scholar] [CrossRef]
- Marhuenda, Y.; Morales, D.; Pardo, M.C. A comparison of uniformity tests. Statistics 2005, 39, 315–327. [Google Scholar] [CrossRef]
- Alizadeh Noughabi, H.A. Entropy-based tests of uniformity: A Monte Carlo power comparison. Commun. Stat. Simul. Comput. 2017, 46, 1266–1279. [Google Scholar] [CrossRef]
- Rousseau, R. Concentration and diversity of availability and use in information systems: A positive reinforcement model. J. Am. Soc. Inf. Sci. 1992, 43, 391–395. [Google Scholar] [CrossRef]
- Leydesdorff, L.; Rafols, I. Indicators of the interdisciplinarity of journals: Diversity, centrality, and citations. J. Inf. 2011, 5, 87–100. [Google Scholar] [CrossRef]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communications. Bell. Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Shannon, C. Prediction and entropy of printed English. Bell. Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Campbell, L.L. Exponential entropy as a measure of extent of a distribution. Probab. Theory Relat. Fields 1966, 5, 217–225. [Google Scholar] [CrossRef]
- Theil, H. Economics and Information Theory; Rand McNally and Company: Chicago, IL, USA, 1967. [Google Scholar]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; Van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stat. Sci. 1997, 6, 17–39. [Google Scholar]
- Oancea, B.; Pirjol, D. Extremal properties of the Theil and Gini measures of inequality. Qual. Quant. 2019, 53, 859–869. [Google Scholar] [CrossRef]
- Hirschman, A.O. The paternity of an index. Am. Econ. Rev. 1964, 54, 761–762. [Google Scholar]
- Gini, C. Índice di Concentrazione e di Dipendenza. Biblioteca dell’Economista, Serie V; Utet Torino: Turin, Italy, 1910; Volume XX, English translation in Riv. Politica Econ. 1997, 87, 769–789. [Google Scholar]
- Atkinson, A.B.; Bourguignon, F. (Eds.) Handbook of Income Distribution; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2. [Google Scholar]
- Cerqueti, R.; Ausloos, M. Statistical assessment of regional wealth inequalities: The Italian case. Qual. Quant. 2015, 49, 2307–2323. [Google Scholar] [CrossRef]
- Cerqueti, R.; Ausloos, M. Socio-economical Analysis of Italy: The case of hagiotoponym cities. Soc. Sci. J. 2015, 52, 561–564. [Google Scholar] [CrossRef]
- Wessa, P. Free Statistics Software, Office for Research Development and Education, Version 1.1.23-r. 2014. Available online: http://www.wessa.net/ (accessed on 4 June 2019).
- Crooks, G.E. On Measures of Entropy and Information. Tech. Note 2017, 9, v7. [Google Scholar]
- Clippe, P.; Ausloos, M. Benford’s law and Theil transform of financial data. Phys. A 2012, 391, 6556–6567. [Google Scholar] [CrossRef]
- Nedić, O.; Drvenica, I.; Ausloos, M.; Dekanski, A. Efficiency in managing peer-review of scientific manuscripts-editors’ perspective. J. Serb. Chem. Soc. 2018, 83, 1391–1405. [Google Scholar] [CrossRef]
- Drvenica, I.; Bravo, G.; Vejmelka, L.; Dekanski, A.; Nedić, O. Peer Review of Reviewers: The Author’s Perspective. Publications 2019, 7, 1. [Google Scholar] [CrossRef]
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| 317 | 322 | 274 | 913 | 604 | 961 | 1008 | 2573 | |
| 2012 | 2013 | 2014 | [2012–2014] | 2014 | 2015 | 2016 | [2014–2016] | |
| January | 0.08202 | 0.10870 | 0.08029 | 0.09091 | 0.09106 | 0.07596 | 0.08532 | 0.08317 |
| February | 0.04732 | 0.05280 | 0.09489 | 0.06353 | 0.07285 | 0.07492 | 0.07639 | 0.07501 |
| March | 0.05994 | 0.09317 | 0.10219 | 0.08434 | 0.07119 | 0.09157 | 0.07937 | 0.08201 |
| April | 0.09779 | 0.08385 | 0.10584 | 0.09529 | 0.08775 | 0.08325 | 0.08730 | 0.08589 |
| May | 0.08202 | 0.05590 | 0.05839 | 0.06572 | 0.07616 | 0.09990 | 0.08333 | 0.08784 |
| June | 0.06940 | 0.07453 | 0.06934 | 0.07119 | 0.06954 | 0.07700 | 0.09325 | 0.08162 |
| July | 0.09779 | 0.09627 | 0.09854 | 0.09748 | 0.07947 | 0.09261 | 0.07937 | 0.08434 |
| August | 0.06940 | 0.09317 | 0.06569 | 0.07667 | 0.05960 | 0.07596 | 0.06349 | 0.06724 |
| September | 0.06625 | 0.09938 | 0.09854 | 0.08762 | 0.07450 | 0.07700 | 0.08036 | 0.07773 |
| October | 0.11987 | 0.09938 | 0.05474 | 0.09310 | 0.11258 | 0.07492 | 0.09325 | 0.09094 |
| November | 0.08202 | 0.07764 | 0.10949 | 0.08872 | 0.07781 | 0.08949 | 0.09028 | 0.08706 |
| December | 0.12618 | 0.06522 | 0.06204 | 0.08543 | 0.12748 | 0.08741 | 0.08829 | 0.09716 |
| 23.278 | 14.075 | 14.964 | 15.811 | 29.497 | 9.377 | 9.333 | 20.236 | |
| entropy | 2.4487 | 2.4620 | 2.4569 | 2.4760 | 2.4621 | 2.4801 | 2.4801 | 2.4809 |
| Mean | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 |
| Std Dev | 0.02359 | 0.01820 | 0.02034 | 0.01145 | 0.01923 | 0.00860 | 0.00837 | 0.00772 |
| 0.03616 | 0.04694 | 0.04265 | 0.06043 | 0.04486 | 0.06614 | 0.06658 | 0.06790 | |
| 0.13051 | 0.11973 | 0.12401 | 0.10624 | 0.12180 | 0.10053 | 0.10008 | 0.09877 | |
| 654.12 | 854.49 | 705.30 | 2287.08 | 1107.62 | 3124.03 | 3287.43 | 5694.50 | |
| 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | |
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| 160 | 146 | 116 | 422 | 336 | 467 | 447 | 1250 | |
| 2012 | 2013 | 2014 | [2012–2014] | 2014 | 2015 | 2016 | [2014–2016] | |
| January | 0.11250 | 0.12329 | 0.12069 | 0.11848 | 0.09524 | 0.08565 | 0.06935 | 0.08240 |
| February | 0.05625 | 0.06849 | 0.10345 | 0.07346 | 0.07143 | 0.08994 | 0.07830 | 0.08080 |
| March | 0.05625 | 0.05479 | 0.09483 | 0.06635 | 0.08929 | 0.09850 | 0.08054 | 0.08960 |
| April | 0.06875 | 0.05479 | 0.14655 | 0.08531 | 0.09226 | 0.08565 | 0.09843 | 0.09200 |
| May | 0.07500 | 0.06164 | 0.05172 | 0.06398 | 0.09226 | 0.11991 | 0.08054 | 0.09840 |
| June | 0.05625 | 0.06849 | 0.07759 | 0.06635 | 0.04762 | 0.07281 | 0.09396 | 0.07360 |
| July | 0.09375 | 0.07534 | 0.11207 | 0.09242 | 0.09226 | 0.07923 | 0.07159 | 0.08000 |
| August | 0.05000 | 0.07534 | 0.06897 | 0.06398 | 0.05952 | 0.05782 | 0.06711 | 0.06160 |
| September | 0.08125 | 0.11644 | 0.09483 | 0.09716 | 0.05357 | 0.08565 | 0.06935 | 0.07120 |
| October | 0.14375 | 0.13699 | 0.05172 | 0.11611 | 0.13095 | 0.07709 | 0.09172 | 0.09680 |
| November | 0.08750 | 0.10959 | 0.04310 | 0.08294 | 0.07738 | 0.07709 | 0.11409 | 0.09040 |
| December | 0.11875 | 0.05479 | 0.03448 | 0.07346 | 0.09821 | 0.07066 | 0.08501 | 0.08320 |
| 18.200 | 17.068 | 18.276 | 20.806 | 23.4286 | 14.8243 | 11.7651 | 19.5802 | |
| entropy | 2.4305 | 2.4291 | 2.4042 | 2.4612 | 2.4496 | 2.4695 | 2.4722 | 2.4769 |
| Mean | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 | 0.08333 |
| Std Dev | 0.02935 | 0.02976 | 0.03455 | 0.01933 | 0.02298 | 0.01551 | 0.01412 | 0.01089 |
| 0.02462 | 0.02381 | 0.01424 | 0.04468 | 0.03737 | 0.05232 | 0.05509 | 0.06155 | |
| 0.14204 | 0.14285 | 0.15243 | 0.12199 | 0.12930 | 0.11435 | 0.11157 | 0.10512 | |
| 373.51 | 351.88 | 270.17 | 921.04 | 691.19 | 1207.53 | 1297.69 | 2813.71 | |
| 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | |
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | [2012–2014] | 2014 | 2015 | 2016 | [2014–2016] | |
| January | 0.6923 | 0.5143 | 0.6364 | 0.6024 | 0.5818 | 0.5479 | 0.3605 | 0.4813 |
| February | 0.6000 | 0.5882 | 0.4615 | 0.5345 | 0.5455 | 0.5833 | 0.4545 | 0.5233 |
| March | 0.4737 | 0.2667 | 0.3929 | 0.3636 | 0.6977 | 0.5227 | 0.4500 | 0.5308 |
| April | 0.3548 | 0.2963 | 0.5862 | 0.4138 | 0.5849 | 0.5000 | 0.5000 | 0.5204 |
| May | 0.4615 | 0.5000 | 0.3750 | 0.4500 | 0.6739 | 0.5833 | 0.4286 | 0.5442 |
| June | 0.4091 | 0.4167 | 0.4737 | 0.4308 | 0.3810 | 0.4595 | 0.4468 | 0.4381 |
| July | 0.4839 | 0.3548 | 0.4815 | 0.4382 | 0.6458 | 0.4157 | 0.4000 | 0.4608 |
| August | 0.3636 | 0.3667 | 0.4444 | 0.3857 | 0.5556 | 0.3699 | 0.4687 | 0.4451 |
| September | 0.6190 | 0.5312 | 0.4074 | 0.5125 | 0.4000 | 0.5405 | 0.3827 | 0.4450 |
| October | 0.6053 | 0.6250 | 0.4000 | 0.5765 | 0.6471 | 0.5000 | 0.4362 | 0.5171 |
| November | 0.5385 | 0.6400 | 0.1667 | 0.4321 | 0.5532 | 0.4186 | 0.5604 | 0.5045 |
| December | 0.4750 | 0.3810 | 0.2353 | 0.3974 | 0.4286 | 0.3929 | 0.4270 | 0.4160 |
| 4.0120 | 4.0970 | 4.1301 | 4.2136 | 3.7919 | 4.1450 | 4.2943 | 4.1883 | |
| sum | 6.0767 | 5.4809 | 5.0610 | 5.5375 | 6.6951 | 5.8343 | 5.3154 | 5.8266 |
| Mean () | 0.5064 | 0.4567 | 0.4217 | 0.4615 | 0.5579 | 0.4862 | 0.4429 | 0.4856 |
| Std Dev | 0.1063 | 0.1271 | 0.1297 | 0.0770 | 0.1058 | 0.0737 | 0.0528 | 0.0432 |
| 0.2939 | 0.2026 | 0.1624 | 0.3075 | 0.3463 | 0.3387 | 0.3373 | 0.3992 | |
| 0.7189 | 0.7109 | 0.6811 | 0.6154 | 0.7695 | 0.6337 | 0.5486 | 0.5719 | |
| t-test | 52.786 | 46.897 | 43.870 | 130.33 | 67.933 | 135.995 | 203.05 | 380.07 |
| z-test | 0.803 | 40.758 | 0.673 | 1.268 | 1.198 | 1.347 | 1.291 | 2.190 |
| p-level | 0.4221 | 0.4484 | 0.5012 | 0.2047 | 0.2309 | 0.1780 | 0.1968 | 0.0285 |
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | [2012–2014] | 2014 | 2015 | 2016 | [2014–2016] | |
| January | 0.25458 | 0.34199 | 0.28763 | 0.30531 | 0.31511 | 0.32963 | 0.36780 | 0.35196 |
| February | 0.30650 | 0.31213 | 0.35686 | 0.33483 | 0.33062 | 0.31441 | 0.35839 | 0.33888 |
| March | 0.35394 | 0.35247 | 0.36705 | 0.36785 | 0.25116 | 0.33909 | 0.35933 | 0.33619 |
| April | 0.36765 | 0.36041 | 0.31308 | 0.36513 | 0.31369 | 0.34657 | 0.34657 | 0.33992 |
| May | 0.35686 | 0.34657 | 0.36781 | 0.35933 | 0.26596 | 0.31441 | 0.36313 | 0.33109 |
| June | 0.36565 | 0.36478 | 0.35394 | 0.36279 | 0.36765 | 0.35732 | 0.35996 | 0.36157 |
| July | 0.35126 | 0.36765 | 0.35191 | 0.36155 | 0.28237 | 0.36489 | 0.36652 | 0.35702 |
| August | 0.36785 | 0.36788 | 0.36041 | 0.36745 | 0.32655 | 0.36787 | 0.35517 | 0.36029 |
| September | 0.29688 | 0.33603 | 0.36583 | 0.34258 | 0.36652 | 0.33253 | 0.36758 | 0.36031 |
| October | 0.30390 | 0.29375 | 0.36652 | 0.31754 | 0.28168 | 0.34657 | 0.36190 | 0.34104 |
| November | 0.33333 | 0.28562 | 0.29863 | 0.36257 | 0.32752 | 0.36453 | 0.32451 | 0.34518 |
| December | 0.35361 | 0.36765 | 0.34045 | 0.36672 | 0.36313 | 0.36705 | 0.36337 | 0.36486 |
| 4.0120 | 4.0969 | 4.1301 | 4.2137 | 3.7919 | 4.1449 | 4.2942 | 4.1883 | |
| Mean | 0.33433 | 0.34141 | 0.34418 | 0.35114 | 0.3160 | 0.34541 | 0.35785 | 0.34903 |
| Std Dev | 0.03597 | 0.02924 | 0.02842 | 0.02131 | 0.03922 | 0.01963 | 0.01205 | 0.01162 |
| 0.26240 | 0.28294 | 0.28734 | 0.30852 | 0.23755 | 0.30615 | 0.33376 | 0.32578 | |
| 0.40627 | 0.39989 | 0.40101 | 0.39375 | 0.39444 | 0.38467 | 0.38195 | 0.37227 | |
| 216.505 | 251.492 | 229.588 | 577.295 | 295.560 | 665.578 | 1060.13 | 1828.53 | |
| 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | |
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | [2012–2014] | 2014 | 2015 | 2016 | [2014–2016] | |
| D | 11.574 | 11.729 | 11.669 | 11.893 | 11.730 | 11.942 | 11.943 | 11.952 |
| 0.08640 | 0.08526 | 0.08570 | 0.08408 | 0.08526 | 0.08373 | 0.08373 | 0.08367 | |
| 0.03619 | 0.02287 | 0.02797 | 0.00893 | 0.02280 | 0.00480 | 0.00480 | 0.00399 | |
| HHI | 0.08945 | 0.08698 | 0.08788 | 0.08478 | 0.08740 | 0.08415 | 0.08410 | 0.08399 |
| 0.15063 | 0.11749 | 0.13139 | 0.07329 | 0.11369 | 0.05402 | 0.05192 | 0.04861 | |
| accepted papers | ||||||||
| D | 11.364 | 11.349 | 11.069 | 11.719 | 11.584 | 11.817 | 11.848 | 11.904 |
| 0.08799 | 0.088114 | 0.09034 | 0.08533 | 0.08633 | 0.08463 | 0.08440 | 0.08401 | |
| 0.05446 | 0.05578 | 0.08073 | 0.02371 | 0.03528 | 0.01539 | 0.01275 | 0.00803 | |
| HHI | 0.09281 | 0.09308 | 0.09646 | 0.08746 | 0.08914 | 0.08598 | 0.08553 | 0.08464 |
| 0.18646 | 0.18949 | 0.22557 | 0.12164 | 0.14335 | 0.09404 | 0.08930 | 0.07027 | |
| accepted papers if submitted in a given month | ||||||||
| D | 55.257 | 60.158 | 62.186 | 67.602 | 44.341 | 63.116 | 73.278 | 65.912 |
| 0.08504 | 0.08634 | 0.08737 | 0.08438 | 0.08478 | 0.08423 | 0.08387 | 0.08364 | |
| 0.02022 | 0.03614 | 0.04727 | 0.01244 | 0.01716 | 0.01070 | 0.00641 | 0.00365 | |
| HHI | 0.08670 | 0.08924 | 0.09056 | 0.08546 | 0.08608 | 0.08509 | 0.08442 | 0.08394 |
| 0.11355 | 0.15211 | 0.15965 | 0.08820 | 0.10083 | 0.08264 | 0.06189 | 0.04808 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ausloos, M.; Nedic, O.; Dekanski, A. Seasonal Entropy, Diversity and Inequality Measures of Submitted and Accepted Papers Distributions in Peer-Reviewed Journals. Entropy 2019, 21, 564. https://doi.org/10.3390/e21060564
Ausloos M, Nedic O, Dekanski A. Seasonal Entropy, Diversity and Inequality Measures of Submitted and Accepted Papers Distributions in Peer-Reviewed Journals. Entropy. 2019; 21(6):564. https://doi.org/10.3390/e21060564
Chicago/Turabian StyleAusloos, Marcel, Olgica Nedic, and Aleksandar Dekanski. 2019. "Seasonal Entropy, Diversity and Inequality Measures of Submitted and Accepted Papers Distributions in Peer-Reviewed Journals" Entropy 21, no. 6: 564. https://doi.org/10.3390/e21060564
APA StyleAusloos, M., Nedic, O., & Dekanski, A. (2019). Seasonal Entropy, Diversity and Inequality Measures of Submitted and Accepted Papers Distributions in Peer-Reviewed Journals. Entropy, 21(6), 564. https://doi.org/10.3390/e21060564







