Abstract
This paper presents a novel method for finding features in the analysis of variable distributions stemming from time series. We apply the methodology to the case of submitted and accepted papers in peer-reviewed journals. We provide a comparative study of editorial decisions for papers submitted to two peer-reviewed journals: the Journal of the Serbian Chemical Society (JSCS) and this MDPI Entropy journal. We cover three recent years for which the fate of submitted papers—about 600 papers to JSCS and 2500 to Entropy—is completely determined. Instead of comparing the number distributions of these papers as a function of time with respect to a uniform distribution, we analyze the relevant probabilities, from which we derive the information entropy. It is argued that such probabilities are indeed more relevant for authors than the actual number of submissions. We tie this entropy analysis to the so called diversity of the variable distributions. Furthermore, we emphasize the correspondence between the entropy and the diversity with inequality measures, like the Herfindahl-Hirschman index and the Theil index, itself being in the class of entropy measures; the Gini coefficient which also measures the diversity in ranking is calculated for further discussion. In this sample, the seasonal aspects of the peer review process are outlined. It is found that the use of such indices, non linear transformations of the data distributions, allow us to distinguish features and evolutions of the peer review process as a function of time as well as comparing the non-uniformity of distributions. Furthermore, t- and z-statistical tests are applied in order to measure the significance (p-level) of the findings, that is, whether papers are more likely to be accepted if they are submitted during a few specific months or during a particular “season”; the predictability strength depends on the journal.
1. Introduction
Authors who submit (by their own assumption) high quality papers to scholarly journals, are interested in knowing if there are factors which may increase the probability that their papers be accepted. One such factor may be related to the month or day of submission, as recently discussed [1]. Indeed, authors might wonder about editors’ and reviewers’ overload at some times of the year. Moreover, the number of submitted papers is relevant for editors and publishers handling machines to the point that artificial intelligence can be useful for helping journal editors [2,3]. More generally, informetrics and bibliometrics are also interested in manuscript submission timing, especially in light of an enormous increase in the number of electronic journals.
From the author’s point of view, rejection is often frustrating, be it due to an “editor desk rejection” or following a review process. A high editor desk rejection rate has sometimes been explained as due to an entrance barrier editor load effect [4]. Thus, it is of interest to observe whether there is a high probability of submission during specific months or seasons. In fact, non uniform submission has already been studied. However, the acceptance distribution, during a year, that is, a “monthly bias”, is rarely studied, because of publisher secrecy. Search engines do not provide any information at all on the timing of rejected papers.
Interestingly, Boja et al. [1] recently examined a large database of journals with high impact factors and reported that a day of the week correlation effect occurs between “when a paper is submitted to a peer-reviewed journal (and) whether that paper is accepted”. However, there was no study of rejected papers because of a lack of data, therefore one may wonder whether, besides a “day of the week” effect, there is some “seasonal” effect. One may indeed imagine that researchers in academic surroundings do not have a constant occupation rate due to teaching classes, holidays, congresses, and even budgetary conditions. Researchers have only specific times during the academic year for producing research papers.
From the “seasonal effect” point view, Shalvi et al. [5] found a discrepancy in the pattern of “submission-per-month” and “acceptance-per-month” for Psychological Science () but not for Social Psychology Bulletin (). Summer months inspired authors to submit more papers to but the subsequent acceptance was not related to the effect of seasonal bias (based on a test for percentages). On the other hand, a very low rate of acceptance was recorded for manuscripts sent in November or December. The number of submissions to , on the contrary, was the greatest during winter months, followed by a reduced “production” in April; however, the rate of acceptance was the highest for papers submitted in the period from August to October. Moreover, a significant “acceptance success dip” was noted for submissions made in winter months. One of the main reasons for such differences between journals was conjectured to lie in different rejection policies; some journals employ desk rejection, whereas others do not.
Schreiber [4] analysed the acceptance rate of a journal—Europhysics Letters ()—for a period of 12 years and found that the rate of manuscript submission exceeded the rate of their acceptance. The data revealed (Table 2 in [4]) that there is a maximum number of submissions in July, defined as a 10% increase compared to the annual mean, together with a minimum in February, even taking into account the “shorter length” of this month. He concluded that significant fluctuations exist between months. The acceptance rate ranged from 45% to 55%; the highest acceptance rate was seen in July and the lowest in January, in the most recent years.
Recently, Ausloos et al. [6] studied submission and also subsequent acceptance data for two journals, a specialized (chemistry) scientific journal and a multidisciplinary journal, respectively, i.e., the Journal of the Serbian Chemical Society (JSCS) (http://shd.org.rs/JSCS/) and Entropy (http://www.mdpi.com/journal/entropy), each over a 3 year time interval. The authors found that fluctuations, expectedly, occur: the number of submissions to is the greatest in July and September and the smallest in May and December. The highest rate of paper submission for was noted in October and December and the lowest in August. Concerning acceptance for , the proportion of accepted/submitted manuscripts is the greatest in January and October. Concerning acceptance for , the number of papers steadily increase from January to a peak in May, followed by a marked dip during summer time, before reaching a peak in October of the order of the May peak.
Concerning the number of submitted manuscripts, it was observed that the acceptance rate in was the highest if papers were submitted in January and February; it was significantly lower if the submission occurred in December. In the case of , the highest rejection rate was for papers submitted in December and March, thus with a January-February peak; the lowest acceptance rate was for manuscripts submitted in June or December; the highest rate being for those sent in spring months, February to May. One recognizes a journal-dependent seasonal shift of the features. Notice that we adapt the word “seasonal”; even though changes in seasons occur on the 21st of various months, we approximate the season transition as occurring on the next 1st day of the following month.
Here, we propose another line of approach in order to study the submission, acceptance, and rejection (number and rate) diversity based on probabilities, with emphasis on the conditional probabilities, thereafter measuring the entropy and other characteristics of the distributions. Indeed, the entropy is a measure of disorder, and one of several ways to measure diversity. Researchers have their own preference [7,8] in measuring diversity. Here below, we practically adapt the classical measure of diversity, as used in ecology, but other cases of interest pertaining to information science [9,10] can be mentioned.
Let us recall that the general equation of diversity is often written in the form [11,12]
in which , and the measured variable. For , reduces to the exponential of the Shannon entropy [13,14]
to which we will only stick here.
Several inequality measures are commonly used in the literature: in the class of entropy related measures, one finds the exponential entropy [15], which measures the extent of a distribution, and the Theil index [16] which emerges as the most popular one [17,18], besides the Herfindahl- Hirschman index [19], measuring “concentrations.” “Finally,” upon ranking according to their size the measured variable, the Gini coefficient [20], is a classical indicator of non-uniform distributions.
The Theil index [16] is defined by
It seems obvious that the Theil index can be expressed in terms of the negative entropy
indicating the deviation from the maximum disorder entropy, ,
The exponential entropy [15] is
The Herfindahl–Hirschman index (HHI) [19] is an indicator of the “concentration” of variables, the “amount of competition” between the months, here. The higher the value of HHI, the smaller the number of months with a large value of (submitted, or accepted, or accepted if submitted) papers in a given month. Formally, adapting the HHI notion to the present case,
Notice that .
The Gini coefficient [20] has been widely used as a measure of income [21] or wealth inequality [22,23]; nowadays, it is widely used in many other fields. In brief, defining first the Lorenz curve as the percentage contributed by the bottom r of the variable population to the total value of the measured (and now ranked) variable , i.e., , one obtains the Gini coefficient as twice the area between this Lorenz curve and the diagonal line in the plane; such a diagonal represents perfect equality; whence, corresponds to perfect equality of the variables.
Having set up the framework and presented the definition of the indices to be calculated, we indicate quantities of interest and turn to the data and data analysis, in Section 2 and Section 3, respectively. Their discussion and comments on the present study, together with a remark on its limitations, are found in the conclusion Section 4.
2. Definitions
In order to develop the method measuring the disorder of the time series, let us recall the necessary data. The raw data can be found in Reference [6]. For completeness, let the time series of submitted and of accepted papers if submitted during a given month to and to be recalled through Figure A1 for the years in which the full data is available, that is, for which the final decisions have been made on the submitted papers.
Let us introduce notations:
- the number of monthly submissions in a given month () in year (y) is called
- the percentage of this set is the probability of submission in a given month for a specific year
- similarly, one can define , as being the number of accepted papers when submitted in year (y) in a specific month (m),
- and for the related percentage, one has ;
- more importantly, for authors, the (conditional) probability of a paper acceptance when submitted in a given month may be considered and estimated before submission
Thereafter, one can deduce the relevant “monthly information entropies”
and the overall information entropy:
in order to pin point whether the yearly distributions are disordered.
Moreover, we can discuss the data by not only comparing different years, but also the cumulated data per month in the examined time interval as if all years are “equivalent”:
- , from which one deduces
- and similarly for the accepted papers , and
- leading to the ratio between cumulated monthly data
- and to the corresponding “monthly cumulated entropy”, ,
- finally to
which will be called the “conditional entropy”.
Relevant values are given in Table 1, Table 2, Table 3 and Table 4 both for and for . The diversity and the inequality index values are given in Table 5. Most of the results stem from the use of a free online software [24].

Table 1.
Number of papers and monthly percentage of papers submitted in a given year (y) and month (m), respectively to JSCS in 2012, 2013, and 2014, and to in 2014, 2015, and 2016; is obtained after summing the events of each year for a given month, i.e., from ; last lines: and entropy, mean, standard deviation, confidence interval, and t-test with significance level; recall that 2.4849 and .

Table 2.
Number of papers and monthly percentage of papers accepted when submitted in a given year (y) and month (m) respectively to JSCS in 2012, 2013, and 2014, and to in 2014, 2015, and 2016; is obtained after summing the events of each year for a given month, i.e., from ; last lines: and entropy, mean, standard deviation, confidence interval, and t-test with significance level; recall 2.4849, and .

Table 3.
Conditional probability of having a paper accepted if submitted in a given month (m) to JSCS or to Entropy in a given year (y), and the corresponding cumulated conditional probability ; the sum of such probabilities is given; we also report the here so called “conditional entropy” (), either or . The distribution total (sum), mean, standard deviation, confidence interval, t- and z-test with p-significance level, are also reported.

Table 4.
Monthly information Entropy and (last line) overall information entropy for specific years and for the cumulated data over the relevant time interval for either journal so investigated; on the last lines one gives the so-called “conditional entropy”, , either or , together with each distribution mean, standard deviation, confidence interval, and t-test with significance level.

Table 5.
Diversity index, the exponential entropy (), Theil index, Herfindahl–Hirschman index, and Gini coefficient, for specific years and for the cumulated data over the relevant time interval for the submitted, accepted, and accepted if submitted papers, respectively, to both investigated journals
3. Data Analysis
3.1. Data
First, notice that the 3-year long time series is not in itself part of the main aim of the paper; this is because we intend to compare data with an equivalent number of degrees of freedom, that is, 11, for all studied cases. Nevertheless, for completeness and in order not to distract readers from our framework, we provide relevant figures in the Appendix A, together with a note on the corresponding discrete Fourier transform. A short note, in the Appendix, recalls the meaning of the (p-) significance level.
3.2. Analysis
The relevant values for the various indices, given in Table 1, Table 2, Table 3 and Table 4, both for and for , serve the following analysis. We consider 3 aspects: (i) a posteriori features findings, (ii) non-linear entropy indices, and (iii) forecasting aspects.
3.2.1. A posteriori features findings
Browsing through Table 1, it can be noticed that the distribution of probabilities of submissions is weaker during the February-May months for , but is rather high for the fall and winter months. For , the highest probability of submissions also occurs in October-December, and is preceded by a low rate of submissions, the lowest being in February and in August, should one say at vacation times. Let us recall that the extremum entropy (for “perfect disorder”) is here .
Apparently this submission evolution pattern is reflected—see Table 2— in the acceptance rate, except for which has a low acceptance rate for papers submitted in winter 2014. For , the weaker acceptance rate occurs for papers submitted during the August–September months, say the end of summer time.
Statistical tests, for example, , can be provided to ensure the validity of these findings for percentages, but taking into account the number of observations. In all cases, such a test demonstrates that the distributions are far from uniform, suggesting looking further for the major deviations. See a discussion of other texts in Section 3.2.3.
However, values only measure the probability of monthly acceptances without considering the number of submissions in a given month. It is in this respect more appropriate to look at the conditional probabilities, , as in Table 3. For , the highest values of are found for winter months: has a notable maximum in January and the lowest for spring-summer time, from March till August. There is a shift of such a pattern for : the highest conditional probabilities occur during spring time, except in 2016.
The corresponding values of the monthly entropy, for the given years and for the cumulated distributions, are found in Table 4. All values of the entropy are remarkably , both for and , suggesting some sort of universality. One can notice that the entropy steadily increases as a function of time both for and , the growth rate being about twice as large for the latter journal. This is somewhat slightly surprising since one should expect an averaging effect in the case of because of the multidisciplinarity of the topics involved. Comparing such values indicates that the distributions are far from uniform (The slight difference between the last lines of Table 3 and Table 4, displaying the “conditional entropy” is merely due to rounding errors.) indeed.
3.2.2. Non-Linear Entropy Indices
The diversity and inequality measures are given in Table 5. The diversity index is remarkably similar for both journals (∼11) for the submitted papers and accepted papers distributions. The similarity holds also for the HHI , although a little bit lower for the journal . The diversity index for the conditional probability distributions is however rather different: both increase as a function of time, indicating an increase in concentrations in favor of relevant months. This increase rate is much higher for than for .
The inequality between months is rather low, as seen in the Gini coefficient; there is a weak inequality between months. However, there is a factor ∼2 in favor of , which we interpret as being due to the greater specificity of , implying a smaller involved community and specially favored topics. This numerical observation reinforces what can be deduced from the Theil index, whence inducing the same conclusion.
3.2.3. Forecasting Aspects
Considering the rather small sizes of both samples (not our fault!), it is of interest to discuss the significance of the findings, in some sense in view of suggesting some “strategy” after the “diagnosis”. The notions of “false positives” and “false negatives”, as in medical testing, can be applied in our framework.
In brief, a ”false positive” occurs as an error when a test result improperly indicates the presence (high probability) of an outcome, when in reality it is not present; obviously, a contrario—a “false negative”—is an error in which a test result improperly indicates no presence of a condition (the result is negative), when in reality it is present. This corresponds to rejecting (or accepting) a null hypothesis, for example, in econometrics. Thus, two statistical tests have been used for such a discussion: (i) the Student test and (ii) the z-test. Recall that they are used if one either does not know or one knows the variance (or standard deviation) of the sample and test distributions. Such characteristics are given in Table 1, Table 2, Table 3 and Table 4 for each relevant quantity.
For completeness, one has also given the confidence interval []. It is easily seen that there is no outlier. This observation would lead us, like other authors, to claim that there is no anomaly in the monthly numbers and subsequent percentages, in contradistinction with the values and tests. We should here point out that the t-Student test leads to a p-value < 0.0001, a quite significant result. Concentrating our attention on the (monthly and annual) conditional probabilities , the z-test gives the significance reported in Table 4. The values (so called , or error of type I) in hypothesis testing, indicate that the correct conclusion is to reject the null hypothesis and to consider the existence of “false positives”. This is essentially due to the sample size. It is remarkable that the order of magnitude differs for and for .
4. Conclusions
The data on the number of submitted papers is relevant for editors and, more so nowadays, for publishers due to the automatic handling of papers. The relative number of accepted papers is less significant in that respect, but the conditional probability of having an accepted paper if it is submitted in a given month is very relevant for authors. Authors expect a fast and (hopefully) positive response from journals as they are probably interested to discover the best timing for their submission in order to avoid possible editor overload and a negative effect in a particular moment. For these authors, the possible seasonal bias issue is expected to be relevant, as they would like to know whether a specific month of submission will increase the chance that their paper will be accepted. Thus, the probability of acceptance, the so called “acceptance rate,” is the relevant variable to be studied. Instead of tests or observing the “confidence interval” on monthly distributions, we have proposed a new line of approach: considering the diversity and inequality in the distributions of papers submitted, accepted, or accepted if submitted in a given month through information indices, like the Shannon entropy [25], the diversity index, the Gini coefficients and the Herfindahl–Hirschman index.
From these case studies, a seasonal bias seems stronger in the specialized () journal. The features are emphasized because we use a non linear transformation of the data, through information concepts, having their usefulness demonstrated in many other fields [26]. In the present cases, the seasonal bias effects are observed. The overall significance and the universality features might have to be re-examined if more data were available. Indeed, the p-values (so-called , or error of type I) in hypothesis testing, indicate that the correct conclusion is to consider the existence of “false positives”.
Our outlined findings suggest intrinsic behavioral hypotheses for future research. Complementary aspects must be used as ingredients in order to understand whether some seasonal bias occurs [27,28]. One has to take into account the scientific work environment, besides the journal favored topics.
Author Contributions
All authors (M.A., O.N. and A.D.) equally contributed their best to all aspects of this paper; conceptualization, methodology; formal analysis; investigation; resources; data curation; writing–original draft preparation; writing revised version, and editing; visualization.
Funding
This research received no external funding.
Acknowledgments
M.A. greatly thanks the MDPI Entropy Editorial staff for gathering and cleaning up the raw data, and in particular Yuejiao Hu, Managing Editor. Thanks also go to the reviewers and editor.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Series Data
The time series of submitted and accepted papers if submitted during a given month to and to are given in Figure A1. The distributions are markedly non-uniform. Nevertheless, with such a short series, one can observe some periods more important than others. One can also observe that , a rather new journal, is attracting more submissions since 2015, and has an increased rejection rate. Some “parallelism” in the numbers of submitted and accepted if submitted papers in a given month seems apparent for .
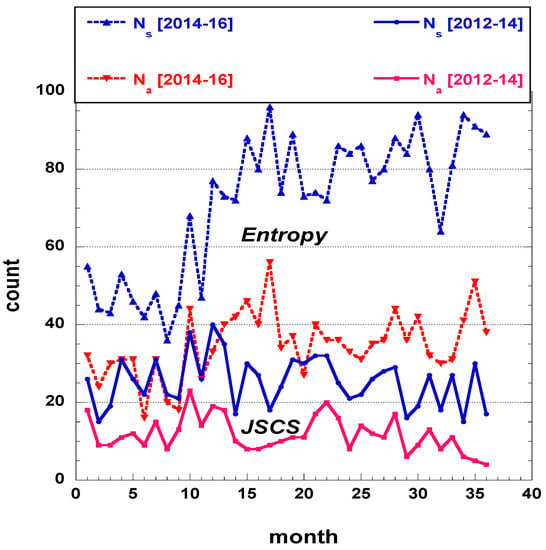
Figure A1.
Number of papers submitted and number of papers accepted if submitted, during a given month, to and to , in the examined 36 months of the 3-year time interval, [2012–2014] and [2014–2016], respectively.
The two largest amplitudes of frequency f in , or (periods), resulting from a Fourier analysis of the 3-year time series for papers submitted or accepted if submitted during a given month to and are given in Table A1. The year period is, in 3 cases, one of the two most important ones; the trimester period is the most important for submitted papers to , and the next largest for to , indicating the more relevant timing for the journal, more prone toward academic authors than .

Table A1.
The two largest amplitudes of frequency f in , or (periods), resulting from a Fourier analysis of the 3-year time series for papers submitted or accepted if submitted during a given month to and , as displayed in Figure A1.
Table A1.
The two largest amplitudes of frequency f in , or (periods), resulting from a Fourier analysis of the 3-year time series for papers submitted or accepted if submitted during a given month to and , as displayed in Figure A1.
| JSCS | Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| f | ||||||||
| 1 | 125.42 | 0.3333 (3) | 66.83 | 0.0833 (12) | 720.23 | 0.0278 (36) | 169.36 | 0.0556 (18) |
| 2 | 94.94 | 0.3889 (2.57) | 51.11 | 0.3333 (3) | 378.38 | 0.0833 (12) | 164.15 | 0.0833 (12) |
Computational notes
This procedure calculates the difference of an observed mean with a hypothesized value. A significance value (p-value) and 95% Confidence Interval (CI) of the observed mean are reported. The p-value is the probability of obtaining the mean observed for the sample if the null hypothesis holds true.
The p-value is calculated using the one sample t-test, with t calculated as:
where the hypothesized mean is k and the standard deviation . In the present context, the hypothesized mean corresponds to that of the uniform distribution. Recall that the p-value is the area of the t distribution, which for degrees of freedom falls outside .
References
- Boja, C.E.; Herţeliu, C.; Dârdală, M.; Ileanu, B.V. Day of the week submission effect for accepted papers in Physica A, PLOS ONE, Nature and Cell. Scientometrics 2018, 117, 887–918. [Google Scholar] [CrossRef]
- Mrowinski, M.J.; Fronczak, A.; Fronczak, P.; Nedic, O.; Ausloos, M. Review times in peer review: Quantitative analysis and modelling of editorial work flows. Scientometrics 2016, 107, 271–286. [Google Scholar] [CrossRef] [PubMed]
- Mrowinski, M.J.; Fronczak, P.; Fronczak, A.; Ausloos, M.; Nedic, O. Artificial intelligence in peer review: How can evolutionary computation support journal editors? PLoS ONE 2017, 12, e0184711. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, M. Seasonal bias in editorial decisions for a physics journal: You should write when you like, but submit in July. Learn. Publ. 2012, 25, 145–151. [Google Scholar] [CrossRef]
- Shalvi, S.; Baas, M.; Handgraaf, M.J.J.; De Dreu, C.K.W. Write when hot—Submit when not: Seasonal bias in peer review or acceptance? Learn. Publ. 2010, 23, 117–123. [Google Scholar] [CrossRef]
- Ausloos, M.; Nedič, O.; Dekanski, A. Correlations between submission and acceptance of papers in peer review journals. Scientometrics 2019, 119, 279–302. [Google Scholar] [CrossRef]
- Marhuenda, Y.; Morales, D.; Pardo, M.C. A comparison of uniformity tests. Statistics 2005, 39, 315–327. [Google Scholar] [CrossRef]
- Alizadeh Noughabi, H.A. Entropy-based tests of uniformity: A Monte Carlo power comparison. Commun. Stat. Simul. Comput. 2017, 46, 1266–1279. [Google Scholar] [CrossRef]
- Rousseau, R. Concentration and diversity of availability and use in information systems: A positive reinforcement model. J. Am. Soc. Inf. Sci. 1992, 43, 391–395. [Google Scholar] [CrossRef]
- Leydesdorff, L.; Rafols, I. Indicators of the interdisciplinarity of journals: Diversity, centrality, and citations. J. Inf. 2011, 5, 87–100. [Google Scholar] [CrossRef]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communications. Bell. Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Shannon, C. Prediction and entropy of printed English. Bell. Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Campbell, L.L. Exponential entropy as a measure of extent of a distribution. Probab. Theory Relat. Fields 1966, 5, 217–225. [Google Scholar] [CrossRef]
- Theil, H. Economics and Information Theory; Rand McNally and Company: Chicago, IL, USA, 1967. [Google Scholar]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; Van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stat. Sci. 1997, 6, 17–39. [Google Scholar]
- Oancea, B.; Pirjol, D. Extremal properties of the Theil and Gini measures of inequality. Qual. Quant. 2019, 53, 859–869. [Google Scholar] [CrossRef]
- Hirschman, A.O. The paternity of an index. Am. Econ. Rev. 1964, 54, 761–762. [Google Scholar]
- Gini, C. Índice di Concentrazione e di Dipendenza. Biblioteca dell’Economista, Serie V; Utet Torino: Turin, Italy, 1910; Volume XX, English translation in Riv. Politica Econ. 1997, 87, 769–789. [Google Scholar]
- Atkinson, A.B.; Bourguignon, F. (Eds.) Handbook of Income Distribution; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2. [Google Scholar]
- Cerqueti, R.; Ausloos, M. Statistical assessment of regional wealth inequalities: The Italian case. Qual. Quant. 2015, 49, 2307–2323. [Google Scholar] [CrossRef]
- Cerqueti, R.; Ausloos, M. Socio-economical Analysis of Italy: The case of hagiotoponym cities. Soc. Sci. J. 2015, 52, 561–564. [Google Scholar] [CrossRef]
- Wessa, P. Free Statistics Software, Office for Research Development and Education, Version 1.1.23-r. 2014. Available online: http://www.wessa.net/ (accessed on 4 June 2019).
- Crooks, G.E. On Measures of Entropy and Information. Tech. Note 2017, 9, v7. [Google Scholar]
- Clippe, P.; Ausloos, M. Benford’s law and Theil transform of financial data. Phys. A 2012, 391, 6556–6567. [Google Scholar] [CrossRef]
- Nedić, O.; Drvenica, I.; Ausloos, M.; Dekanski, A. Efficiency in managing peer-review of scientific manuscripts-editors’ perspective. J. Serb. Chem. Soc. 2018, 83, 1391–1405. [Google Scholar] [CrossRef]
- Drvenica, I.; Bravo, G.; Vejmelka, L.; Dekanski, A.; Nedić, O. Peer Review of Reviewers: The Author’s Perspective. Publications 2019, 7, 1. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).