Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress
Abstract
1. Introduction
2. Materials and Methods
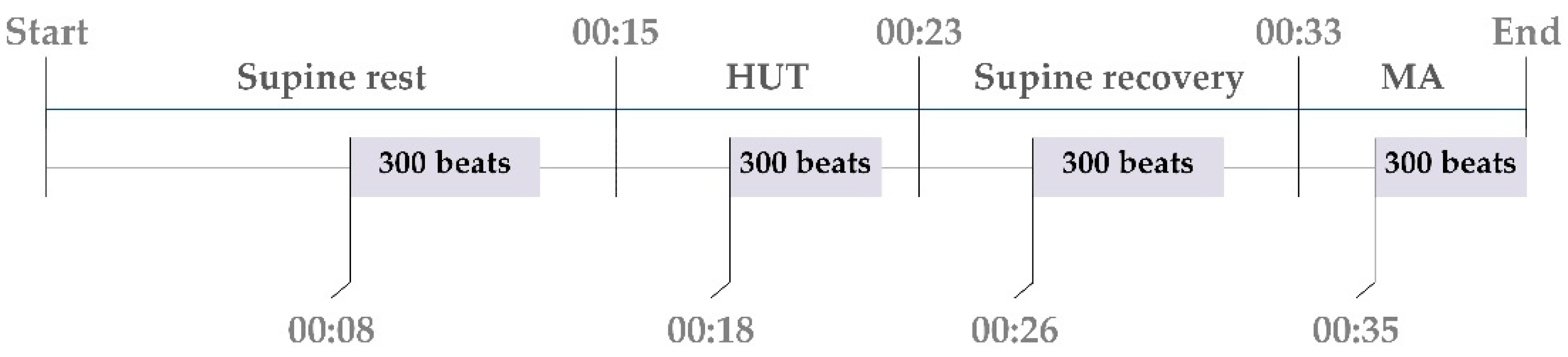
2.1. Experimental Protocol
2.2. Time Series Extraction
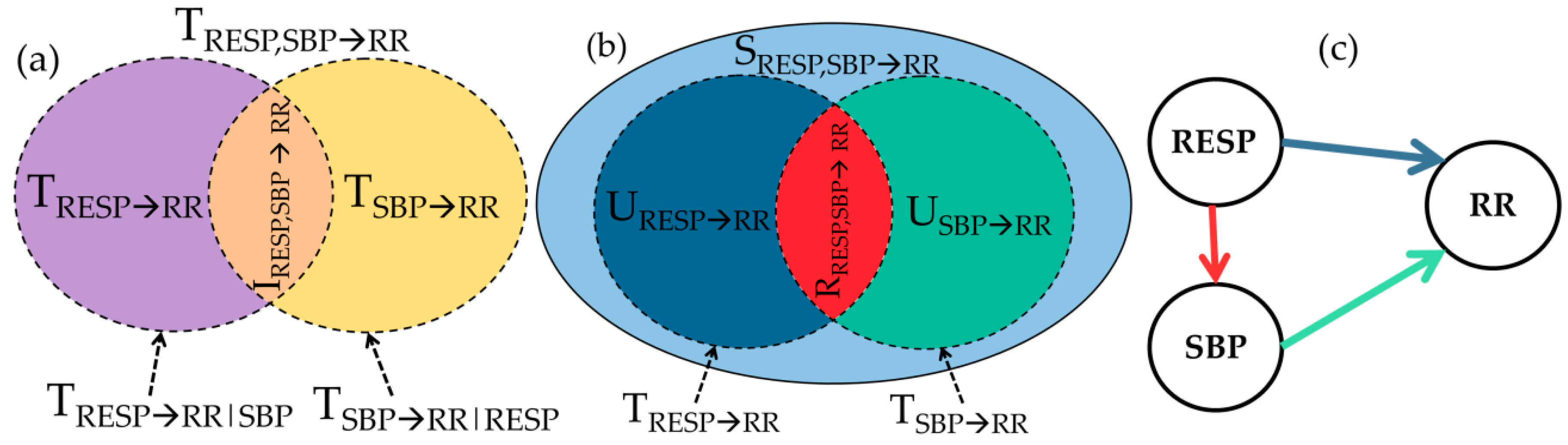
2.3. Multiscale Information Decomposition
2.4. Data Analysis and Interpretation
2.5. Statistical Analysis
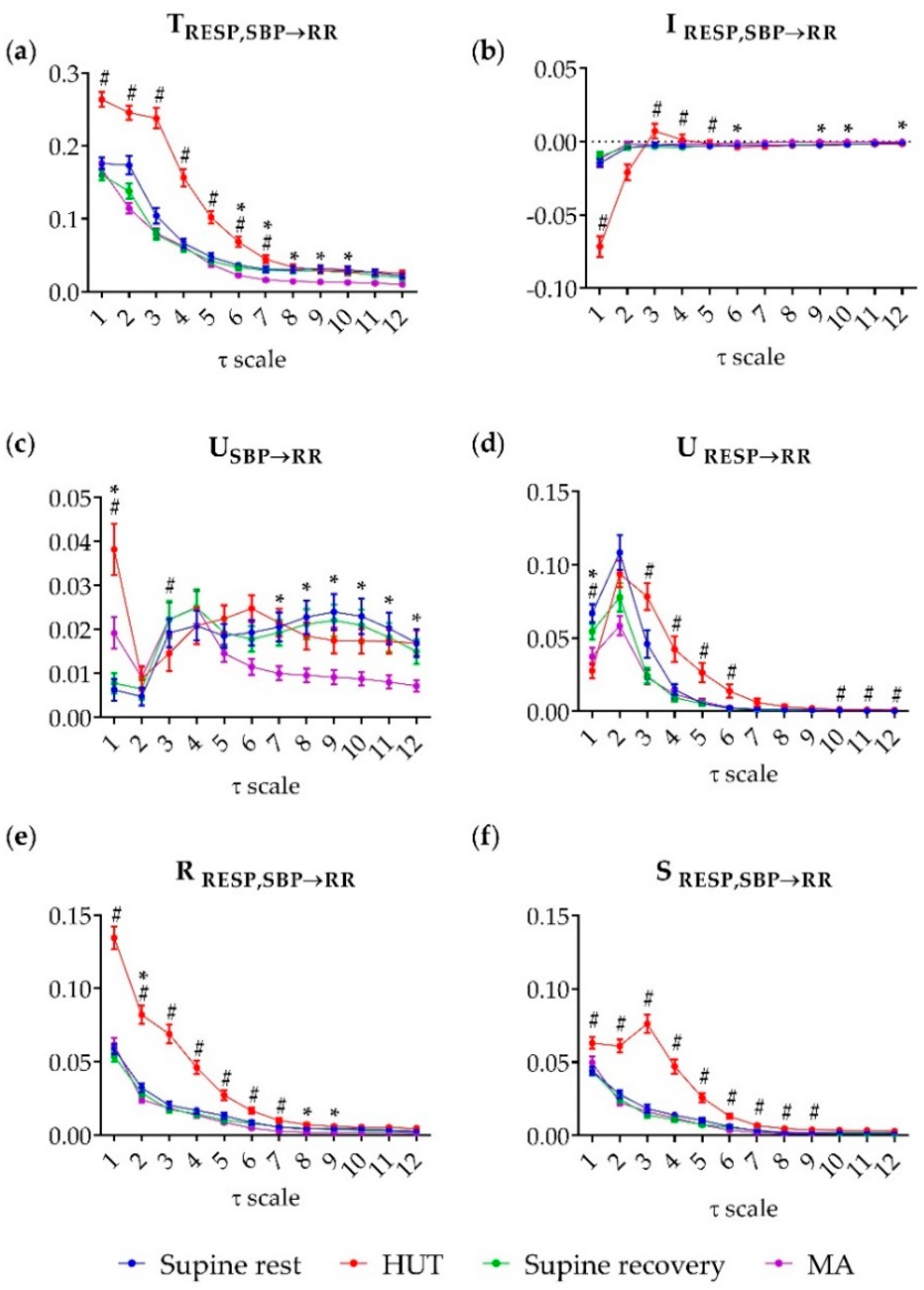
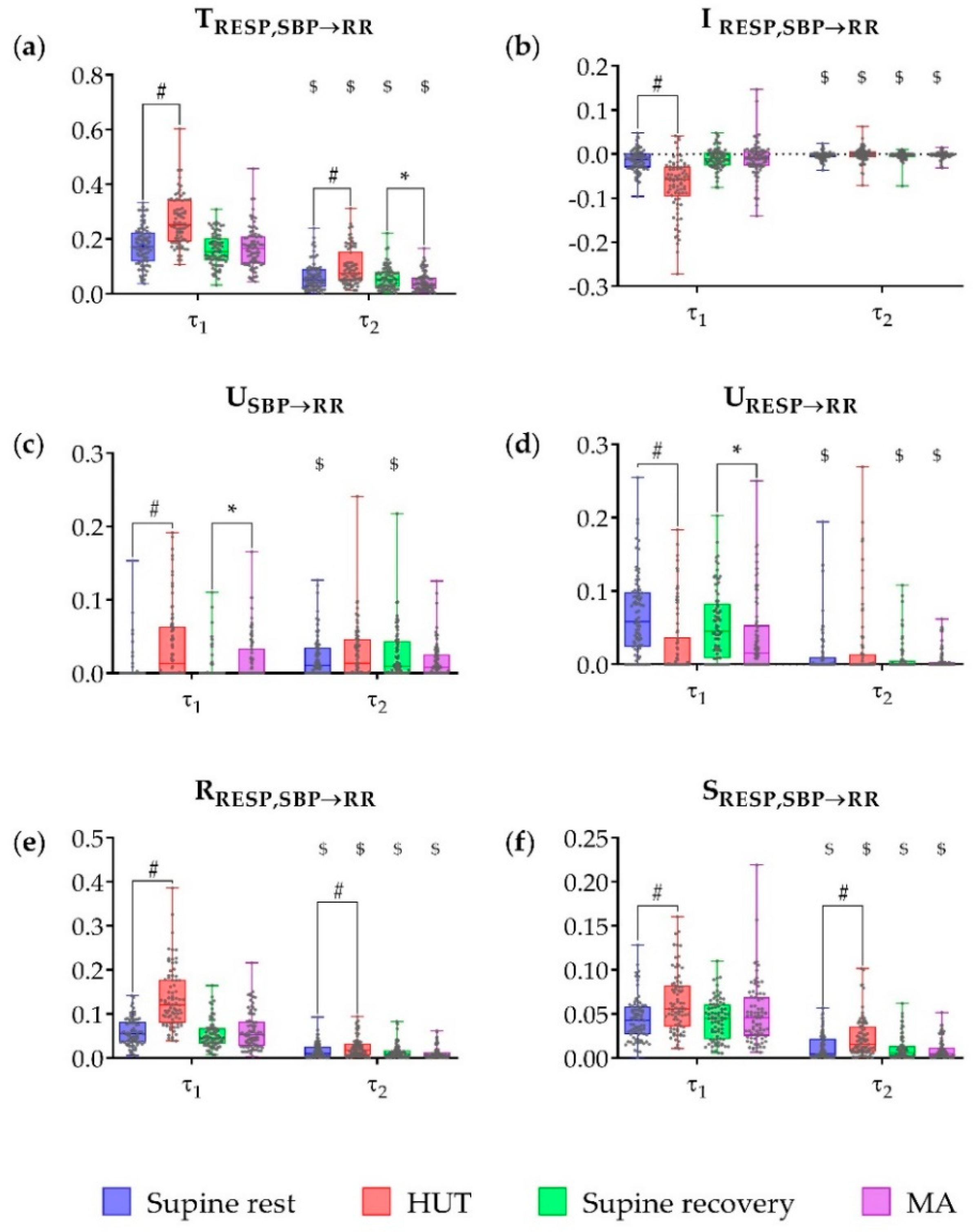
3. Results
4. Discussion
4.1. Partial Information Decomposition of Cardiovascular and Cardiorespiratory Interactions During Postural and Mental Stress—Raw Data Analysis
4.2. Multiscale Information Decomposition of Cardiovascular and Cardiorespiratory Interactions—Focus on Slower Oscillations
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
| τ1 | τ2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Supine Rest vs. HUT | Supine Recovery vs. MA | Supine Rest vs. HUT | Supine Recovery vs. MA | |||||
| p-Value | Kendall’s W | p-Value | Kendall’s W | p-Value | Kendall’s W | p-Value | Kendall’s W | |
| TRESP,SBP→RR | <0.001 | 0.286 | 0.771 | 0.286 | <0.001 | 0.167 | 0.019 | 0.167 |
| IRESP,SBP→RR | <0.001 | 0.319 | 1.000 | 0.319 | 0.095 | 0.017 | 0.664 | 0.017 |
| USBP→RR | <0.001 | 0.200 | 0,002 | 0.200 | 0.895 | 0.014 | 0.129 | 0.014 |
| URESP→RR | <0.001 | 0.167 | 0.031 | 0.167 | 0.461 | 0.007 | 0.870 | 0.007 |
| RRESP,SBP→RR | <0.001 | 0.420 | 0.107 | 0.420 | 0.017 | 0.058 | 0.612 | 0.058 |
| SRESP,SBP→RR | 0.003 | 0.043 | 0.660 | 0.043 | <0.001 | 0.106 | 0.696 | 0.106 |
| Supine Rest | HUT | Supine Recovery | MA | |||||
|---|---|---|---|---|---|---|---|---|
| p-Value | Kendall’s W | p-Value | Kendall’s W | p-Value | Kendall’s W | p-Value | Kendall’s W | |
| TRESP,SBP→RR | <0.001 | 0.760 | <0.001 | 0.805 | <0.001 | 0.852 | <0.001 | 0.900 |
| IRESP,SBP→RR | 0.001 | 0.148 | <0.001 | 0.716 | 0.006 | 0.080 | 0.010 | 0.111 |
| USBP→RR | <0.001 | 0.331 | 0.321 | 0.001 | <0.001 | 0.319 | 0.964 | 0.021 |
| URESP→RR | <0.001 | 0.562 | 0.174 | 0.055 | <0.001 | 0.486 | <0.001 | 0.216 |
| RRESP,SBP→RR | <0.001 | 0.632 | <0.001 | 0.949 | <0.001 | 0.673 | <0.001 | 0.760 |
| SRESP,SBP→RR | <0.001 | 0.805 | <0.001 | 0.592 | <0.001 | 0.900 | <0.001 | 0.760 |
References
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, F.; McCraty, R.; Zerr, C.L. A healthy heart is not a metronome: an integrative review of the heart’s anatomy and heart rate variability. Front. Psychol. 2014, 5, 1040. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Schulz, S.; Schroeder, R.; Baumert, M.; Caminal, P. Methods derived from nonlinear dynamics for analysing heart rate variability. Philos. Trans. Ser. A, Math., Phys., Eng. Sci. 2009, 367, 277–296. [Google Scholar] [CrossRef]
- McCraty, R.; Atkinson, M.; Tomasino, D.; Bradley, R.T. The Coherent Heart: Heart-brain Interactions, Psychophysiological Coherence, and the Emergence of System-wide Order; HearthMath Research Center, Institute of HeartMath: Boulder Creek, CA, USA, 2006. [Google Scholar]
- Schumann, A.; Schulz, S.; Voss, A.; Scharbrodt, S.; Baumert, M.; Bar, K.J. Baroreflex Coupling Assessed by Cross-Compression Entropy. Front. Phys. 2017, 8, 282. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.A.; Taylor, J.A. Short-term cardiovascular oscillations in man: measuring and modelling the physiologies. J. Phys. 2002, 542, 669–683. [Google Scholar] [CrossRef]
- Katona, P.G.; Poitras, J.W.; Barnett, G.O.; Terry, B.S. Cardiac vagal efferent activity and heart period in the carotid sinus reflex. Am. J. Phys. 1970, 218, 1030–1037. [Google Scholar] [CrossRef]
- Heart rate variability: standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996, 93, 1043–1065. [CrossRef]
- Voss, A.; Kurths, J.; Kleiner, H.J.; Witt, A.; Wessel, N. Improved analysis of heart rate variability by methods of nonlinear dynamics. J. Electrocardiol. 1995, 28, 81–88. [Google Scholar] [CrossRef]
- Dick, T.E.; Hsieh, Y.H.; Dhingra, R.R.; Baekey, D.M.; Galan, R.F.; Wehrwein, E.; Morris, K.F. Cardiorespiratory coupling: common rhythms in cardiac, sympathetic, and respiratory activities. Prog. Brain Res. 2014, 209, 191–205. [Google Scholar] [CrossRef]
- Bar, K.J.; Schuhmacher, A.; Hofels, S.; Schulz, S.; Voss, A.; Yeragani, V.K.; Maier, W.; Zobel, A. Reduced cardio-respiratory coupling after treatment with nortriptyline in contrast to S-citalopram. J. Affect. Disord. 2010, 127, 266–273. [Google Scholar] [CrossRef]
- Marwan, N.; Zou, Y.; Wessel, N.; Riedl, M.; Kurths, J. Estimating coupling directions in the cardiorespiratory system using recurrence properties. Philos. Trans. Ser. A, Math., Phys., Eng. Sci. 2013, 371, 20110624. [Google Scholar] [CrossRef]
- Peupelmann, J.; Quick, C.; Berger, S.; Hocke, M.; Tancer, M.E.; Yeragani, V.K.; Bar, K.J. Linear and non-linear measures indicate gastric dysmotility in patients suffering from acute schizophrenia. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2009, 33, 1236–1240. [Google Scholar] [CrossRef]
- Penzel, T.; Porta, A.; Stefanovska, A.; Wessel, N. Recent advances in physiological oscillations. Physiol. Meas. 2017, 38, E1–E7. [Google Scholar] [CrossRef]
- Nollo, G.; Faes, L.; Porta, A.; Antolini, R.; Ravelli, F. Exploring directionality in spontaneous heart period and systolic pressure variability interactions in humans: implications in the evaluation of baroreflex gain. Am. J. Physiol. Heart Circ. Physiol. 2005, 288, 1777–1785. [Google Scholar] [CrossRef]
- Silvani, A.; Calandra-Buonaura, G.; Johnson, B.D.; Van Helmond, N.; Barletta, G.; Cecere, A.G.; Joyner, M.J.; Cortelli, P. Physiological Mechanisms Mediating the Coupling between Heart Period and Arterial Pressure in Response to Postural Changes in Humans. Front. Physiol. 2017, 8, 163. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Mechanisms of causal interaction between short-term RR interval and systolic arterial pressure oscillations during orthostatic challenge. J. Appl. Physiol. 2013, 114, 1657–1667. [Google Scholar] [CrossRef] [PubMed]
- Nollo, G.; Faes, L.; Porta, A.; Pellegrini, B.; Ravelli, F.; Del Greco, M.; Disertori, M.; Antolini, R. Evidence of unbalanced regulatory mechanism of heart rate and systolic pressure after acute myocardial infarction. Am. J. Physiol. Heart Circ. Physiol. 2002, 283, 1200–1207. [Google Scholar] [CrossRef][Green Version]
- Porta, A.; Furlan, R.; Rimoldi, O.; Pagani, M.; Malliani, A.; Van De Borne, P. Quantifying the strength of the linear causal coupling in closed loop interacting cardiovascular variability signals. Biol. Cybern. 2002, 86, 241–251. [Google Scholar] [CrossRef]
- Lenis, G.; Kircher, M.; Lázaro, J.; Bailón, R.; Gil, E.; Doessel, O. Separating the effect of respiration on the heart rate variability using Granger’s causality and linear filtering. Biomed. Signal Process. Control 2017, 31, 272–287. [Google Scholar] [CrossRef]
- Porta, A.; Baselli, G.; Lombardi, F.; Montano, N.; Malliani, A.; Cerutti, S. Conditional entropy approach for the evaluation of the coupling strength. Biol. Cybern. 1999, 81, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Information-based detection of nonlinear Granger causality in multivariate processes via a nonuniform embedding technique. Phys. Rev. E, Stat., Nonlinear, Soft Matter Phys. 2011, 83, 051112. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Porta, A. Information domain approach to the investigation of cardio-vascular, cardio-pulmonary, and vasculo-pulmonary causal couplings. Front. Phys. 2011, 2, 80. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Cucino, R.; Cerutti, S.; Antolini, R.; Nollo, G. Causal transfer function analysis to describe closed loop interactions between cardiovascular and cardiorespiratory variability signals. Biol. Cybern. 2004, 90, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Bassani, T.; Bari, V.; Tobaldini, E.; Takahashi, A.C.; Catai, A.M.; Montano, N. Model-based assessment of baroreflex and cardiopulmonary couplings during graded head-up tilt. Comput. Biol. Med. 2012, 42, 298–305. [Google Scholar] [CrossRef]
- Javorka, M.; Krohova, J.; Czippelova, B.; Turianikova, Z.; Lazarova, Z.; Javorka, K.; Faes, L. Basic cardiovascular variability signals: mutual directed interactions explored in the information domain. Physiol. Meas. 2017, 38, 877–894. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Nollo, G.; Porta, A. Non-uniform multivariate embedding to assess the information transfer in cardiovascular and cardiorespiratory variability series. Comput. Biol. Med. 2012, 42, 290–297. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Porta, A.; Nollo, G.; Javorka, M. Information Decomposition in Multivariate Systems: Definitions, Implementation and Application to Cardiovascular Networks. Entropy 2017, 19, 5. [Google Scholar] [CrossRef]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- Faes, L.; Bari, V.; Ranucci, M.; Porta, A. Multiscale Decomposition of Cardiovascular and Cardiorespiratory Information Transfer under General Anesthesia. In Proceedings of the 40th International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI USA, 17–21 July 2018; pp. 4607–4610. [Google Scholar] [CrossRef]
- Javorka, M.; Krohova, J.; Czippelova, B.; Turianikova, Z.; Lazarova, Z.; Wiszt, R.; Faes, L. Towards understanding the complexity of cardiovascular oscillations: Insights from information theory. Comput. Biol. Med. 2018, 98, 48–57. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: an experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E, Stat., Nonlinear, Soft Matter Phys. 2015, 91, 052802. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Badra, L.J.; Cooke, W.H.; Hoag, J.B.; Crossman, A.A.; Kuusela, T.A.; Tahvanainen, K.U.; Eckberg, D.L. Respiratory modulation of human autonomic rhythms. Am. J. Phys. Heart Circ. Physiol. 2001, 280, 2674–2688. [Google Scholar] [CrossRef] [PubMed]
- Eckberg, D.L. Point:counterpoint: respiratory sinus arrhythmia is due to a central mechanism vs. respiratory sinus arrhythmia is due to the baroreflex mechanism. J. Appl. Physiol. 2009, 106. [Google Scholar] [CrossRef] [PubMed]
- Koepchen, H.P.; Klussendorf, D.; Sommer, D. Neurophysiological background of central neural cardiovascular-respiratory coordination: basic remarks and experimental approach. J. Auton. Nerv. Syst. 1981, 3, 335–368. [Google Scholar] [CrossRef]
- Porta, A.; Bari, V.; De Maria, B.; Takahashi, A.C.M.; Guzzetti, S.; Colombo, R.; Catai, A.M.; Raimondi, F.; Faes, L. Quantifying Net Synergy/Redundancy of Spontaneous Variability Regulation via Predictability and Transfer Entropy Decomposition Frameworks. IEEE Trans. Bio-Med. Eng. 2017, 64, 2628–2638. [Google Scholar] [CrossRef]
- Karemaker, J.M. Counterpoint: respiratory sinus arrhythmia is due to the baroreflex mechanism. J. Appl. Physiol. 2009, 106, 1742–1743, discussion 1744. [Google Scholar] [CrossRef] [PubMed]
- Krohova, J.; Czippelova, B.; Turianikova, Z.; Lazarova, Z.; Wiszt, R.; Javorka, M.; Faes, L. Information domain analysis of respiratory sinus arrhythmia mechanisms. Physiol. Res. 2018, 67, 611–618. [Google Scholar] [CrossRef]
- Hirsch, J.A.; Bishop, B. Respiratory sinus arrhythmia in humans: how breathing pattern modulates heart rate. Am. J. Physiol. 1981, 241, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Baselli, G.; Rimoldi, O.; Malliani, A.; Pagani, M. Assessing baroreflex gain from spontaneous variability in conscious dogs: role of causality and respiration. Am. J. Physiol. Heart Circ. Physiol. 2000, 279, 2558–2567. [Google Scholar] [CrossRef] [PubMed]
- Milde, T.; Schwab, K.; Walther, M.; Eiselt, M.; Schelenz, C.; Voss, A.; Witte, H. Time-variant partial directed coherence in analysis of the cardiovascular system. A methodological study. Physiol. Meas. 2011, 32, 1787–1805. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krohova, J.; Faes, L.; Czippelova, B.; Turianikova, Z.; Mazgutova, N.; Pernice, R.; Busacca, A.; Marinazzo, D.; Stramaglia, S.; Javorka, M. Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress. Entropy 2019, 21, 526. https://doi.org/10.3390/e21050526
Krohova J, Faes L, Czippelova B, Turianikova Z, Mazgutova N, Pernice R, Busacca A, Marinazzo D, Stramaglia S, Javorka M. Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress. Entropy. 2019; 21(5):526. https://doi.org/10.3390/e21050526
Chicago/Turabian StyleKrohova, Jana, Luca Faes, Barbora Czippelova, Zuzana Turianikova, Nikoleta Mazgutova, Riccardo Pernice, Alessandro Busacca, Daniele Marinazzo, Sebastiano Stramaglia, and Michal Javorka. 2019. "Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress" Entropy 21, no. 5: 526. https://doi.org/10.3390/e21050526
APA StyleKrohova, J., Faes, L., Czippelova, B., Turianikova, Z., Mazgutova, N., Pernice, R., Busacca, A., Marinazzo, D., Stramaglia, S., & Javorka, M. (2019). Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress. Entropy, 21(5), 526. https://doi.org/10.3390/e21050526








