Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy
Abstract
1. Introduction
2. EEMD-Based Feature Space Reconstruction
2.1. A Brief Overview of EMD and EEMD
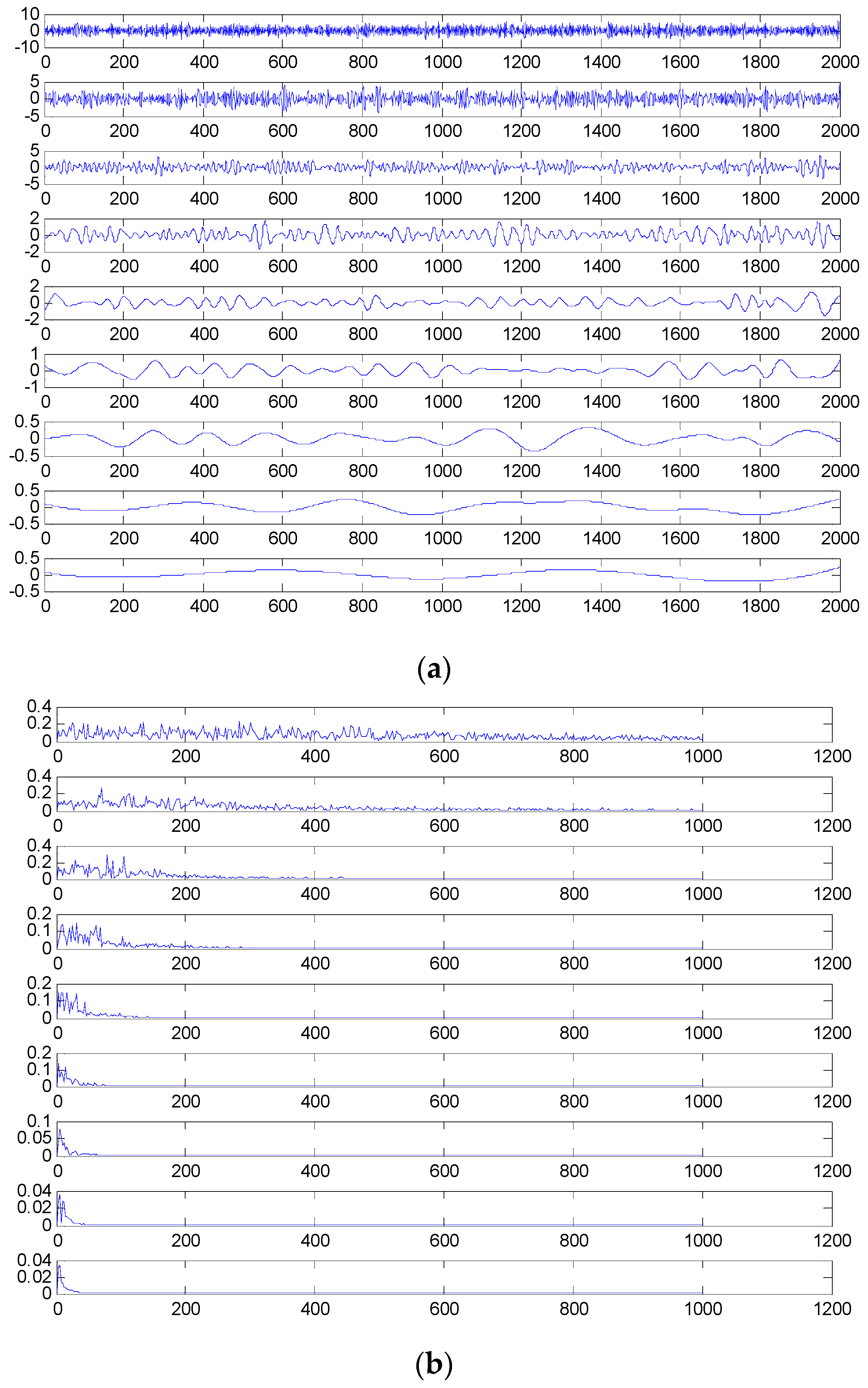
2.2. Feature Space Reconstruction Based on EEMD (FSRE)
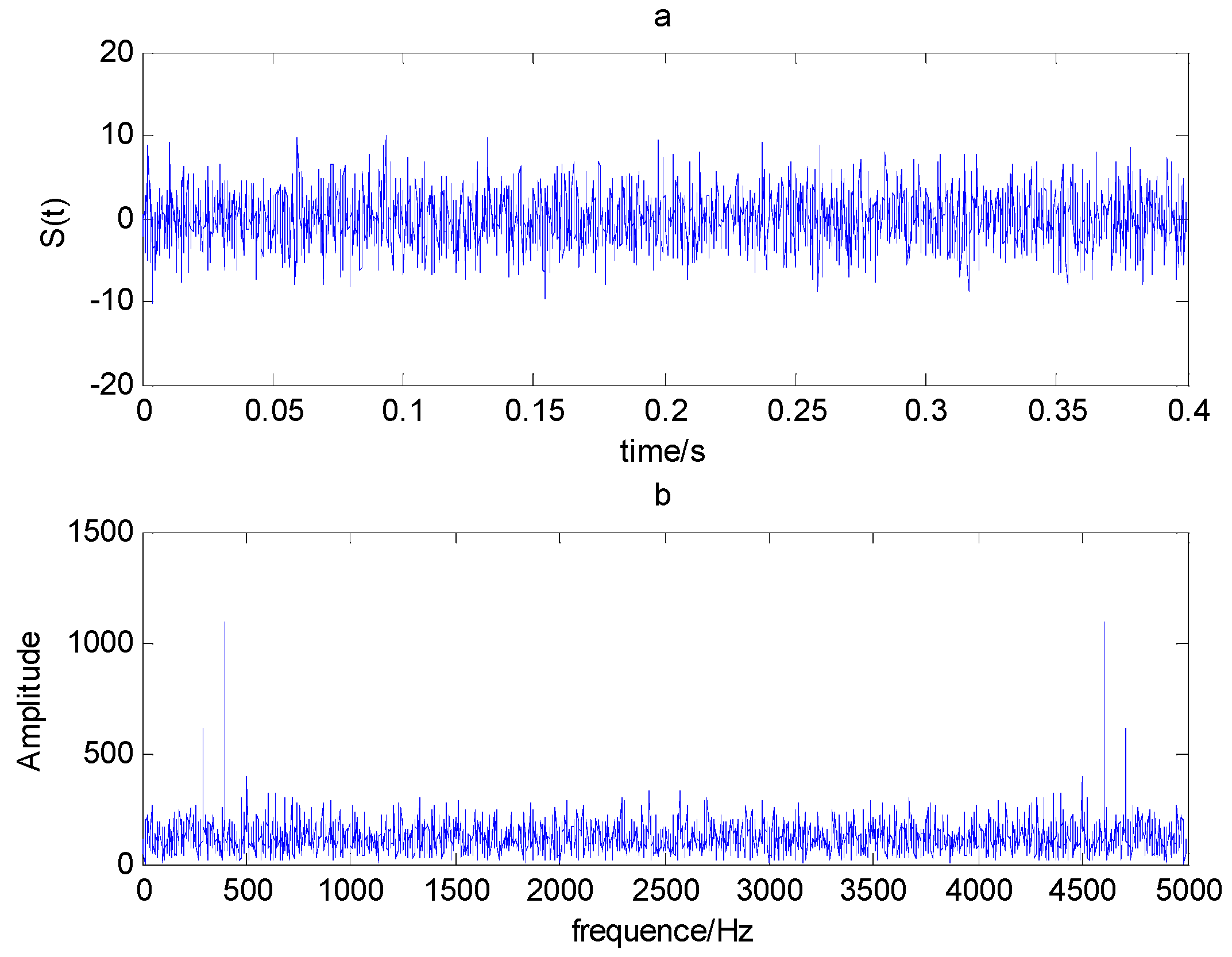
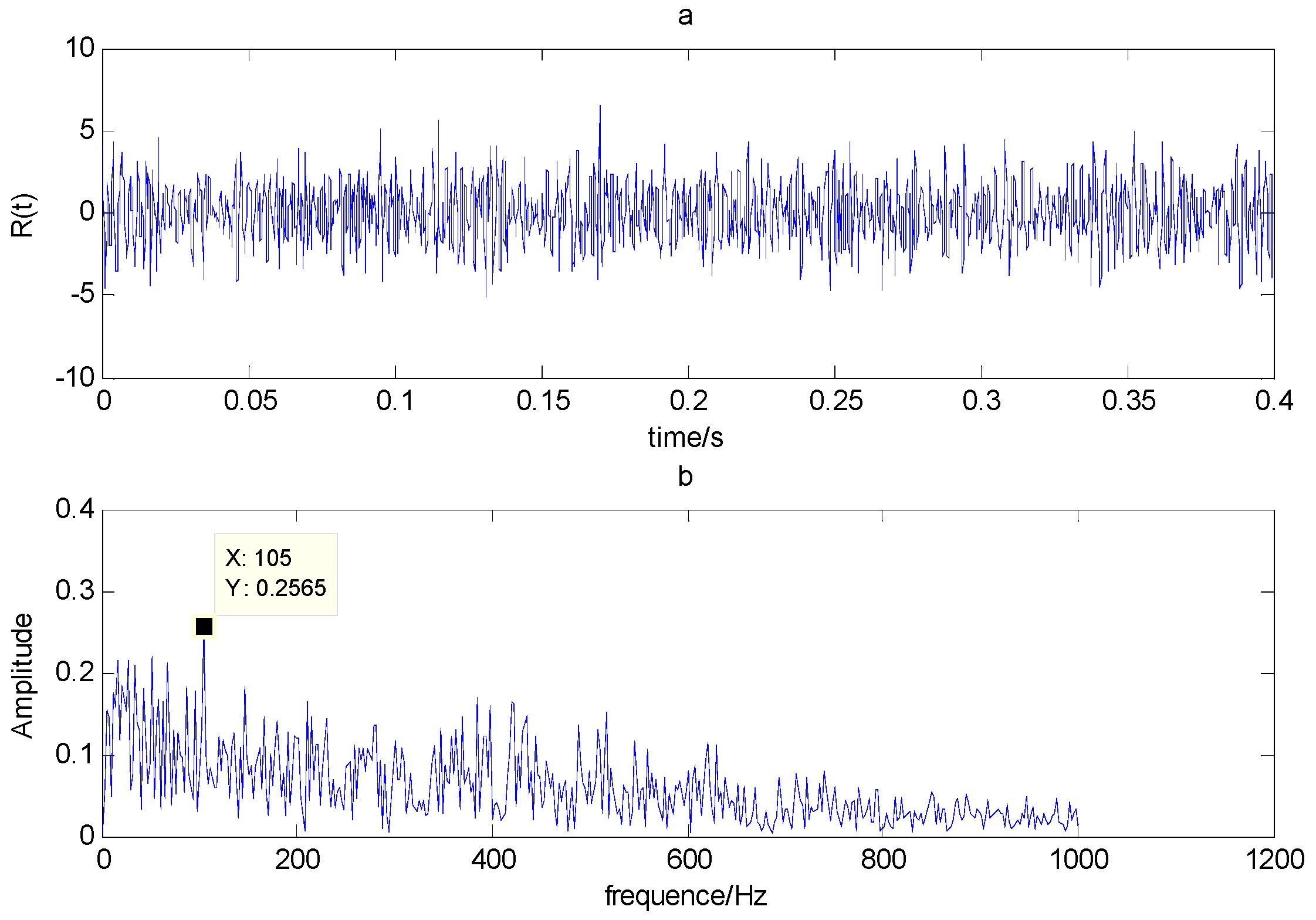
2.3. Analysis of Simulating Bearing Fault Signals
3. Permutation Entropy and Multiscale Permutation Entropy
3.1. Permutation Entropy
3.2. Multiscale Permutation Entropy
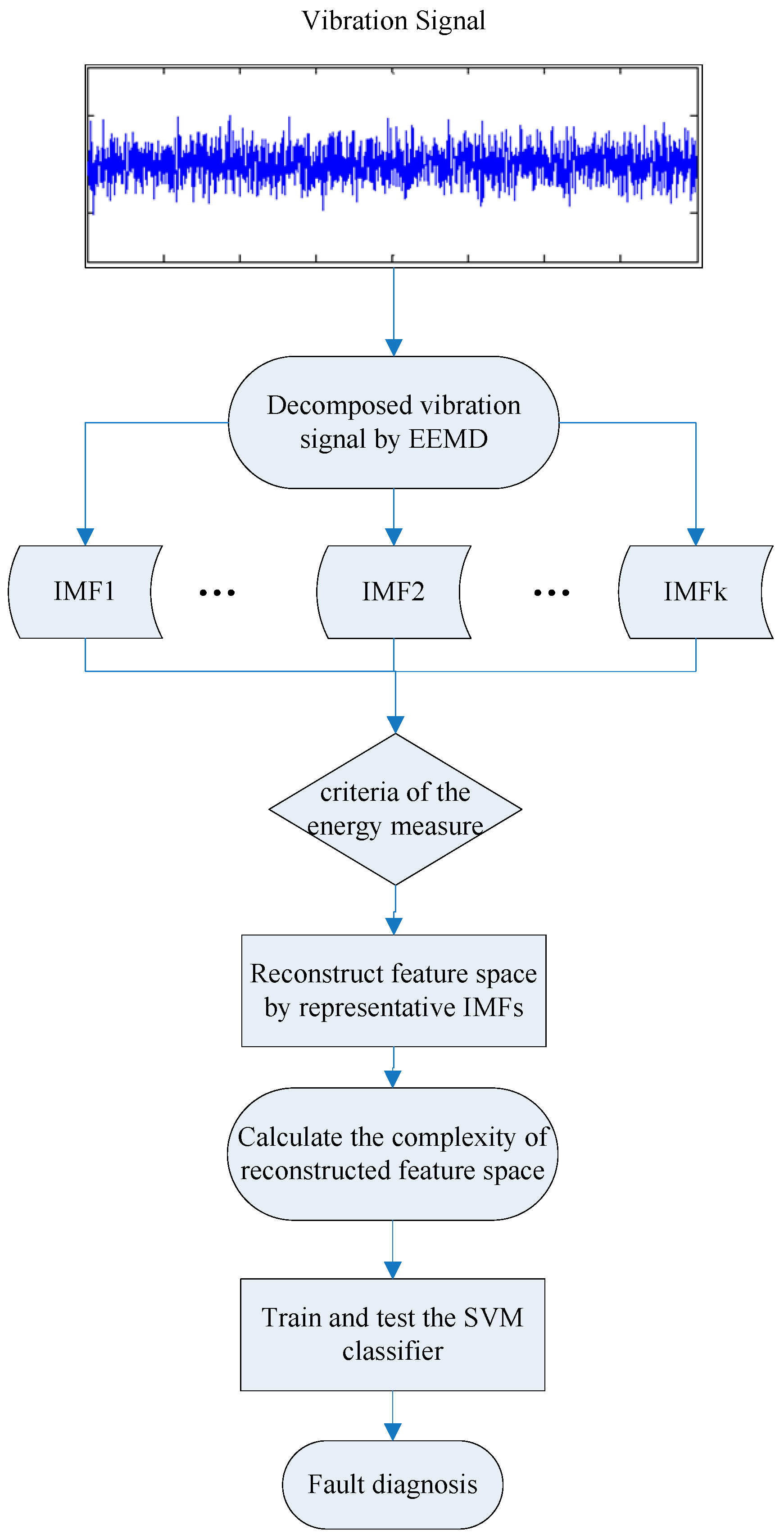
4. The Proposed Method
5. Experimental Results
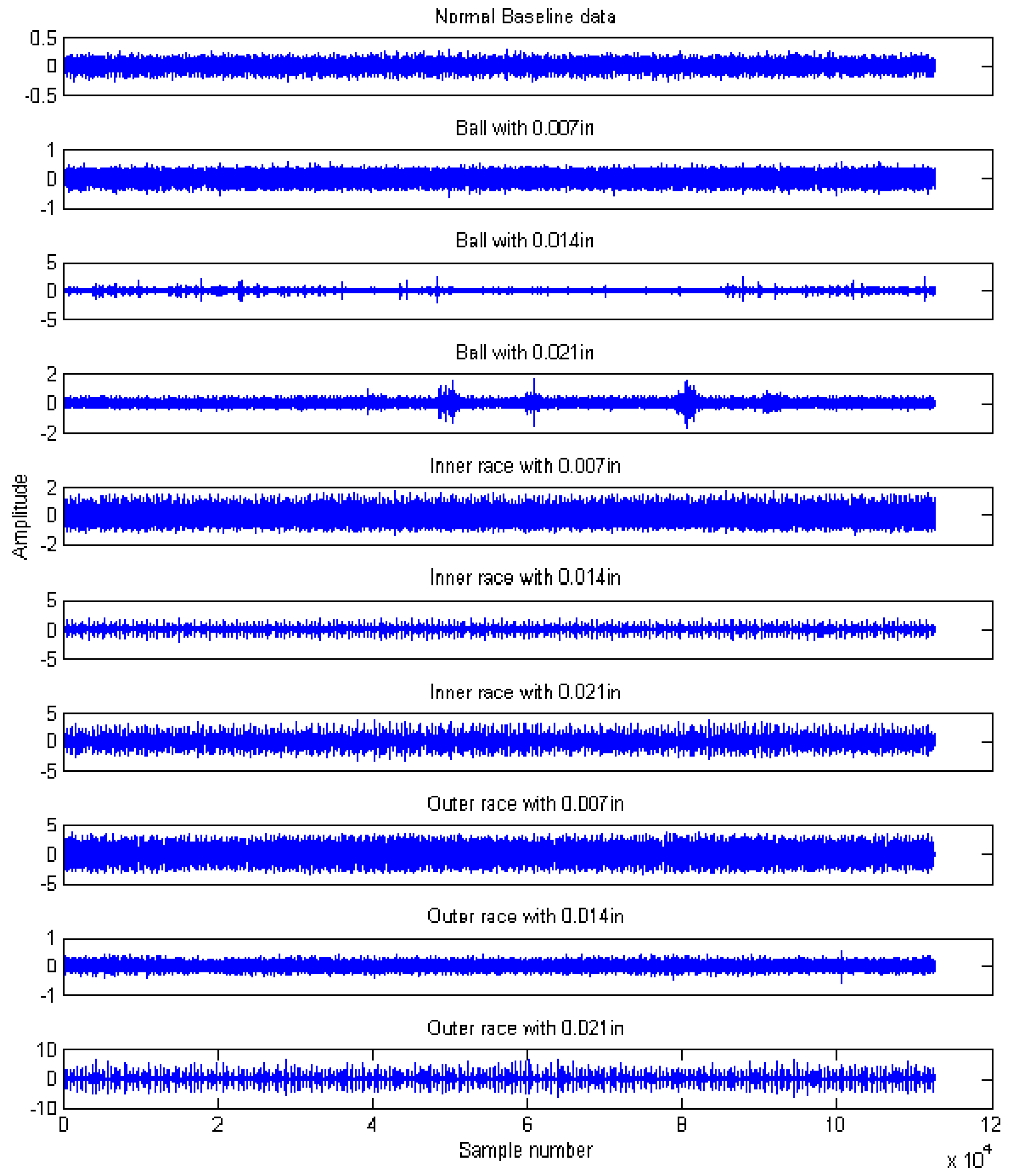
5.1. Experimental Data Description
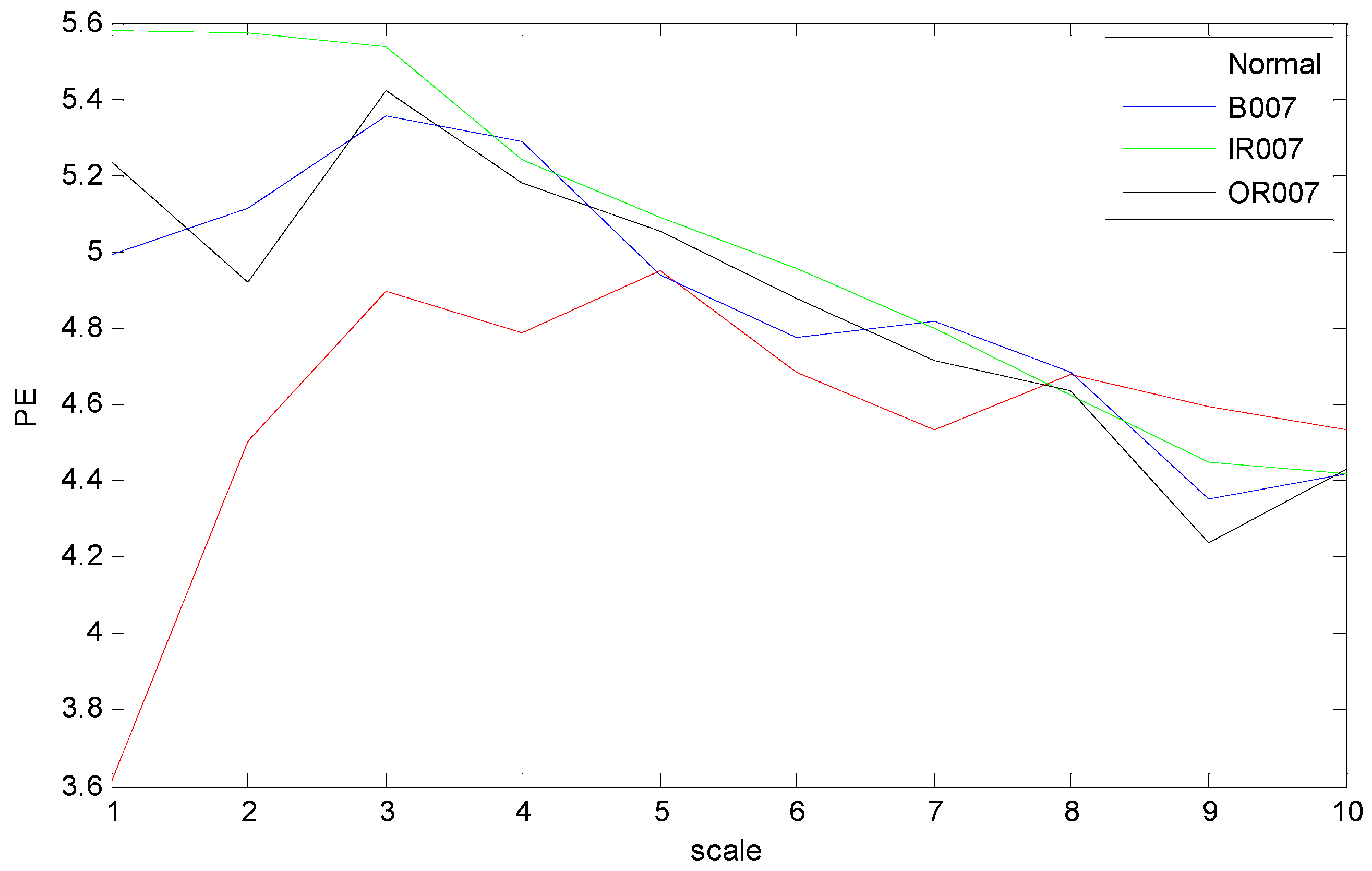
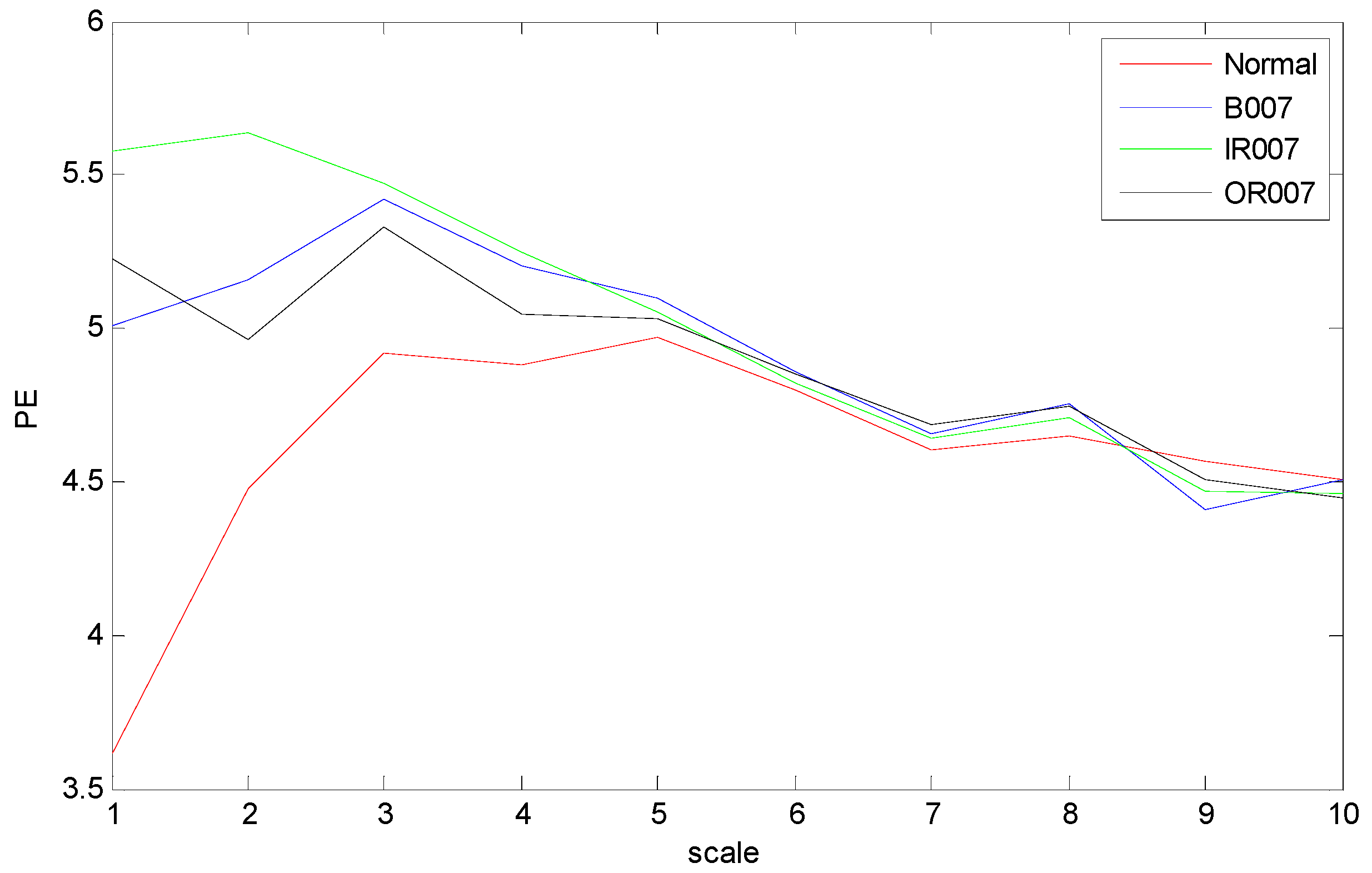
5.2. Results and Analysis
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agarwal, D.; Singh, C.K. Model-Based Fault Detection on Modern Automotive Engines. In Advanced Engine Diagnostics; Springer: Singapore, 2019; pp. 167–204. [Google Scholar]
- Fu, W.; Tan, J.; Zhang, X.; Chen, T.; Wang, K. Blind parameter identification of MAR model and mutation hybrid GWO-SCA optimized SVM for fault diagnosis of rotating machinery. Complexity 2019, 2019, 3264969. [Google Scholar] [CrossRef]
- López-Estrada, F.R.; Theilliol, D.; Astorga-Zaragoza, C.M.; Ponsart, J.C.; Valencia-Palomo, G.; Camas-Anzueto, J. Fault diagnosis observer for descriptor Takagi-Sugeno systems. Neurocomputing 2019, 331, 10–17. [Google Scholar] [CrossRef]
- Gómez-Peñate, S.; Valencia-Palomo, G.; López-Estrada, F.R.; Astorga-Zaragoza, C.; Osornio-Rios, R.A.; Santos-Ruiz, I. Sensor Fault Diagnosis Based on a Sliding Mode and Unknown Input Observer for Takagi-Sugeno Systems with Uncertain Premise Variables. Asian J. Control 2019, 21, 339–353. [Google Scholar] [CrossRef]
- Sonoda, D.; de Souza, A.Z.; da Silveira, P.M. Fault identification based on artificial immunological systems. Electr. Power Syst. Res. 2018, 156, 24–34. [Google Scholar] [CrossRef]
- Heo, S.; Lee, J.H. Fault detection and classification using artificial neural networks. IFAC-PapersOnLine 2018, 51, 470–475. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.D.L.; López-Estrada, F.R.; Puig, V.; Pérez-Pérez, E.J.; Mina-Antonio, J.D.; Valencia-Palomo, G. Diagnosis of Fluid Leaks in Pipelines Using Dynamic PCA. IFAC-PapersOnLine 2018, 51, 373–380. [Google Scholar] [CrossRef]
- Martin, H.R. Statistical moment analysis as a means of surface damage detection. In Proceedings of the 7th International Modal Analysis Conference; Society for Experimental Mechanics: Las Vegas, NV, USA, 1989; Volume 1, pp. 1016–1021. [Google Scholar]
- Volker, E.; Martin, H.R. Application of kurtosis to damage mapping. In Proceedings of the International Modal Analysis Conference, Los Angeles, CA, USA, 3–6 February 1986; pp. 629–633. [Google Scholar]
- Martin, H.R.; Honarvar, F. Application of statistical moments to bearing failure detection. Appl. Acoust. 1995, 44, 67–77. [Google Scholar] [CrossRef]
- Peter, W.T.; Peng, Y.H.; Yam, R. Wavelet analysis and envelope detection for rolling element bearing fault diagnosis—Their effectiveness and flexibilities. J. Vib. Acoust. 2001, 123, 303–310. [Google Scholar]
- Zheng, G.T.; Wang, W.J. A new cepstral analysis procedure of recovering excitations for transient components of vibration signals and applications to rotating machinery condition monitoring. J. Vib. Acoust. 2001, 123, 222–229. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Li, C.; Tan, J. Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM. Energy Convers. Manag. 2019, 187, 356–377. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Zhou, J.; Xu, Y.; Tan, J.; Chen, T. A hybrid approach for multi-step wind speed forecasting based on multi-scale dominant ingredient chaotic analysis, KELM and synchronous optimization strategy. Sustainability 2019, 11, 1804. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Rotary machine health diagnosis based on empirical mode decomposition. J. Vib. Acoust. 2008, 130, 21007. [Google Scholar] [CrossRef]
- Yu, D.; Cheng, J.; Yang, Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mech. Syst. Signal Process. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs. Meas. Sci. Technol. 2009, 20, 125701. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Qu, H.; Ma, W.; Zhao, J.; Wang, T. Prediction method for network traffic based on maximum correntropy criterion. China Commun. 2013, 10, 134–145. [Google Scholar]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Clarià, F.; Baranowski, R.; Orłowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef]
- Azami, H.; Fernández, A.; Escudero, J. Refined multiscale fuzzy entropy based on standard deviation for biomedical signal analysis. Med. Biol. Eng. Comput. 2017, 55, 2037–2052. [Google Scholar] [CrossRef]
- Yeh, C.H.; Shi, W. Generalized multiscale Lempel–Ziv complexity of cyclic alternating pattern during sleep. Nonlinear Dyn. 2018, 93, 1899–1910. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Cao, Y.; Tung, W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, J.; Xiao, H.; Zhang, W.; Zhu, W.; Li, C. Multifault diagnosis for rolling element bearings based on intrinsic mode permutation entropy and ensemble optimal extreme learning machine. Adv. Mech. Eng. 2014, 6, 803919. [Google Scholar] [CrossRef]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the 9th International Multitopic Conference (INMIC ’05), Karachi, Pakistan, 24–25 December 2005. [Google Scholar]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.; Wang, C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.K.; Kankar, P.K. A multiscale permutation entropy based approach to select wavelet for fault diagnosis of ball bearings. J. Vib. Control 2015, 21, 3123–3131. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Multiscale permutation entropy based rolling bearing fault diagnosis. Shock Vib. 2014, 2014, 154291. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Weighted multiscale permutation entropy of financial time series. Nonlinear Dyn. 2014, 78, 2921–2939. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 15 February 2011). [CrossRef]
- Cheng, J.; Yu, D.; Tang, J.; Yang, Y. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery. Shock Vib. 2009, 16, 89–98. [Google Scholar] [CrossRef]
- Fu, W.; Wang, K.; Li, C.; Li, X.; Li, Y.; Zhong, H. Vibration trend measurement for a hydropower generator based on optimal variational mode decomposition and an LSSVM improved with chaotic sine cosine algorithm optimization. Meas. Sci. Technol. 2019, 30, 015012. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 15 October 2018).
- Zhang, X.; Liang, Y.; Zhou, J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]


| Working Conditions | Defect Size (inches) | Number of Training Data Points | Number of Testing Data Points | Label of Classification |
|---|---|---|---|---|
| Normal | 0 | 80 | 30 | 0 |
| Ball 1 | 0.007 | 80 | 30 | 1 |
| Ball 2 | 0.014 | 80 | 30 | 2 |
| Ball 3 | 0.021 | 80 | 30 | 3 |
| Inner race 1 | 0.007 | 80 | 30 | 4 |
| Inner race 2 | 0.014 | 80 | 30 | 5 |
| Inner race 3 | 0.021 | 80 | 30 | 6 |
| Outer race 1 | 0.007 | 80 | 30 | 7 |
| Outer race 2 | 0.014 | 80 | 30 | 8 |
| Outer race 3 | 0.021 | 80 | 30 | 9 |
| Group | Fault Label | Label of Classification | Number of Training Data Points | Number of Testing Data Points |
|---|---|---|---|---|
| 1 | Normal | 0 | 80 | 30 |
| B007 | 1 | |||
| IR007 | 2 | |||
| OR007 | 3 | |||
| 2 | Normal | 0 | 80 | 30 |
| B007 | 1 | |||
| B021 | 2 | |||
| IR007 | 3 | |||
| IR021 | 4 | |||
| OR007 | 5 | |||
| OR021 | 6 | |||
| 3 | Normal | 0 | 80 | 30 |
| B007 | 1 | |||
| B014 | 2 | |||
| B021 | 3 | |||
| IR007 | 4 | |||
| IR014 | 5 | |||
| IR021 | 6 | |||
| OR007 | 7 | |||
| OR014 | 8 | |||
| OR021 | 9 |
| Approach | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| PE | 92.50% | 85.88% | 73.25% |
| MPE | 98.33% | 94.14% | 87.33% |
| MSE | 97.17% | 92.46% | 84.46% |
| IMPE | 100% | 95.85% | 91.90% |
| Proposed method | 100% | 98.5% | 94.7% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhou, J. Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy 2019, 21, 519. https://doi.org/10.3390/e21050519
Zhang W, Zhou J. Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy. 2019; 21(5):519. https://doi.org/10.3390/e21050519
Chicago/Turabian StyleZhang, Weibo, and Jianzhong Zhou. 2019. "Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy" Entropy 21, no. 5: 519. https://doi.org/10.3390/e21050519
APA StyleZhang, W., & Zhou, J. (2019). Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy, 21(5), 519. https://doi.org/10.3390/e21050519




