1. Introduction
Portfolio selection theory is an important part of modern quantitative finance. Generally, investors allocate the funds among different assets to maximize expected returns by choosing an optimal investment strategy, which is known as the portfolio selection problem. Since the classical portfolio selection programming was raised by Markowitz [
1], who proposed the mean-variance model in which return was quantified as the mean and risk as the variance, there have been numerous studies surrounding Markowitz’s work. As research continues to deepen, new models involving other risk indicators have been introduced and enriched the research field. For example, Ballestero [
2] presented mean-semi-variance in place of mean-variance owing to the fact that investors actually merely consider the risk when the returns are lower than their expected returns. Macedo et al. [
3] was devoted to studying the application of multi-objective evolutionary algorithms in the portfolio optimization, within a mean-semi-variance framework, which took into account adverse return variations rather than overall variations. Meanwhile, transaction cost is also an important factor in portfolios, which has been studied by many scholars. For example, Beraldi et al. [
4] aimed at dealing with complex transaction costs within portfolio management models effectively. With the increase of experts’ research on financial market, the vagueness and ambiguity of information were increasingly recognized, and the fuzzy set theory raised by Zadeh [
5] was then stretched into portfolio selections. Since then, a paradigm shift has taken place while modeling portfolios, and many scholars have studied the fuzzy portfolio to deal with the uncertainty in actual problems, such as [
6,
7], depending on the possibility measure. Furthermore, Liu and Liu [
8] transformed the exact historical data into fuzzy numbers and constrained fuzzy expected value models on the basis of the credibility measure, which is consistent with the vagueness, so as to overcome the limitations of possibility measure. In accordance with the credibility measure, Huang [
9] originally put forward semi-variance to express fuzzy variance and utilized a fuzzy simulation based on the genetic algorithm to solve the formed mean-semi-variance model.
In probability theory, many researchers have investigated and accepted mean-entropy models [
10,
11] and mean-cross entropy models [
10]; the former maximizes the uncertainty of investment return for improving diversification, and the latter minimizes the divergence of investment return from the a priori one. In fuzzy set theory, different from the probabilistic environment, Huang [
12] used entropy as a measure of risk and proposed two credibility-based fuzzy mean-entropy models to illustrate the effect of entropy in portfolios. Furthermore, cross-entropy was adopted by Qin et al. [
13] in portfolio problems, and a hybrid intelligent algorithm was designed to deal with different models. With the development of research, models and applications involving entropy have received great attention. For example, Ray and Majumder [
14] proposed a fuzzy mean-variance-skewness-entropy model with triangular fuzzy returns to facilitate a more reasonable investment decision. Zhou et al. [
15] found that semi-entropy was positively correlated with entropy and variance so that the semi-entropy can be directly proven as a surrogate indicator of risk, and an illustrative example showed that the mean-semi-entropy models of fuzzy portfolios can significantly improve the dispersibility. Tian et al. [
16] established the bi-objective optimization model on the basis of fuzzy cross-entropy so as to identify the criterion weights and obtain a final ranking result.
Though great progress has been made in embedding fuzzy programming approaches in portfolios, most research on fuzzy portfolios is in the framework of a single period, and also, some scholars have studied the multi-period fuzzy portfolio selection problems. In the real world, investors tend to invest their assets from time to time, which makes it reasonable for single-period portfolio selection problems to evolve into multi-period portfolio selection problems. Yan et al. [
17] originally formulated a class of multi-period semi-variance models, and a hybrid genetic algorithm was applied to solve the model. Moreover, Yan and Li [
18] established a multi-period semi-variance model considering the stochastic exchange rate, which was proven to be effective. Peng et al. [
19] proposed an asset-liability mean-variance model, using a nested mean-variance game formulation due to its time inconsistency. Within the framework of credibility theory, Guo et al. [
20] designed a fuzzy simulation-based genetic algorithm to settle the fuzzy multi-period mean-variance model involving V-shaped transaction costs. Similarly, Zhang and Liu [
21] presented a multi-period credibilistic mean-variance model, aiming to maximize the terminal wealth and minimize its risk. Besides, Mohebbi and Najaf [
22] formulated a bi-objective mean-VaR portfolio selection model with multiple periods and transaction cost considerations based on credibility theory and adopted an interactive dynamic programming method to solve this model.
Table 1 summaries the literature mentioned above from the aspect of risk indicators, objective, period, and theory considered in modeling. Most of them were committed to researching one certain aspect, such as going into depth for a risk indicator, discussing multiple objectives, and studying multiple cycles. Considering that the current research mainly focuses on proposing new portfolio selection models composed of returns and a few risk indicators, such as the mean-variance model and the mean-variance-entropy model, few research puts so many risk indicators into one paper. Therefore, in order to study the extent to which these indicators affect the model, a portfolio selection model is proposed from the perspective of studying different risk indicators and their impacts in a multi-period multi-objective portfolio selection problem under the fuzzy environment. Because there exist many risk indicators, we choose variance, semi-variance, entropy, and semi-entropy, which are commonly discussed in portfolios. Meanwhile, for dealing with the multi-objective issues, a polynomial goal programming (PGP) was embedded. Ultimately, from the perspective of empirical data, the priorities to which investors with different risk preferences prefer different risk indicators or portfolio selection models involving different combination of risk indicators are given, helping investors make more rational decisions.
After this brief Introduction, this paper introduces the conceptions of credibility theory, i.e., credibilistic expectation, variance, semi-variance, entropy, and semi-entropy, in
Section 2; then, based on the PGP method, a multi-period polynomial goal programming model is presented in
Section 3, which considers transaction costs, upper and lower bounds, investment proportion, and short-sale to a large extent; in
Section 4, the defuzzification portfolio selection model is solved by an adjusted genetic algorithm; followed by
Section 5 and
Section 6, providing an empirical application to demonstrate the results of the comparison of models and the final conclusion, respectively.
5. Empirical Experiments
In this section, filtering all stocks of the Shanghai Stock Exchange (SSE) 50 index, 29 stocks with complete ten-year historical data (December 2007–2017) were selected on Wind (a data service software). There were two main considerations in choosing the ten-year data. On the one hand, the acquisition of fuzzy numbers was consistent. On the other hand, the long-existing stocks are safer for investors.
For each stock, we obtained the closing prices of 121 months. By the formula of monthly return
, we obtained 120 historical yield rates, which were sorted by reference to Bermúdez et al. [
35]. The 40–60 sample percentiles of the monthly returns were regarded as the cores of each fuzzy return, while the 5–40 and 60–95 sample percentiles expressed the left-hand and right-hand spreads of each trapezoidal fuzzy number. Hence, 29 trapezoidal fuzzy variables were achieved (see
Table 4). Furthermore, in the ensuing demonstration, the constant parameters in the models were adopted as:
,
,
. By using the software MATLAB, we set the parameters of the designed algorithm as: the population size was
, the crossover probability
, the mutation probability
, and the number of generations
10,000. With regard to the polynomial model corresponding to
,
, and
,
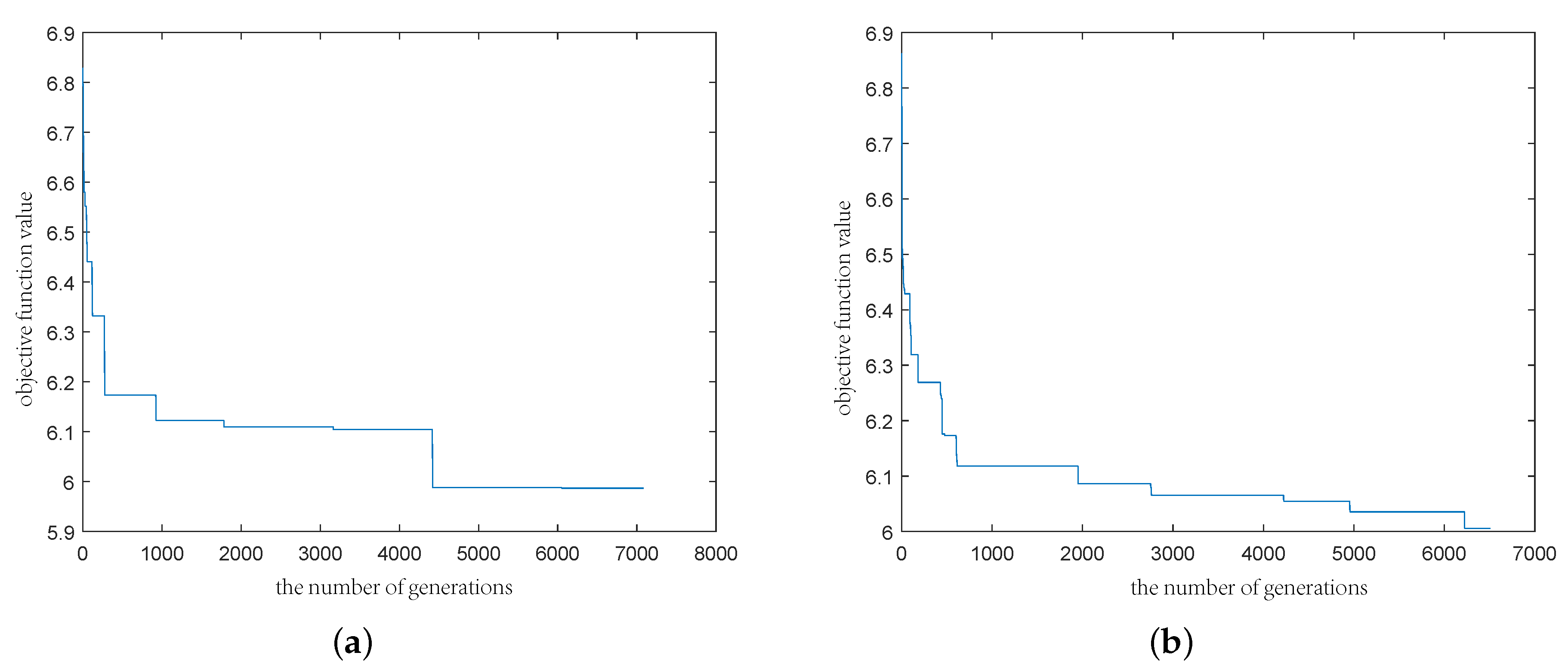
Figure 1a,b show how the objective function value changes with the number of generations. The first experiment converges around 4000 and the second converges around 6000. Thus, in order to ensure the reliability of the results, we set
10,000.
Table 5 provides the aspired values
, and
, which were obtained by separately handling the five sub-individual objective models. Because of too many periods and experimental data, in order to be brief, we just show the results of the last three issues of the whole 12 periods in the tables.
We embedded the aspired values in the objective and constraints of the model to settle the models involving different combinations of objective functions. Simultaneously, two groups were constructed by assigning a binary value to the corresponding (i = 2, 3, 4, 5) so as to analyze the performance of different risk indicators. Specifically, Group 1 consisted of the overall expected return and a risk indicator, including the return-variance model (RVM), RSvM, RHM, and RShM, respectively; the corresponding were 1-1-0-0-0, 1-0-1-0-0, 1-0-0-1-0, and 1-0-0-0-1. Group 2 consisted of the overall expected return and two risk indicators, including the return-variance-entropy model (RVHM), RVShM, RSvHM, and RSvShM, respectively; the corresponding were 1-1-0-1-0, 1-1-0-0-1, 1-0-1-1-0, and 1-0-1-0-1.
Table 6 presents the results of each objective value of the models in Group 1 in Periods 10–12. By observing the results of Periods 10–12, comparing RVM and RS
vM, the variance, semi-variance, entropy, and semi-entropy of the former were smaller, indicating that the risk was smaller, while the latter had better expected return. According to the comprehensive CrSR index, the RS
vM model was better. In addition, comparing RHM and RS
hM, the variance, semi-variance, entropy, and semi-entropy of the latter were smaller, showing that the risk was smaller, while the former had better expected return. The comprehensive CrSR index expressed that the RHM model was better. Overall, the largest expected return was obtained by RHM, followed by RS
hM; relatively speaking, they were income preferences. For the remaining risk indicators including variance, semi-variance, entropy, and semi-entropy, RVM had the lowest risk and RS
vM the second, indicating that they were risk aversions. Here, we used the indicator CrSR to balance the return and risk, and the results showed that RHM was the best, followed by RS
hM, suggesting that the return had a greater contribution to the CrSR.
Table 7 presents the results of each objective value of the models in Group 2 in Periods 10–12. By observing the results of Periods 10–12, comparing RVHM and RVS
hM, the variance, semi-variance, entropy, and semi-entropy of the latter were smaller, indicating that the risk was smaller, while the former had better expected return. According to the comprehensive CrSR index, the RVHM model was better. In addition, comparing RS
vHM and RS
vS
hM, the former had better expected return, and its risk was relatively smaller in terms of probability; thus, the comprehensive CrSR index was obviously better. Compare the models RVHM and RS
vHM, which both contain the entropy issue, and models RVS
hM and RS
vS
hM, which both contain the semi-entropy issue; the semi-variance issue prefers the expected return, while the variance issue contributes greatly to avoiding risk. Overall, the largest expected return was obtained by RS
vHM, followed by RS
vS
hM; relatively speaking, they were income preferences. For the remaining risk indicators including variance, semi-variance, entropy, and semi-entropy, RVS
hM had the lowest risk, and RVHM was the second, indicating that they were risk aversions. Here, we used the indicator CrSR to balance the return and risk, and the results showed that RS
vHM was the best, followed by RS
vS
hM.
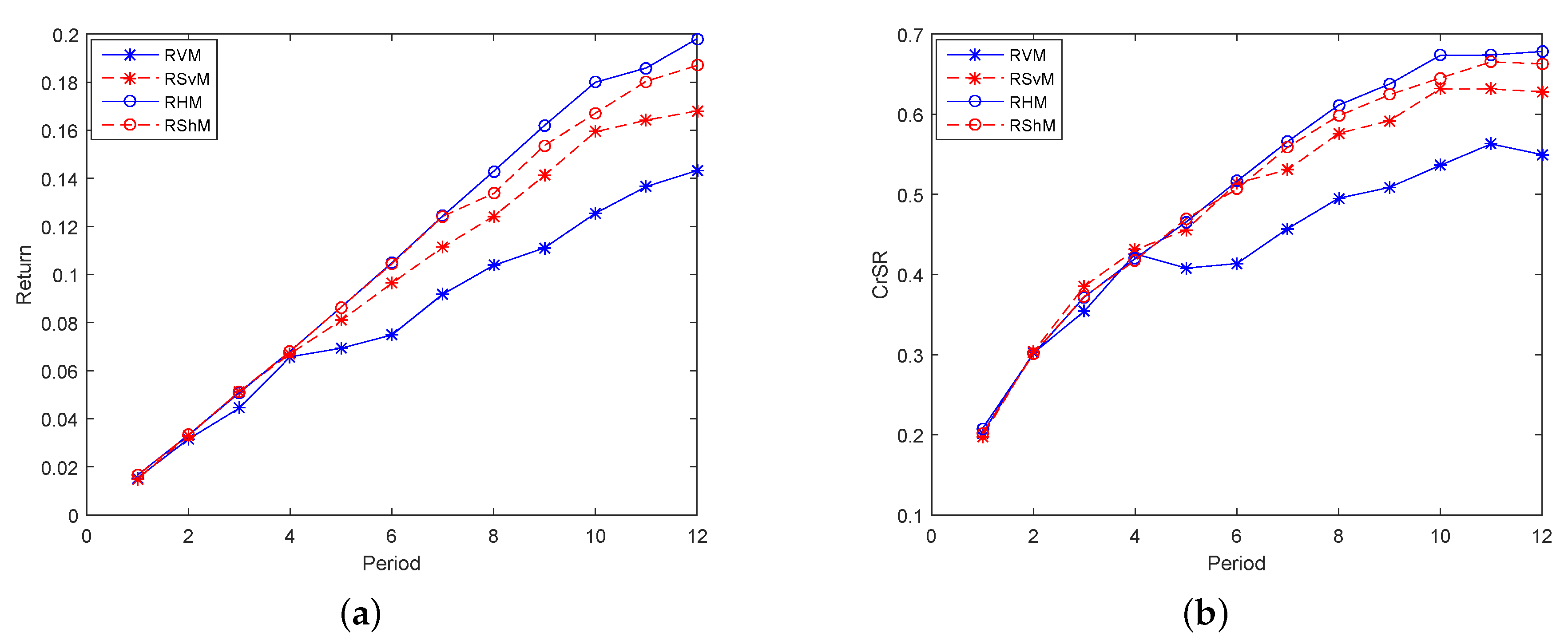
To better illustrate the above analysis, we conduct a study of each indicator in the 12 periods. Firstly, study models consisting of two indicators, one return indicator and one risk indicator, made up Group 1.
Figure 2a,b, respectively, shows the expected returns and CrSRs of models in Group 1 in 12 periods, and their trends were basically the same. For investors who prefer incomes, the larger the expected returns and CrSRs are, the better the model is. Obviously, entropy plays the most important role, followed by semi-entropy. Therefore, for risk-averse investors, the four risk indicators with basically consistent trends in
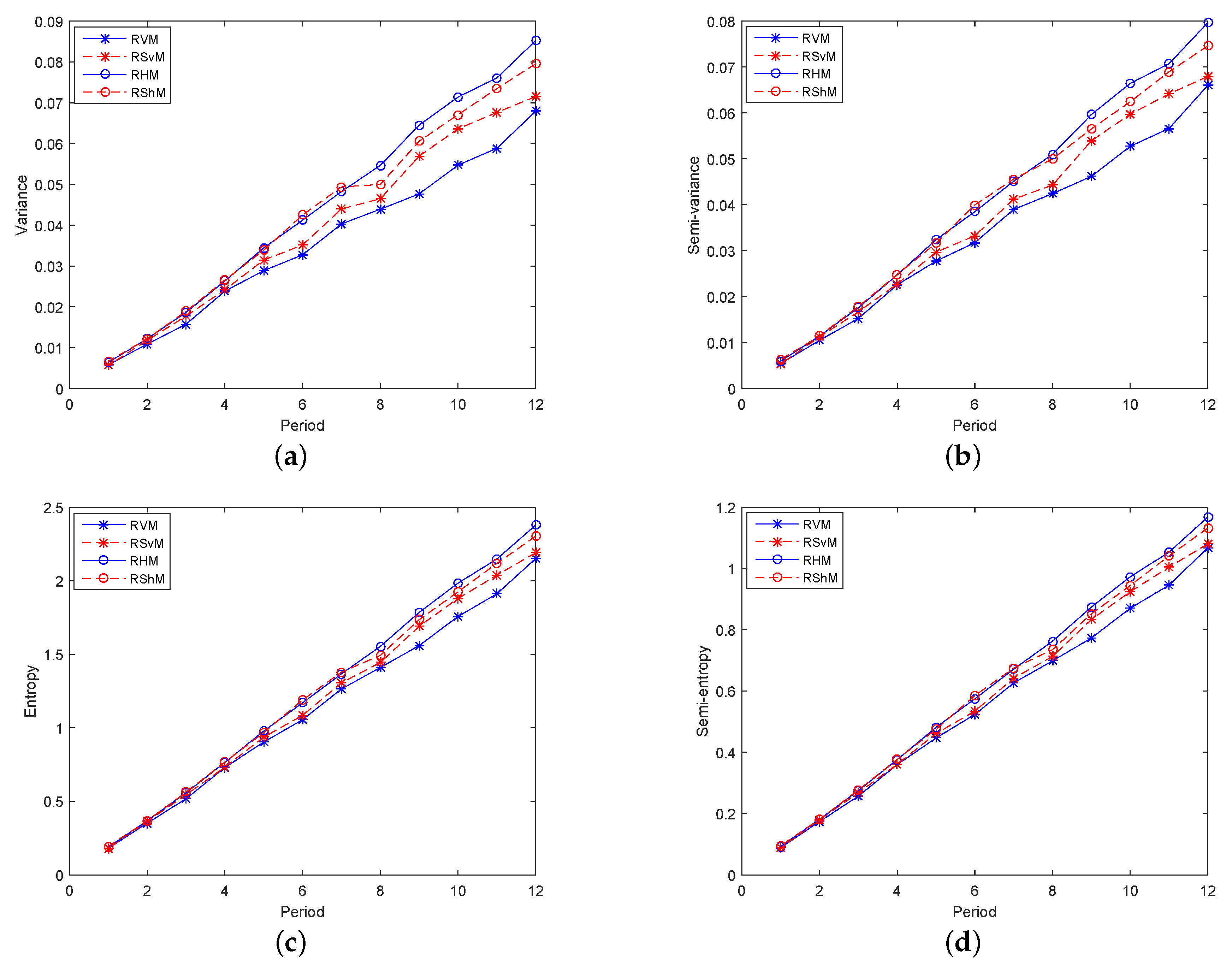
Figure 3a–d shows that the contribution of variance was the largest, followed by semi-variance. Hence, for investors who balance incomes and risks, RHM was chosen in the high-yield models, and RS
vM was chosen in the low-risk models because their corresponding CrSRs were relatively higher.
To sum up, for the models in Group 1, the four risk indicators can be divided into two categories: one is the income-preference index composed of entropy and semi-entropy, and the other one is the risk aversion index composed of variance and semi-variance. In terms of performance, entropy was the best from the perspective of profit, and the variance was optimal from the perspective of risk. In equilibrium, the entropy was optimal in the high-yield fields, and the semi-variance performed best in the low-risk fields.
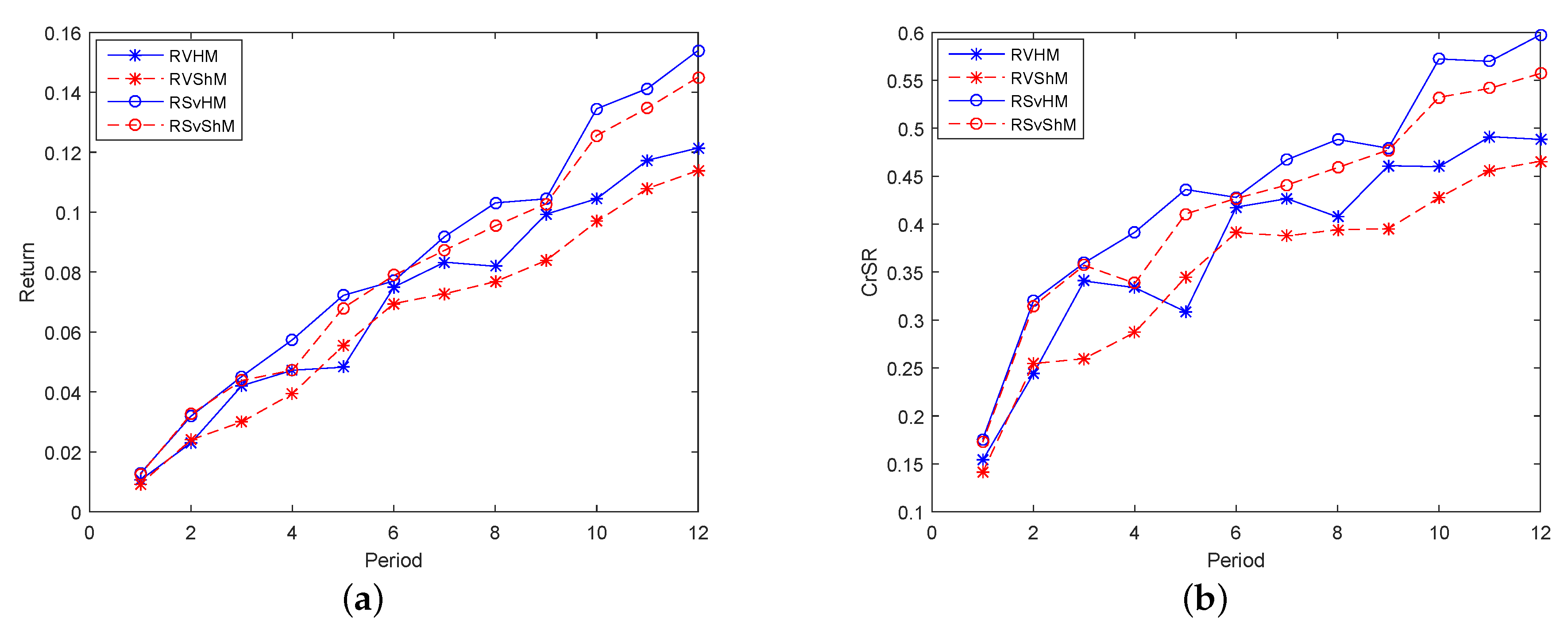
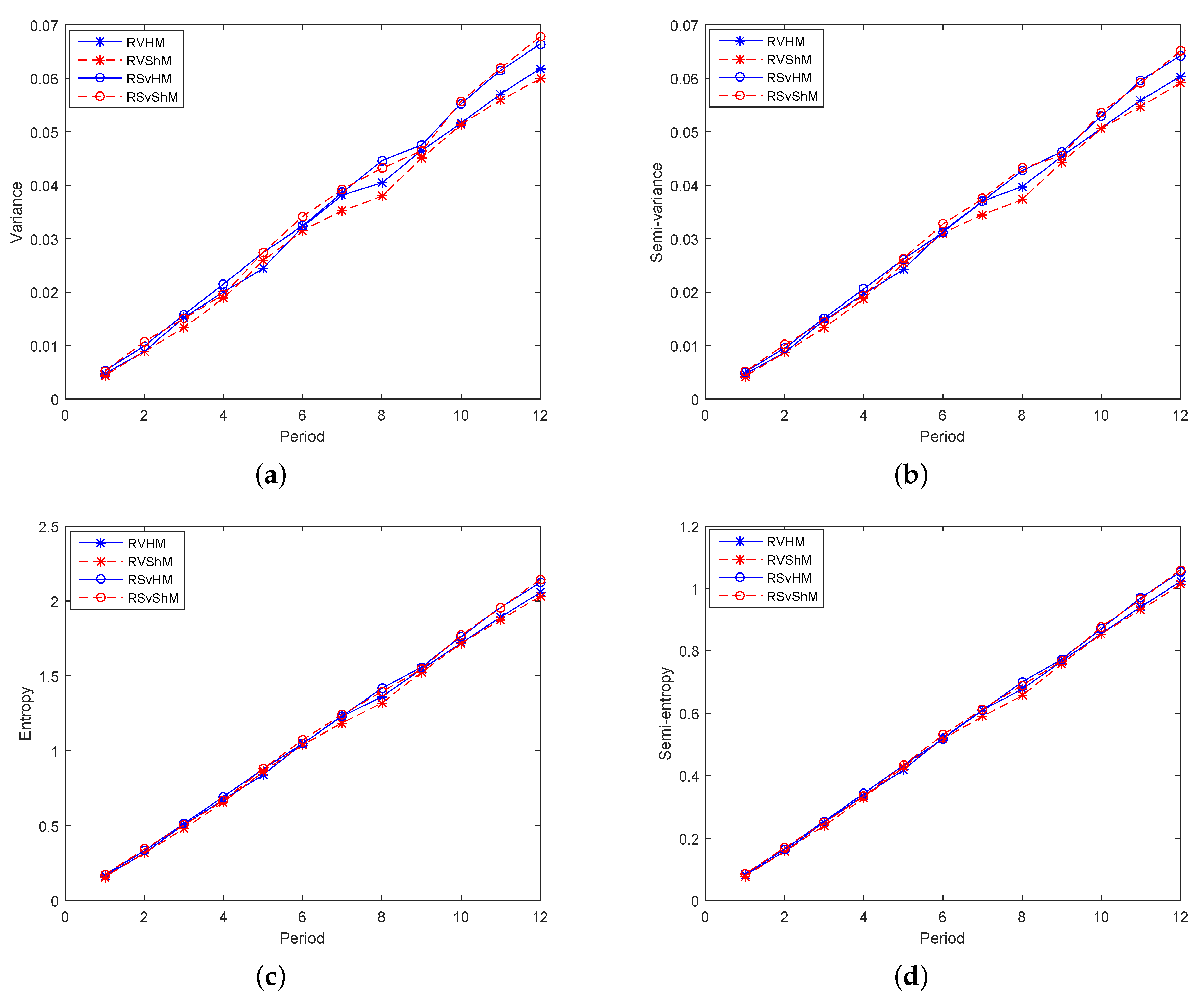
Secondly, models consisting of three indicators were studied, that is one return indicator and two risk indicators made up Group 2. For investors who prefer incomes,
Figure 4a,b shows that RS
vHM and RS
vS
hM were higher than RVHM and RVS
hM. For models with three indicators, the semi-variance element was more helpful for expected returns and CrSRs than variance, and the model with entropy named RS
vHM was the best. In addition, for investors who avoid risks,
Figure 5a–d displays that the results of the four risk indicators were quite close, and the risks of RVHM and RVS
hM were smaller than those of RS
vHM and RS
vS
hM, indicating that the variance had a greater effect on risk aversions and that the model with semi-entropy named RVS
hM was the best. Hence, for investors who balance incomes and risks, RS
vHM was chosen in the high-yield models, and RVHM was chosen in the low-risk models because of their higher CrSRs.
To sum up, for the models in Group 2, the risks of the four models were roughly equivalent. Similarly, the four models can be divided into two categories: one is the risk-avoidance models based on variance, and the other one is the income-preference models based on semi-variance. In terms of performance, RSvHM was the optimal from the perspective of profit, and RVShM performed best from the perspective of risk. In terms of balance, RSvHM was the best in the high-yield fields, and RVHM was optimal in the low-risk fields.