Mechanical Fault Diagnosis of a DC Motor Utilizing United Variational Mode Decomposition, SampEn, and Random Forest-SPRINT Algorithm Classifiers
Abstract
1. Introduction
2. Variational Mode Decomposition (VMD)
2.1. A Brief Description of VMD
- For each modal function , the marginal spectrum is obtained by a Hilbert transformation.
- The exponent-modified method is utilized to move the spectrum of modal functions to their estimated central frequencies.
- The bandwidth of each modal function is obtained by Gauss smoothing.
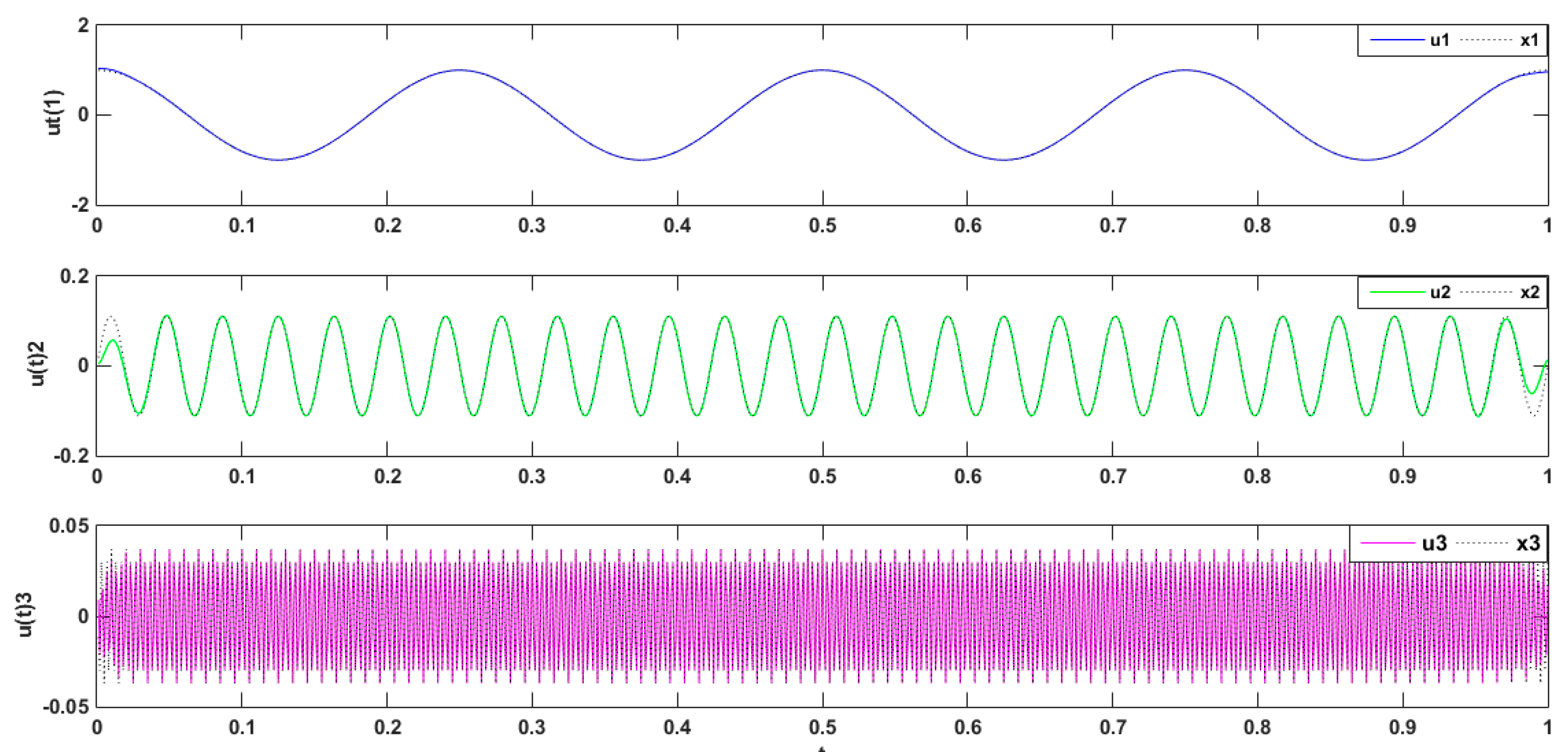
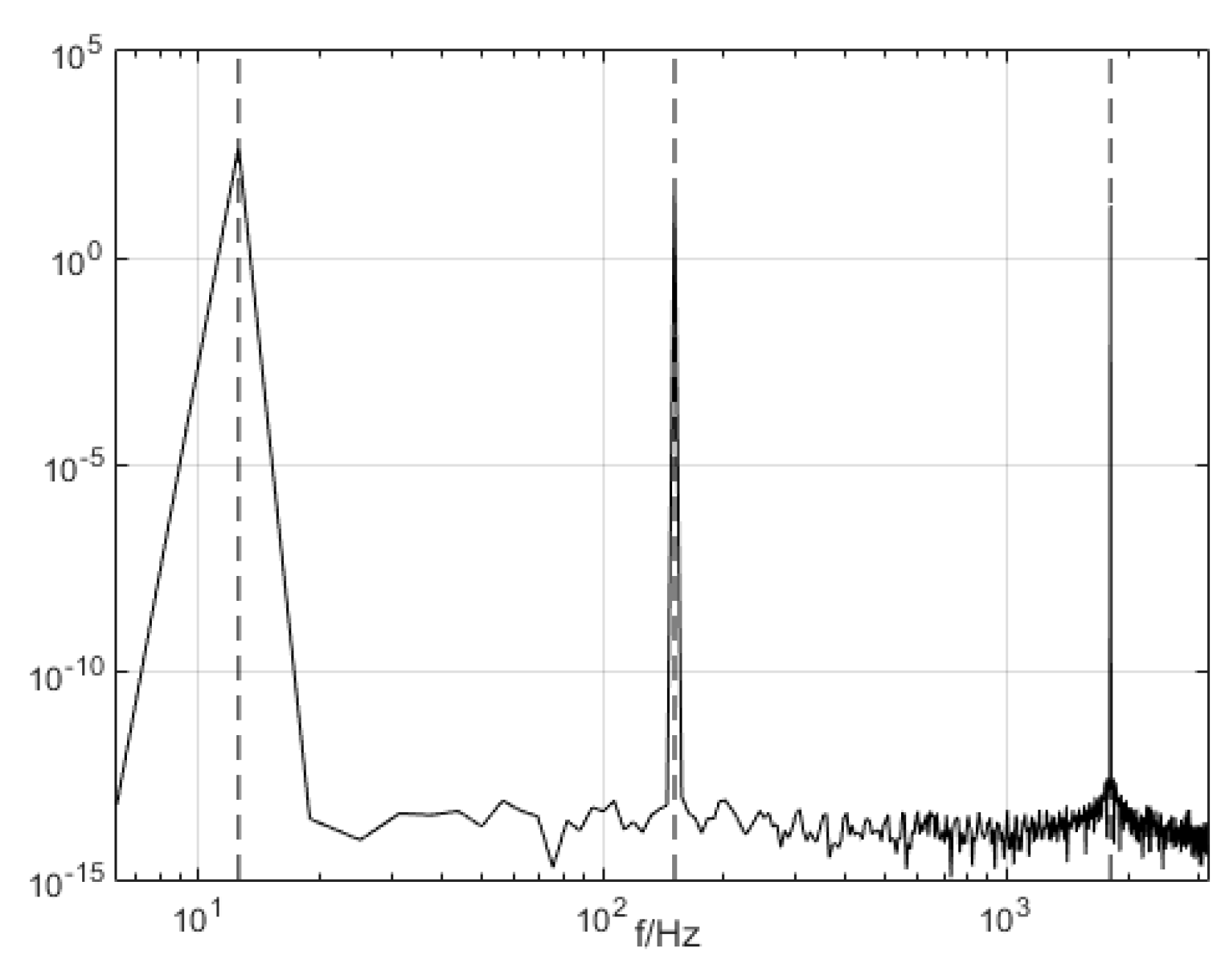
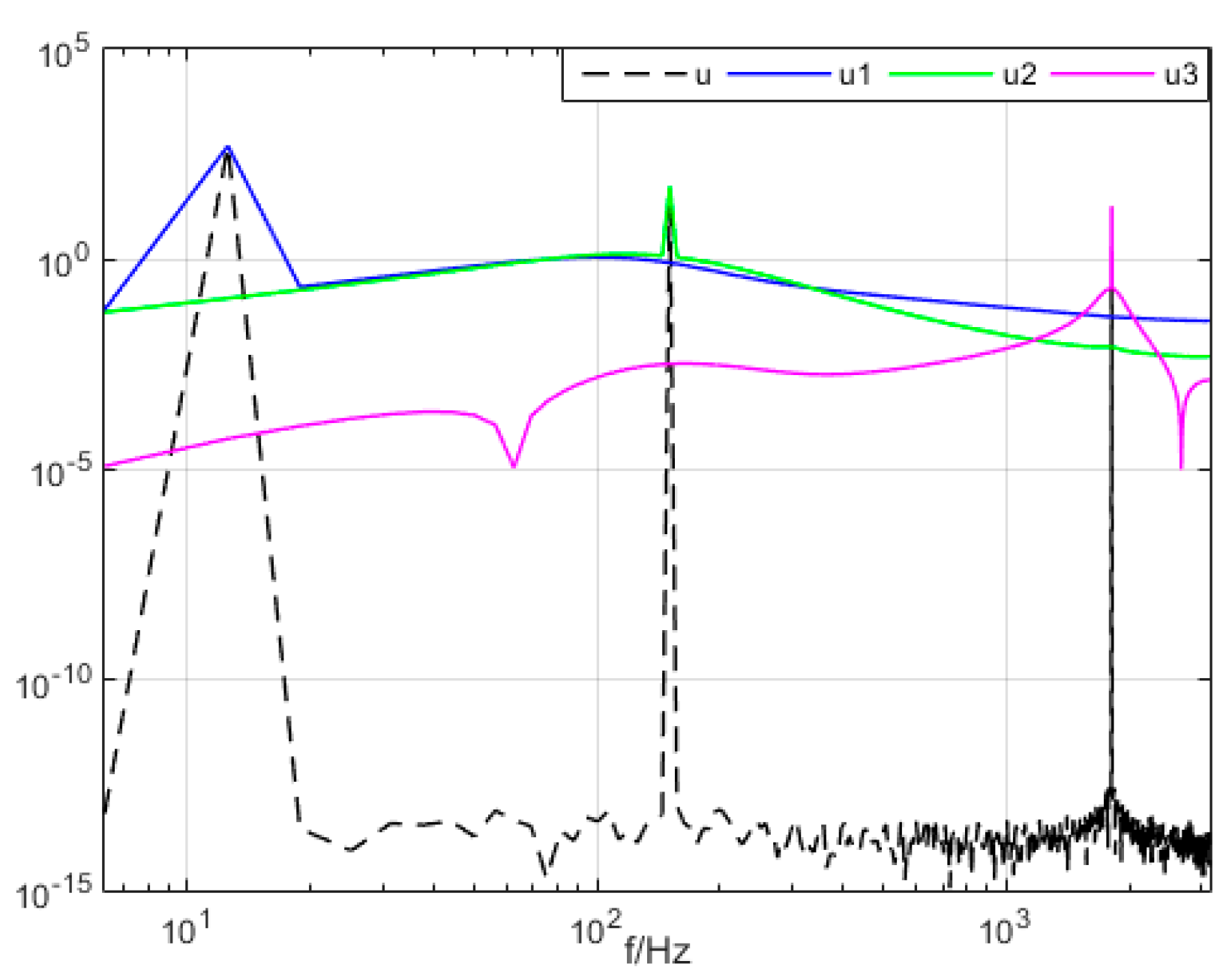
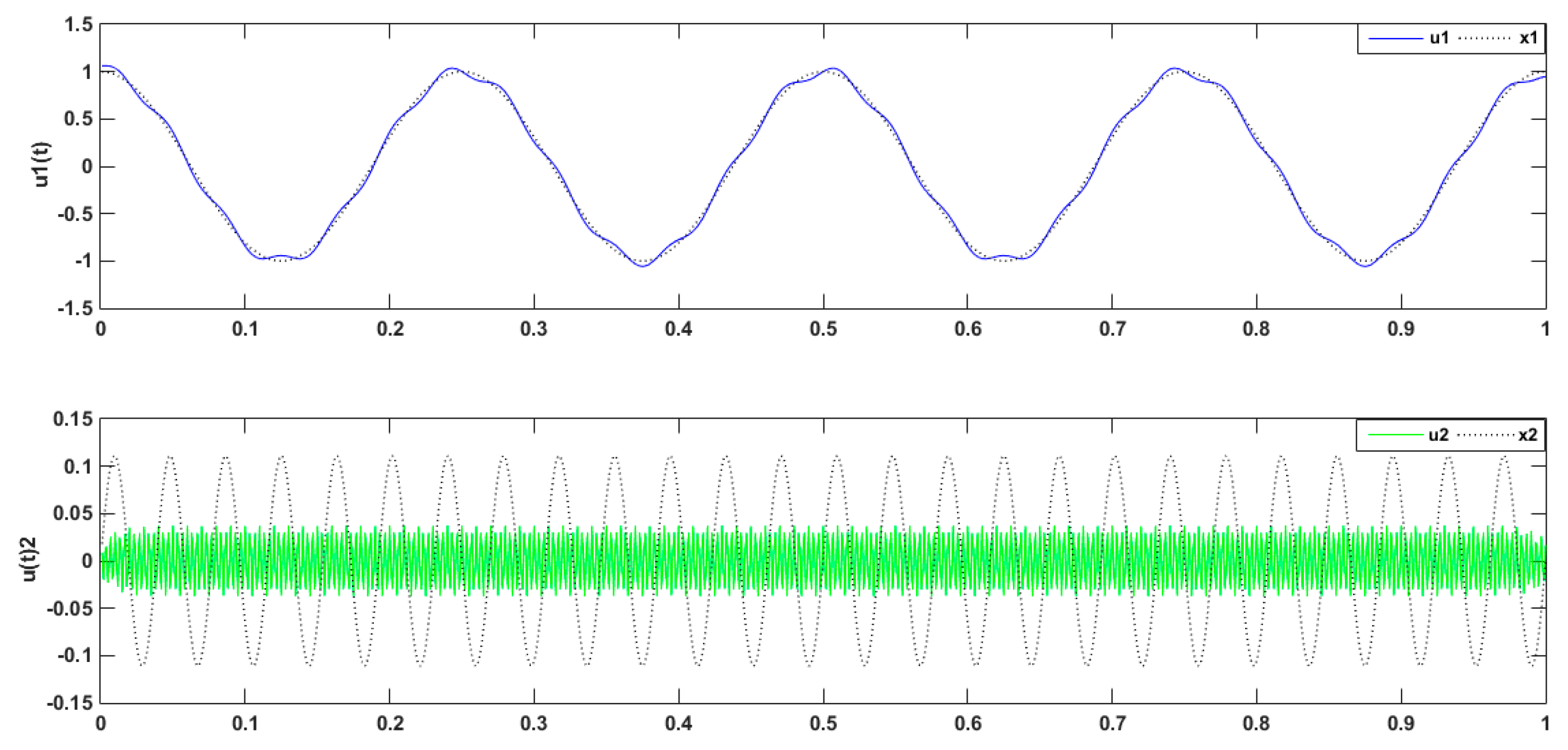
2.2. VMD Algorithm Simulation
2.3. Study of the Parameter Decomposition Modes of the VMD
Simulation Experimental Results
3. Sample Entropy
- As for , the number of j whose distance between and is less than or equal to r is counted and denoted as Bi. For , there is:
- Define as
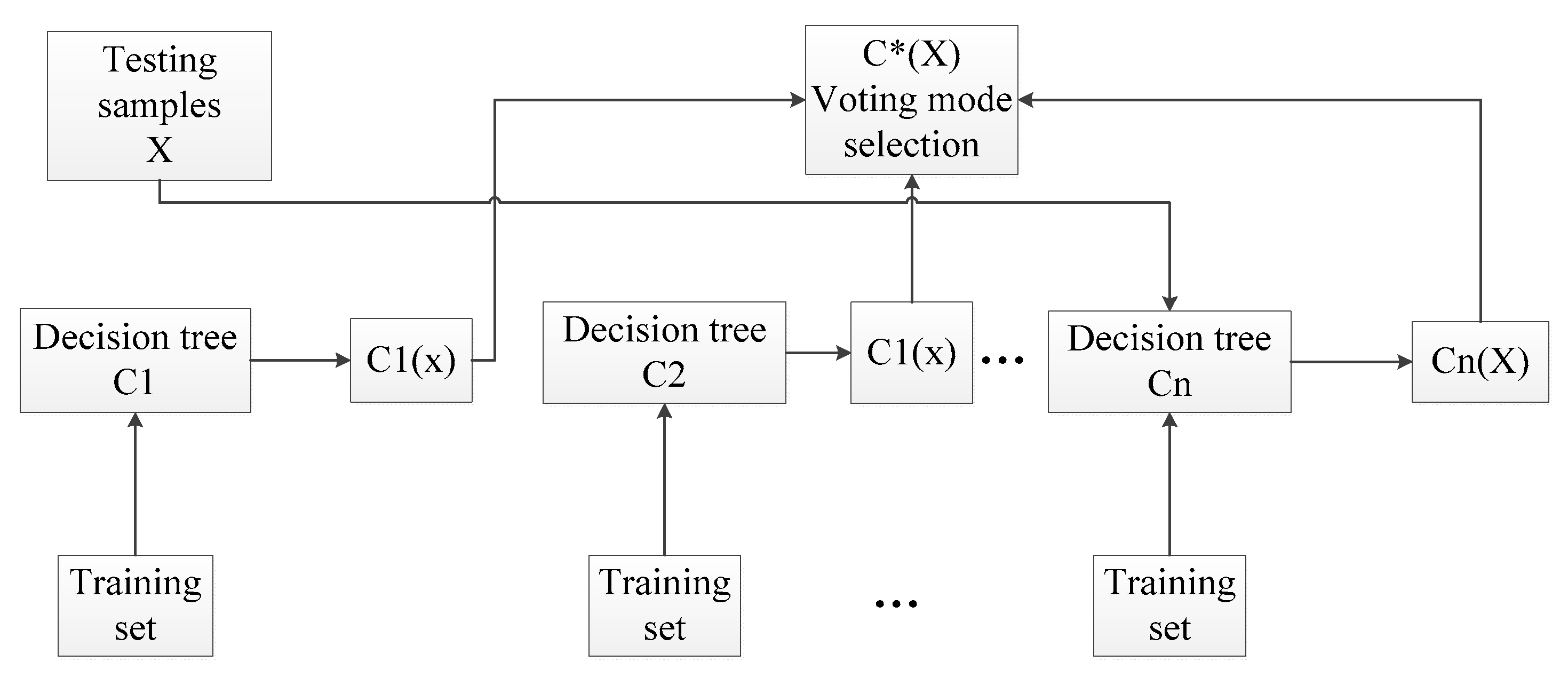
4. Random Forest
4.1. Bootstrap Resampling Algorithm
4.2. Bagging Algorithm
- Produce T training sets randomly through the bootstrap method of resampling;
- Each training set is used to generate the corresponding decision tree;
- As for the test set sample X, each decision tree is applied to test the corresponding categories;
- Choose the category that has the most outcomes from the decision tree for testing sample X through voting.
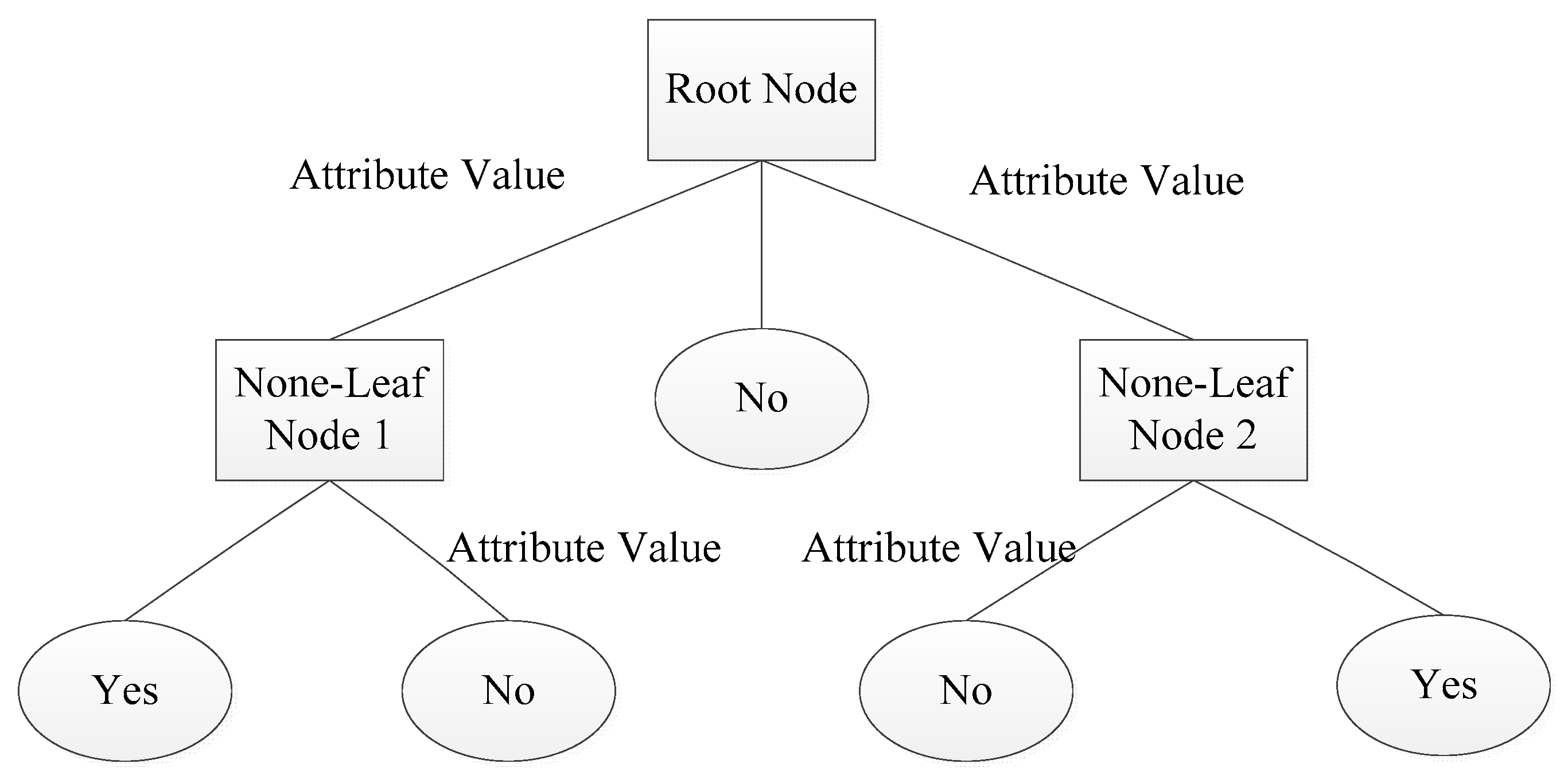
4.3. Decision Tree
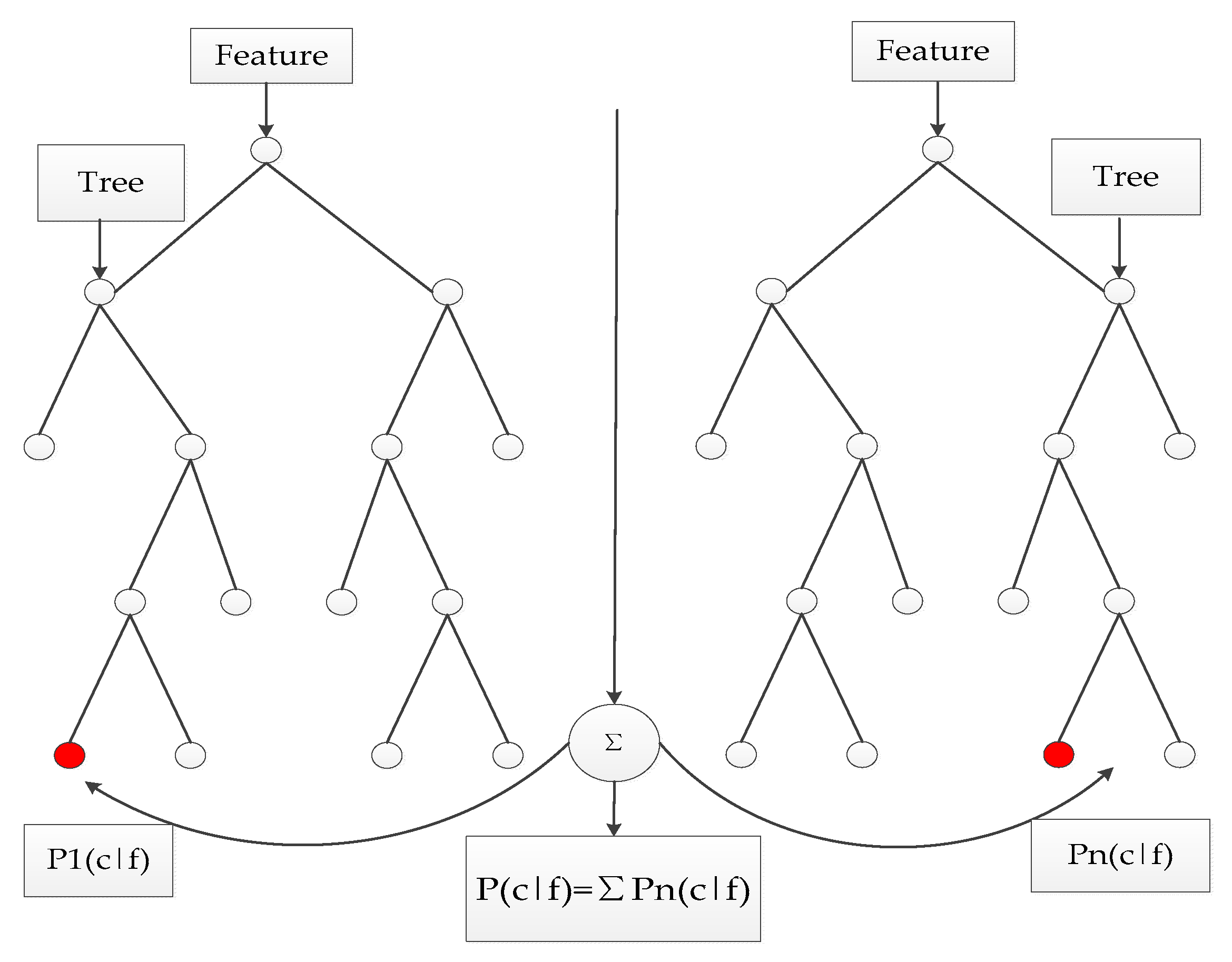
4.4. Random Forest Algorithm
- Samples are collected by the bootstrap method, and training sets will be generated randomly;
- Each training set is employed to generate the corresponding decision tree ;
- Every tree grows intact without pruning;
- As for the test set sample X, it gets the corresponding category by testing each decision number;
- The category with the most output from T decision tree is taken as the category of test set sample X by voting.
4.5. Random Forest-United SPRINT Algorithm
- The random forest utilizes the bootstrap resampling method to extract 63.2% of the samples from the original training sample set to generate a subsample set, where each subsample corresponds to a classification tree. At the same time, the original samples that are not sampled are called out-of-bag data (OOB). OOB data are used to evaluate the classification accuracy of classifiers.
- Each sub-sample set becomes a single classification tree. At each tree node, m feature vectors are picked out of M feature vectors, according to the empirical formula . According to the principle of minimum nonpurity of nodes, feature is chosen as the classification attribute of the node.
- According to the feature , the node is divided into two branches, and then the best feature from the remaining features is searched. The classification tree can grow sufficiently and the impurity of each node can be minimized through the above method.
- In the classification phase, the classification label is a combination of the results of all classification trees. RF is based on the voting principle.
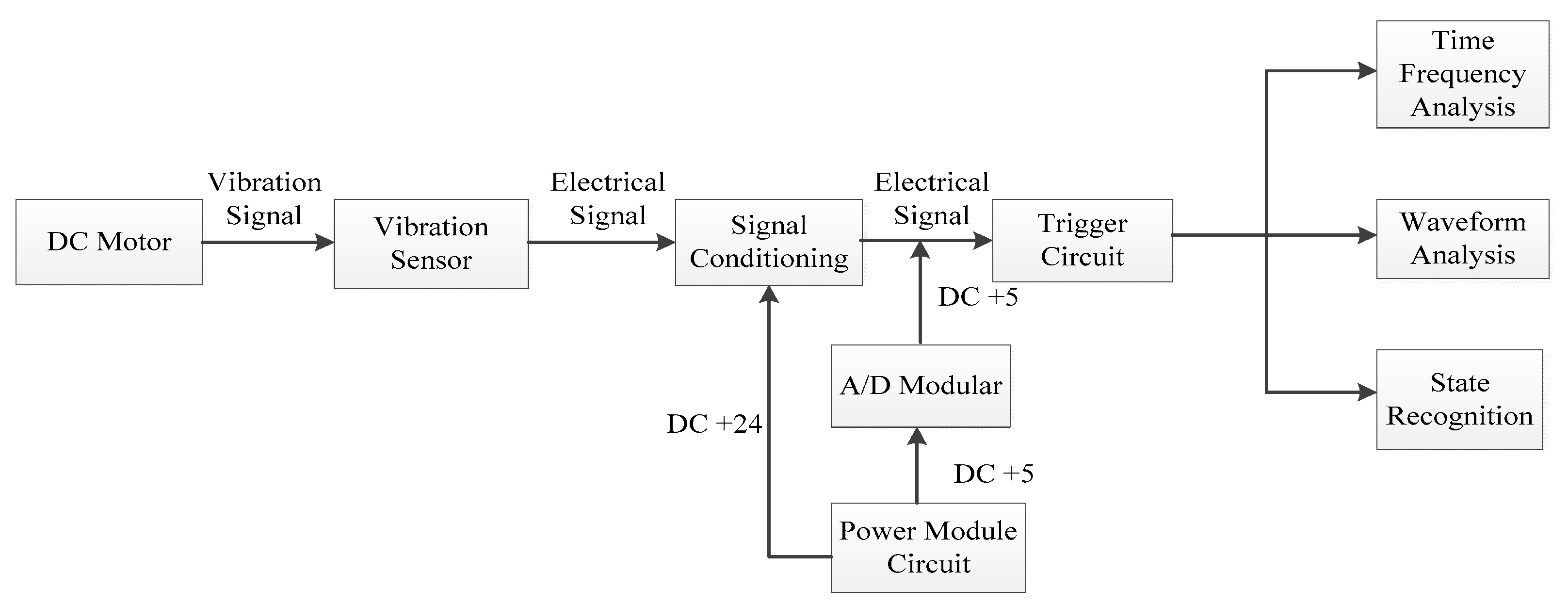
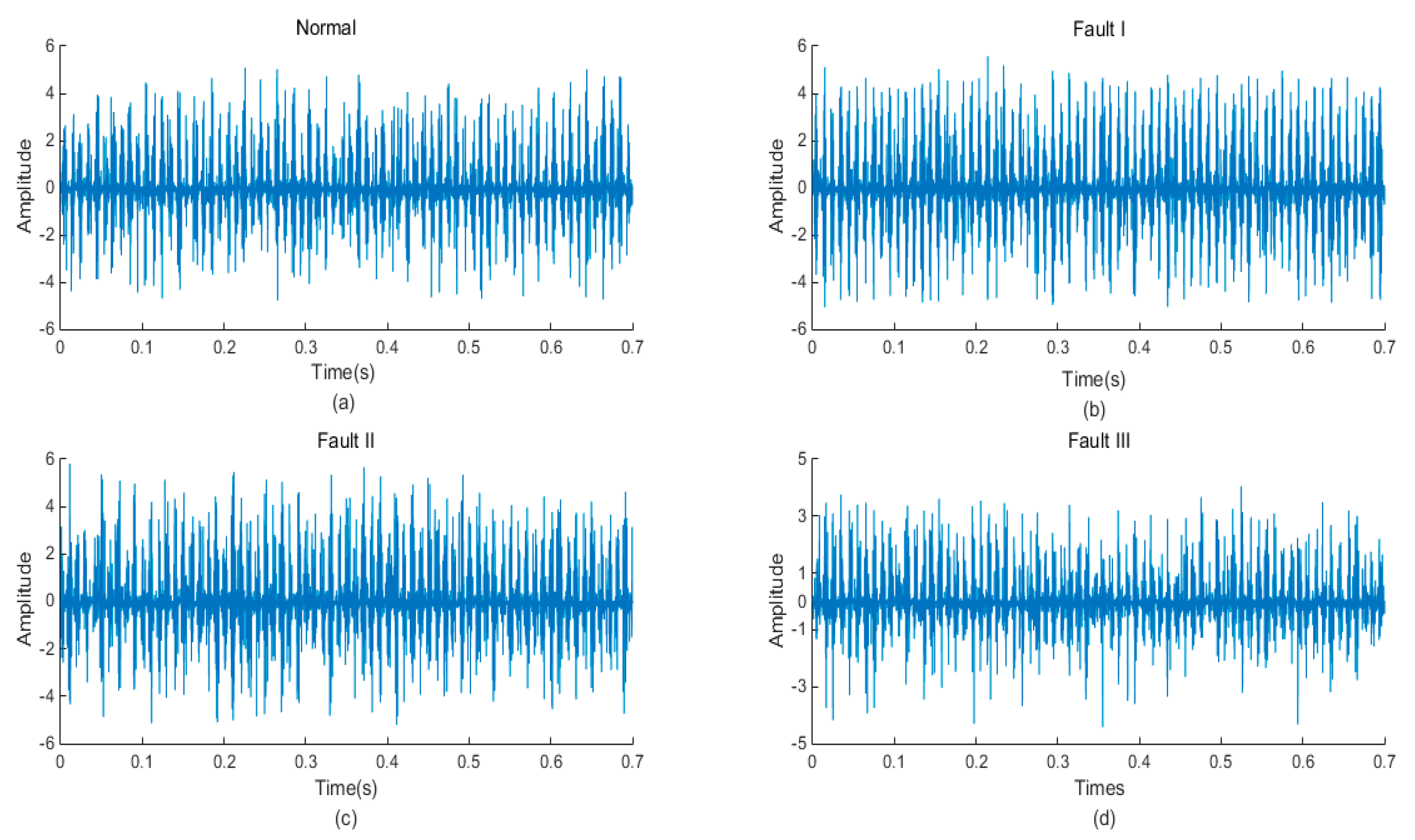
5. Experimental Results and Analysis
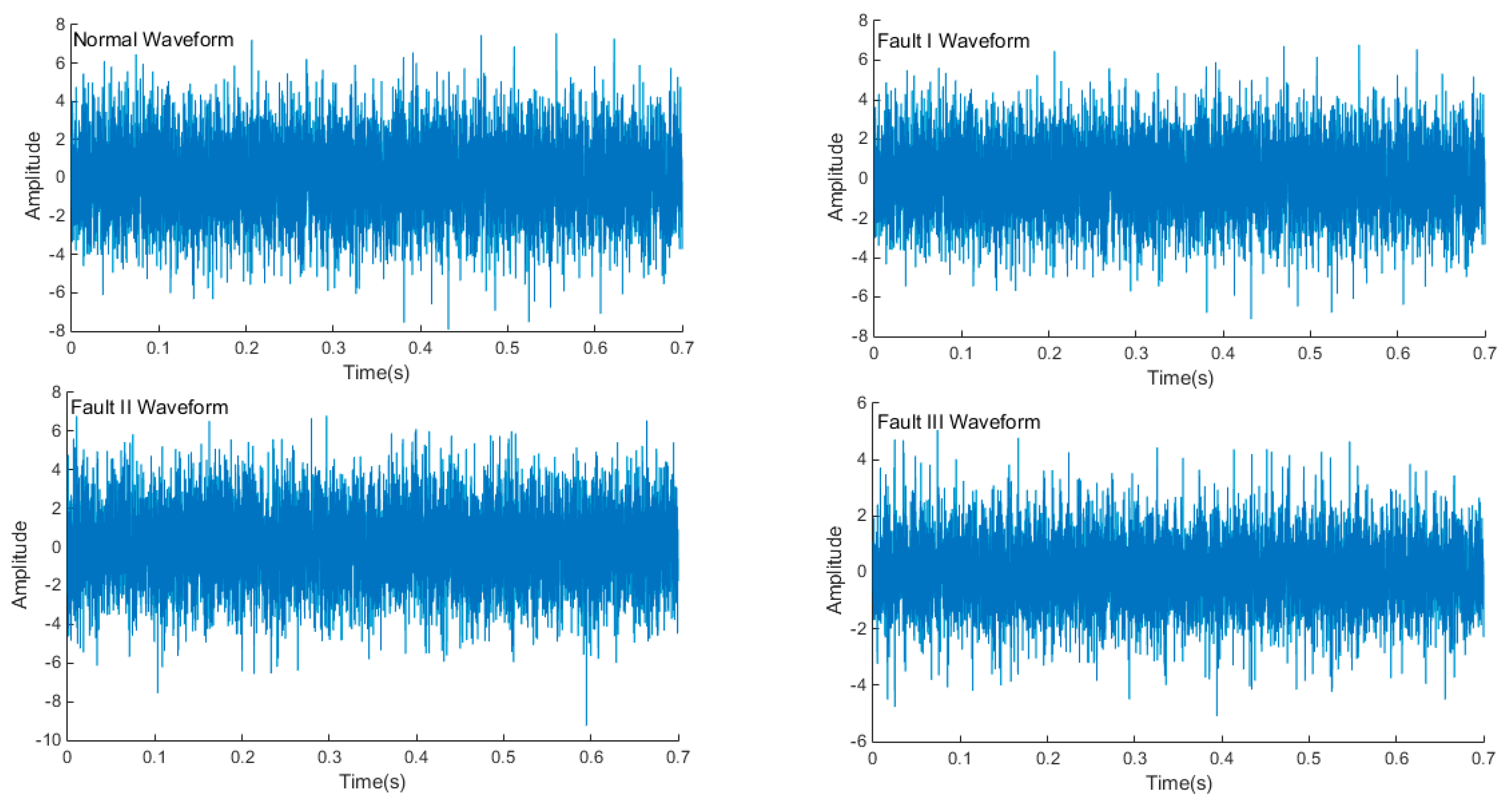
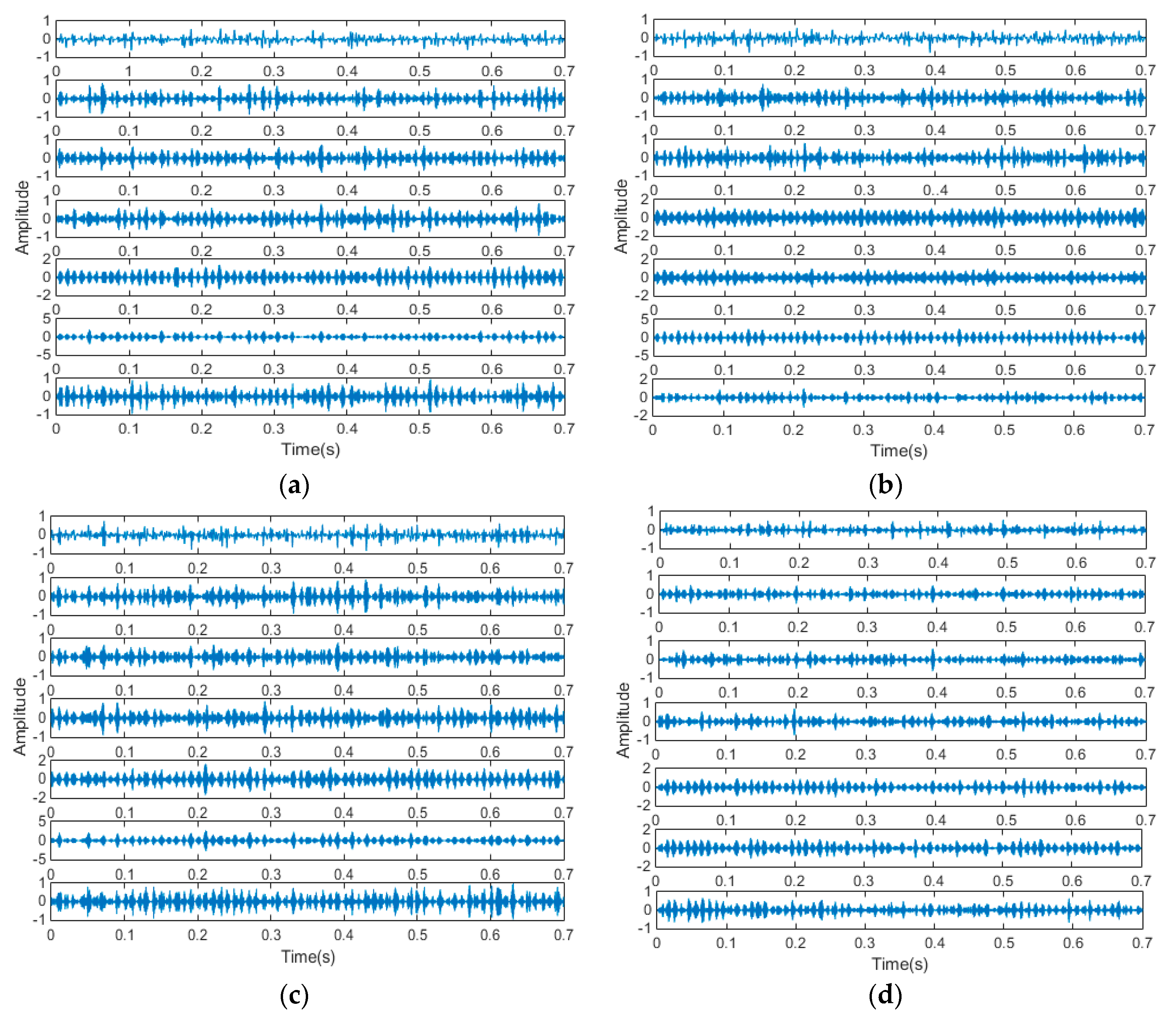
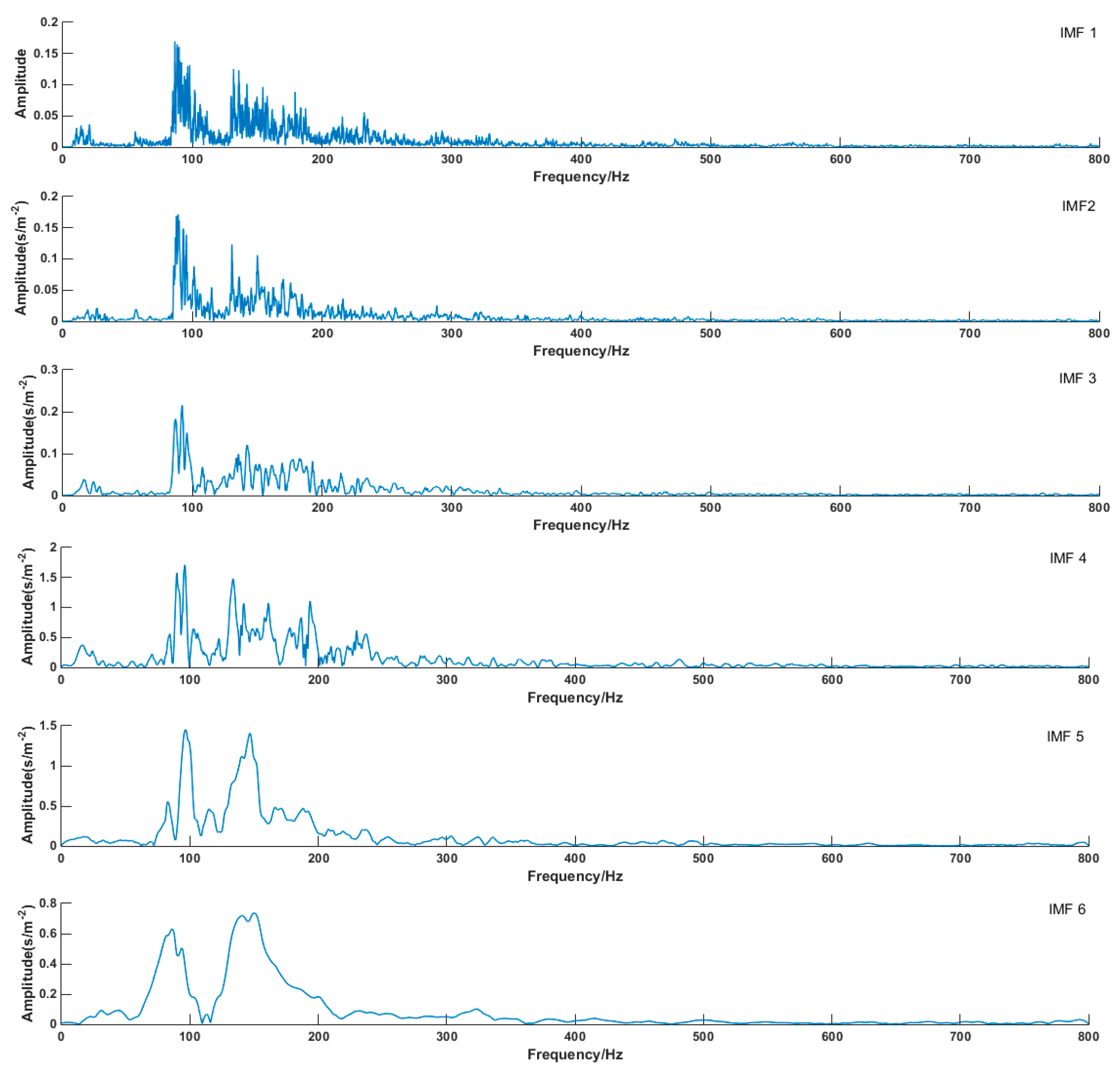
5.1. Signal Decomposition and Feature Extraction
5.2. Feature Extraction
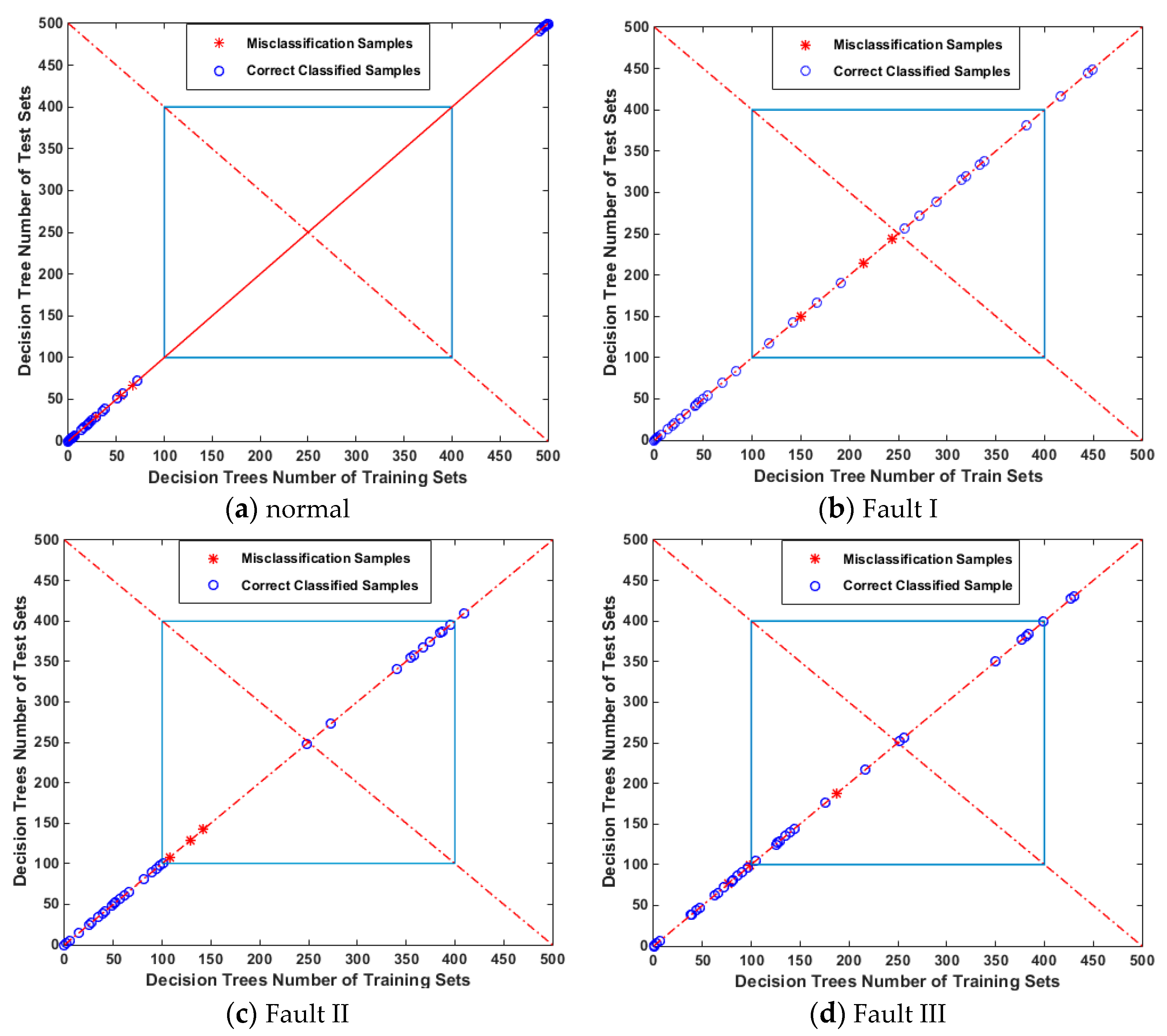
5.3. Fault Diagnosis of the DC Motor
6. Conclusions
- Compared with EMD, LMD, and EWT methods, the VMD method can better decompose the signals into a series of physically meaningful modes, and it also can solve the mode aliasing well.
- The proposed SampEn method is more superior in feature extraction. The feature curves of different types of signals obtained by the SampEn method are more dispersed than approximate entropy method, which is good for classification.
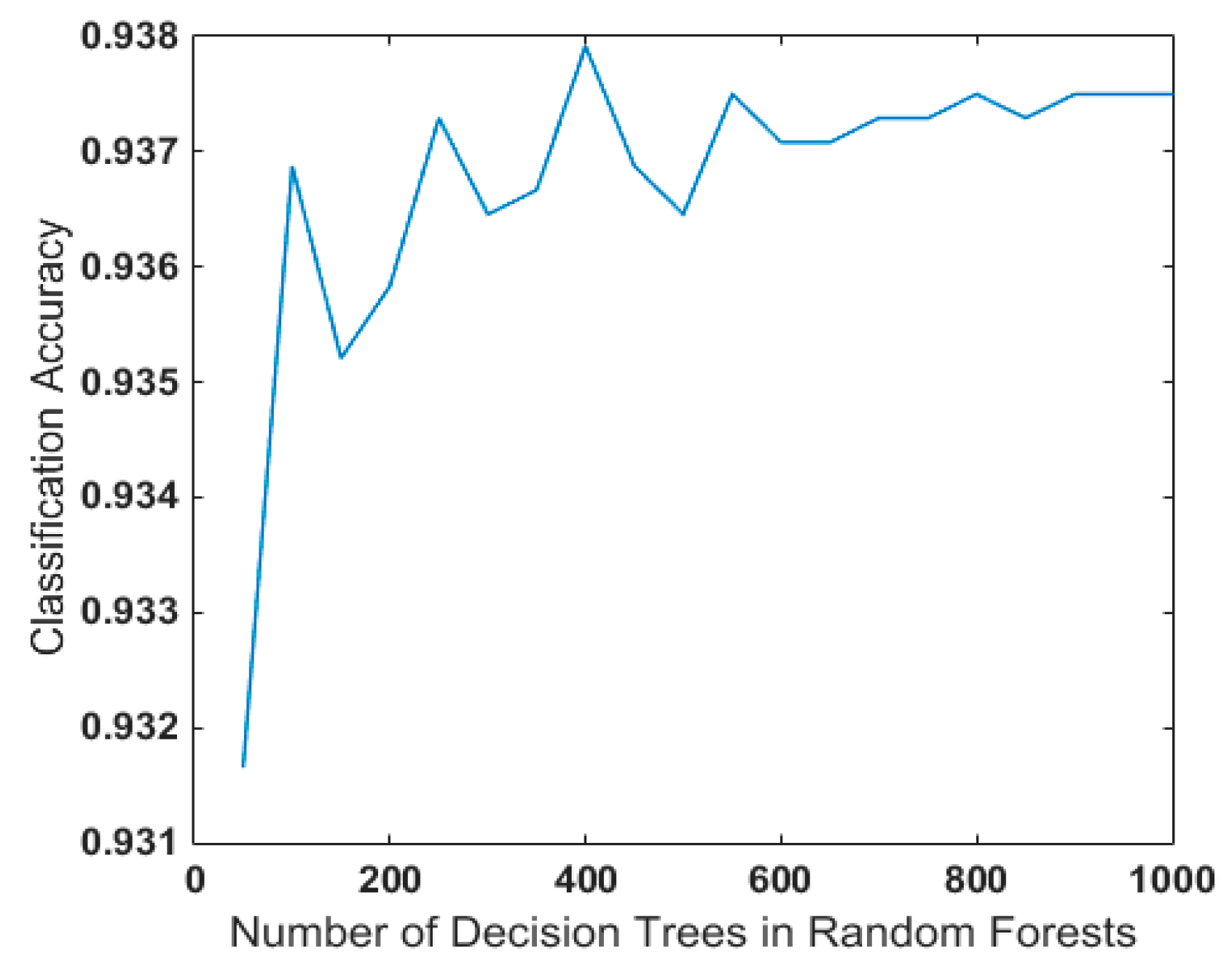
- The parameter “tree” of RF needs to be determined, which usually depends on human choice. Combined with SPRINT, the loop traversal method can effectively find the best parameter of the decision tree.
- According to the final recognition rates, the VMD-SampEn feature extraction method and the optimal RF classifier are more suitable for mechanical fault diagnosis of DC motors. The proposed RF-SPRINT method provides a new idea for mechanical feature extraction of DC motors.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Z.; Guo, W.; Hu, J.; Ma, W. A hybrid intelligent multi-fault detection method for rotating machinery based on RSGWPT, KPCA and Twin SVM. ISA Trans. 2016, 66, 249. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Grap. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Manana, M.; Arroyo, A.; Renedo, C.J.; Perez, S.; Delgado, F. Field winding fault diagnosis in DC motors during manufacturing using thermal monitoring. Appl. Therm. Eng. 2011, 31, 978–983. [Google Scholar] [CrossRef]
- Zhong, T.; Li, Y.; Wu, N.; Nie, P.; Yang, B. A study on the stationarity and Gaussianity of the background noise in land-seismic prospecting. Geophysics 2015, 80, 67–82. [Google Scholar] [CrossRef]
- Yin, J.; Wang, W.; Man, Z.; Khoo, S. Statistical modeling of gear vibration signals and its application to detecting and diagnosing gear faults. Inf. Sci. 2014, 259, 295–303. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and Localization Diagnosis of a Defective Ball Bearing Based on Vertical-Horizontal Synchronization Signal Analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8706. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Fan, X.; Fan, X.; Huang, H.Z. Rolling element bearing fault detection using an improved combination of Hilbert and wavelet transforms. J. Mech. Sci. Technol. 2009, 23, 3292–3301. [Google Scholar] [CrossRef]
- Daubechies, I. The Wavelet Transform. Time-Frequency Localisation and Signal Analysis. J. Renew. Susain. Energy 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, H.; Hui, W.; Rui, M. Application of improved EMD algorithm for the fault diagnosis of reciprocating pump valves with spring failure. In Proceedings of the 9th International Symposium on Signal Processing and Its Application, Sharjah, UAE, 12–15 February 2007. [Google Scholar]
- Hu, X.; Peng, S.; Hwang, W.L. EMD Revisited: A New Understanding of the Envelope and Resolving the Mode-Mixing Problem in AM-FM Signals. IEEE Trans. Signal Process. 2012, 60, 1075–1086. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets—Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Ling, X.; Li, Y. Application of Empirical Wavelet Transform in Fault Diagnosis of Rotary Mechanisms. J. Chin. Soc. Power Eng. 2015, 12, 975–981. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Two-Dimensional Variational Mode Decomposition. In Energy Minimization Methods in Computer Vision and Pattern Recognition; Tai, X.C., Bae, E., Chan, T.F., Lysaker, M., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Pérez-Pérez, E.J.; Mina-Antonio, J.D.; Valencia-Palomo, G. Diagnosis of Fluid Leaks in Pipelines Using Dynamic PCA. IFAC 2018, 51, 373–380. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; Bermúdez, J.R.; López-Estrada, F.R.; Puig, V.; Torres, L.; Delgado-Aguiñaga, J.A. Online leak diagnosis in pipelines using an EKF-based and steady-state mixed approach. Control Eng. Pract. 2018, 81, 55–64. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Comparative study between VMD and EMD in bearing fault diagnosis. In Proceedings of the 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014. [Google Scholar] [CrossRef]
- Luo, J. Wavelet Fractal Technology and Its Application to Aeroengine Fault Diagnoisis. J. Projectiles Rockets Missiles Guidance 2006. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L.S. Feature Extraction Based on Morlet Wavelet And Its Application For Mechanical Fault Diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Rosenstein, M.T. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Cheng, J.; Yu, D.; Yang, Y. Fault Diagnosis for Rotor System Based on EMD and Fractal Dimension. China Mech. Eng. 2005, 6, 1088–1091. [Google Scholar]
- Goldberger, A.L. Non-linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef]
- Li, Y.; Shao, W.; Pu, Y.; Wang, H.; Kui-Long, Z.; Wei-Guo, Z.; Yu-Long, T. Application of Lyapunov Exponents to Fault Diagnosis of Rolling Bearing. Noise Vib. Control 2007, 5, 104–105. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Basaran, C.; Yan, Y. A Thermodynamic Framework for Damage Mechanics of Solder Joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. Lond. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Leonid, S.; Sergei, S. Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [PubMed]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Zhang, C., Ma, Y.Q., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Felsenstein, J. Confidence Limits on Phylogenies: An Approach Using the Bootstrap. Evolution 1985, 39, 783–791. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction on decision tree. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Tripoliti, E.E.; Fotiadis, D.I.; Manis, G. Dynamic construction of Random Forests: Evaluation using biomedical engineering problems. In Proceedings of the 10th IEEE International Conference on Information Technology and Applications in Biomedicine, Corfu, Greece, 3–5 November 2010. [Google Scholar]
- Sun, J.; Wang, C.; Sun, J.; Wang, L. Analog circuit fault diagnosis based on PCA and LVQ. J. Circuits Syst. 2013, 8. [Google Scholar] [CrossRef]
- He, X.; Wang, H.; Lu, J.; Jiang, W. Analog circuit fault diagnosis method based on preferred wavelet packet and ELM. Chin. J. Sci. Instrum. 2013, 34, 2614–2619. [Google Scholar]
- Yan, X.; Jia, M.; Xiang, L. Compound fault diagnosis of rotating machinery based on OVMD and a 1.5-dimension envelope spectrum. Meas. Sci. Technol. 2016, 27, 075002. [Google Scholar] [CrossRef]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Peng, Z.K.; Tse, P.W.; Chu, F.L. A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Fault Diagnosis Method for Rolling Bearing’s Weak Fault Based on Minimum Entropy Deconvolution and Sparse Decomposition. J. Mech. Eng. 2013, 49, 88–94. [Google Scholar] [CrossRef]
- Pincus, S.M. Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 2010, 954, 245–267. [Google Scholar] [CrossRef]
- Alcaraz, R.; Rieta, J.J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal Process. Control 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Sathyadevan, S.; Nair, R.R. Comparative Analysis of Decision Tree Algorithms: ID3, C4.5 and Random Forest. In Computational Intelligence in Data Mining; Jain, L., Behera, H., Mandal, J., Mohapatra, D., Eds.; Springer: New Delhi, India, 2015; pp. 549–562. [Google Scholar]
- Luo, Z.K.; Sun, H.Y.; Wang, D. An Improved SPRINT Algorithm. Adv. Mater. Res. 2012, 532–533, 1685–1690. [Google Scholar] [CrossRef]
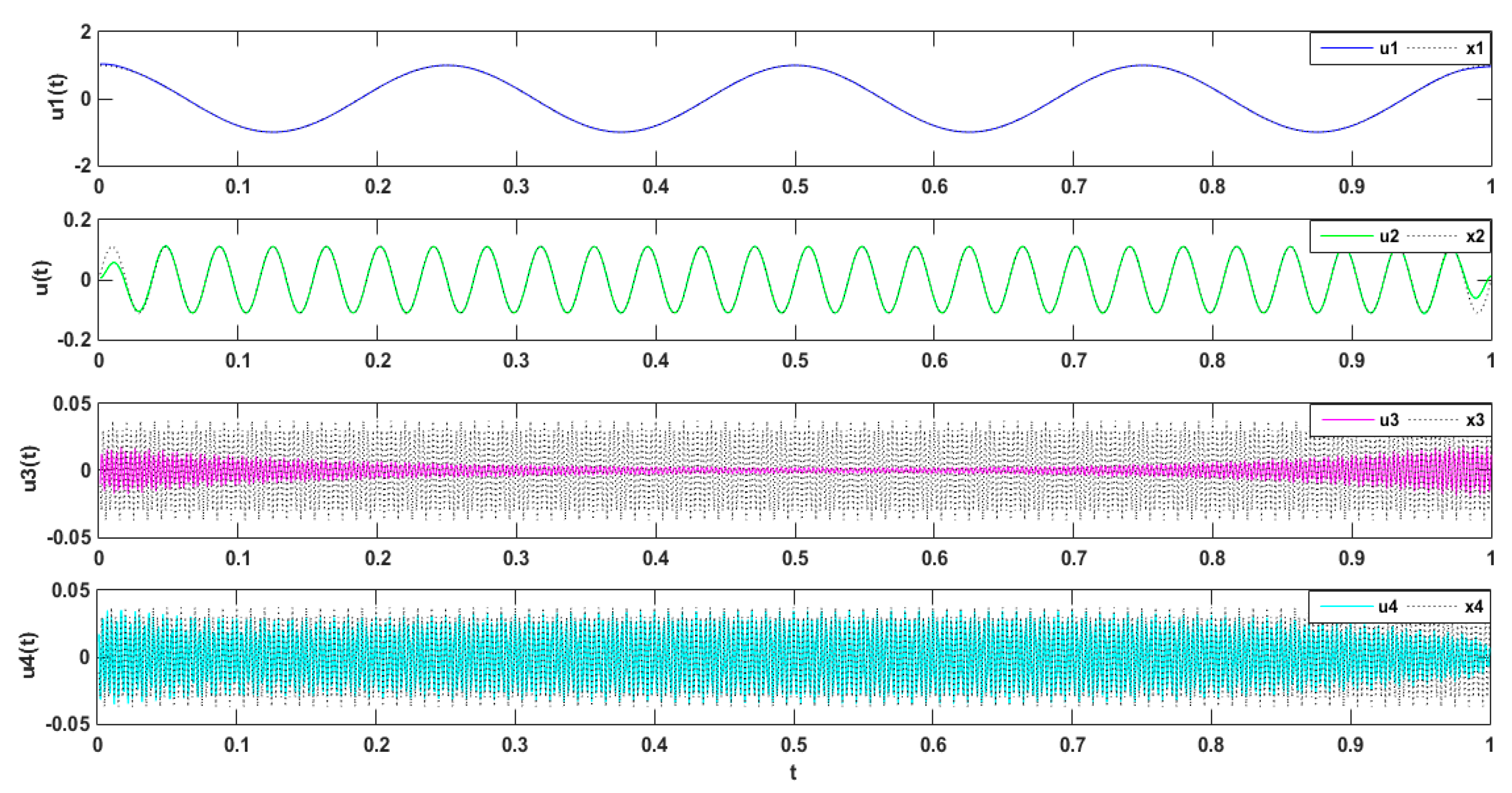
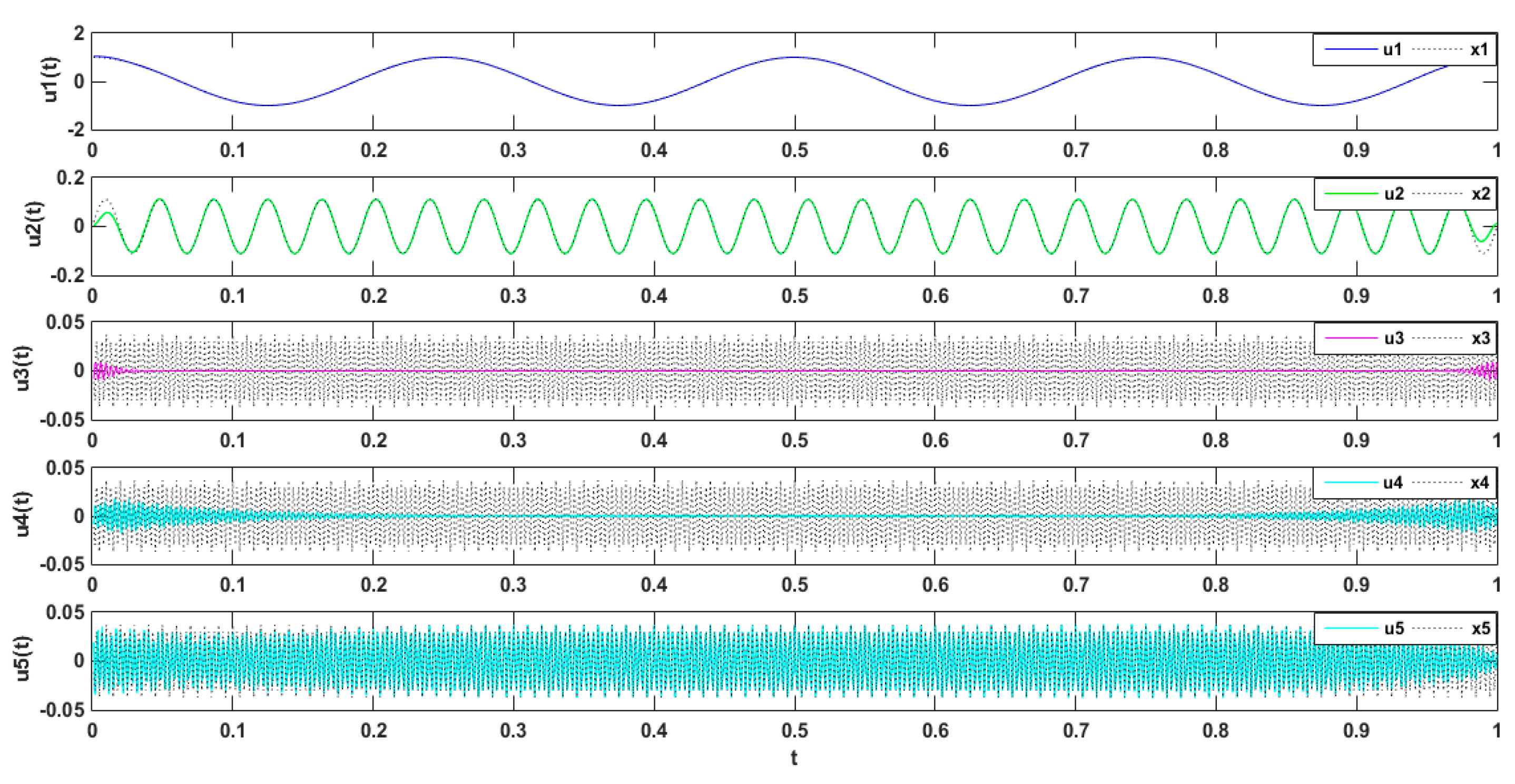
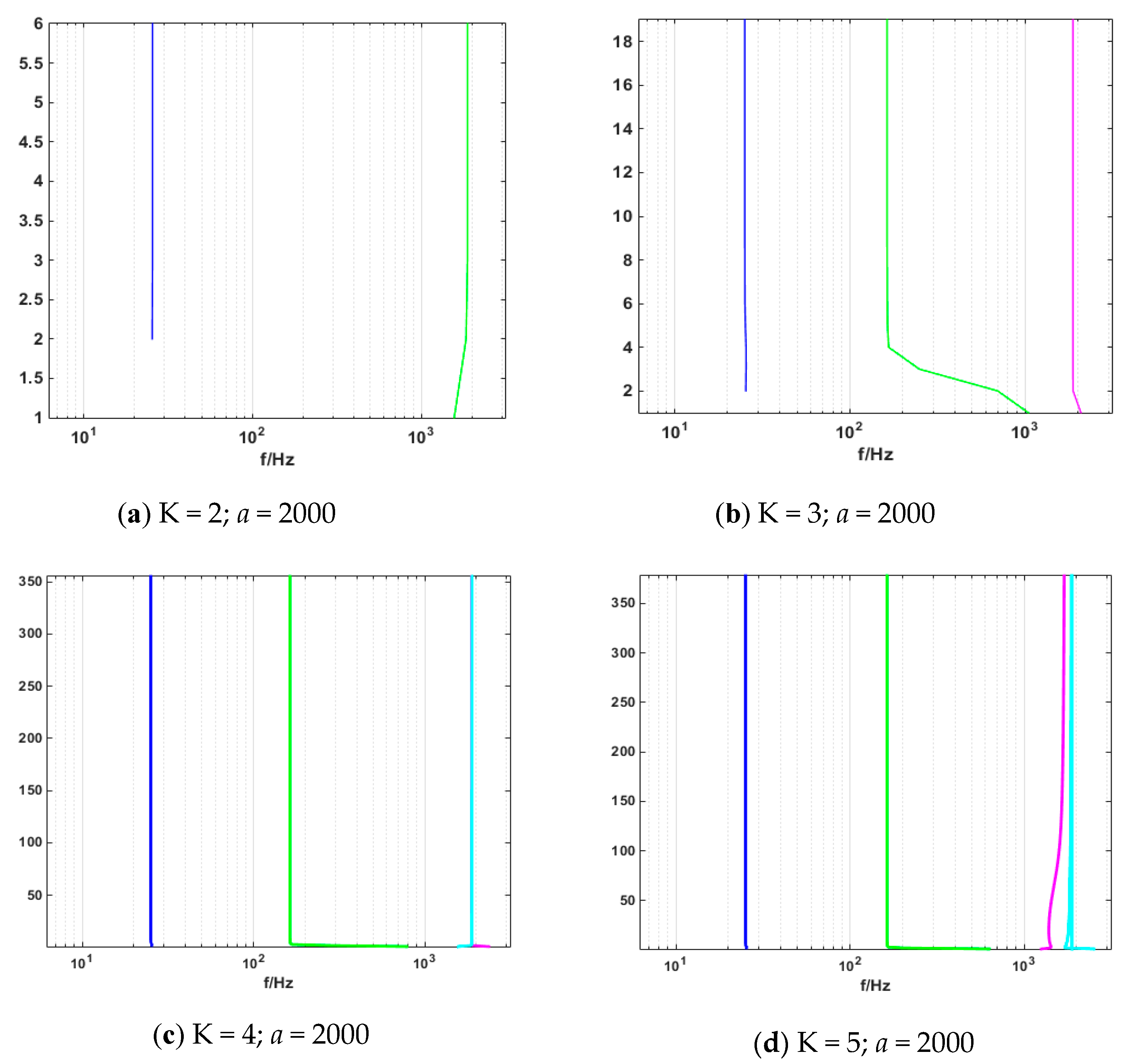



| Mode Value | Center Frequency | ||||
|---|---|---|---|---|---|
| U1 | U2 | U3 | U4 | U5 | |
| K = 2 | 25.76 | 1884.32 | |||
| K = 3 | 25.13 | 163.36 | 1884.96 | ||
| K = 4 | 25.13 | 163.36 | 1884.96 | 1884.96 | |
| K = 5 | 25.13 | 163.36 | 1763.06 | 1874.27 | 1885.58 |
| Model Value | Center Frequency | |||||||
|---|---|---|---|---|---|---|---|---|
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | |
| K = 3 | 95.86 | 456.25 | 554.80 | |||||
| K = 4 | 89.69 | 200.74 | 462.75 | 554.80 | ||||
| K = 5 | 87.17 | 198.56 | 372.27 | 464.10 | 554.96 | |||
| K = 6 | 83.56 | 117.50 | 283.25 | 384.21 | 463.85 | 645.28 | ||
| K = 7 | 83.56 | 117.49 | 283.21 | 382.64 | 464.32 | 553.70 | 645.28 | |
| K = 8 | 21.67 | 98.64 | 183.31 | 285.25 | 382.27 | 464.32 | 553.70 | 554.88 |
| Model Value | Correlation Coefficient | |||||||
|---|---|---|---|---|---|---|---|---|
| K = 3 | 0.3366 | 0.5512 | 0.5930 | |||||
| K = 4 | 0.3029 | 0.3213 | 0.5485 | 0.5916 | ||||
| K = 5 | 0.2945 | 0.3055 | 0.3417 | 0.5324 | 0.5876 | |||
| K = 6 | 0.2928 | 0.3029 | 0.3355 | 0.5258 | 0.5669 | 0.3570 | ||
| K = 7 | 0.2824 | 0.2825 | 0.2844 | 0.3191 | 0.5202 | 0.5650 | 0.3553 | |
| K = 8 | 0.1996 | 0.2681 | 0.2720 | 0.2808 | 0.3176 | 0.5467 | 0.5176 | 0.3548 |
| Motor Types | Label | SampEn I | SampEn II | SampEn III | SampEn IV | SampEn V | SampEn VI | SampEn VII | Desired Output |
|---|---|---|---|---|---|---|---|---|---|
| Normal | 1 | 0.3241 | 0.4299 | 0.3757 | 0.2647 | 0.1455 | 0.2659 | 0.4664 | 1 |
| 0.3091 | 0.4368 | 0.3818 | 0.2506 | 0.1338 | 0.2599 | 0.4445 | 1 | ||
| 0.2914 | 0.4567 | 0.3811 | 0.2742 | 0.1630 | 0.2888 | 0.4837 | 1 | ||
| Fault I | 2 | 0.2239 | 0.5127 | 0.2319 | 0.1434 | 0.1818 | -0.5116 | 0.3566 | 2 |
| 0.2854 | 0.2787 | 0.2934 | 0.2787 | 0.2018 | 0.8924 | 0.4550 | 2 | ||
| 0.3838 | 0.4191 | 0.4041 | 0.3033 | 0.1318 | -0.8236 | 0.6149 | 2 | ||
| Fault II | 3 | 0.3084 | 0.3857 | 0.5754 | 0.2425 | 0.7845 | 0.3938 | 0.6215 | 3 |
| 0.0684 | 0.5457 | 0.5754 | 0.2625 | 1.5645 | 0.4307 | 0.2915 | 3 | ||
| 0.2384 | 0.5557 | 0.5130 | 0.2225 | 1.4085 | 0.4553 | 0.5515 | 3 | ||
| Fault III | 4 | 0.2749 | 0.6835 | 0.1855 | 0.1931 | 0.1958 | 0.3765 | 0.5568 | 4 |
| 0.4348 | 0.3811 | 0.1955 | 0.5119 | 0.2458 | 0.3519 | 0.4968 | 4 | ||
| 0.4840 | 0.5323 | 0.1755 | 0.2435 | 0.3758 | 0.3273 | 0.4568 | 4 |
| Classifier | Experimental Parameters | Recognition Rate | ||||
|---|---|---|---|---|---|---|
| Normal | Fault I | Fault II | Fault III | All Test Samples | ||
| LQV | Hidden Layer = 5; | 75% | 75% | 80% | 80% | 77.5% |
| Hidden Layer = 20; | 85% | 90% | 90% | 90% | 88.75% | |
| Hidden Layer = 40 | 80% | 85% | 85% | 85% | 83.75% | |
| ELM | Activation Function (Sin); | 80% | 80% | 85% | 85% | 82.5% |
| Activation Function (Sig); | 85% | 90% | 90% | 90% | 88.75% | |
| Activation Function (Hardlim) | 80% | 85% | 85% | 85% | 84.5% | |
| Decision Tree | Decision Tree (100); | 85% | 80% | 80% | 85% | 83.75% |
| Decision Tree (500) | 95% | 90% | 85% | 85% | 88.75% | |
| Decision Tree (800) | 90% | 85% | 80% | 80% | 83.5% | |
| Random Forest | Decision Tree (100); | 100% | 90% | 90% | 90% | 92.5% |
| Decision Tree (500) | 100% | 95% | 90% | 90% | 93.75% | |
| Decision Tree (800) | 95% | 90% | 90% | 90% | 91.25% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Liu, M.; Qin, H.; Li, B. Mechanical Fault Diagnosis of a DC Motor Utilizing United Variational Mode Decomposition, SampEn, and Random Forest-SPRINT Algorithm Classifiers. Entropy 2019, 21, 470. https://doi.org/10.3390/e21050470
Guo Z, Liu M, Qin H, Li B. Mechanical Fault Diagnosis of a DC Motor Utilizing United Variational Mode Decomposition, SampEn, and Random Forest-SPRINT Algorithm Classifiers. Entropy. 2019; 21(5):470. https://doi.org/10.3390/e21050470
Chicago/Turabian StyleGuo, Zijian, Mingliang Liu, Huabin Qin, and Bing Li. 2019. "Mechanical Fault Diagnosis of a DC Motor Utilizing United Variational Mode Decomposition, SampEn, and Random Forest-SPRINT Algorithm Classifiers" Entropy 21, no. 5: 470. https://doi.org/10.3390/e21050470
APA StyleGuo, Z., Liu, M., Qin, H., & Li, B. (2019). Mechanical Fault Diagnosis of a DC Motor Utilizing United Variational Mode Decomposition, SampEn, and Random Forest-SPRINT Algorithm Classifiers. Entropy, 21(5), 470. https://doi.org/10.3390/e21050470




