Symmetry and Shannon Measure of Ordering: Paradoxes of Voronoi Tessellation
Abstract
:1. Introduction
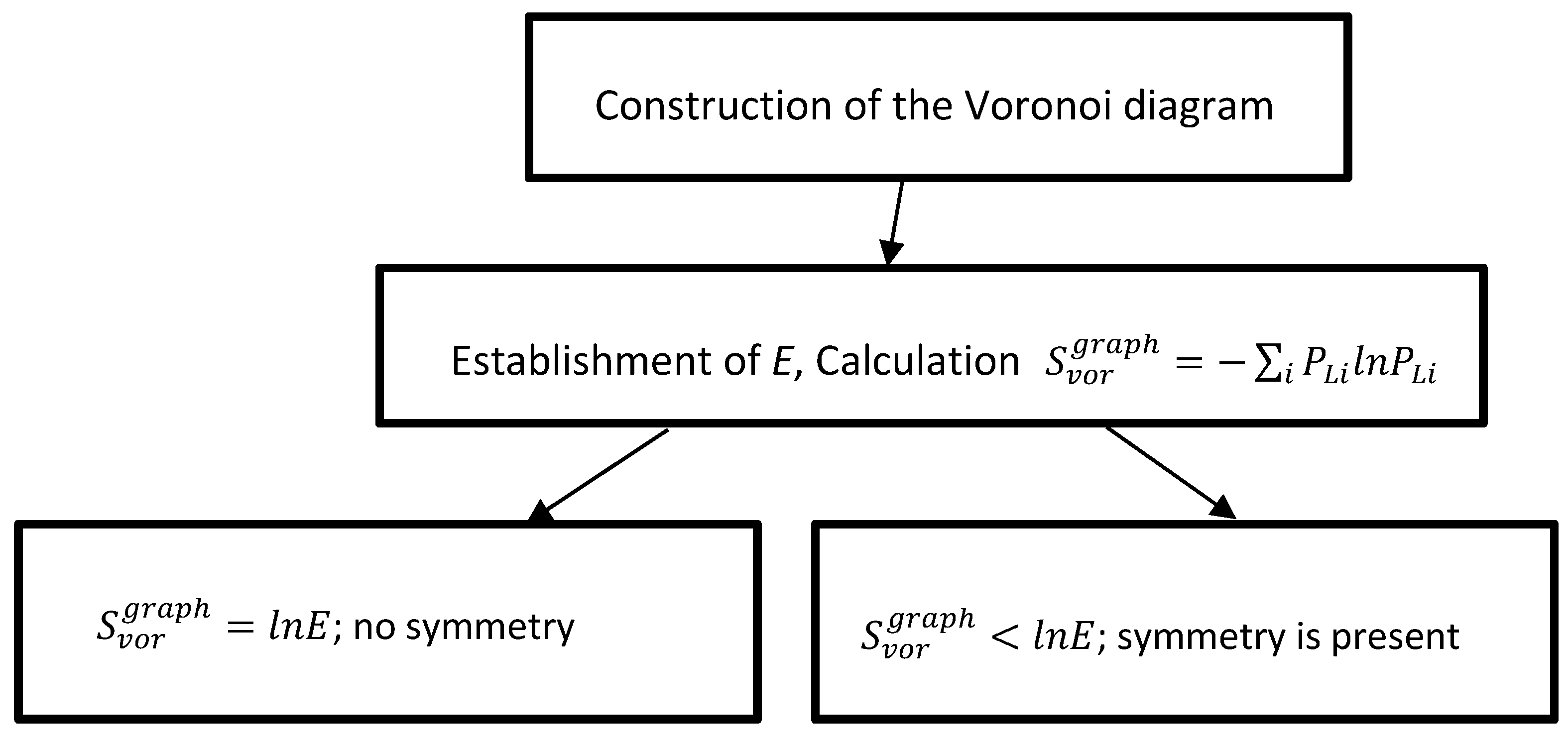
2. Results and Discussion
2.1. 2D Patterns Demonstrating Symmetry and Their Voronoi Tessellations
2.2. Revealing Symmetry in 2D Patterns with Voronoi Diagrams
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Van Fraassen, B.C. Laws and Symmetry; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Rosen, J. Symmetry in Science: An Introduction to the General Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Hall, B.C. Quantum Theory for Mathematicians. Graduate Texts in Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Chatterjee, S.K. Crystallography and the World of Symmetry; Springer: Berlin, Germany, 2008. [Google Scholar]
- El-Batanouny, M.; Wooten, F. Symmetry and Condensed Matter Physics–A Computational Approach; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Darvas, G. Symmetry: Cultural-historical and Ontological Aspects of Science-Arts Relations; Birkhauser: Basel, Switzerland, 2007. [Google Scholar]
- Hargittai, I.; Pickover, C.A. Spiral Symmetry; World Scientific: Singapore, 1992. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ben Naim, A. Shannon’s Measure of information and Boltzmann’s H-Theorem. Entropy 2017, 19, 48. [Google Scholar] [CrossRef]
- Ben-Naim, A. Information Theory; World Scientific: Singapore, 2017. [Google Scholar]
- Ben-Naim, A. A Farewell to Entropy: Statistical Thermodynamics Based on Information; World Scientific: Singapore, 2008. [Google Scholar]
- Ben Naim, A. An Informational Theoretical Approach to the Entropy of Liquids and Solutions. Entropy 2018, 20, 514. [Google Scholar] [CrossRef]
- Ben-Naim, A. Entropy, the Truth the Whole Truth and Nothing but the Truth; World Scientific: Singapore, 2016. [Google Scholar]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les paralléloèdres primitifs. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar]
- Liebling, T.M.; Pournin, L. Voronoi diagrams and Delaunay triangulations: Ubiquitous Siamese Twins. Doc. Math. 2012, ISMP, 419–431. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.; Aktaev, N.; Dombrovsky, L.; Nosonovsky, M. Characterization of self-assembled 2D patterns with Voronoi Entropy. Entropy 2018, 20, 956. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Frenkel, M.; Bormashenko, E.; Nosonovsky, M. Small levitating ordered droplet clusters: Stability, symmetry, and Voronoi Entropy. J. Phys. Chem. Lett. 2017, 8, 5599–5602. [Google Scholar] [CrossRef] [PubMed]
- Weaire, D.; Rivier, N. Soap, cells and statistics—random patterns in two dimensions. Contemporary Phys. 1984, 25, 59–99. [Google Scholar] [CrossRef]
- Descartes, R. Principia Philosophiae; Ludovicus Elzevirius: Amsterdam, The Netherlands, 1644; ISBN 978-90-277-1754-2. [Google Scholar]
- Bormashenko, E.; Frenkel, M.; Legchenkova, I. Is the Voronoi Entropy a True Entropy? Comments on “Entropy, Shannon’s Measure of Information and Boltzmann’s H-Theorem”, Entropy 2017, 19, 48. Entropy 2019, 21, 251. [Google Scholar] [CrossRef]
- Limaye, A.V.; Narhe, R.D.; Dhote, A.M.; Ogale, S.B. Evidence for convective effects in breath figure formation on volatile fluid surfaces. Phys. Rev. Lett. 1996, 76, 3762–3765. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.P.; Blunt, M.O.; Pauliac-Vaujour, E.; Stannard, A.; Moriarty, P.; Vancea, I.; Thiele, U. Controlling pattern formation in nanoparticle assemblies via directed solvent dewetting. Phys. Rev. Lett. 2007, 99, 116103. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.X.; Thorpe, S.M.; Windle, A.H. The geometrical properties of irregular two-dimensional Voronoi tessellations. Philos. Mag. A 2001, 81, 2765–2783. [Google Scholar] [CrossRef]
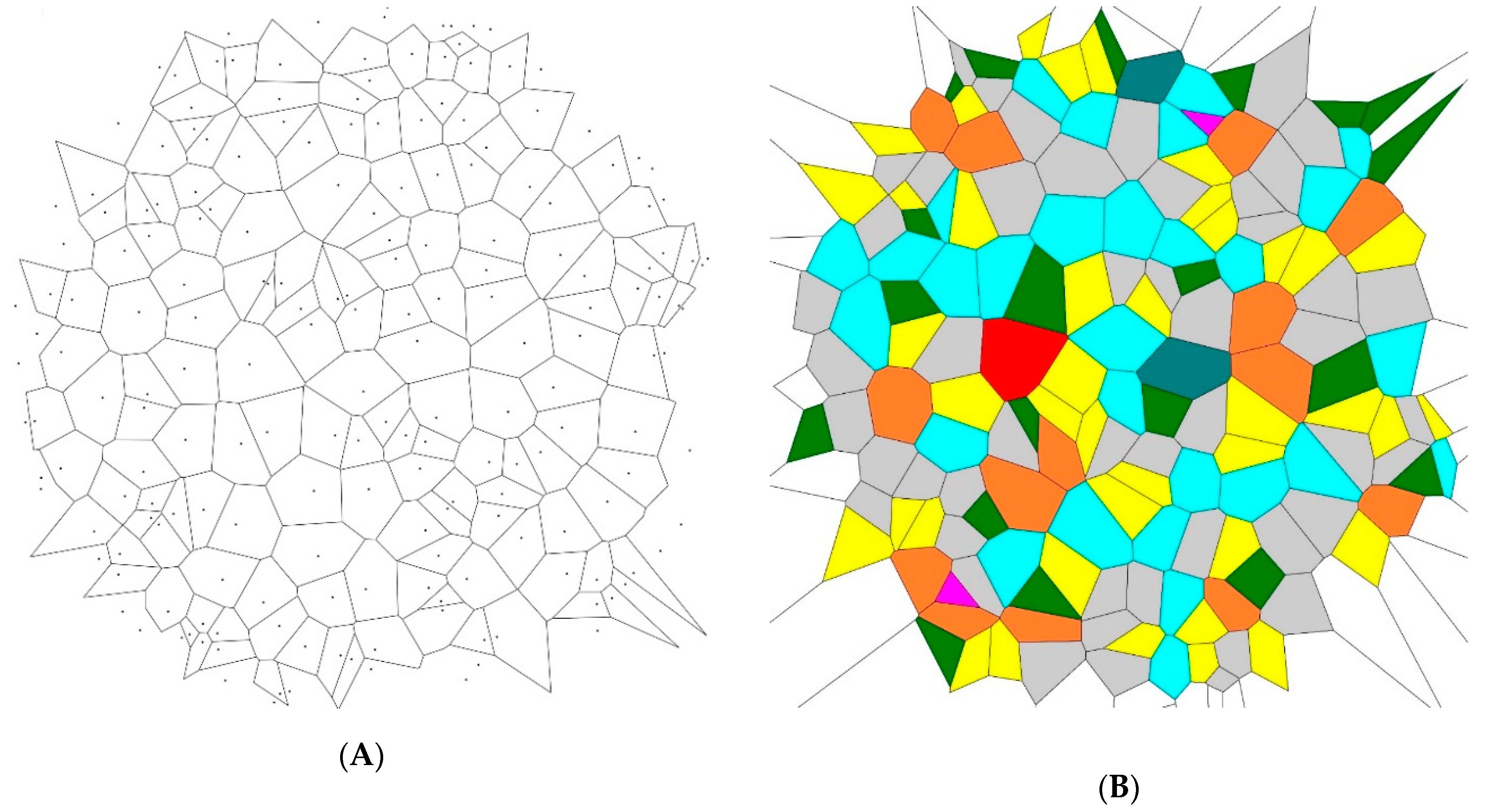
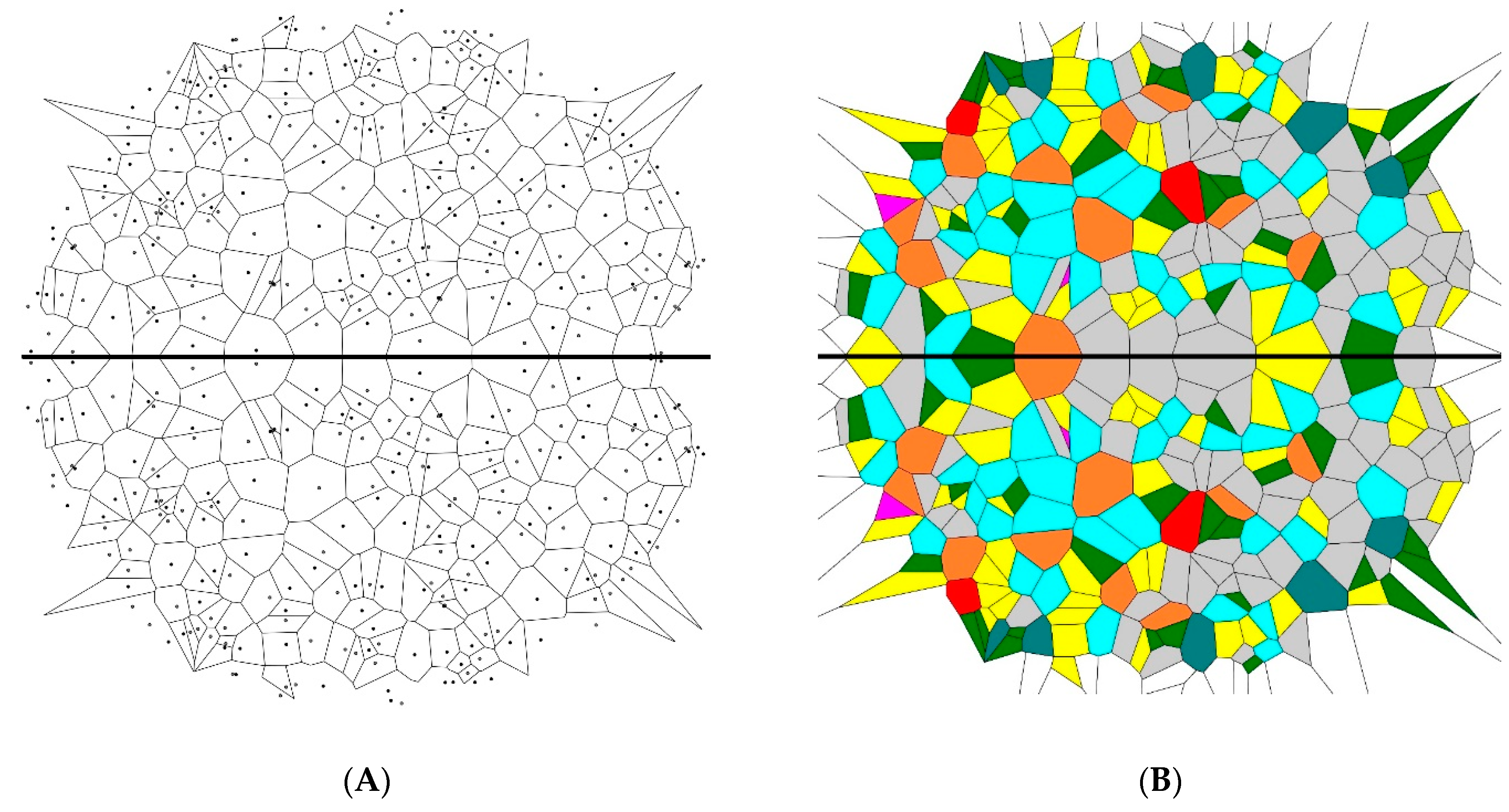

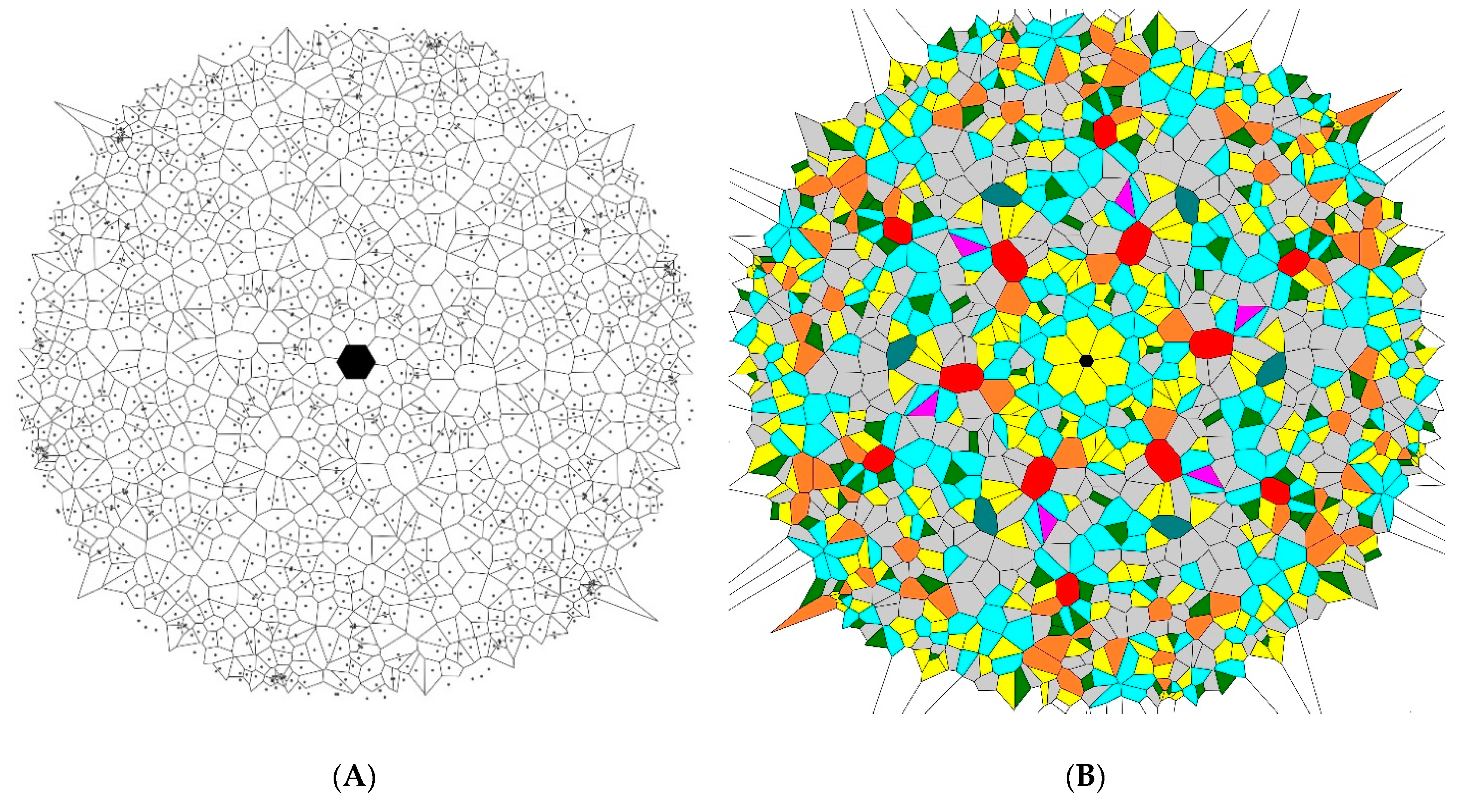

| Sample | Voronoi Entropy | Standard Deviation | Random Sample | Voronoi Entropy | Standard Deviation |
|---|---|---|---|---|---|
| Initial set of points (200 random points) | 1.66 | ±0.05 | 200 random points set | 1.66 | ±0.05 |
| Mirror reflection (400 points) | 1.64 | ±0.05 | 400 random points set | 1.66 | ±0.04 |
| Point reflection (400 points) | 1.66 | ±0.06 | |||
| Six-fold rotational symmetry (1200 points) | 1.65 | ±0.07 | 1200 random points set | 1.68 | ±0.02 |
| Initial set of points (1000 random points) | 1.68 | ±0.02 | 1000 random points set | 1.68 | ±0.02 |
| Mirror reflection (2000 points) | 1.68 | ±0.01 | 2000 random points set | 1.67 | ±0.01 |
| Point reflection (2000 points) | 1.67 | ±0.02 | |||
| Six-fold rotational symmetry (6000 points) | 1.67 | ±0.02 | 6000 random points set | 1.68 | ±0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Symmetry and Shannon Measure of Ordering: Paradoxes of Voronoi Tessellation. Entropy 2019, 21, 452. https://doi.org/10.3390/e21050452
Bormashenko E, Legchenkova I, Frenkel M. Symmetry and Shannon Measure of Ordering: Paradoxes of Voronoi Tessellation. Entropy. 2019; 21(5):452. https://doi.org/10.3390/e21050452
Chicago/Turabian StyleBormashenko, Edward, Irina Legchenkova, and Mark Frenkel. 2019. "Symmetry and Shannon Measure of Ordering: Paradoxes of Voronoi Tessellation" Entropy 21, no. 5: 452. https://doi.org/10.3390/e21050452
APA StyleBormashenko, E., Legchenkova, I., & Frenkel, M. (2019). Symmetry and Shannon Measure of Ordering: Paradoxes of Voronoi Tessellation. Entropy, 21(5), 452. https://doi.org/10.3390/e21050452







