On the Statistical Properties of Multiscale Permutation Entropy: Characterization of the Estimator’s Variance
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background
2.1.1. Permutation Entropy
2.1.2. Multiscale Permutation Entropy
2.2. Variance of MPE Statistic
2.3. MPE Cramér–Rao Lower Bound
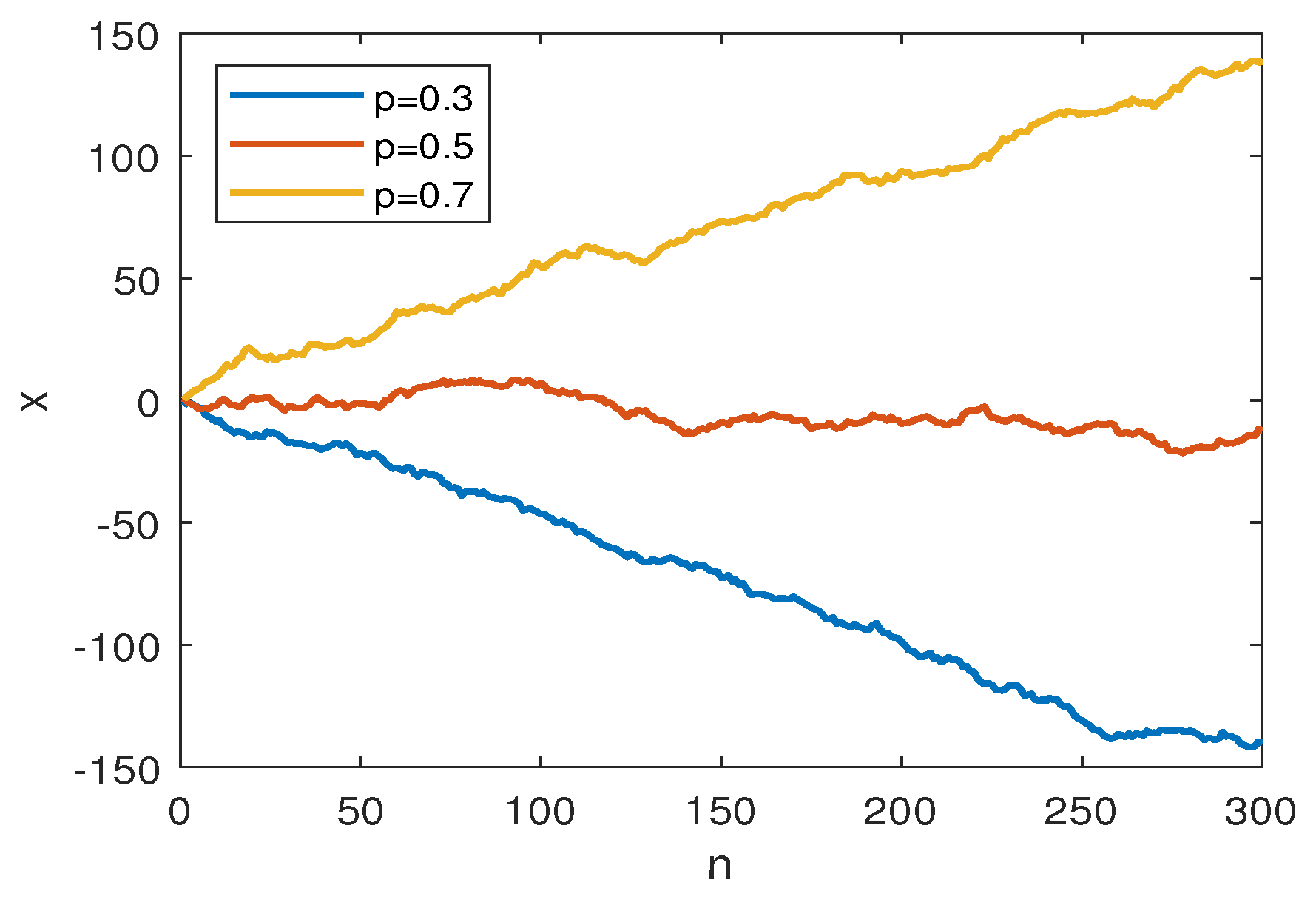
2.4. Simulations
3. Results and Discussion
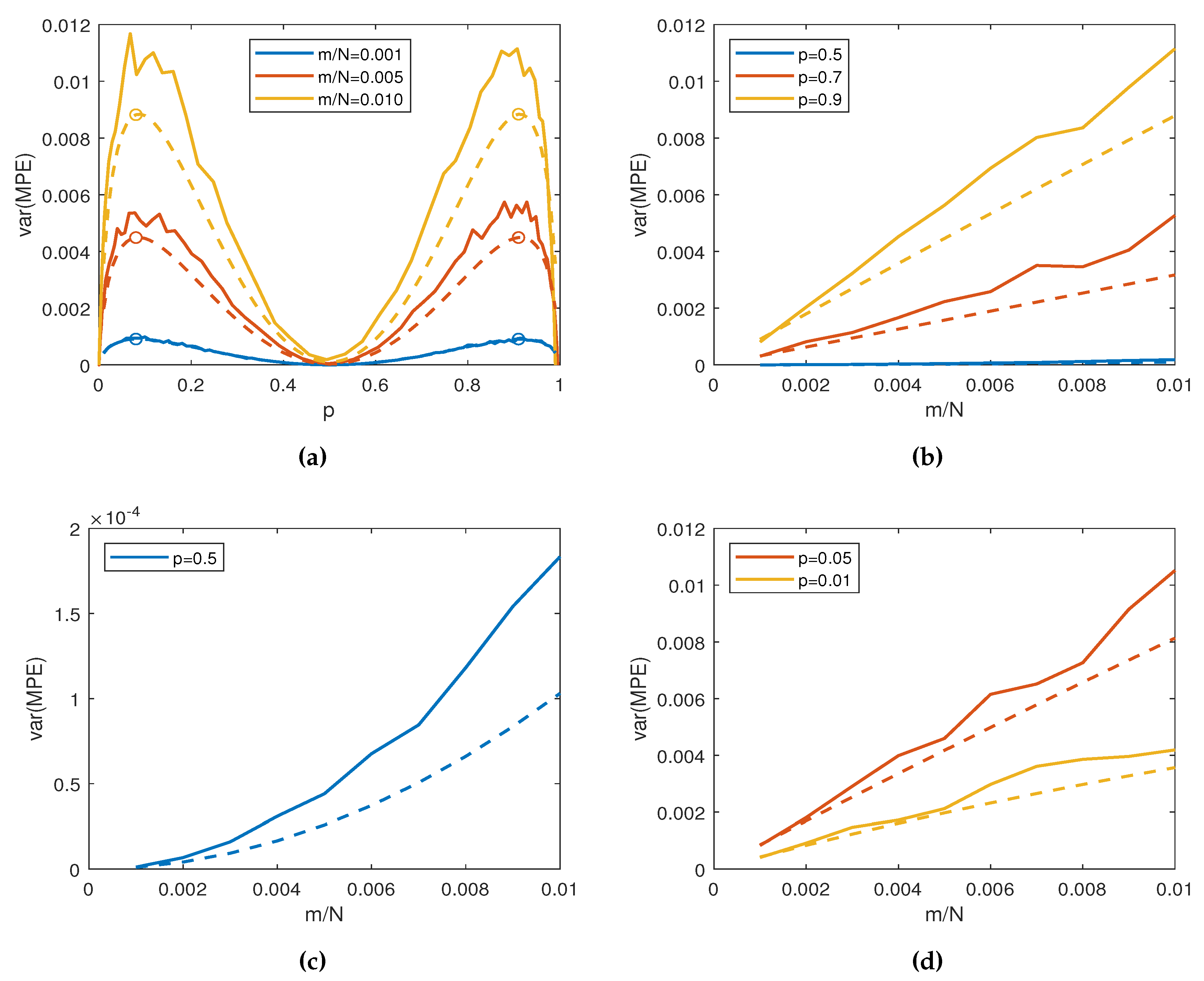
3.1. Results
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PE | Permutation Entropy |
| MSE | Multiscale Entropy |
| MPE | Multiscale Permutation Entropy |
| CRLB | Cramér–Rao Lower Bound |
Appendix A. Multinomial Moment Matrices
Appendix B. Cramér–Rao Lower Bound of MPE
References
- Shannon, C.E. A Mathematical Theory of Communication. SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Peng, C.K.; Lipsitz, L.A. What is physiologic complexity and how does it change with aging and disease? Neurobiol. Aging 2002, 23, 23–26. [Google Scholar] [CrossRef]
- Cashaback, J.G.A.; Cluff, T.; Potvin, J.R. Muscle fatigue and contraction intensity modulates the complexity of surface electromyography. J. Electromyogr. Kinesiol. 2013, 23, 78–83. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chen, P.; Luo, X.; Wu, M.; Liao, L.; Yang, S.; Rangayyan, R.M. Measuring signal fluctuations in gait rhythm time series of patients with Parkinson’s disease using entropy parameters. Biomed. Signal Process. Control 2017, 31, 265–271. [Google Scholar] [CrossRef]
- Aquino, A.L.L.; Ramos, H.S.; Frery, A.C.; Viana, L.P.; Cavalcante, T.S.G.; Rosso, O.A. Characterization of electric load with Information Theory quantifiers. Physica A 2017, 465, 277–284. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Aziz, W.; Arif, M. Multiscale Permutation Entropy of Physiological Time Series. In Proceedings of the 2005 Pakistan Section Multitopic Conference, Karachi, Pakistan, 24–25 December 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Wu, C.W.; Wu, S.D. Refined Composite Multiscale Permutation Entropy to Overcome Multiscale Permutation Entropy Length Dependence. IEEE Signal Process. Lett. 2015, 22, 2364–2367. [Google Scholar] [CrossRef]
- Bandt, C.; Shiha, F. Order Patterns in Time Series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Permutation entropy of fractional Brownian motion and fractional Gaussian noise. Phys. Lett. A 2008, 372, 4768–4774. [Google Scholar] [CrossRef]
- Little, D.J.; Kane, D.M. Permutation entropy of finite-length white-noise time series. Phys. Rev. E 2016, 94, 022118. [Google Scholar] [CrossRef] [PubMed]
- Dávalos, A.; Jabloun, M.; Ravier, P.; Buttelli, O. Theoretical Study of Multiscale Permutation Entropy on Finite-Length Fractional Gaussian Noise. In Proceedings of the 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 1092–1096. [Google Scholar]
- Friedlander, B.; Francos, J.M. Estimation of Amplitude and Phase Parameters of Multicomponent Signals. IEEE Trans. Signal Process. 1995, 43, 917–926. [Google Scholar] [CrossRef]
- Miller, K.S. On the Inverse of the Sum of Matrices. Math. Mag. 1981, 54, 67–72. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dávalos, A.; Jabloun, M.; Ravier, P.; Buttelli, O. On the Statistical Properties of Multiscale Permutation Entropy: Characterization of the Estimator’s Variance. Entropy 2019, 21, 450. https://doi.org/10.3390/e21050450
Dávalos A, Jabloun M, Ravier P, Buttelli O. On the Statistical Properties of Multiscale Permutation Entropy: Characterization of the Estimator’s Variance. Entropy. 2019; 21(5):450. https://doi.org/10.3390/e21050450
Chicago/Turabian StyleDávalos, Antonio, Meryem Jabloun, Philippe Ravier, and Olivier Buttelli. 2019. "On the Statistical Properties of Multiscale Permutation Entropy: Characterization of the Estimator’s Variance" Entropy 21, no. 5: 450. https://doi.org/10.3390/e21050450
APA StyleDávalos, A., Jabloun, M., Ravier, P., & Buttelli, O. (2019). On the Statistical Properties of Multiscale Permutation Entropy: Characterization of the Estimator’s Variance. Entropy, 21(5), 450. https://doi.org/10.3390/e21050450




