Assessing the Performance of Hierarchical Forecasting Methods on the Retail Sector
Abstract
:1. Introduction
2. Pure Forecasting Models
2.1. State Space Models
2.1.1. Estimation of State Space Models
2.1.2. Information Criteria for Model Selection
2.2. ARIMA Models
Information Criteria for Model Selection
3. Hierarchical Forecasting
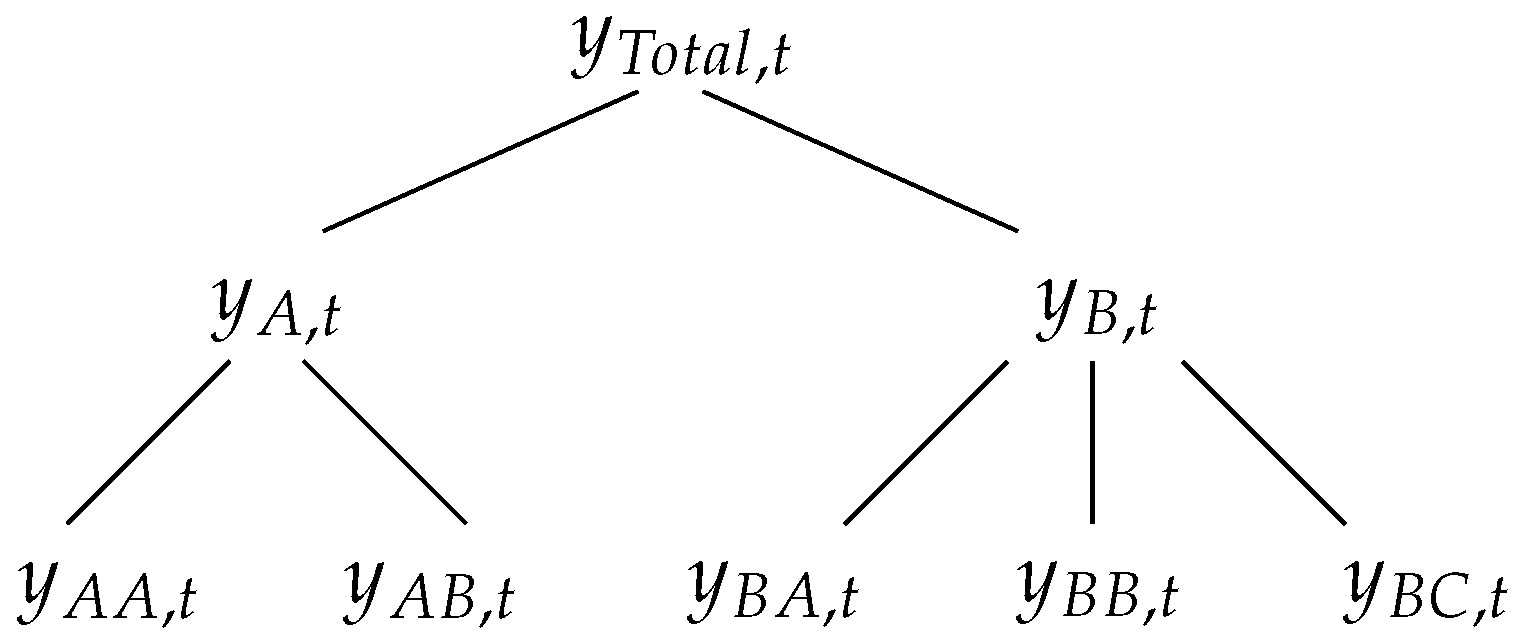
3.1. Hierarchical Time-Series
3.2. Hierarchical Forecasting Methods
4. Empirical Study
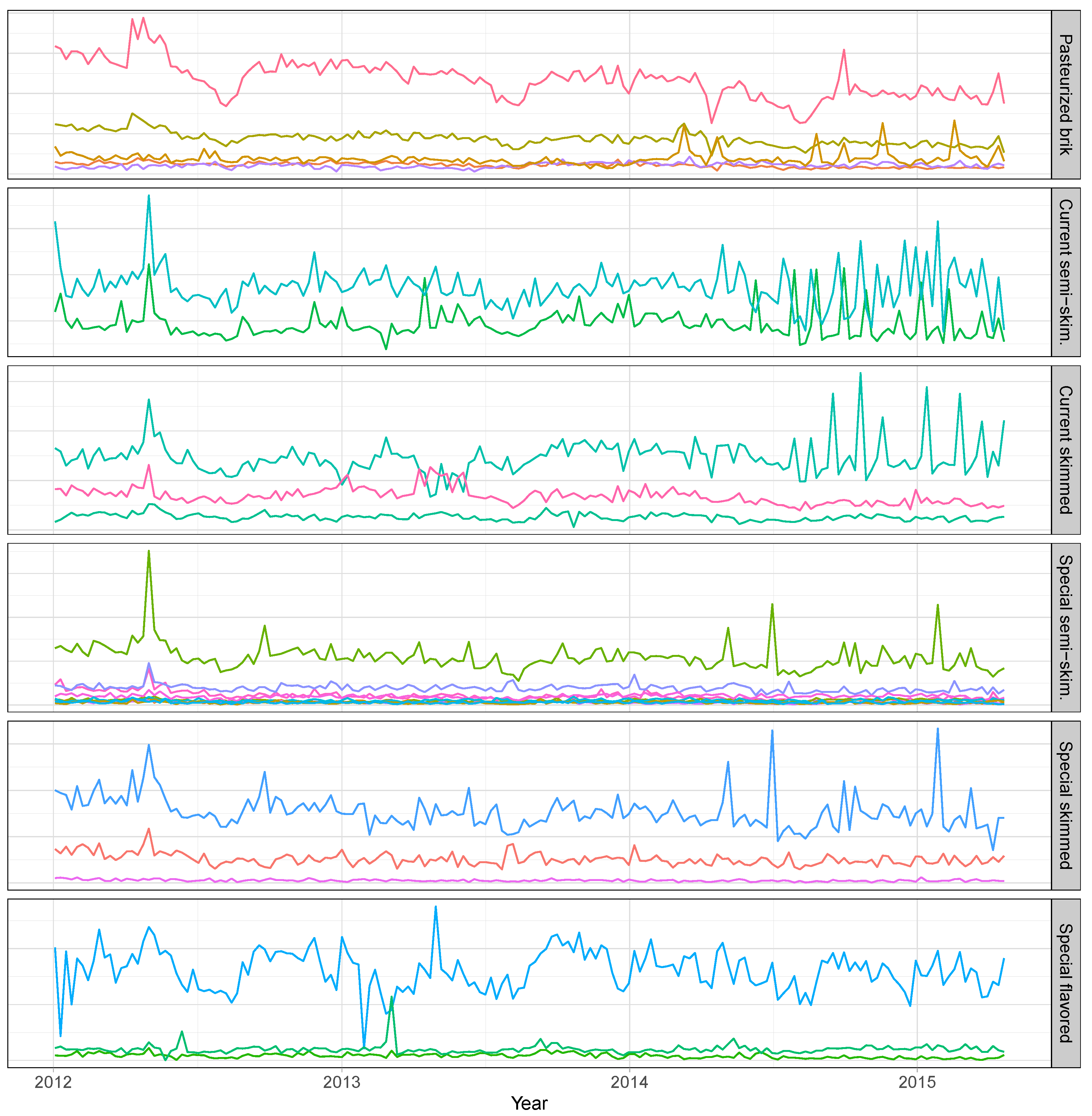
4.1. Case Study Data
4.2. Experimental Setup
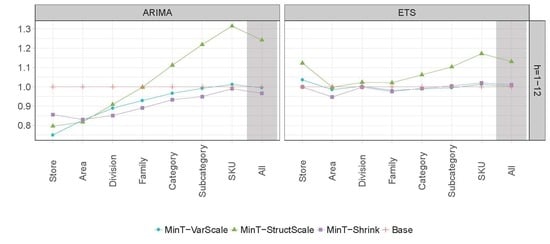
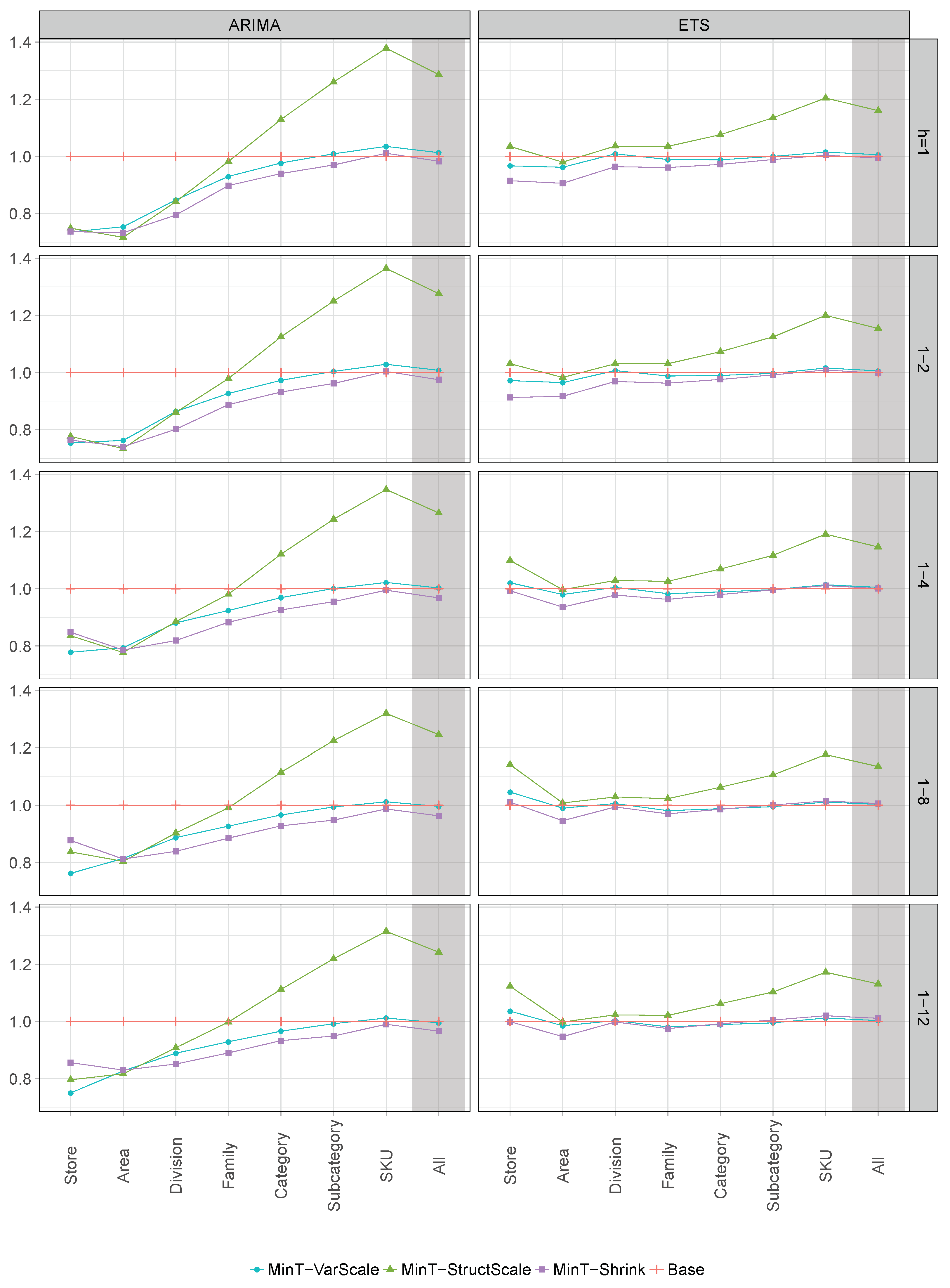
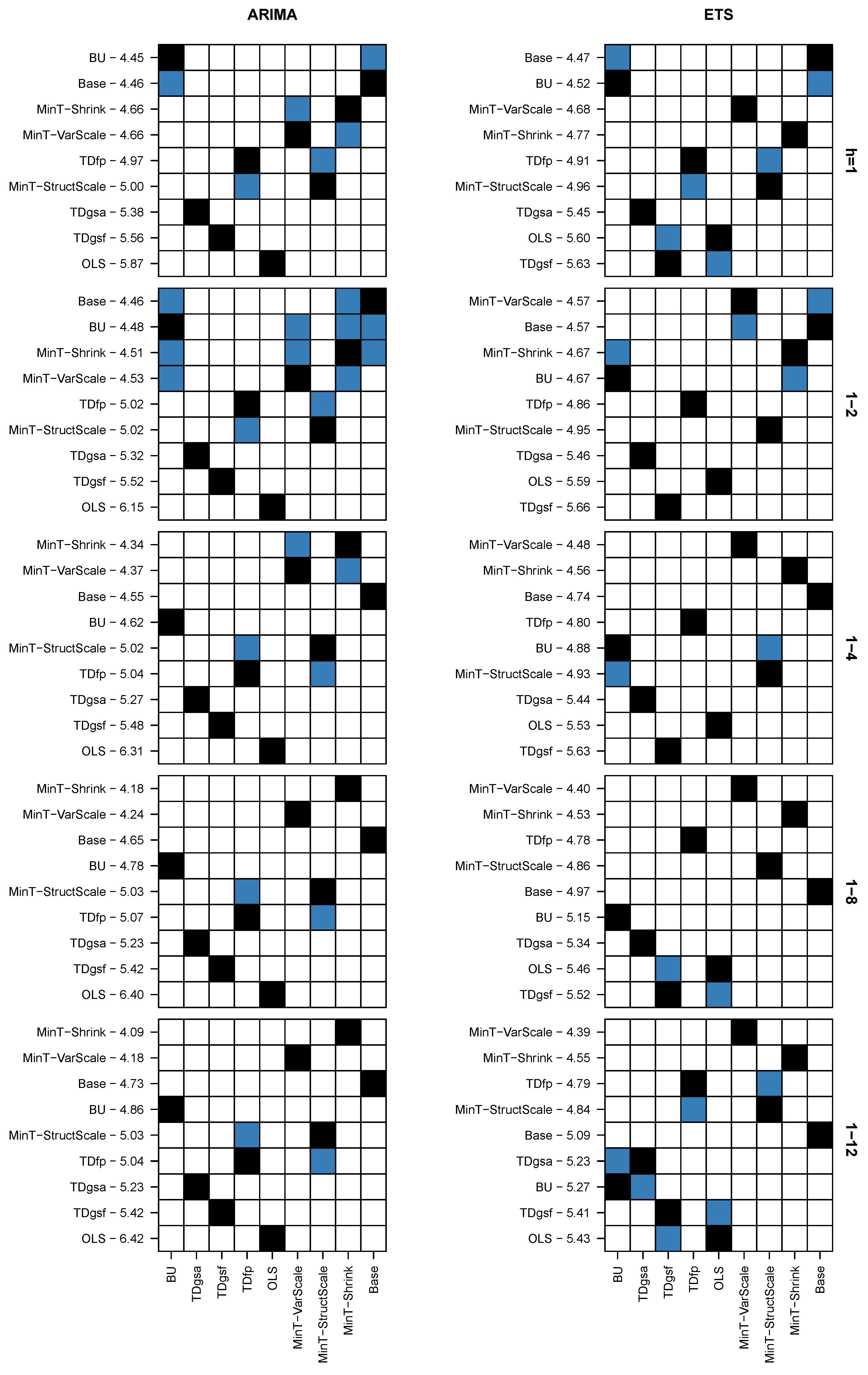
4.3. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fildes, R.; Ma, S.; Kolassa, S. Retail forecasting: Research and practice. Working paper. Available online: http://eprints.lancs.ac.uk/128587/ (accessed on 24 April 2019).
- Kremer, M.; Siemsen, E.; Thomas, D.J. The sum and its parts: Judgmental hierarchical forecasting. Manag. Sci. 2016, 62, 2745–2764. [Google Scholar] [CrossRef]
- Pennings, C.L.; van Dalen, J. Integrated hierarchical forecasting. Eur. J. Oper. Res. 2017, 263, 412–418. [Google Scholar] [CrossRef]
- Orcutt, G.H.; Watts, H.W.; Edwards, J.B. Data aggregation and information loss. Am. Econ. Rev. 1968, 58, 773–787. [Google Scholar]
- Dunn, D.M.; Williams, W.H.; Dechaine, T.L. Aggregate versus subaggregate models in local area forecasting. J. Am. Stat. Assoc. 1976, 71, 68–71. [Google Scholar] [CrossRef]
- Shlifer, E.; Wolff, R.W. Aggregation and proration in forecasting. Manag. Sci. 1979, 25, 594–603. [Google Scholar] [CrossRef]
- Kohn, R. When is an aggregate of a time series efficiently forecast by its past? J. Econom. 1982, 18, 337–349. [Google Scholar] [CrossRef]
- Gross, C.W.; Sohl, J.E. Disaggregation methods to expedite product line forecasting. J. Forecast. 1990, 9, 233–254. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Ahmed, R.A.; Hyndman, R.J. Hierarchical forecasts for Australian domestic tourism. Int. J. Forecast. 2009, 25, 146–166. [Google Scholar] [CrossRef]
- Dangerfield, B.J.; Morris, J.S. Top-down or bottom-up: Aggregate versus disaggregate extrapolations. Int. J. Forecast. 1992, 8, 233–241. [Google Scholar] [CrossRef]
- Widiarta, H.; Viswanathan, S.; Piplani, R. Forecasting aggregate demand: An analytical evaluation of top-down versus bottom-up forecasting in a production planning framework. Int. J. Prod. Econ. 2009, 118, 87–94. [Google Scholar] [CrossRef]
- Syntetos, A.A.; Babai, Z.; Boylan, J.E.; Kolassa, S.; Nikolopoulos, K. Supply chain forecasting: Theory, practice, their gap and the future. Eur. J. Oper. Res. 2016, 252, 1–26. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Ahmed, R.A.; Athanasopoulos, G.; Shang, H.L. Optimal combination forecasts for hierarchical time series. Comput. Stat. Data Anal. 2011, 55, 2579–2589. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Lee, A.; Wang, E. Fast computation of reconciled forecasts for hierarchical and grouped time series. Comput. Stat. Data Anal. 2016, 97, 16–32. [Google Scholar] [CrossRef]
- Wickramasuriya, S.L.; Athanasopoulos, G.; Hyndman, R.J. Optimal forecast reconciliation for hierarchical and grouped time series through trace minimization. J. Am. Stat. Assoc. 2018. [Google Scholar] [CrossRef]
- Erven, T.; Cugliari, J. Game-Theoretically Optimal Reconciliation of Contemporaneous Hierarchical Time Series Forecasts. In Modeling and Stochastic Learning for Forecasting in High Dimensions; Antoniadis, A., Poggi, J.M., Brossat, X., Eds.; Springer: Cham, Switzerland, 2015; Volume 217, pp. 297–317. [Google Scholar]
- Mircetic, D.; Nikolicic, S.; Stojanovic, Đ; Maslaric, M. Modified top down approach for hierarchical forecasting in a beverage supply chain. Transplant. Res. Procedia 2017, 22, 193–202. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; Online Open-access Textbooks, 2018. Available online: https://OTexts.com/fpp2/ (accessed on 24 April 2019).
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Ramos, P.; Santos, N.; Rebelo, R. Performance of state space and ARIMA models for consumer retail sales forecasting. Robot. Comput. Integr. Manuf. 2015, 34, 151–163. [Google Scholar] [CrossRef]
- Ramos, P.; Oliveira, J.M. A procedure for identification of appropriate state space and ARIMA models based on time-series cross-validation. Algorithms 2016, 9, 76. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Canova, F.; Hansen, B.E. Are seasonal patterns constant over time? A test for seasonal stability. J. Bus. Econ. Stat. 1985, 13, 237–252. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Hamilton, J. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Theil, H. Linear Aggregation of Economic Relations; North-Holland: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Zellner, A.; Tobias, J. A note on aggregation, disaggregation and forecasting performance. J. Forecast. 2000, 19, 457–465. [Google Scholar] [CrossRef]
- Grunfeld, Y.; Griliches, Z. Is aggregation necessarily bad? Rev. Econ. Stat. 1960, 42, 1–13. [Google Scholar] [CrossRef]
- Lutkepohl, H. Forecasting contemporaneously aggregated vector ARMA processes. J. Bus. Econ. Stat. 1984, 2, 201–214. [Google Scholar] [CrossRef]
- McLeavey, D.W.; Narasimhan, S. Production Planning and Inventory Control; Allyn and Bacon Inc.: Boston, MA, USA, 1974. [Google Scholar]
- Fliedner, G. An investigation of aggregate variable timesSeries forecast strategies with specific subaggregate time series statistical correlation. Comput. Oper. Res. 1999, 26, 1133–1149. [Google Scholar] [CrossRef]
- Athanasopoulos, G.; Hyndman, R.J.; Kourentzes, N.; Petropoulos, F. Forecasting with temporal hierarchies. Eur. J. Oper. Res. 2017, 262, 60–74. [Google Scholar] [CrossRef]
- Schäfer, J.; Strimmer, K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005, 4, 151–163. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: the forecast package for R. J. Stat. Softw. 2008, 26, 1–22. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Predictability of monthly temperature and precipitation using automatic time series forecasting methods. Acta Geophys. 2018, 66, 807–831. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. One-step ahead forecasting of geophysical processes within a purely statistical framework. Geosci. Lett. 2018, 5, 12. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stoch. Environ. Res. Risk Assess. 2019. [Google Scholar] [CrossRef]
- Hyndman, R.; Lee, A.; Wang, E.; Wickramasuriya, S. hts: Hierarchical and Grouped Time Series, 2018. R package Version 5.1.5. Available online: https://pkg.earo.me/hts/ (accessed on 24 April 2019).
- Davydenko, A.; Fildes, R. Measuring forecasting accuracy: The case of judgmental adjustments to SKU-level demand forecasts. Int. J. Forecast. 2013, 29, 510–522. [Google Scholar] [CrossRef]
- Fildes, R.; Petropoulos, F. Simple versus complex selection rules for forecasting many time series. J. Bus. Res. 2015, 68, 1692–1701. [Google Scholar] [CrossRef]
- Fleming, P.J.; Wallace, J.J. How not to lie with statistics: The correct way to summarize benchmark results. Commun. ACM 1986, 29, 218–221. [Google Scholar] [CrossRef]
- Kourentzes, N.; Athanasopoulos, G. Cross-temporal coherent forecasts for Australian tourism. Ann. Tourism Res. 2019, 75, 393–409. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kourentzes, N.; Svetunkov, I.; Schaer, O. tsutils: Time Series Exploration, Modelling and Forecasting, 2019. R package Version 0.9.0. Available online: https://rdrr.io/cran/tsutils/ (accessed on 24 April 2019).
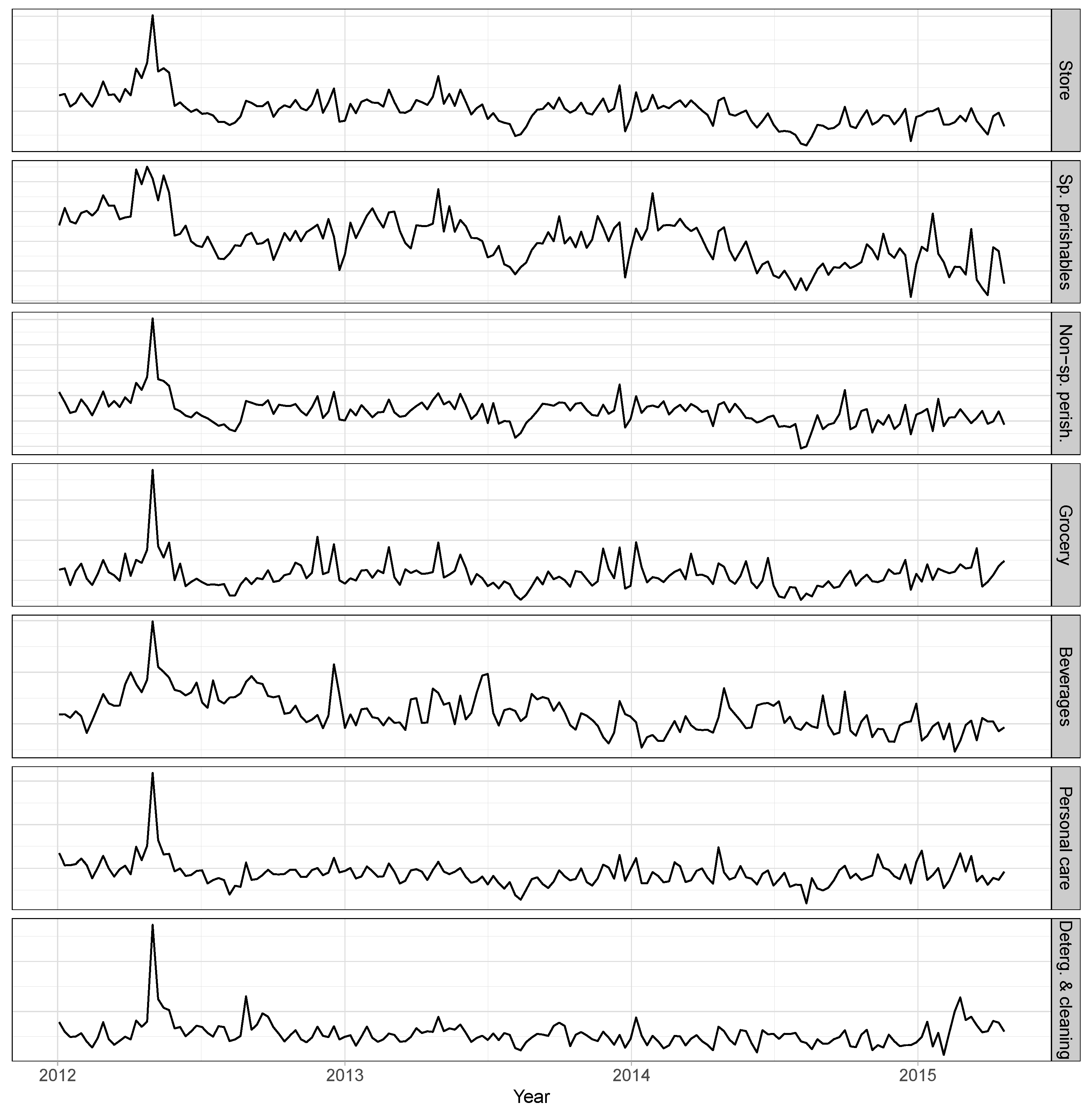

| Area | Divisions | Families | Categories | Subcategories | SKUs |
|---|---|---|---|---|---|
| Specialized perishables | 6 | 19 | 50 | 102 | 193 |
| Non-specialized perishables | 4 | 16 | 48 | 117 | 287 |
| Grocery | 3 | 14 | 51 | 144 | 309 |
| Beverages | 4 | 6 | 16 | 32 | 103 |
| Personal care | 2 | 9 | 19 | 37 | 59 |
| Detergents & cleaning | 2 | 9 | 19 | 27 | 37 |
| Total | 21 | 73 | 203 | 459 | 988 |
| Area | Division | Families | Categories | Subcategories | SKUs |
|---|---|---|---|---|---|
| Non-specialized perishables | Milk | Raw | Pasteurized | Brik | 5 |
| UHT | Current | Semi-skimmed | 2 | ||
| Skimmed | 3 | ||||
| Special | Semi-skimmed | 10 | |||
| Skimmed | 3 | ||||
| Flavored | 3 |
| ARIMA | ETS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Rank | Rank | |||||||||||
| Top-level: Store | |||||||||||||
| BU | 2.074 | 2.179 | 2.489 | 2.569 | 2.237 | 9 | 1.748 | 1.721 | 1.869 | 1.990 | 1.914 | 9 | |
| TD | 1 | 1 | 1 | 1 | 1 | 6.5 | 1 | 1 | 1 | 1 | 1 | 4.6 | |
| TD | 1 | 1 | 1 | 1 | 1 | 6.5 | 1 | 1 | 1 | 1 | 1 | 4.6 | |
| TD | 1 | 1 | 1 | 1 | 1 | 6.5 | 1 | 1 | 1 | 1 | 1 | 4.6 | |
| OLS | 0.949 | 0.951 | 0.959 | 0.950 | 0.947 | 4 | 0.985 | 0.990 | 0.998 | 1 | 0.999 | 2.5 | |
| MinT-VarScale | 0.736 | 0.754 | 0.778 | 0.762 | 0.750 | 1 | 0.967 | 0.972 | 1.021 | 1.046 | 1.036 | 5 | |
| MinT-StructScale | 0.749 | 0.777 | 0.836 | 0.837 | 0.796 | 2.4 | 1.035 | 1.031 | 1.099 | 1.142 | 1.123 | 8 | |
| MinT-Shrink | 0.737 | 0.764 | 0.848 | 0.877 | 0.856 | 2.6 | 0.915 | 0.913 | 0.993 | 1.011 | 0.999 | 2.1 | |
| Base | 1 | 1 | 1 | 1 | 1 | 6.5 | 1 | 1 | 1 | 1 | 1 | 4.6 | |
| Level 1: Area | |||||||||||||
| BU | 1.096 | 1.154 | 1.242 | 1.274 | 1.268 | 8.6 | 1.264 | 1.274 | 1.314 | 1.327 | 1.288 | 9 | |
| TD | 0.895 | 0.899 | 0.922 | 0.950 | 0.972 | 5 | 1.077 | 1.074 | 1.069 | 1.092 | 1.083 | 7.6 | |
| TD | 0.886 | 0.888 | 0.911 | 0.938 | 0.961 | 4 | 1.067 | 1.063 | 1.057 | 1.080 | 1.071 | 6.6 | |
| TD | 1.020 | 1.012 | 1.002 | 1.009 | 1.015 | 7 | 1.021 | 1.009 | 0.998 | 0.998 | 0.998 | 4.5 | |
| OLS | 1.189 | 1.186 | 1.150 | 1.134 | 1.125 | 8.4 | 1.123 | 1.079 | 1.004 | 0.990 | 0.977 | 5.3 | |
| MinT-VarScale | 0.754 | 0.763 | 0.794 | 0.814 | 0.827 | 2.8 | 0.962 | 0.965 | 0.980 | 0.990 | 0.985 | 2.3 | |
| MinT-StructScale | 0.717 | 0.734 | 0.777 | 0.804 | 0.817 | 1 | 0.980 | 0.983 | 0.997 | 1.008 | 0.998 | 3.9 | |
| MinT-Shrink | 0.733 | 0.741 | 0.786 | 0.812 | 0.830 | 2.2 | 0.906 | 0.917 | 0.936 | 0.946 | 0.947 | 1 | |
| Base | 1 | 1 | 1 | 1 | 1 | 6 | 1 | 1 | 1 | 1 | 1 | 4.8 | |
| Level 2: Division | |||||||||||||
| BU | 1.082 | 1.131 | 1.175 | 1.212 | 1.192 | 7.6 | 1.278 | 1.278 | 1.277 | 1.256 | 1.227 | 8 | |
| TD | 1.081 | 1.098 | 1.130 | 1.146 | 1.138 | 5.8 | 1.259 | 1.219 | 1.190 | 1.156 | 1.132 | 6 | |
| TD | 1.089 | 1.104 | 1.136 | 1.151 | 1.142 | 7 | 1.269 | 1.226 | 1.197 | 1.162 | 1.137 | 7 | |
| TD | 1.091 | 1.091 | 1.082 | 1.068 | 1.056 | 5.6 | 1.026 | 1.020 | 1.002 | 1.004 | 1.006 | 3.6 | |
| OLS | 1.966 | 1.953 | 1.994 | 2.029 | 2.027 | 9 | 1.523 | 1.495 | 1.461 | 1.471 | 1.457 | 9 | |
| MinT-VarScale | 0.848 | 0.864 | 0.881 | 0.887 | 0.889 | 2.4 | 1.009 | 1.007 | 1.005 | 1.006 | 1.003 | 3.4 | |
| MinT-StructScale | 0.842 | 0.861 | 0.885 | 0.903 | 0.908 | 2.6 | 1.036 | 1.031 | 1.029 | 1.029 | 1.023 | 5 | |
| MinT-Shrink | 0.795 | 0.802 | 0.819 | 0.839 | 0.851 | 1 | 0.964 | 0.969 | 0.978 | 0.994 | 0.998 | 1 | |
| Base | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 1 | 1 | 1 | 1 | 2 | |
| Level 3: Family | |||||||||||||
| BU | 1.016 | 1.022 | 1.031 | 1.040 | 1.036 | 5 | 1.083 | 1.083 | 1.073 | 1.067 | 1.061 | 6.4 | |
| TD | 1.194 | 1.182 | 1.174 | 1.155 | 1.130 | 7 | 1.217 | 1.176 | 1.132 | 1.079 | 1.043 | 6.8 | |
| TD | 1.200 | 1.188 | 1.179 | 1.159 | 1.134 | 8 | 1.223 | 1.181 | 1.136 | 1.083 | 1.046 | 7.8 | |
| TD | 1.101 | 1.094 | 1.079 | 1.079 | 1.075 | 6 | 1.024 | 1.018 | 1.008 | 1.005 | 1.005 | 4 | |
| OLS | 2.348 | 2.314 | 2.338 | 2.405 | 2.399 | 9 | 1.567 | 1.542 | 1.533 | 1.524 | 1.503 | 9 | |
| MinT-VarScale | 0.930 | 0.927 | 0.924 | 0.927 | 0.929 | 2 | 0.989 | 0.988 | 0.983 | 0.981 | 0.981 | 2 | |
| MinT-StructScale | 0.982 | 0.979 | 0.981 | 0.991 | 0.998 | 3 | 1.035 | 1.031 | 1.026 | 1.023 | 1.021 | 5 | |
| MinT-Shrink | 0.898 | 0.888 | 0.883 | 0.885 | 0.890 | 1 | 0.961 | 0.963 | 0.963 | 0.970 | 0.975 | 1 | |
| Base | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 1 | 1 | 1 | 1 | 3 | |
| Level 4: Category | |||||||||||||
| BU | 1.014 | 1.015 | 1.019 | 1.029 | 1.029 | 4 | 1.027 | 1.028 | 1.027 | 1.028 | 1.027 | 4.2 | |
| TD | 1.300 | 1.290 | 1.271 | 1.249 | 1.233 | 7 | 1.295 | 1.263 | 1.219 | 1.159 | 1.122 | 7 | |
| TD | 1.306 | 1.296 | 1.276 | 1.253 | 1.237 | 8 | 1.302 | 1.269 | 1.224 | 1.163 | 1.125 | 8 | |
| TD | 1.129 | 1.121 | 1.108 | 1.107 | 1.103 | 5.1 | 1.033 | 1.031 | 1.028 | 1.027 | 1.030 | 4.8 | |
| OLS | 2.463 | 2.418 | 2.403 | 2.398 | 2.375 | 9 | 1.636 | 1.618 | 1.602 | 1.563 | 1.537 | 9 | |
| MinT-VarScale | 0.977 | 0.973 | 0.969 | 0.966 | 0.966 | 2 | 0.988 | 0.990 | 0.989 | 0.988 | 0.989 | 1.8 | |
| MinT-StructScale | 1.129 | 1.125 | 1.121 | 1.115 | 1.112 | 5.9 | 1.076 | 1.073 | 1.069 | 1.063 | 1.062 | 6 | |
| MinT-Shrink | 0.940 | 0.932 | 0.926 | 0.928 | 0.933 | 1 | 0.972 | 0.976 | 0.980 | 0.986 | 0.992 | 1.2 | |
| Base | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | |
| Level 5: Subcategory | |||||||||||||
| BU | 1.008 | 1.009 | 1.012 | 1.015 | 1.014 | 3.8 | 1.011 | 1.009 | 1.009 | 1.009 | 1.009 | 4 | |
| TD | 1.326 | 1.301 | 1.274 | 1.231 | 1.208 | 6.8 | 1.314 | 1.270 | 1.220 | 1.155 | 1.117 | 7 | |
| TD | 1.335 | 1.309 | 1.282 | 1.238 | 1.215 | 7.8 | 1.323 | 1.278 | 1.228 | 1.161 | 1.123 | 8 | |
| TD | 1.155 | 1.143 | 1.131 | 1.122 | 1.115 | 5 | 1.052 | 1.046 | 1.044 | 1.039 | 1.039 | 5 | |
| OLS | 2.478 | 2.426 | 2.408 | 2.378 | 2.353 | 9 | 1.677 | 1.651 | 1.626 | 1.582 | 1.558 | 9 | |
| MinT-VarScale | 1.009 | 1.004 | 1.001 | 0.994 | 0.992 | 2.8 | 1.000 | 0.997 | 0.997 | 0.995 | 0.995 | 1.7 | |
| MinT-StructScale | 1.260 | 1.250 | 1.243 | 1.225 | 1.219 | 6.4 | 1.135 | 1.125 | 1.117 | 1.106 | 1.103 | 6 | |
| MinT-Shrink | 0.970 | 0.962 | 0.955 | 0.948 | 0.949 | 1 | 0.989 | 0.992 | 0.996 | 1.001 | 1.005 | 1.8 | |
| Base | 1 | 1 | 1 | 1 | 1 | 2.4 | 1 | 1 | 1 | 1 | 1 | 2.5 | |
| Bottom-level: SKU | |||||||||||||
| BU | 1 | 1 | 1 | 1 | 1 | 2.1 | 1 | 1 | 1 | 1 | 1 | 1.5 | |
| TD | 1.381 | 1.355 | 1.321 | 1.267 | 1.243 | 6.2 | 1.387 | 1.346 | 1.293 | 1.217 | 1.177 | 7 | |
| TD | 1.393 | 1.366 | 1.331 | 1.276 | 1.251 | 7.4 | 1.398 | 1.357 | 1.303 | 1.225 | 1.184 | 8 | |
| TD | 1.182 | 1.166 | 1.148 | 1.129 | 1.126 | 5 | 1.080 | 1.079 | 1.075 | 1.068 | 1.069 | 5 | |
| OLS | 2.077 | 2.038 | 2.009 | 1.972 | 1.959 | 9 | 1.506 | 1.496 | 1.479 | 1.448 | 1.433 | 9 | |
| MinT-VarScale | 1.035 | 1.029 | 1.022 | 1.012 | 1.012 | 4 | 1.015 | 1.016 | 1.014 | 1.011 | 1.012 | 3.6 | |
| MinT-StructScale | 1.378 | 1.364 | 1.347 | 1.320 | 1.315 | 7.4 | 1.204 | 1.200 | 1.191 | 1.177 | 1.172 | 6 | |
| MinT-Shrink | 1.011 | 1.004 | 0.995 | 0.987 | 0.990 | 1.8 | 1.004 | 1.009 | 1.011 | 1.015 | 1.020 | 3.4 | |
| Base | 1 | 1 | 1 | 1 | 1 | 2.1 | 1 | 1 | 1 | 1 | 1 | 1.5 | |
| ARIMA | ETS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Rank | Rank | |||||||||||
| All | |||||||||||||
| BU | 1.006 | 1.008 | 1.010 | 1.013 | 1.012 | 3.7 | 1.013 | 1.013 | 1.013 | 1.012 | 1.012 | 4 | |
| TD | 1.343 | 1.320 | 1.292 | 1.248 | 1.225 | 6.8 | 1.346 | 1.306 | 1.256 | 1.186 | 1.148 | 7 | |
| TD | 1.353 | 1.329 | 1.301 | 1.255 | 1.232 | 7.8 | 1.356 | 1.315 | 1.264 | 1.193 | 1.154 | 8 | |
| TD | 1.163 | 1.150 | 1.134 | 1.121 | 1.117 | 5 | 1.064 | 1.061 | 1.057 | 1.052 | 1.052 | 5 | |
| OLS | 2.223 | 2.182 | 2.159 | 2.132 | 2.116 | 9 | 1.565 | 1.549 | 1.530 | 1.496 | 1.477 | 9 | |
| MinT-VarScale | 1.013 | 1.008 | 1.003 | 0.996 | 0.995 | 2.9 | 1.006 | 1.006 | 1.005 | 1.003 | 1.003 | 2.6 | |
| MinT-StructScale | 1.286 | 1.276 | 1.265 | 1.246 | 1.242 | 6.4 | 1.160 | 1.154 | 1.146 | 1.135 | 1.131 | 6 | |
| MinT-Shrink | 0.983 | 0.975 | 0.968 | 0.963 | 0.966 | 1 | 0.994 | 0.998 | 1.001 | 1.006 | 1.011 | 2 | |
| Base | 1 | 1 | 1 | 1 | 1 | 2.4 | 1 | 1 | 1 | 1 | 1 | 1.4 | |
| Top-level | 0.592 | 0.572 | 0.549 | 0.563 | 0.617 |
| Level 1 | 1.007 | 0.98 | 0.958 | 0.947 | 0.929 |
| Level 2 | 1.075 | 1.01 | 0.962 | 0.914 | 0.913 |
| Level 3 | 0.986 | 0.961 | 0.931 | 0.902 | 0.894 |
| Level 4 | 0.985 | 0.967 | 0.95 | 0.921 | 0.905 |
| Level 5 | 0.984 | 0.969 | 0.955 | 0.937 | 0.925 |
| Bottom-level | 1.007 | 0.998 | 0.987 | 0.972 | 0.961 |
| All | 0.998 | 0.985 | 0.971 | 0.953 | 0.941 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, J.M.; Ramos, P. Assessing the Performance of Hierarchical Forecasting Methods on the Retail Sector. Entropy 2019, 21, 436. https://doi.org/10.3390/e21040436
Oliveira JM, Ramos P. Assessing the Performance of Hierarchical Forecasting Methods on the Retail Sector. Entropy. 2019; 21(4):436. https://doi.org/10.3390/e21040436
Chicago/Turabian StyleOliveira, José Manuel, and Patrícia Ramos. 2019. "Assessing the Performance of Hierarchical Forecasting Methods on the Retail Sector" Entropy 21, no. 4: 436. https://doi.org/10.3390/e21040436
APA StyleOliveira, J. M., & Ramos, P. (2019). Assessing the Performance of Hierarchical Forecasting Methods on the Retail Sector. Entropy, 21(4), 436. https://doi.org/10.3390/e21040436