A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery
Abstract
:1. Introduction
2. Review of Early Fault Diagnosis Approaches
2.1. FFD-Based Early Fault Diagnosis
2.1.1. Adaptive Decomposition Methods
Empirical Mode Composition
Ensemble Empirical Mode Composition
Local Mean Decomposition
Empirical Wavelet Transform
Variational Mode Decomposition
2.1.2. Wavelet Transform
2.1.3. Sparse Decomposition
2.2. AI-Based Early Fault Diagnosis
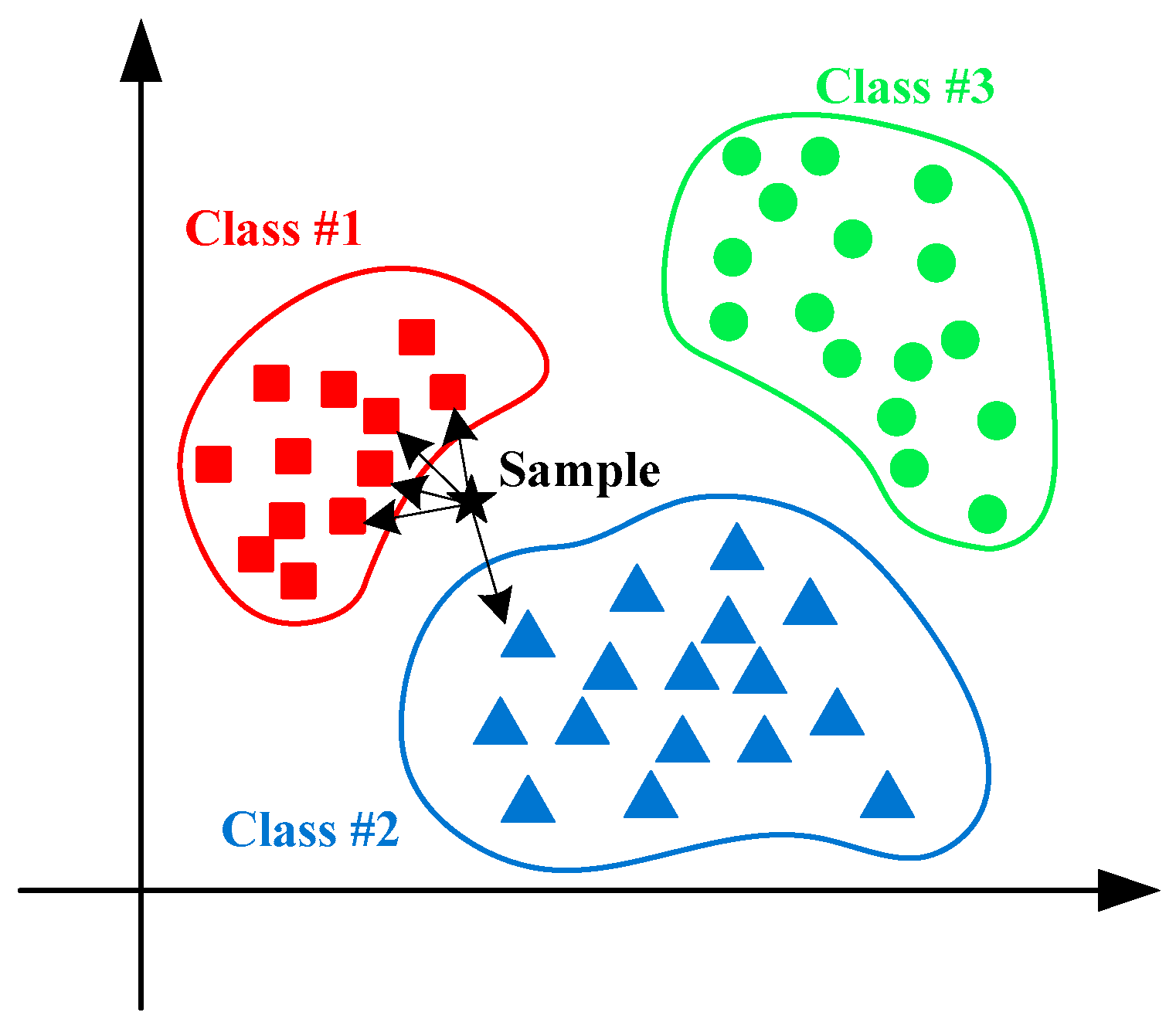
2.2.1. KNN
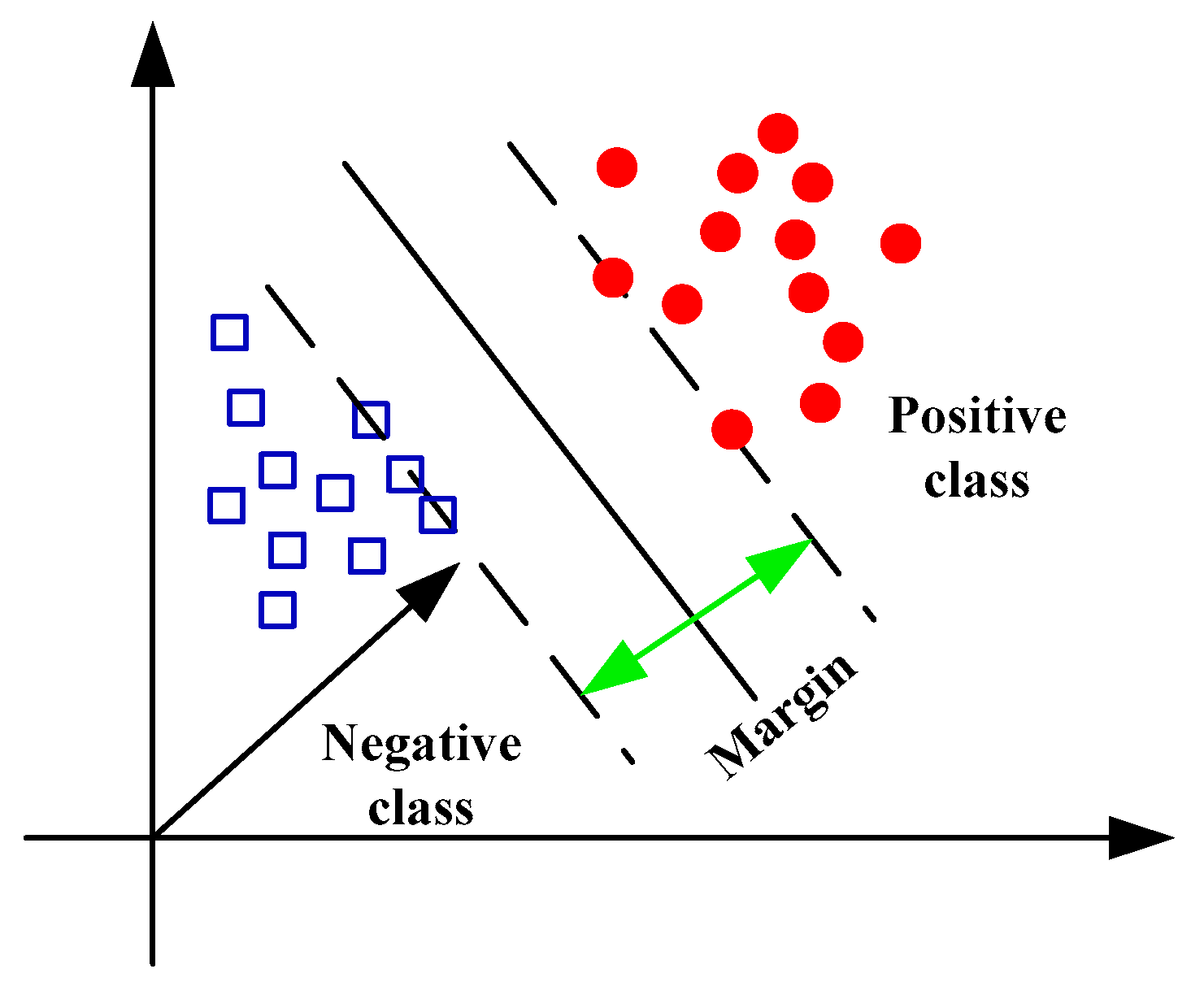
2.2.2. SVM
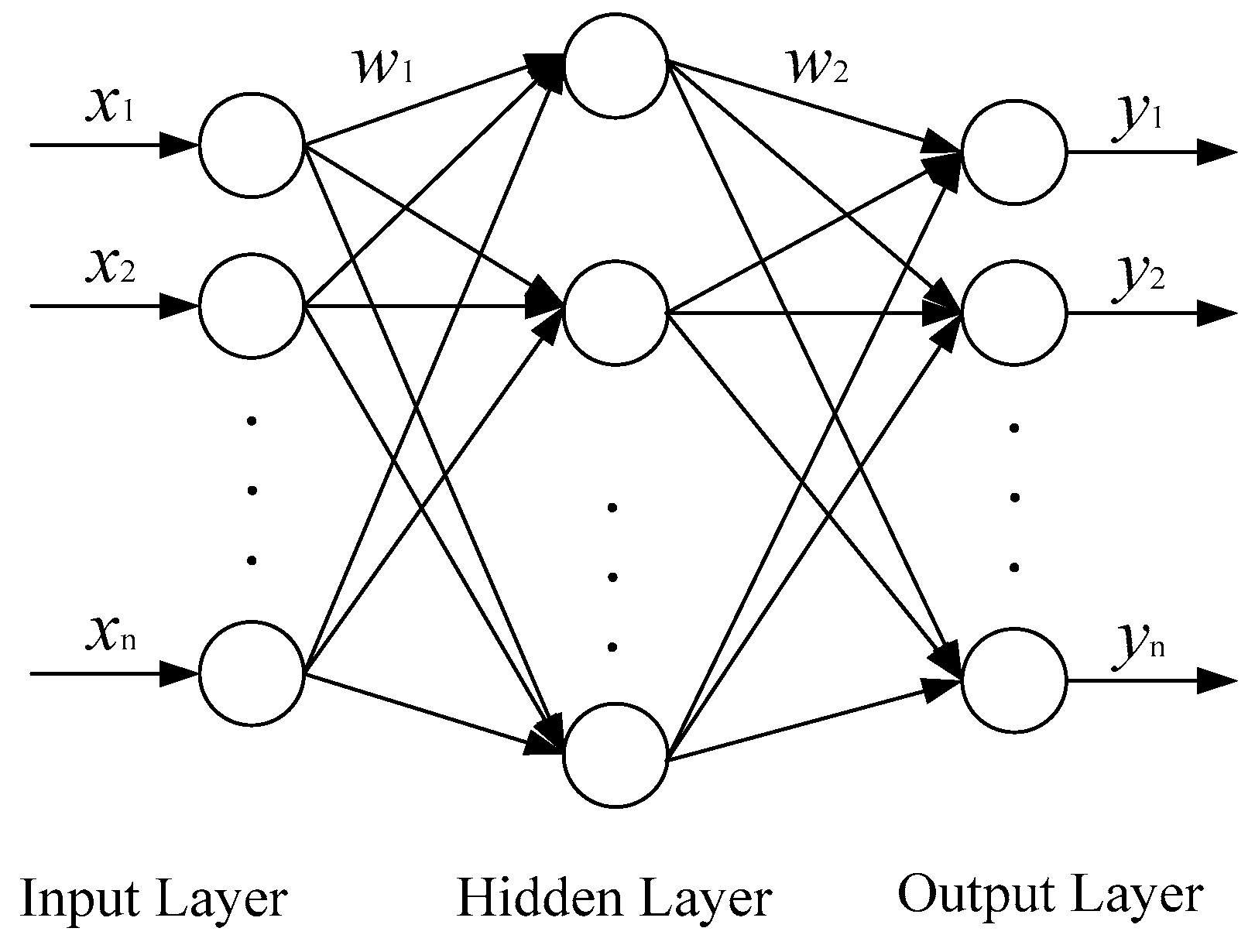
2.2.3. Neural network
3. Applications of FFD in Early Fault Diagnosis of Rotating Machinery
3.1. Adaptive Decomposition Methods
3.1.1. EMD
3.1.2. EEMD
3.1.3. LMD
3.1.4. EWT
3.1.5. VMD
3.1.6. Other Adaptive Methods
3.2. Wavelet Transform Methods
3.3. Sparse Representation Methods
3.4. Other Fault Frequency Based Methods
4. Applications of AI in Early Fault Diagnosis of Rotating Machinery
4.1. KNN
4.2. SVM
4.3. Neural Network
4.4. Other Methods
5. Discussion and Conclusions
- (1)
- Research on EFD based on multi-information fusion should be developed. In real applications, usually, multiple channel signals are measured simultaneously, such as vibration signals, current signals, torque signals, and rotating encoder signals. The extension of EFD techniques to multivariate versions can extract more characteristic fault information, which is vital for detection of weak fault symptoms at an early fault stage.
- (2)
- The calculation efficiency of EFD techniques deserves further research. Many EFD methods are proposed to improve the early fault detection ability at the cost of time consumption, which cannot meet the requirements of online condition monitoring. Therefore, how to improve the calculation efficiency of EFD is another research topic for early fault detection.
- (3)
- Most EFD methods are tested to be powerful on one test rig and the reliability test results on other machines are unknown. In real applications, the robustness of EFD methods should be studied, aiming to be effective for multiple machines.
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The entropy algorithm and its variants in the fault diagnosis of rotating machinery: A review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Li, H.; Xu, F.; Liu, H.; Zhang, X. Incipient fault information determination for rolling element bearing based on synchronous averaging reassigned wavelet scalogram. Measurement 2015, 65, 1–10. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Shen, C.; He, Q.; Kong, F.; Tse, P.W. A fast and adaptive varying-scale morphological analysis method for rolling element bearing fault diagnosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 6, 1362–1370. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and localization diagnosis of a defective ball bearing based on vertical-horizontal synchronization signal analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8706. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F.; Chu, F. HVSRMS localization formula and localization law: Localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process. 2019, 120, 608–629. [Google Scholar] [CrossRef]
- Lu, K.; Jin, Y.; Chen, Y.; Yang, Y.; Hou, L.; Zhang, Z.; Li, Z.; Fu, C. Review for order reduction based on proper orthogonal decomposition and outlooks of applications in mechanical systems. Mech. Syst. Signal Process. 2019, 123, 264–297. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Wang, X.; Liu, B.; Liang, X. Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. J. Sound Vib. 2018, 428, 72–86. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Alper, E.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Li, Y.; Feng, K.; Liang, X.; Zuo, M.J. A fault diagnosis method for planetary gearboxes under non-stationary working conditions using improved Vold-Kalman filter and multi-scale sample entropy. J. Sound Vib. 2019, 439, 271–286. [Google Scholar] [CrossRef]
- Mao, W.; He, L.; Yan, Y.; Wang, J. Online sequential prediction of bearings imbalanced fault diagnosis by extreme learning machine. Mech. Syst. Signal Process. 2017, 83, 450–473. [Google Scholar] [CrossRef]
- Yu, J.; Lv, J. Weak fault feature extraction of rolling bearings using local mean decomposition-based multilayer hybrid denoising. IEEE Trans. Instrum. Meas. 2017, 66, 3148–3159. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Q.; Wang, L.; Cheng, L.; Zhou, J. Early fault detection method for rotating machinery based on harmonic-assisted multivariate empirical mode decomposition and transfer entropy. Entropy 2018, 20, 873. [Google Scholar] [CrossRef]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- Stępień, K.; Makieła, W. An analysis of deviations of cylindrical surfaces with the use of wavelet transform. Metrol. Meas. Syst. 2013, 20, 139–150. [Google Scholar] [CrossRef]
- Gupta, P.; Pradhan, M.K. Fault detection analysis in rolling element bearing: A review. Mater. Today Proc. 2017, 4, 2085–2094. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, Z.; Vong, C.; Han, J. A patent analysis of prognostics and health management (PHM) innovations for electrical systems. IEEE Access 2018, 6, 18088–18107. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process. 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Si, S.; Huang, S. Entropy based fault classification using the Case Western Reserve University data: A benchmark study. IEEE Trans. Reliab. 2019, 1–14. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, J. Dual serial vortex-induced energy harvesting system for enhanced energy harvesting. AIP Adv. 2018, 8, 075221. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Naha, A.; Samanta, A.K.; Routray, A.; Deb, A.K. Low complexity motor current signature analysis using sub-nyquist strategy with reduced data length. IEEE Trans. Instrum. Meas. 2017, 66, 3249–3259. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, C.; Jia, X.; Peng, X. Fault diagnosis of reciprocating compressor valve with the method integrating acoustic emission signal and simulated valve motion. Mech. Syst. Signal Process. 2015, 56, 197–212. [Google Scholar] [CrossRef]
- Shibata, K.; Takahashi, A.; Shirai, T. Fault diagnosis of rotating machinery through visualization of sound signals. Mech. Syst. Signal Process. 2000, 14, 229–241. [Google Scholar] [CrossRef]
- Han, C.F.; He, H.Q.; Wei, C.C.; Horng, J.H.; Chiu, Y.L.; Hwang, Y.C.; Lin, J.F. Techniques developed for fault diagnosis of long-range running ball screw drive machine to evaluate lubrication condition. Measurement 2018, 126, 274–288. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J. Health assessment of rotating machinery using a rotary encoder. IEEE Trans. Ind. Electron. 2018, 65, 2548–2556. [Google Scholar] [CrossRef]
- Ciabattoni, L.; Ferracuti, F.; Freddi, A.; Monteriù, A. Statistical spectral analysis for fault diagnosis of rotating machines. IEEE Trans. Ind. Electron. 2018, 65, 4301–4310. [Google Scholar] [CrossRef]
- Samuel, P.D.; Pines, D.J. A review of vibration-based techniques for helicopter transmission diagnostics. J. Sound Vib. 2005, 282, 475–508. [Google Scholar] [CrossRef]
- Dalvand, F.; Dalvand, S.; Sharafi, F.; Pecht, M. Current noise cancellation for bearing fault diagnosis using time shifting. IEEE Trans. Ind. Electron. 2017, 64, 8138–8147. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. Health condition monitoring and early fault diagnosis of bearings using SDF and intrinsic characteristic-scale decomposition. IEEE Trans. Instrum. Meas. 2016, 9, 2174–2189. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A comparative study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to bearing defect diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Cheng, J.; Yu, D.; Yang, Y. Application of support vector regression machines to the processing of end effects of Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 1197–1211. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Long, S.R.; Shen, S.S.; Qu, W.; Gloersen, P.; Fan, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar]
- Smith, J. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 23, 443–454. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Hess-Nielsen, N.; Wickerhauser, M.V. Wavelets and time-frequency analysis. Proc. IEEE 1996, 84, 523–540. [Google Scholar] [CrossRef]
- Mallat, S.G. A wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Elsevier Press: Amsterdam, The Netherlands; Boston, MA, USA, 2008. [Google Scholar]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Cui, L.; Wu, N.; Ma, C.; Wang, H. Quantitative fault analysis of roller bearings based on a novel matching pursuit method with a new step-impulse dictionary. Mech. Syst. Signal Process. 2016, 68, 34–43. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Liu, L. A windowing and mapping strategy for gear tooth fault detection of a planetary gearbox. Mech. Syst. Signal Process. 2016, 80, 445–459. [Google Scholar] [CrossRef]
- Ding, Y.; He, W.; Chen, B.; Zi, Y.; Selesnick, I.W. Detection of faults in rotating machinery using periodic time-frequency sparsity. J. Sound Vib. 2016, 382, 357–378. [Google Scholar] [CrossRef]
- Du, Z.; Chen, X.; Zhang, H.; Yan, R. Sparse feature identification based on union of redundant dictionary for wind turbine gearbox fault diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 6594–6605. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Lin, H. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vib. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- Wang, L.; Cai, G.; You, W.; Huang, W.; Zhou, Z. Transients extraction based on averaged random orthogonal matching pursuit algorithm for machinery fault diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 3237–3248. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, Y.; Zuo, M.J.; Chu, F.; Chen, X. Atomic decomposition and sparse representation for complex signal analysis in machinery fault diagnosis: A review with examples. Measurement 2017, 103, 106–132. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Wang, J.; Neskovic, P.; Cooper, L.N. Neighborhood size selection in the k-nearest-neighbor rule using statistical confidence. Pattern Recognit. 2006, 39, 417–423. [Google Scholar] [CrossRef]
- Sain, S.R. The nature of statistical learning theory. Technometrics 1996, 38, 409. [Google Scholar] [CrossRef]
- Knerr, S.; Personnaz, L.; Dreyfus, G. Single-layer learning revisited: A stepwise procedure for building and training a neural network. In Neurocomputing; Springer: Berlin/Heidelberg, Germany, 1990; pp. 41–50. [Google Scholar]
- Platt, J.C.; Cristianini, N.; Shawe-Taylor, J.S.; Wang, H. Large margin DAGs for multiclass classification. Adv. Neural Inf. Process. Syst. 2000, 547–553. [Google Scholar]
- Vural, V.; Dy, J.G. A hierarchical method for multi-class support vector machines. In Proceedings of the Twenty-First International Conference on Machine Learning-ICML, Banff, AB, Canada, 4–8 July 2004; p. 105. [Google Scholar]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Dybala, J.; Zimroz, R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Zhu, K.; Song, X.; Xue, D. Incipient fault diagnosis of roller bearings using empirical mode decomposition and correlation coefficient. J. Vibroeng. 2013, 15, 597–603. [Google Scholar]
- Dybala, J.; Galezia, A. A novel method of gearbox health vibration monitoring using empirical mode decomposition. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2014; Volume 333, pp. 225–234. [Google Scholar]
- Li, Y.; Xu, M.; Liang, X.; Huang, W. Application of bandwidth EMD and adaptive multiscale morphology analysis for incipient fault diagnosis of rolling bearings. IEEE Trans. Ind. Electron. 2017, 64, 6506–6517. [Google Scholar] [CrossRef]
- Zhao, S.; Liang, L.; Xu, G.; Wang, J. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mech. Syst. Signal Process. 2013, 40, 154–177. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, G. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Parey, A.; Pachori, R.B. Variable cosine windowing of intrinsic mode functions: Application to gear fault diagnosis. Measurement 2012, 45, 415–426. [Google Scholar] [CrossRef]
- Chen, H.; Chen, P.; Chen, W.; Wu, C. Wind turbine gearbox fault diagnosis based on improved EEMD and Hilbert square demodulation. Appl. Sci. 2017, 7, 128. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Zvokelj, M.; Zupan, S.; Prebil, I. EEMD-based multiscale ICA method for slewing bearing fault detection and diagnosis. J. Sound Vib. 2016, 370, 394–423. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, G.; Shan, X.; Hu, X. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Measurement 2015, 73, 55–67. [Google Scholar] [CrossRef]
- Guo, W. An Enhanced Extraction Method Based on EEMD for Processing a Bearing Vibration Signal with Multiple Vibration Sources; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Imaouchen, Y.; Kedadouche, M.; Alkama, R.; Thomas, M. A frequency-weighted energy operator and complementary ensemble empirical mode decomposition for bearing fault detection. Mech. Syst. Signal Process. 2017, 82, 103–116. [Google Scholar] [CrossRef]
- Li, M.; Wang, H.; Tang, G.; Yuan, H. An improved method based on CEEMD for fault diagnosis of rolling bearing. Adv. Mech. Eng. 2014, 6, 676205. [Google Scholar] [CrossRef]
- Tabrizi, A.; Garibaldi, L.; Fasana, A.; Marchesiello, S. Performance improvement of ensemble empirical mode decomposition for roller bearings damage detection. Shock Vib. 2015, 2015, 964805. [Google Scholar] [CrossRef]
- Jiang, H.; Li, C.; Li, H. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mech. Syst. Signal Process. 2013, 36, 225–239. [Google Scholar] [CrossRef]
- Liu, W.Y.; Zhang, W.H.; Han, J.G.; Wang, G.F. A new wind turbine fault diagnosis method based on the local mean decomposition. Renew. Energy 2012, 48, 411–415. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J.; Qu, J.; Tian, T. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes. Mech. Syst. Signal Process. 2013, 40, 56–75. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Xiang, J.; Zi, Y. Application of local mean decomposition to the surveillance and diagnostics of low-speed helical gearbox. Mech. Mach. Theory 2012, 47, 62–73. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Yang, Y.; Xu, M. Earlyfault diagnosis of rotating machinery by combining differential rational spline-based LMD and K-L divergence. IEEE Trans. Instrum. Meas. 2017, 66, 3077–3090. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Wang, Z.; Wang, J. Weak feature enhancement in machinery fault diagnosis using empirical wavelet transform and an improved adaptive bistable stochastic resonance. ISA Trans. 2019, 84, 283–295. [Google Scholar] [CrossRef]
- Chen, J.; Pan, J.; Li, Z.; Zi, Y. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Merainani, B.; Benazzouz, D.; Rahmoune, C. Early detection of tooth crack damage in gearbox using empirical wavelet transform combined by Hilbert transform. J. Vib. Control 2017, 23, 1623–1634. [Google Scholar] [CrossRef]
- Lu, Y.; Xie, R.; Liang, S.Y. Detection of weak fault using sparse empirical wavelet transform for cyclic fault. Int. J. Adv. Manuf. Technol. 2018, 99, 1195–1201. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.; Wang, X. Incipient fault feature extraction of rolling bearings based on the MVMD and Teager energy operator. ISA Trans. 2018, 80, 297–311. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved AR-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Yang, K.; Wang, G.; Dong, Y.; Zhang, Q. Early chatter identification based on an optimized variational mode decomposition. Mech. Syst. Signal Process. 2019, 115, 238–254. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Z.; Cao, J.; Gong, T. An optimized variational mode decomposition for extracting weak feature of viscoelastic sandwich cylindrical structures. Meas. Sci. Technol. 2018, 29, 035006. [Google Scholar] [CrossRef]
- Han, D.; Su, X.; Shi, P. Weak fault signal detection of rotating machinery based on multistable stochastic resonance and VMD-AMD. Shock Vib. 2018, 2018, 4252438. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W. An improved VMD with empirical mode decomposition and its application in incipient fault detection of rolling bearing. IEEE Access 2018, 6, 44483–44493. [Google Scholar] [CrossRef]
- Elasha, F.; Mba, D.; Ruiz-Carcel, C. Effectiveness of adaptive filter algorithms and spectral kurtosis in bearing faults detection in a gearbox. Vib. Eng. Technol. Mach. 2015, 219–229. [Google Scholar]
- Zhao, M.; Jia, X. A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery. Mech. Syst. Signal Process. 2017, 94, 129–147. [Google Scholar] [CrossRef]
- Ibrahim, G.; Albarbar, A.; Abouhnik, A.; Shnibha, R. Adaptive filtering based system for extracting gearbox condition feature from the measured vibrations. Measurement 2013, 46, 2029–2034. [Google Scholar] [CrossRef]
- Mei, J.; Jia, J.; Zeng, R.; Zhou, B. A multi-order FRFT self-adaptive filter based on segmental frequency fitting and early fault diagnosis in gears. Measurement 2016, 91, 532–540. [Google Scholar] [CrossRef]
- Romero, A.; Lage, Y.; Soua, S.; Wang, B. Vestas V90-3MW wind turbine gearbox health assessment using a vibration-based condition monitoring system. Shock Vib. 2016, 2016, 6423587. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, Q.; Li, J.; Zhu, Z. A wavelet-based statistical approach for monitoring and diagnosis of compound faults with application to rolling bearings. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1563–1572. [Google Scholar] [CrossRef]
- He, W.; Miao, Q.; Azarian, M.; Pecht, M. Health monitoring of cooling fan bearings based on wavelet filter. Mech. Syst. Signal Process. 2015, 64, 149–161. [Google Scholar] [CrossRef]
- Cui, H.; Qiao, Y.; Yin, Y.; Hong, M. An investigation on early bearing fault diagnosis based on wavelet transform and sparse component analysis. Struct. Health Monit. Int. J. 2017, 16, 39–49. [Google Scholar] [CrossRef]
- Cui, H.; Qiao, Y.; Yin, Y.; Hong, M. An investigation of rolling bearing early diagnosis based on high-frequency characteristics and self-adaptive wavelet de-noising. Neurocomputing 2016, 216, 649–656. [Google Scholar] [CrossRef]
- Wang, D.; Shen, C.; Tse, P.W. A novel adaptive wavelet stripping algorithm for extracting the transients caused by bearing localized faults. J. Sound Vib. 2013, 332, 6871–6890. [Google Scholar] [CrossRef]
- Combet, F.; Gelman, L.; LaPayne, G. Novel detection of local tooth damage in gears by the wavelet bicoherence. Mech. Syst. Signal Process. 2012, 26, 218–228. [Google Scholar] [CrossRef]
- Moumene, I.; Ouelaa, N. Application of the wavelets multiresolution analysis and the high-frequency resonance technique for gears and bearings faults diagnosis. Int. J. Adv. Manuf. Technol. 2016, 83, 1315–1339. [Google Scholar] [CrossRef]
- Chen, J.L.; Zi, Y.Y.; He, Z.J. Construction of adaptive redundant multiwavelet packet and its application to compound faults detection of rotating machinery. Sci. China Technol. Sci. 2012, 55, 2083–2090. [Google Scholar] [CrossRef]
- He, S.L.; Zi, Y.Y.; Zhao, C.L. Maximal-overlap adaptive multiwavelet for detecting transient vibration responses from dynastic signal of rotating machineries. Sci. China Technol. Sci. 2014, 57, 136–150. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Xu, M.; Huang, W. Early fault feature extraction of rolling bearing based on ICD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2017, 86, 204–223. [Google Scholar] [CrossRef]
- Fan, Q.; Ikejo, K.; Nagamura, K.; Kawada, M. Application of statistical parameters and discrete wavelet transform to gear damage diagnosis. J. Adv. Mech. Des. Syst. Manuf. 2014, 8. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.N. Online unbalanced rotor fault detection of an IM drive based on both time and frequency domain analyses. IEEE Trans. Ind. Appl. 2017, 53, 4087–4096. [Google Scholar] [CrossRef]
- Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Ramirez-Cortes, J.; Morales-Caporal, R. Vibration analysis of partially damaged rotor bar in induction motor under different load condition using DWT. Shock Vib. 2016, 2016, 3530464. [Google Scholar] [CrossRef]
- Jayakumar, K.; Thangavel, S. Industrial drive fault diagnosis through vibration analysis using wavelet transform. J. Vib. Control 2017, 23, 2003–2013. [Google Scholar] [CrossRef]
- Fan, Q.; Ikejo, K.; Nagamura, K.; Kawada, M. The design of a new sparsogram for fast bearing fault diagnosis: Parts 1 and 2. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar]
- Yang, D.; Li, H.; Hu, Y.; Zhao, H. Vibration condition monitoring system for wind turbine bearings based on noise suppression with multi-point data fusion. Renew. Energy 2016, 92, 104–116. [Google Scholar] [CrossRef]
- Elmorsy, M.; Achtenova, G. Application of optimal morlet wavelet filter for bearing fault diagnosis. SAE Int. J. Passeng. Cars Mech. Syst. 2015, 8, 817–824. [Google Scholar] [CrossRef]
- Yiakopoulos, C.; Koutsoudaki, M.; Gryllias, K.; Antoniadis, I. Improving the performance of univariate control charts for abnormal detection and classification. Mech. Syst. Signal Process. 2017, 86, 122–150. [Google Scholar] [CrossRef]
- Elmorsy, M.; Achtenova, G. Value of optimal wavelet function in gear fault diagnosis. SAE Int. J. Veh. Dyn. Stab. NVH 2017, 1, 390–399. [Google Scholar] [CrossRef]
- Wang, D.; Guo, W.; Wang, X. A joint sparse wavelet coefficient extraction and adaptive noise reduction method in recovery of weak bearing fault features from a multi-component signal mixture. Appl. Soft Comput. 2013, 13, 4097–4104. [Google Scholar] [CrossRef]
- Tang, H.; Chen, J.; Dong, G. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Lv, Y.; Luo, J.; Yi, C. Enhanced orthogonal matching pursuit algorithm and its application in mechanical equipment fault diagnosis. Shock Vib. 2017, 2017, 4896056. [Google Scholar] [CrossRef]
- Mo, D.; Cui, L.; Wang, J.; Xu, Y. The delayed correlation envelope analysis technique based on sparse signal decomposition method and its application to bearing early fault diagnosis. Contemp. Des. Manuf. Technol. 2013, 819, 292–296. [Google Scholar] [CrossRef]
- Cui, L.; Wang, J.; Lee, S.; Kawada, M. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis. J. Sound Vib. 2014, 333, 2840–2862. [Google Scholar] [CrossRef]
- Tang, G.; Yang, Q.; Wang, H.Q.; Luo, G. Sparse classification of rotating machinery faults based on compressive sensing strategy. Mechatronics 2015, 31, 60–67. [Google Scholar] [CrossRef]
- Li, X.; Deng, W.; Zhao, H.; Zheng, G. Study on a novel fault diagnosis method of rolling bearing in motor. Recent Pat. Mech. Eng. 2016, 9, 144–152. [Google Scholar] [CrossRef]
- Hu, A.J.; Lin, J.F.; Sun, S.F. A novel approach of impulsive signal extraction for early fault detection of rolling element bearing. Shock Vib. 2017, 2017, 9375491. [Google Scholar]
- Raj, A.S.; Murali, N. Early classification of bearing faults using morphological operators and fuzzy inference. IEEE Trans. Ind. Electron. 2013, 60, 567–574. [Google Scholar] [CrossRef]
- Dong, G.; Chen, J.; Zhao, F. Incipient bearing fault feature extraction based on minimum entropy deconvolution and K-singular value decomposition. J. Manuf. Sci. Eng. Trans. ASME 2017, 139, 101006. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A.; Guilbault, R. Nonlinear parameters for monitoring gear: Comparison between Lempel-Ziv, approximate entropy, and sample entropy complexity. Shock Vib. 2015, 2015, 959380. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Fault diagnosis of rolling bearing’s early weak fault based on minimum entropy de-convolution and fast Kurtogram algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2890–2907. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: An useful tool for characterizing non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Antoni, J.; Xin, G.; Hamzaoui, N. Fast computation of the spectral correlation. Mech. Syst. Signal Process. 2017, 92, 248–277. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G. Spectral kurtosis based on AR model for fault diagnosis and condition monitoring of rolling bearing. J. Mech. Sci. Technol. 2012, 26, 301–306. [Google Scholar] [CrossRef]
- Jeong, I.K.; Kang, M.; Kim, J.; Kim, J.M. Enhanced DET-based fault signature analysis for reliable diagnosis of single and multiple-combined bearing defects. Shock Vib. 2015, 2015, 814650. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Shan, H.; Lin, J. Early fault diagnosis of bearings using an improved spectral kurtosis by maximum correlated kurtosis deconvolution. Sensors 2015, 15, 29363–29377. [Google Scholar] [CrossRef]
- Li, H.K.; Ren, Y.J.; Yang, R. Incipient feature extraction for rolling element bearing based on particle filter preprocessing and kurtogram. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016. [Google Scholar]
- Chen, X.; Xiao, L.; Zhang, X.; Liu, Z. A heterogeneous fault diagnosis method for bearings in gearbox. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1491–1499. [Google Scholar] [CrossRef]
- Masmoudi, M.L.; Etien, E.; Moreau, S.; Sakout, A. Single point bearing fault diagnosis using simplified frequency model. Electr. Eng. 2017, 99, 455–465. [Google Scholar] [CrossRef]
- Dong, G.; Chen, J.; Zhao, F. A frequency-shifted bispectrum for rolling element bearing diagnosis. J. Sound Vib. 2015, 339, 396–418. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Dong, J.M.; Xiao, W.B. Application of the horizontal slice of cyclic bispectrum in rolling element bearings diagnosis. Mech. Syst. Signal Process. 2012, 26, 229–243. [Google Scholar] [CrossRef]
- Dong, G.; Chen, J. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2012, 33, 212–236. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, X.; Fei, J.; Zhao, Y. Study on fault diagnosis of rolling bearing based on time-frequency generalized dimension. Shock Vib. 2015, 2015, 808457. [Google Scholar] [CrossRef]
- Siegel, D.; Al-Atat, H.; Shauche, V.; Liao, L. Novel method for rolling element bearing health assessment-A tachometer-less synchronously averaged envelope feature extraction technique. Mech. Syst. Signal Process. 2012, 29, 362–376. [Google Scholar] [CrossRef]
- Park, C.S.; Choi, Y.C.; Kim, Y.H. Early fault detection in automotive ball bearings using the minimum variance cepstrum. Mech. Syst. Signal Process. 2013, 38, 534–548. [Google Scholar] [CrossRef]
- Fu, S.; Liu, K.; Xu, Y.; Liu, Y. Rolling bearing diagnosing method based on time domain analysis and adaptive fuzzy C-means clustering. Shock Vib. 2016, 2016, 9412787. [Google Scholar]
- Li, C.; Valente, J.; Sanchez, R.V.; Cerrada, M. Fuzzy determination of informative frequency band for bearing fault detection. J. Intell. Fuzzy Syst. 2016, 30, 3513–3525. [Google Scholar] [CrossRef]
- Liu, H.; Han, S.; Yang, J.; Liu, S. Improving the weak feature extraction by adaptive stochastic resonance in cascaded piecewise-linear system and its application in bearing fault detection. J. Vibroeng. 2017, 19, 2506–2520. [Google Scholar]
- Liao, Z.; Song, L.; Chen, P.; Zuo, S. An automatic filtering method based on an improved genetic algorithm-with application to rolling bearing fault signal extraction. IEEE Sens. J. 2017, 17, 6340–6349. [Google Scholar] [CrossRef]
- Javorskyj, I.; Kravets, I.; Matsko, I.; Yuzefovych, R. Periodically correlated random processes: Application in early diagnostics of mechanical systems. Mech. Syst. Signal Process. 2017, 83, 406–438. [Google Scholar] [CrossRef]
- Igba, J.; Alemzadeh, K.; Durugbo, C.; Eiriksson, E.T. Analysing RMS and peak values of vibration signals for condition monitoring of wind turbine gearboxes. Renew. Energy 2016, 91, 90–106. [Google Scholar] [CrossRef]
- Shao, Y.; Su, D.; Al-Habaibeh, A.; Yu, W. A new fault diagnosis algorithm for helical gears rotating at low speed using an optical encoder. Measurement 2016, 93, 449–459. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Gear crack detection using modified TSA and proposed fault indicators for fluctuating speed conditions. Measurement 2016, 90, 560–575. [Google Scholar] [CrossRef]
- Jin, X.; Chow, T.W. Anomaly detection of cooling fan and fault classification of induction motor using Mahalanobis-Taguchi system. Expert Syst. Appl. 2013, 40, 5787–5795. [Google Scholar] [CrossRef]
- Georgoulas, G.; Karvelis, P.; Loutas, T.; Stylios, C.D. Rolling element bearings diagnostics using the symbolic aggregate approximation. Mech. Syst. Signal Process. 2015, 60, 229–242. [Google Scholar] [CrossRef]
- Gao, J.; Wang, R.; Zhang, R.; Li, Y. A novel fault diagnosis method for rotating machinery based on S transform and morphological pattern spectrum. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1575–1584. [Google Scholar] [CrossRef]
- Rajeswari, C.; Sathiyabhama, B.; Devendiran, S.; Manivannan, K. Diagnostics of gear faults using ensemble empirical mode decomposition, hybrid binary bat algorithm and machine learning algorithms. J. Vibroeng. 2015, 17, 1169–1187. [Google Scholar]
- Geramifard, O.; Xu, J.X.; Panda, S.K. Fault detection and diagnosis in synchronous motors using hidden Markov model-based semi-nonparametric approach. Eng. Appl. Artif. Intell. 2013, 26, 1919–1929. [Google Scholar] [CrossRef]
- Holguin-Londono, M.; Cardona-Morales, O.; Sierra-Alonso, E.F.; Mejia-Henao, J.D. Machine fault detection based on filter bank similarity features using acoustic and vibration analysis. Math. Probl. Eng. 2016, 2016, 7906834. [Google Scholar] [CrossRef]
- Fan, Q.; Ikejo, K.; Nagamura, K.; Kawada, M. Gear damage diagnosis and classification based on support vector machines. J. Adv. Mech. Des. Syst. Manuf. 2014, 8, 21–24. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zhang, X.; Wang, S. Time-frequency atoms-driven support vector machine method for bearings incipient fault diagnosis. Mech. Syst. Signal Process. 2016, 75, 345–370. [Google Scholar] [CrossRef]
- Fernandez-Francos, D.; Martinez-Rego, D.; Fontenla-Romero, O.; Alonso-Betanzos, A. Automatic bearing fault diagnosis based on one-class v-SVM. Comput. Ind. Eng. 2013, 64, 357–365. [Google Scholar] [CrossRef]
- Shen, C.; Wang, D.; Liu, Y.; Kong, F. Recognition of rolling bearing fault patterns and sizes based on two-layer support vector regression machines. Smart Struct. Syst. 2014, 13, 453–471. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.; Bechhoefer, E.; Benbouzid, M. Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR. Appl. Acoust. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, M.; Deng, W.; Yang, X. A new feature extraction method based on EEMD and multi-scale fuzzy entropy for motor bearing. Entropy 2016, 19, 14. [Google Scholar] [CrossRef]
- Fan, Q.; Ikejo, K.; Nagamura, K.; Kawada, M. Diagnosis for gear tooth surface damage by empirical mode decomposition in cyclic fatigue test. J. Adv. Mech. Des. Syst. Manuf. 2014, 8. [Google Scholar] [CrossRef]
- Tabrizi, A.; Garibald, L.; Fasana, A.; Marchesiello, S. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica 2015, 50, 865–874. [Google Scholar] [CrossRef]
- Wu, C.; Chen, T.; Jiang, R.; Ning, L. A novel approach to wavelet selection and tree kernel construction for diagnosis of rolling element bearing fault. J. Intell. Manuf. 2017, 28, 1847–1858. [Google Scholar] [CrossRef]
- Konar, P.; Sil, J.; Chattopadhyay, P. Knowledge extraction using data mining for multi-class fault diagnosis of induction motor. Neurocomputing 2015, 166, 14–25. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.M. Singular value decomposition based feature extraction approaches for classifying faults of induction motors. Mech. Syst. Signal Process. 2013, 41, 348–356. [Google Scholar] [CrossRef]
- Jedlinski, L.; Jonak, J. Early fault detection in gearboxes based on support vector machines and multilayer perceptron with a continuous wavelet transform. Appl. Soft Comput. 2015, 30, 636–641. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Soleimani, A.; Khadem, S.E. Early fault detection of rotating machinery through chaotic vibration feature extraction of experimental data sets. Chaos Solitons Fractals 2015, 78, 61–75. [Google Scholar] [CrossRef]
- Eren, L. Bearing fault detection by one-dimensional convolutional neural networks. Math. Probl. Eng. 2017, 2017, 8617315. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sanchez, R.V. Multi-layer neural network with deep belief network for gearbox fault diagnosis. J. Vibroeng. 2015, 17, 2379–2392. [Google Scholar]
- Martin-del-Campo, S.; Sandin, F. Online feature learning for condition monitoring of rotating machinery. Eng. Appl. Artif. Intell. 2017, 64, 187–196. [Google Scholar] [CrossRef]
- Almeida, L.F.; Bizarria, J.W.; Bizarria, F.C.; Mathias, M.H. Condition-based monitoring system for rolling element bearing using a generic multi-layer perceptron. J. Vib. Control 2015, 21, 3456–3464. [Google Scholar] [CrossRef]
- Li, K.; Chen, P.; Wang, H. Intelligent diagnosis method for rotating machinery using wavelet transform and ant colony optimization. IEEE Sens. J. 2012, 12, 2474–2484. [Google Scholar] [CrossRef]
- Brkovic, A.; Gajic, D.; Savic-Gajic, J.; Gligorijevic, I.; Georgieva, O. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.; Mi, S.; Liu, P.; Liu, D. Applying the fuzzy lattice neurocomputing (FLN) classifier model to gear fault diagnosis. Neural Comput. Appl. 2013, 22, 627–636. [Google Scholar] [CrossRef]
- Cruz-Vega, I.; Rangel-Magdaleno, J.; Ramirez-Cortes, J.; Peregrina-Barreto, H. Automatic progressive damage detection of rotor bar in induction motor using vibration analysis and multiple classifiers. J. Mech. Sci. Technol. 2017, 31, 2651–2662. [Google Scholar] [CrossRef]
- Martinez-Rego, D.; Fontenla-Romero, O.; Alonso-Betanzos, A.; Principe, J.C. Fault detection via recurrence time statistics and one-class classification. Pattern Recognit. Lett. 2016, 84, 8–14. [Google Scholar] [CrossRef]
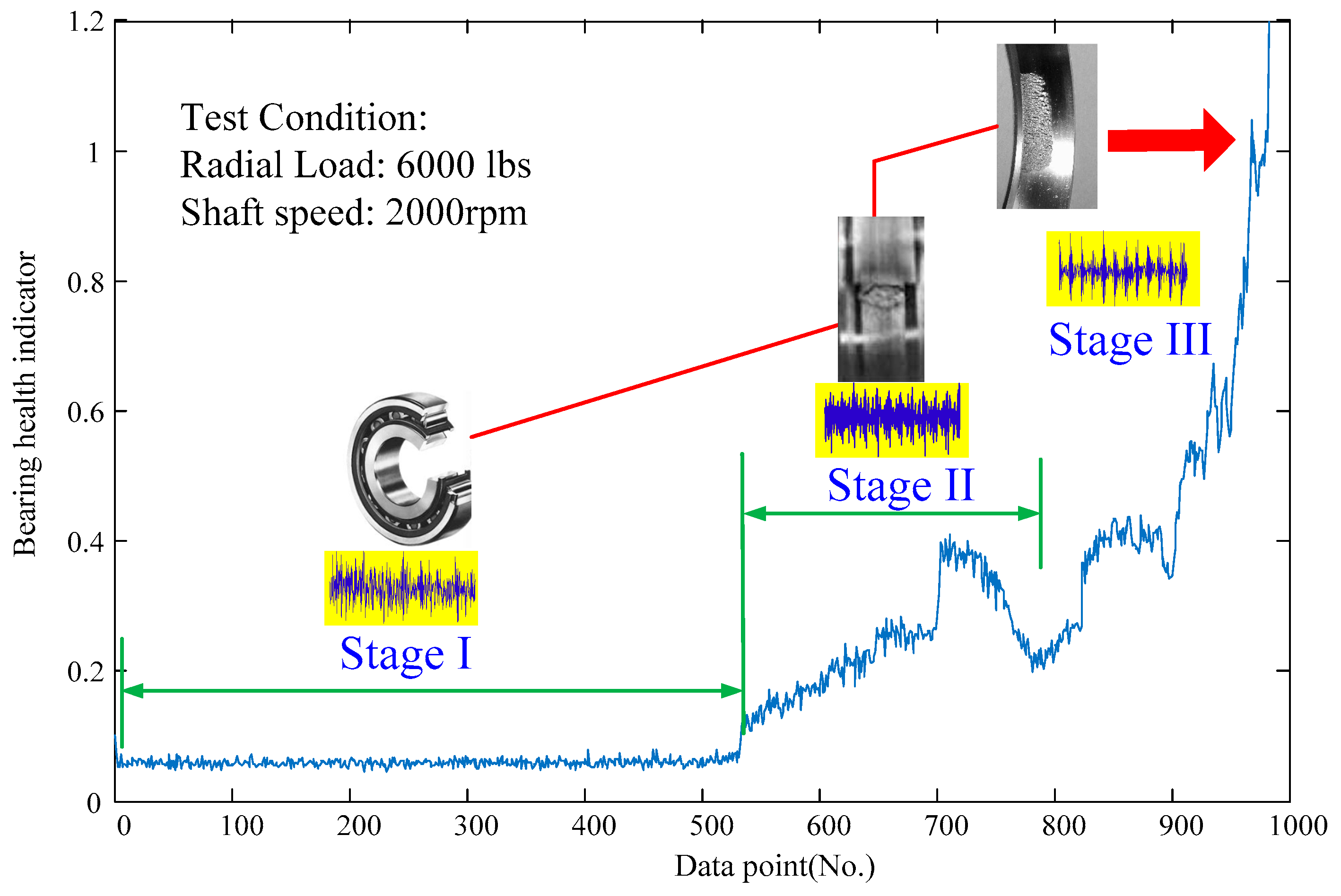
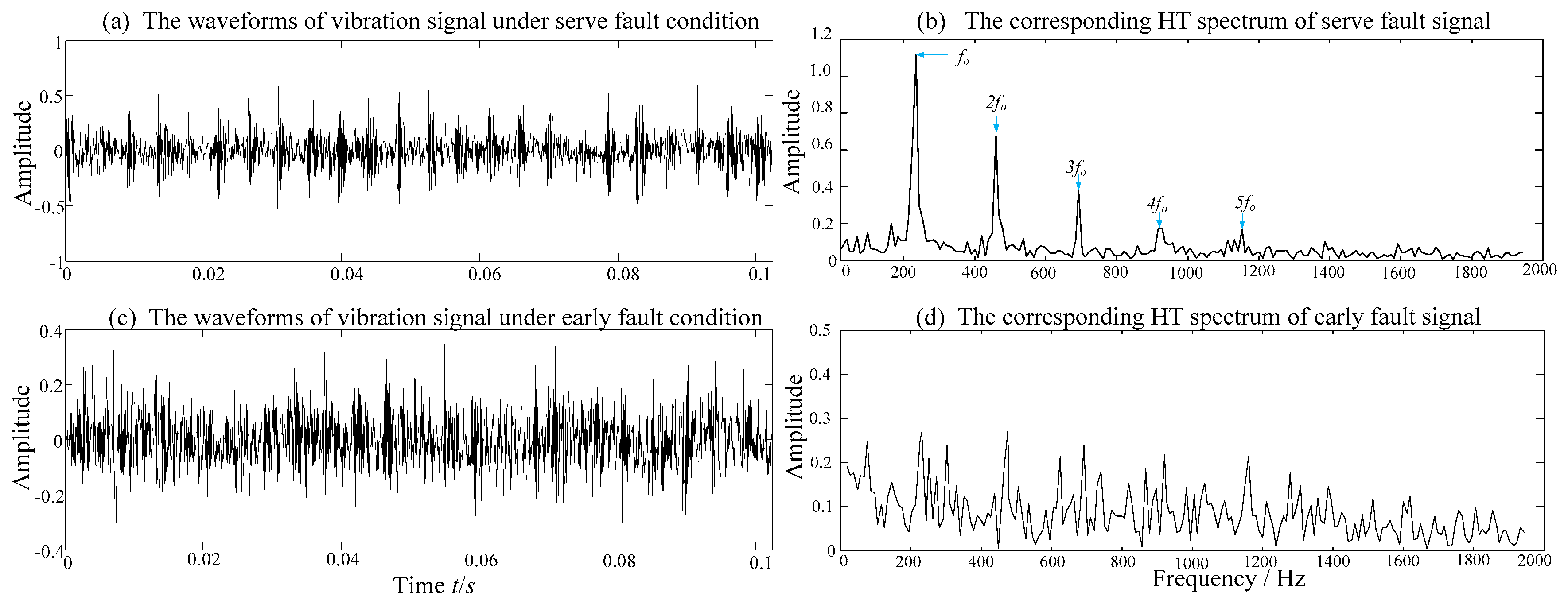
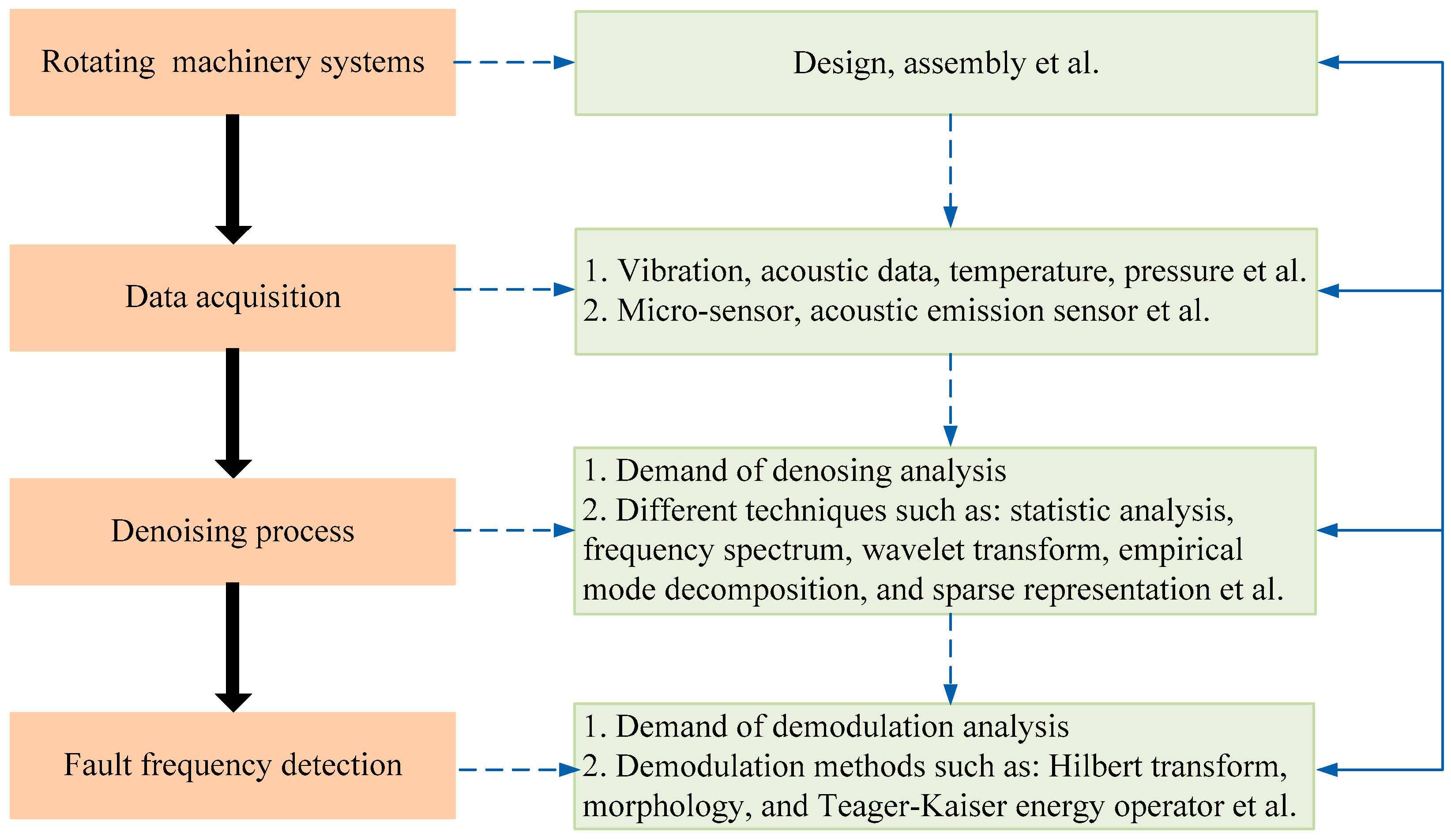
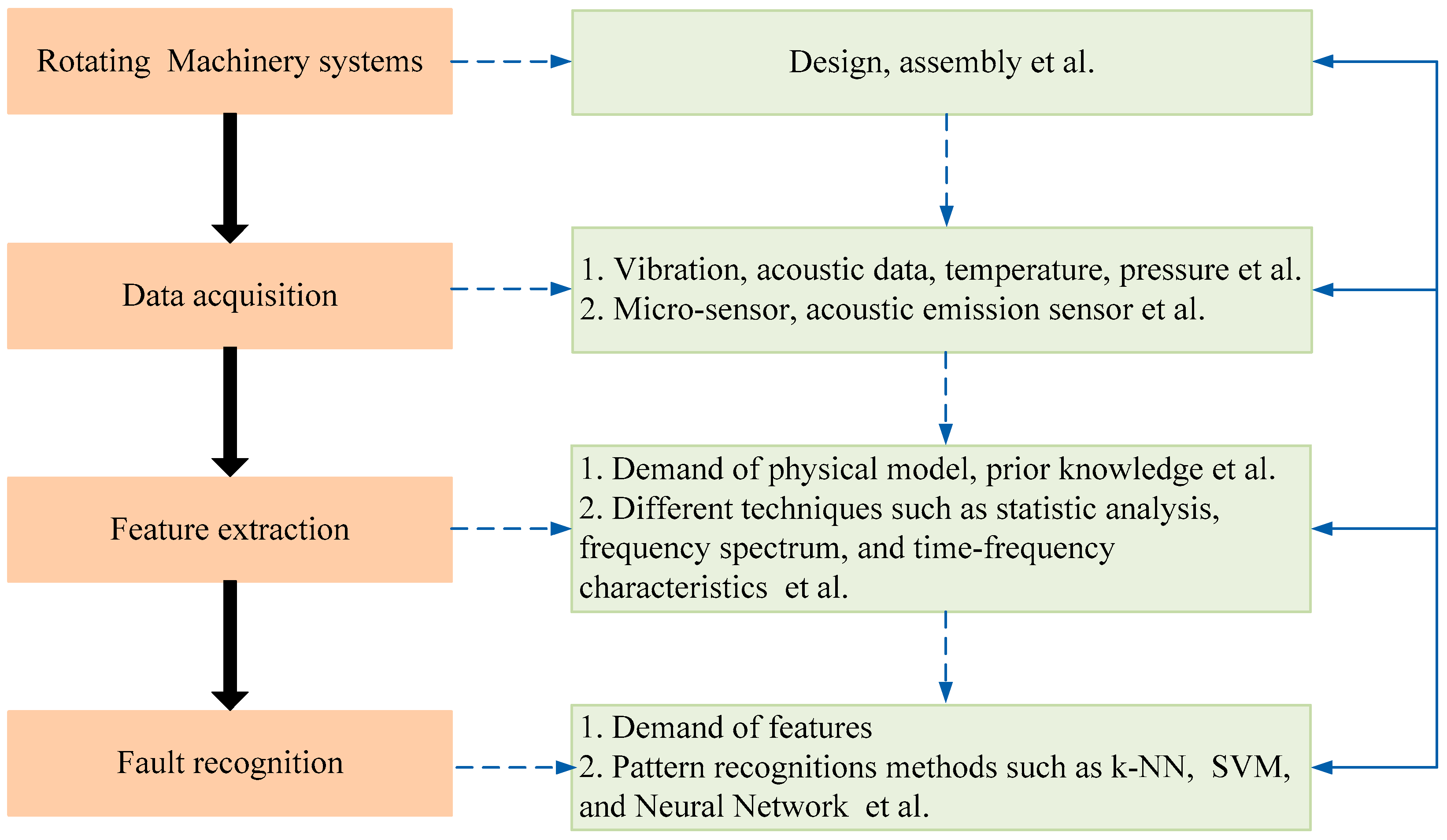
| Authors | Methodologies |
|---|---|
| Dybała et al. [60] | EMD |
| Zhu et al. [61] | EMD + correlation coefficient |
| Dybała et al. [62] | EMD |
| Li et al. [63] | Bandwidth EMD + adaptive multiscale morphological analysis |
| Zhao et al. [64] | Approximate entropy + EMD |
| Lv et al. [65] | Multivariate EMD |
| Parey et al. [66] | EMD + variable cosine window |
| Authors | Methodologies |
|---|---|
| Guo et al. [71] | EEMD + similarity criterion |
| Imaouchen et al. [72] | Complementary EEMD |
| Li et al. [73] | Complementary EEMD |
| Tabrizi et al. [74] | Performance improved EEMD |
| Wang et al. [68] | EEMD + tunable Q-factor wavelet transform |
| Žvokelj et al. [69] | Independent component analysis multivariate monitoring + EEMD |
| Chen et al. [67] | EEMD + Hilbert Square Demodulation |
| Chen et al. [70] | EEMD + adaptive stochastic resonance |
| Jiang et al. [75] | EEMD + multiwavelet packet |
| Authors | Methodologies |
|---|---|
| Li et al. [79] | Differential rational spline-based LMD |
| Liu et al. [76] | LMD |
| Feng et al. [77] | LMD |
| Wang et al. [78] | LMD |
| Authors | Methodologies |
|---|---|
| Chen et al. [81] | Wavelet spatial neighboring coefficient + EWT |
| Boualem et al. [82] | EWT + Hilbert Transform |
| Zhang et al. [80] | Bistable stochastic resonance + EWT |
| Lu et al. [83] | Kurtogram + EWT + sparse regression |
| Authors | Methodologies |
|---|---|
| Ma et al. [84] | Adaptive scale space spectrum segmentation + VMD + Teager energy operator |
| Li et al. [85] | Improved autoregressive-Minimum entropy deconvolution + VMD |
| Yang et al. [86] | Optimized VMD + simulated annealing |
| Guo et al. [87] | VMD + parameter optimization |
| Han et al. [88] | Rescaling subsampling compression + analytical mode decomposition + VMD |
| Jiang et al. [89] | EMD + VMD |
| Authors | Methodologies |
|---|---|
| Elasha et al. [90] | Least mean squares (LMS)+fast block LMS |
| Zhao et al. [91] | Reweighted singular value decomposition |
| Ibrahim et al. [92] | Least mean squares algorithm |
| Mei et al. [93] | Multi-order self-adaptive filter |
| Romero et al. [94] | Machine learning + intrinsic characteristic-scale decomposition |
| Authors | Methodologies |
|---|---|
| Fan et al. [95] | Wavelet transform |
| He et al. [96] | Wavelet transform |
| Cui et al. [97] | Wavelet transform + time–frequency analysis + blind source Separation theory |
| Morsy et al. [111] | Morlet wavelet Filter + envelope detection |
| Yiakopoulos [112] | Morphological + Complex Shifted Morlet Wavelets. |
| Cui et al. [98] | High-frequency characteristics + self-adaptive wavelet de-noising |
| Wang et al. [114] | Complex Morlet wavelet coefficients + sparsity measurement |
| Tse et al. [109] | Wavelet transform + envelope analysis |
| Wang et al. [99] | Adaptive wavelet stripping algorithm |
| Morsy et al. [113] | Maximum Kurtosis + Morlet wavelet |
| Combet et al. [100] | Wavelet bicoherence |
| Moumene et al. [101] | Wavelets multiresolution analysis + the high-frequency resonance |
| Fan et al. [105] | Discrete wavelet transform |
| Karuppaiah et al. [108] | HAAR wavelet |
| Rahman et al. [106] | Discrete wavelet transform |
| Rangel-Magdaleno et al. [107] | Discrete wavelet transform + motor current signature analysis |
| Chen et al. [102] | Adaptive redundant multiwavelet packet |
| He et al. [103] | Adaptive multiwavelet |
| Yang et al. [110] | EMD + autocorrelation de-noising + wavelet package decomposition |
| Li et al. [104] | Intrinsic character-scale decomposition + tunable Q-factor wavelet transform. |
| Authors | Methodologies |
|---|---|
| Lv et al. [116] | Atomic sparse decomposition + genetic algorithm |
| Li et al [120] | Resonance-based sparse signal decomposition + principal component analysis |
| Tang et al. [115] | Shift-invariant sparse coding |
| Mo et al. [117] | Delayed correlation envelope+ sparse decomposition |
| Cui et al. [118] | Sparse decomposition + adaptive impulse dictionary |
| Tang et al. [119] | Sparse representation + compressive sensing |
| Authors | Methodologies |
|---|---|
| Aijun et al. [121] | Morphological operators |
| Raj et al. [122] | Morphological operators + fuzzy system |
| Dong et al. [123] | Minimum entropy deconvolution + K-singular value decomposition |
| Antoni J. [126] | Short-time Fourier-transform-based estimator of the spectral kurtosis |
| Antoni J. [127] | Fast computation of the kurtogram |
| Li et al. [132] | Particle Filter + Kurtogram |
| Wang et al. [125] | Minimum entropy de-convolution + Fast Kurtogram |
| Cong et al. [129] | Spectral kurtosis + autoregressive model |
| Jeong et al. [130] | Spectral kurtosis |
| Chen et al. [133] | Mean envelope Kurtosis + envelope analysis |
| Jia et al. [131] | Maximum correlated kurtosis deconvolution |
| Masmoudi et al. [134] | Time synchronous averaging |
| Dong et al. [135] | Frequency-shifted bispectrum |
| Zhou et al. [136] | Cyclic bispectrum |
| Dong et al. [137] | Wigner–Ville spectrum |
| Yuan et al. [138] | Multi-fractal analysis |
| Siegel et al. [139] | Tachometer-less synchronously averaged envelope |
| Park et al. [140] | Minimum variance cepstrum |
| Fu et al. [141] | Adaptive fuzzy-means clustering |
| Li et al. [142] | Informative frequency band |
| Liu et al. [143] | Adaptive SR + quantum particle swarm |
| Liao et al. [144] | Improved genetic algorithm |
| Kedadouche et al. [124] | Approximate entropy + sample entropy + Lempel-Ziv Complexity. |
| Javorskyj et al. [145] | Periodically correlated random processes |
| Igba et al. [146] | Root mean square (RMS) + peak values |
| Shao et al. [147] | RMS in angle domain |
| Sharma et al. [148] | Modified time synchronous averaging |
| Jin et al. [149] | Mahalanobis distance |
| Authors | Methodologies |
|---|---|
| Georgoulas et al. [150] | Symbolic Aggregate approximation + KNN |
| Gao et al. [151] | Stransform + morphological pattern spectrum + KNN |
| Rajeswari et al. [152] | EEMD + hybrid binary bat + KNN |
| Geramifard et al. [153] | Hidden Markov model + KNN |
| Holguín-Londoño [154] | Filter bank + KNN |
| Authors | Methodologies |
|---|---|
| Shen et al. [158] | Statistical feature + SVM |
| Liu et al. [156] | Impact time frequency dictionary + SVM |
| Fernández-Francos et al. [157] | Band-pass filters and Hilbert Transform + ν-SVM |
| Zhao et al. [160] | EEMD + multi-scale fuzzy entropy + SVM |
| Tabrizi et al. [162] | WPD + EEMD + SVM |
| Wu et al. [163] | Continuous wavelet transform+ SVM |
| Fan et al. [155] | Statistical parameters + PCA + SVM |
| Kang et al. [165] | Singular value decomposition+ SVM |
| Konar et al. [164] | CWT + GA + SVM |
| Saidi et al. [159] | Spectral kurtosis + SVM |
| Authors | Methodologies |
|---|---|
| Eren et al. [169] | 1D convolutional neural networks |
| Jedlinski et al. [166] | CWT + multilayer perceptron network |
| Chen et al. [170] | Multi-layer neural networks |
| Bin et al. [167] | Wavelet packet transform+ EMD + BP neural network |
| Soleimani et al. [168] | Chaotic behavior features + neural network |
| Authors | Methodologies |
|---|---|
| Martin-del-Campo et al. [171] | Dictionary learning |
| Almeida et al. [172] | Time-domain features + generic multi-layer perceptron |
| Li et al. [173] | Wavelet transformation + ant colony optimization |
| Brkovic et al. [174] | Wavelet transformation + quadratic classifier |
| Li et al. [175] | Fuzzy lattice neurocomputing |
| Cruz-Vega et al. [176] | Discrete wavelet + binary classification tree |
| Martínez-Rego et al. [177] | Time domain features + one-class classifier |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Li, Y.; Xu, M.; Huang, W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy 2019, 21, 409. https://doi.org/10.3390/e21040409
Wei Y, Li Y, Xu M, Huang W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy. 2019; 21(4):409. https://doi.org/10.3390/e21040409
Chicago/Turabian StyleWei, Yu, Yuqing Li, Minqiang Xu, and Wenhu Huang. 2019. "A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery" Entropy 21, no. 4: 409. https://doi.org/10.3390/e21040409
APA StyleWei, Y., Li, Y., Xu, M., & Huang, W. (2019). A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy, 21(4), 409. https://doi.org/10.3390/e21040409





