Satellite Quantum Communications When Man-in-the-Middle Attacks Are Excluded
Abstract
:1. Introduction
2. Results
3. Discussion
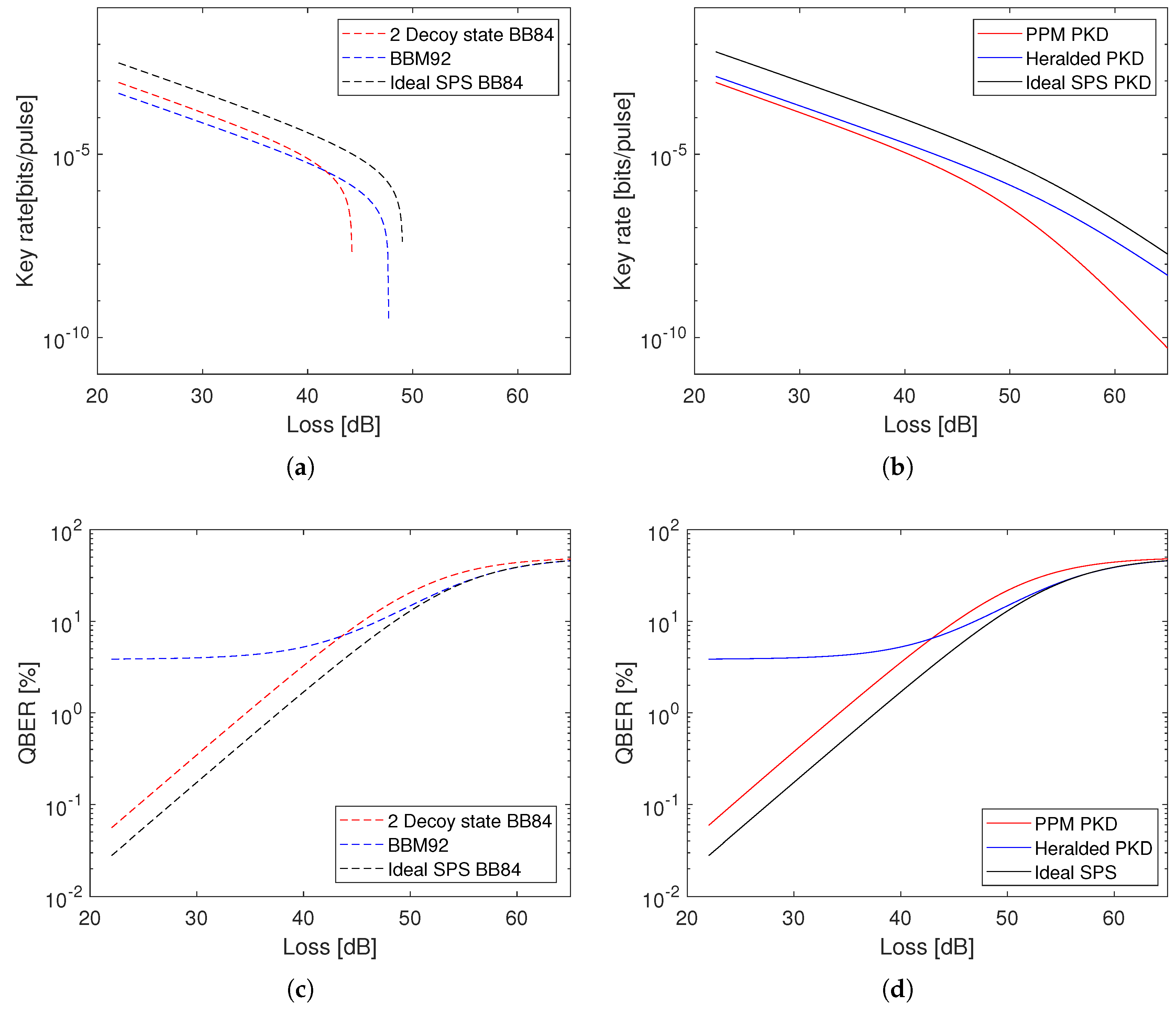
3.1. Weak Coherent Pulse (WCP) Source
3.2. Spontaneous Parametric Down Conversion (SPDC) Photon Pair Source
3.3. Single Photon Source (SPS)
3.4. Summary
4. Materials and Methods
5. Conclusions
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QKD | Quantum key distrbution |
| FSO | Free space optics |
| PKD | Photon key distribution |
| SPS | Single photon source |
| WCP | Weak coherent pulse |
| PPM | Pulse position modulation |
| BB84 | Bennett Brassard 1984 (QKD protocol [24]) |
| BBM92 | Bennett Brassard Mermin 1992 (QKD protocol [15]) |
| QBER | Quantum bit error rate |
| COW | Coherent one way (QKD protocol [27]) |
| SPDC | Spontaneous parametric down conversion |
References
- Vernam, G.S. Cipher Printing Telegraph Systems For Secret Wire and Radio Telegraphic Communications. Trans. Am. Inst. Electr. Eng. 1926, XLV, 295–301. [Google Scholar] [CrossRef]
- Roback, E. Advanced Encryption Standard (AES); Technical Report 141; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Bedington, R.; Arrazola, J.M.; Ling, A. Progress in satellite quantum key distribution. NPJ Quantum Inf. 2017, 3, 30. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Diamanti, E.; Lo, H.K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Sasaki, M. Quantum networks: Where should we be heading? Quantum Sci. Technol. 2017, 2. [Google Scholar] [CrossRef]
- Wyner, A.D. The Wire-Tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Poor, H.V.; Schaefer, R.F. Wireless physical layer security. Proc. Natl. Acad. Sci. USA 2017, 114, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, M.; Ito, T.; Kitamura, M.; Endo, H.; Tsuzuki, O.; Toyoshima, M.; Takenaka, H.; Takayama, Y.; Shimizu, R.; Takeoka, M.; et al. Free-space optical wiretap channel and experimental secret key agreement in 7.8 km terrestrial link. Opt. Express 2018, 26, 19513–19523. [Google Scholar] [CrossRef]
- Tan, Y.C.; Chandrasekara, R.; Cheng, C.; Ling, A. Silicon avalanche photodiode operation and lifetime analysis for small satellites. Opt. Express 2013, 21, 16946–16954. [Google Scholar] [CrossRef]
- Bourgoin, J.P.; Meyer-Scott, E.; Higgins, B.L.; Helou, B.; Erven, C.; Hübel, H.; Kumar, B.; Hudson, D.; D’Souza, I.; Girard, R.; et al. A comprehensive design and performance analysis of low Earth orbit satellite quantum communication. New J. Phys. 2013, 15, 023006. [Google Scholar] [CrossRef]
- Liao, S.K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
- Haber, R.; Garbe, D.; Schilling, K.; Rosenfeld, W. QUBE—A CubeSat for Quantum Key Distribution Experiments. Proc. AIAA/USU Conf. Small Satell. 2018, 49. [Google Scholar] [CrossRef]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.K. Practical decoy state for quantum key distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef]
- Naughton, D.; Bedington, R.; Barraclough, S.; Islam, T.; Griffin, D.; Smith, B. Design considerations for an optical link supporting intersatellite quantum key distribution. Opt. Eng. 2019, 58, 016106. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Ren, J.G.; Liao, S.K.; Zhang, L.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-to-Ground Entanglement-Based Quantum Key Distribution. Phys. Rev. Lett. 2017, 119, 200501. [Google Scholar] [CrossRef]
- Grieve, J.A.; Bedington, R.; Tang, Z.; Chandrasekara, R.C.; Ling, A. SpooQySats: CubeSats to demonstrate quantum key distribution technologies. Acta Astronaut. 2018, 151, 103–106. [Google Scholar] [CrossRef]
- Tang, Z.; Chandrasekara, R.; Tan, Y.C.; Cheng, C.; Sha, L.; Hiang, G.C.; Oi, D.K.L.; Ling, A. Generation and Analysis of Correlated Pairs of Photons aboard a Nanosatellite. Phys. Rev. Appl. 2016, 5, 054022. [Google Scholar] [CrossRef]
- Janossy, L. Rate of n-fold Accidental Coincidences. Nature 1944, 153, 165. [Google Scholar] [CrossRef]
- Grieve, J.A.; Chandrasekara, R.; Tang, Z.; Cheng, C.; Ling, A. Correcting for accidental correlations in saturated avalanche photodiodes. Opt. Express 2016, 24, 3592. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Li, Y.H.; Zou, W.J.; Li, Z.P.; Shen, Q.; Liao, S.K.; Ren, J.G.; Yin, J.; Chen, Y.A.; Peng, C.Z.; et al. Bell Test over Extremely High-Loss Channels: Towards Distributing Entangled Photon Pairs between Earth and the Moon. Phys. Rev. Lett. 2018, 120, 140405. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Vogl, T.; Lecamwasam, R.; Buchler, B.C.; Lu, Y.; Lam, P.K. Space-compatible cavity-enhanced single-photon generation with hexagonal boron nitride. arXiv 2019, arXiv:1902.03019. [Google Scholar]
- Ma, X.; Fung, C.H.F.; Lo, H.K. Quantum key distribution with entangled photon sources. Phys. Rev. 2007, 76, 012307. [Google Scholar] [CrossRef]
- Branciard, C.; Gisin, N.; Lutkenhaus, N.; Scarani, V. Zero-Error Attacks and Detection Statistics in the Coherent One-Way Protocol for Quantum Cryptography. Quant. Inf. Comput. 2007, 7, 639–664. [Google Scholar] [CrossRef]
| Photon Source | QKD Protocol | PKD Encoding (Example) |
|---|---|---|
| Weak coherent pulse (WCP) | Decoy state BB84 | Pulse position modulation (PPM) |
| Spontaneous parametric down conversion (SPDC) pairs | BBM92 (entanglement-based BB84) | Heralded Left or Right-handed polarized photons |
| Ideal single photon source (SPS) | Single photon BB84 | Left or Right-handed polarized photons |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vergoossen, T.; Bedington, R.; Grieve, J.A.; Ling, A. Satellite Quantum Communications When Man-in-the-Middle Attacks Are Excluded. Entropy 2019, 21, 387. https://doi.org/10.3390/e21040387
Vergoossen T, Bedington R, Grieve JA, Ling A. Satellite Quantum Communications When Man-in-the-Middle Attacks Are Excluded. Entropy. 2019; 21(4):387. https://doi.org/10.3390/e21040387
Chicago/Turabian StyleVergoossen, Tom, Robert Bedington, James A. Grieve, and Alexander Ling. 2019. "Satellite Quantum Communications When Man-in-the-Middle Attacks Are Excluded" Entropy 21, no. 4: 387. https://doi.org/10.3390/e21040387
APA StyleVergoossen, T., Bedington, R., Grieve, J. A., & Ling, A. (2019). Satellite Quantum Communications When Man-in-the-Middle Attacks Are Excluded. Entropy, 21(4), 387. https://doi.org/10.3390/e21040387





