Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes
Abstract
:1. Introduction
2. Preliminaries
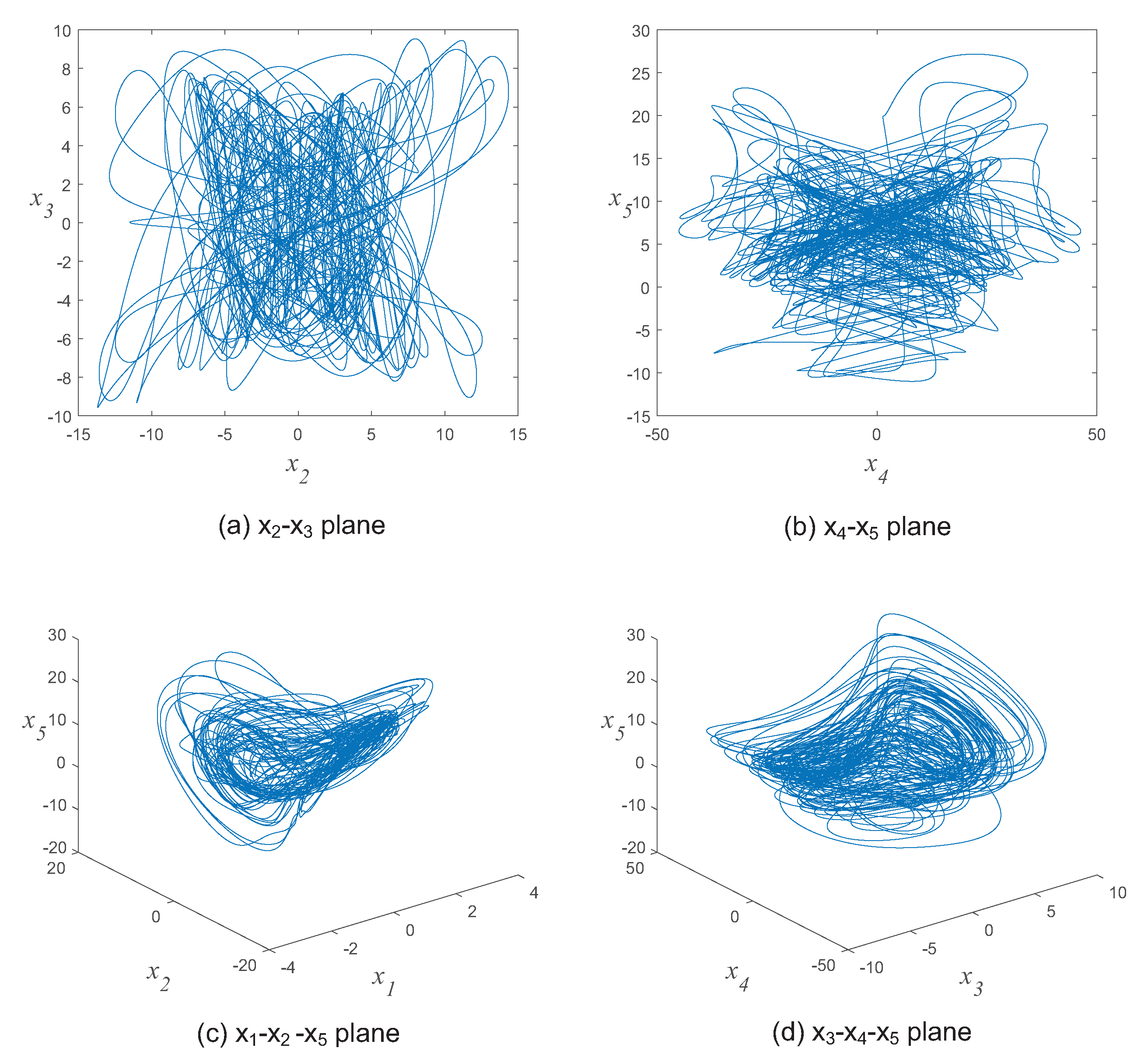
2.1. Hyperchaotic Systems
2.2. Filtering
2.3. DNA Computing
2.4. Latin Square
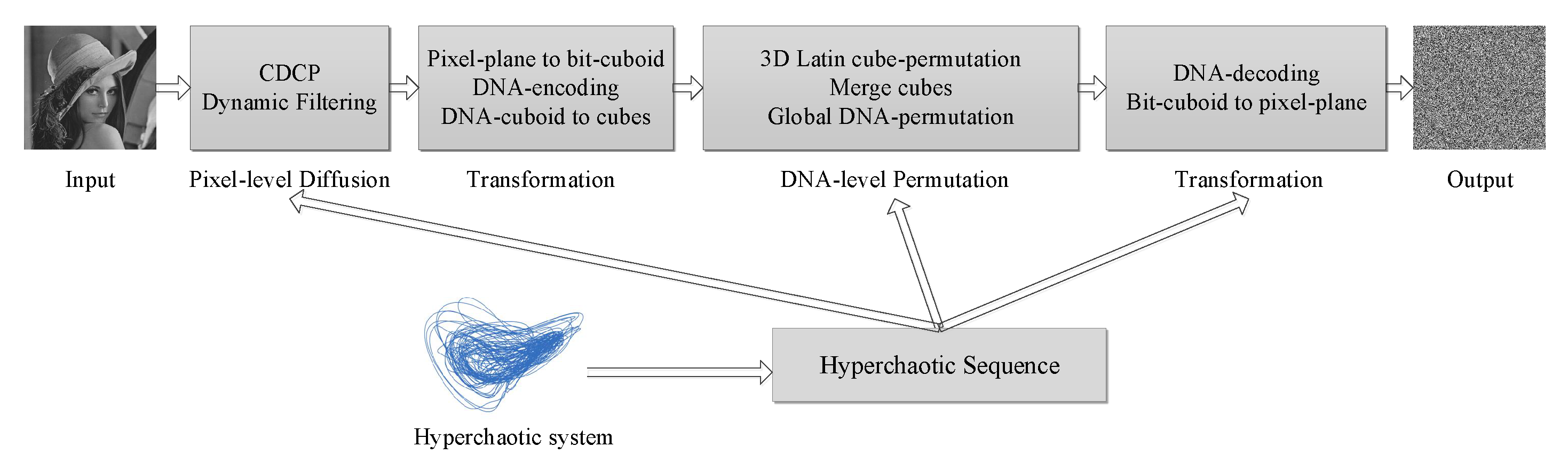
3. The Proposed Image Encryption Approach
3.1. Hyperchaotic Sequence Generation
- Step 1:
- The sequences generated by the first iterations are discarded to eliminate the adverse effects.
- Step 2:
- The 5D hyperchaotic system continues to iterate to generate sequences long enough for image encryption. In the th iteration, we can obtain five state values denoted as .
- Step 3:
- When the iteration completes, a hyperchaotic sequence S can be obtained by contacting all the as
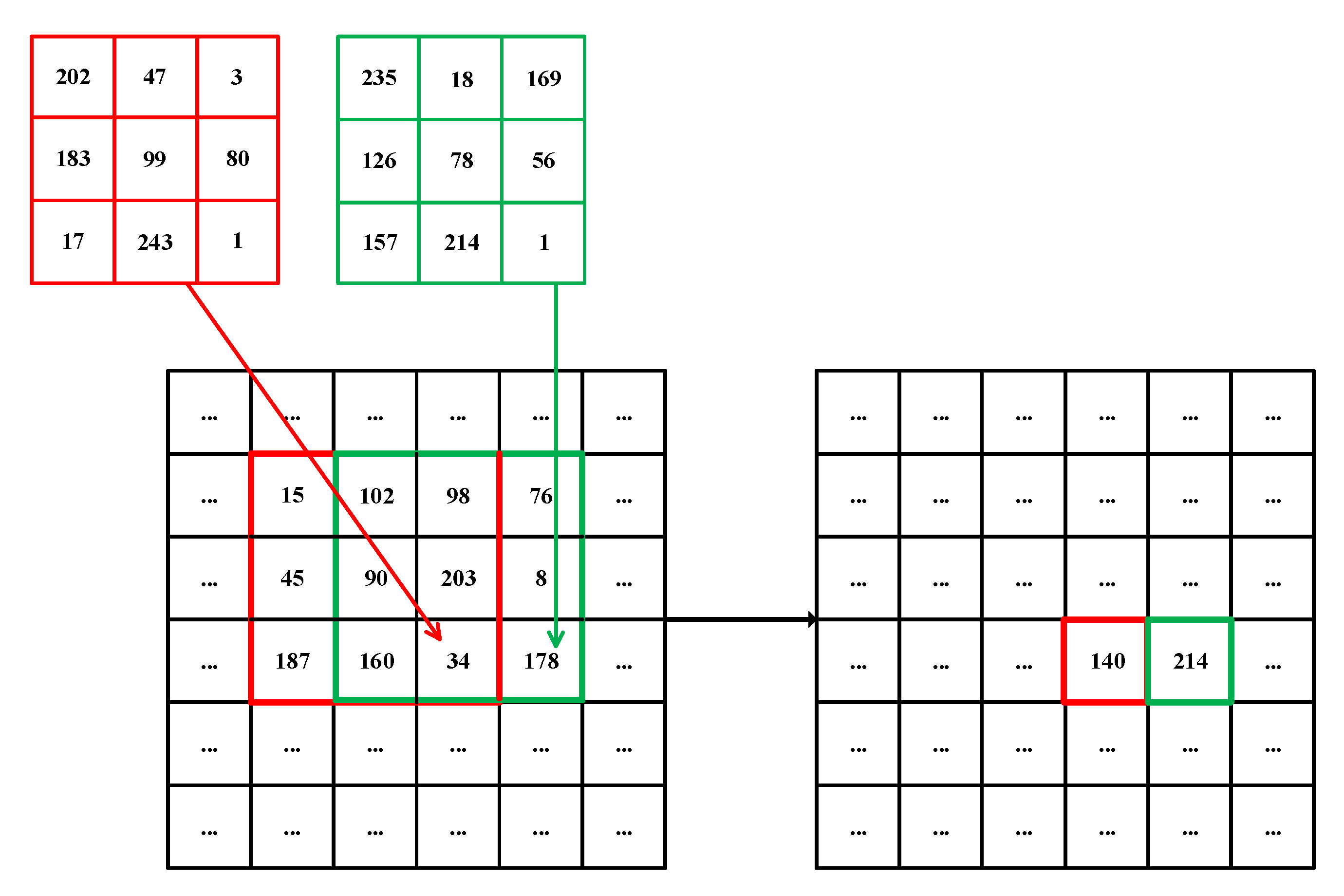
3.2. Dynamic Filtering
3.3. Image to Cubes
- Step 1:
- Given an image with size , where , and d represent the height, width, and depth, respectively, calculate the number of the pixels .
- Step 2:
- Let , if L is an integer, jump to Step 3, else jump to Step 4.
- Step 3:
- Get a cube with size , return.
- Step 4:
- Define , find the biggest K that meets ; then we get a cube with size .
- Step 5:
- Update , if , return; else jump to Step 2.
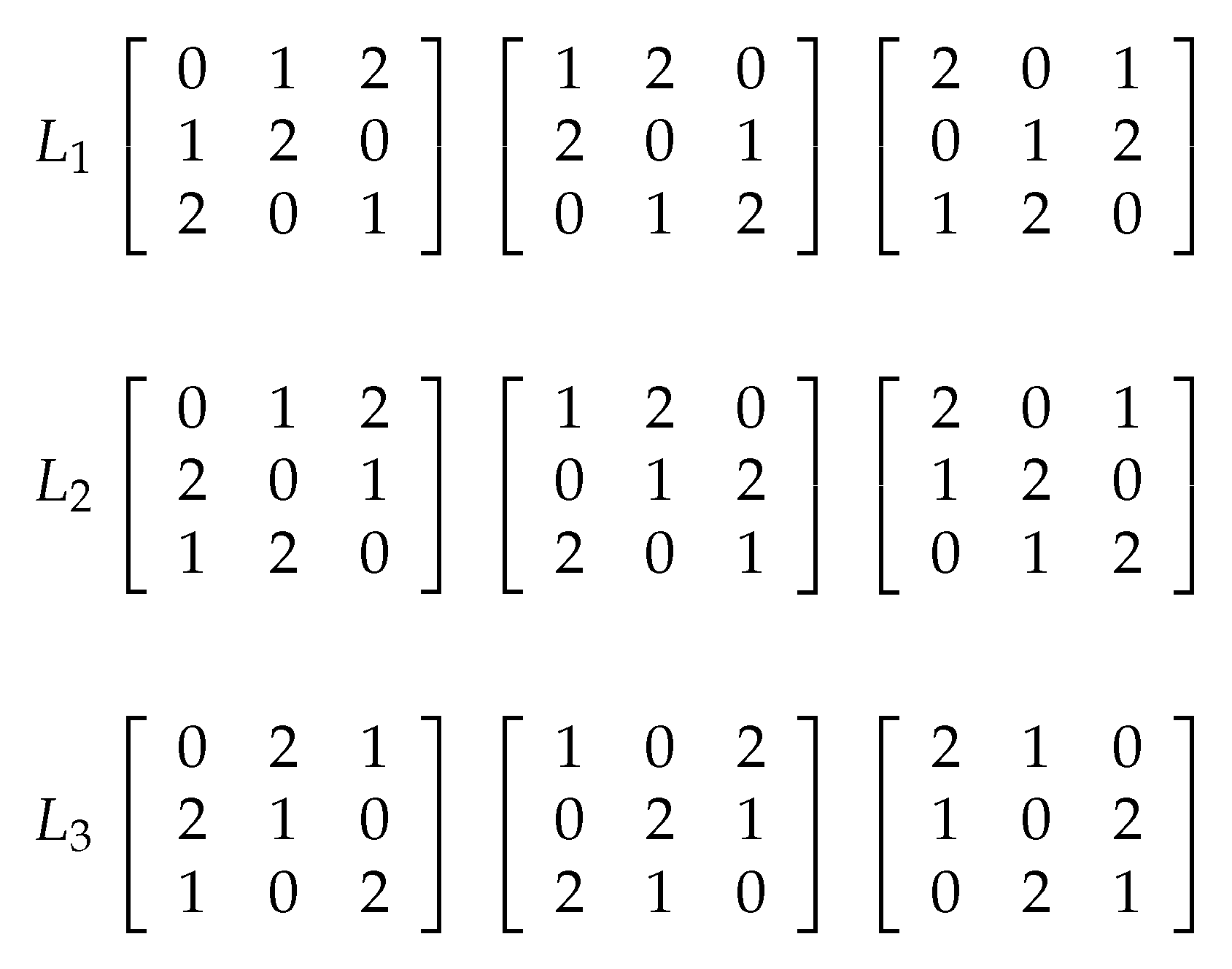
3.4. 3D Latin Cube
3.5. DFDLC: The Proposed Image Encryption Approach with Dynamic Filtering and Latin Cubes
- Step 1:
- Step 2:
- Conduct CDCP with pixels of the image. This operation expands a little change in one pixel of the plain image to very large changes in a variety of pixels of the cipher image.
- Step 3:
- Dynamic filtering on the image. For each pixel, firstly, generate a kernel with the hyperchaotic sequence and set the right-bottom grid to 1. Secondly, do convolution with the kernel and corresponding sub-region of the image associated with the pixel. Thirdly, use the result of the convolution as the new value of the pixel in the cipher image.
- Step 4:
- Transform the pixel image to a DNA image. For each pixel, use an encoding rule decided by the hyperchaotic sequence to encode one pixel into a string with 4 nucleic acids. The DNA encoding rule (Rule N) can be formulated as: , where x is a corresponding value in the hyperchaotic sequence regarding the pixel.
- Step 5:
- Transform the DNA image into one or several cubes using I2C.
- Step 6:
- Conduct DNA-level Latin cube permutation. For each DNA-level cube, generate a Latin cube and then change the position of each nucleic acid according to the Latin cube. In addition, the DNA XOR operation is conducted on the DNA-level cube with a generated DNA cube from the hyperchaotic sequence.
- Step 7:
- Integrate all the DNA-level cubes into a DNA image.
- Step 8:
- Conduct global DNA permutation as described in [2].
- Step 9:
- Decode the DNA image into a pixel image. For each nucleic acid, the DNA encoding rule is decided as the encoding rule in Step 6. The pixel image is the cipher image.
4. Experimental Results
4.1. Experimental Settings
4.2. Security Key Analysis
4.2.1. Key Space
4.2.2. Sensitivity to Security Key
4.3. Statistical Analysis
4.3.1. Histogram Analysis
4.3.2. Information Entropy
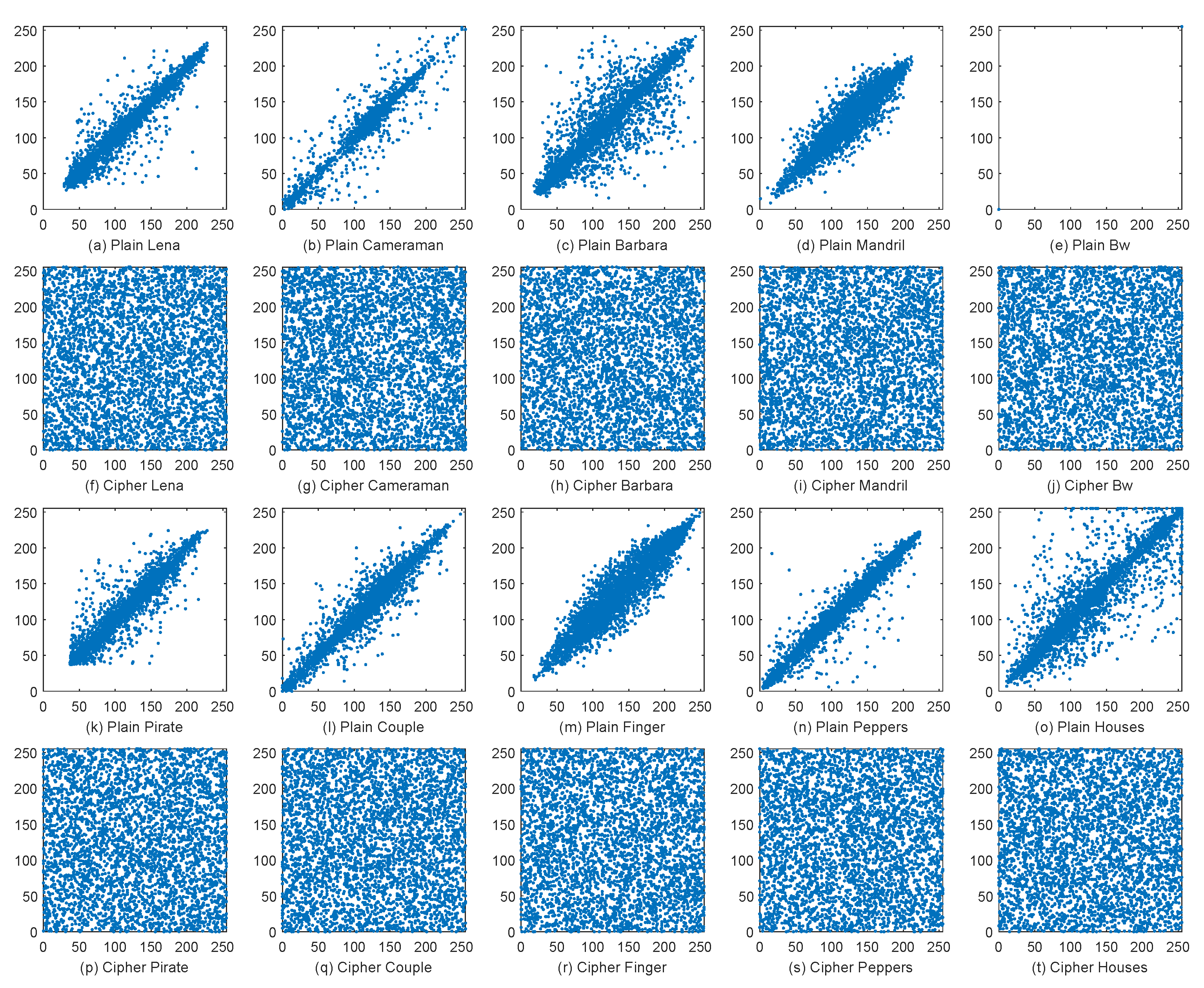
4.3.3. Correlation Analysis
4.4. Analysis of Resisting Differential Attacks
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahmad, J.; Hwang, S.O.; Ali, A. An experimental comparison of chaotic and non-chaotic image encryption schemes. Wirel. Pers. Commun. 2015, 84, 901–918. [Google Scholar] [CrossRef]
- Li, T.; Yang, M.; Wu, J.; Jing, X. A novel image encryption algorithm based on a fractional-order hyperchaotic system and DNA computing. Complexity 2017, 2017, 9010251. [Google Scholar] [CrossRef]
- Abd El-Latif, A.A.; Abd-El-Atty, B.; Talha, M. Robust encryption of quantum medical images. IEEE Access 2018, 6, 1073–1081. [Google Scholar] [CrossRef]
- Guillén-Fernández, O.; Meléndez-Cano, A.; Tlelo-Cuautle, E.; Núñez-Pérez, J.C.; de Jesus Rangel-Magdaleno, J. On the synchronization techniques of chaotic oscillators and their FPGA-based implementation for secure image transmission. PLoS ONE 2019, 14, e0209618. [Google Scholar] [CrossRef] [PubMed]
- Flores-Vergara, A.; García-Guerrero, E.; Inzunza-González, E.; López-Bonilla, O.; Rodríguez-Orozco, E.; Cárdenas-Valdez, J.; Tlelo-Cuautle, E. Implementing a chaotic cryptosystem in a 64-bit embedded system by using multiple-precision arithmetic. Nonlinear Dyn. 2019, 1–20. [Google Scholar] [CrossRef]
- Li, X.; Xie, Z.; Wu, J.; Li, T. Image encryption based on dynamic filtering and bit cuboid operations. Complexity 2019, 2019, 7485621. [Google Scholar] [CrossRef]
- Praveenkumar, P.; Thenmozhi, K.; Rayappan, J.B.B.; Amirtharajan, R. Inbuilt Image Encryption and Steganography Security Solutions for Wireless Systems: A Survey. Res. J. Inf. Tech. 2017, 9, 46–63. [Google Scholar]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Guan, Z.H.; Huang, F.; Guan, W. Chaos-based image encryption algorithm. Phys. Lett. A 2005, 346, 153–157. [Google Scholar] [CrossRef]
- Huang, X. A designed image encryption algorithm based on chaotic systems. J. Comput. Theor. Nanosci. 2012, 9, 2130–2135. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, G.; Jin, H.; Noonan, J.P. Image encryption using the two-dimensional logistic chaotic map. J. Electron. Imaging 2012, 21, 013014. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Xiang, Y. Quantum image encryption using intra and inter bit permutation based on logistic map. IEEE Access 2019, 7, 6937–6946. [Google Scholar] [CrossRef]
- Flores-Vergara, A.; Inzunza-González, E.; García-Guerrero, E.E.; López-Bonilla, O.R.; Rodríguez-Orozco, E.; Hernández-Ontiveros, J.M.; Cárdenas-Valdez, J.R.; Tlelo-Cuautle, E. Implementing a Chaotic Cryptosystem by Performing Parallel Computing on Embedded Systems with Multiprocessors. Entropy 2019, 21, 268. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.W.; Liao, X.; Chen, G. A new chaos-based fast image encryption algorithm. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Sahari, M.L.; Boukemara, I. A pseudo-random numbers generator based on a novel 3D chaotic map with an application to color image encryption. Nonlinear Dyn. 2018, 94, 723–744. [Google Scholar] [CrossRef]
- Zhou, N.; Yan, X.; Liang, H.; Tao, X.; Li, G. Multi-image encryption scheme based on quantum 3D Arnold transform and scaled Zhongtang chaotic system. Quantum Inf. Process. 2018, 17, 338. [Google Scholar] [CrossRef]
- Cvitanović, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G.; Whelan, N.; Wirzba, A. Chaos: Classical and Quantum; Niels Bohr Institute: Copenhagen, Denmark, 2005. [Google Scholar]
- Gangadhar, C.; Rao, K.D. Hyperchaos based image encryption. Int. J. Bifurcation Chaos. 2009, 19, 3833–3839. [Google Scholar] [CrossRef]
- Ye, G.; Wong, K.W. An image encryption scheme based on time-delay and hyperchaotic system. Nonlinear Dyn. 2013, 71, 259–267. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K.; Chen, Y.; Liu, X. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Zhang, L.M.; Sun, K.H.; Liu, W.H.; He, S.B. A novel color image encryption scheme using fractional-order hyperchaotic system and DNA sequence operations. Chin. Phys. B 2017, 26, 100504. [Google Scholar] [CrossRef]
- Bouslehi, H.; Seddik, H. Innovative image encryption scheme based on a new rapid hyperchaotic system and random iterative permutation. Multimed. Tools Appl. 2018, 77, 30841–30863. [Google Scholar] [CrossRef]
- Zhou, H.; Wilke, V.S. Research on image selective encryption and compression algorithm under hyperchaotic system. J. Intell. Fuzzy Syst. 2018, 35, 4329–4337. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Lu, Y.; Zhang, M.; Chen, Y. A novel color image encryption algorithm based on genetic recombination and the four-dimensional memristive hyperchaotic system. Chin. Phys. B 2016, 25, 100503. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Wang, Y. Quantum image compression-encryption scheme based on quantum discrete cosine transform. Int. J. Theor. Phys. 2018, 57, 2904–2919. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Inf. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Alfalou, A.; Brosseau, C.; Abdallah, N.; Jridi, M. Simultaneous fusion, compression, and encryption of multiple images. Opt. Express 2011, 19, 24023–24029. [Google Scholar] [CrossRef]
- Li, T.; Zhou, M. ECG classification using wavelet packet entropy and random forests. Entropy 2016, 18, 285. [Google Scholar] [CrossRef]
- Annaby, M.H.; Rushdi, M.A.; Nehary, E.A. Color image encryption using random transforms, phase retrieval, chaotic maps, and diffusion. Opt. Laser Eng. 2018, 103, 9–23. [Google Scholar] [CrossRef]
- Li, T.; Hu, Z.; Jia, Y.; Wu, J.; Zhou, Y. Forecasting Crude Oil Prices Using Ensemble Empirical Mode Decomposition and Sparse Bayesian Learning. Energies 2018, 11, 1882. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, T.; Shi, J.; Qian, Z. A CEEMDAN and XGBOOST-based approach to forecast crude oil prices. Complexity 2019, 2019, 4392785. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A novel fault diagnosis method based on integrating empirical wavelet transform and fuzzy entropy for motor bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Q.; Wei, X. A novel image encryption scheme based on DNA coding and multi-chaotic maps. Adv. Sci. Lett. 2010, 3, 447–451. [Google Scholar] [CrossRef]
- Wu, X.; Kan, H.; Kurths, J. A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl. Soft. Comput. 2015, 37, 24–39. [Google Scholar] [CrossRef]
- Faragallah, O.S.; Alzain, M.A.; El-Sayed, H.S.; Al-Amri, J.F.; El-Shafai, W.; Afifi, A.; Naeem, E.A.; Soh, B. Block-based optical color image encryption based on double random phase encoding. IEEE Access 2019, 7, 4184–4194. [Google Scholar] [CrossRef]
- Naeem, E.A.; Abd Elnaby, M.M.; Soliman, N.F.; Abbas, A.M.; Faragallah, O.S.; Semary, N.; Hadhoud, M.M.; Alshebeili, S.A.; Abd El-Samie, F.E. Efficient implementation of chaotic image encryption in transform domains. J. Syst. Softw. 2014, 97, 118–127. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X.; Ren, Y. JPEG encryption for image rescaling in the encrypted domain. J. Vis. Commun. Image Represent. 2015, 26, 9–13. [Google Scholar] [CrossRef]
- Lima, J.B.; da Silva, E.S.; Campello de Souza, R.M. Cosine transforms over fields of characteristic 2: Fast computation and application to image encryption. Signal Process. Image Commun. 2017, 54, 130–139. [Google Scholar] [CrossRef]
- Wu, J.; Guo, F.; Liang, Y.; Zhou, N. Triple color images encryption algorithm based on scrambling and the reality-preserving fractional discrete cosine transform. Optik 2014, 125, 4474–4479. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, M.; Zhou, N. Image encryption scheme based on random fractional discrete cosine transform and dependent scrambling and diffusion. J. Mod. Opt. 2017, 64, 334–346. [Google Scholar] [CrossRef]
- Chen, B.; Yu, M.; Tian, Y.; Li, L.; Wang, D.; Sun, X. Multiple-parameter fractional quaternion Fourier transform and its application in colour image encryption. IET Image Process. 2018, 12, 2238–2249. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, H.; Li, P.; Zhao, Y. Design and implementation of color image encryption based on qubit rotation about axis. Chin. J. Electron. 2018, 27, 799–807. [Google Scholar] [CrossRef]
- Liansheng, S.; Xiao, Z.; Chongtian, H.; Ailing, T.; Asundi, A.K. Silhouette-free interference-based multiple-image encryption using cascaded fractional Fourier transforms. Opt. Laser Eng. 2019, 113, 29–37. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. A novel image encryption scheme based on self-synchronous chaotic stream cipher and wavelet transform. Entropy 2018, 20, 445. [Google Scholar] [CrossRef]
- Lv, X.; Liao, X.; Yang, B. A novel scheme for simultaneous image compression and encryption based on wavelet packet transform and multi-chaotic systems. Multimed. Tools Appl. 2018, 77, 28633–28663. [Google Scholar] [CrossRef]
- Vaish, A.; Kumar, M. Color image encryption using MSVD, DWT and Arnold transform in fractional Fourier domain. Optik 2017, 145, 273–283. [Google Scholar] [CrossRef]
- Raja, S.P. Joint medical image compression-encryption in the cloud using multiscale transform-based image compression encoding techniques. Sadhana-Acad. Proc. Eng. Sci. 2019, 44, 28. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Design of image cipher using block-based scrambling and image filtering. Inf. Sci. 2017, 396, 97–113. [Google Scholar] [CrossRef]
- Hua, Z.; Xu, B.; Jin, F.; Huang, H. Image encryption using josephus problem and filtering diffusion. IEEE Access 2019, 7, 8660–8674. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y.; Noonan, J.P.; Agaian, S. Design of image cipher using latin squares. Inf. Sci. 2014, 264, 317–339. [Google Scholar] [CrossRef]
- Panduranga, H.T.; Kumar, S.K.N.; Kiran. Image encryption based on permutation-substitution using chaotic map and Latin Square Image Cipher. Eur. Phys. J. Spec. Top. 2014, 223, 1663–1677. [Google Scholar] [CrossRef]
- Xu, M.; Tian, Z. A novel image encryption algorithm based on self-orthogonal Latin squares. Optik 2018, 171, 891–903. [Google Scholar] [CrossRef]
- Xu, M.; Tian, Z. A novel image cipher based on 3D bit matrix and latin cubes. Inf. Sci. 2019, 478, 1–14. [Google Scholar] [CrossRef]
- Wang, H.; Li, X. A novel hyperchaotic system with infinitely many heteroclinic orbits coined. Chaos Solitons Fractals 2018, 106, 5–15. [Google Scholar] [CrossRef]
- Pano-Azucena, A.; Tlelo-Cuautle, E.; Rodriguez-Gomez, G.; de la Fraga, L. FPGA-based implementation of chaotic oscillators by applying the numerical method based on trigonometric polynomials. AIP Adv. 2018, 8, 075217. [Google Scholar] [CrossRef]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef]
- Zhu, C.; Hu, Y.; Sun, K. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern. J. Electron. Inf. Tech. 2012, 34, 1735–1743. [Google Scholar] [CrossRef]
- Zhan, K.; Wei, D.; Shi, J.; Yu, J. Cross-utilizing hyperchaotic and DNA sequences for image encryption. J. Electron. Imaging 2017, 26, 013021. [Google Scholar] [CrossRef]
- Stinson, D.R. Cryptography: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Li, Y.; Song, X. A new image encryption algorithm based on the fractional-order hyperchaotic Lorenz system. Chin. Phys. B 2013, 22, 010504. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. J. Sel. Areas Telecommun. 2011, 31–38. [Google Scholar]
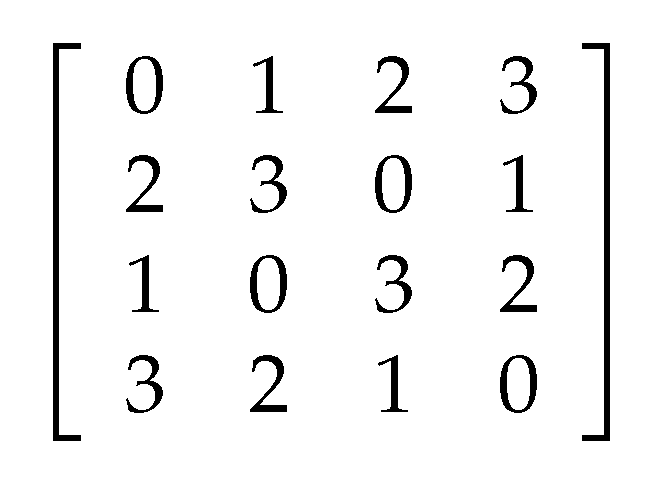
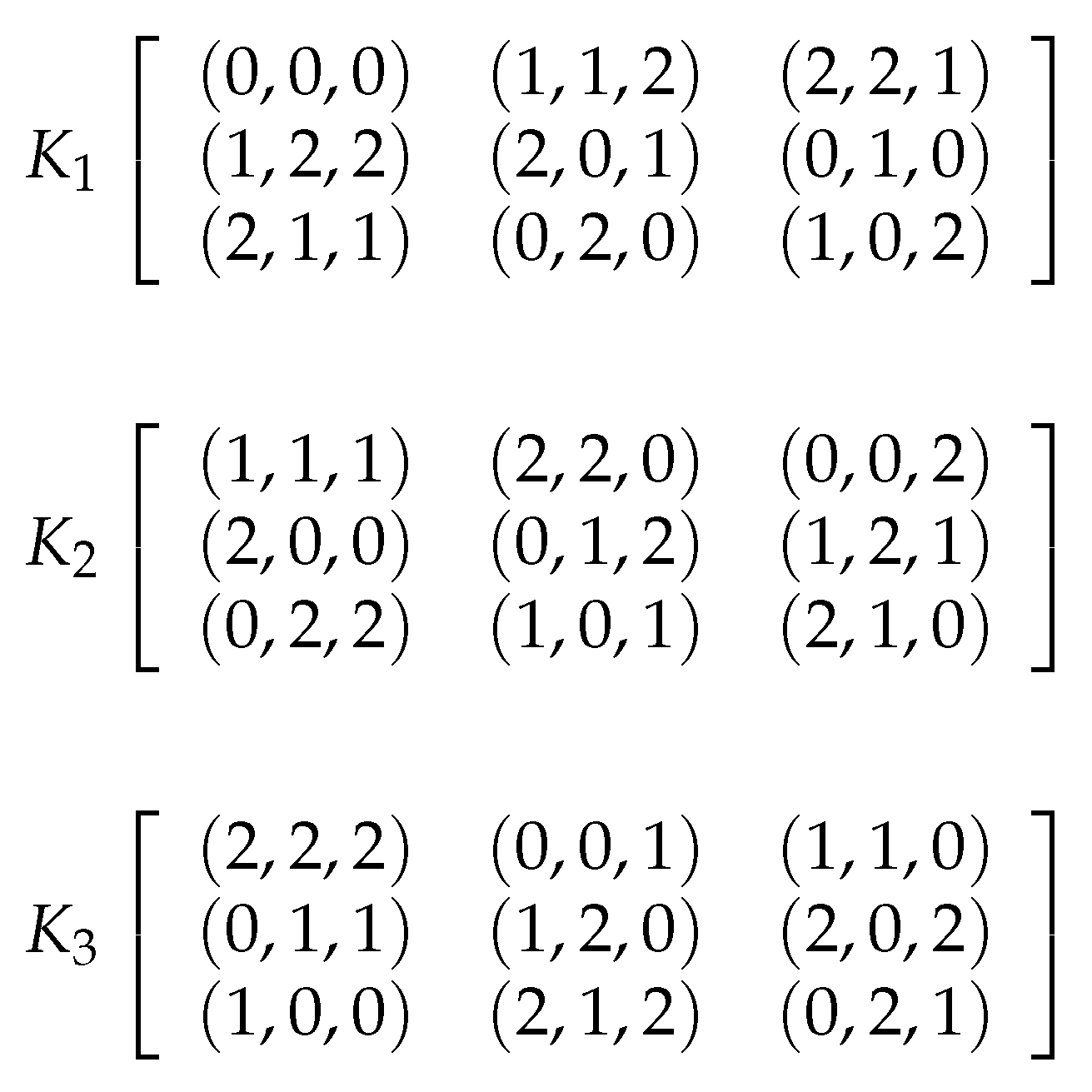

| RULE | Rule 1 | Rule 2 | Rule 3 | Rule 4 | Rule 5 | Rule 6 | Rule 7 | Rule 8 |
|---|---|---|---|---|---|---|---|---|
| 00 | A | T | T | A | C | G | C | G |
| 01 | C | G | C | G | A | A | T | T |
| 10 | G | C | G | C | T | T | A | A |
| 11 | T | A | A | T | G | C | G | C |
| ++ | A | C | G | T |
| A | C | A | T | G |
| C | A | C | G | T |
| G | T | G | C | A |
| T | G | T | A | C |
| -- | A | C | G | T |
| A | C | G | T | A |
| C | A | C | G | T |
| G | T | A | C | G |
| T | G | T | A | C |
| A | C | G | T | |
| A | A | C | G | T |
| C | C | A | T | G |
| G | G | T | A | C |
| T | T | G | C | A |
| Image | Size () | Image | Size () |
|---|---|---|---|
| Lena | Cameraman | ||
| Barbara | Mandril | ||
| Bw | Pirate | ||
| Couple | Finger | ||
| Peppers | Houses |
| Image | Input | Cipher Images | |||||
|---|---|---|---|---|---|---|---|
| DFDLC | FHDNA [2] | HCDNA [61] | CDCP [60] | IC-BSIF [51] | DFBC [6] | ||
| Lena | 7.4455 | 7.9993 | 7.9993 | 7.9994 | 7.9993 | 7.9994 | 7.9994 |
| Cameraman | 7.0480 | 7.9992 | 7.9993 | 7.9981 | 7.9993 | 7.9993 | 7.9992 |
| Barbara | 7.6321 | 7.9993 | 7.9994 | 7.9993 | 7.9992 | 7.9993 | 7.9993 |
| Mandril | 7.2925 | 7.9994 | 7.9992 | 7.9992 | 7.9993 | 7.9993 | 7.9993 |
| Bw | 1.0000 | 7.9993 | 7.9992 | 7.9158 | 7.9992 | 7.9993 | 7.9993 |
| Pirate | 7.2367 | 7.9994 | 7.9993 | 7.9988 | 7.9993 | 7.9994 | 7.9993 |
| Couple | 7.0572 | 7.9993 | 7.9992 | 7.9992 | 7.9993 | 7.9992 | 7.9993 |
| Finger | 6.7279 | 7.9993 | 7.9994 | 7.9990 | 7.9992 | 7.9994 | 7.9993 |
| Peppers | 7.5925 | 7.9993 | 7.9994 | 7.9991 | 7.9993 | 7.9993 | 7.9994 |
| Houses | 7.6548 | 7.9992 | 7.9993 | 7.9993 | 7.9994 | 7.9994 | 7.9993 |
| Image | Input | Cipher Images | ||||||
|---|---|---|---|---|---|---|---|---|
| DFDLC | FHDNA [2] | HCDNA [61] | CDCP [60] | IC-BSIF [51] | DFBC [6] | |||
| Lena | 0.9691 | 0.0023 | 0.0000 | −0.0015 | −0.0004 | −0.0032 | 0.0002 | |
| 0.9841 | 0.0009 | −0.0022 | −0.0020 | 0.0028 | 0.0013 | 0.0010 | ||
| 0.9639 | 0.0008 | 0.0004 | 0.0024 | 0.0016 | −0.0009 | 0.0006 | ||
| Cameraman | 0.9830 | 0.0011 | 0.0013 | 0.0004 | −0.0001 | −0.0015 | −0.0008 | |
| 0.9887 | 0.0009 | 0.0033 | 0.0003 | 0.0019 | 0.0010 | −0.0013 | ||
| 0.9746 | −0.0002 | −0.0000 | −0.0013 | 0.0010 | −0.0012 | −0.0002 | ||
| Barbara | 0.8940 | −0.0003 | −0.0022 | 0.0010 | −0.0026 | −0.0002 | 0.0027 | |
| 0.9572 | 0.0030 | −0.0002 | 0.0004 | 0.0006 | −0.0004 | −0.0029 | ||
| 0.8942 | −0.0029 | −0.0000 | −0.0009 | 0.0005 | 0.0010 | −0.0005 | ||
| Mandril | 0.9322 | 0.0022 | 0.0016 | −0.0007 | 0.0012 | 0.0026 | −0.0006 | |
| 0.9100 | 0.0005 | 0.0035 | −0.0001 | 0.0009 | −0.0001 | −0.0018 | ||
| 0.8647 | −0.0023 | −0.0025 | −0.0017 | −0.0004 | 0.0001 | 0.0016 | ||
| Bw | 1.0000 | 0.0019 | 0.0006 | 0.0004 | −0.0004 | 0.0003 | 0.0000 | |
| 0.9922 | −0.0006 | 0.0009 | 0.0013 | 0.0001 | −0.0005 | −0.0002 | ||
| 0.9961 | −0.0012 | −0.0012 | −0.0002 | 0.0005 | 0.0002 | −0.0016 | ||
| Pirate | 0.9593 | −0.0000 | 0.0015 | −0.0023 | −0.0012 | −0.0026 | −0.0012 | |
| 0.9675 | 0.0009 | 0.0057 | −0.0000 | −0.0008 | −0.0006 | 0.0013 | ||
| 0.9432 | 0.0015 | 0.0001 | 0.0011 | 0.0006 | 0.0005 | 0.0005 | ||
| Couple | 0.9451 | 0.0012 | 0.0013 | 0.0014 | −0.0001 | −0.0006 | −0.0009 | |
| 0.9514 | 0.0025 | −0.0026 | 0.0008 | 0.0001 | 0.0023 | 0.0022 | ||
| 0.9116 | 0.0017 | −0.0011 | −0.0007 | 0.0005 | −0.0008 | −0.0024 | ||
| Finger | 0.9343 | −0.0001 | 0.0002 | 0.0007 | −0.0023 | 0.0004 | −0.0025 | |
| 0.9168 | 0.0002 | −0.0025 | 0.0029 | −0.0032 | −0.0009 | 0.0004 | ||
| 0.8664 | 0.0017 | 0.0005 | −0.0022 | −0.0010 | 0.0030 | −0.0006 | ||
| Peppers | 0.9733 | 0.0003 | −0.0045 | 0.0000 | −0.0003 | −0.0031 | 0.0008 | |
| 0.9763 | −0.0010 | −0.0049 | −0.0005 | 0.0003 | −0.0010 | −0.0003 | ||
| 0.9650 | 0.0011 | −0.0012 | −0.0005 | −0.0025 | 0.0017 | −0.0010 | ||
| Houses | 0.9077 | 0.0020 | 0.0006 | 0.0004 | 0.0026 | 0.0001 | −0.0002 | |
| 0.9173 | 0.0015 | 0.0004 | −0.0032 | 0.0002 | 0.0017 | 0.0006 | ||
| 0.8439 | 0.0020 | 0.0021 | 0.0038 | −0.0011 | 0.0034 | 0.0002 | ||
| Range | [0.8439,1.000] | [−0.0023,0.0030] | [−0.0049, 0.0057] | [−0.0032, 0.0038] | [−0.0032, 0.0028] | [−0.0032, 0.0034] | [−0.0029, 0.0027] | |
| Interval Width | 0.1561 | 0.0053 | 0.0106 | 0.0070 | 0.0060 | 0.0066 | 0.0056 | |
| Image | DFDLC | FHDNA [2] | HCDNA [61] | CDCP [60] | BSIF [51] | DFBC [6] |
|---|---|---|---|---|---|---|
| Lena | 99.6103/0.0129/10 | 99.5814/0.0119/6 | 43.5948/16.8360/0 | 99.6201/0.2837/5 | 99.6166/0.0109/10 | 99.5995/0.0002/10 |
| Cameraman | 99.6055/0.0126/10 | 99.5795/0.0137/4 | 64.6306/31.1442/0 | 99.6146/0.2372/6 | 99.6057/0.0121/10 | 99.6143/0.0002/10 |
| Barbara | 99.6171/0.0075/10 | 99.5842/0.0099/8 | 37.8473/19.6663/0 | 99.6048/0.2136/6 | 99.6165/0.0144/10 | 99.5833/0.0002/10 |
| Mandril | 99.6047/0.0117/10 | 99.5774/0.0125/3 | 51.2024/28.3679/0 | 99.5697/0.2107/4 | 99.6070/0.0117/10 | 99.5998/0.0001/10 |
| Bw | 99.6030/0.0094/10 | 99.3196/0.2433/1 | 47.5142/15.7628/0 | 99.6362/0.2321/5 | 99.6180/0.0142/10 | 99.6033/0.0000/10 |
| Pirate | 99.6176/0.0133/10 | 99.5812/0.0127/4 | 35.8150/27.9995/0 | 99.6403/0.3222/7 | 99.6116/0.0116/10 | 99.5751/0.0002/0 |
| Couple | 99.6089/0.0133/10 | 99.5779/0.0076/5 | 58.1698/27.5116/0 | 99.5718/0.1939/3 | 99.6079/0.0112/10 | 99.5586/0.0001/0 |
| Finger | 99.6097/0.0158/10 | 99.5792/0.0152/4 | 60.3329/29.8886/0 | 99.5984/0.1420/6 | 99.6171/0.0096/10 | 99.6132/0.0002/10 |
| Peppers | 99.6099/0.0154/9 | 99.5800/0.0119/5 | 45.6316/38.2206/0 | 99.5493/0.2509/4 | 99.6099/0.0150/9 | 99.6166/0.0001/10 |
| Houses | 99.6130/0.0126/10 | 99.5795/0.0083/6 | 63.0733/19.2267/0 | 99.6039/0.2053/7 | 99.6135/0.0119/10 | 99.6151/0.0001/10 |
| Image | DFDLC | FHDNA [2] | HCDNA [61] | CDCP [60] | BSIF [51] | DFBC [6] |
|---|---|---|---|---|---|---|
| Lena | 33.4504/0.0466/9 | 33.2700/0.0490/0 | 18.5974/9.5490/0 | 33.5212/0.0775/6 | 33.4714/0.0339/10 | 33.4818/0.0005/10 |
| Cameraman | 33.4909/0.0457/9 | 33.3010/0.0320/0 | 27.0047/13.9227/0 | 33.4222/0.0658/7 | 33.4755/0.0485/10 | 33.4406/0.0005/10 |
| Barbara | 33.4451/0.0350/10 | 33.2533/0.0431/0 | 13.6480/8.2289/0 | 33.4464/0.1075/7 | 33.4722/0.0476/9 | 33.4808/0.0007/10 |
| Mandril | 33.4704/0.0334/10 | 33.2988/0.0336/0 | 22.2006/14.1993/0 | 33.4467/0.0928/5 | 33.4449/0.0423/10 | 33.5136/0.0003/10 |
| Bw | 33.4334/0.0471/10 | 32.0705/1.0272/0 | 18.5654/6.1072/0 | 33.4555/0.1144/4 | 33.4500/0.0468/10 | 41.6585/0.0010/0 |
| Pirate | 33.4736/0.0275/10 | 33.3021/0.0431/1 | 14.8888/14.1945/0 | 33.4664/0.0766/8 | 33.4644/0.0328/10 | 33.4668/0.0003/10 |
| Couple | 33.4282/0.0385/9 | 33.2796/0.0381/0 | 17.8782/7.3362/0 | 33.4293/0.1011/9 | 33.4632/0.0439/10 | 33.4717/0.0003/10 |
| Finger | 33.4311/0.0504/8 | 33.2907/0.0413/0 | 26.0775/14.9380/0 | 33.4911/0.1004/6 | 33.4856/0.0399/9 | 33.5263/0.0006/10 |
| Peppers | 33.4618/0.0432/10 | 33.2735/0.0347/0 | 19.8106/18.6275/0 | 33.4626/0.0752/6 | 33.4301/0.0379/10 | 33.4525/0.0009/10 |
| Houses | 33.4634/0.0358/10 | 33.3322/0.0273/1 | 22.1296/7.4892/0 | 33.4721/0.0467/10 | 33.4448/0.0343/10 | 33.4545/0.0004/10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Shi, J.; Li, X.; Wu, J.; Pan, F. Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes. Entropy 2019, 21, 319. https://doi.org/10.3390/e21030319
Li T, Shi J, Li X, Wu J, Pan F. Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes. Entropy. 2019; 21(3):319. https://doi.org/10.3390/e21030319
Chicago/Turabian StyleLi, Taiyong, Jiayi Shi, Xinsheng Li, Jiang Wu, and Fan Pan. 2019. "Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes" Entropy 21, no. 3: 319. https://doi.org/10.3390/e21030319
APA StyleLi, T., Shi, J., Li, X., Wu, J., & Pan, F. (2019). Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes. Entropy, 21(3), 319. https://doi.org/10.3390/e21030319







