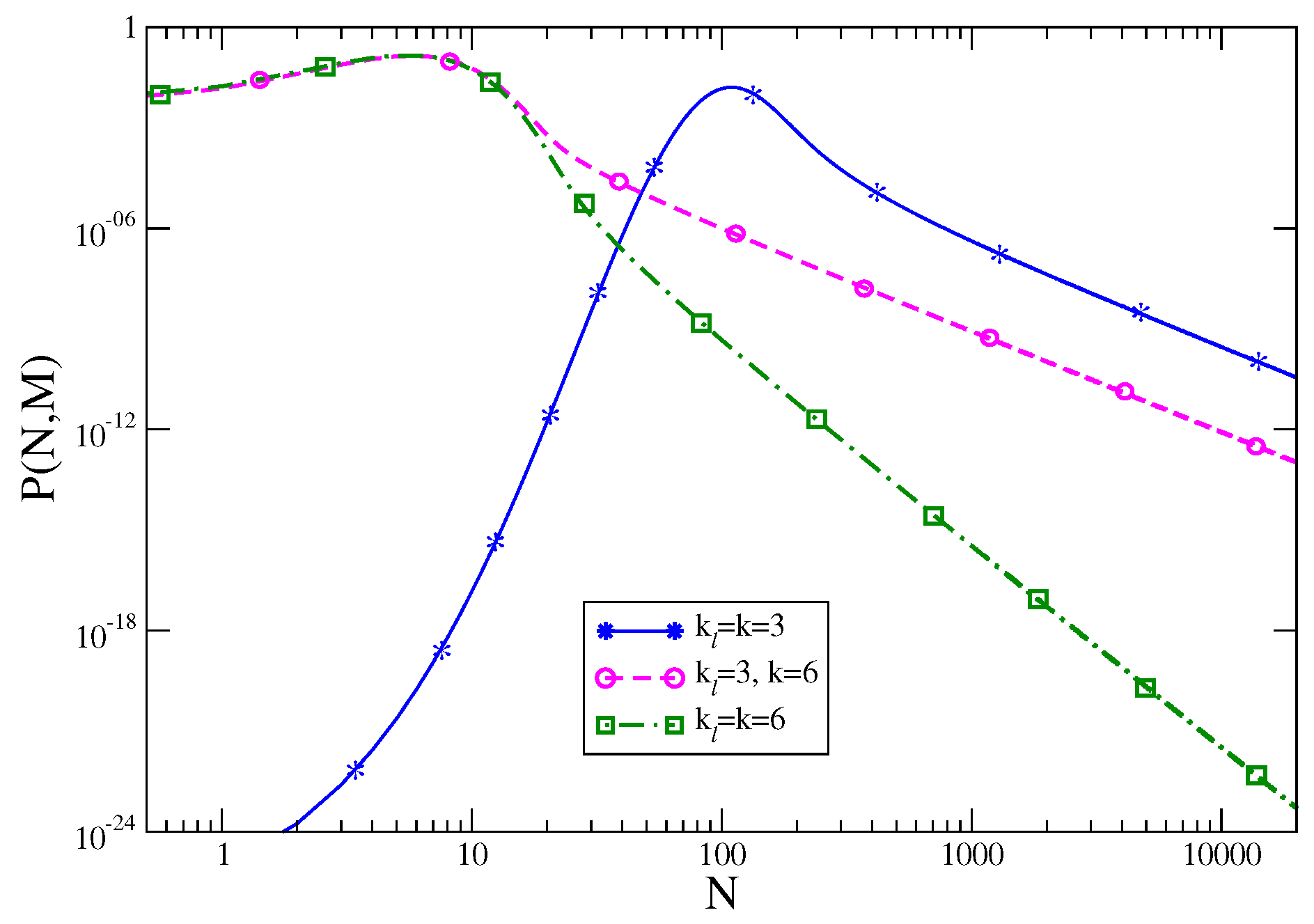
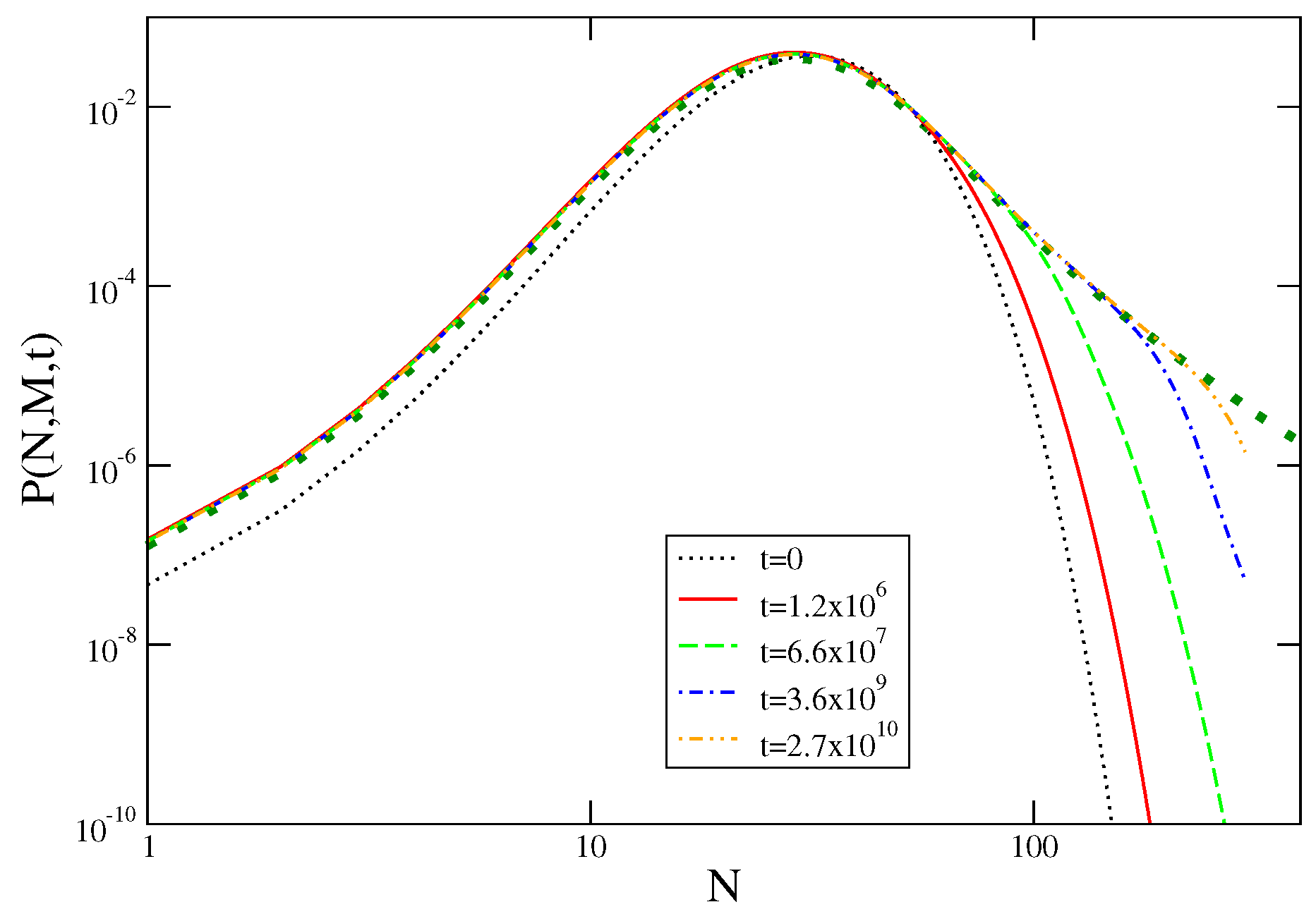
1. Introduction
Quantitative predictions on the occurrence of rare events can be very useful particularly when these events can produce macroscopic effects on the system. This occurs, for instance, when a large fluctuation triggers the decay of a metastable state [
1] leading the system to a completely different thermodynamic condition. Other examples with rare deviations producing important effects are found in many other contexts, as in information theory [
2] and finance [
3].
For a collective variable
N, namely a quantity formed by the addition of many microscopic contributions, such as the energy of a perfect gas or the mass of an aggregate, typical fluctuations are regulated by the central limit theorem. Rare events, instead, may go beyond the theorem’s validity and are described by large deviations theory [
4,
5] which, in principle, aims at describing the whole spectrum of possible fluctuations, no matter how large or rare they are, by means of their full probability distribution
.
It has been found that, in many cases,
exhibits a singular behavior, in that it is non-differentiable around some value (or values)
of the fluctuating variable [
3,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]. Such singularities have an origin akin to those observed in the thermodynamic potentials of systems at criticality. Indeed, a correspondence can be shown between
and the free energy of a companion system, related to the one under study by a duality map [
4,
34,
35,
36], which is interested by a phase-transition.
Recently, a great effort has been devoted to the characterization of these singular behaviors in the large deviation functions of different models where analytical results can be obtained. This has unveiled a rich phenomenology which shares common features. In most cases non-analyticities are a consequence of a particular condensation phenomenon denoted as condensation of fluctuations.
It occurs when a significant contribution to the fluctuations is built within a limited part of phase-space, or is provided by just one of the degrees of freedom of the system. This is analogous to what happens, for instance, in the usual condensation of a gas when it concentrates in a liquid drop, or in the well-known Bose–Einstein condensation, where the mode with vanishing wavevector contributes macroscopically. However, while usual condensation represents the typical behavior of the system, the condensation of fluctuations can only be observed when certain rare events take place.
Another interesting feature of systems with singular probability distributions can be their extreme sensibility to small perturbations. Usually, the properties of a system made of many constituents or degrees of freedom do not change much if some features of a single particle are slightly changed. This is true both for the average properties and for the fluctuations. For instance, neither the average energy of a gas nor its fluctuations change appreciably if the mass of one single molecule is increased a bit. This is simply because this particle is only one out of an Avogadro number. However, when condensation of fluctuations occurs, one can observe a giant response if the perturbed degree of freedom is exactly the one that contributes macroscopically to the fluctuation.
Singular probability distributions raise the question about the validity of the fluctuation relations (FRs). These relations have been extensively studied recently [
40,
41] because they reflect general symmetries of the deviations of certain quantities and are believed to contribute to a general understanding of non-equilibrium states. In particular, FRs connect the probability of observing events with a certain value
N of the fluctuating variable, to the probability of the events associated to the opposite value
. Among other open issues on the subject, one is represented by the case of singular fluctuations. Indeed, the singularity in
usually separates two regions where fluctuations have very different properties. For instance, on one side of
one can have a standard situation where all the degrees of freedom contribute, whereas on the other side fluctuations can condense and be determined by the contribution of a single degree. Clearly, if
N is such that
N and
fall on different branches of
, namely on the two sides of
, the mechanism whereby an FR can be fulfilled must be highly non-trivial. In general, singular probability distributions may, or may not, exhibit the FR and a general understanding of this point is still not achieved.
This paper is a brief review devoted to the discussion of singular probability distributions where, without any presumption of neither completeness or mathematical rigor, we present examples of models where such non-analyticities show up, we highlight the mathematical mechanism producing condensation, and we discuss some relevant aspects related to the subject, such as those mentioned above. We do that in a physically oriented spirit, providing whenever possible an intuitive interpretation and a simple perspective. Non-differentiable probability distributions have been previously reviewed also in [
42], where however the authors focus on different models and complementary aspects with respect to those addressed in this paper.
The paper is organized as follows. In
Section 2 we recall some basic results of probability theory and introduce some notations. In
Section 3 we present some models of statistical mechanics where non-differentiable probability distributions have been computed for different collective quantities. In
Section 4 we illustrate in detail some phenomena related to the singular distribution function, mainly using the urn model as a paradigm, and discuss how similar behaviors arise in other systems. We also discuss the topic of the fluctuation relations. More specific features, such as giant response and observability, are then presented in
Section 5, and, finally, some conclusions are drawn in
Section 6.
2. Probability Distributions: Generalities
We consider a generic stochastic system, whose physical state is defined by the random variable
x taking values on a suitable phase space. We will be mainly interested in the behavior of collective random variables, that are defined as the sum of a large number of microscopic random variables. For these quantities some general results can be derived [
5]. As an example let us consider the sum
of a sequence of
M random variables
, with empirical mean
The quantities
can represent a sequence of states of a system (for instance, the position of a particle along a trajectory) or an ensemble of variables describing its microscopic constituents (e.g., the energies of the single particles of a gas). In the case of independent identically distributed variables, with expectation
and finite variance
, one has that the empirical mean tends to
for large
M, namely
where
is a small quantity and hereafter
(also
or
) is the probability of an event
E. The above equation represents the Law of Large Numbers.
As a further step, one can describe the statistical behavior of the small fluctuations of
around the average
,
, introducing the quantity
which, for very large
M, and for
, has the following distribution function
This result is the central limit theorem (CLT), that holds also in the case of weakly correlated variables.
More in general, fluctuations of arbitrary size of the quantity
can, under certain conditions, be characterized by the large deviation principle (LDP)
where
is the so called rate function. When
has a single absolute maximum (in
), the rate function is positive everywhere but for
, where it vanishes. It is easy to obtain the CLT Equation (
4) from the LDP Equation (
5) by expanding up to second order the function
around
. However, as we will discuss in detail below, there are interesting cases where the LDP in the form Equation (
5) is not satisfied.
A simple example where LDP holds and the rate function can be easily computed is obtained by considering
as dichotomous variables taking the value
with probability
q and
with probability
. Then, using the Stirling approximation, one obtains the explicit expression for the rate function:
Expanding Equation (
6) around the mean
one has the CLT
4. General Features of Singular Probability Distributions
In this section we will discuss some general properties of singular probability distributions observed in the different models mentioned above, focusing on the common physical interpretation and on the underlying mathematical structure.
4.1. Duality
The singular behavior of the probability distribution seen in the examples of the previous section has an interpretation akin to the occurrence of phase transitions in ordinary critical phenomena. In order to discuss this point we can refer to the Gaussian model as a paradigm. The partition function is
where
is the probability of microscopic configurations as specified by the field
. For instance, in a canonical setting it is
, where
is the inverse temperature
; in this case
Z depends on
T and
V, the volume. On the other hand the probability of the collective variable
N of Equation (
9) can be written as
In view of Equation (
15), one can recognize Equation (
16) as a partition function as well. However this is not the partition function of the original model that is, in this example, the Gaussian one. Instead,
in Equation (
16) can be interpreted as the partition function of a dual system that can be obtained from the original one upon removing all the configurations such that the argument of the delta function in Equation (
16) does not vanish. In other words, this is the model one arrives at upon constraining configurations in a certain way. In this case the requirement is that the variance of
must equal a given value
N. Such a system, a Gaussian model with a constraint on the variance, is the spherical model of Berlin and Kac [
58].
The equilibrium properties of the spherical model are exactly known. For fixed
N, there is a phase-transition at a critical temperature
, from a disordered phase for
to an ordered one below
. Equivalently, still in the Berlin–Kac model, if one keeps
T fixed, the transition occurs changing the variance
defined in Equation (
9) upon crossing a critical value
. The ordered phase is found for
, in this case. The presence of such a phase transition crossing
determines a singularity of the partition function
of the spherical model (Equation (
16)) at
. However the same quantity
is also the probability distribution of the quantity
in the context originally considered, the Gaussian model. This explains what one observes in
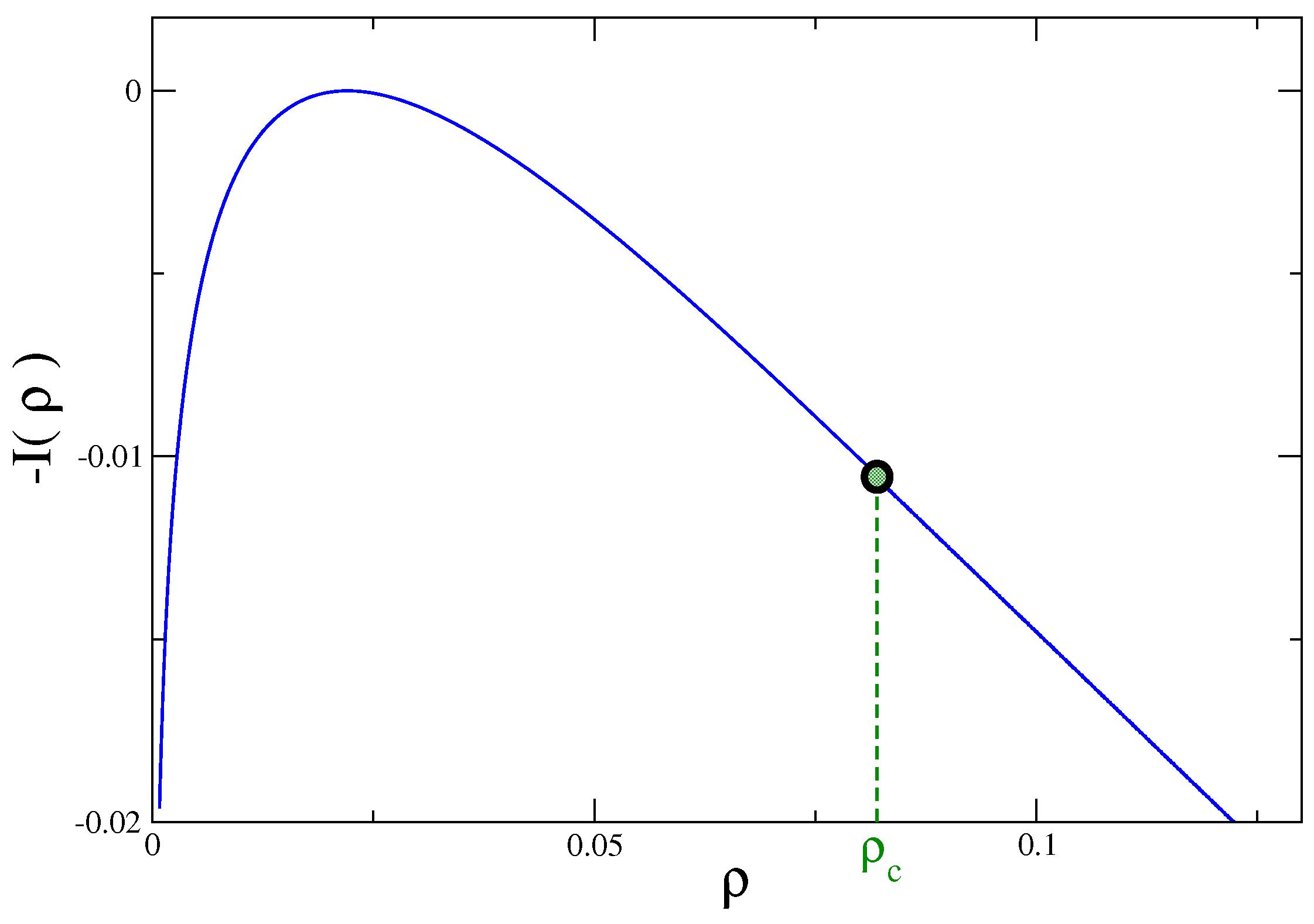
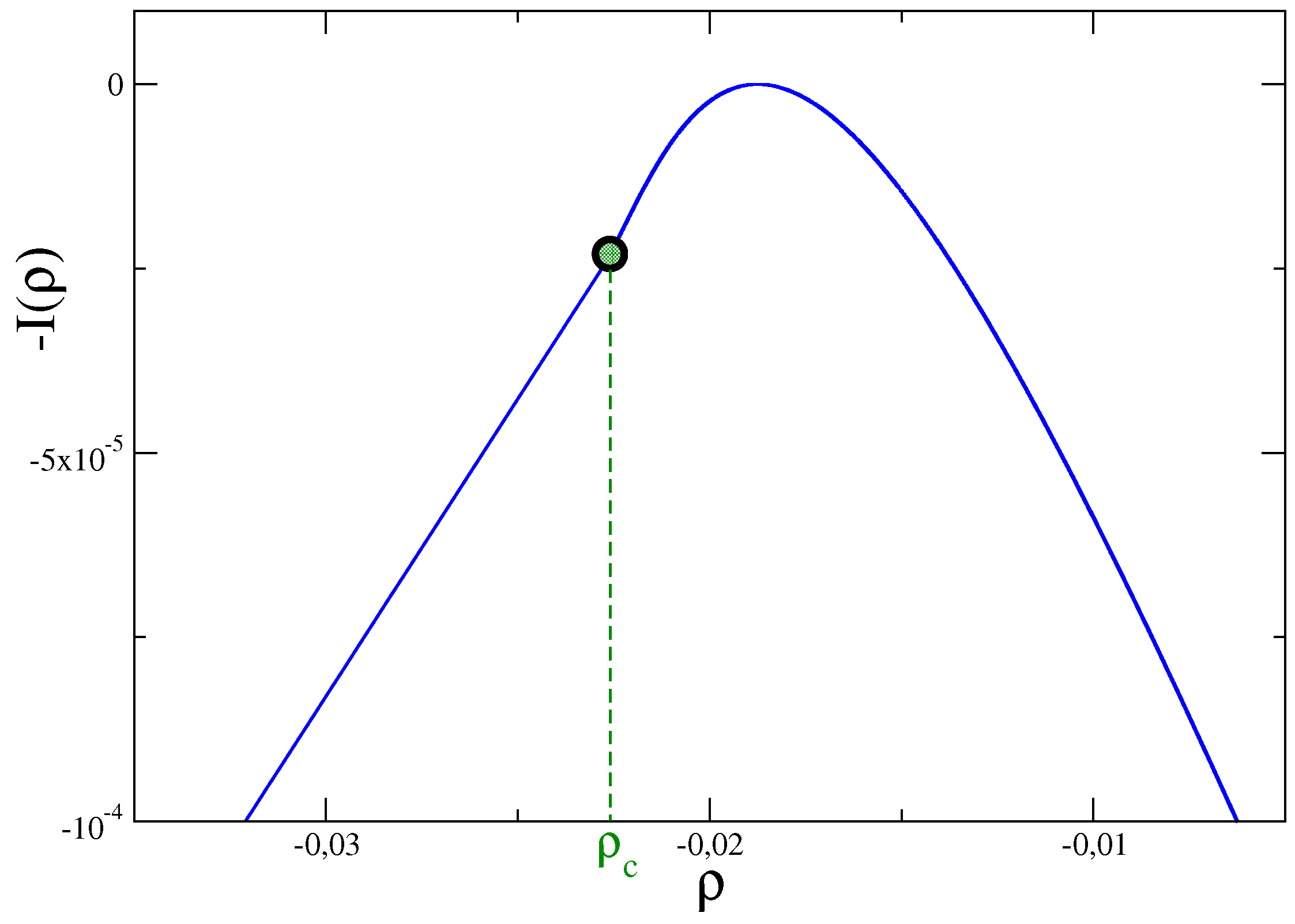
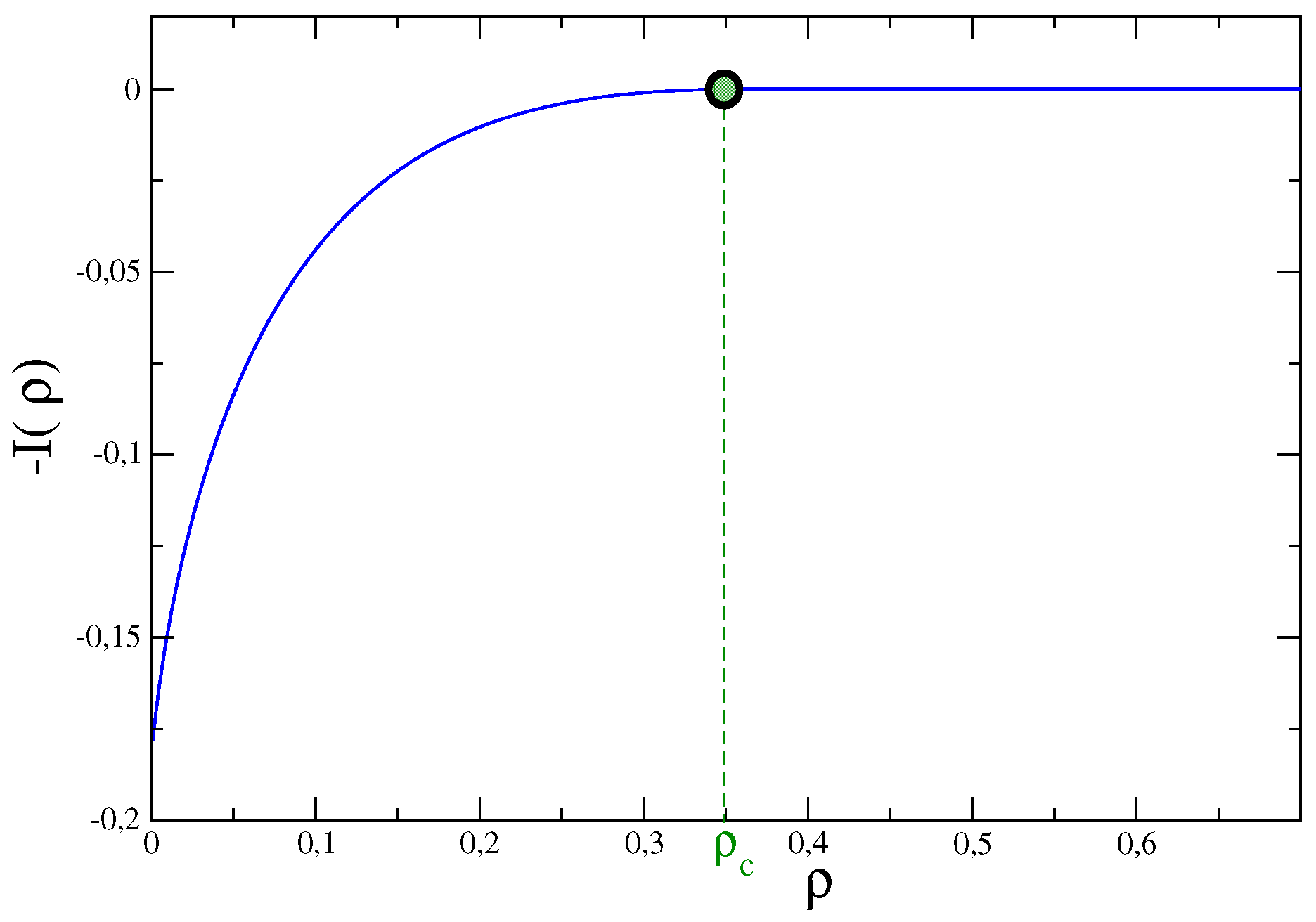
Figure 1.
is the value of
N marked by a dot in this figure, where the singular behavior shows up.
This dual interpretation of , as a probability distribution of a collective variable in the original model, or as a partition function in a dual model, may help to understand why singularities are manifested in the probability distributions. Indeed, if one asks the question: why a simple model without phase transitions, such as the Gaussian model, exhibits a non trivial singularity in the probability distribution , the answer can be that, although the original model is quite simple, the dual one is far from being trivial, with a phase-transition induced by the presence of the constraint. This generates anomalous behavior in the fluctuation spectrum of the original model.
We have discussed the fact that imposing a constraint to the Gaussian model we change the system into a dual one that is interested by a phase transition, since this is the spherical model. Is this an isolated example or has this feature some generality? The answer is that it occurs quite often. Besides the above mentioned spherical model, another well known example where the same mechanism is at work is the perfect boson gas. There is no phase transition in a gas with a non conserved number
N of bosons, as in the case of photons, but if the number
N of particles is fixed Bose–Einstein condensation happens. The partition function of the conserved bosons, for a given volume and temperature, has a singularity at a certain value of the boson number
(or density). This singularity corresponds to the critical number of particles below which the condensed phase develops. According to the duality principle discussed above, this implies that the probability distribution of the number of bosons in a system of, say, photons, where this number is allowed to fluctuate, will be singular at the same value
of the random variable
N [
33]. The very urn model is another instructive example. One can consider a model, dual to the one discussed in
Section 3.3, where the total number of balls is conserved [
21]. Marbles can only be exchanged among boxes and their density
is an external control parameter. This model is known to be interested, for
, by a phase transition crossing
. Notice that, since
is a control parameter, having
in this dual model is not a rare event (as in the model introduced in
Section 3.3). A similar situation is found in related models such as the zero range process [
18,
21,
28].
4.2. Condensation
In order to see how singularities may come about in another perspective we will discuss the phenomenon in the framework of the urn models, where the physical meaning is probably more transparent in term of a condensation mechanism. Something similar occurs also in the other models considered in
Section 3, regardless of the fact that the rate function is well defined or not.
Let us consider the conditional probability
that one of the
M a priori equivalent urns contains
n particles, given that there are
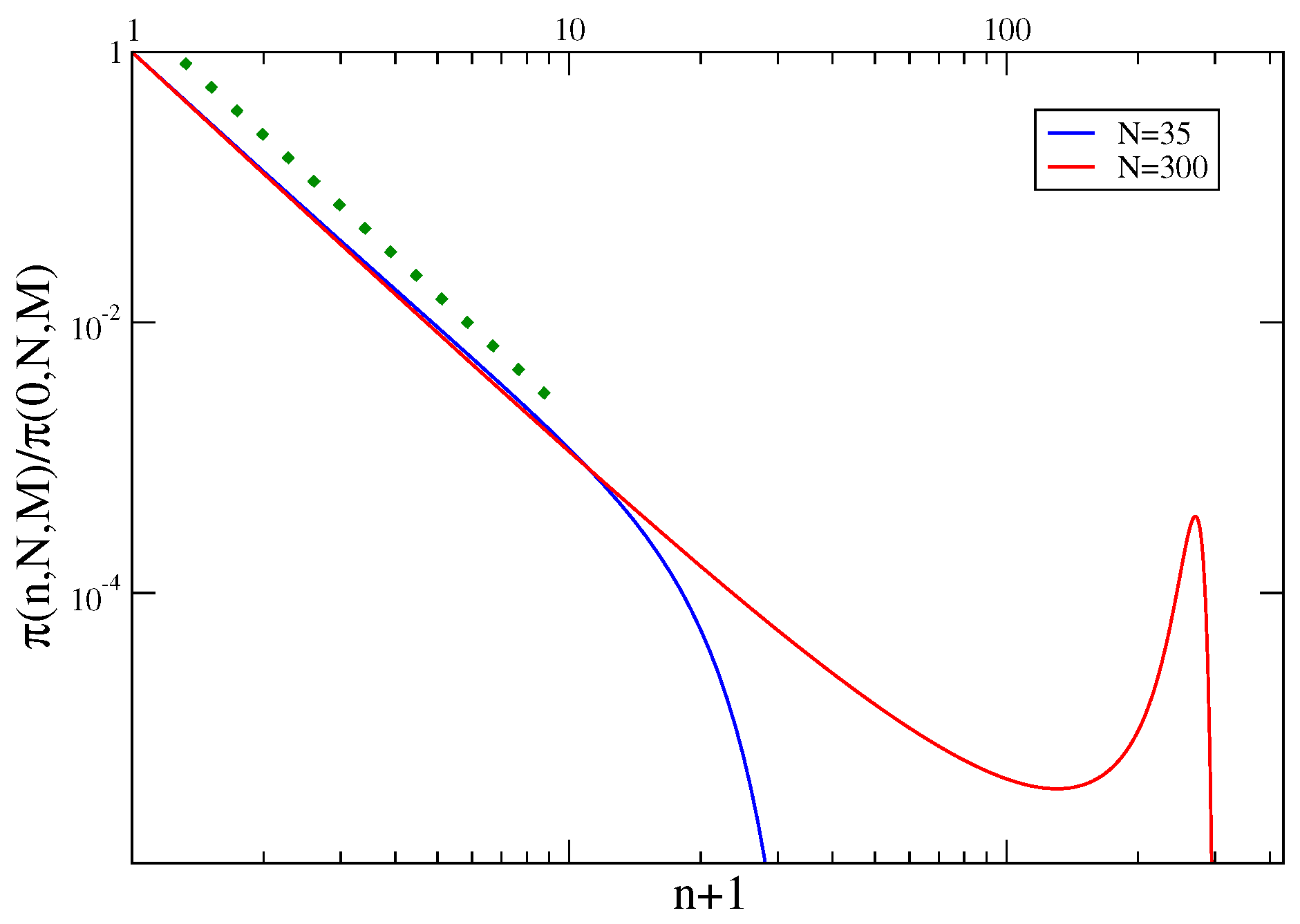
N particles in the whole system. This quantity can be evaluated exactly and is shown in
Figure 5 (normalized by its value in
to better compare curves with different
N in a single figure). Let us discuss its properties. First of all
vanishes for
, since it is impossible that an urn contains more particles than the whole system. Secondly, for small
n one has
(dotted green line in
Figure 5). This means that, as far as very few particles are stored in the tagged urn, the condition on the total number of balls is irrelevant.
More interestingly, at large
n,
, different behaviors are observed in the region of relatively small
N, and in the one with relatively large
N, exemplified by
and
, respectively, in
Figure 5. In the former case
is exponentially damped at large
n, meaning that accommodating many particles in a single urn is probabilistically very unfavorable. In the latter case there is a peak at a value of
n or of order
N. This means that a significant fraction of the total number of particles is located in a single urn. This is the condensation phenomenon. (We will see in the next section that in this particular model occurs when
and for sufficiently large densities). The essence of a condensation phenomenon is that a given quantity is not fairly distributed among many degrees of freedom, but is concentrated in a single one. This is particularly clear in the urn model, where one particular urn contains a macroscopic fraction of balls.
One easily realizes that something similar occurs in the other example models discussed in
Section 3. For instance, in the model of
Section 3.1, writing
in terms of the Fourier components
of the field
as
one can show that while for
(or equivalently
) all the Fourier components add up to realize the sum in Equation (
17) in a comparable way, for
the term with
alone provides the most important contribution to the sum. A similar mechanism, with the dominance of the
term, is also at work in the example of
Section 3.2. In the Maxwell–Lorentz particle model (
Section 3.4) one has that normal entropy fluctuations are formed by the addition of many contributions associated to many short flights of the probe particle. However above the critical threshold
they are associated to a single event which is responsible for a macroscopic contribution to the entropy production. This event is a long flight of the probe particle with no collisions with the scatterers. For more details and a very accurate analytical description of these kinds of behaviors in a similar system re-framed in the context of active particles, see the recent work [
48].
4.3. Mathematical Mechanism
In the previous section we have discussed the phenomenon of condensation on physical grounds. In this section we show the underlying mathematical mechanism. We will give a description as simple as possible, without presumption of mathematical rigor, in the framework of the urn model.
The probability distribution of the total number of particles
N reads
where
is the Kronecker function and in the leftmost sum the variables
run from 0 to
∞. Using the representation
of the
function one arrives at
where
and we have confused
with
for large
M. Still for large
M, the integral in Equation (
20) can be evaluated by the steepest descent method as
where
with
the value of
z for which the argument in the exponential of Equation (
20) has its maximum value. This in turn is given by the following implicit saddle-point equation
where
Let us study this equation. Clearly, it must be
in order for the sums hidden in
Q and
to converge. It can also be easily seen that
and that this function increases with
z up to
where
is a finite positive number. The function
is shown in
Figure 6, for two values of the parameter
k. As it is clear from this figure, for
the saddle point Equation (
24) admits a solution only for
. It is trivial to show that
. However nothing prevents fluctuations with
to occur. How can we recover the model solution for
? We know that for such high densities urns are no longer equivalent: there is one—say the first—which hosts an extensive number of particles and condensation occurs. In a physically oriented approach, we can take into account this fact by writing, in place of Equation (
18), the following
The factor
M in front of the r.h.s. stems from the fact that there are
M ways to chose the urn (denoted as 1) to be singled out. Repeating the mathematical manipulations as in Equations (
18) and (
20), but only on the sum
, one arrives at
Evaluating the integral with the steepest descent method, the saddle point equation is now
Notice that in a normal situation, where condensation does not occur, in the thermodynamic limit where
with fixed
, the typical number of particles in a single urn does not depend on the number of urns. Therefore the last term on the r.h.s. of Equation (
29) is negligible and one goes back to the previous saddle point Equation (
24). However, when condensation occurs (i.e., with
and
) the only possibility to close the model equations is to have the last term in Equation (
29) finite. In conclusion one has
Clearly we are in the presence of a phase-transition resembling the ferro-paramagnetic or the gas–liquid transitions. There are two phases with qualitatively different behaviors. However, at variance with usual phase transitions, here the parameter producing the transition is not an external one that can be varied at will, but the value of the spontaneously fluctuating variable
N. Another difference with usual phase transitions is the fact that here there is no interaction among urns. Despite that, urns are not completely independent due to the constraint over the number of particles represented by the Kronecker function in Equations (
18) and (
27). This constraint can be regarded as an effective interaction determining the transition (it can be easily seen, in fact, that without such conservation there is no transition).
Notice that it is in the normal phase and in the condensed phase, therefore this quantity represents the order parameter of the transition. Despite the fact that a priori the system (i.e., the Hamiltonian) is invariant under a permutation of the urns, namely all boxes are equal, this property is not shared by the physical realization of the actual state of the system when condensation occurs, since one urn behaves very differently from the others. We are in the presence of spontaneous symmetry breaking.
As a final remark, let us note that the phenomenon of condensation in the sum of many identically distributed variables is not specific to an algebraic decay of
, or to the discrete value of the variable
n. Indeed it is found [
31] that it occurs provided that
. Condensation in the presence of a stretched exponential
, for instance, has been discussed in [
59,
60]. Finally, we mention the fact that in the context of Lévy flights the phenomenon of condensation is usually referred to as the big jump principle [
61].
4.4. Fluctuation Relation
The Fluctuation Relation is one of the few general results of non-equilibrium statistical mechanics, expressing an asymmetry property of the fluctuations of some extensive (in time or in number of degrees of freedom) quantities
N [
40]. The FR reads
where
c is a constant, and
stands for sub-linear corrections in
M. Usually, the exponential form of the FR is related to two properties of
: (i) it satisfies a LDP Equation (
5), and (ii) the rate function
has the symmetry:
These two conditions, with
different from 0 and
∞, are known to be sufficient for
to satisfy a FR (see, e.g., [
4] and references therein).
It is interesting to consider the validity of an FR in the case of probability distributions with singularities. First, let us note that, when the singularity appears in zero, as in the case of the “kink” mentioned in
Section 3.5, then the validity of an FR is clearly not affected by the singularity. More in general, the FR can also be satisfied by a pdf for which a standard (namely, with a leading exponential scaling in
M) LDP does not hold. This can be observed for instance in the driven Maxwell–Lorentz gas described in
Section 3.4. In this model it has been shown [
11] that the entropy production calculated over a time
t satisfies an FR, even though the far positive tail of its pdf scales exponentially with
rather than
t. In this case the validity of the FR can be exploited to extract some information on the behavior of the probability distribution in the regions where the stretched-exponential scaling takes place.
The FR Equation (
32) in the presence of a singular rate function has been also observed [
37], besides the already mentioned Maxwell-Lorentz case , in some large time limit for the exchanged heat, in the large-
model of
Section 3.2. More recently, it has been shown [
39] that the rate function of the heat exchanged by a set of uncoupled Brownian oscillators with the thermostat during a non-stationary relaxation process does not satisfy an FR in the form Equation (
31). Although, even in this case, the rate function shows a singular behavior in the limit of a large number of degrees of freedom, the lack of a standard FR is not necessarily related to the presence of the singularity.
6. Summary and Conclusions
In this paper we have shortly reviewed the issue of probability distributions characterized by non-analyticities. Naively, this feature could be considered as a rare manifestation of curious mathematical pathologies occurring in scholarly model with uncertain relations to the physical world. In reality, singular probability distributions have been shown analytically to occur in very simple and fundamental models of statistical mechanics, such as the Gaussian one, and not only in weird non-equilibrium states but also in equilibrium. Furthermore, they have been detected in numerical simulations and, most importantly, also in real experiments. This widespread occurrence points towards an underlying general mechanism for the development of singularities in the fluctuation probability. This paper has been conceived in order to highlight and discuss, at a simple and physically oriented level, at least some of such general features.
In the first part of the paper, after recalling basic and general concepts of probability theory we have reviewed some models where singular fluctuation spectra have been observed. These range from the aforementioned Gaussian model to the spherical limit of a ferromagnet, from the so-called urn model to a description of the Maxwell–Lorentz gas. In all these cases the deviations of certain collective observables are described by non-analytical probability distributions, which, in the case when LDP holds, are characterized by the presence of exponential branches.
The non-analytical behavior has been interpreted as due to the same mechanism whereby singularities develop in the thermodynamic functions of systems experiencing phase transitions. Indeed we have discussed the fact that a singular fluctuation distribution function can be mapped onto a thermodynamic potential of a dual model with a critical point. The singularity appears similarly to what one observes in thermodynamic functions when a condensation transition is present. When such feature occurs at the level of fluctuations, at variance with the usual examples of condensation, one speaks of condensation of fluctuations.
Singularities of the probability distributions can have a scarce practical relevance if they occur in regions where fluctuations have a negligible chance to be observed. However, in some of the cases considered in this paper the non-analytical behavior is associated to the breakdown of the large deviation principle. As a result, large fluctuations of macrovariables have a better chance to be observed even in systems with a relatively large number of degrees of freedom. In this case the presence of singularities not only can be observed, but its effects can be appreciated. Perhaps, one of the most intriguing one is the so called giant susceptibility, whereby slightly tuning the properties of even one single component, say a molecule of a gas, can have catastrophic consequences on the behavior of the whole system.
Non-analyticity points in the probability distributions also influence the way in which rare fluctuations are developed out of typical state where they are absent. Indeed, it has been shown that large fluctuations in the region where condensation occurs are formed by means of a complex slow dynamics which resembles, once again a manifestation of a dual behavior, that of systems brought across a phase transition. The knowledge of the dynamical path leading to a rare fluctuation may have important consequences in those cases when such deviations lead to catastrophic events, as in the case of extinctions or bankruptcies.
Among the several perspectives of future studies in this context, we mention the possibility to explore the role of correlated noise on the large deviations, for instance in models of active particles where some analytical results can be obtained [
66]; the meaning of singularities, which are related to non-equilibrium phase transitions, within the general framework of the macroscopic fluctuation theory [
67]; the relation between the presence of singularities and the validity of the fluctuation relation for entropy production or related quantities in more general cases; the role of correlations among random variables in the anomalous large deviations, as observed for instance in conditioned random walks [
68] and Brownian motion [
69]; the effect of inhomogeneous rates in bulk-driven exclusion processes [
70].