Thermodynamic Relations among Isotropic Material Properties in Conditions of Plane Shear Stress
Abstract
1. Introduction
2. The Gibbs Equation and Generalized Free Energy
3. Relations among the Material Properties
3.1. Entropy Representation
3.1.1.
3.1.2.
3.1.3.
3.1.4.
3.2. Volume Representation
3.2.1.
3.2.2.
3.2.3.
3.2.4.
3.3. Shear-Angle Representation
3.3.1.
3.3.2.
3.3.3.
3.3.4.
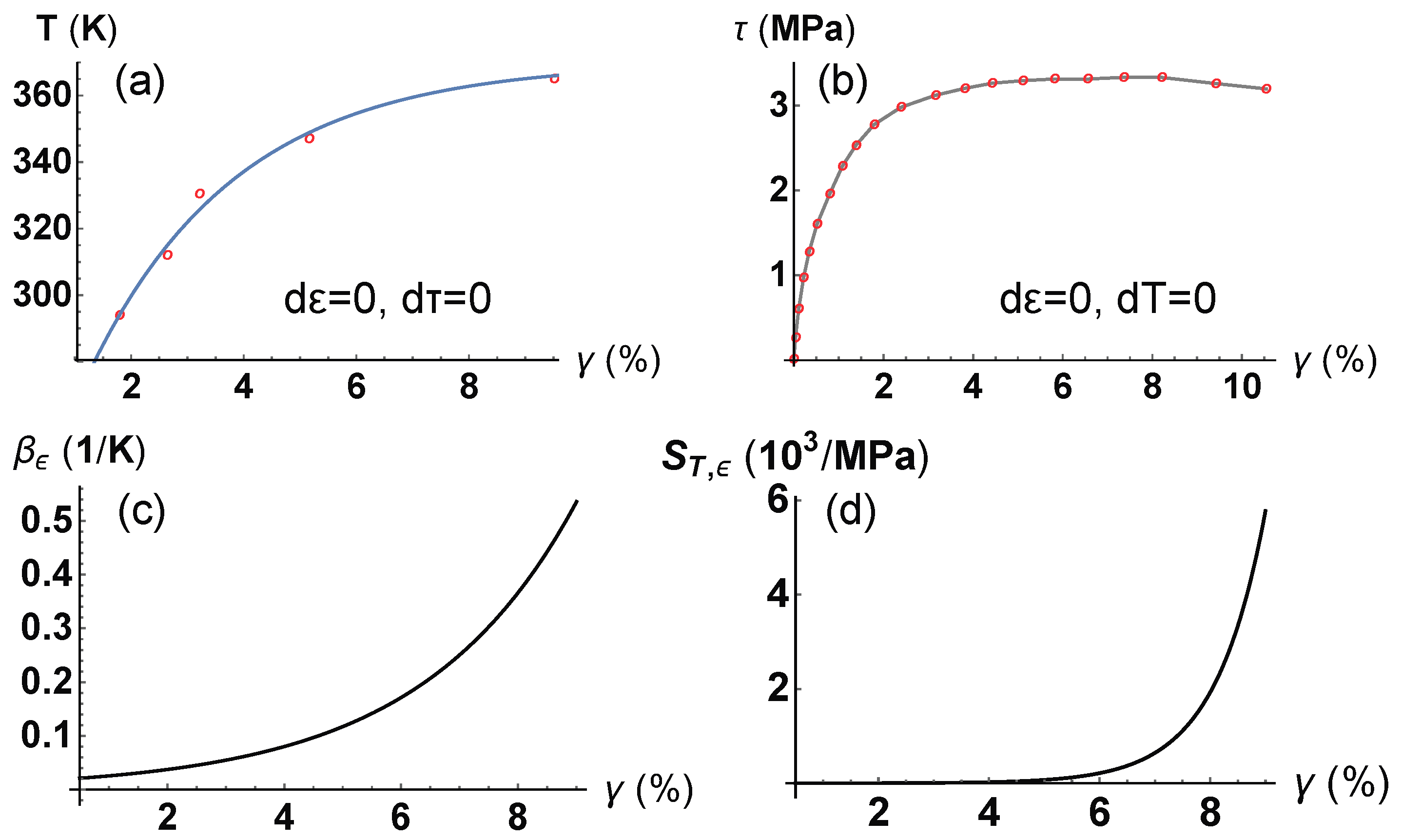
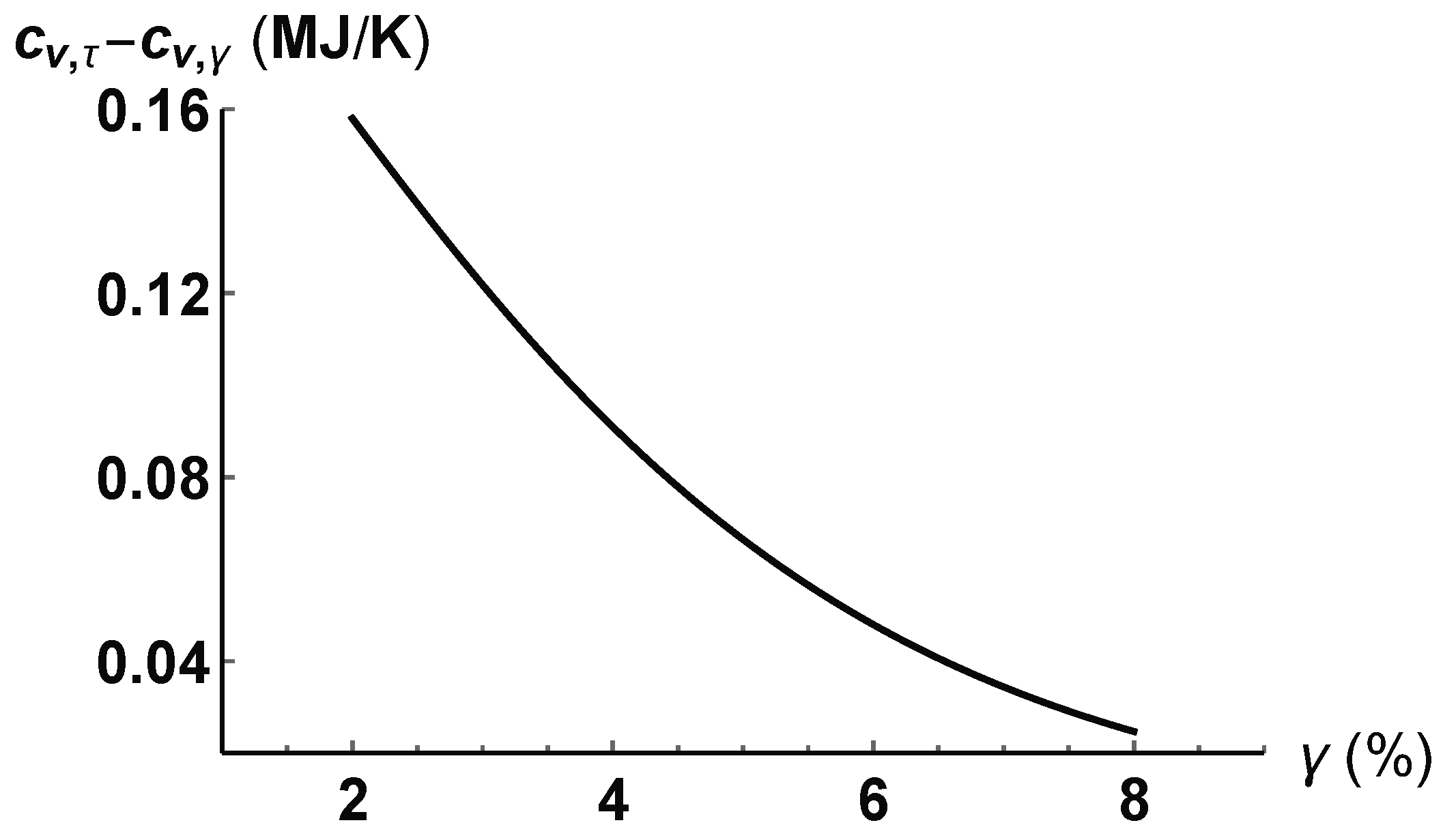
4. Application
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gibbs, J.W. The Collected Works of J. Willard Gibbs, Volume I: Thermodynamics; Yale University Press: New Haven, CT, USA, 1928. [Google Scholar]
- Poirier, J.P. Introduction to the Physics of the Earth’s Interior; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259. [Google Scholar] [CrossRef] [PubMed]
- Dyre, J.C. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953. [Google Scholar] [CrossRef]
- Charbonneau, P.; Kurchan, J.; Parisi, G.; Urbani, P.; Zamponi, F. Glass and jamming transitions: From exact results to finite-dimensional descriptions. Ann. Rev. Condens. Matter Phys. 2017, 8, 265–288. [Google Scholar] [CrossRef]
- Xu, B.; Falk, M.L.; Li, J.; Kong, L. Predicting Shear Transformation Events in Metallic Glasses. Phys. Rev. Lett. 2018, 120, 125503. [Google Scholar] [CrossRef] [PubMed]
- Burns, S. 77 new thermodynamic identities among crystalline elastic material properties leading to a shear modulus constitutive law in isotropic solids. J. Appl. Phys. 2018, 124, 085114. [Google Scholar] [CrossRef]
- Guzzetta, G. Relating Deformation and Thermodynamics: An Opportunity for Rethinking Basic Concepts of Continuum Mechanics. Entropy 2013, 15, 2548–2569. [Google Scholar] [CrossRef]
- Berezovski, A.; Ván, P. Internal Variables in Thermoelasticity; Springer: Berlin, Germany, 2017. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics; Springer: Berlin, Germany, 2004; pp. 1–579. [Google Scholar]
- Callen, H. Thermodynamics and an Introduction to Thermodynamics; Wiley India Pvt. Ltd.: New Delhi, India, 2006. [Google Scholar]
- Brillouin, L. Influence de la Température sur L’élasticité d’un Solide; Gauthier-Villars: Paris, France, 1940. (In French) [Google Scholar]
- Menikoff, R.; Plohr, B.J. The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 1989, 61, 75. [Google Scholar] [CrossRef]
- Ponkratz, U.; Holzapfel, W.B. Equations of state for wide ranges in pressure and temperature. J. Phys. Condens. Matter 2004, 16, S963. [Google Scholar] [CrossRef]
- Heuzé, O. General form of the Mie–Grüneisen equation of state. C. R. Mec. 2012, 340, 679–687. [Google Scholar] [CrossRef]
- Holzapfel, W.B. Coherent thermodynamic model for solid, liquid and gas phases of elements and simple compounds in wide ranges of pressure and temperature. Solid State Sci. 2018, 80, 31–34. [Google Scholar] [CrossRef]
- Fung, Y.C. Foundations of Solid Mechanics; Prentice Hall: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- Born, M. Thermodynamics of crystals and melting. J. Chem. Phys. 1939, 7, 591–603. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Burns, S. Elastic shear modulus constitutive law found from entropy considerations. J. Appl. Phys. 2018, 124, 085904. [Google Scholar] [CrossRef]
- Reynolds, O. LVII. On the dilatancy of media composed of rigid particles in contact. With experimental illustrations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1885, 20, 469–481. [Google Scholar] [CrossRef]
- Li, J.C.M. Physical chemistry of some microstructural phenomena. Metall. Trans. A 1978, 9, 1353–1380. [Google Scholar]
- Hencky, H. Uber die Form des Elastizitatsgesetzes bei ideal elastischen Stoffen. Zeit. Tech. Phys. 1928, 9, 215–220. [Google Scholar]
- Fitzgerald, J.E. A tensorial Hencky measure of strain and strain rate for finite deformations. J. Appl. Phys. 1980, 51, 5111–5115. [Google Scholar] [CrossRef]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. A 1962, 269, 500–527. [Google Scholar]
- Brace, W.; Paulding, B., Jr.; Scholz, C. Dilatancy in the fracture of crystalline rocks. J. Geophys. Res. 1966, 71, 3939–3953. [Google Scholar] [CrossRef]
- Nur, A. Dilatancy, pore fluids, and premonitory variations of ts/tp travel times. Bull. Seismol. Soc. Am. 1972, 62, 1217–1222. [Google Scholar]
- Barnes, H. Shear-thickening (“Dilatancy”) in suspensions of nonaggregating solid particles dispersed in Newtonian liquids. J. Rheol. 1989, 33, 329–366. [Google Scholar] [CrossRef]
- Schneebeli, G. Une analogie mecanique pour les terres sans cohesion. C. R. Hebd. Seances L’academie Sci. 1956, 243, 125–126. [Google Scholar]
- Sibille, L.; Froiio, F. A numerical photogrammetry technique for measuring microscale kinematics and fabric in Schneebeli materials. Granul. Matter 2007, 9, 183. [Google Scholar] [CrossRef]
- DeWit, R. Elastic constants and thermal expansion averages of a nontextured polycrystal. J. Mech. Mater. Struct. 2008, 3, 195–212. [Google Scholar] [CrossRef]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1934, 143, 307–326. [Google Scholar] [CrossRef]
- Hueckel, T.; Pellegrini, R. Effective stress and water pressure in saturated clays during heating–cooling cycles. Can. Geotech. J. 1992, 29, 1095–1102. [Google Scholar] [CrossRef]
| s | |||
|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porporato, A.; Calabrese, S.; Hueckel, T. Thermodynamic Relations among Isotropic Material Properties in Conditions of Plane Shear Stress. Entropy 2019, 21, 295. https://doi.org/10.3390/e21030295
Porporato A, Calabrese S, Hueckel T. Thermodynamic Relations among Isotropic Material Properties in Conditions of Plane Shear Stress. Entropy. 2019; 21(3):295. https://doi.org/10.3390/e21030295
Chicago/Turabian StylePorporato, Amilcare, Salvatore Calabrese, and Tomasz Hueckel. 2019. "Thermodynamic Relations among Isotropic Material Properties in Conditions of Plane Shear Stress" Entropy 21, no. 3: 295. https://doi.org/10.3390/e21030295
APA StylePorporato, A., Calabrese, S., & Hueckel, T. (2019). Thermodynamic Relations among Isotropic Material Properties in Conditions of Plane Shear Stress. Entropy, 21(3), 295. https://doi.org/10.3390/e21030295






