Feedback Schemes for the Action-Dependent Wiretap Channel with Noncausal State at the Transmitter
Abstract
:1. Introduction
- (1)
- How should the feedback scheme in [9] be extended to the action-dependent wiretap channel with noncausal state?
- (2)
- (1)
- We propose a new lower bound on the secrecy capacity of the action-dependent wiretap channel with noncausal state and noiseless feedback, which is constructed according to a hybrid feedback scheme similar to that in [9].
- (2)
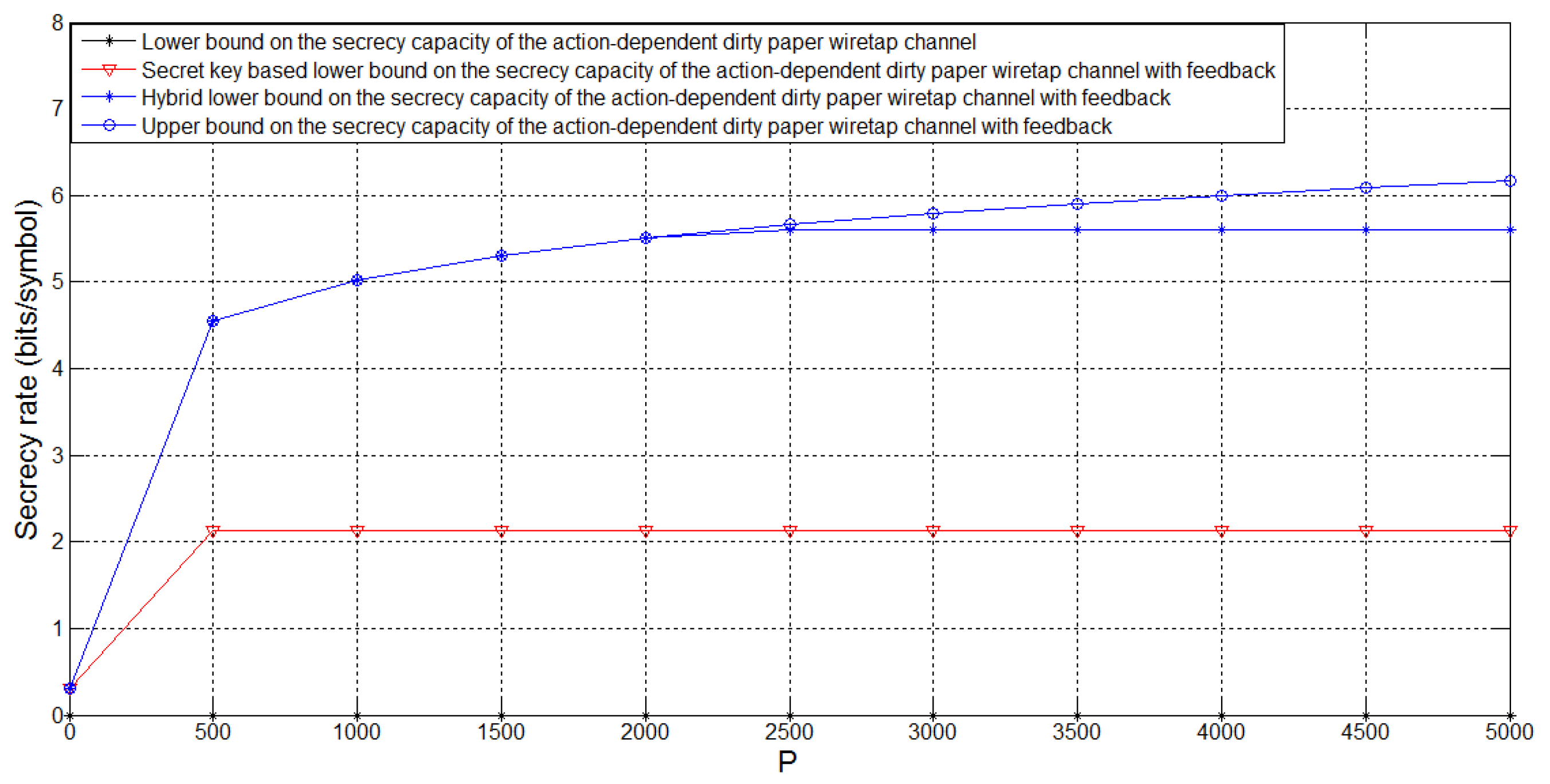
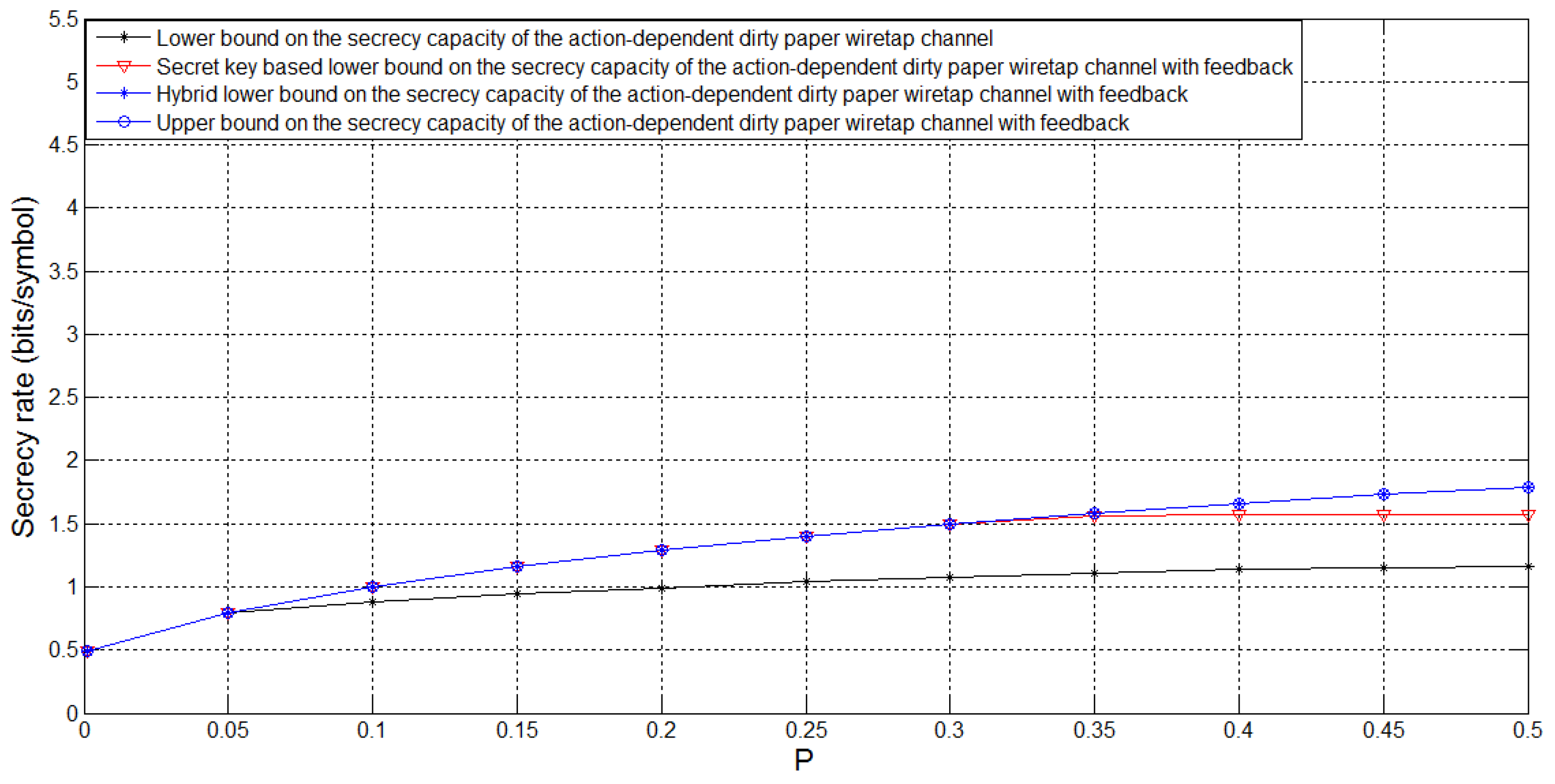
- From a Gaussian example, which is also called the action-dependent dirty paper wiretap channel with noiseless feedback, we show that our new lower bound on the secrecy capacity is larger than the secret key based lower bound. Moreover, we find that our new lower bound achieves the secrecy capacity for some special cases.
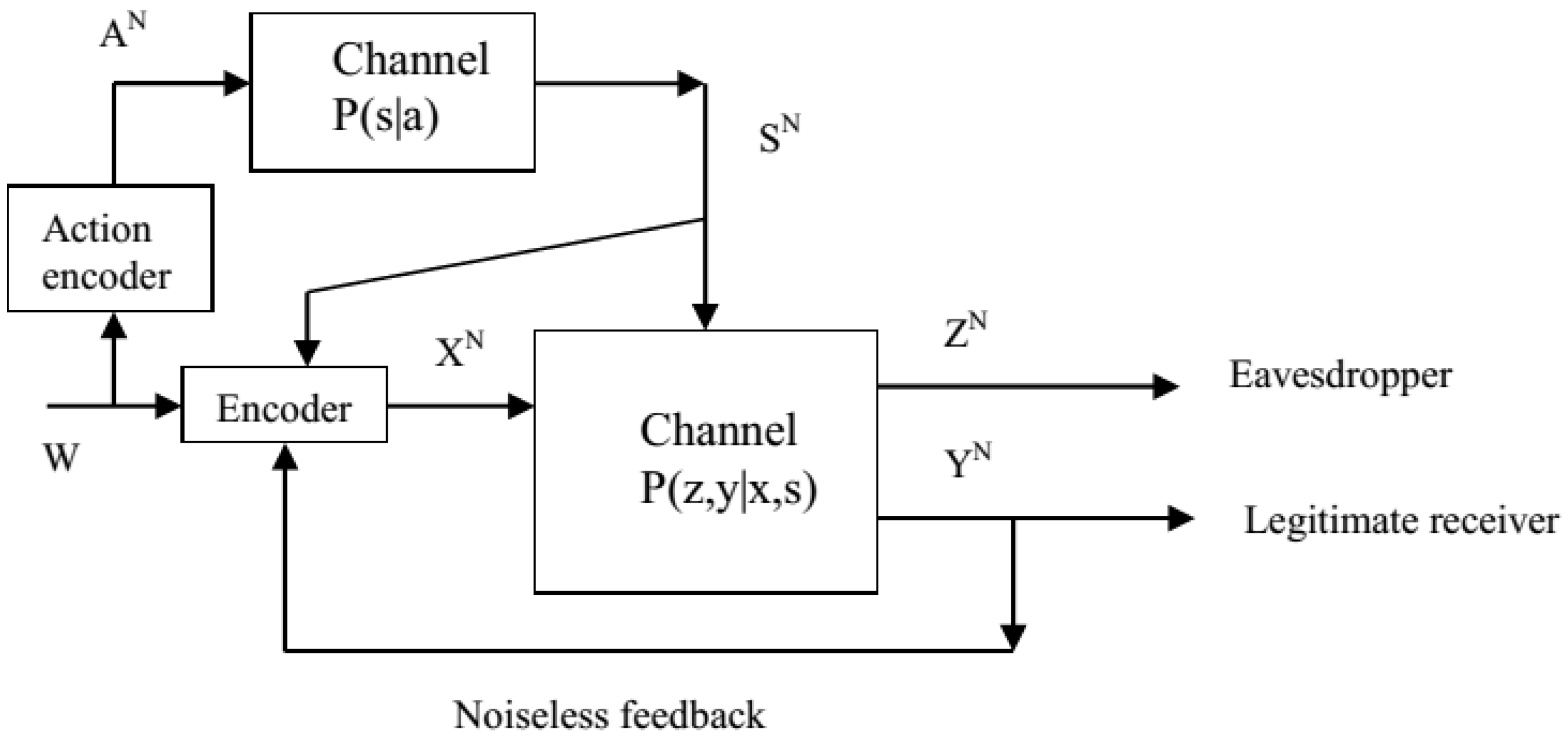
2. Problem Formulation and New Result
3. Proof of Theorem 1
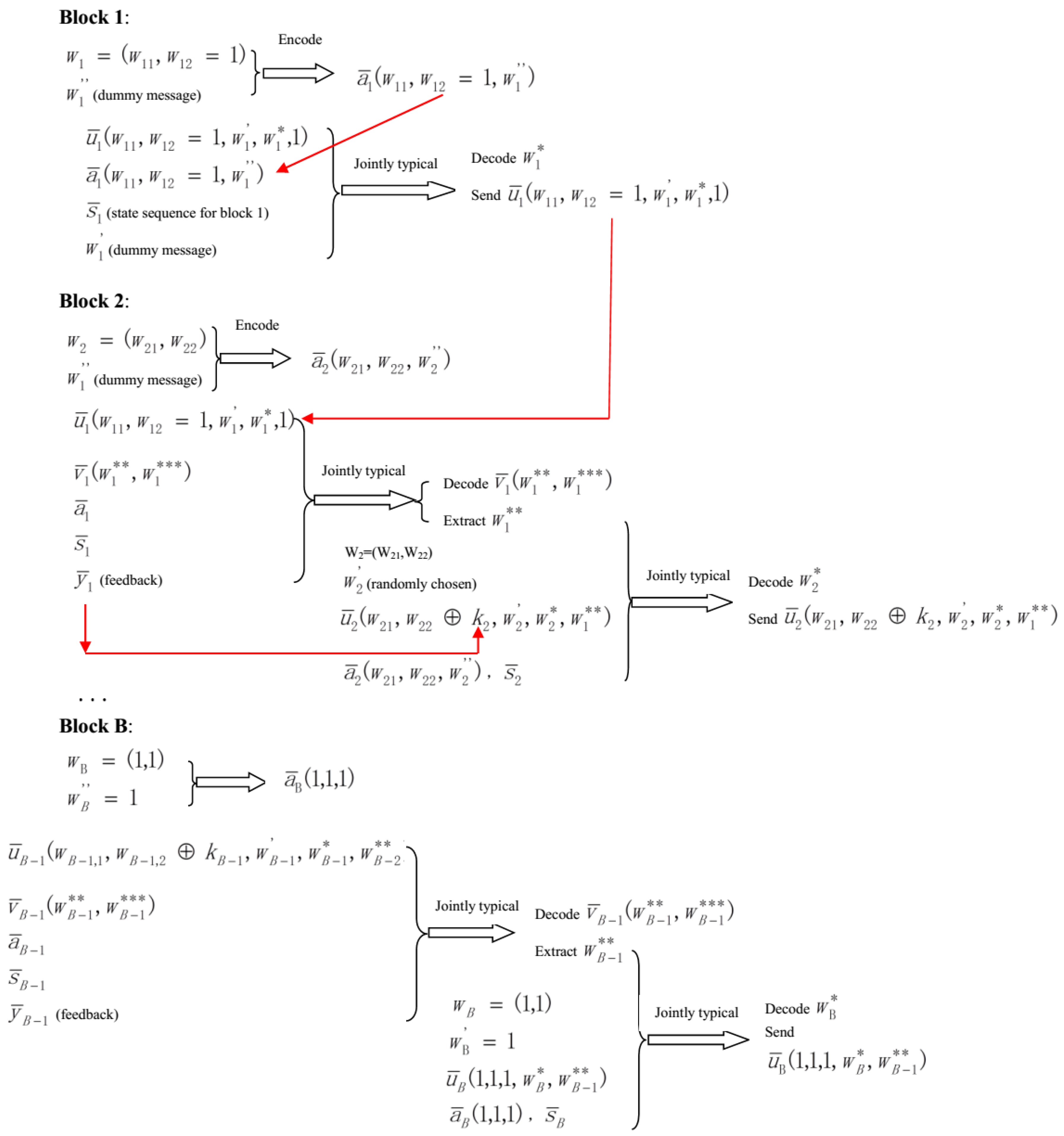
3.1. Code-Book Construction and Transmission Scheme
- Similar to the coding scheme in [9], suppose that the overall transmission consists of B blocks, and the codeword length in each block is N.
- The overall message W is composed of B components (), and each component () is the message transmitted in block b. The value of belongs to the set . Next, split into two parts , and the values of and , respectively, belong to the sets and . Note that .
- Analogously, the randomly produced dummy messages and , which are used to confuse the wiretapper, also consist of B components ( and ), and the components and () are transmitted in block b. Here, note that and are uniformly drawn from the sets and , respectively.
- The auxiliary message , which is used to cooperate with the channel state, consists of B components (), and the value of () belongs to the set .
- The help information and , which is used to ameliorate the legitimate receiver’s decoding performance, consists of B components ( and ), and the value of and (), respectively, belongs to the sets and .
- In block b (), the random vectors , , , , , and are denoted by , , , , , and , respectively. In addition, let be a collection of the random vectors for all blocks. Analogously, we have , , , , and . The vector value is written in lower case letter.
- In block b (), randomly produce i.i.d. codewords with respect to (w.r.t.) , and label them as , where , and .
- In block b (), randomly produce i.i.d. codewords w.r.t. , and label them as , where , , , and .
- For each possible value of and , randomly produce i.i.d. codewords on the basis of . Then, label these as , where and .
- For given and , the transmitted sequence is i.i.d. produced on the basis of the probability .
- For block 1, the transmitter chooses . Next, define , for given and the state sequence , the transmitter selects an index such that are jointly typical. If no such exists, declare an encoding error. If multiple exist, randomly pick out one. Based on the Covering Lemma [22], the encoding error tends to zero if
- For block b (), before transmission, produce a mapping (this mapping is generated exactly the same as that in [1]). Based on this mapping, generate a random variable (RV) taking values in , and for . The RV is used as a secret key and it is not known to the eavesdropper, and is independent of the real transmitted messages and for block b. Notice that is a realization of . The mapping is revealed to all parties. First, since the transmitter knows its own , , and , he tries to find a such that are jointly typical. For the case that more than one exist, randomly pick one; if no such exists, declare an encoding error. According to the Covering Lemma [22], the encoding error approaches to zero ifwhere (1) is from the definition in Equation (6), which implies that . Next, the transmitter chooses . Finally, since the transmitter obtains , he extracts and tries to find a such that are jointly typical. If no such exists, declare an encoding error. If multiple exist, randomly pick out one. Based on the Covering Lemma [22], the encoding error tends to zero if Equation (10) holds. The codeword is picked for transmission.
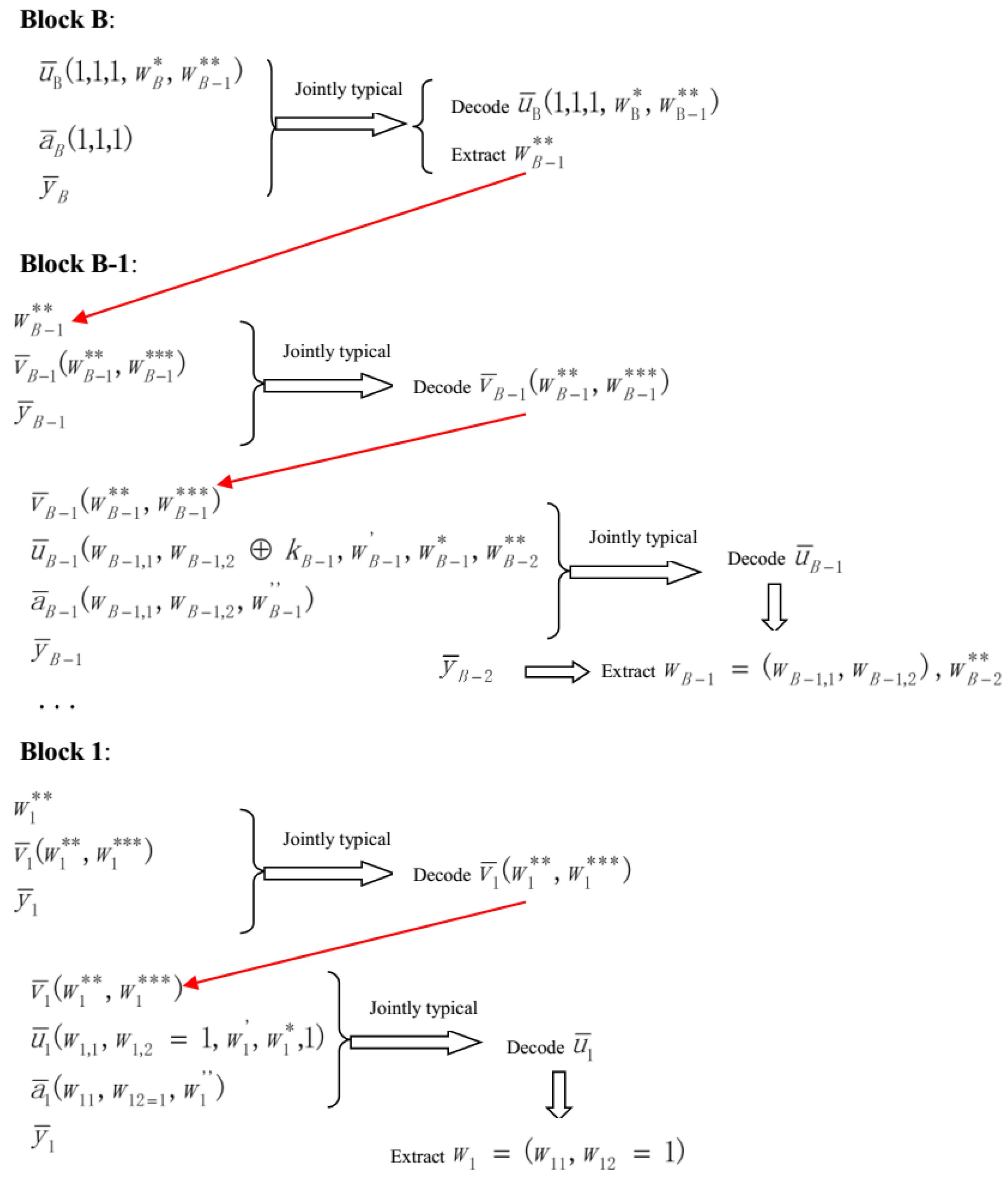
- At block B, first, the transmitter chooses . Next, after receiving the feedback , the transmitter tries to find a such that are jointly typical. After decoding such , the transmitter extracts and tries to find a such that are jointly typical. If no such exists, declare an encoding error. If multiple exist, randomly pick out one. The codeword is picked for transmission.
3.2. Equivocation Analysis
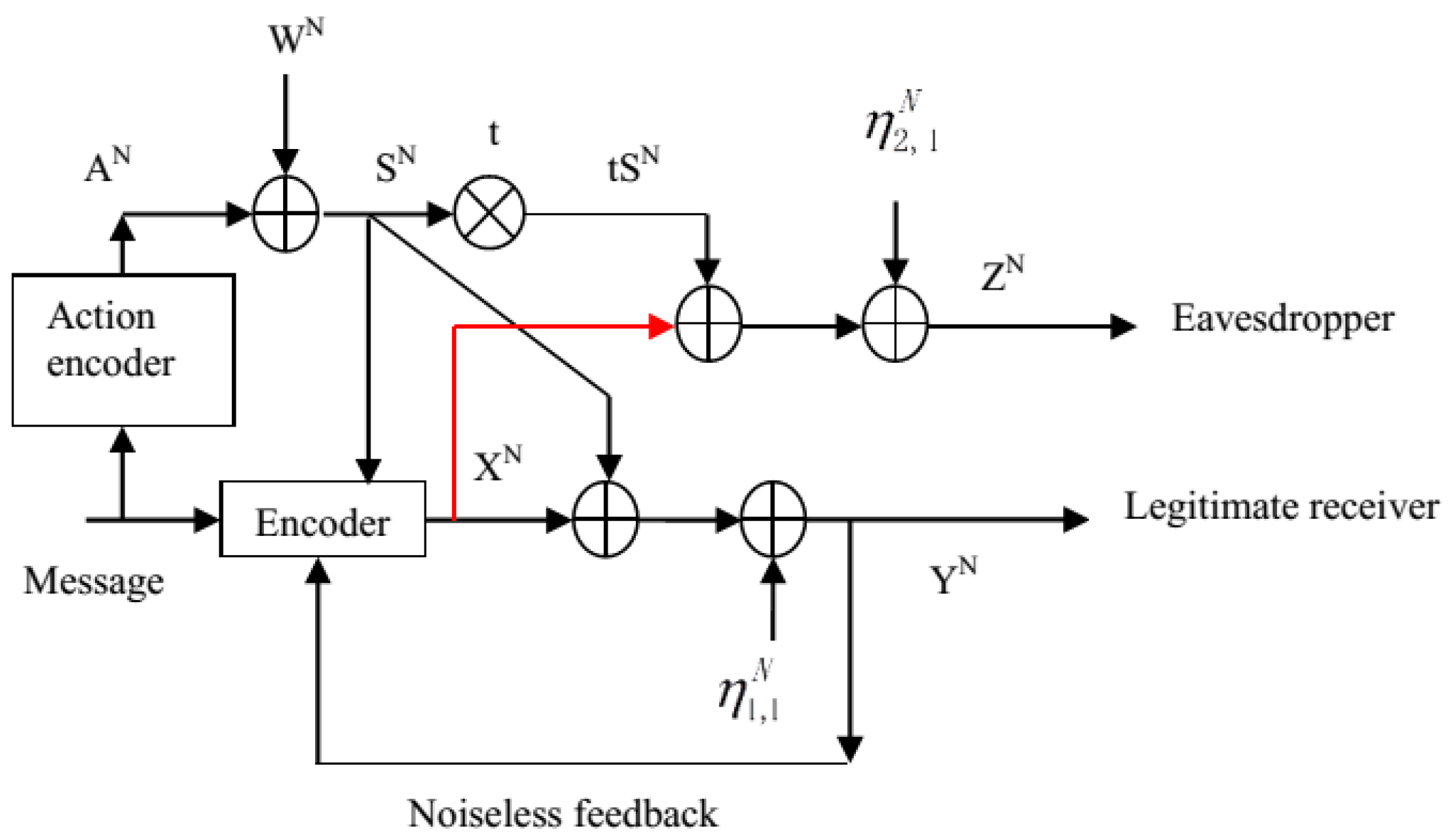
4. The Action-Dependent Dirty Paper Wiretap Channel with Noiseless Feedback
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Ahlswede, R.; Cai, N. Transmission, identification and common randomness capacities for wire-tap channels with secure feedback from the decoder. In General Theory of Information Transfer and Combinatorics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 258–275. [Google Scholar]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Ardestanizadeh, E.; Franceschetti, M.; Javidi, T.; Kim, Y. Wiretap channel with secure rate-limited feedback. IEEE Trans. Inf. Theory 2009, 55, 5353–5361. [Google Scholar] [CrossRef]
- Schaefer, R.F.; Khisti, A.; Poor, H.V. Secure broadcasting using independent secret keys. IEEE Trans. Commun. 2018, 66, 644–661. [Google Scholar] [CrossRef]
- Ekrem, E.; Ulukus, S. Secrecy capacity of a class of broadcast channels with an eavesdropper. EURASIP J. Wirel. Commun. Netw. 2009, 2009, 1–29. [Google Scholar] [CrossRef]
- Cohen, A.; Cohen, A. Wiretap channel with causal state information and secure rate-limited feedback. IEEE Trans. Commun. 2016, 64, 1192–1203. [Google Scholar] [CrossRef]
- Dai, B.; Ma, Z.; Luo, Y. Finite state Markov wiretap channel with delayed feedback. IEEE Trans. Inf. Forensics Secur. 2017, 12, 746–760. [Google Scholar] [CrossRef]
- Dai, B.; Ma, Z.; Xiao, M.; Tang, X.; Fan, P. Secure communication over finite state multiple-access wiretap channel with delayed feedback. IEEE J. Sel. Areas Commun. 2018, 36, 723–736. [Google Scholar] [CrossRef]
- Dai, B.; Luo, Y. An improved feedback coding scheme for the wiretap channel. IEEE Trans. Inf. Forensics Secur. 2019, 14, 262–271. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Tsybakov, B.S. Coding in memories with defective cells. Probl. Control Inf. Theory 1974, 10, 52–60. [Google Scholar]
- Gel’fand, S.I.; Pinsker, M.S. Coding for channel with random parameters. Probl. Control Inf. Theory 1980, 9, 19–31. [Google Scholar]
- Costa, M.H.M. Writing on dirty paper. IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Weissman, T. Capacity of channels with action-dependent states. IEEE Trans. Inf. Theory 2010, 56, 5396–5411. [Google Scholar] [CrossRef]
- Chen, Y.; Han Vinck, A.J. Wiretap channel with side information. IEEE Trans. Inf. Theory 2008, 54, 395–402. [Google Scholar] [CrossRef]
- Dai, B.; Luo, Y. Some new results on wiretap channel with side information. Entropy 2012, 14, 1671–1702. [Google Scholar] [CrossRef]
- El-Halabi, M.; Liu, T.; Georghiades, C.N.; Shamai, S. Secret writing on dirty paper: A deterministic view. IEEE Trans. Inf. Theory 2012, 58, 3419–3429. [Google Scholar] [CrossRef]
- Mitrpant, C.; Han Vinck, A.J.; Luo, Y. An achievable region for the gaussian wiretap channel with side information. IEEE Trans. Inf. Theory 2006, 52, 2181–2190. [Google Scholar] [CrossRef]
- Leung-Yan-Cheong, S.K.; Hellman, M.E. The Gaussian wire-tap channel. IEEE Trans. Inf. Theory 1978, 24, 451–456. [Google Scholar] [CrossRef]
- Dai, B.; Ma, Z.; Fang, X. Feedback enhances the security of state-dependent degraded broadcast channels with confidential messages. IEEE Trans. Inf. Forensics Secur. 2015, 10, 1529–1542. [Google Scholar] [CrossRef]
- Dai, B.; Han Vinck, A.J.; Luo, Y.; Tang, X. Wiretap channel with action-dependent channel state information. Entropy 2013, 15, 445–473. [Google Scholar] [CrossRef]
- Dai, B.; Han Vinck, A.J.; Luo, Y. Wiretap channel in the presence of action-dependent states and noiseless feedback. J. Appl. Math. 2013, 2013, 1–17. [Google Scholar] [CrossRef]
- El Gamal, A.; Kim, Y.H. Information measures and typicality. In Network Information Theory; Cambridge University Press: Cambridge, UK, 2011; pp. 17–37. ISBN 978-1-107-00873-1. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yu, L.; Dai, B. Feedback Schemes for the Action-Dependent Wiretap Channel with Noncausal State at the Transmitter. Entropy 2019, 21, 278. https://doi.org/10.3390/e21030278
Zhang H, Yu L, Dai B. Feedback Schemes for the Action-Dependent Wiretap Channel with Noncausal State at the Transmitter. Entropy. 2019; 21(3):278. https://doi.org/10.3390/e21030278
Chicago/Turabian StyleZhang, Haonan, Linman Yu, and Bin Dai. 2019. "Feedback Schemes for the Action-Dependent Wiretap Channel with Noncausal State at the Transmitter" Entropy 21, no. 3: 278. https://doi.org/10.3390/e21030278
APA StyleZhang, H., Yu, L., & Dai, B. (2019). Feedback Schemes for the Action-Dependent Wiretap Channel with Noncausal State at the Transmitter. Entropy, 21(3), 278. https://doi.org/10.3390/e21030278




