A Monotone Path Proof of an Extremal Result for Long Markov Chains
Abstract
1. Introduction
2. The Gaussian Version
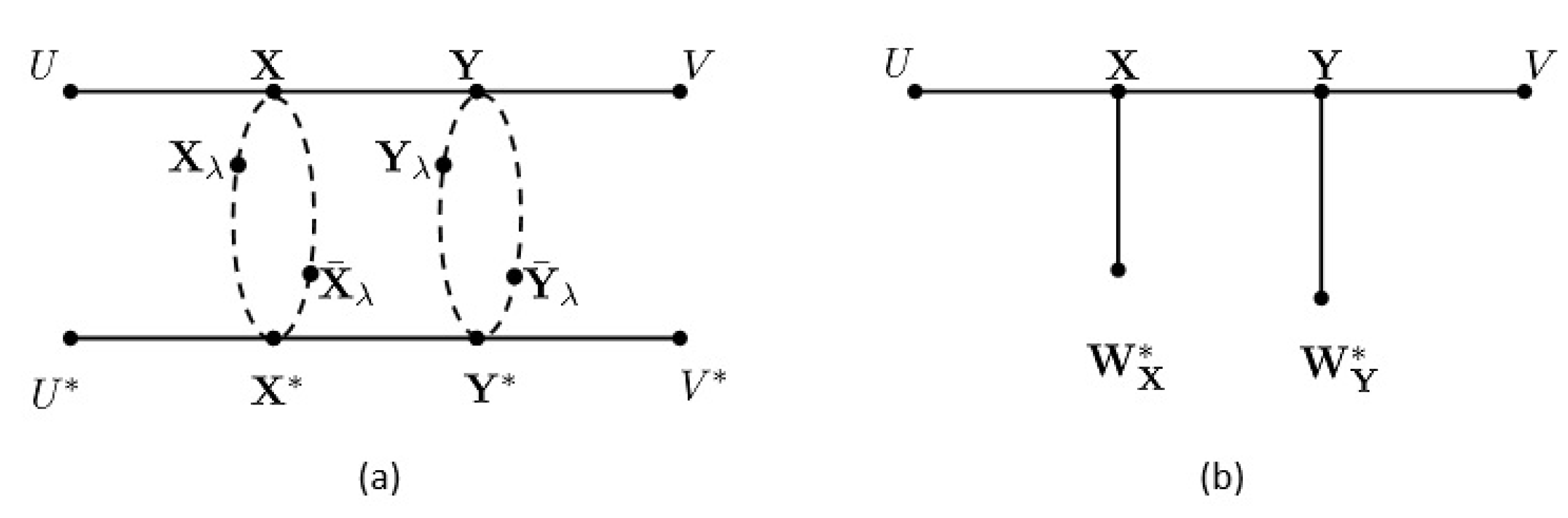
3. The Key Construction
4. Proof of Theorem 1
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
Appendix C. Proof of Lemma 3
Appendix D. Proof of Lemma 4
References
- Bergmans, P. A simple converse for broadcast channels with additive white Gaussian noise (corresp.). IEEE Trans. Inf. Theory 1974, 20, 279–280. [Google Scholar] [CrossRef]
- Weingarten, H.; Steinberg, Y.; Shamai, S. The capacity region of the Gaussian multiple-input multiple-output broadcast channel. IEEE Trans. Inf. Theory 2006, 52, 3936–3964. [Google Scholar] [CrossRef]
- Prabhakaran, V.; Tse, D.; Ramchandran, K. Rate region of the quadratic Gaussian CEO problem. In Proceedings of the IEEE International Symposium on Information Theory, (ISIT), Chicago, IL, USA, 27 June–2 July 2004; p. 117. [Google Scholar]
- Oohama, Y. Rate-distortion theory for Gaussian multiterminal source coding systems with several side informations at the decoder. IEEE Trans. Inf. Theory 2005, 51, 2577–2593. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J. Vector Gaussian two-terminal source coding. IEEE Trans. Inf. Theory 2013, 59, 3693–3708. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J. Vector Gaussian multiterminal source coding. IEEE Trans. Inf. Theory 2014, 60, 5533–5552. [Google Scholar] [CrossRef]
- Liu, T.; Shamai, S. A note on the secrecy capacity of the multiple-antenna wiretap channel. IEEE Trans. Inf. Theory 2009, 55, 2547–2553. [Google Scholar] [CrossRef]
- Chen, J. Rate region of Gaussian multiple description coding with individual and central distortion constraints. IEEE Trans. Inf. Theory 2009, 55, 3991–4005. [Google Scholar] [CrossRef]
- Motahari, A.S.; Khandani, A.K. Capacity bounds for the Gaussian interference channel. IEEE Trans. Inf. Theory 2009, 55, 620–643. [Google Scholar] [CrossRef]
- Shang, X.; Kramer, G.; Chen, B. A new outer bound and the noisy-interference sum-rate capacity for Gaussian interference channels. IEEE Trans. Inf. Theory 2009, 55, 689–699. [Google Scholar] [CrossRef]
- Annapureddy, V.S.; Veeravalli, V.V. Gaussian interference networks: Sum capacity in the low interference regime and new outer bounds on the capacity region. IEEE Trans. Inf. Theory 2009, 55, 3032–3050. [Google Scholar] [CrossRef]
- Song, L.; Chen, J.; Wang, J.; Liu, T. Gaussian robust sequential and predictive coding. IEEE Trans. Inf. Theory 2013, 59, 3635–3652. [Google Scholar] [CrossRef]
- Song, L.; Chen, J.; Tian, C. Broadcasting correlated vector Gaussians. IEEE Trans. Inf. Theory 2015, 61, 2465–2477. [Google Scholar] [CrossRef]
- Khezeli, K.; Chen, J. A source-channel separation theorem with application to the source broadcast problem. IEEE Trans. Inf. Theory 2016, 62, 1764–1781. [Google Scholar] [CrossRef]
- Tian, C.; Chen, J.; Diggavi, S.N.; Shamai, S. Matched multiuser Gaussian source channel communications via uncoded schemes. IEEE Trans. Inf. Theory 2017, 63, 4155–4171. [Google Scholar] [CrossRef]
- Geng, Y.; Nair, C. The capacity region of the two-receiver Gaussian vector broadcast channel with private and common messages. IEEE Trans. Inf. Theory 2014, 60, 2087–2104. [Google Scholar] [CrossRef]
- Geng, Y.; Nair, C. Reflection and summary of the paper: The capacity region of the two-receiver Gaussian vector broadcast channel with private and common messages. IEEE IT Soc. Newlett. 2017, 67, 5–7. [Google Scholar]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Blachman, N.M. The convolution inequality for entropy powers. IEEE Trans. Inf. Theory 1965, 11, 267–271. [Google Scholar] [CrossRef]
- Dembo, A.; Cover, T.M.; Thomas, J.A. Information theoretic inequalities. IEEE Trans. Inf. Theory 1991, 37, 1501–1518. [Google Scholar] [CrossRef]
- Liu, T.; Viswanath, P. An extremal inequality motivated by multiterminal information-theoretic problems. IEEE Trans. Inf. Theory 2007, 53, 1839–1851. [Google Scholar] [CrossRef]
- Courtade, T.A. An Extremal Conjecture: Experimenting With Online Collaboration. Information Theory b-Log. 5 March 2013. Available online: http://blogs.princeton.edu/blogit/2013/03/05/ (accessed on 15 March 2013).
- Courtade, T.A.; Jiao, J. An extremal inequality for long Markov chains. arXiv, 2014; arXiv:1404.6984v1. [Google Scholar]
- Courtade, T.A. A strong entropy power inequality. IEEE Trans. Inf. Theory 2018, 64, 2173–2192. [Google Scholar] [CrossRef]
- Palomar, D.P.; Verdú, S. Gradient of mutual information in linear vector Gaussian channels. IEEE Trans. Inf. Theory 2006, 52, 141–154. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Y.; Yu, W.; Chen, J. On the optimal fronthaul compression and decoding strategies for uplink cloud radio access networks. IEEE Trans. Inf. Theory 2016, 62, 7402–7418. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. Inequalities: Theory of Majorization and Its Applications; Academic Press: New York, NY, USA, 1979. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, J. A Monotone Path Proof of an Extremal Result for Long Markov Chains. Entropy 2019, 21, 276. https://doi.org/10.3390/e21030276
Wang J, Chen J. A Monotone Path Proof of an Extremal Result for Long Markov Chains. Entropy. 2019; 21(3):276. https://doi.org/10.3390/e21030276
Chicago/Turabian StyleWang, Jia, and Jun Chen. 2019. "A Monotone Path Proof of an Extremal Result for Long Markov Chains" Entropy 21, no. 3: 276. https://doi.org/10.3390/e21030276
APA StyleWang, J., & Chen, J. (2019). A Monotone Path Proof of an Extremal Result for Long Markov Chains. Entropy, 21(3), 276. https://doi.org/10.3390/e21030276