Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method
Abstract
:1. Introduction
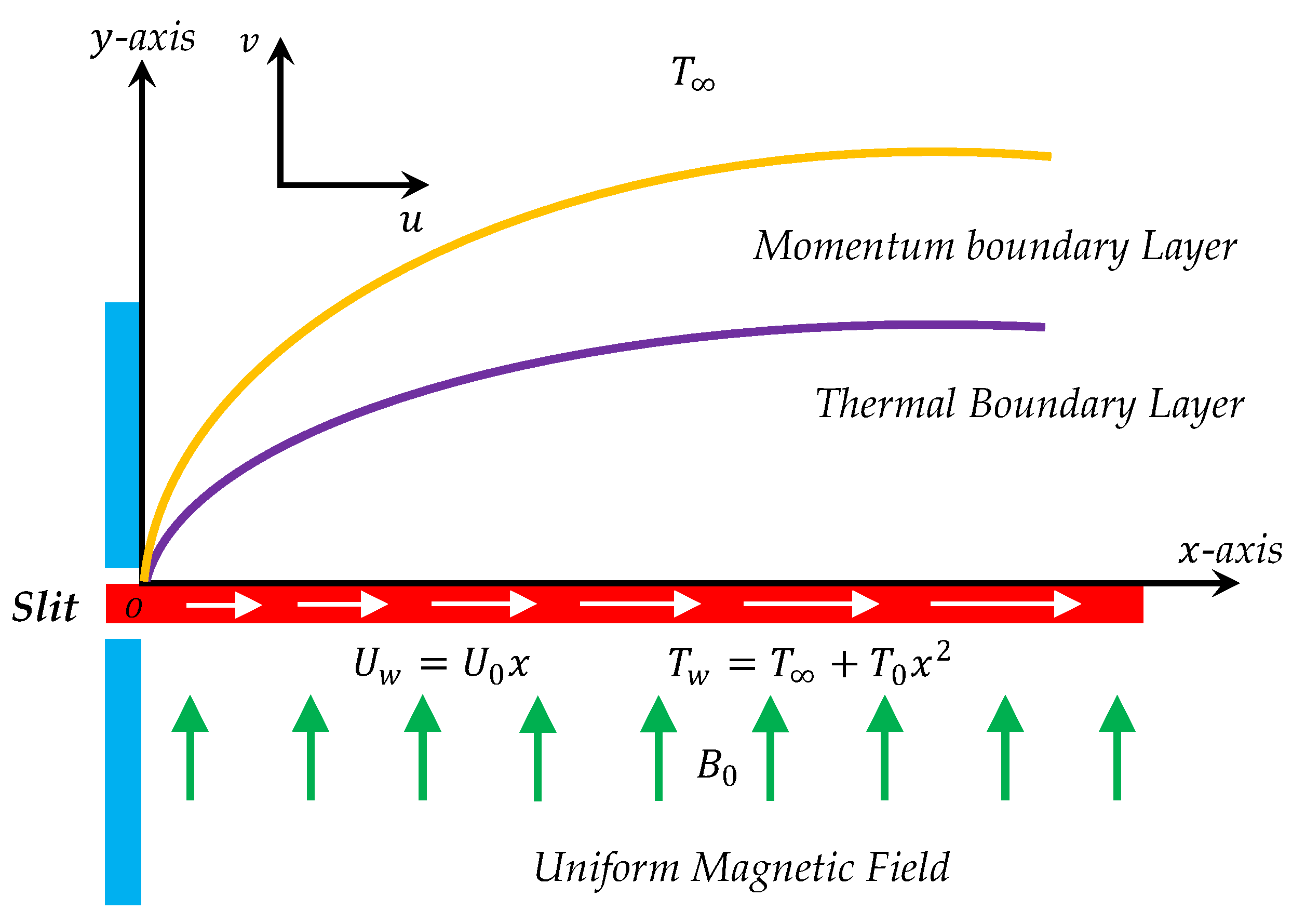
2. Flow and Heat Transfer Analysis
2.1. Closed Form Solutions
2.2. Second Law Analysis
3. Solution Methodology
3.1. Gear-Generalized Differential Quadrature Method (GGDQM)
3.2. Validation of the Numerical Results
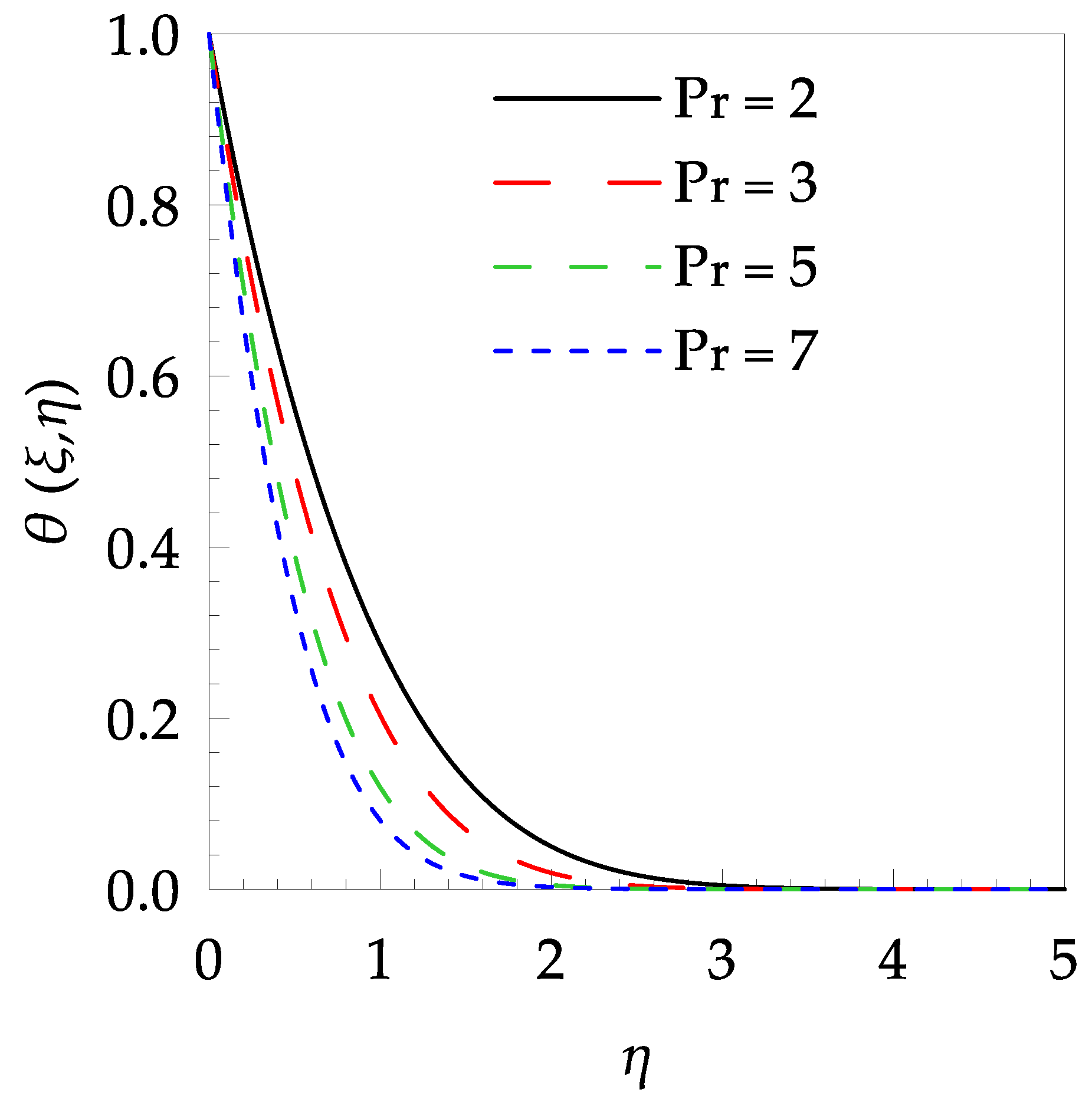
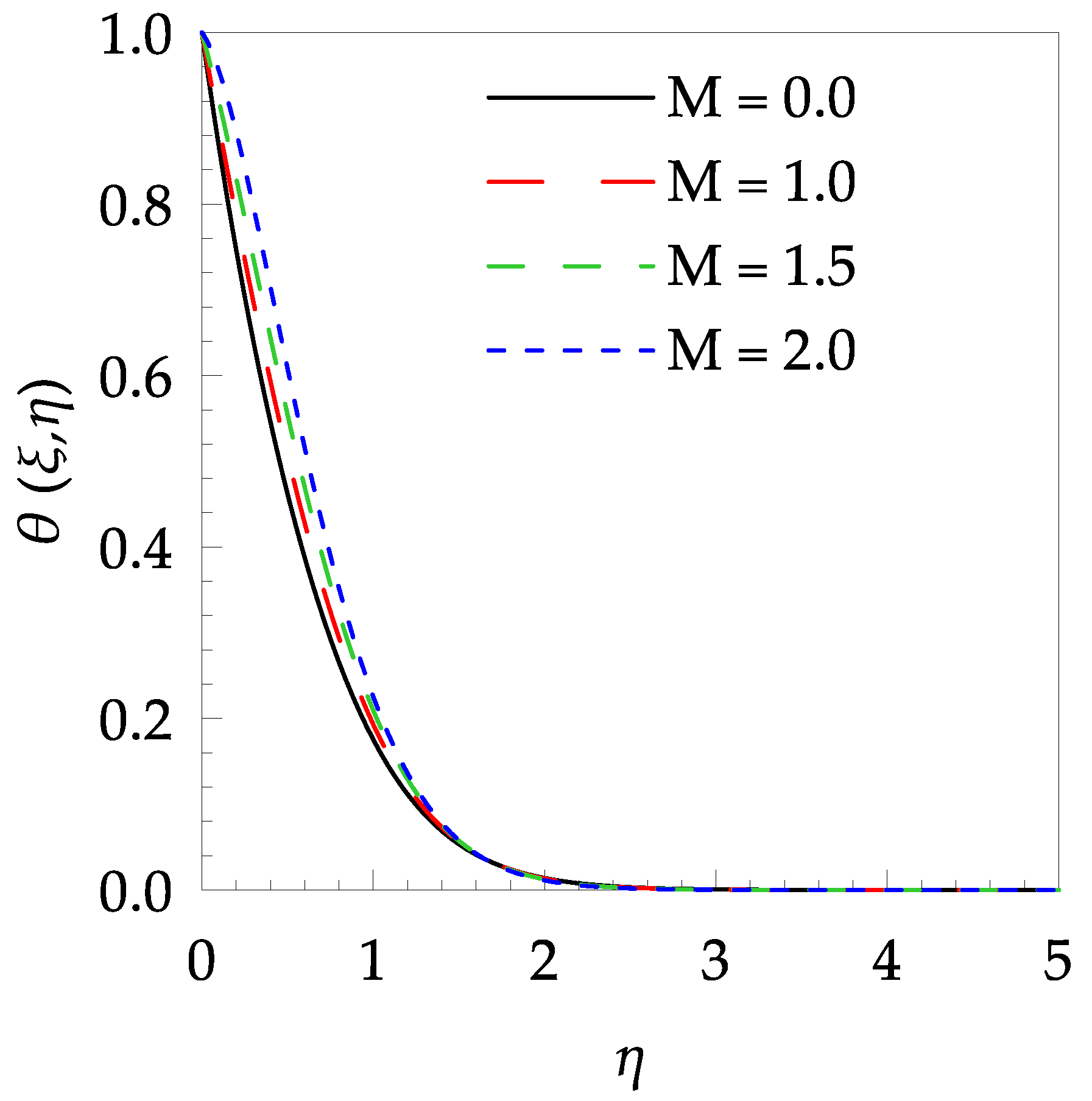
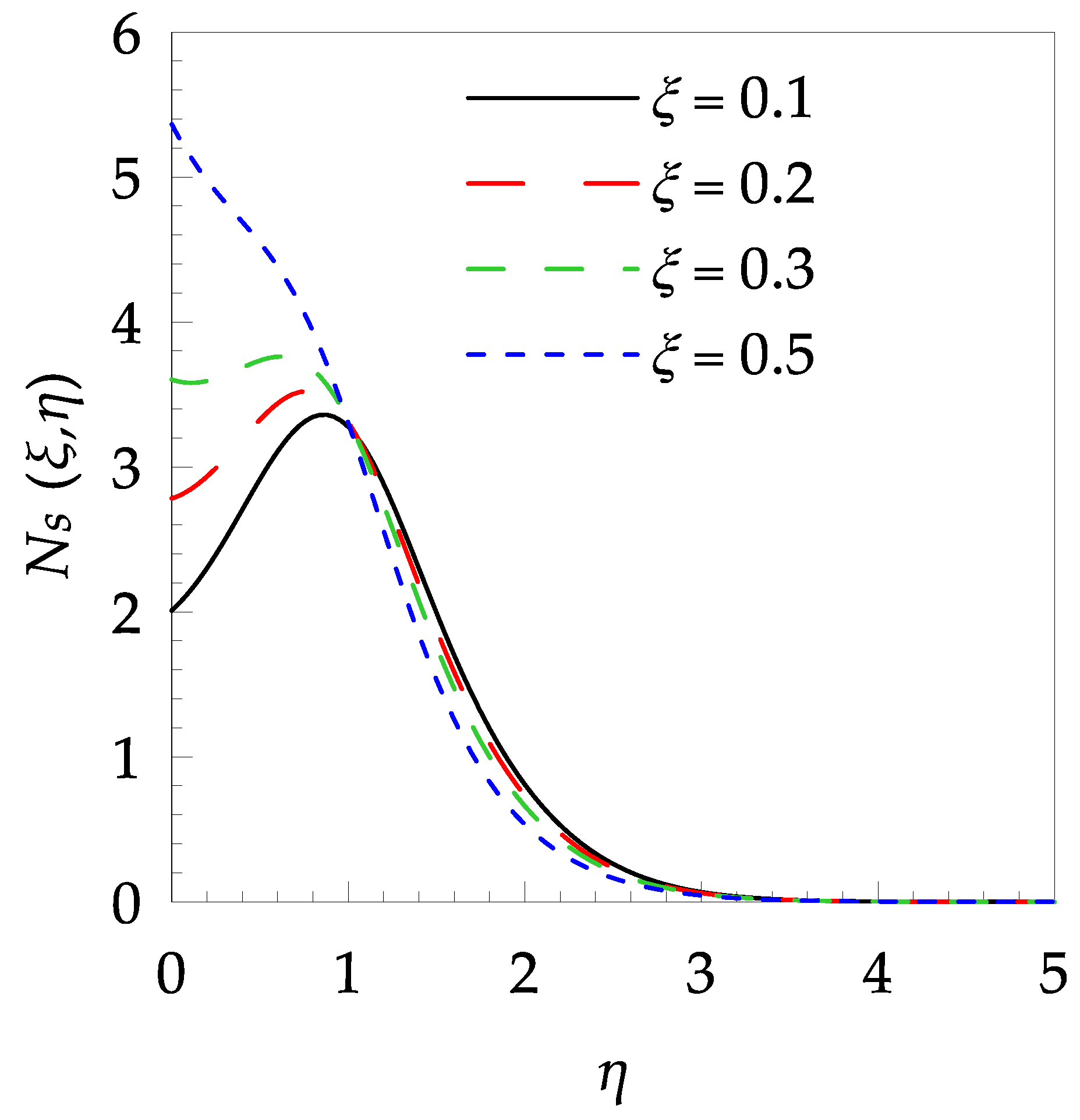
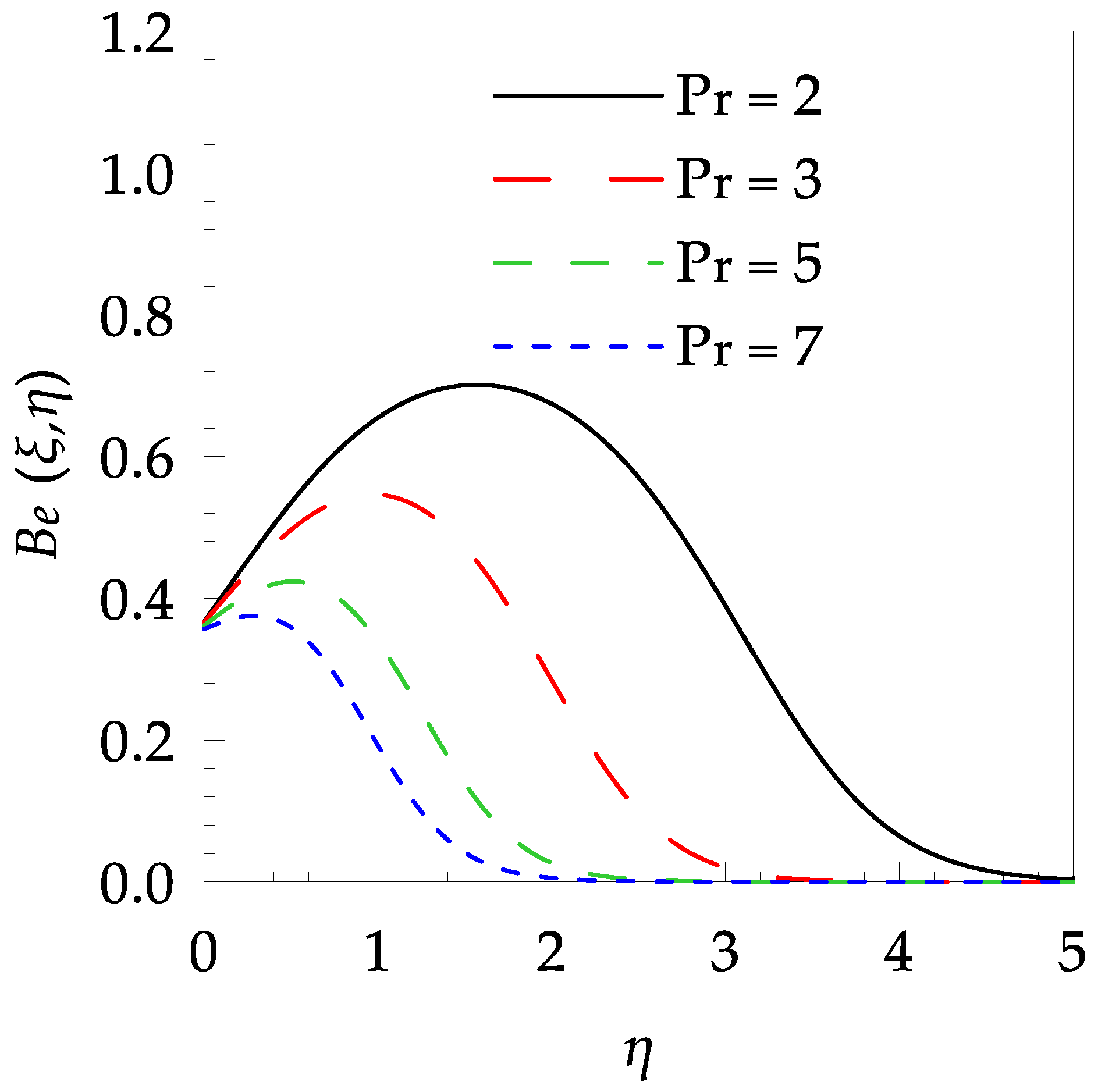
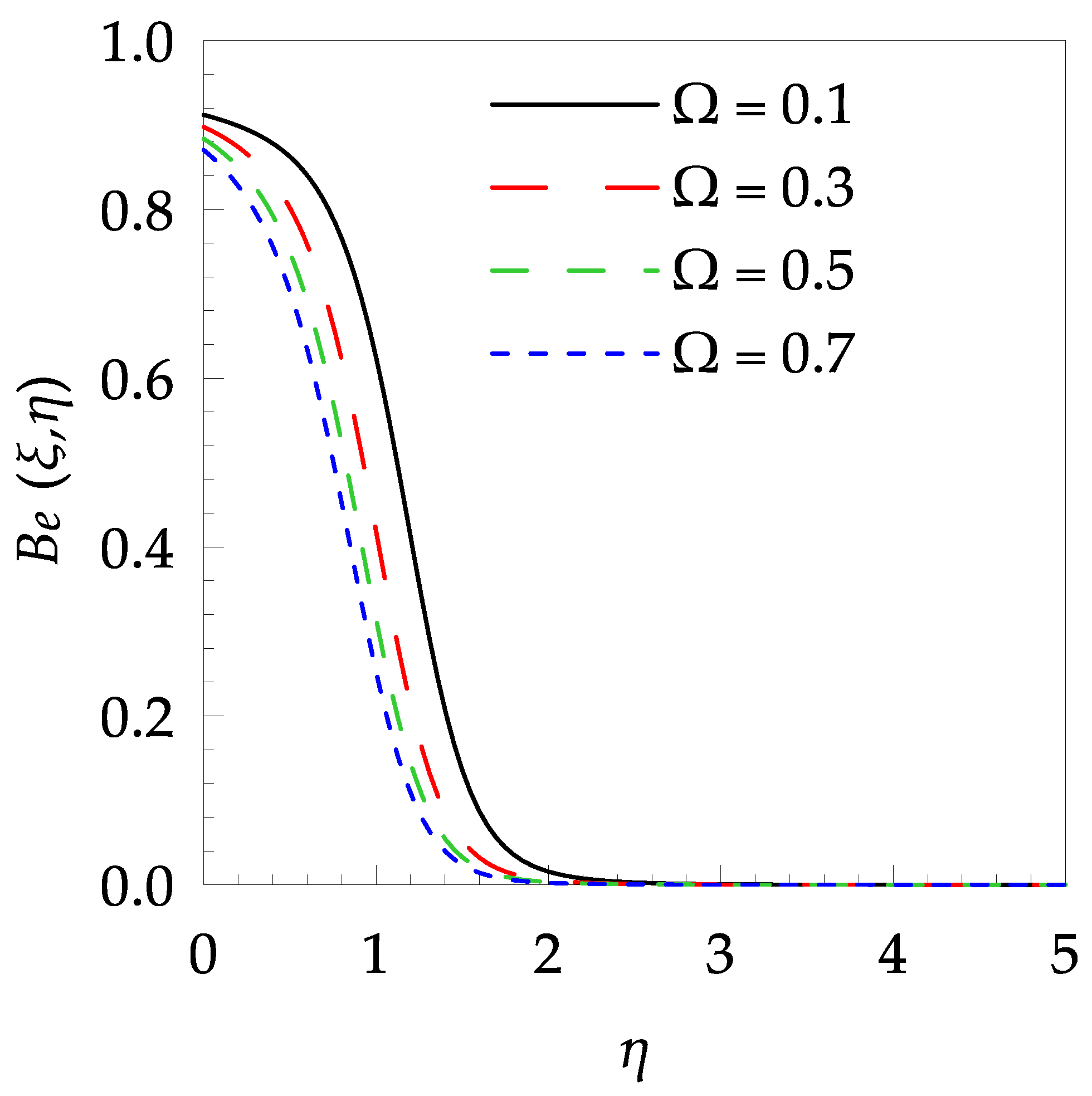
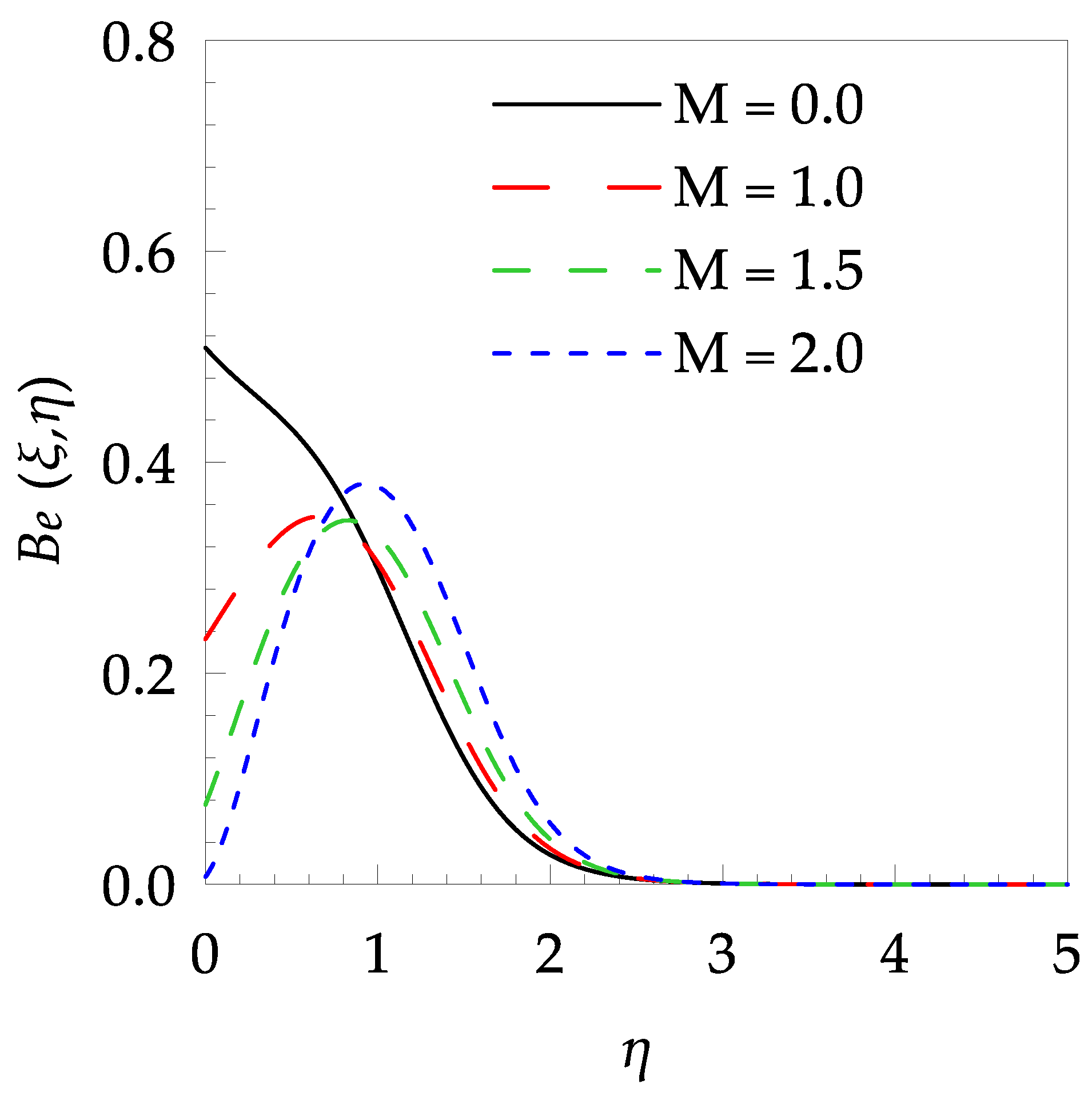
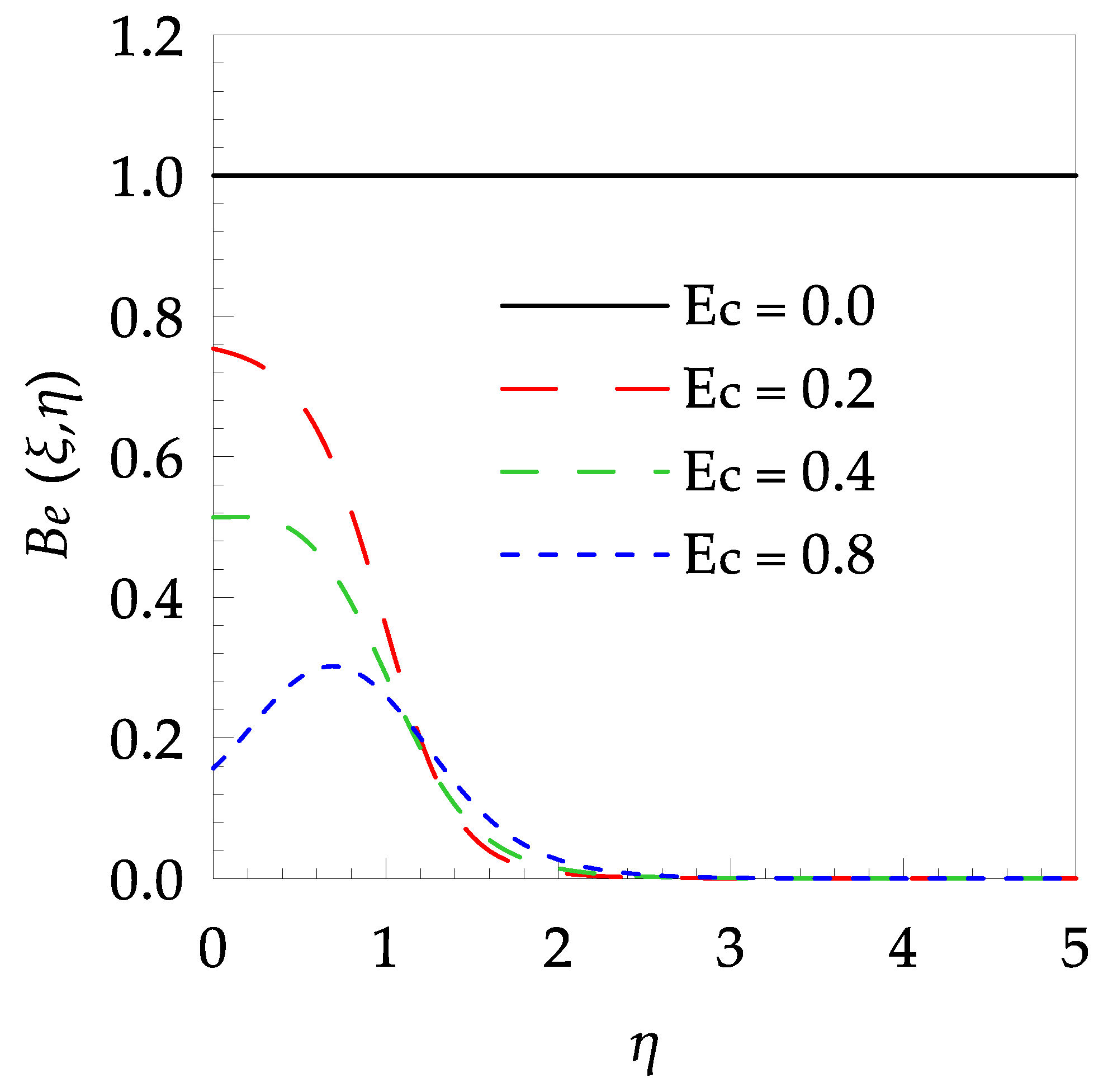
4. Results and Discussion
5. Closing Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transfer 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. The thermodynamic design of heat and mass transfer processes and devices. Int. J. Heat Fluid Flow 1987, 8, 258–276. [Google Scholar] [CrossRef]
- Makinde, O.D. Irreversibility analysis for a gravity driven non-Newtonian liquid film along an inclined isothermal plate. Phys. Scr. 2006, 74, 642–645. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S.; Tshehla, M.S. Thermodynamics analysis of variable viscosity hydromagnetic Couette flow in a rotating system with Hall effects. Entropy 2015, 17, 7811–7826. [Google Scholar] [CrossRef]
- Chamkha, A.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy generation and natural convection of CuO-water nanofluid in C-shaped cavity under magnetic field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Basaran, C.; Yan, C.Y. A thermodynamic framework for damage mechanics of solder joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Yao, W.; Basaran, C. Computational damage mechanics of electromigration and thermomigration. J. Appl. Phys. 2013, 114, 79–99. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamic entropy and analysis of damage state of complex systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Sosnovskiy, L.; Sherbakov, S. Mechanothermodynamics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für Angew. Math. und Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the role of entropy generation in processes involving fatigue. Entropy 2012, 14, 24–31. [Google Scholar] [CrossRef]
- Chamkha, A.J. MHD flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Int. Commun. Heat Mass Transf. 2003, 30, 413–422. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. Eng. 2010, 41, 651–655. [Google Scholar] [CrossRef]
- Reddy, P.S.; Chamkha, A.J. Soret and Dufour Effects on Unsteady MHD Heat and Mass Transfer from a Permeable Stretching Sheet with Thermophoresis and Non-Uniform Heat Generation/Absorption. J. Appl. Fluid Mech. 2016, 9, 2443–2455. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Prakash, M. Temperature dependent viscosity and thermal conductivity effects on hydromagnetic flow over a slendering stretching sheet. J. Niger. Math. Soc. 2015, 34, 318–330. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Layek, G.C. Thermal boundary layer in flow due to an exponentially stretching surface with an exponentially moving free stream. Model. Simul. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Abid, H.; Khan, I.; Sharidan, S. Analytical solution for suction and injection flow of a viscoplastic Casson fluid past a stretching surface in the presence of viscous dissipation. Neural Comput. Appl. 2016, 2016, 1–9. [Google Scholar]
- Khan, Z.H.; Qasim, M.; Ishfaq, N.; Khan, W.A. Dual Solutions of MHD Boundary Layer Flow of a Micropolar Fluid with Weak Concentration over a Stretching/Shrinking Sheet. Commun. Theor. Phys. 2017, 67, 449–457. [Google Scholar] [CrossRef]
- Pop, I.; Na, T.Y. Unsteady flow past a stretching sheet. Mech. Res. Commun. 1996, 23, 413–422. [Google Scholar] [CrossRef]
- Chang, C.; Wang, C.; Miklavcic, M.; Du, Q. Impulsive Stretching of a Surface in a Viscous Fluid. SIAM J. Appl. Math. 1997, 57, 1–14. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Zheng, L.C.; Jin, X.; Zhang, X.X.; Zhang, J.H. Unsteady heat and mass transfer in MHD flow over an oscillatory stretching surface with Soret and Dufour effects. Acta Mech. Sin. 2013, 29, 667–675. [Google Scholar] [CrossRef]
- Aurangzaib, A.R.; Kasim, M.; Mohammad, N.F.; Shafie, S. Unsteady MHD Mixed Convection Flow with Heat and Mass Transfer over a Vertical Plate in a Micropolar Fluid-Saturated Porous Medium. J. Appl. Sci. Eng. 2013, 16, 141–150. [Google Scholar]
- Malvandi, A.; Hedayati, F.; Ganji, D.D.; Rostamiyan, Y. Unsteady boundary layer flow of nanofluid past a permeable stretching/shrinking sheet with convective heat transfer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 1175–1184. [Google Scholar] [CrossRef]
- Motsa, S.S.; Makukula, Z.G. On a Bivariate Spectral Homotopy Analysis Method for Unsteady Mixed Convection Boundary Layer Flow, Heat, and Mass Transfer due to a Stretching Surface in a Rotating Fluid. J. Appl. Math. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Motsa, S.S. On the practical use of the spectral homotopy analysis method and local linearisation method for unsteady boundary-layer flows caused by an impulsively stretching plate. Numer. Algorithms 2014, 66, 865–883. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sarojamma, G.; Sreelakshmi, K.; Kalyani, C. Dual solutions of an unsteady flow, heat and mass transfer of an electrically conducting fluid over a shrinking sheet in the presence of radiation and viscous dissipation. Int. J. Mech. Sci. 2017, 130, 119–132. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1992, 95, 227–230. [Google Scholar] [CrossRef]
- Xu, H.; Liao, S.J.; Pop, I. Series solutions of unsteady three-dimensional MHD flow and heat transfer in the boundary layer over an impulsively stretching plate. Eur. J. Mech. B/Fluids 2007, 26, 15–27. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Methods Appl. Mech. Eng. 2019, 344, 319–333. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput. Methods Appl. Mech. Eng. 2019, 344, 306–318. [Google Scholar] [CrossRef]
- Salem, A.M. Entropy generation for magnetohydrodynamic heat transfer over a non-isothermal stretching sheet with variable viscosity. IMA J. Appl. Math. 2015, 80, 255–272. [Google Scholar] [CrossRef]
- Das, S.; Sarkar, B.C.; Jana, R.N. Entropy Generation in MHD Free Convective Boundary Layer Flow Past an Inclined Flat Plate Embedded in a Porous Medium with Hall Currents. Int. J. Comput. Appl. 2013, 84, 36–46. [Google Scholar]
- Rashidi, M.M.; Freidoonimehr, N. Analysis of Entropy Generation in MHD Stagnation-Point Flow in Porous Media with Heat Transfer. Int. J. Comput. Methods Eng. Sci. Mech. 2014, 15, 345–355. [Google Scholar] [CrossRef]
- Govindaraju, M.; Vishnu Ganesh, N.; Ganga, B.; Abdul Hakeem, A.K. Entropy generation analysis of magneto hydrodynamic flow of a nanofluid over a stretching sheet. J. Egypt. Math. Soc. 2015, 23, 429–434. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohammadi, F.; Abbasbandy, S.; Alhuthali, M.S. Entropy Generation Analysis for Stagnation Point Flow in a Porous Medium over a Permeable Stretching Surface. J. Appl. Fluid Mech. 2015, 8, 753–765. [Google Scholar] [CrossRef]
- Hakeem, A.K.A.; Govindaraju, M.; Ganga, B.; Kayalvizhi, M. Second law analysis for radiative MHD slip flow of a nanofluid over a stretching sheet with non-uniform heat source effect. Sci. Iran. 2016, 23, 1524–1538. [Google Scholar]
- Afridi, I.M.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, S.A. Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy 2017, 19, 10. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I. Effects of Energy Dissipation and Variable Thermal Conductivity on Entropy Generation Rate in Mixed Convection Flow. J. Therm. Sci. Eng. Appl. 2018, 10, 1–6. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Makinde, O.D. Second Law Analysis of Boundary Layer Flow with Variable Fluid Properties. J. Heat Transfer 2017, 139, 1–6. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy 2018, 20, 43. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Amine, A.; Animasaun, I.L.; Afridi, M.I.; Qasim, M.; Sehaqui, R. Magneto-Convection of Alumina - Water Nanofluid Within Thin Horizontal Layers Using the Revised Generalized Buongiorno’s Model. Front. Heat Mass Transf. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 1–27. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. Numerical Analysis of the Onset of Longitudinal Convective Rolls in a Porous Medium Saturated by an Electrically Conducting Nanofluid in the Presence of an External Magnetic Field. Results Phys. 2017, 7, 2134–2152. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Sehaqui, R. A Semi-Analytical Analysis of Electro-Thermo-Hydrodynamic Stability in Dielectric Nanofluids Using Buongiorno’s Mathematical Model Together with More Realistic Boundary Conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Mishra, S.R.; Rashidi, M.M.; Sehaqui, R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model. Eur. Phys. J. Plus 2018, 133, 1–16. [Google Scholar] [CrossRef]
- Afridi, I.M.; Qasim, M.; Wakif, A.; Hussanan, A. Second Law Analysis of Dissipative Nanofluid Flow over a Curved Surface in the Presence of Lorentz Force: Utilization of the Chebyshev–Gauss–Lobatto Spectral Method. Nanomaterials 2019, 9, 195. [Google Scholar] [CrossRef] [PubMed]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Spectral relaxation method and spectral quasilinearization method for solving unsteady boundary layer flow problems. Adv. Math. Phys. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Agbaje, T.M.; Motsa, S.S. Comparison between spectral perturbation and spectral relaxation approach for unsteady heat and mass transfer by MHD mixed convection flow over an impulsively stretched vertical surface with chemical reaction effect. J. Interpolat. Approx. Sci. Comput. 2015, 1, 48–83. [Google Scholar] [CrossRef]





| SPM [54] | SRM [54] | GGDQM | ||
|---|---|---|---|---|
| 0.7 | −0.6278318239 | −0.6278318241 | −0.6278318240 | −0.6278318238 |
| 1.5 | −0.9704104930 | −0.9704104933 | −0.9704104926 | −0.9704104929 |
| 3.0 | −1.4270081804 | −1.4270081807 | −1.4270081793 | −1.4270081804 |
| 5.0 | −1.8845313181 | −1.8845313184 | −1.8845313162 | −1.8845313181 |
| 7.0 | −2.2577308115 | −2.2577308118 | −2.2577308091 | −2.2577308115 |
| 10 | −2.7291527800 | −2.7291527804 | −2.7291527770 | −2.7291527800 |
| Exact Results | GGDQM | Exact Results | GGDQM | |
|---|---|---|---|---|
| 0.0 | −0.56418958 | −0.56418958 | −1.0000000 | −1.0000000 |
| 1.0 | −0.56418958 | −0.56418958 | −1.4142135 | −1.4142135 |
| 1.5 | −0.56418958 | −0.56418958 | −1.8027756 | −1.8027756 |
| 2.0 | −0.56418958 | −0.56418958 | −2.2360679 | −2.2360679 |
| Exact Results | GGDQM | Exact Results | GGDQM | |||
|---|---|---|---|---|---|---|
| 4.0 | 0.0 | 1.0 | −1.2732395 | −1.2732395 | 4.0000000 | 4.0000000 |
| 4.0 | 1.0 | 1.0 | −1.2732395 | −1.2732395 | −4.0000000 | −3.9999999 |
| 4.0 | 1.5 | 1.0 | −1.2732395 | −1.2732395 | −14.0000000 | −14.0000000 |
| 4.0 | 2.0 | 1.0 | −1.2732395 | −1.2732395 | −28.0000000 | −28.0000000 |
| 6.0 | 0.5 | 0.0 | 0.0000000 | 0.0000000 | 12.0000000 | 12.0000000 |
| 6.0 | 0.5 | 0.5 | −0.9549296 | −0.9549296 | 7.5000000 | 7.4999999 |
| 6.0 | 0.5 | 1.5 | −2.8647889 | −2.8647889 | −1.5000000 | −1.5000001 |
| 6.0 | 0.5 | 2.0 | −3.8197186 | −3.8197186 | −6.0000000 | −6.0000001 |
| Method | ||||||
|---|---|---|---|---|---|---|
| 0.01 | 0.001 | 0.0005 | 0.0002 | 0.0001 | ||
| 0.1 | SRM [53] | −0.61046835 | −0.61046762 | −0.61046761 | −0.61046761 | −0.61046761 |
| SQLM [53] | −0.61045544 | −0.61046674 | −0.61046742 | −0.61046758 | −0.61046761 | |
| GGDQM | −0.61041972 | −0.61046718 | −0.61046751 | −0.61046759 | −0.61046761 | |
| 0.3 | SRM [53] | −0.70126751 | −0.70126681 | −0.70126680 | −0.70126680 | −0.70126680 |
| SQLM [53] | −0.70126943 | −0.70126664 | −0.70126676 | −0.70126679 | −0.70126680 | |
| GGDQM | −0.70125747 | −0.70126671 | −0.70126678 | −0.70126680 | −0.70126680 | |
| 0.5 | SRM [53] | −0.78982903 | −0.78982837 | −0.78982837 | −0.78982837 | −0.78982837 |
| SQLM [53] | −0.78981759 | −0.78982831 | −0.78982835 | −0.78982836 | −0.78982837 | |
| GGDQM | −0.78982519 | −0.78982833 | −0.78982836 | −0.78982836 | −0.78982837 | |
| 0.7 | SRM [53] | −0.87626715 | −0.87626654 | −0.87626653 | −0.87626653 | −0.87626653 |
| SQLM [53] | −0.87625663 | −0.87626652 | −0.87626653 | −0.87626653 | −0.87626653 | |
| GGDQM | −0.87626547 | −0.87626652 | −0.87626653 | −0.87626653 | −0.87626653 | |
| 0.9 | SRM [53] | −0.96053875 | −0.96053800 | −0.96053800 | −0.96053800 | −0.96053800 |
| SQLM [53] | −0.96053069 | −0.96053800 | −0.96053800 | −0.96053800 | −0.96053800 | |
| GGDQM | −0.96053779 | −0.96053799 | −0.96053799 | −0.96053800 | −0.96053800 | |
| CPU Time (s) | |||
|---|---|---|---|
| SRM [53] | SQLM [53] | GGDQM | |
| 0.1 | 01.93 | 04.72 | 5.019 |
| 0.3 | 06.01 | 14.67 | 5.326 |
| 0.5 | 10.69 | 24.19 | 5.612 |
| 0.7 | 15.08 | 33.29 | 5.930 |
| 0.9 | 19.57 | 42.65 | 6.320 |
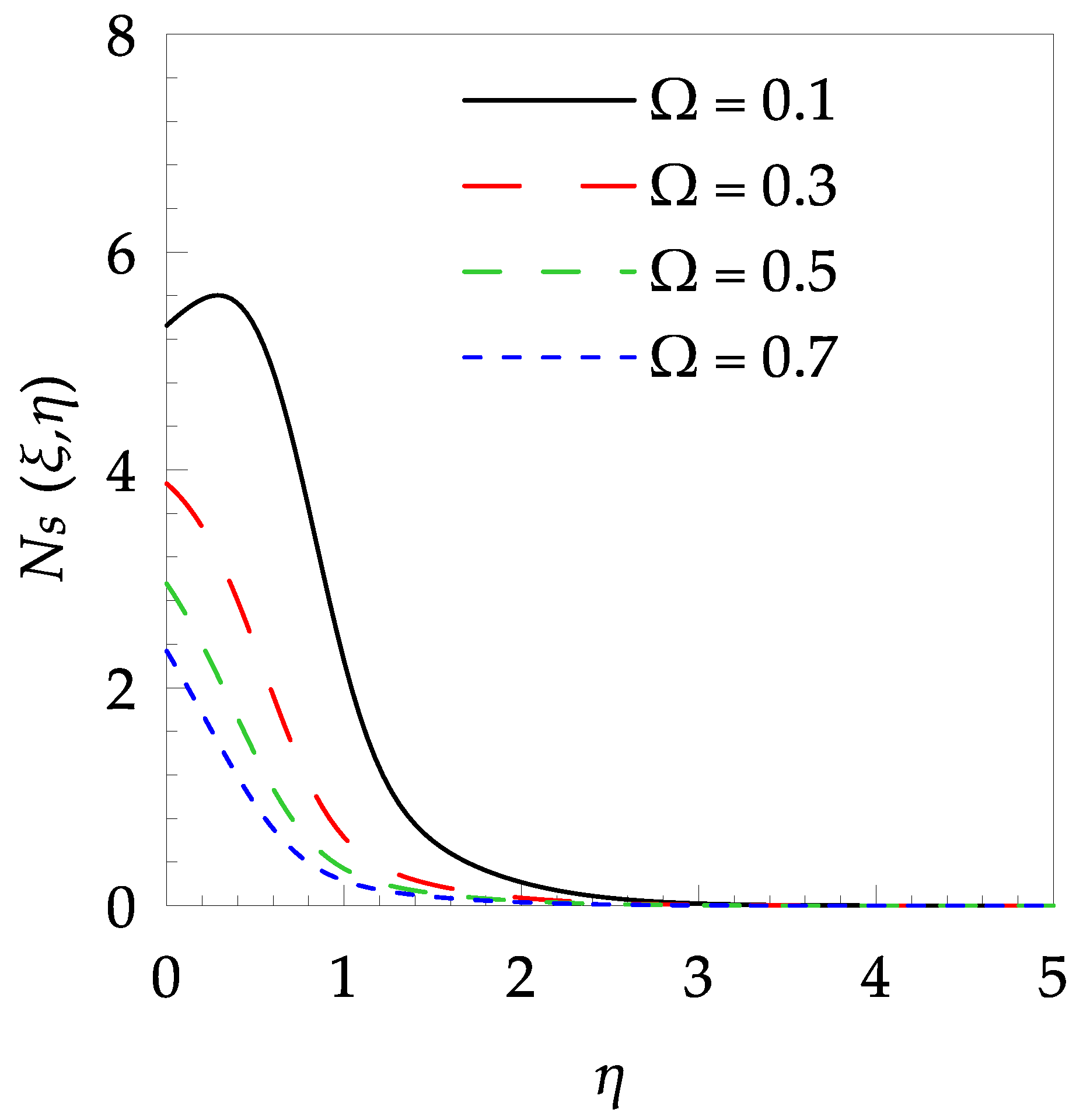
| 0.1 | 6.0 | 0.8 | 0.7 | 2.0415507 | 2.1732328 |
| 0.2 | 1.6200792 | 1.8904622 | |||
| 0.3 | 1.4625827 | 1.8127995 | |||
| 0.5 | 1.3401177 | 1.7802112 | |||
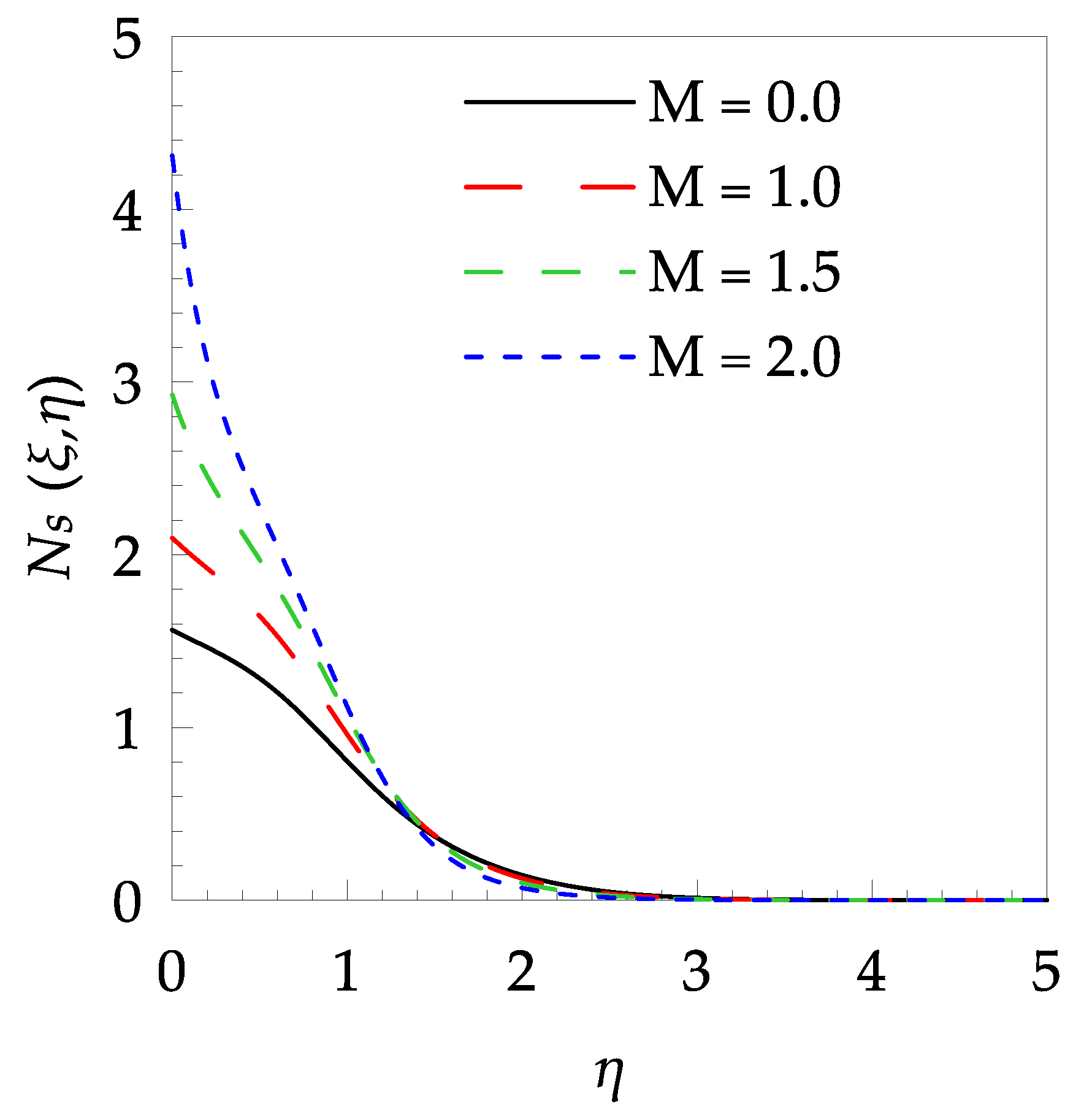
| 0.5 | 2.0 | 1.5 | 0.2 | 1.8162426 | 1.5214377 |
| 3.0 | 1.8162426 | 1.8609960 | |||
| 5.0 | 1.8162426 | 2.3780814 | |||
| 7.0 | 1.8162426 | 2.7823358 | |||
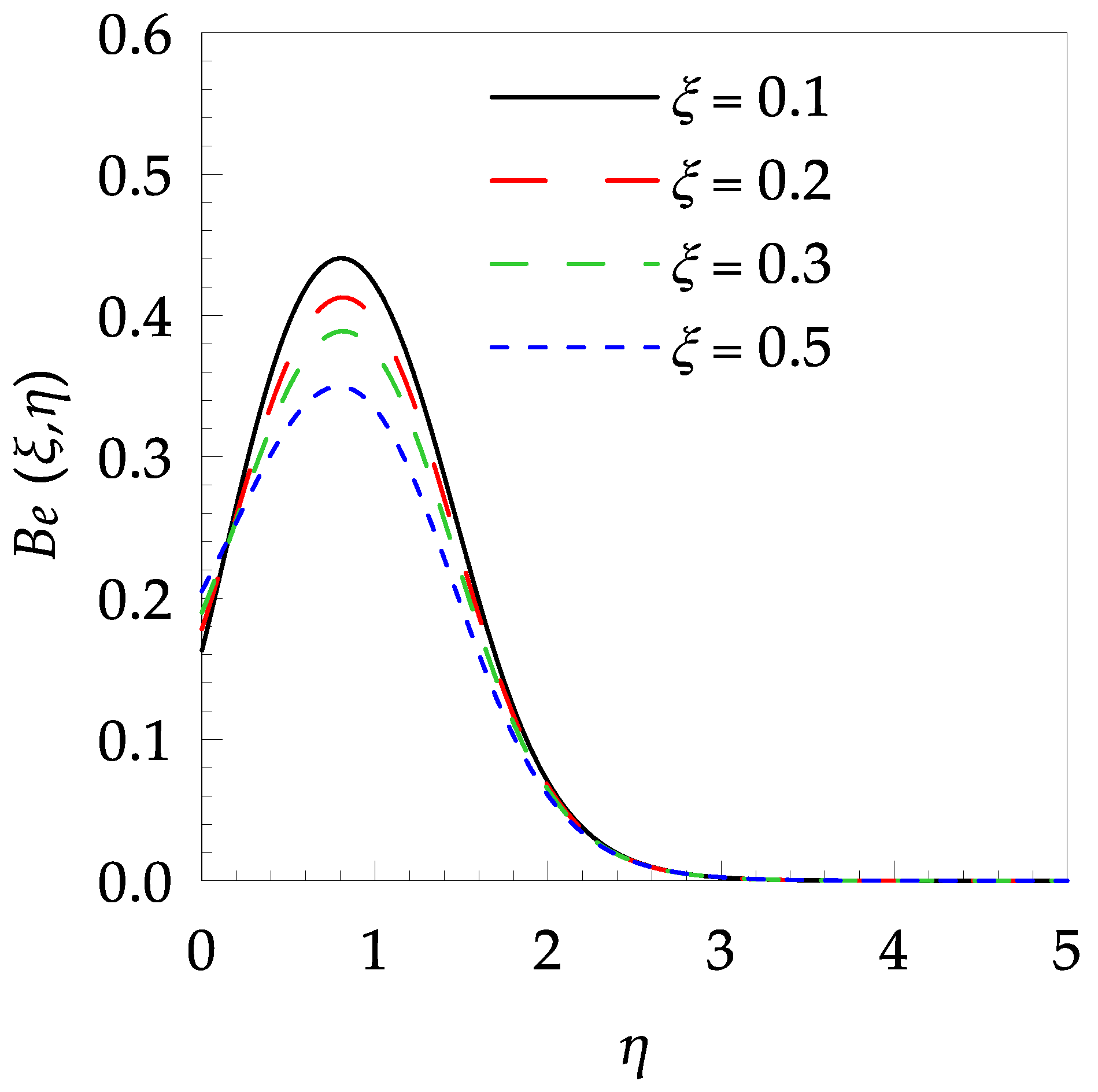
| 0.3 | 5.0 | 0.0 | 0.5 | 1.2803321 | 2.6073736 |
| 1.0 | 1.5602619 | 2.0405642 | |||
| 1.5 | 1.8757871 | 1.3748750 | |||
| 2.0 | 2.2665979 | 0.5145979 | |||
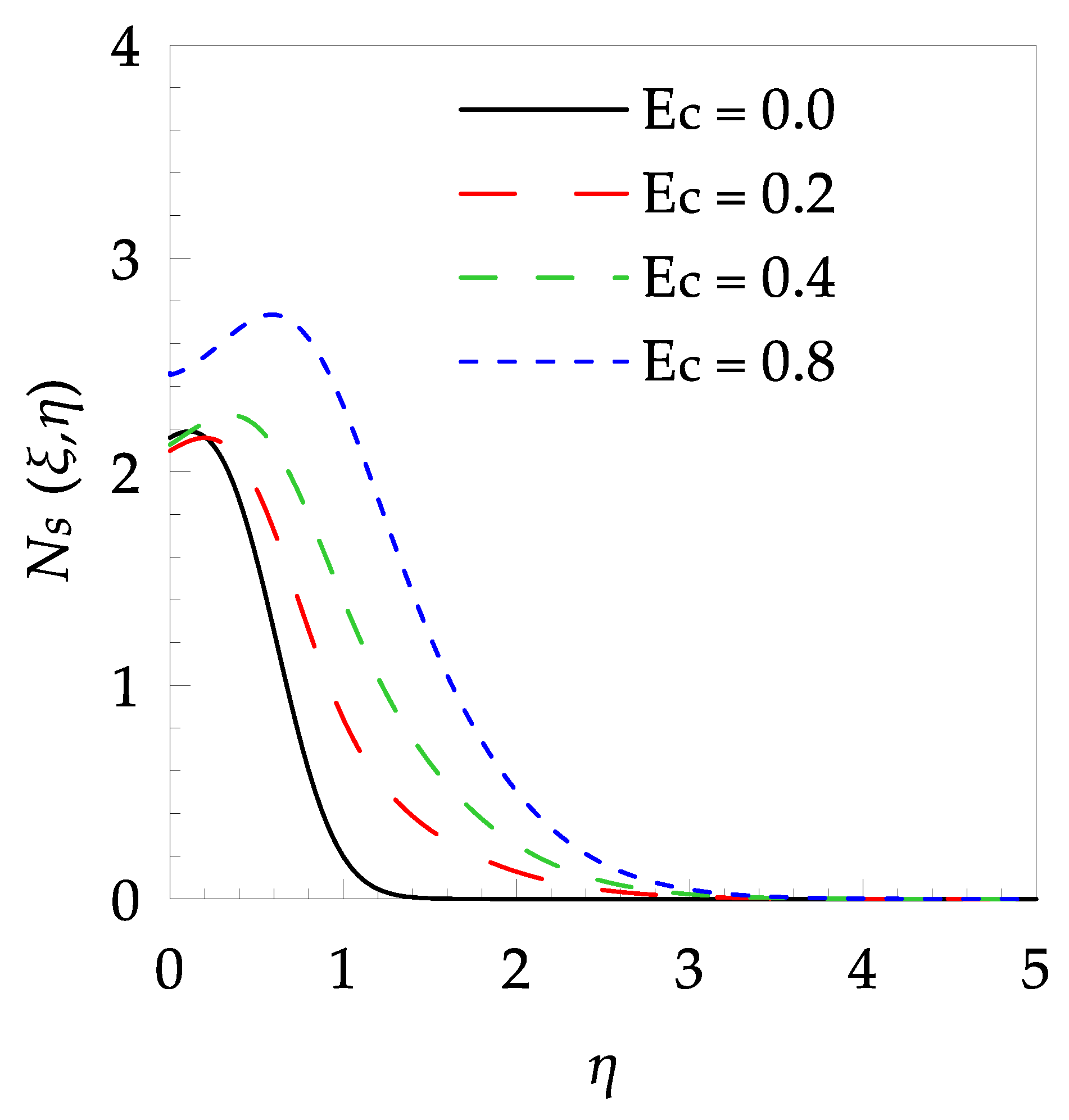
| 0.2 | 7.0 | 0.5 | 0.0 | 1.5276915 | 4.6016634 |
| 0.2 | 1.5276915 | 3.9378840 | |||
| 0.4 | 1.5276915 | 3.2741046 | |||
| 0.8 | 1.5276915 | 1.9465459 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasim, M.; Afridi, M.I.; Wakif, A.; Thoi, T.N.; Hussanan, A. Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method. Entropy 2019, 21, 240. https://doi.org/10.3390/e21030240
Qasim M, Afridi MI, Wakif A, Thoi TN, Hussanan A. Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method. Entropy. 2019; 21(3):240. https://doi.org/10.3390/e21030240
Chicago/Turabian StyleQasim, Muhammad, Muhammad Idrees Afridi, Abderrahim Wakif, T. Nguyen Thoi, and Abid Hussanan. 2019. "Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method" Entropy 21, no. 3: 240. https://doi.org/10.3390/e21030240
APA StyleQasim, M., Afridi, M. I., Wakif, A., Thoi, T. N., & Hussanan, A. (2019). Second Law Analysis of Unsteady MHD Viscous Flow over a Horizontal Stretching Sheet Heated Non-Uniformly in the Presence of Ohmic Heating: Utilization of Gear-Generalized Differential Quadrature Method. Entropy, 21(3), 240. https://doi.org/10.3390/e21030240







