Entropic Effects in Polymer Nanocomposites
Abstract
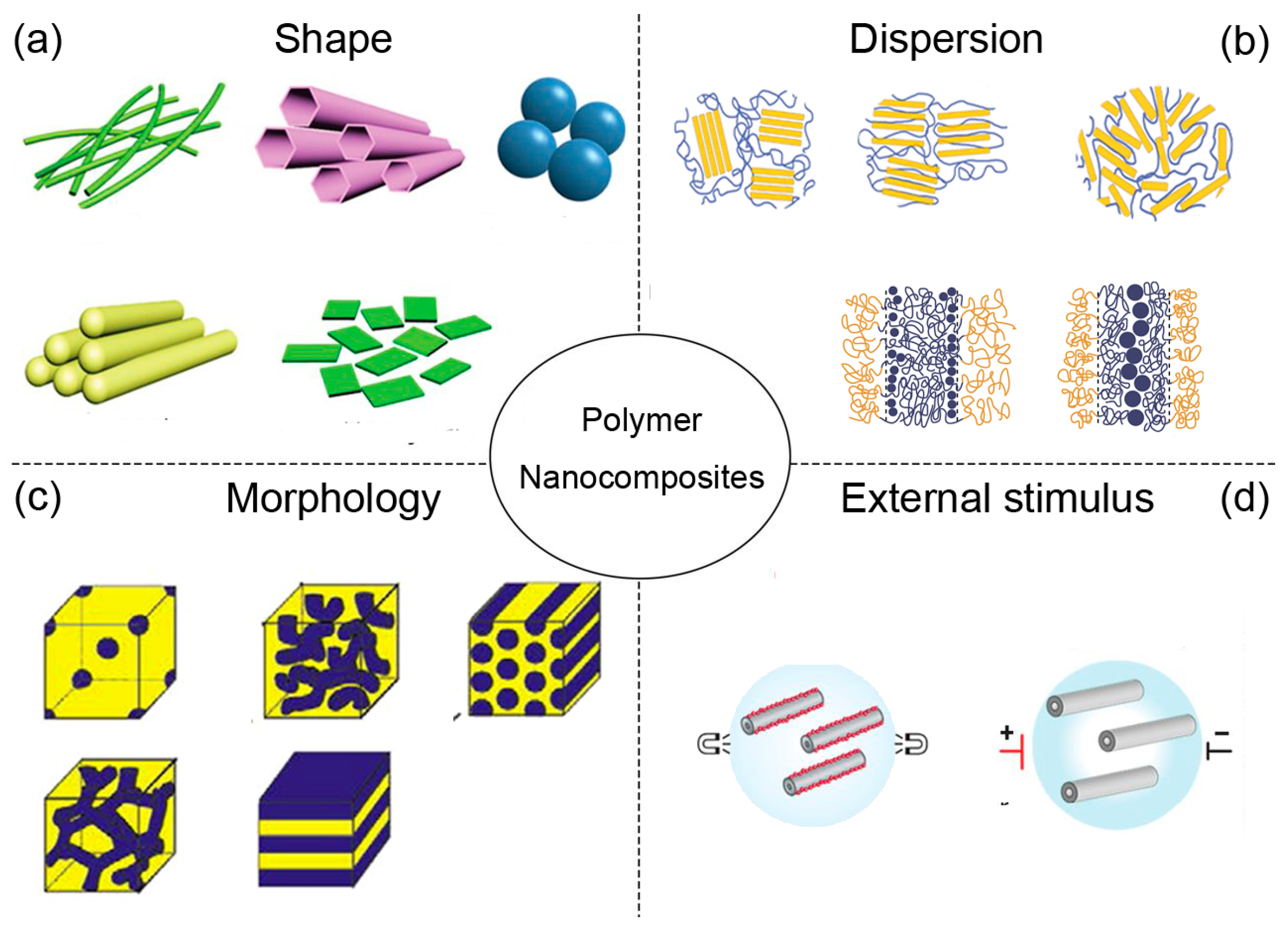
:1. Introduction
2. Methods and Models of Molecular Simulations
2.1. Molecular Dynamics
2.2. Monte Carlo
3. Entropy-Induced Transition Due to Nanoparticles
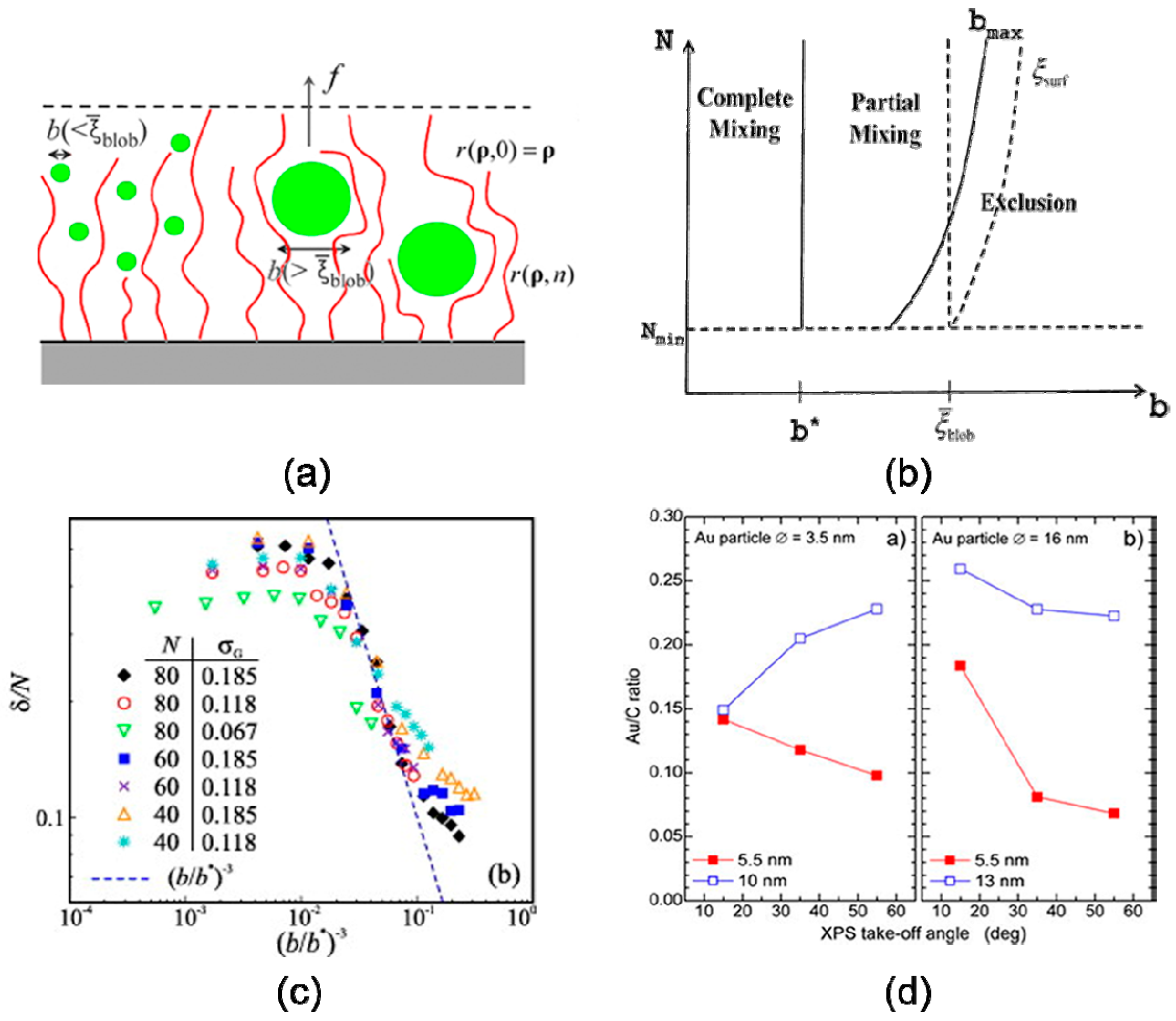
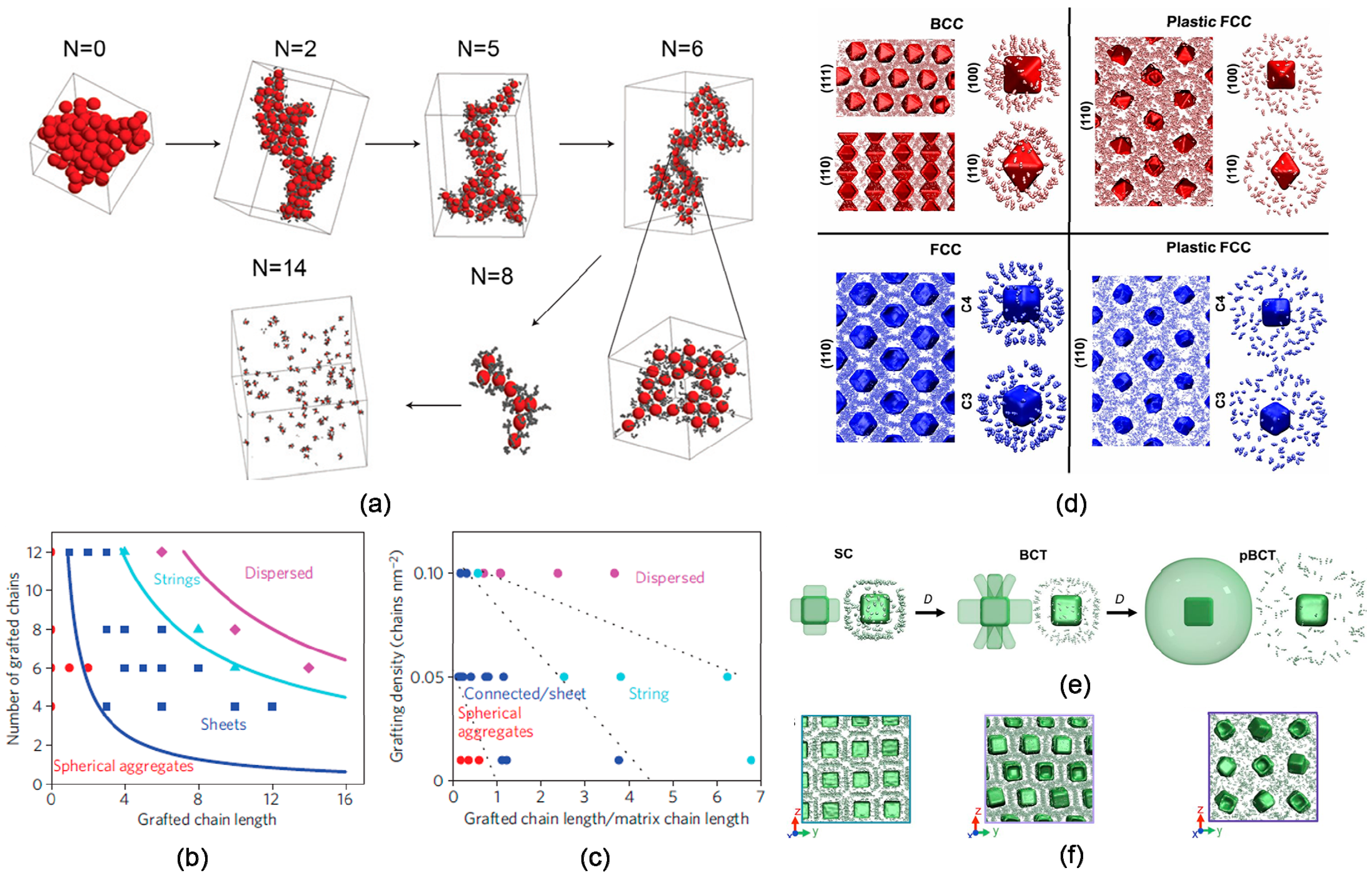
3.1. Particle Size
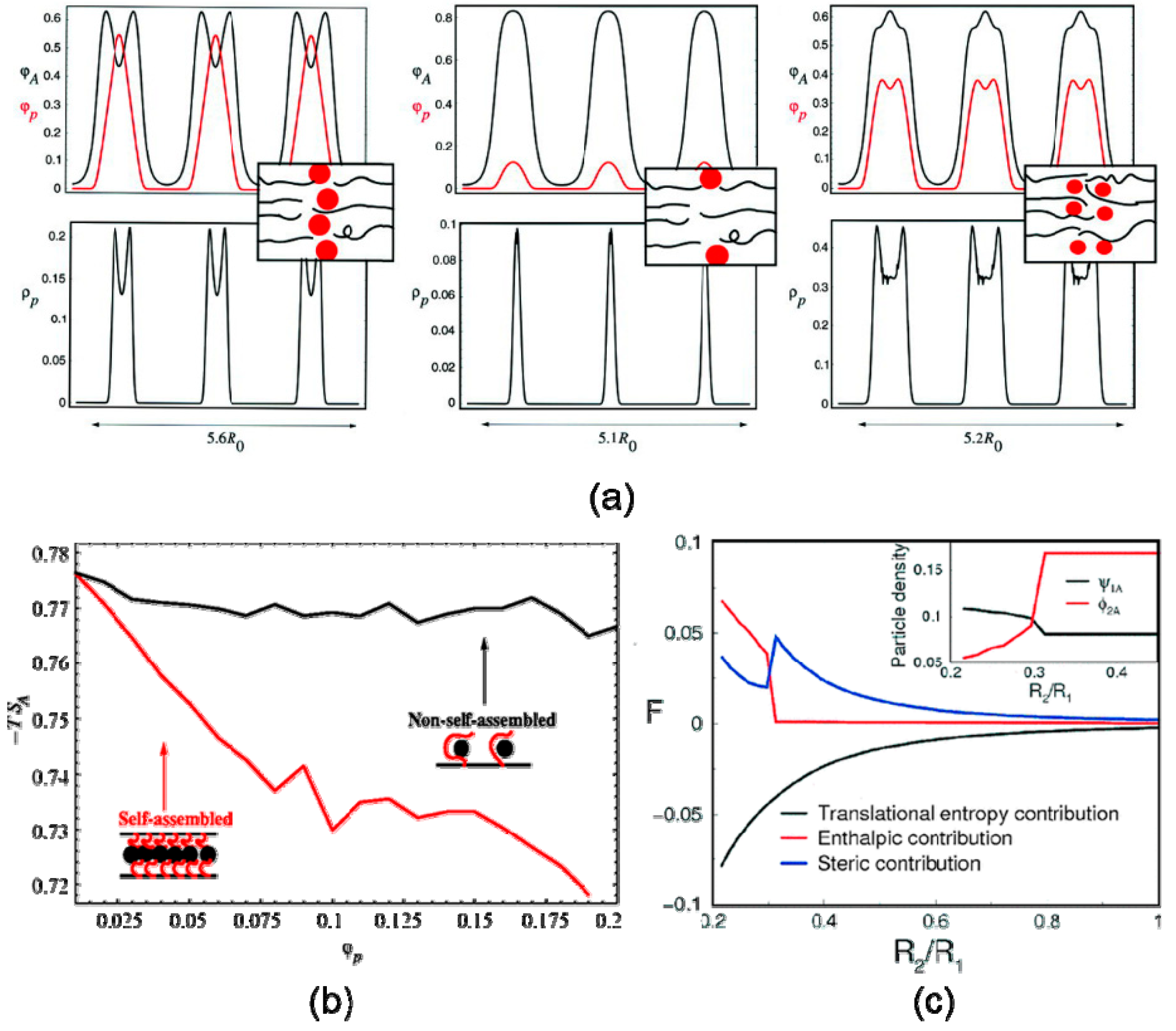
3.2. Volume Fraction
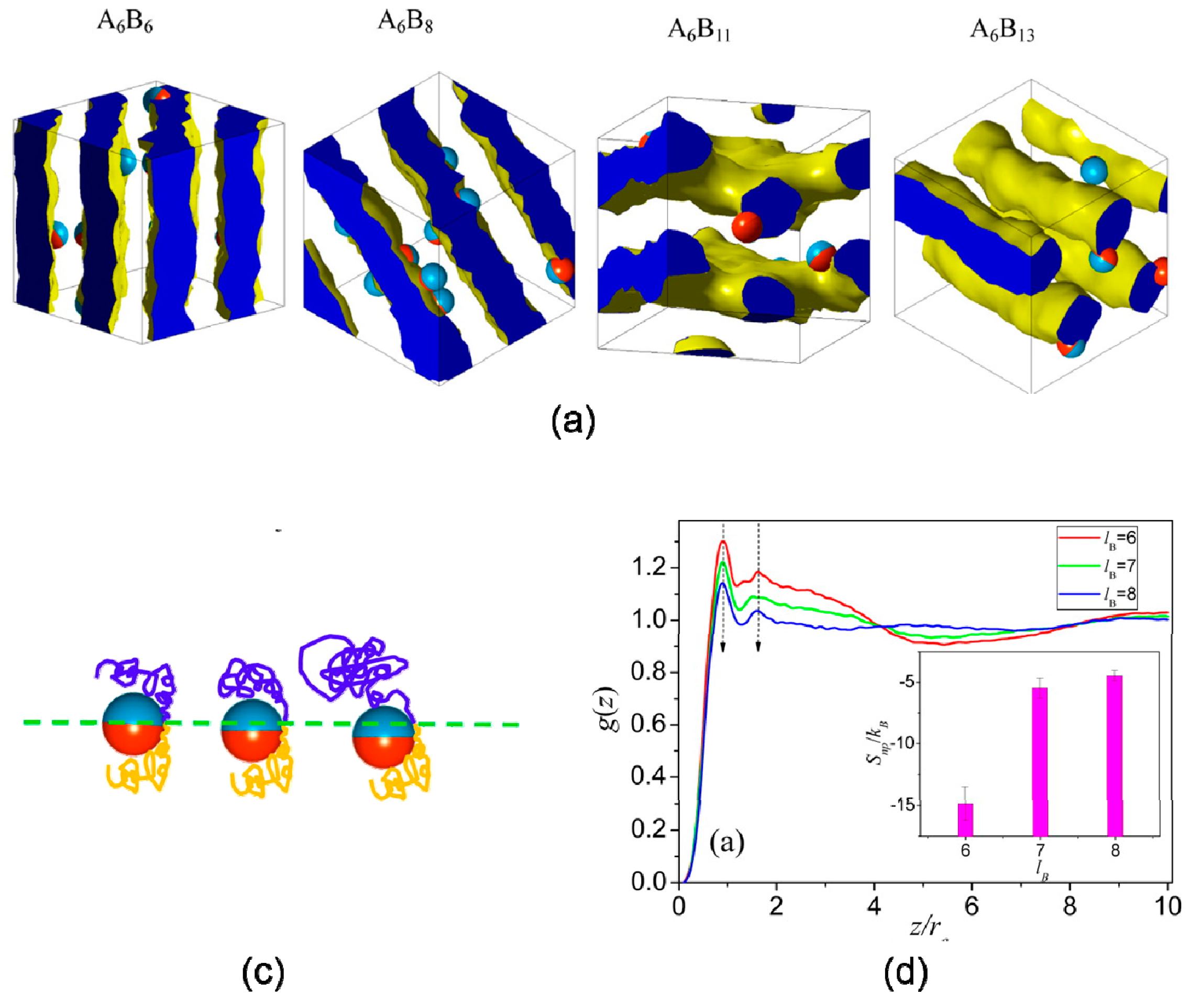
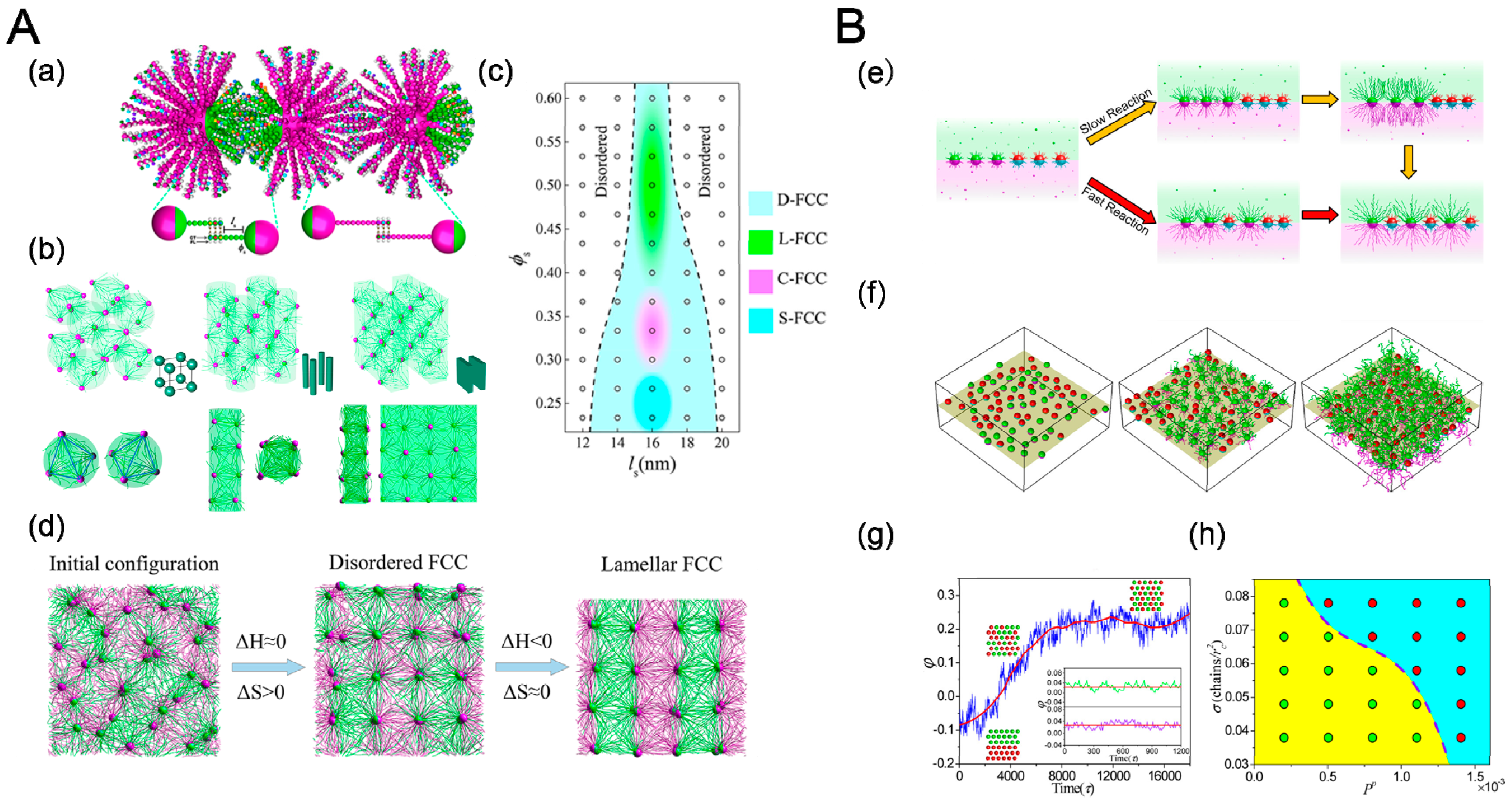
3.3. Shape
4. Entropy-Induced Transition by External Conditions
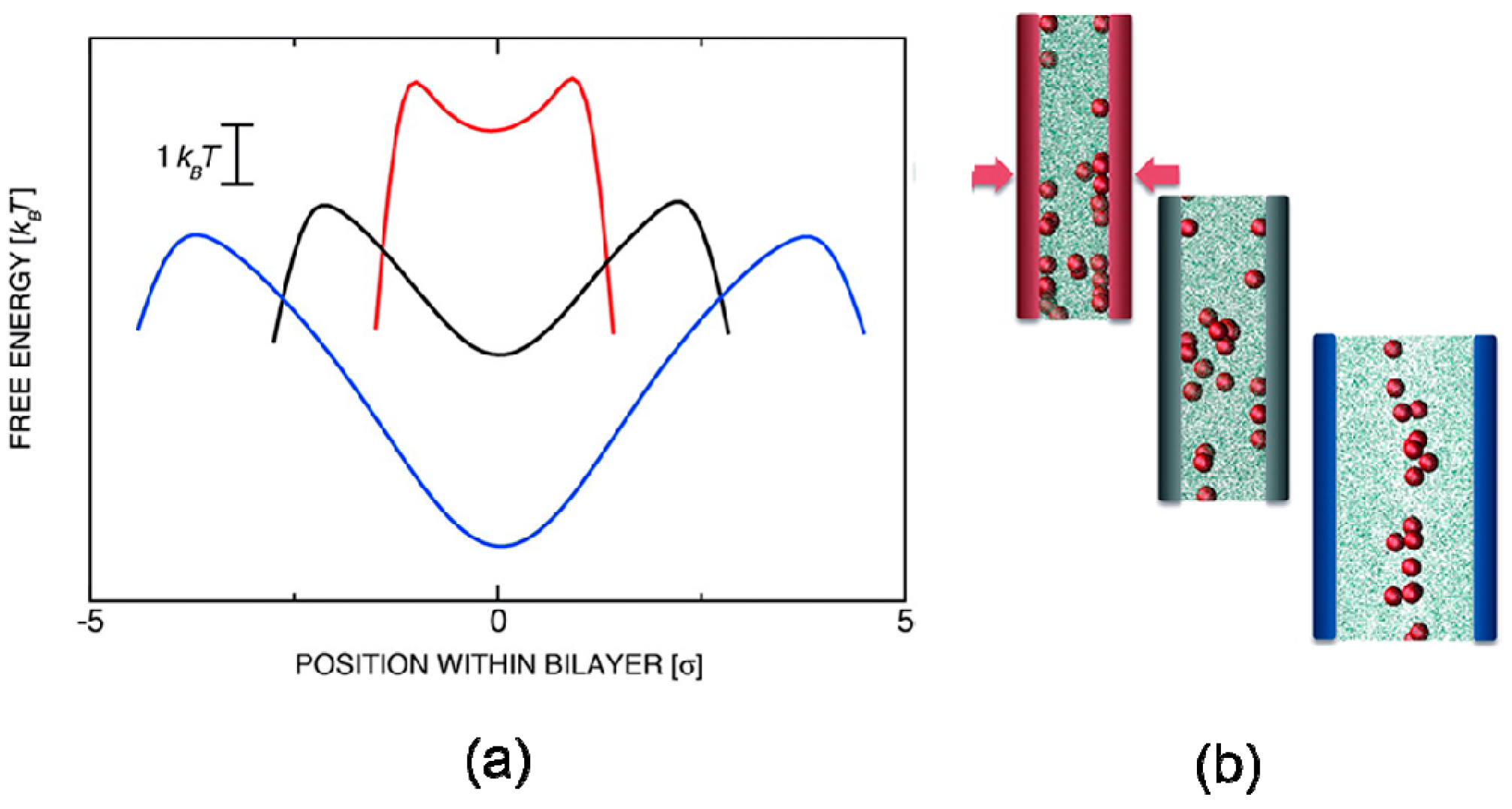
4.1. Confinement
4.2. External Field
4.3. Heating/Cooling
4.4. Reaction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle polymer composites: where two small worlds meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Bishop, K.J.; Wilmer, C.E.; Soh, S.; Grzybowski, B.A. Nanoscale forces and their uses in self-assembly. Small 2010, 5, 1600–1630. [Google Scholar] [CrossRef] [PubMed]
- Sevim, S.; Sorrenti, A.; Franco, C.; Furukawa, S.; Pané, S.; deMello, A.J.; Puigmartí-Luis, J. Self-assembled materials and supramolecular chemistry within microfluidic environments: from common thermodynamic states to non-equilibrium structures. Chem. Soc. Rev. 2018, 47, 3788–3803. [Google Scholar] [CrossRef] [PubMed]
- Böker, A.; He, J.; Russell, T.P.; Emrick, T.S. Self-assembly of nanoparticles at interfaces. Soft Matter 2010, 3, 1231–1248. [Google Scholar] [CrossRef]
- Stamm, M.; Sommer, J.U. Polymer-nanoparticle films: Entropy and enthalpy at play. Nat. Mat. 2007, 6, 260. [Google Scholar] [CrossRef] [PubMed]
- Escobedo, F.A. Engineering entropy in soft matter: the bad, the ugly and the good. Soft Matter 2014, 10, 8388–8400. [Google Scholar] [CrossRef] [PubMed]
- Behl, M.; Razzaq, M.Y.; Lendlein, A. Multifunctional shape-memory polymers. Adv. Mater. 2010, 22, 3388–3410. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Huang, Z.; Chen, P.; Cui, T.; Zhang, X.; Miao, B.; Yan, L.T. Optimal reactivity and improved self-healing capability of structurally dynamic polymers grafted on Janus nanoparticles governed by chain stiffness and spatial organization. Small 2017, 13, 1603155. [Google Scholar] [CrossRef]
- Dong, B.; Huang, Z.; Chen, H.; Yan, L.T. Chain-stiffness-induced entropy effects mediate interfacial assembly of Janus nanoparticles in block copolymers: From interfacial nanostructures to optical responses. Macromolecules 2015, 48, 5385–5393. [Google Scholar] [CrossRef]
- Nagel, S.R. Experimental soft-matter science. Rev. Mod. Phys. 2017, 89, 025002. [Google Scholar] [CrossRef]
- Dong, B.; Guo, R.; Yan, L.T. Coassembly of Janus nanoparticles in asymmetric diblock copolymer scaffolds: unconventional entropy effect and role of interfacial topology. Macromolecules 2014, 47, 4369–4379. [Google Scholar] [CrossRef]
- Thompson, R.B.; Rasmussen, K.; Lookman, T. Origins of elastic properties in ordered block copolymer/nanoparticle composites. Nano Lett. 2004, 4, 2455–2459. [Google Scholar] [CrossRef]
- Zhao, Y.; Thorkelsson, K.; Mastroianni, A.J.; Schilling, T.; Luther, J.M.; Rancatore, B.J.; Matsunaga, K.; Jinnai, H.; Wu, Y.; Poulsen, D.; et al. Small-molecule-directed nanoparticle assembly towards stimuli-responsive nanocomposites. Nat. Mater. 2009, 8, 979–985. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Guo, R.; Xu, G.; Huang, Z.; Yan, L.T. Entropy-mediated mechanical response of the interfacial nanoparticle patterning. Nano Lett. 2014, 14, 6910–6916. [Google Scholar] [CrossRef] [PubMed]
- Manna, L.; Scher, E.C.; Alivisatos, A.P. Shape control of colloidal semiconductor nanocrystals. J. Clust. Sci. 2002, 13, 521–532. [Google Scholar] [CrossRef]
- Ghezelbash, A.; Koo, B.; Korgel, B.A. Self-assembled stripe patterns of CdS nanorods. Nano Lett. 2006, 6, 1832–1836. [Google Scholar] [CrossRef] [PubMed]
- Arjmand, M.; Sadeghi, S.; Khajehpour, M.; Sundararaj, U. Carbon nanotube/graphene nanoribbon/polyvinylidene fluoride hybrid nanocomposites: rheological and dielectric properties. J. Phys. Chem. C 2017, 121, 169–181. [Google Scholar] [CrossRef]
- Sadeghi, S.; Arjmand, M.; Navas, I.O.; Yazdi, A.Z.; Sundararaj, U. Effect of nanofiller geometry on network formation in polymeric nanocomposites: Comparison of rheological and electrical properties of multiwalled carbon nanotube and graphene nanoribbon. Macromolecules 2017, 50, 3954–3967. [Google Scholar] [CrossRef]
- Biswas, A.; Bayer, I.S.; Biris, A.S.; Wang, T.; Dervishi, E.; Faupel, F. Advances in top-down and bottom-up surface nanofabrication: Techniques, applications & future prospects. Adv. Colloid Interfac. 2012, 170, 2–27. [Google Scholar]
- Knorowski, C. Dynamics and Statics of Polymer Nanocomposite Self-assembly via Molecular Dynamics; Iowa State University: Ames, IA, USA, 2015. [Google Scholar]
- Yan, L.T. Self-Assembling Systems: Theory and Simulation; John Wiley & Sons: Oxford, UK, 2016. [Google Scholar]
- Mao, X.; Chen, Q.; Granick, S. Entropy favours open colloidal lattices. Nat. Mater. 2013, 12, 217–222. [Google Scholar] [CrossRef]
- Eldridge, M.D.; Madden, P.A.; Frenkel, D. Entropy-driven formation of a superlattice in a hard-sphere binary mixture. Nature 1993, 365, 35–37. [Google Scholar] [CrossRef]
- Manoharan, V.; Elsesser, M.; Pine, D. Dense packing and symmetry in small clusters of microspheres. Science 2003, 301, 483–487. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Laderman, B.; Sacanna, S.; Chaikin, P. Re-entrant solidification in polymer–colloid mixtures as a consequence of competing entropic and enthalpic attractions. Nat. Mater. 2015, 14, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Lubchenko, V.; Wolynes, P.G. Theory of structural glasses and supercooled liquids. Annu. Rev. Phys. Chem. 2007, 58, 235–266. [Google Scholar] [CrossRef]
- Parisi, G.; Zamponi, F. Mean field theory of the glass transition and jamming of hard spheres. Rev. Mod. Phys. 2010, 82, 789–845. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Thompson, R.B.; Ginzburg, V.V.; Matsen, M.W.; Balazs, A.C. Predicting the mesophases of copolymer-nanoparticle composites. Science 2001, 292, 2469–2472. [Google Scholar] [CrossRef]
- Kim, J.U.; O’Shaughnessy, B. Nanoinclusions in dry polymer brushes. Macromolecules 2009, 39, 413–425. [Google Scholar] [CrossRef]
- Huang, Z.; Lu, C.; Dong, B.; Xu, G.; Ji, C.; Zhao, K.; Yan, L.T. Chain stiffness regulates entropy-templated perfect mixing at single-nanoparticle level. Nanoscale 2015, 8, 1024. [Google Scholar] [CrossRef]
- Shin, H.; Schweizer, K.S. Theory of two-dimensional self-assembly of Janus colloids: crystallization and orientational ordering. Soft Matter 2013, 10, 262–274. [Google Scholar] [CrossRef]
- Berkovich, R.; Fernandez, V.I.; Stirnemann, G.; Valle-Orero, J.; Fernandez, J.M. Segmentation and the entropic elasticity of modular proteins. J. Phys. Chem. Lett. 2018, 9, 4707–4713. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.A.; Antonaglia, J.; Millan, J.A.; Engel, M.; Glotzer, S.C. Shape and symmetry determine two-dimensional melting transitions of hard regular polygons. Phys. Rev. X. 2017, 7, 021001. [Google Scholar] [CrossRef]
- Anders, G.V.; Klotsa, D.; Ahmed, N.K.; Engel, M.; Glotzer, S.C. Understanding shape entropy through local dense packing. PNAS 2014, 111, E4812–E4821. [Google Scholar] [CrossRef] [PubMed]
- Anders, G.V.; Ahmed, N.K.; Smith, R.; Engel, M.; Glotzer, S.C. Entropically patchy particles: Engineering valence through shape entropy. ACS Nano 2014, 8, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Petukhov, A.V.; Meijer, J.M.; Vroege, G.J. Particle shape effects in colloidal crystals and colloidal liquid crystals: Small-angle X-ray scattering studies with microradian resolution. Curr. Opin. Colloid Interface Sci. 2015, 20, 272–281. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N.Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Frenkel, D. Order through entropy. Nat. Mater. 2015, 14, 9. [Google Scholar] [CrossRef]
- Bhat, R.R.; Genzer, J.; Chaney, B.N.; Sugg, H.W.; Liebmann-Vinson, A. Controlling the assembly of nanoparticles using surface grafted molecular and macromolecular gradients. Nanotech. 2003, 14, 1145–1152. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, Q.; Emrick, T.; Balazs, A.C.; Russell, T.P. Entropy-driven segregation of nanoparticles to cracks in multilayered composite polymer structures. Nat. Mater. 2006, 5, 229–233. [Google Scholar]
- Chen, P.; Yang, Y.; Dong, B.; Huang, Z.; Zhu, G.; Cao, Y.; Yan, L.T. Polymerization-induced interfacial self-assembly of Janus nanoparticles in block copolymers: reaction-mediated entropy effects, diffusion dynamics, and tailorable micromechanical behaviors. Macromolecules 2017, 50, 2078–2091. [Google Scholar] [CrossRef]
- Yaneva, J.; Dimitrov, D.I.; Milchev, A.; Binder, K. Nanoinclusions in polymer brushes with explicit solvent – a molecular dynamics investigation. J. Colloid. Interface. Sci. 2009, 336, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 2002, 22, 1255–1256. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polym. Sci. 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Alexander, S. Adsorption of chain molecules with a polar head a scaling description. J. Physique 1977, 38, 983–987. [Google Scholar] [CrossRef]
- De Gennes, P.G. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069. [Google Scholar] [CrossRef]
- Zhu, G.; Huang, Z.; Xu, Z.; Yan, L.T. Tailoring interfacial nanoparticle organization through entropy. Acc. Chem. Res. 2018, 51, 900–909. [Google Scholar] [CrossRef] [PubMed]
- Allegra, G.; Raos, G.; Vacatello, M. Theories and simulations of polymer-based nanocomposites: from chain statistics to reinforcement. Prog. Polym. Sci. 2008, 33, 683–731. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Application; Academic Press: Massachusetts, MA, USA, 2002. [Google Scholar]
- Sarkar, B.; Alexandridis, P. Block copolymer–nanoparticle composites: structure, functional properties, and processing. Prog. Poly. Sci. 2015, 40, 33–62. [Google Scholar] [CrossRef]
- Shang, X.; Kroger, M.; Leimkuhler, B. Assessing numerical methods for molecular and particle simulation. Soft Matter 2017, 13, 8565–8578. [Google Scholar] [CrossRef]
- Hoheisel, T.N.; Hur, K.; Wiesner, U.B. Block copolymer-nanoparticle hybrid self-assembly. Prog. Polym. Sci. 2011, 40, 3–32. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A review of multiscale computational methods in polymeric materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Zeng, Q.; Yu, A.; Lu, G.Q. Multiscale modeling and simulation of polymer nanocomposites. Prog. Poly. Sci. 2008, 33, 191–269. [Google Scholar] [CrossRef]
- Allen, P.; Tildesley, D. Computer simulation of liquids; Oxford Science Publ, Clarendon Press: New York, NY, USA, 1989. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Gujrati, P.D. Hierarchy of relaxation times and residual entropy: a nonequilibrium approach. Entropy 2018, 20, 149. [Google Scholar] [CrossRef]
- Evans, M.R.; Foster, D.P.; Godrèche, C.; Mukamel, D. Spontaneous symmetry breaking in a one dimensional driven diffusive system. Phys. Rev. Lett. 1995, 74, 208. [Google Scholar] [CrossRef] [PubMed]
- Stratford, K.; Adhikari, R.; Pagonabarraga, I.; Desplat, J.C.; Cates, M.E. Colloidal jamming at interfaces: a route to fluid-bicontinuous gels. Science 2005, 309, 2198–2201. [Google Scholar] [CrossRef] [PubMed]
- Arkin, A.; Ross, J.; McAdams, H.H. Stochastic kinetic analysis of developmental pathway bifurcation in phage infected escherichia coli cells. Genetics 1998, 149, 1633–1648. [Google Scholar]
- Warren, P.B.; Allen, R.J. Trajectory reweighting for non-equilibrium steady states. Mol. Phys. 2018, 116, 3104–3113. [Google Scholar] [CrossRef]
- Warmflash, A.; Bhimalapuram, P.; Dinner, A.R. Umbrella sampling for nonequilibrium processes. J. Chem. Phys. 2007, 127, 154112. [Google Scholar] [CrossRef]
- Valeriani, C.; Allen, R.J.; Morelli, M.J.; Frenkel, D.; ten Wolde, P.R. Computing stationary distributions in equilibrium and nonequilibrium systems with forward flux sampling. J. Chem. Phys. 2007, 127, 114109. [Google Scholar] [CrossRef]
- Mehlig, B.; Heermann, D.W.; Forrest, B.M. Hybrid Monte Carlo method for condensed-matter systems. Phys. Rev. B 1992, 45, 679–685. [Google Scholar] [CrossRef]
- Prokhorenko, S.; Kalke, K.; Nahas, Y.; Bellaiche, L. Large scale hybrid Monte Carlo simulations for structure and property prediction. NPJ Comput. Mater. 2018, 4, 80. [Google Scholar] [CrossRef]
- Kim, J.U.; O’Shaughnessy, B. Morphology selection of nanoparticle dispersions by polymer media. Phys. Rev. Lett. 2002, 89, 238301. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Thompson, R.B.; Jasnow, D.; Balazs, A.C. Entropically driven formation of hierarchically ordered nanocomposites. Phys. Rev. Lett. 2002, 89, 155503. [Google Scholar] [CrossRef] [PubMed]
- Bockstaller, M.R.; Lapetnikov, Y.; Margel, S.; Thomas, E.L. Size-selective organization of enthalpic compatibilized nanocrystals in ternary block copolymer/particle mixtures. J. Am. Chem. Soc. 2003, 125, 5276–5277. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.J.; Chiu, J.J.; Yi, G.R.; Pine, D.J.; Kramer, E.J. Nanoparticle-induced phase transitions in diblock-copolymer films. Adv. Mater. 2010, 17, 2618–2622. [Google Scholar] [CrossRef]
- Sides, S.W.; Kim, B.J.; Kramer, E.J.; Fredrickson, G.H. Hybrid particle-field simulations of polymer nanocomposites. Phys. Rev. Lett. 2006, 96, 250601. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.K.; Feng, X.Q.; Yu, S.W. Controllable nanostructural rransitions in grafted nanoparticle–block copolymer composites. Nano. Res. 2010, 3, 356–362. [Google Scholar] [CrossRef]
- Akcora, P.; Liu, H.; Kumar, S.K.; Moll, J.; Li, Y.; Benicewicz, B.C.; Schadler, L.S.; Acehan, D.; Panagiotopoulos, A.Z.; Pryamitsyn, V.; et al. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. [Google Scholar] [CrossRef]
- O’Brien, M.N.; Girard, M.; Lin, H.X.; Millan, J.A.; Olvera de la Cruz, M.; Lee, B.; Mirkin, C.A. Exploring the zone of anisotropy and broken symmetries in DNA-mediated nanoparticle crystallization. PNAS 2016, 113, 10485–10490. [Google Scholar] [CrossRef]
- Gooneie, A.; Holzer, C. Reinforced local heterogeneities in interfacial tension distribution in polymer blends by incorporating carbon nanotubes. Polymer 2017, 125, 90–101. [Google Scholar] [CrossRef]
- Gooneie, A.; Sapkota, J.; Shirole, A.; Holzer, C. Length controlled kinetics of self-assembly of bidisperse nanotubes/nanorods in polymers. Polymer 2017, 118, 236–248. [Google Scholar] [CrossRef]
- He, L.L.; Liang, H.J.; Zhang, L.X. Mono- or bidisperse nanorods mixtures in diblock copolymers. Polymer 2010, 51, 3303–3314. [Google Scholar] [CrossRef]
- Daoulas, K.C.; And, V.A.H.; Mavrantzas, V.G. Detailed atomistic simulation of a polymer melt/solid interface: structure, density, and conformation of a thin film of polyethylene melt adsorbed on graphite. Macromolecules 2005, 38, 5780–5795. [Google Scholar] [CrossRef]
- Gooneie, A.; Gonzalez-Gutierrez, J.; Holzer, C. Atomistic modelling of confined polypropylene chains between ferric oxide substrates at melt temperature. Polymers 2016, 8, 361. [Google Scholar] [CrossRef]
- Anastassiou, A.; Mavrantzas, V.G. Molecular Structure and Work of Adhesion of Poly(n-butyl acrylate) and Poly(n-butyl acrylate-co-acrylic acid) on alpha-Quartz, alpha-Ferric Oxide, and alpha-Ferrite from Detailed Molecular Dynamics Simulations. Macromolecules 2015, 48, 8262–8284. [Google Scholar] [CrossRef]
- Lee, J.Y.; Shou, Z.; Balazs, A.C. Modeling the self-assembly of copolymer-nanoparticle mixtures confined between solid surfaces. Phys. Rev. Lett. 2003, 91, 136103. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S.; Lee, J.Y.; Buxton, G.A.; Balazs, A.C. Using nanocomposite coatings to heal surface defects. Macromolecules 2004, 37, 9160–9168. [Google Scholar] [CrossRef]
- Lee, J.Y.; Buxton, G.A.; Balazs, A.C. Using nanoparticles to create self-healing composites. J. Chem. Phys. 2004, 121, 5531–5540. [Google Scholar] [CrossRef]
- Smith, K.A.; Tyagi, S.; Balazs, A.C. Healing surface defects with nanoparticle-filled polymer coatings: effect of particle geometry. Macromolecules 2005, 38, 10138–10147. [Google Scholar] [CrossRef]
- Curk, T.; Martinez-Veracoechea, F.J.; Frenkel, D.; Dobnikar, J. Nanoparticle organization in sandwiched polymer brushes. Nano Letter. 2014, 14, 2617–2622. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.; Emrick, T.; Russell, T.P. Stabilizing liquid drops in nonequilibrium shapes by the interfacial jamming of nanoparticles. Science 2013, 342, 460–463. [Google Scholar] [CrossRef] [PubMed]
- Taylor, S.L.; Evans, R.; Royall, C.P. Temperature as an external field for colloid–polymer mixtures: ‘quenching’ by heating and ‘melting’ by cooling. J. Phys. Condens. Matt. 2012, 24, 464128. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.Z.; Merlitz, H.; Wu, C.X.; Sommer, J.U. Polymer-induced inverse-temperature crystallization of nanoparticles on a substrate. ACS Nano 2013, 7, 9920–9926. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Xu, Z.; Yang, Y.; Dai, X.; Yan, L.T. Hierarchical crystals formed from DNA-functionalized Janus nanoparticles. ACS Nano 2018, 12, 9467–9475. [Google Scholar] [CrossRef] [PubMed]
- Thaner, R.V.; Kim, Y.; Li, T.; Macfarlane, R.J.; Nguyen, S.T.; Olvera de la Cruz, M.; Mirkin, C.A. Entropy-driven crystallization behavior in DNA-mediated nanoparticle assembly. Nano Lett. 2015, 15, 5545. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, P.; Cao, Y.; Huang, Z.; Zhu, G.; Xu, Z.; Dai, X.; Chen, S.; Miao, B.; Yan, L.T. How Implementation of entropy in driving structural ordering of nanoparticles relates to assembly kinetics: insight into reaction-induced interfacial assembly of Janus nanoparticles. Langmuir 2018, 34, 9477–9488. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Hou, C.; Xu, Z.; Yang, Y.; Zhu, G.; Chen, P.; Huang, Z.; Yan, L.-T. Entropic Effects in Polymer Nanocomposites. Entropy 2019, 21, 186. https://doi.org/10.3390/e21020186
Dai X, Hou C, Xu Z, Yang Y, Zhu G, Chen P, Huang Z, Yan L-T. Entropic Effects in Polymer Nanocomposites. Entropy. 2019; 21(2):186. https://doi.org/10.3390/e21020186
Chicago/Turabian StyleDai, Xiaobin, Cuiling Hou, Ziyang Xu, Ye Yang, Guolong Zhu, Pengyu Chen, Zihan Huang, and Li-Tang Yan. 2019. "Entropic Effects in Polymer Nanocomposites" Entropy 21, no. 2: 186. https://doi.org/10.3390/e21020186
APA StyleDai, X., Hou, C., Xu, Z., Yang, Y., Zhu, G., Chen, P., Huang, Z., & Yan, L.-T. (2019). Entropic Effects in Polymer Nanocomposites. Entropy, 21(2), 186. https://doi.org/10.3390/e21020186




