The Optimized Multi-Scale Permutation Entropy and Its Application in Compound Fault Diagnosis of Rotating Machinery
Abstract
:1. Introduction
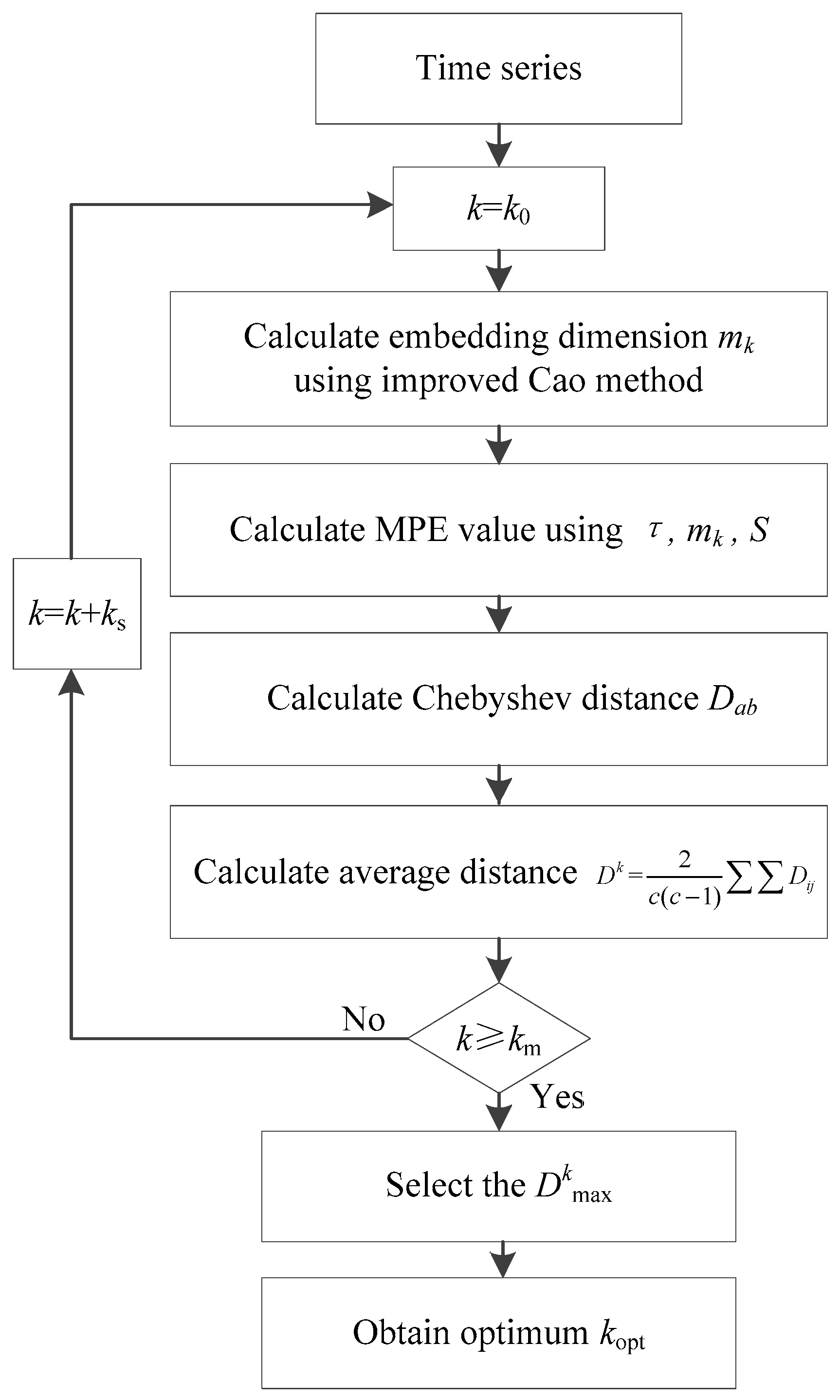
2. Optimized Multi-Scale Permutation Entropy
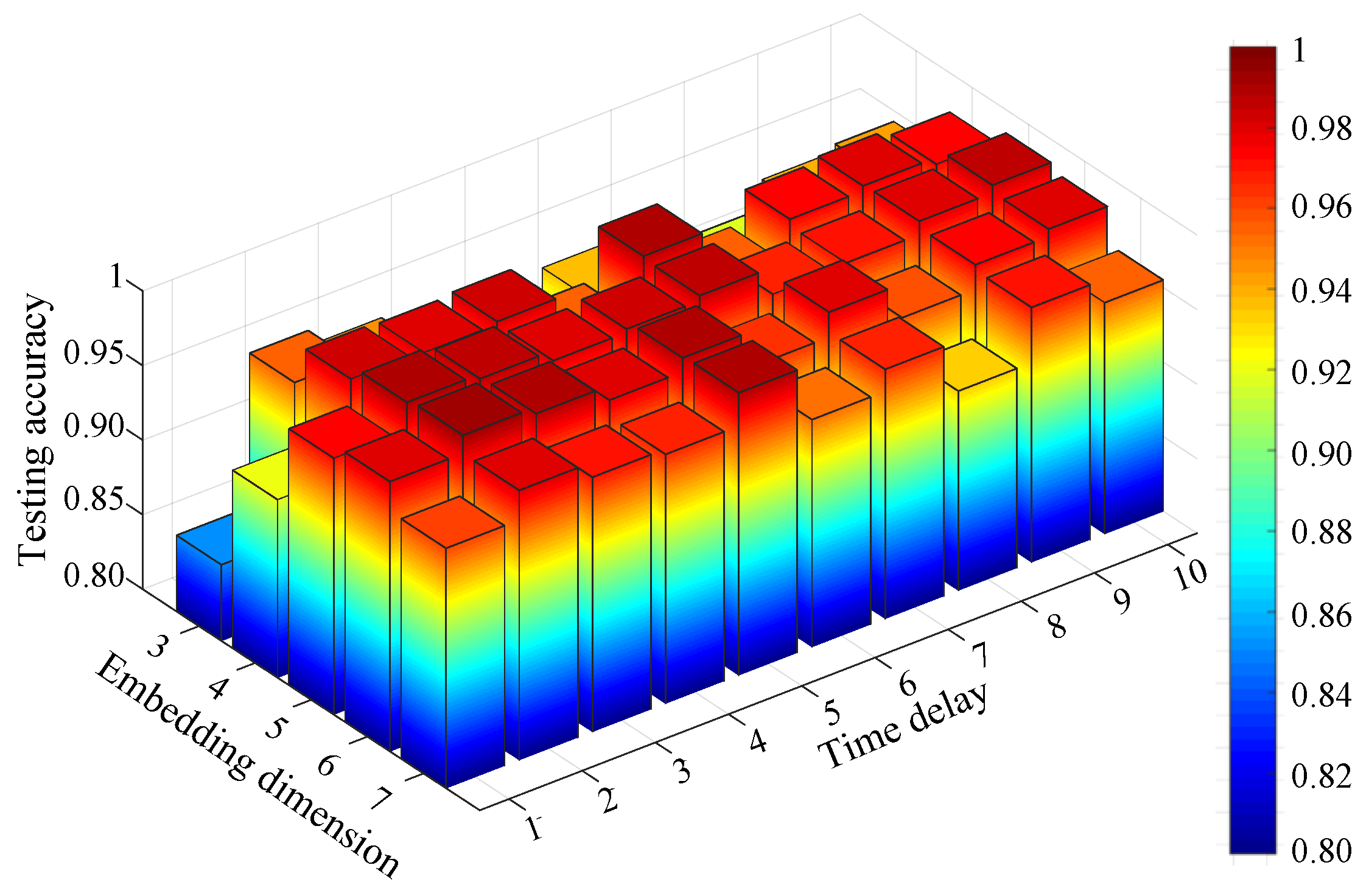
2.1. Time Delay Calculation Based on Mutual Information
2.2. Embedding Dimension Calculation Based on Improved Cao Method
2.2.1. Embedding Dimension Calculation
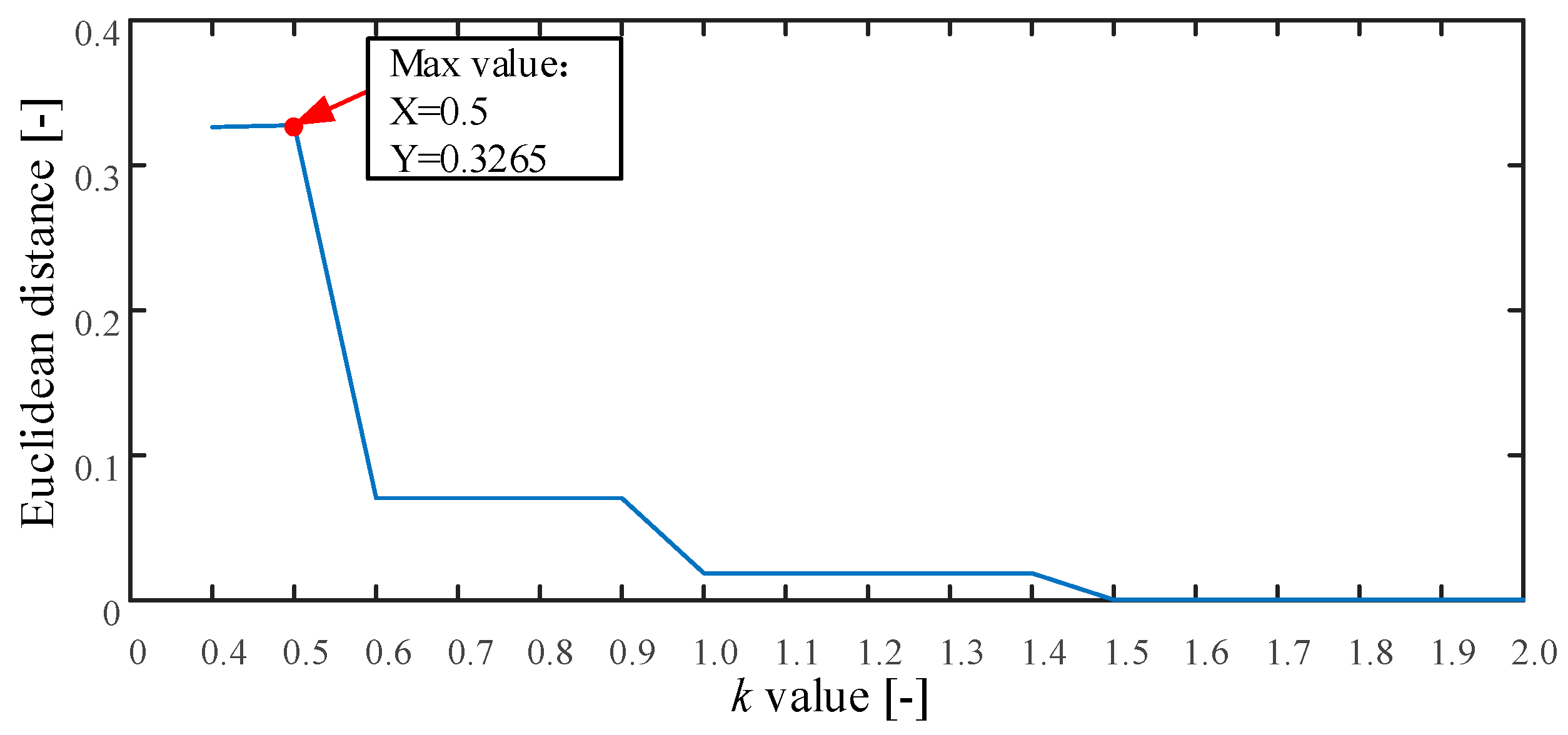
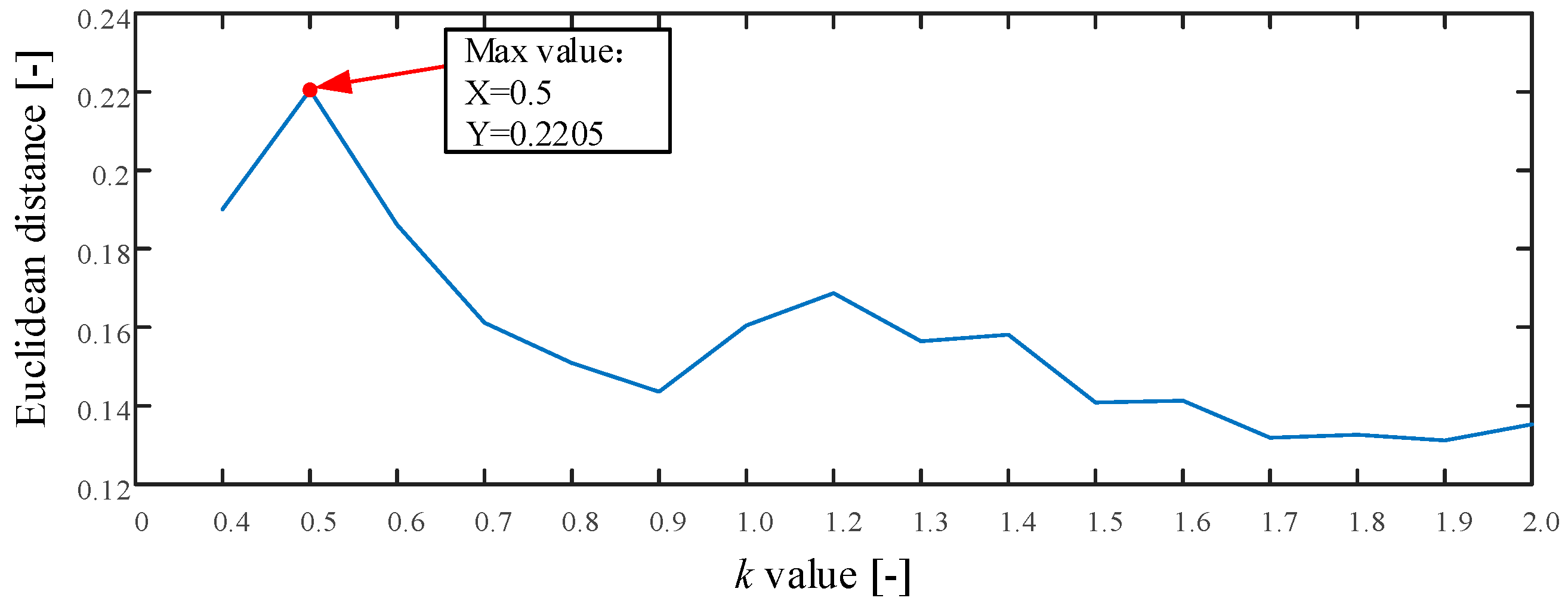
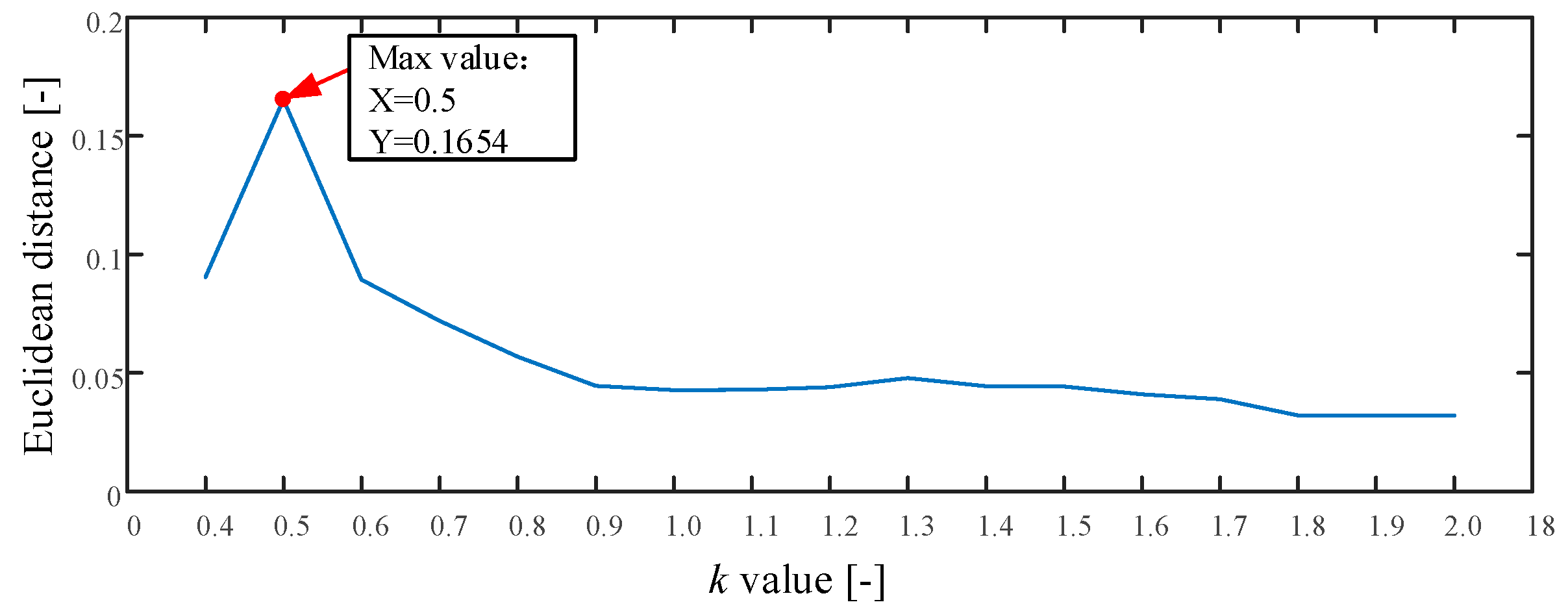
2.2.2. Threshold Adjustment using Chebyshev Distance
2.3. Procedures of OMPE Method
3. Simulation Validation
4. Experimental Validation
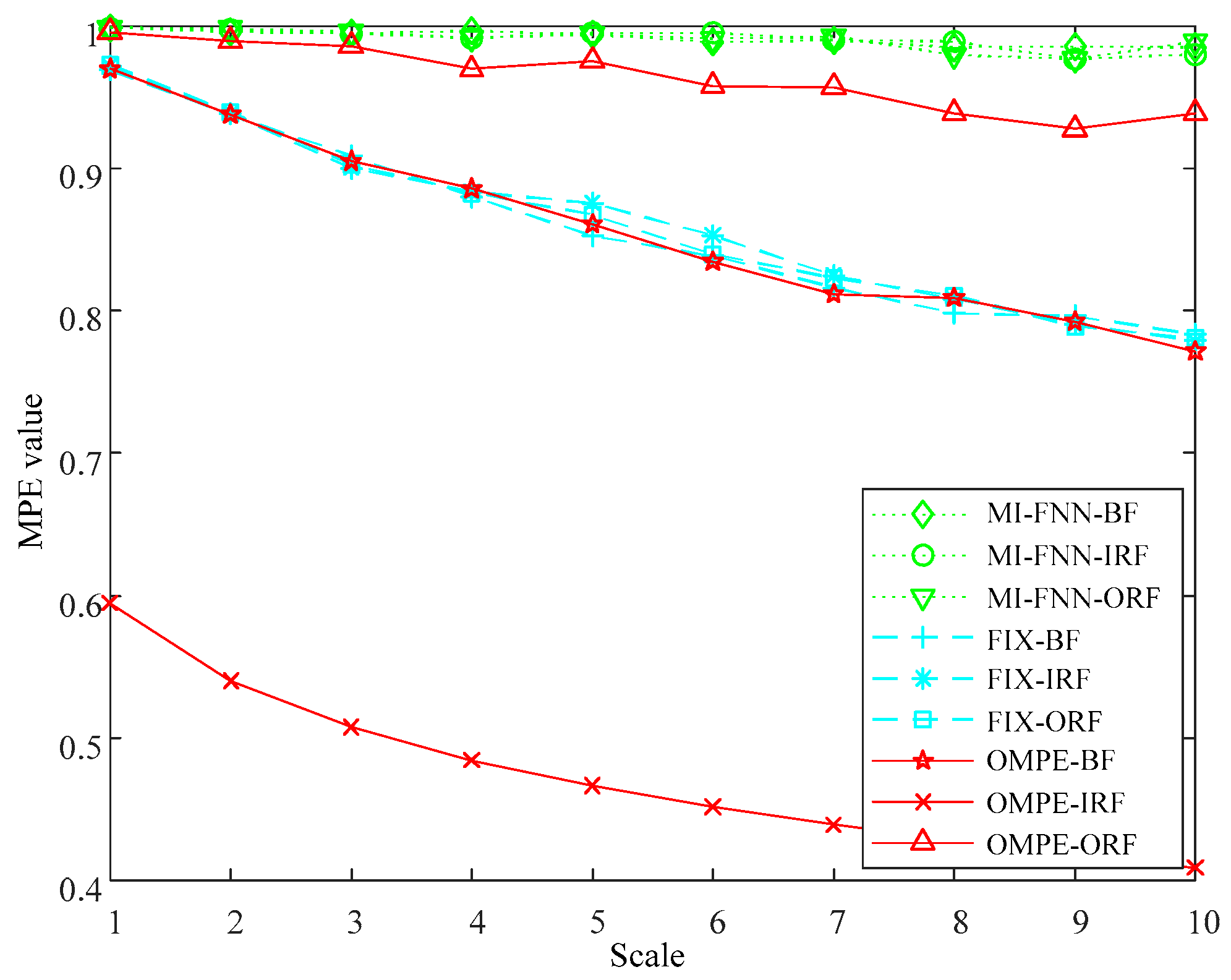
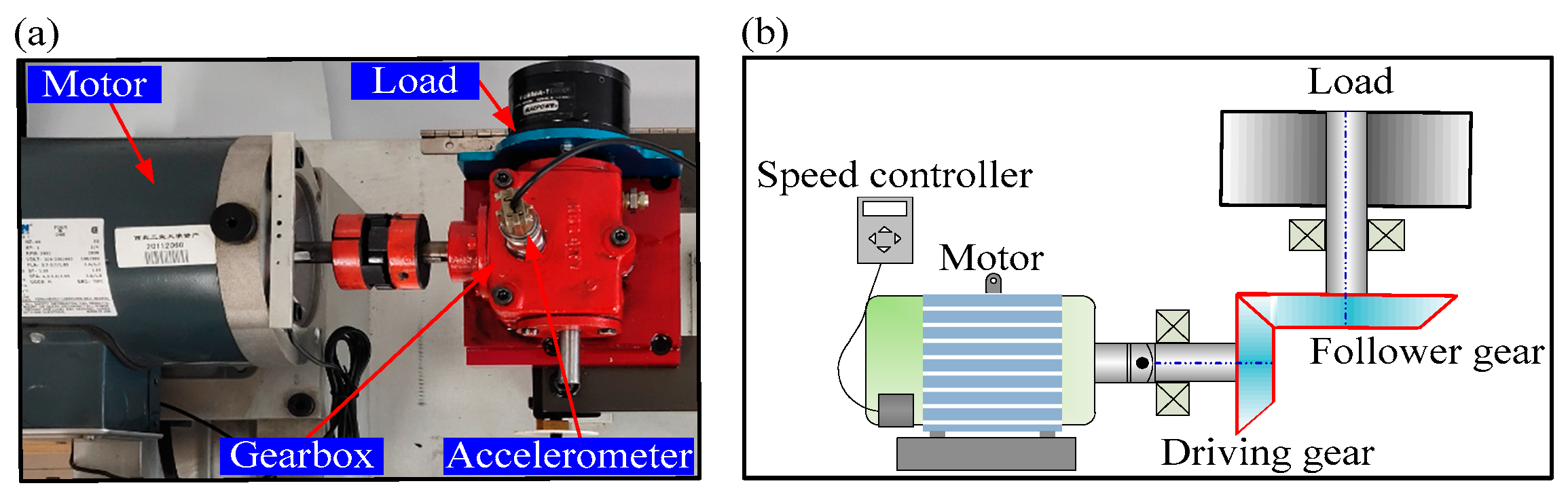
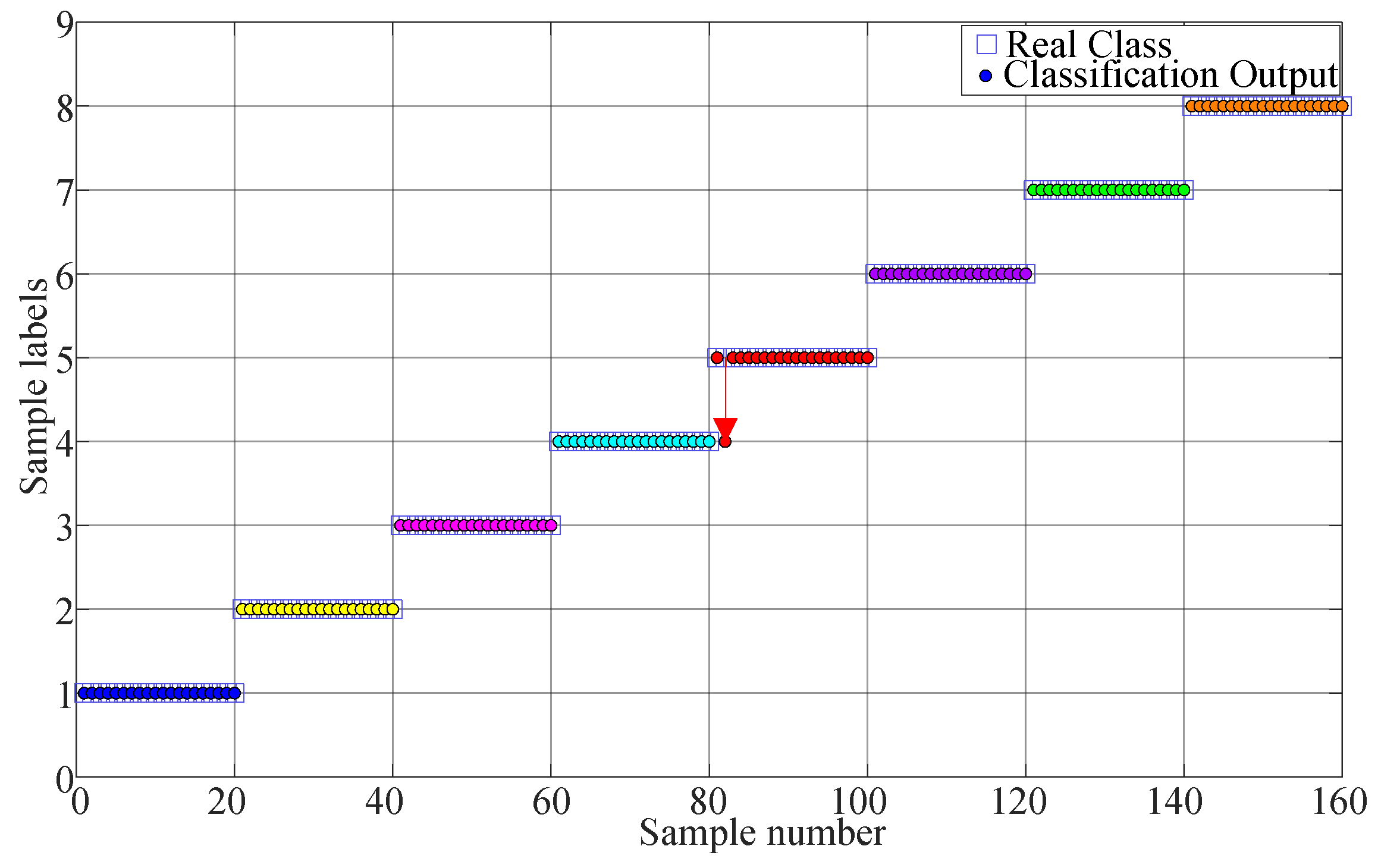
4.1. Experiment 1: Compound Gear Fault
4.2. Experiment 2: Compound Bearing and Unbalance Rotor Fault
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Tung, W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.K.; Kankar, P.K. Ball Bearing Fault Diagnosis using Supervised and Unsupervised Machine Learning Methods. Int. J. Acoust. Vib. 2015, 20, 244–250. [Google Scholar] [CrossRef]
- Tang, G.; Wang, X.; He, Y. A Novel Method of Fault Diagnosis for Rolling Bearing Based on Dual Tree Complex Wavelet Packet Transform and Improved Multiscale Permutation Entropy. Math. Probl. Eng. 2016, 2016, 5432648. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process. 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Xiong, Q.; Luo, D.; Mei, G.; Zhang, T. A rolling bearing fault diagnosis strategy based on improved multiscale permutation entropy and least squares SVM. J. Mech. Sci. Technol. 2017, 31, 2711–2722. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, J. Dual serial vortex-induced energy harvesting system for enhanced energy harvesting. AIP Adv. 2018, 8, 075221. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Wang, X.; Liu, B.; Liang, X. Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. J. Sound Vib. 2018, 428, 72–86. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Zhao, L.-Y.; Wang, L.; Yan, R.-Q. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Decomposition and Multi-Scale Permutation Entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Wu, T.-Y.; Wang, C.-C. Multi-Scale Analysis Based Ball Bearing Defect Diagnostics Using Mahalanobis Distance and Support Vector Machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, P.-H.; Wu, C.-W.; Ding, J.-J.; Wang, C.-C. Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Tiwari, R.; Gupta, V.K.; Kankar, P. Bearing fault diagnosis based on multi-scale permutation entropy and adaptive neuro fuzzy classifier. J. Vib. Control 2015, 21, 461–467. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Multiscale Permutation Entropy Based Rolling Bearing Fault Diagnosis. Shock Vib. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Yao, D.; Yang, J.; Bai, Y.; Cheng, X. Railway rolling bearing fault diagnosis based on multi-scale intrinsic mode function permutation entropy and extreme learning machine classifier. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Qing-Fang, M.; Yu-Hua, P.; Pei-Jun, X. A new method of determining the optimal embedding dimension based on nonlinear prediction. Chin. Phys. 2007, 16, 1252–1257. [Google Scholar] [CrossRef]
- Chun-Hua, B.; Xin-Bao, N. Determining the minimum embedding dimension of nonlinear time series based on prediction method. Chin. Phys. 2004, 13, 633–636. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Yang, S.; Cheng, J. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Investigation of Fault Feature Extraction and Early Fault Diagnosis for Rolling Bearings. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Gul, A.; Perperoglou, A.; Khan, Z.; Mahmoud, O.; Miftahuddin, M.; Adler, W.; Lausen, B. Ensemble of a subset of kNN classifiers. Adv. Data Anal. Classif. 2018, 12, 827–840. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Si, S.; Huang, S. Entropy based fault classification using the Case Western Reserve University data: A benchmark study. IEEE Trans. Reliab. 2018. [Google Scholar] [CrossRef]



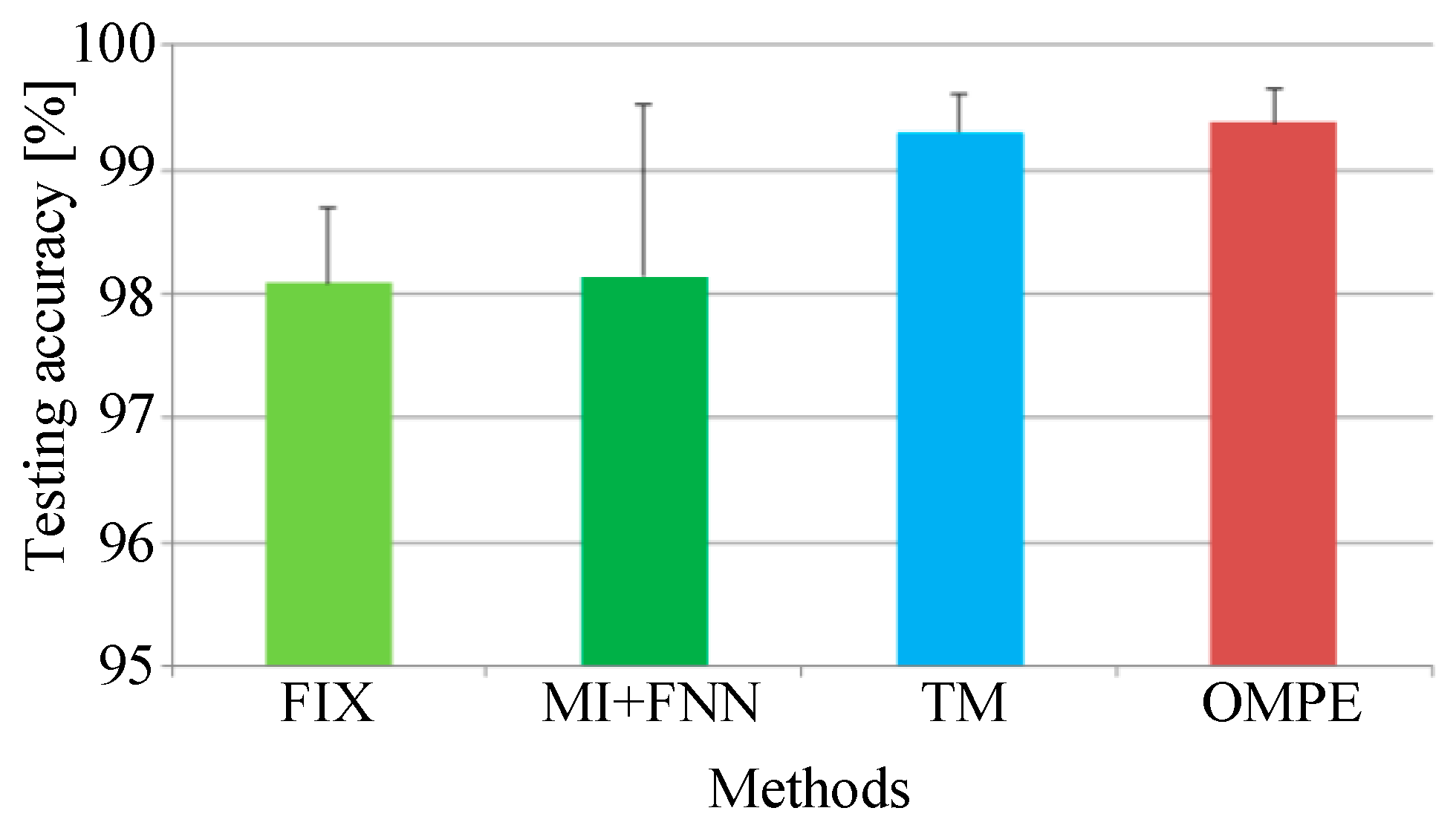

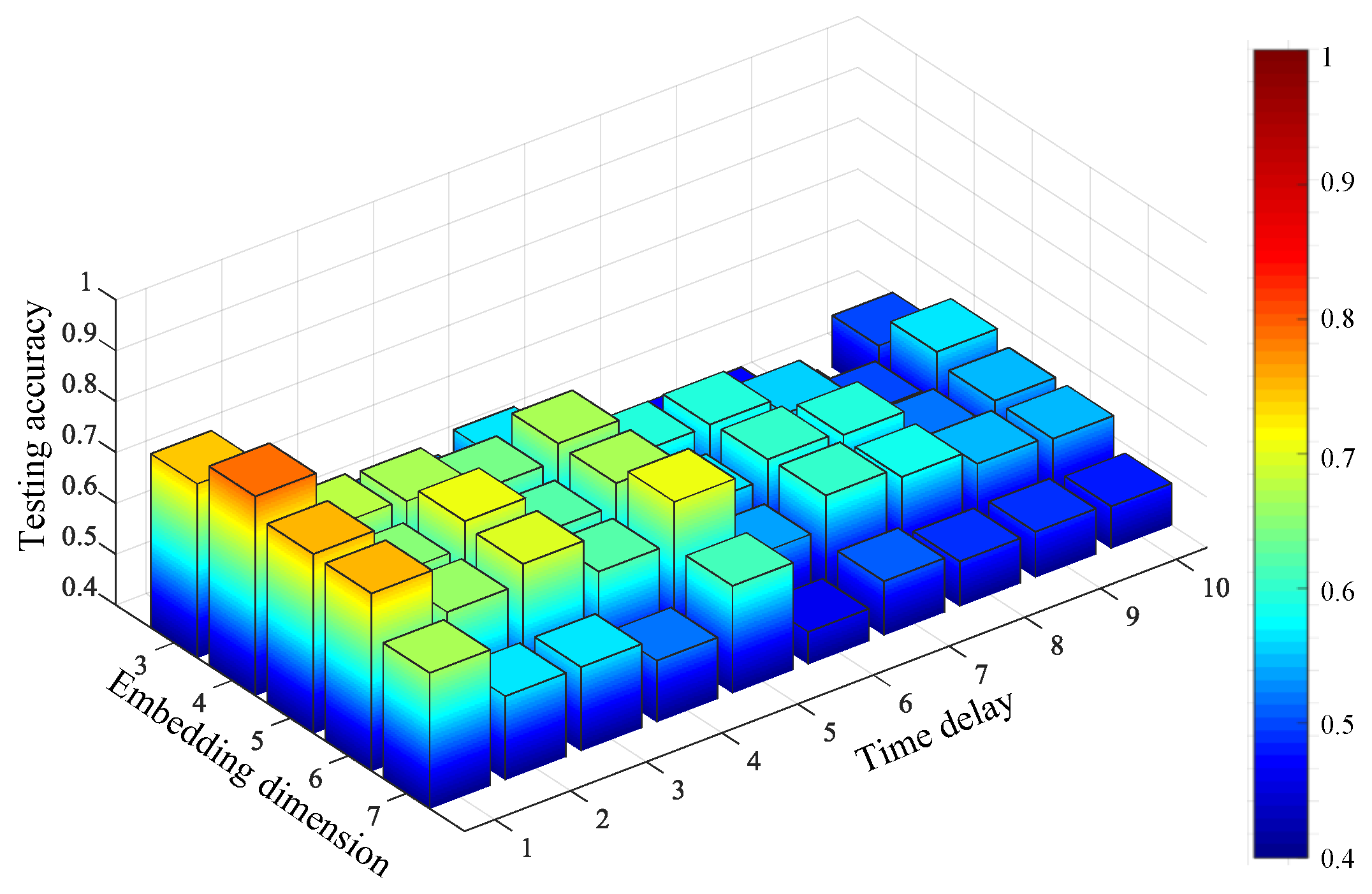
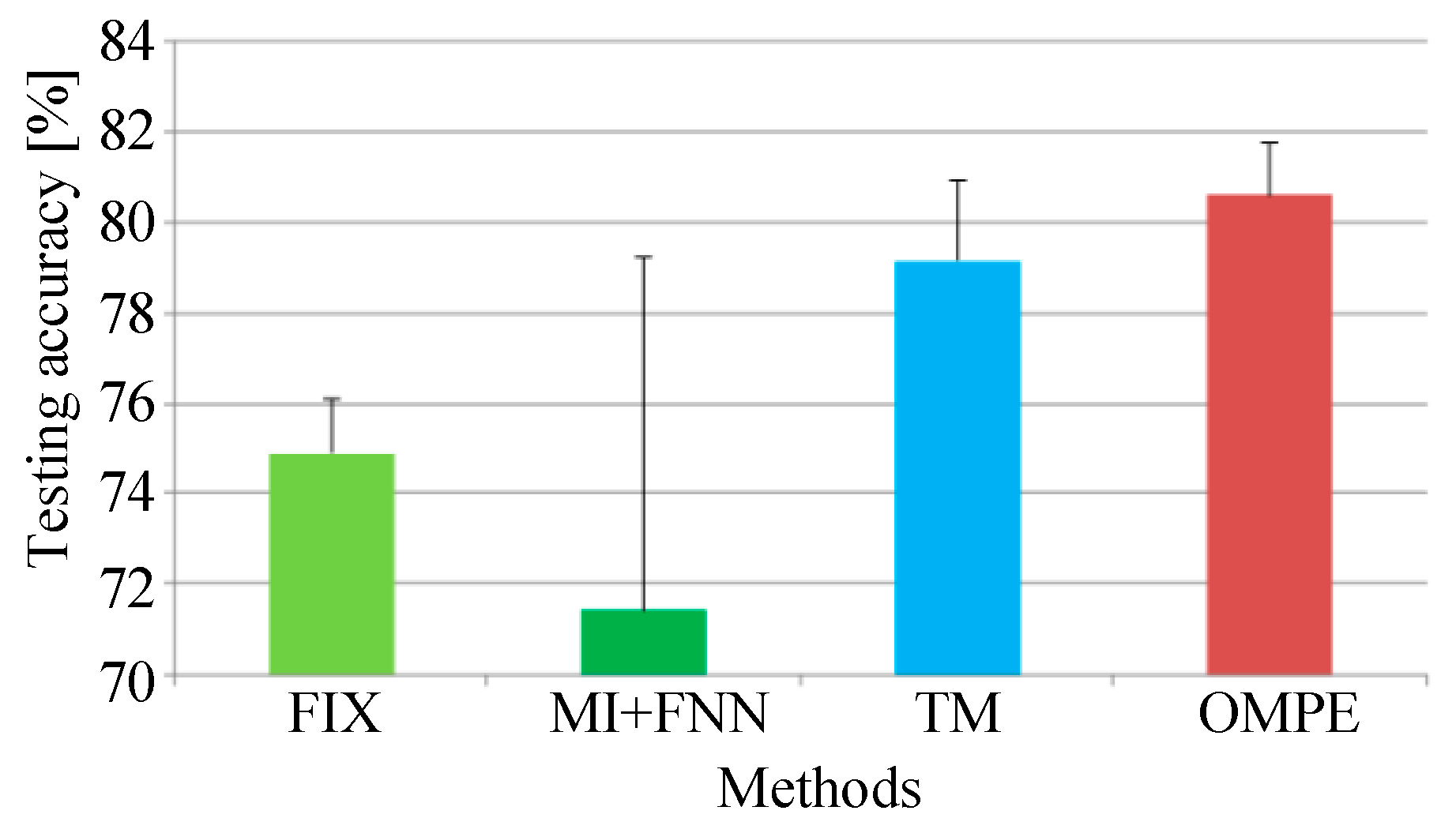
| Parameters | Embedding Dimension | Time Delay | |||||
|---|---|---|---|---|---|---|---|
| Methods | BF | IRF | ORF | BF | IRF | ORF | |
| FIX method | 6 | 6 | 6 | 1 | 1 | 1 | |
| MI-FNN method | 4 | 4 | 4 | 3 | 2 | 2 | |
| Proposed OMPE method | 6 | 9 | 5 | 3 | 2 | 2 | |
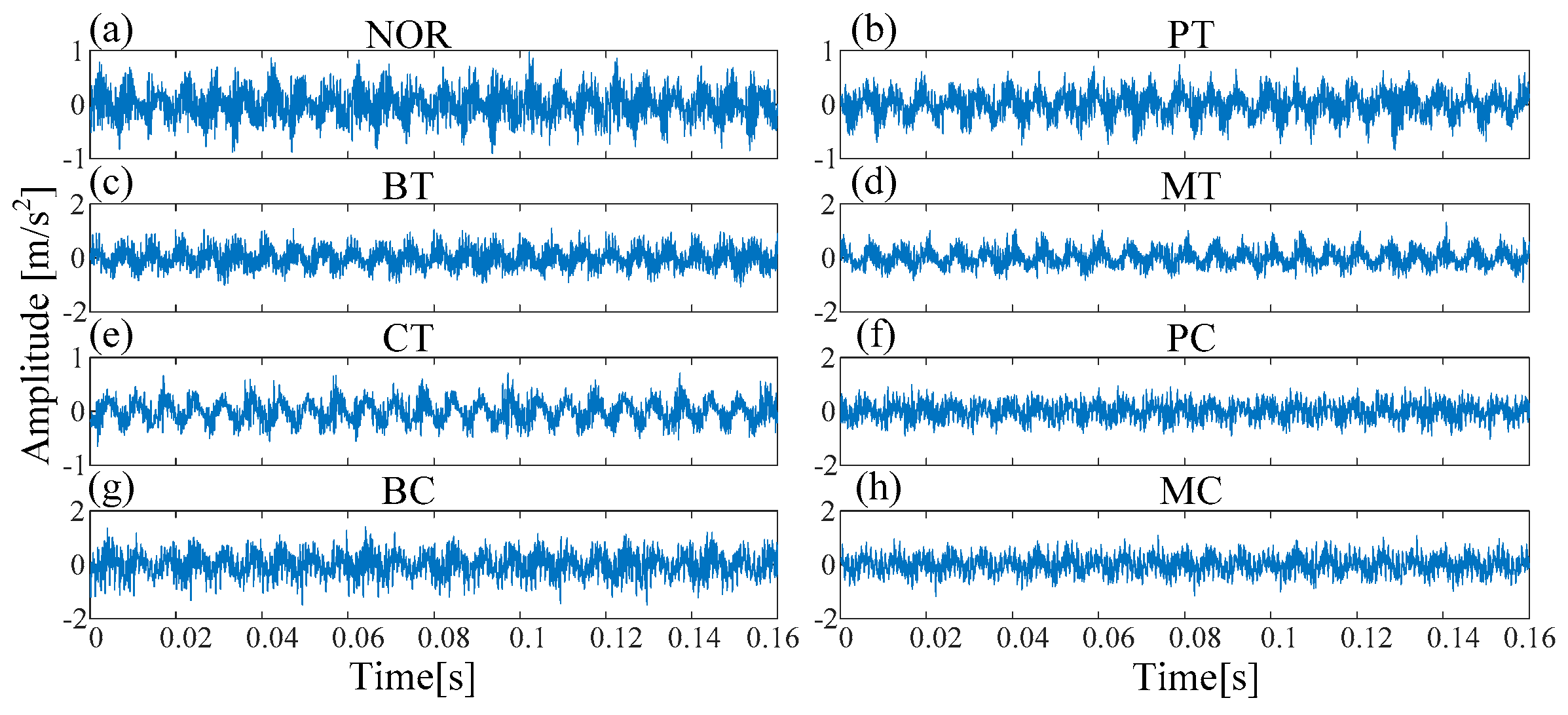
| Fault Type | PT | MT | CT | PC | MC | BC | NOR | BT | |
|---|---|---|---|---|---|---|---|---|---|
| Parameters | |||||||||
| Embedding dimension | 5 | 6 | 6 | 6 | 6 | 7 | 6 | 7 | |
| Time delay | 3 | 2 | 3 | 2 | 2 | 2 | 2 | 2 | |
| Class label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Bearing Type | MB ER-12K |
|---|---|
| Number of rolling elements | 8 |
| Rolling element diameter | 0.3125 inch |
| Pitch diameter | 1.318 inch |
| Contact angle | 0° |
| Sampling frequency | 12,800 Hz |
| Rotating speed | 3000 RPM |
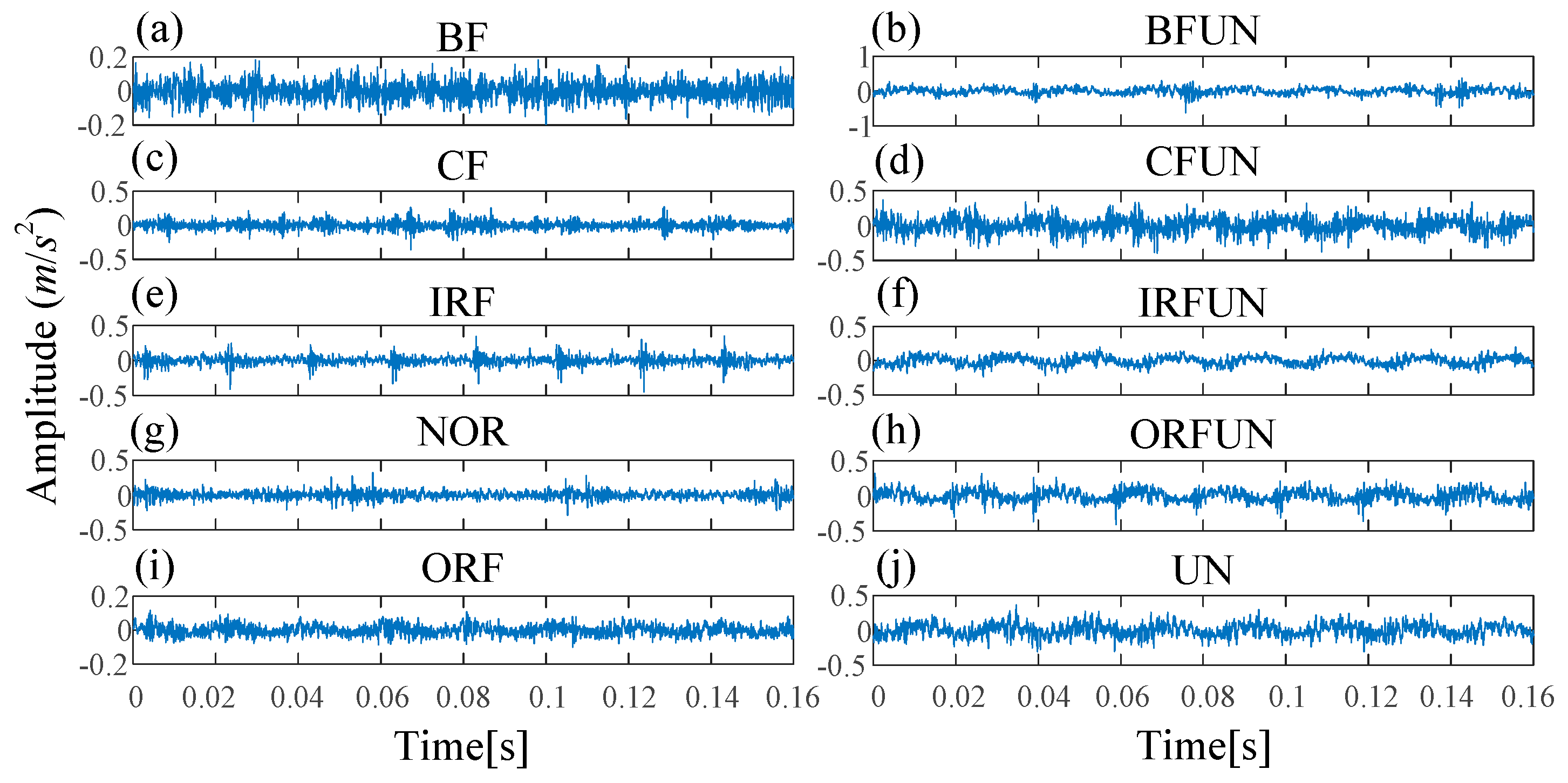
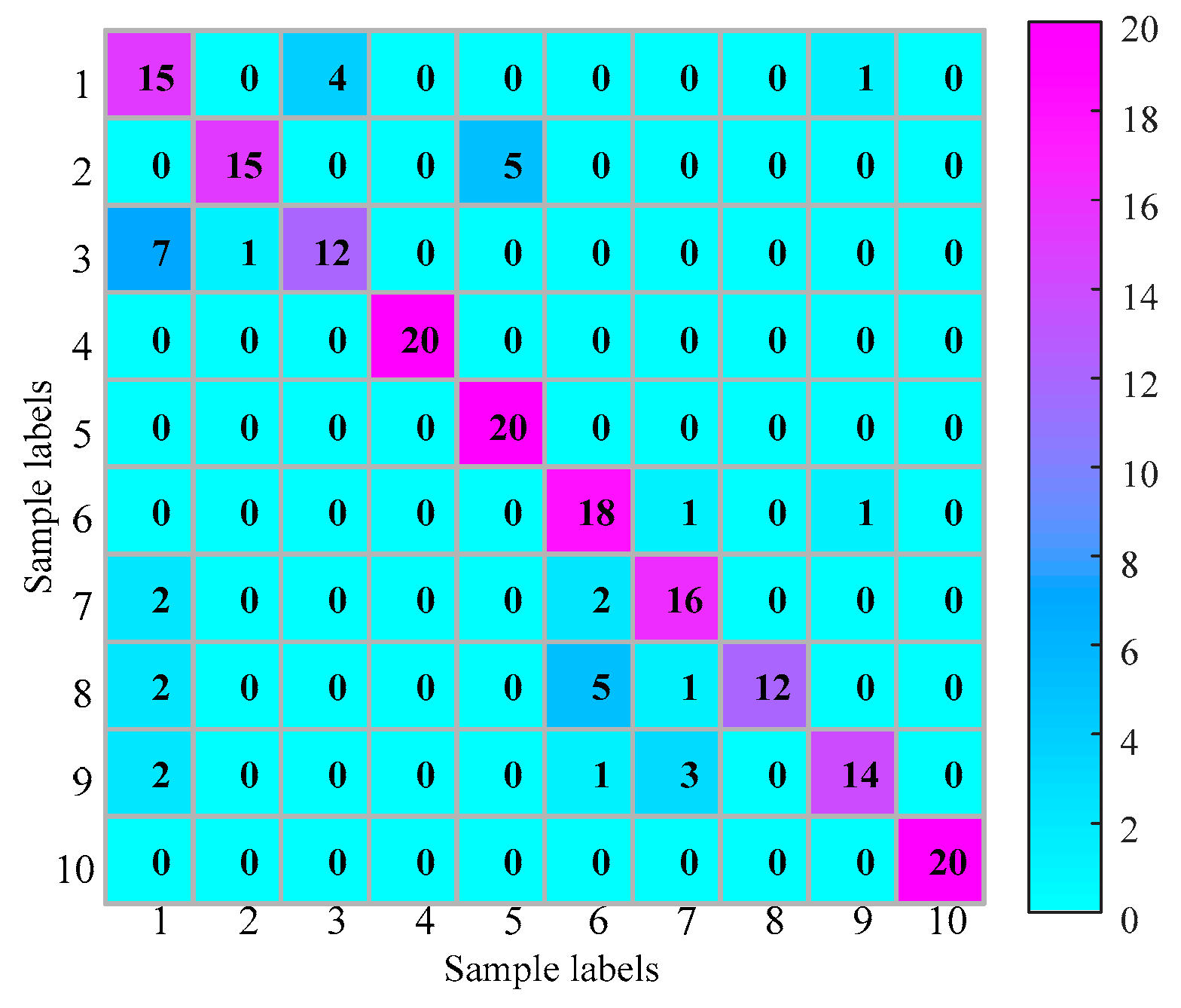
| Fault Type | BF | CF | IRF | NOR | ORF | BFUN | CFUN | IRFUN | ORFUN | UN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | |||||||||||
| Embedding dimension | 6 | 6 | 6 | 5 | 6 | 6 | 6 | 6 | 6 | 7 | |
| Time delay | 3 | 2 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 2 | |
| Class label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Si, S.; Wei, Y.; Li, Y. The Optimized Multi-Scale Permutation Entropy and Its Application in Compound Fault Diagnosis of Rotating Machinery. Entropy 2019, 21, 170. https://doi.org/10.3390/e21020170
Wang X, Si S, Wei Y, Li Y. The Optimized Multi-Scale Permutation Entropy and Its Application in Compound Fault Diagnosis of Rotating Machinery. Entropy. 2019; 21(2):170. https://doi.org/10.3390/e21020170
Chicago/Turabian StyleWang, Xianzhi, Shubin Si, Yu Wei, and Yongbo Li. 2019. "The Optimized Multi-Scale Permutation Entropy and Its Application in Compound Fault Diagnosis of Rotating Machinery" Entropy 21, no. 2: 170. https://doi.org/10.3390/e21020170
APA StyleWang, X., Si, S., Wei, Y., & Li, Y. (2019). The Optimized Multi-Scale Permutation Entropy and Its Application in Compound Fault Diagnosis of Rotating Machinery. Entropy, 21(2), 170. https://doi.org/10.3390/e21020170






