Application of Entropy Spectral Method for Streamflow Forecasting in Northwest China
Abstract
1. Introduction
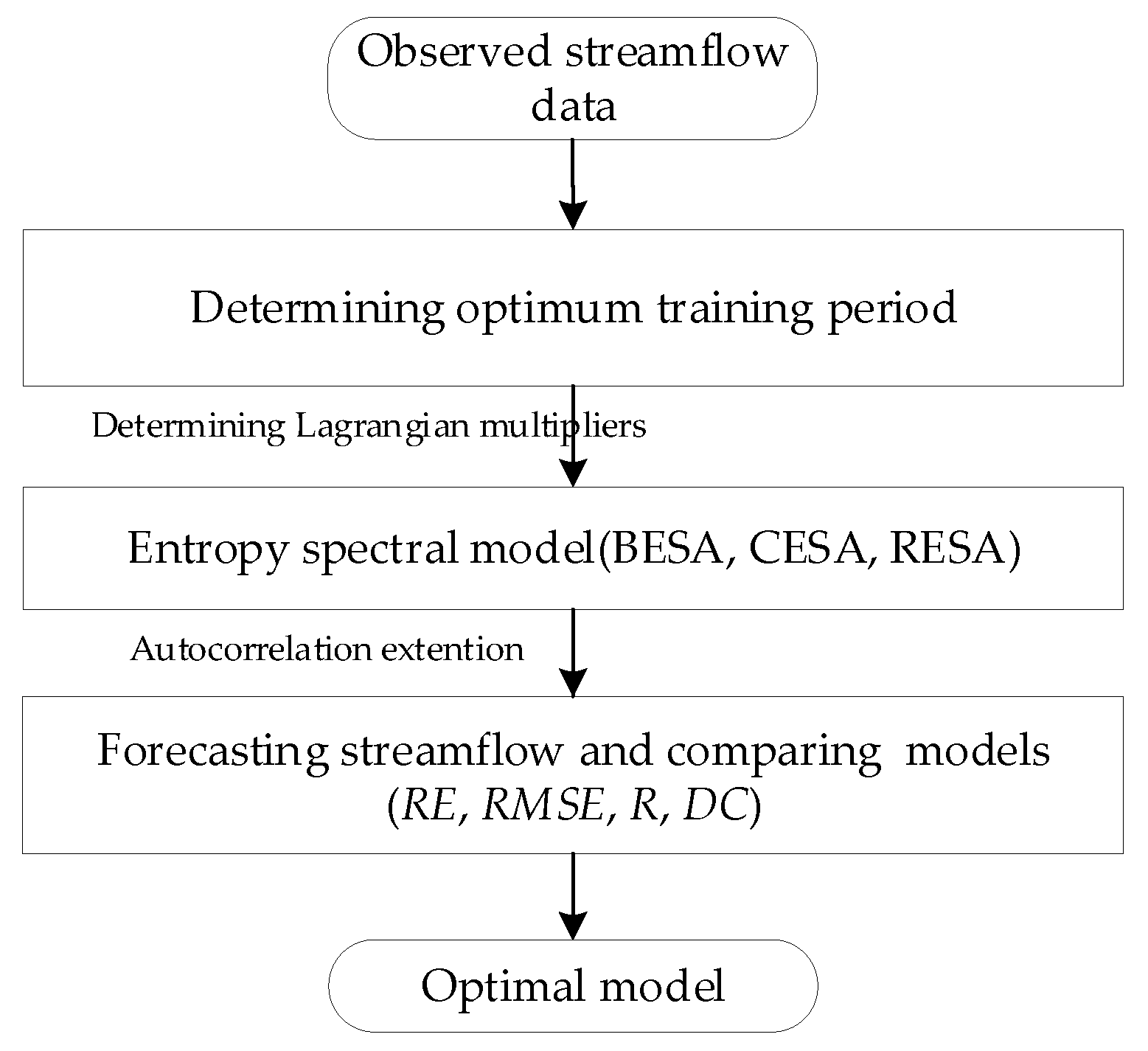
2. Methods
2.1. Deriving Spectral Density Function
2.2. Calculating Lagrangian Multipliers
2.3. Forecasting Streamflow
2.4. Evaluating the Precision of Forecasting Results
3. Application
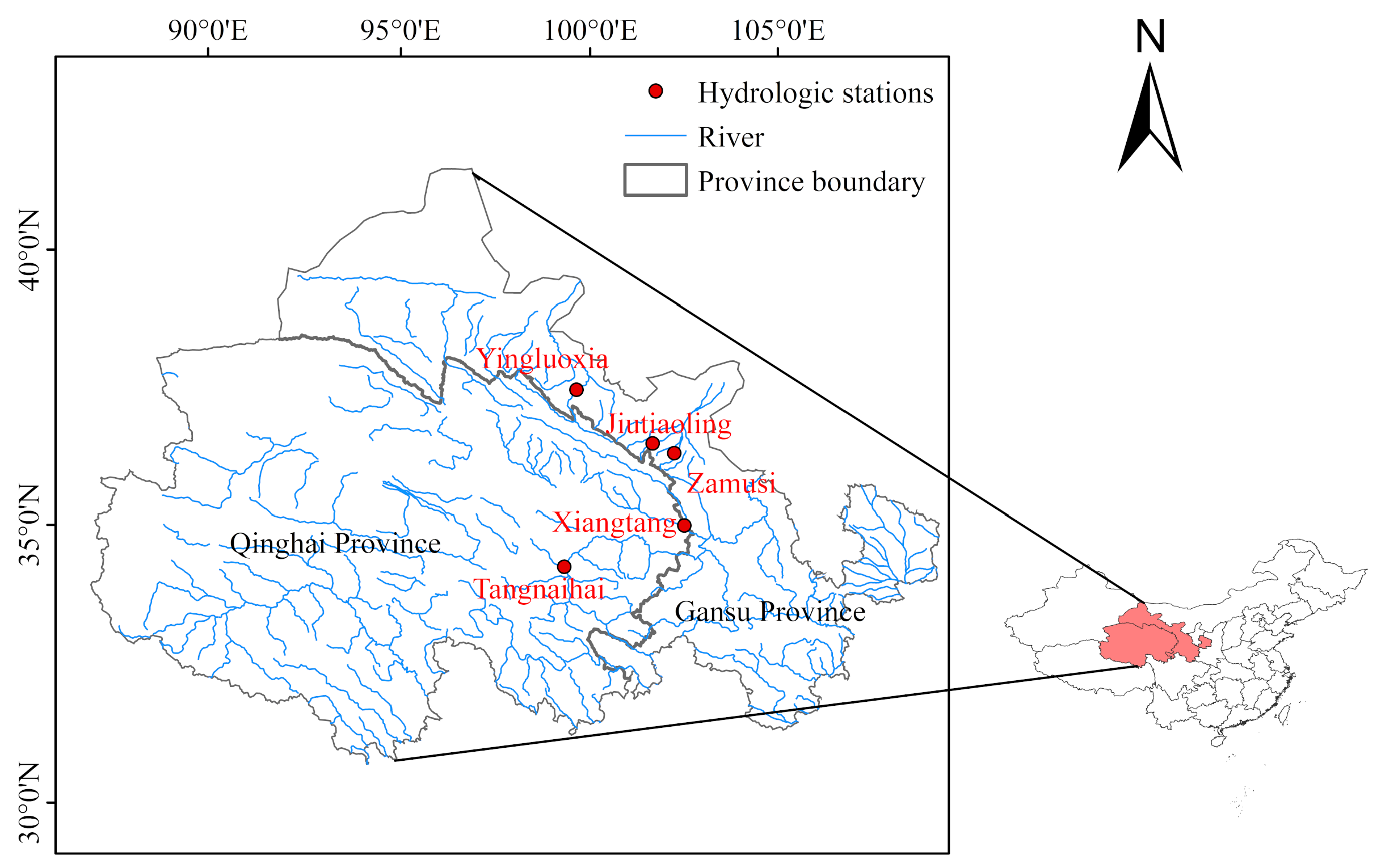
3.1. Data Preprocessing
3.2. Determining Training Period
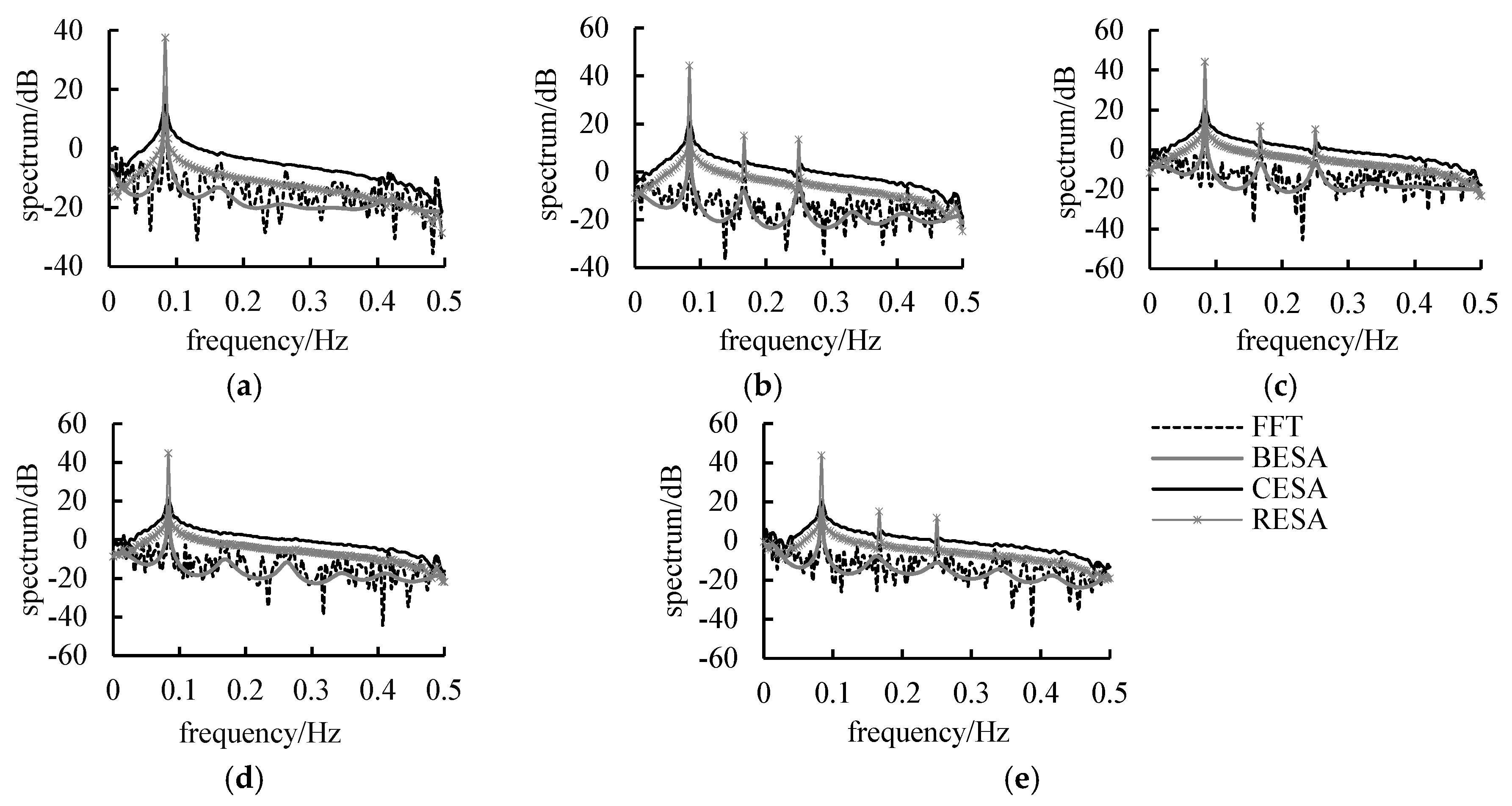
3.3. Estimating Spectral Density
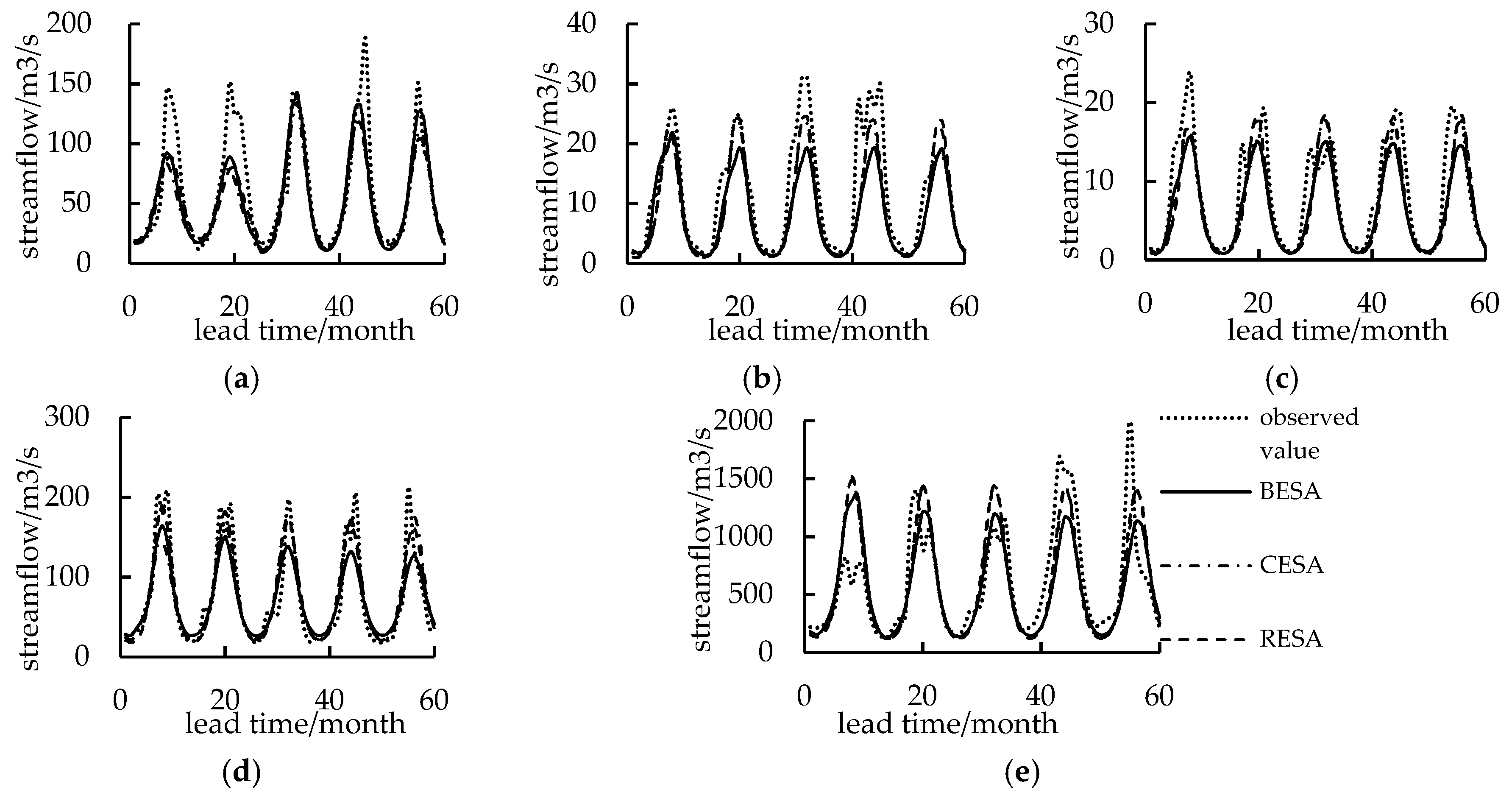
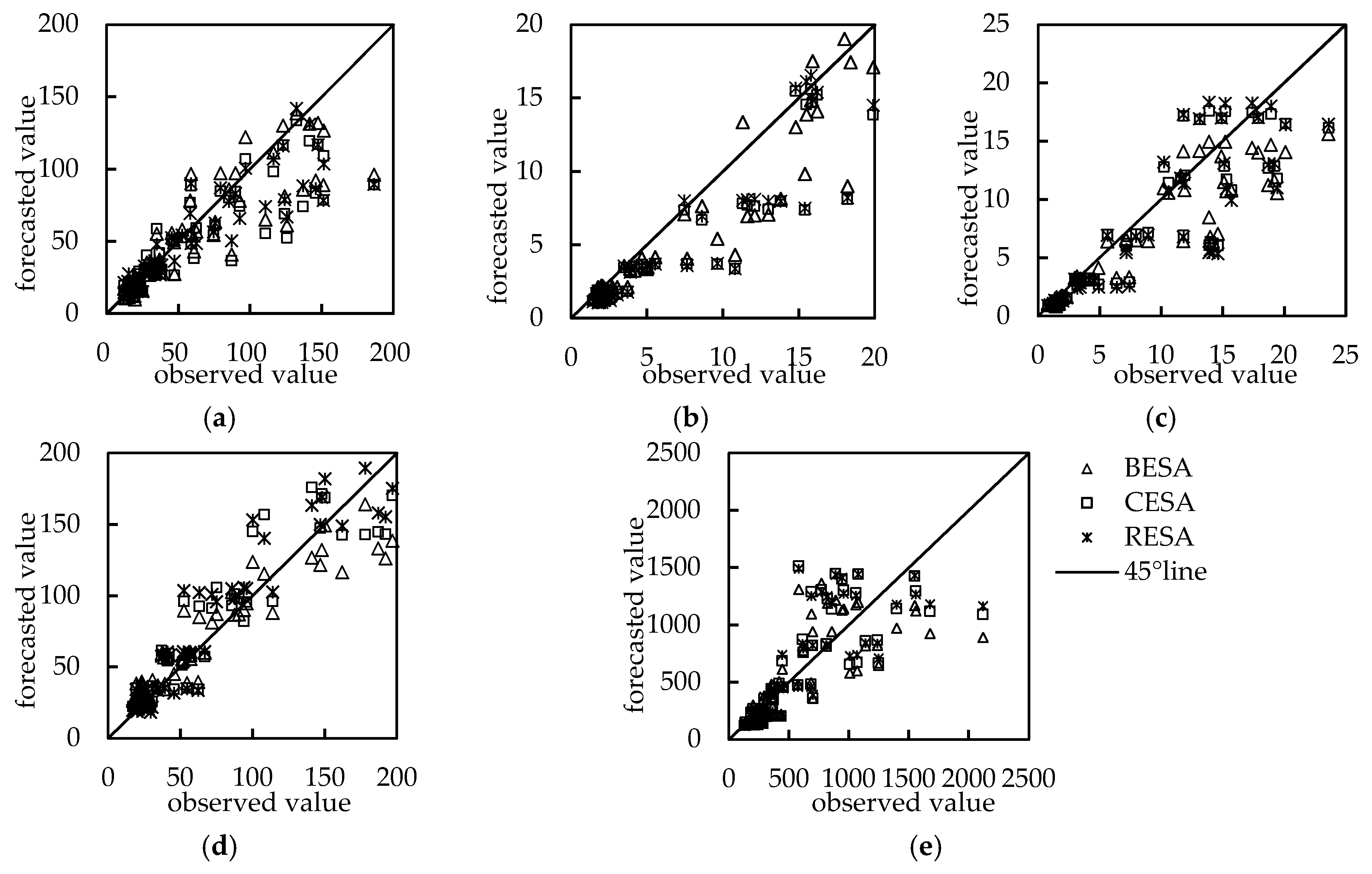
3.4. Streamflow Forecasting Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Determination of the Prior Spectral Density Function for RESA Method
| Number | Period | Spectral Density Function |
|---|---|---|
| Assumption 1 | None | |
| Assumption 2 | 12 months | , |
| Assumption 3 | 12 months, 6 months | , , |
| Assumption 4 | 12 months, 4 months | , , |
| Assumption 5 | 12 months, 4 months, 6 months | , , |
| Assumption 6 | 12 months, 4 months, 6 months | , , , |
| Hydrologic Station | Assumption 1 | Assumption 2 | Assumption 3 | Assumption 4 | Assumption 5 | Assumption 6 |
|---|---|---|---|---|---|---|
| Yingluoxia | 3.4663 | 1.4495 | 1.4536 | 1.4638 | 1.4636 | 1.4629 |
| Zamusi | 3.2100 | 1.3080 | 1.2888 | 1.2735 | 1.2508 | 1.2502 |
| Jiutiaoling | 3.5851 | 1.3211 | 1.2961 | 1.2622 | 1.2267 | 1.2303 |
| Xiangtang | 3.2742 | 1.3225 | 1.3227 | 1.3274 | 1.3237 | 1.3230 |
| Tangnaihai | 3.1384 | 1.4834 | 1.4239 | 1.4790 | 1.4158 | 1.4163 |
References
- Zhou, Z.; Ju, J.; Su, X.; Singh, V.; Zhang, G. Comparison of Two Entropy Spectral Analysis Methods for Streamflow Forecasting in Northwest China. Entropy 2017, 19, 597. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Configurational entropy theory for streamflow forecasting. J. Hydrol. 2015, 521, 1–17. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Maximum entropy spectral analysis for streamflow forecasting. Phys. A 2016, 442, 91–99. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Minimum relative entropy theory for streamflow forecasting with frequency as a random variable. Stoch. Environ. Res. Risk Assess. 2016, 30, 1545–1563. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Application of minimum relative entropy theory for streamflow forecasting. Stoch. Environ. Res. Risk Assess. 2017, 31, 587–608. [Google Scholar] [CrossRef]
- Burg, J.P. Maximum Entropy Spectral Analysis. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1975. [Google Scholar]
- Huo, C.; Chen, N.; Liu, H. Application of time series free regreession model in dynamic simulation and prediction of groundwater in irrigation area. Geotech. Investig. Surv. 1990, 1, 36–38. [Google Scholar]
- Krstanovic, P.F.; Singh, V.P. A real-time flood forecasting model based on maximum-entropy spectral analysis: I. Development. Water Resour. Manag. 1993, 7, 109–129. [Google Scholar] [CrossRef]
- Frieden, B.R. Restoring with maximum likelihood and maximum Entropy. J. Opt. Soc. Am. 1972, 62, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Gull, S.F.; Daniell, G.J. Image reconstruction from incomplete and noisy data. Nature 1978, 272, 686–690. [Google Scholar] [CrossRef]
- Nadeu, C. Finite length cepstrum modelling—A simple spectrum estimation technique. Signal Proc. 1992, 26, 49–59. [Google Scholar] [CrossRef]
- Shore, J.E. Minimum Cross-Entropy Spectral Analysis; Naval Research Laboratory: Washington, DC, USA, 1979.
- Shore, J.E. Minimum cross-entropy spectral-analysis. IEEE Trans. Acoust. Speech 1981, 29, 230–237. [Google Scholar] [CrossRef]
- Tzannes, M.A.; Politis, D.; Tzannes, N.S. A general method of minimum cross-entropy spectral estimation. IEEE Trans. Acoust. Speech 1985, 33, 748–752. [Google Scholar] [CrossRef]
- Woodbury, A.; Ulrych, T.J. Minimum relative entropy and probabilistic inversion in groundwater hydrology. Stoch. Hydrol. Hydraul. 1998, 12, 317–358. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H. Entropy Theory for Streamflow Forecasting. Environ. Process. 2015, 2, 449–460. [Google Scholar] [CrossRef]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. B 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Burg, J.P. Maximum entropy spectral analysis. In Proceedings of the 37th Meeting of Society Exploration Geophysics, Oklahoma City, OK, USA, 31 October 1967; pp. 34–41. [Google Scholar]
- Jam, D.; Singh, V.P. A comparison of transformation methods for flood frequency analysis. J. Am. Water Resour. 1986, 22, 903–910. [Google Scholar] [CrossRef]
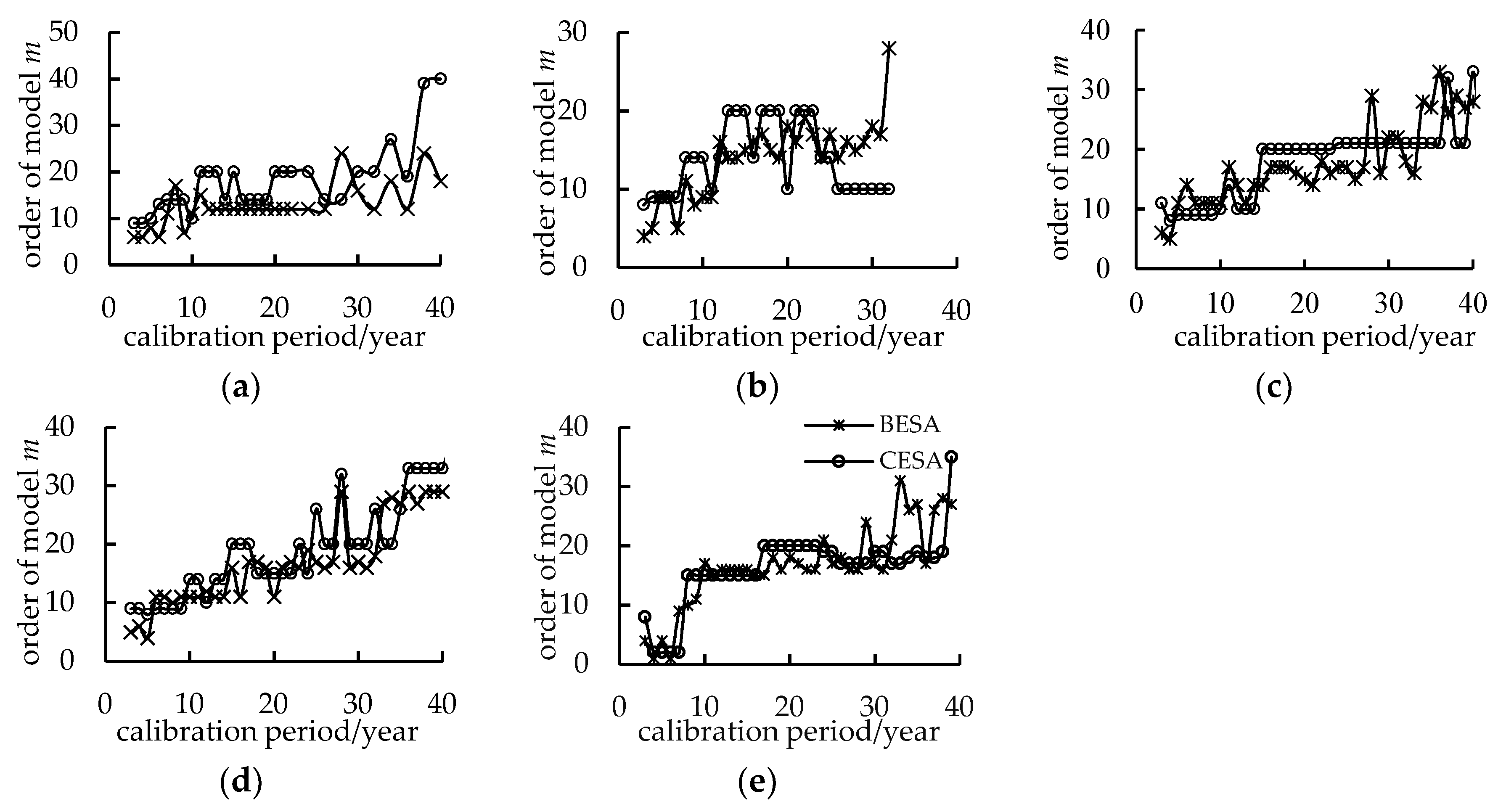
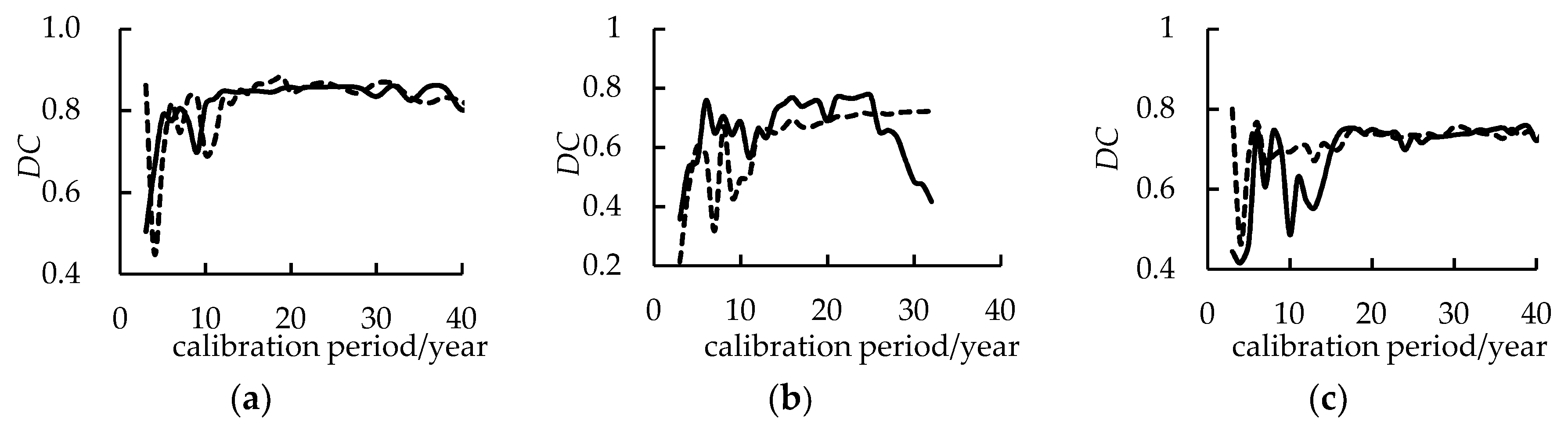
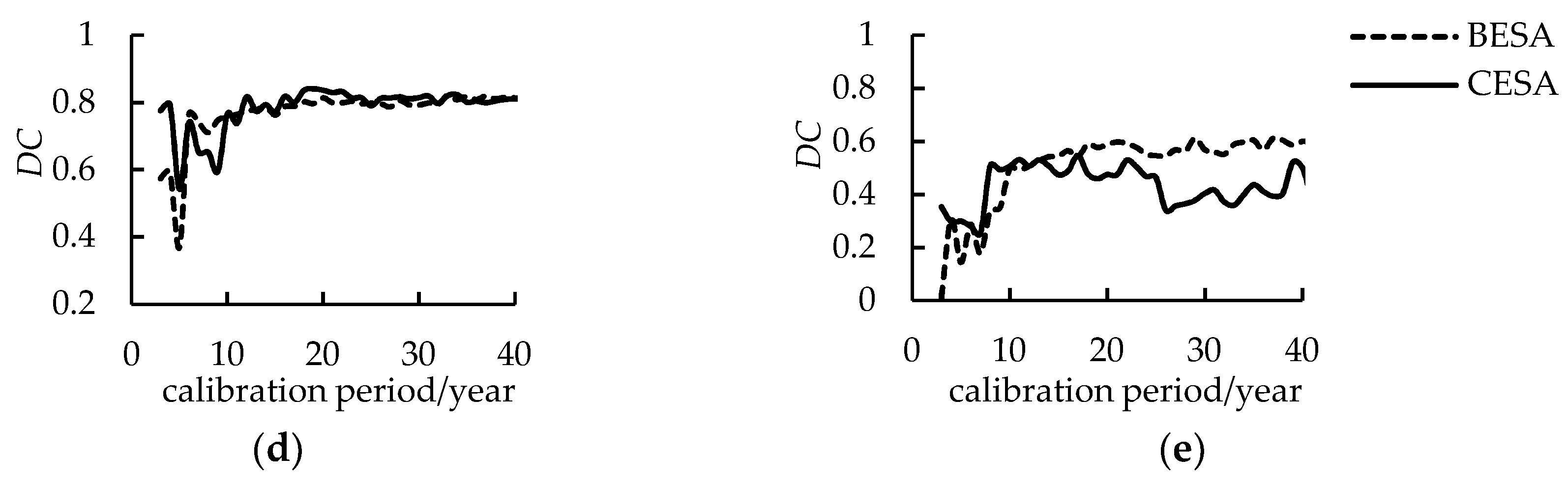
| Criterion | A | B | C |
|---|---|---|---|
| DC | ≥0.9 | 0.9~0.7 | 0.7~0.5 |
| Hydrologic Station | Longitude | Latitude | River | Catchment Area (km2) | Control Area (km2) | Annual Runoff (m3/s) |
|---|---|---|---|---|---|---|
| Yingluoxia | 100°11′ E | 38°48′ N | Hei River | 130,000 | 10.009 | 51 |
| Zamusi | 102°34′ E | 37°42′ N | Zamu River | 851 | 851 | 8 |
| Jiutiaoling | 102°03′ E | 37°52′ N | Xiying River | 1120 | 1077 | 10 |
| Xiangtang | 102°51′ E | 36°22′ N | Datong River | 15.133 | 15,126 | 88 |
| Tangnaihai | 100°09′ E | 35°30′ N | Yellow River | 752,443 | 121,972 | 633 |
| Hydrologic Stations | Yingluoxia | Zamusi | Jiutiaoling | Xiangtang | Tangnaihai |
|---|---|---|---|---|---|
| Returned value | 1 | 1 | 1 | 1 | 1 |
| p Value | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| Confidence coefficient (%) | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 |
| Hydrological Station | BESA | CESA | RESA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RE | RMSE m3/s | R | DC | RE | RMSE m3/s | R | DC | RE | RMSE m3/s | R | DC | |
| Yingluoxia | 0.173 | 18.348 | 0.934 | 0.859 | 0.194 | 16.807 | 0.942 | 0.882 | 0.196 | 16.571 | 0.944 | 0.885 |
| Zamusi | 0.216 | 3.395 | 0.924 | 0.734 | 0.259 | 3.303 | 0.892 | 0.748 | 0.268 | 3.521 | 0.876 | 0.714 |
| Jiutiaoling | 0.224 | 4.972 | 0.911 | 0.716 | 0.273 | 4.771 | 0.911 | 0.739 | 0.276 | 4.592 | 0.911 | 0.758 |
| Xiangtang | 0.260 | 27.237 | 0.924 | 0.797 | 0.232 | 25.760 | 0.907 | 0.818 | 0.234 | 22.636 | 0.928 | 0.859 |
| Tangnaihai | 0.315 | 303.303 | 0.765 | 0.545 | 0.324 | 302.749 | 0.780 | 0.547 | 0.326 | 291.922 | 0.796 | 0.579 |
| Hydrological Station | BESA | CESA | RESA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RE | RMSE m3/s | R | DC | RE | RMSE m3/s | R | DC | RE | RMSE m3/s | R | DC | |
| Yingluoxia | 0.179 | 8.01 | 0.943 | 0.870 | 0.239 | 10.54 | 0.939 | 0.787 | 0.231 | 10.51 | 0.943 | 0.788 |
| Zamusi | 0.224 | 3.00 | 0.936 | 0.726 | 0.255 | 3.15 | 0.901 | 0.692 | 0.263 | 3.47 | 0.887 | 0.665 |
| Jiutiaoliing | 0.229 | 4.02 | 0.863 | 0.654 | 0.257 | 4.42 | 0.864 | 0.631 | 0.268 | 4.40 | 0.864 | 0.636 |
| Xiangang | 0.245 | 12.72 | 0.857 | 0.807 | 0.233 | 13.11 | 0.841 | 0.750 | 0.259 | 15.36 | 0.847 | 0.683 |
| Tangnaihai | 0.261 | 153.08 | 0.802 | 0.630 | 0.276 | 165.70 | 0.813 | 0.567 | 0.284 | 158.23 | 0.827 | 0.605 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhou, Z.; Su, X.; Ayantobo, O.O. Application of Entropy Spectral Method for Streamflow Forecasting in Northwest China. Entropy 2019, 21, 132. https://doi.org/10.3390/e21020132
Zhang G, Zhou Z, Su X, Ayantobo OO. Application of Entropy Spectral Method for Streamflow Forecasting in Northwest China. Entropy. 2019; 21(2):132. https://doi.org/10.3390/e21020132
Chicago/Turabian StyleZhang, Gengxi, Zhenghong Zhou, Xiaoling Su, and Olusola O. Ayantobo. 2019. "Application of Entropy Spectral Method for Streamflow Forecasting in Northwest China" Entropy 21, no. 2: 132. https://doi.org/10.3390/e21020132
APA StyleZhang, G., Zhou, Z., Su, X., & Ayantobo, O. O. (2019). Application of Entropy Spectral Method for Streamflow Forecasting in Northwest China. Entropy, 21(2), 132. https://doi.org/10.3390/e21020132





