Multi-Type Node Detection in Network Communities
Abstract
1. Introduction
2. Methodology
2.1. Definition of Important Measures and Terms
2.1.1. Similarity Measure
2.1.2. Modularity
2.1.3. Betweeness Centrality
2.1.4. Bridging Coefficient and Bridging Centrality
2.1.5. Clustering Coefficient
2.2. The Algorithm
| Algorithm 1 Multi-type Node Detection Algorithm |
| Input: Network G; desired number of partitions P Output: , , , Q
|
2.3. Properties of an Isolated Bridge-Node
- They are bridge-nodes.
- They have degree .
- They have no path linking back to them. In other words, they do not share common nodes with any other node on the network. i.e., . Therefore, they have zero node similarity values with all of their neighbours.
3. Results, Evaluation and Discussion
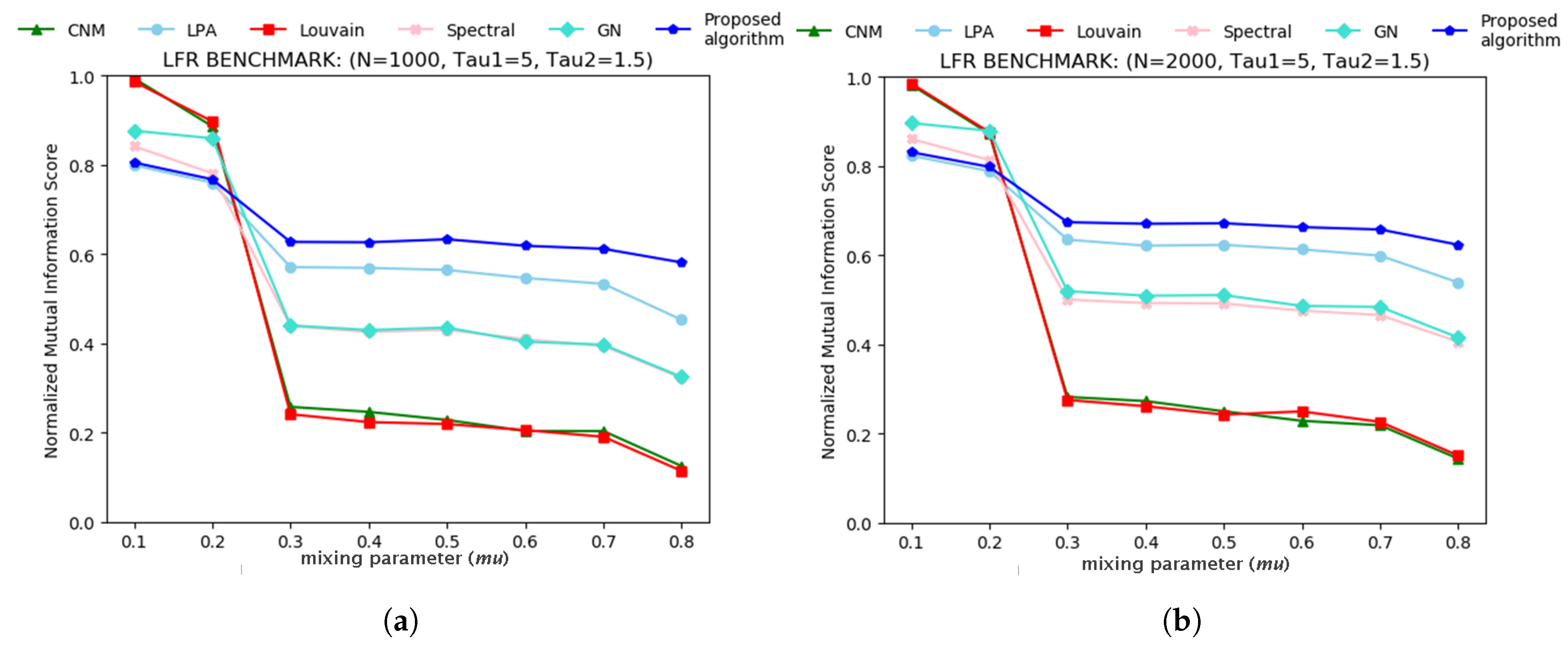
3.1. Tests on Artificial Networks
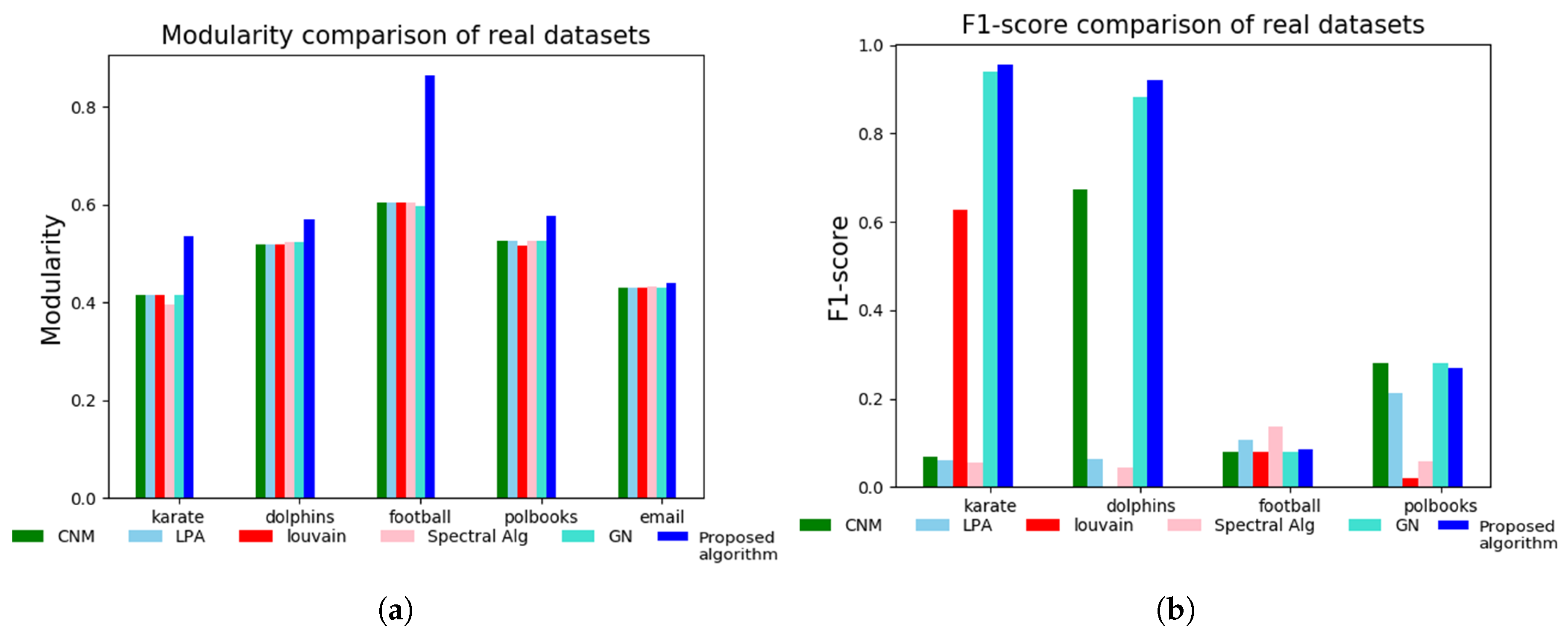
3.2. Tests on Real-World Network Datasets
3.2.1. Zachary’s Karate Club Network
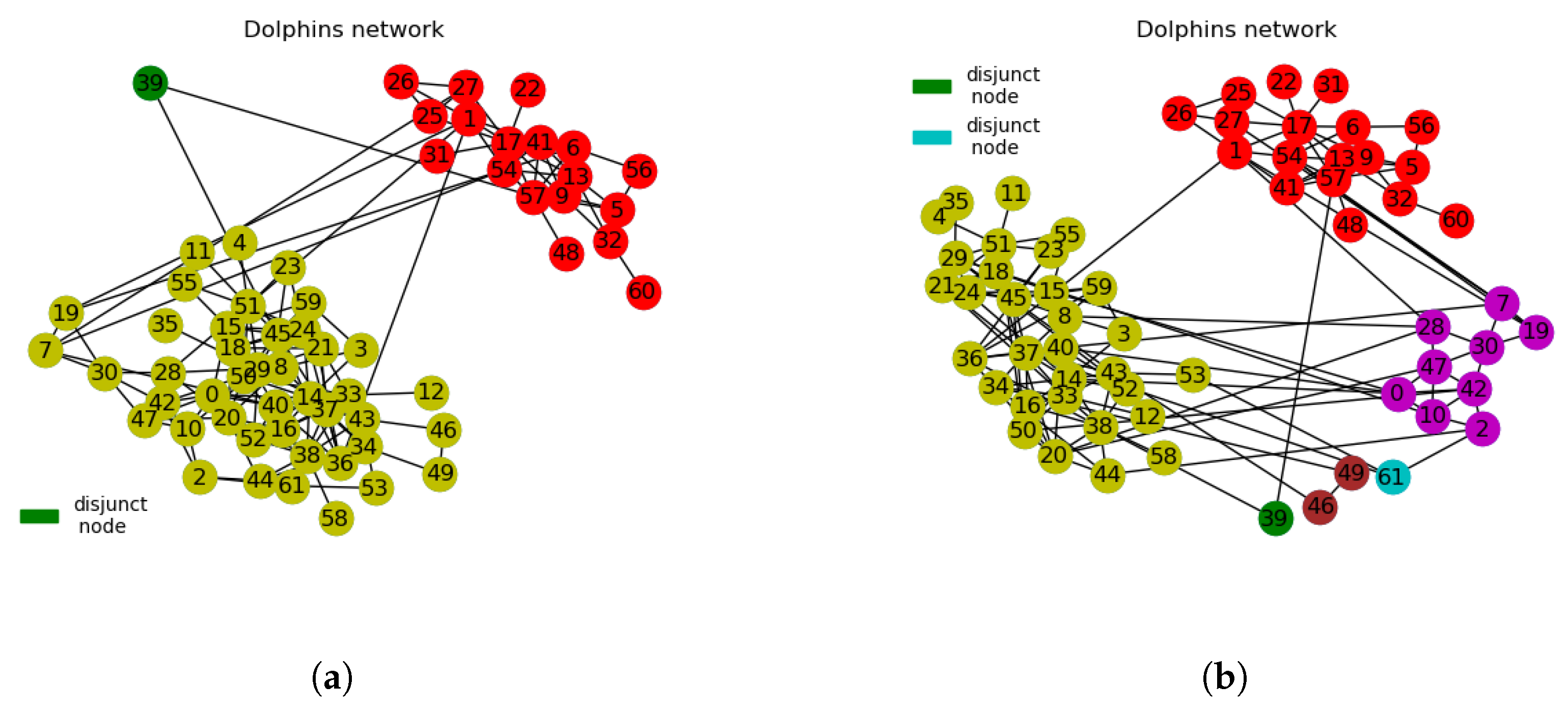
3.2.2. Dolphins Network
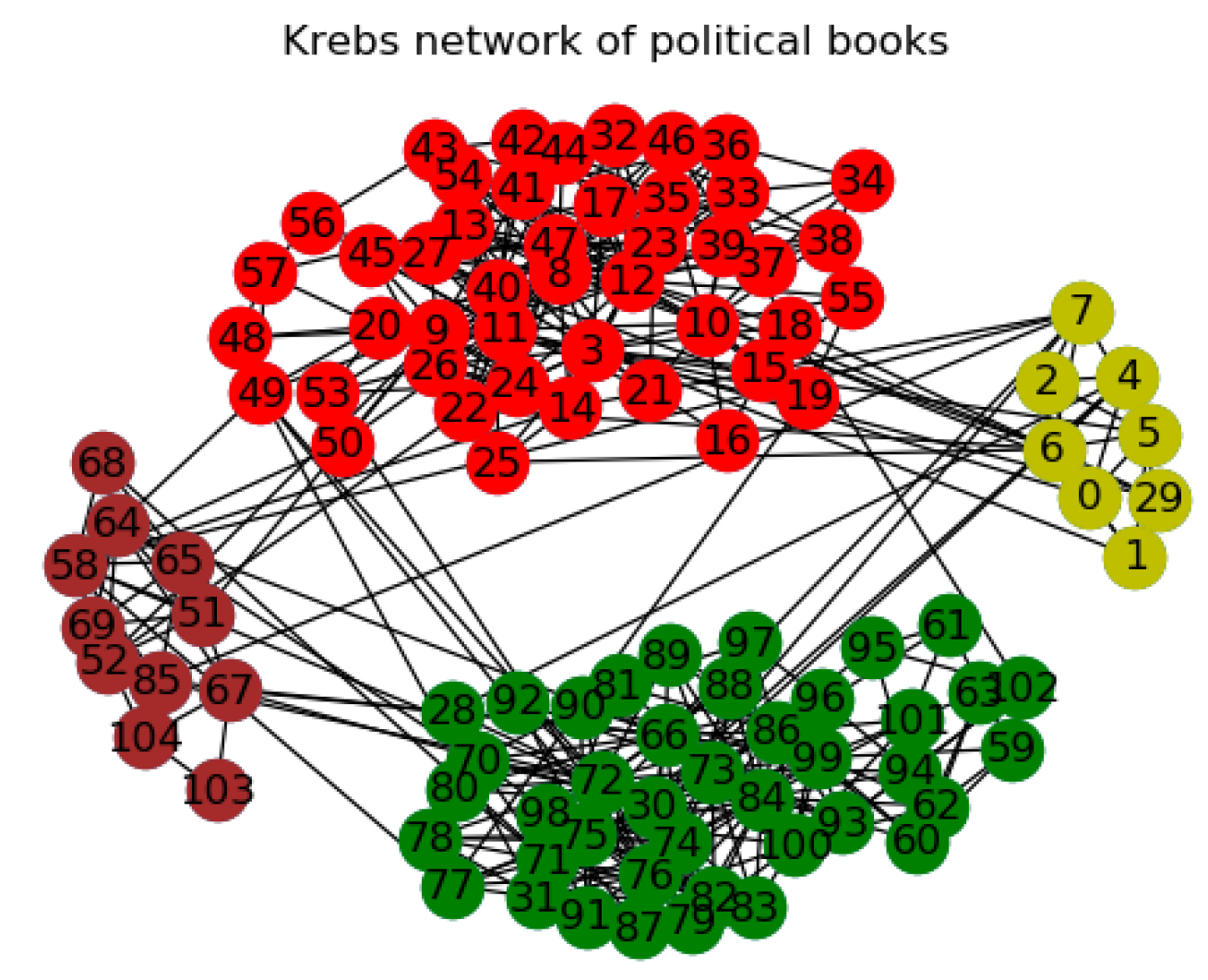
3.2.3. The Other Networks
3.2.4. Computational Complexity Analysis
3.2.5. Limitations and Future Works
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Notes
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Sonia, C.; Gilles, C.; Pierre, H.; Sylvain, P.; Alberto, C. Finding communities in networks in the strong and almost-strong sense. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Zarandi, F.D.; Rafsanjani, M.K. Community detection in complex networks using structural similarity. Phys. A 2018, 503, 882–891. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Cho, Y.; Zhang, A.; Ramanathan, M. Bridging centrality: Identifying bridging nodes in scale-free networks. In Proceedings of the KDD-06, Philadelphia, PA, USA, 20–23 August 2006. [Google Scholar]
- Hwang, W.; Ramanathan, M.; Kim, T.; Zhang, A. Bridging centrality: Graph mining from element level to group level. In Proceedings of the 14th ACM SIGKDD International Conference on KDD, Las Vegas, NV, USA, 24–27 August 2008. [Google Scholar]
- Nanda, S.; Kotz, D. Localized bridging centrality. In Handbook of Optimization in Complex Networks; Thai, M., Pardalos, P., Eds.; SOIA: New York, NY, USA, 2012; pp. 197–218. [Google Scholar]
- Yanqing, H.; Hongbin, C.; Zhang, P.; Menghui, L.; Zengru, D.; Ying, F. Comparative definition of community and corresponding identifying algorithm. Phys. Rev. E 2008, 78, 026121. [Google Scholar] [CrossRef]
- Enugala, R.; Rajamani, L.; Ali, K.; Kurapati, S. Community detection in dynamic social networks: A survey. IJRA 2015, 2, 278–285. [Google Scholar] [CrossRef]
- Baruah, A.K.; Bora, T. Bridging centrality: Identifying bridging nodes in transportation networks. IJANA 2018, 9, 3669–3673. [Google Scholar]
- Aloise, D.; Caporossi, G.; Hansen, P.; Liberti, L.; Perron, S.; Ruiz, M. Modularity maximization in networks by variable neighborhood search. In Proceedings of the 10th DIMACS Implementation Challenge Workshop, Atlanta, GA, USA, 13–14 February 2012; p. 113. [Google Scholar] [CrossRef]
- Chen, M.; Kuzmin, K.; Szymanski, B.K. Community detection via maximization of modularity and its variants. IEEE Trans. Comp. Soc. Syst. 2014, 1, 46–65. [Google Scholar] [CrossRef]
- Greeshma, V.; Vani, K.S. Community detection in networks using page rank vectors. IJBB 2015, 5. [Google Scholar] [CrossRef]
- Scripps, J.; Tan, P. Clustering in the presence of bridge-nodes. In Proceedings of the 2006 SIAM International Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006. [Google Scholar] [CrossRef]
- Saoud, B.; Moussaoui, A. Node similarity and modularity for finding communities in networks. Phys. A 2018, 492, 1958–1966. [Google Scholar] [CrossRef]
- De Montgolfier, F.; Soto, M.; Viennot, L. Asymptotic modularity of some graph classes. In Algorithms and Computation; Asano, S.N., Okamoto, Y., Watanabe, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 435–444. [Google Scholar]
- Chen, M.; Kuzmin, K.; Szymanski, B.K. Extension of modularity density for overlapping community structure. In Proceedings of the IEEE/ACM ASONAM, Beijing, China, 17–20 August 2014; pp. 856–863. [Google Scholar] [CrossRef]
- Yuan, C.; Chai, Y.; Wei, S.B. Feature analysis and modeling of the network community structure. CTP 2012, 58, 604–612. [Google Scholar] [CrossRef]
- Jiang, Y.; Jia, C.; Yu, J. An efficient community detection method based on rank centrality. Phys. A 2013, 392, 2182–2194. [Google Scholar] [CrossRef]
- Zalik, K.R.; Zalik, A.B. Framework for detecting communities of unbalanced sizes in networks. Phys. A 2018, 490, 24–37. [Google Scholar] [CrossRef]
- Ahn, Y.Y.; Bagrow, J.P.; Lehmann, S. Link communities reveal multiscale complexity in networks. Nature 2010, 466, 761–764. [Google Scholar] [CrossRef]
- We use interchangeably disjoint nodes for cluster nodes and disjunct nodes for isolated or neutral nodes. In this context, disjunct nodes refer to nodes that do not belong to any communities after network divisions. They appear to be neutral in adhering to clusters or communities. What we refer to as disjunct nodes in this paper is quite different from singleton nodes with degree value of 1.
- Peel, L.; Larremore, D.B.; Clauset, A. The ground truth about metadata and community detection in networks. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef]
- Newman, M. Fast algorithm for detecting community structure in networks. Phys. Rev. E Stat. Nonlinear Soft. Matter Phys. 2004, 69, 066133. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On Spectral Clustering: Analysis and an Algorithm. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; MIT Press: Cambridge, MA, USA, 2001; pp. 849–856. [Google Scholar]
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community detection in networks: A multidisciplinary review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- Malliaros, F.; Vazirgiannis, M. Clustering and Community Detection in Directed Networks: A Survey. Phys. Rep. 2013, 533. [Google Scholar] [CrossRef]
- The bridging centrality of a node is the product of the betweeness centrality of the node and its bridging coefficient [6,7].
- Radicchi, F.; Castellano, C.; Cecconi, F.; Loreto, V.; Parisi, D. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 2004, 101, 2658–2663. [Google Scholar] [CrossRef]
- Freeman, L. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using networkx. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; Varoquaux, T.V., Millman, J., Eds.; Pasadena: California, CA, USA, 2008; pp. 11–15. [Google Scholar]
- Oliphant, T.E. A Guide to NumPy. 2006. Available online: https://www.scipy.org/citing.html (accessed on 3 December 2019).
- Walt, S.V.; Colbert, S.C.; Varoquaux, G. The numpy array: A structure for efficient numerical computation. MCSE 2011, 13, 22. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. MCSE 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, E.; Peterson, P. Scipy: Open Source Scientific Tools for Python. Available online: https://www.bibsonomy.org/bibtex/24b71448b262807648d60582c036b8e02/neurokernel (accessed on 29 November 2019).
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E 2008, 78, 046110. [Google Scholar] [CrossRef]
- Zachary, W. An information flow model for conflict and fission in small groups. JAR 1976, 33, 473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Krebs, V. Krebs Amazon Political Books Dataset; Unpublished work; 2019. [Google Scholar]
- Available online: http://www-personal.umich.edu/~mejn/netdata/football.zip (accessed on 3 December 2019).
- Yin, H.; Benson, A.; Leskovec, J.; Gleich, D. Local Higher-Order Graph Clustering. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 555–564. [Google Scholar]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph Evolution: Densification and Shrinking Diameters. arXiv 2007, arXiv:physics/0603229. [Google Scholar] [CrossRef]
- Kovacs, I.; Barabasi, A.L. Destruction Perfected. Nature 2015, 524, 38–39. [Google Scholar] [CrossRef] [PubMed]
- Akabane, A.T.; Immich, R.; Pazzi, R.W.; Madeira, E.R.M.; Villas, L.A. Distributed Egocentric Betweenness Measure as a Vehicle Selection Mechanism in VANETs: A Performance Evaluation Study. Sensors 2018, 18, 2731. [Google Scholar] [CrossRef] [PubMed]
- Butcher, N. Jaccard Coefficients. Available online: https://www3.nd.edu/~kogge/courses/cse60742-Fall2018/Public/StudentWork/KernelPaperFinal/jaccard-butcher3.pdf (accessed on 29 November 2019).
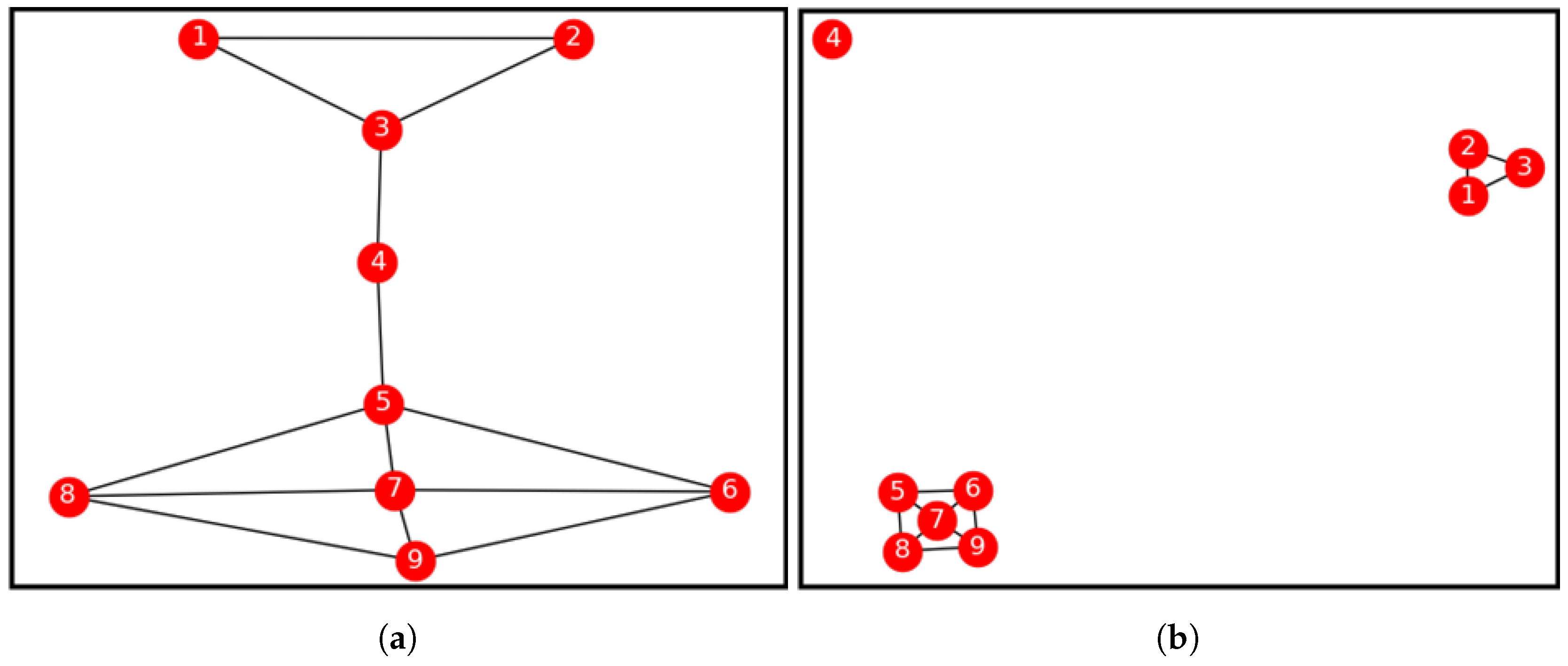

| Iteration Count | Node ID. | Bridge Centrality Value | Neighbours. | Node Similarity Value |
|---|---|---|---|---|
| 1st | 4 | 0.4592 | 3 | 0 |
| 5 | 0 | |||
| 2nd | 7 | 0.0045 | 5 | 0.2857 |
| 6 | 0.2857 | |||
| 8 | 0.2857 | |||
| 9 | 0.2857 |
| Edge | Edge-Betweeness Value |
|---|---|
| 0.2778 | |
| 0.2500 | |
| 0.0972 | |
| 0.0972 |
| Network | Ground-Truth | Description | Ref | |
|---|---|---|---|---|
| Karate Club | 34/78 | 2 | Friendship network of karate club members | [42] |
| Dolphin | 62/159 | 2 | Association network of bottlenose dolphins | [43] |
| Polbooks | 105/441 | 3 | A co-purchasing network of political books | [44] |
| Football | 115/613 | 12 | A game-scheduling network of teams | [45] |
| Email EU | 1005/16706 | 42 | European research institution’s email data | [46,47] |
| Modularity Q and Number of Communities (C) | ||||||
|---|---|---|---|---|---|---|
| Network | CNM | LPA | Louvain | SPA | GN | Proposed Algorithm |
| Karate | 0.4198 | 0.4198 | 0.4156 | 0.4188 | 0.4188 | 0.5789 |
| Dolphin | 0.5188 | 0.5196 | 0.5268 | 0.5188 | 0.4156 | 0.6989 |
| Polbooks | 0.5266 | 0.5268 | 0.5270 | 0.5270 | 0.5266 | 0.5905 |
| Football | 0.6046 | 0.6043 | 0.6044 | 0.6046 | 0.6043 | 0.8641 |
| 0.4324 | 0.4306 | 0.4322 | 0.4314 | 0.4328 | 0.4415 | |
| Network | CNM | LPA | Louvain | SPA | GN | Proposed Algorithm |
|---|---|---|---|---|---|---|
| Karate | 0.0037 | 0.0012 | 0.0110 | 0.0110 | 0.0467 | 0.0311 |
| Dolphin | 0.0147 | 0.0101 | 0.0301 | 0.0604 | 0.1264 | 0.0960 |
| Polbooks | 0.0232 | 0.0061 | 0.0400 | 0.0712 | 1.3444 | 0.8653 |
| Football | 0.0513 | 0.0290 | 0.0655 | 0.1937 | 5.5780 | 3.5012 |
| Email EU | 2.3331 | 0.1486 | 1.3961 | 1.4739 | 324.79 | 6804.38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezeh, C.; Tao, R.; Zhe, L.; Yiqun, W.; Ying, Q. Multi-Type Node Detection in Network Communities. Entropy 2019, 21, 1237. https://doi.org/10.3390/e21121237
Ezeh C, Tao R, Zhe L, Yiqun W, Ying Q. Multi-Type Node Detection in Network Communities. Entropy. 2019; 21(12):1237. https://doi.org/10.3390/e21121237
Chicago/Turabian StyleEzeh, Chinenye, Ren Tao, Li Zhe, Wang Yiqun, and Qu Ying. 2019. "Multi-Type Node Detection in Network Communities" Entropy 21, no. 12: 1237. https://doi.org/10.3390/e21121237
APA StyleEzeh, C., Tao, R., Zhe, L., Yiqun, W., & Ying, Q. (2019). Multi-Type Node Detection in Network Communities. Entropy, 21(12), 1237. https://doi.org/10.3390/e21121237





