Permutation Entropy and Statistical Complexity Analysis of Brazilian Agricultural Commodities
Abstract
1. Introduction
2. Methodology
2.1. Permutation Entropy
2.2. Complexity Entropy Causality Plane
3. Data and Analysis
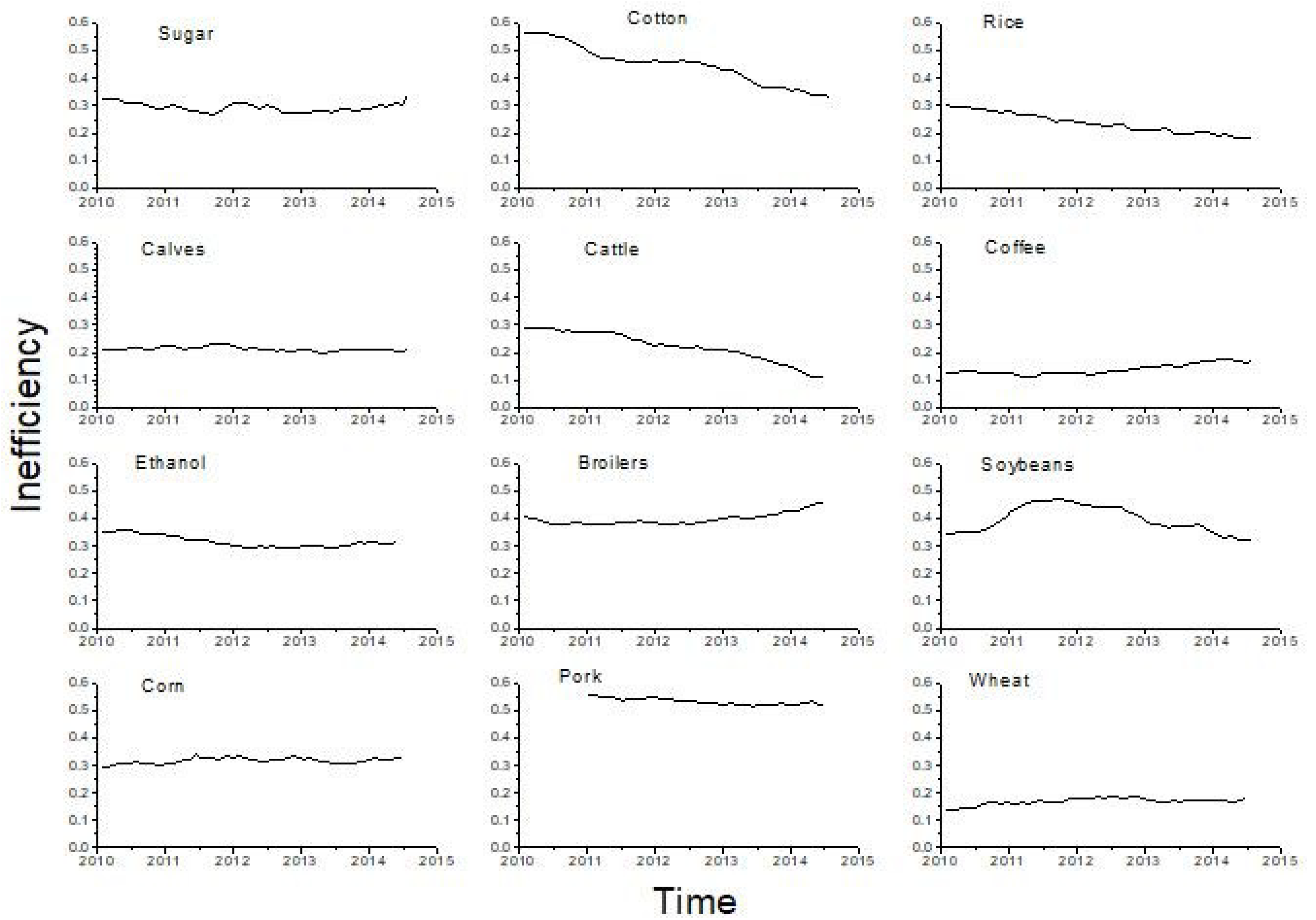
4. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Roberts, M.J.; Schlenker, W. Identifying supply and demand elasticities of agricultural commodities: Implications for the US ethanol mandate. Am. Econ. Rev. 2013, 103, 2265–2295. [Google Scholar] [CrossRef]
- Nazlioglu, S.; Soytas, U. Oil price, agricultural commodity prices, and the dollar: A panel cointegration and causality analysis. Energy Econ. 2012, 34, 1098–1104. [Google Scholar] [CrossRef]
- Adämmer, P.; Bohl, M.T. Speculative bubbles in agricultural prices. Q. Rev. Econ. Financ. 2015, 55, 67–76. [Google Scholar] [CrossRef]
- Beckmann, J.; Czudaj, R. Volatility transmission in agricultural futures markets. Econ. Model. 2014, 36, 541–546. [Google Scholar] [CrossRef]
- He, L.Y.; Chen, S.P. Nonlinear bivariate dependency of price–volume relationships in agricultural commodity futures markets: A perspective from multifractal detrended cross-correlation analysis. Phys. A Stat. Mech. Its Appl. 2011, 390, 297–308. [Google Scholar] [CrossRef]
- He, L.Y.; Chen, S.P. Multifractal detrended cross-correlation analysis of agricultural futures markets. Chaos Solitons Fractals 2011, 44, 355–361. [Google Scholar] [CrossRef]
- Liu, L. Cross-correlations between crude oil and agricultural commodity markets. Phys. A Stat. Mech. Its Appl. 2014, 395, 293–302. [Google Scholar] [CrossRef]
- Siqueira, E.L., Jr.; Stošić, T.; Bejan, L.; Stošić, B. Correlations and cross-correlations in the Brazilian agrarian commodities and stocks. Phys. A Stat. Mech. Its Appl. 2010, 389, 2739–2743. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Commodity futures and market efficiency. Energy Econ. 2014, 42, 50–57. [Google Scholar] [CrossRef]
- Zunino, L.; Tabak, B.M.; Serinaldi, F.; Zanin, M.; Pérez, D.G.; Rosso, O.A. Commodity predictability analysis with a permutation information theory approach. Phys. A Stat. Mech. Its Appl. 2011, 390, 876–890. [Google Scholar] [CrossRef]
- Tabak, B.M.; Serra, T.R.; Cajueiro, D.O. Topological properties of commodities networks. Eur. Phys. J. B 2010, 74, 243–249. [Google Scholar] [CrossRef]
- Hochman, G.; Rajagopal, D.; Timilsina, G.; Zilberman, D. Quantifying the causes of the global food commodity price crisis. Biomass Bioenergy 2014, 68, 106–114. [Google Scholar] [CrossRef]
- Ivanic, M.; Martin, W.; Zaman, H. Estimating the short-run poverty impacts of the 2010–11 surge in food prices. World Dev. 2012, 40, 2302–2317. [Google Scholar] [CrossRef]
- Bellemare, M.F. Rising food prices, food price volatility, and social unrest. Am. J. Agric. Econ. 2015, 97, 1–21. [Google Scholar] [CrossRef]
- Rosegrant, M.W.; Cline, S.A. Global food security: Challenges and policies. Science 2003, 302, 1917–1919. [Google Scholar] [CrossRef]
- FAO. 2018. The State of Agricultural Commodity Markets. In Agricultural Trade, Climate Change and Food Security; FAO: Rome, Italy, 2018. [Google Scholar]
- Mueller, B.; Mueller, C. The political economy of the Brazilian model of agricultural development: Institutions versus sectoral policy. Q. Rev. Econ. Financ. 2016, 62, 12–20. [Google Scholar] [CrossRef]
- Ceballos, F.; Hernandez, M.A.; Minot, N.; Robles, M. Transmission of Food Price Volatility from International to Domestic Markets: Evidence from Africa, Latin America, and South Asia. In Food Price Volatility and Its Implications for Food Security and Policy; Springer: Cham, Switzerland, 2016; pp. 303–328. [Google Scholar]
- Balcombe, K.; Bailey, A.; Brooks, J. Threshold effects in price transmission: The case of Brazilian wheat, maize, and soya prices. Am. J. Agric. Econ. 2007, 89, 308–323. [Google Scholar] [CrossRef]
- Hertel, T.W.; Tyner, W.E.; Birur, D.K. The global impacts of biofuel mandates. Energy J. 2010, 31, 75–100. [Google Scholar] [CrossRef]
- Kristoufek, L.; Janda, K.; Zilberman, D. Comovements of ethanol-related prices: Evidence from Brazil and the USA. Gcb Bioenergy 2016, 8, 346–356. [Google Scholar] [CrossRef]
- Cabrera, B.L.; Schulz, F. Volatility linkages between energy and agricultural commodity prices. Energy Econ. 2016, 54, 190–203. [Google Scholar] [CrossRef]
- He, L.Y.; Chen, S.P. Are developed and emerging agricultural futures markets multifractal? A comparative perspective. Phys. A Stat. Mech. Its Appl. 2010, 389, 3828–3836. [Google Scholar] [CrossRef]
- Kristoufek, L.; Janda, K.; Zilberman, D. Correlations between biofuels and related commodities before and during the food crisis: A taxonomy perspective. Energy Econ. 2012, 34, 1380–1391. [Google Scholar] [CrossRef]
- Kristoufek, L.; Janda, K.; Zilberman, D. Regime-dependent topological properties of biofuels networks. Eur. Phys. J. B 2013, 86, 40. [Google Scholar] [CrossRef]
- Lima CR, A.; de Melo, G.R.; Stosic, B.; Stosic, T. Cross-correlations between Brazilian biofuel and food market: Ethanol versus sugar. Phys. A Stat. Mech. Its Appl. 2019, 513, 687–693. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Phys. A Stat. Mech. Its Appl. 2010, 389, 1891–1901. [Google Scholar] [CrossRef]
- Zunino, L.; Bariviera, A.F.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. On the efficiency of sovereign bond markets. Phys. A Stat. Mech. Its Appl. 2012, 391, 4342–4349. [Google Scholar] [CrossRef]
- Bariviera, A.F.; Zunino, L.; Rosso, O.A. An analysis of high-frequency cryptocurrencies prices dynamics using permutation-information-theory quantifiers. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 075511. [Google Scholar] [CrossRef]
- Bariviera, A.F.; Zunino, L.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. Efficiency and credit ratings: A permutation-information-theory analysis. J. Stat. Mech. Theory Exp. 2013, 2013, PO8007. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Graff, G.; Graff, B.; Kaczkowska, A.; Makowiec, D.; Amigó, J.M.; Piskorski, J.; Guzik, P. Ordinal pattern statistics for the assessment of heart rate variability. Eur. Phys. J. Spec. Top. 2013, 222, 525–534. [Google Scholar] [CrossRef]
- Zeng, K.; Ouyang, G.; Chen, H.; Gu, Y.; Liu, X.; Li, X. Characterizing dynamics of absence seizure EEG with spatial-temporal permutation entropy. Neurocomputing 2018, 275, 577–585. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Consolini, G.; De Michelis, P. Permutation entropy analysis of complex magnetospheric dynamics. J. Atmos. Sol.-Terr. Phys. 2014, 115, 25–31. [Google Scholar] [CrossRef]
- Barreiro, M.; Marti, A.C.; Masoller, C. Inferring long memory processes in the climate network via ordinal pattern analysis. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 013101. [Google Scholar] [CrossRef]
- Saco, P.M.; Carpi, L.C.; Figliola, A.; Serrano, E.; Rosso, O.A. Entropy analysis of the dynamics of El Niño/Southern Oscillation during the Holocene. Phys. A Stat. Mech. Its Appl. 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Mihailović, D.T.; Nikolić-Đorić, E.; Drešković, N.; Mimić, G. Complexity analysis of the turbulent environmental fluid flow time series. Phys. A Stat. Mech. Its Appl. 2014, 395, 96–104. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Phys. A Stat. Mech. Its Appl. 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Weighted permutation entropy based on different symbolic approaches for financial time series. Phys. A Stat. Mech. Its Appl. 2016, 443, 137–148. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Legnani, W.; Traversaro, F.; Redelico, F.O.; Cymberknop, L.J.; Armentano, R.L.; Rosso, O.A. Analysis of ischaemic crisis using the informational causal entropy-complexity plane. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 075518. [Google Scholar] [CrossRef] [PubMed]
- Weck, P.J.; Schaffner, D.A.; Brown, M.R.; Wicks, R.T. Permutation entropy and statistical complexity analysis of turbulence in laboratory plasmas and the solar wind. Phys. Rev. E 2015, 91, 023101. [Google Scholar] [CrossRef] [PubMed]
- Maggs, J.E.; Morales, G.J. Permutation entropy analysis of temperature fluctuations from a basic electron heat transport experiment. Plasma Phys. Control. Fusion 2013, 55, 085015. [Google Scholar] [CrossRef]
- Siddagangaiah, S.; Li, Y.; Guo, X.; Chen, X.; Zhang, Q.; Yang, K.; Yang, Y. A complexity-based approach for the detection of weak signals in ocean ambient noise. Entropy 2016, 18, 101. [Google Scholar] [CrossRef]
- Sippel, S.; Lange, H.; Mahecha, M.D.; Hauhs, M.; Bodesheim, P.; Kaminski, T.; Rosso, O.A. Diagnosing the dynamics of observed and simulated ecosystem gross primary productivity with time causal information theory quantifiers. PLoS ONE 2016, 11, e0164960. [Google Scholar] [CrossRef]
- Stosic, T.; Telesca, L.; de Souza Ferreira, D.V.; Stosic, B. Investigating anthropically induced effects in streamflow dynamics by using permutation entropy and statistical complexity analysis: A case study. J. Hydrol. 2016, 540, 1136–1145. [Google Scholar] [CrossRef]
- Jovanovic, T.; García, S.; Gall, H.; Mejía, A. Complexity as a streamflow metric of hydrologic alteration. Stoch. Environ. Res. Risk Assess. 2017, 31, 2107–2119. [Google Scholar] [CrossRef]
- Serinaldi, F.; Zunino, L.; Rosso, O.A. Complexity–entropy analysis of daily stream flow time series in the continental United States. Stoch. Environ. Res. Risk Assess. 2014, 28, 1685–1708. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Phys. A Stat. Mech. Its Appl. 2006, 369, 439–462. [Google Scholar] [CrossRef]
- CEPEA. Available online: https://www.cepea.esalq.usp.br/br (accessed on 26 October 2019).
- Cavalett, O.; Junqueira, T.L.; Dias, M.O.; Jesus, C.D.; Mantelatto, P.E.; Cunha, M.P.; Bonomi, A. Environmental and economic assessment of sugarcane first generation biorefineries in Brazil. Clean Technol. Environ. Policy 2012, 14, 399–410. [Google Scholar] [CrossRef]
- Da Silva, V.P.; van der Werf, H.M.; Soares, S.R.; Corson, M.S. Environmental impacts of French and Brazilian broiler chicken production scenarios: An LCA approach. J. Environ. Manag. 2014, 133, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Hamadi, H.; Bassil, C.; Nehme, T. News surprises and volatility spillover among agricultural commodities: The case of corn, wheat, soybean and soybean oil. Res. Int. Bus. Financ. 2017, 41, 148–157. [Google Scholar] [CrossRef]
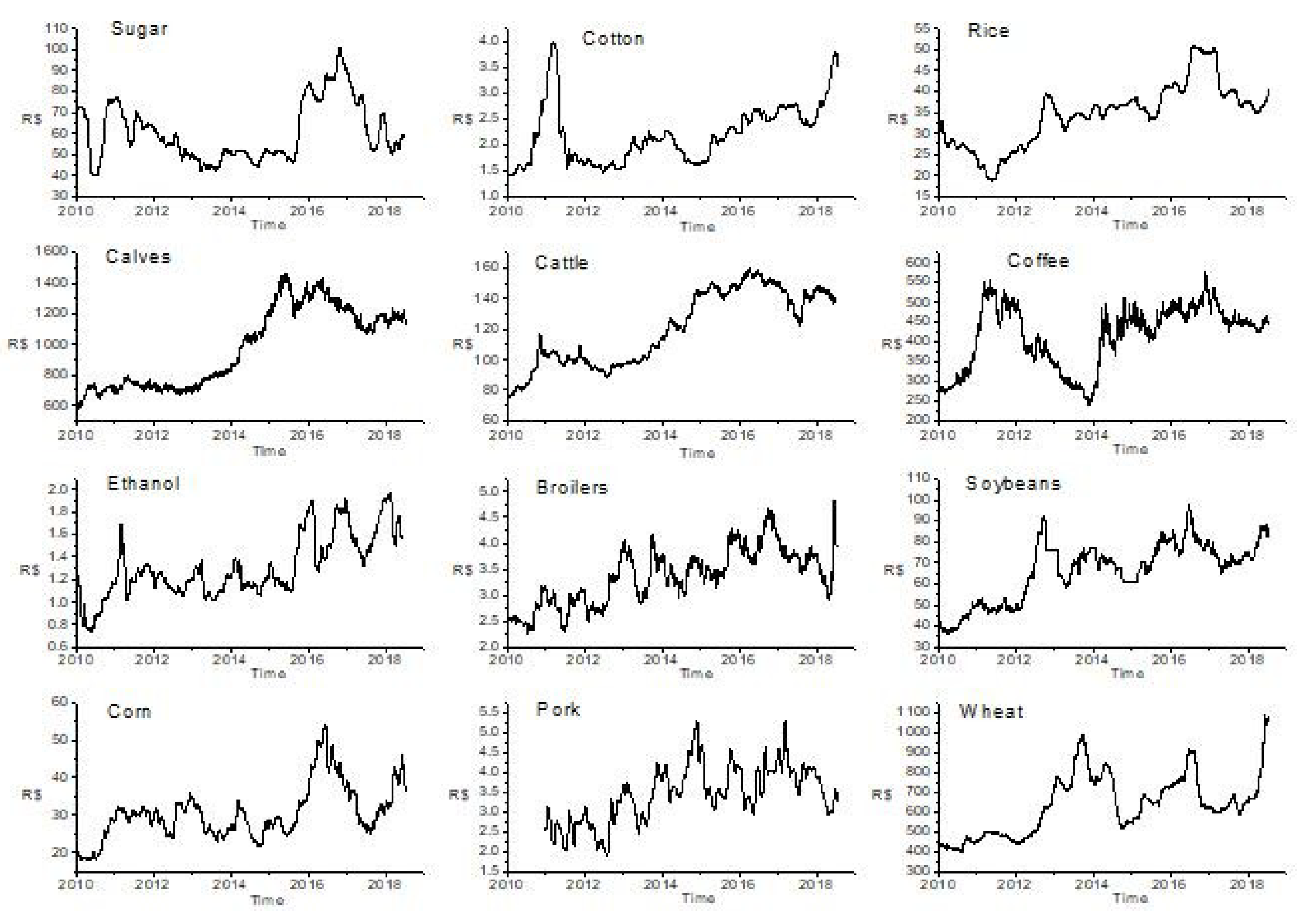
| Name | Currency (Brazilian Real–R$)/ Unit of Measure |
|---|---|
| Sugar | R$/bag of 50 kg |
| Cotton | R$/pound (0.453597 kg) |
| Rice | R$/bag of 50 kg |
| Calves | R$/head |
| Cattle | R$/15 kg |
| Coffee | R$/bag of 60 kg |
| Ethanol | R$/liter |
| Broilers | R$/Kg |
| Corn | R$/bag of 60 kg |
| Soybeans | R$/bag of 60 kg |
| Pork | R$/Kg |
| Wheat | R$/Ton |
| d = 4 | d = 5 | |||||||
|---|---|---|---|---|---|---|---|---|
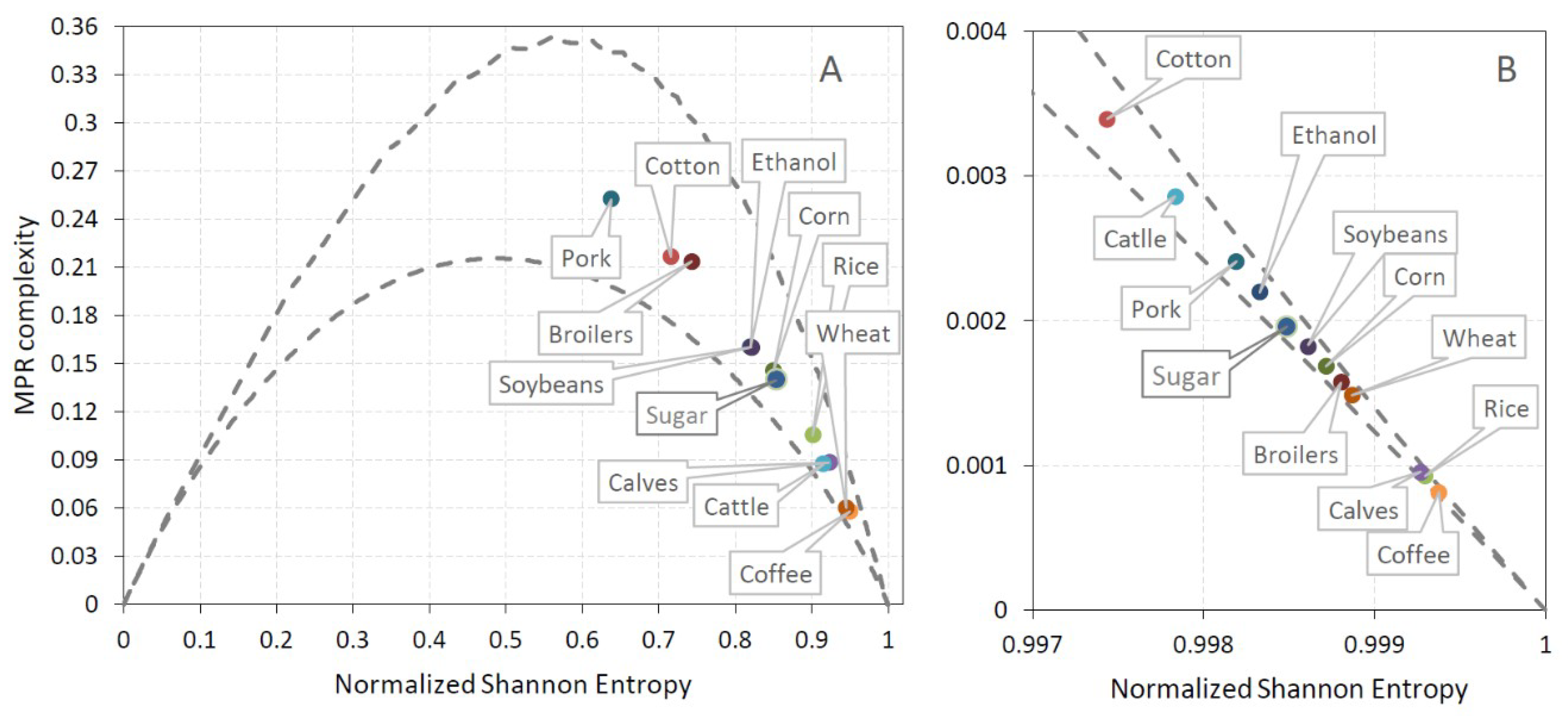
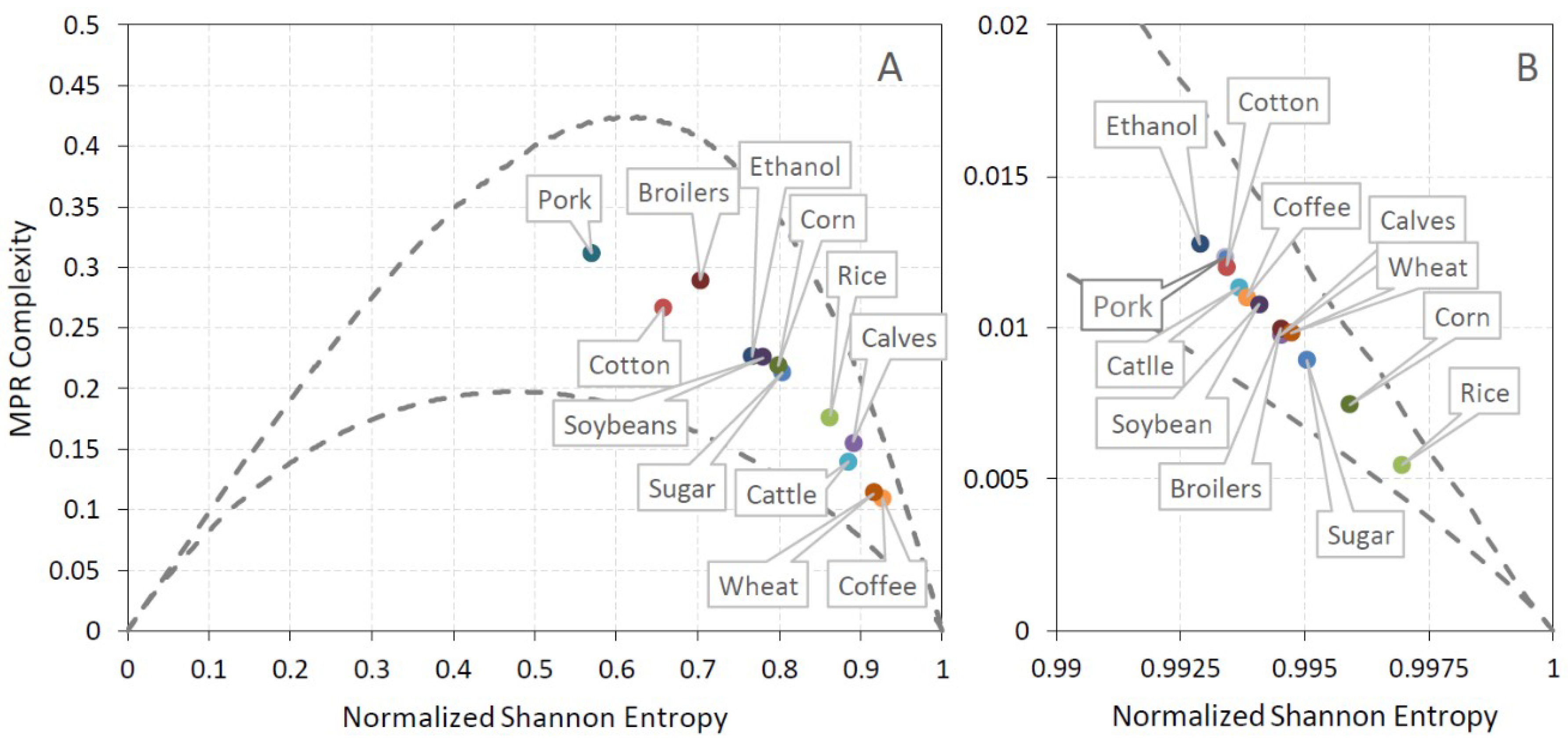
| Position | Commodities | PE | CP | Commodities | PE | CP | ||
| Coffee | 0.950 | 0.058 | 0.076 | Coffee | 0.926 | 0.109 | 0.132 | |
| Wheat | 0.946 | 0.060 | 0.081 | Wheat | 0.916 | 0.114 | 0.142 | |
| Calves | 0.923 | 0.088 | 0.117 | Cattle | 0.884 | 0.139 | 0.181 | |
| Cattle | 0.915 | 0.088 | 0.122 | Calves | 0.891 | 0.155 | 0.189 | |
| Rice | 0.901 | 0.106 | 0.144 | Rice | 0.862 | 0.176 | 0.224 | |
| Sugar | 0.854 | 0.140 | 0.202 | Sugar | 0.803 | 0.213 | 0.290 | |
| Corn | 0.850 | 0.146 | 0.209 | Corn | 0.798 | 0.219 | 0.298 | |
| Soybeans | 0.822 | 0.160 | 0.240 | Soybeans | 0.780 | 0.226 | 0.316 | |
| Ethanol | 0.820 | 0.161 | 0.241 | Ethanol | 0.766 | 0.227 | 0.326 | |
| Broilers | 0.744 | 0.214 | 0.334 | Broilers | 0.703 | 0.289 | 0.414 | |
| Cotton | 0.716 | 0.217 | 0.357 | Cotton | 0.657 | 0.267 | 0.434 | |
| Pork | 0.638 | 0.253 | 0.441 | Pork | 0.570 | 0.312 | 0.531 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Araujo, F.H.A.; Bejan, L.; Rosso, O.A.; Stosic, T. Permutation Entropy and Statistical Complexity Analysis of Brazilian Agricultural Commodities. Entropy 2019, 21, 1220. https://doi.org/10.3390/e21121220
de Araujo FHA, Bejan L, Rosso OA, Stosic T. Permutation Entropy and Statistical Complexity Analysis of Brazilian Agricultural Commodities. Entropy. 2019; 21(12):1220. https://doi.org/10.3390/e21121220
Chicago/Turabian Stylede Araujo, Fernando Henrique Antunes, Lucian Bejan, Osvaldo A. Rosso, and Tatijana Stosic. 2019. "Permutation Entropy and Statistical Complexity Analysis of Brazilian Agricultural Commodities" Entropy 21, no. 12: 1220. https://doi.org/10.3390/e21121220
APA Stylede Araujo, F. H. A., Bejan, L., Rosso, O. A., & Stosic, T. (2019). Permutation Entropy and Statistical Complexity Analysis of Brazilian Agricultural Commodities. Entropy, 21(12), 1220. https://doi.org/10.3390/e21121220






