Entropy Rate Estimation for English via a Large Cognitive Experiment Using Mechanical Turk
Abstract
1. Introduction
2. Entropy Rate Estimation
2.1. Entropy Rate and n-Gram Entropy
2.2. Shannon’s Method
2.3. Cover King’s Method
2.4. Summary of the Scales Used in Previous Studies
3. Cognitive Experiment Using Mechanical Turk
3.1. The Mechanical Turk Framework
3.2. Experimental Design
- The number of characters still available for use.
- The preceding characters.
- The set of incorrect characters already used.
3.3. Experimental Outcomes
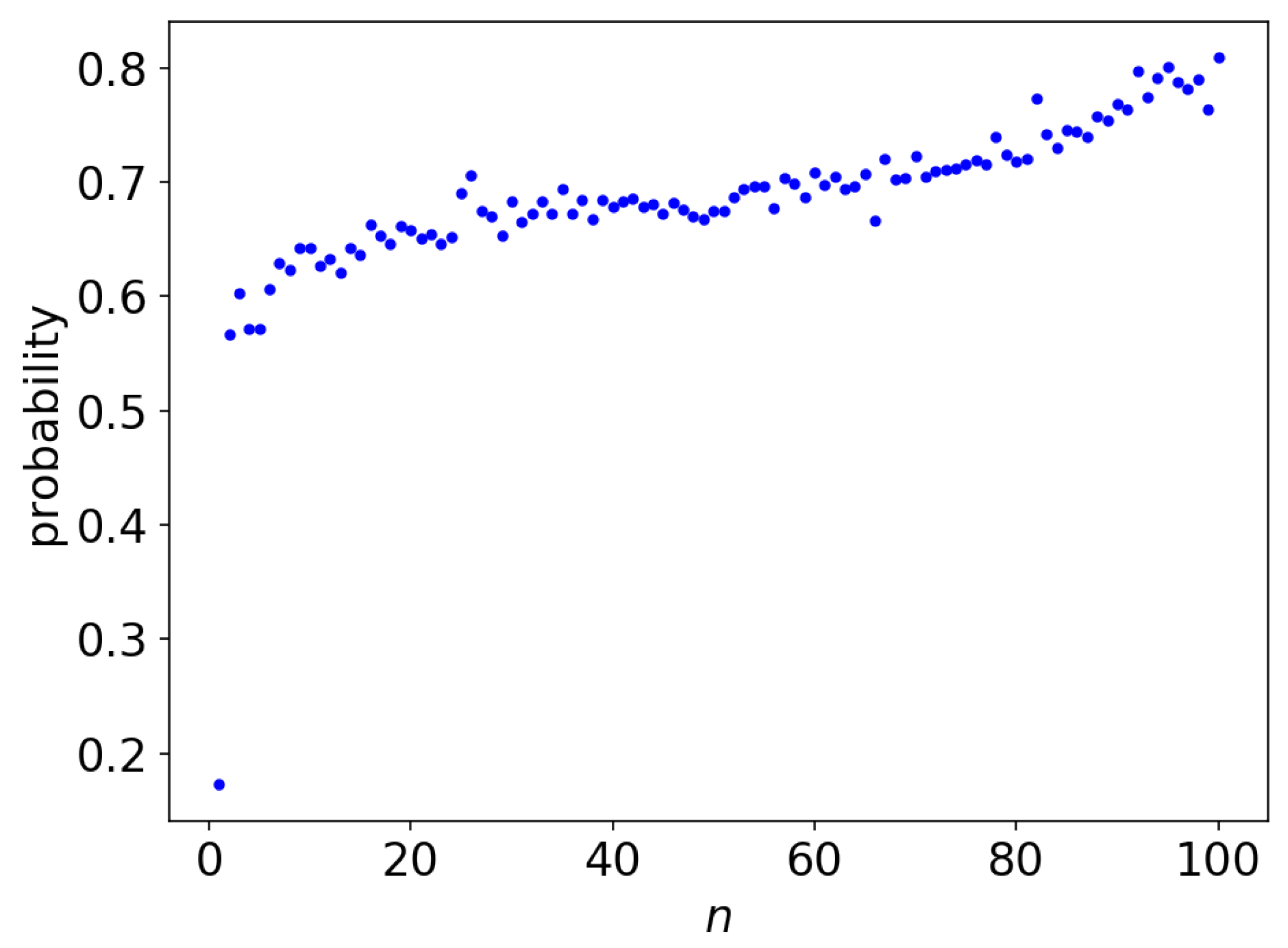
3.4. Human Prediction Accuracy with Respect to Context Length
3.5. The Datapoints of the Bounds for n
4. Extrapolation of the Bounds with an Ansatz Function
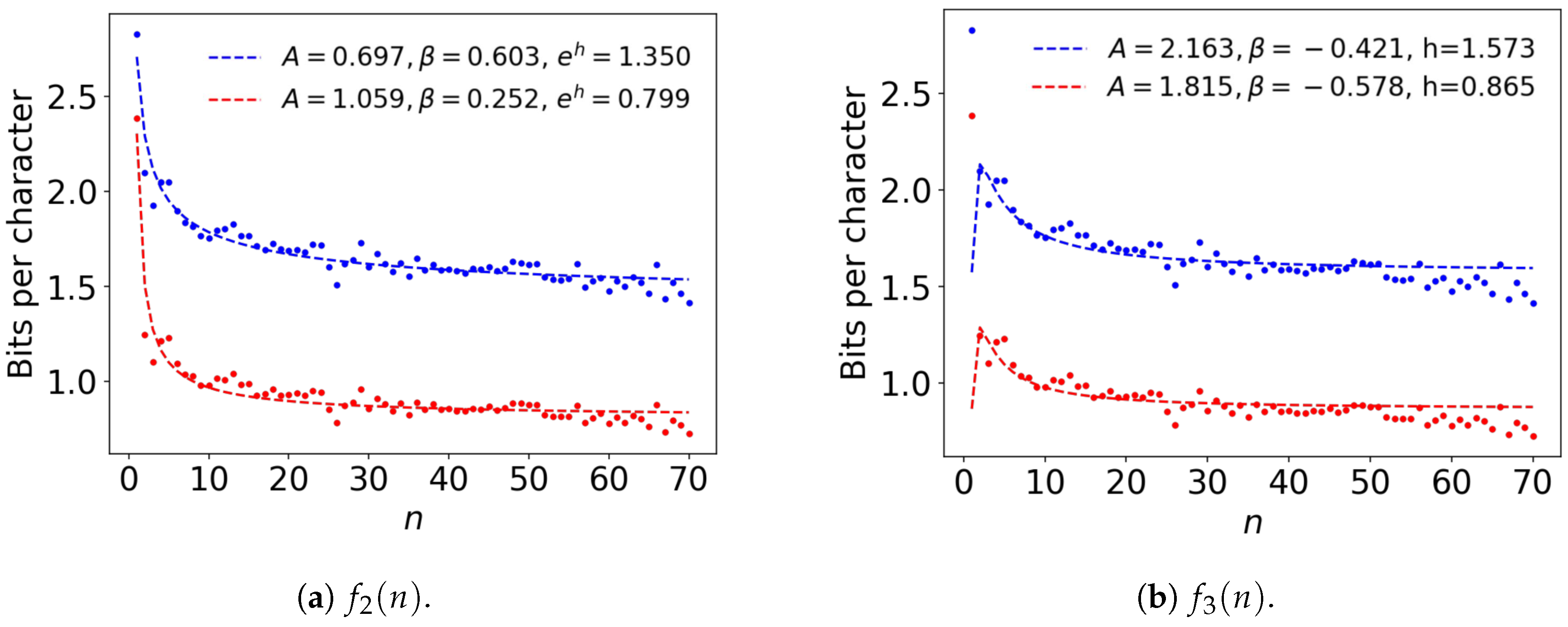
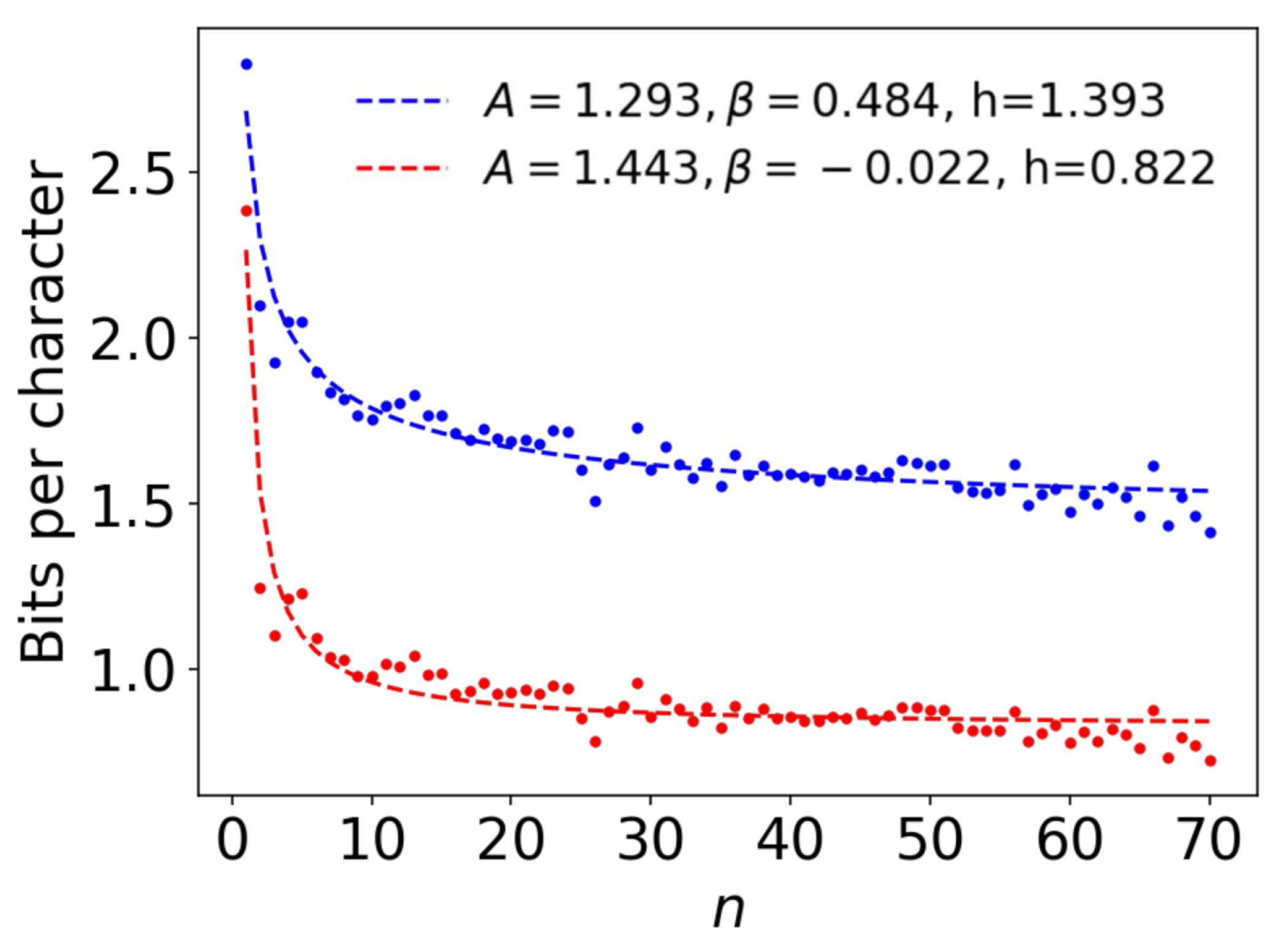
4.1. Ansatz Functions
4.2. Comparison among Ansatz Functions Using All Estimates
5. Analysis via the Bootstrap Technique
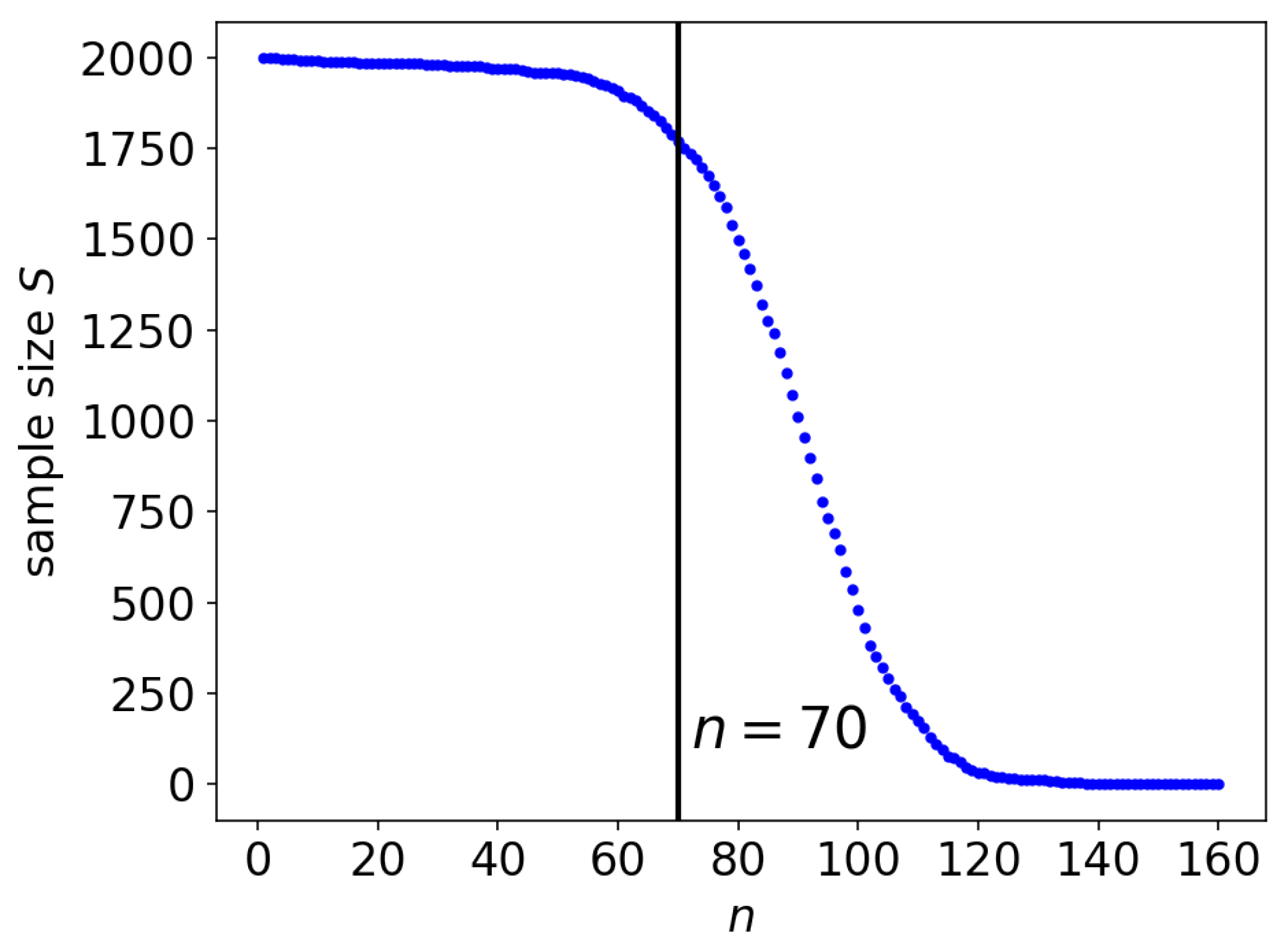
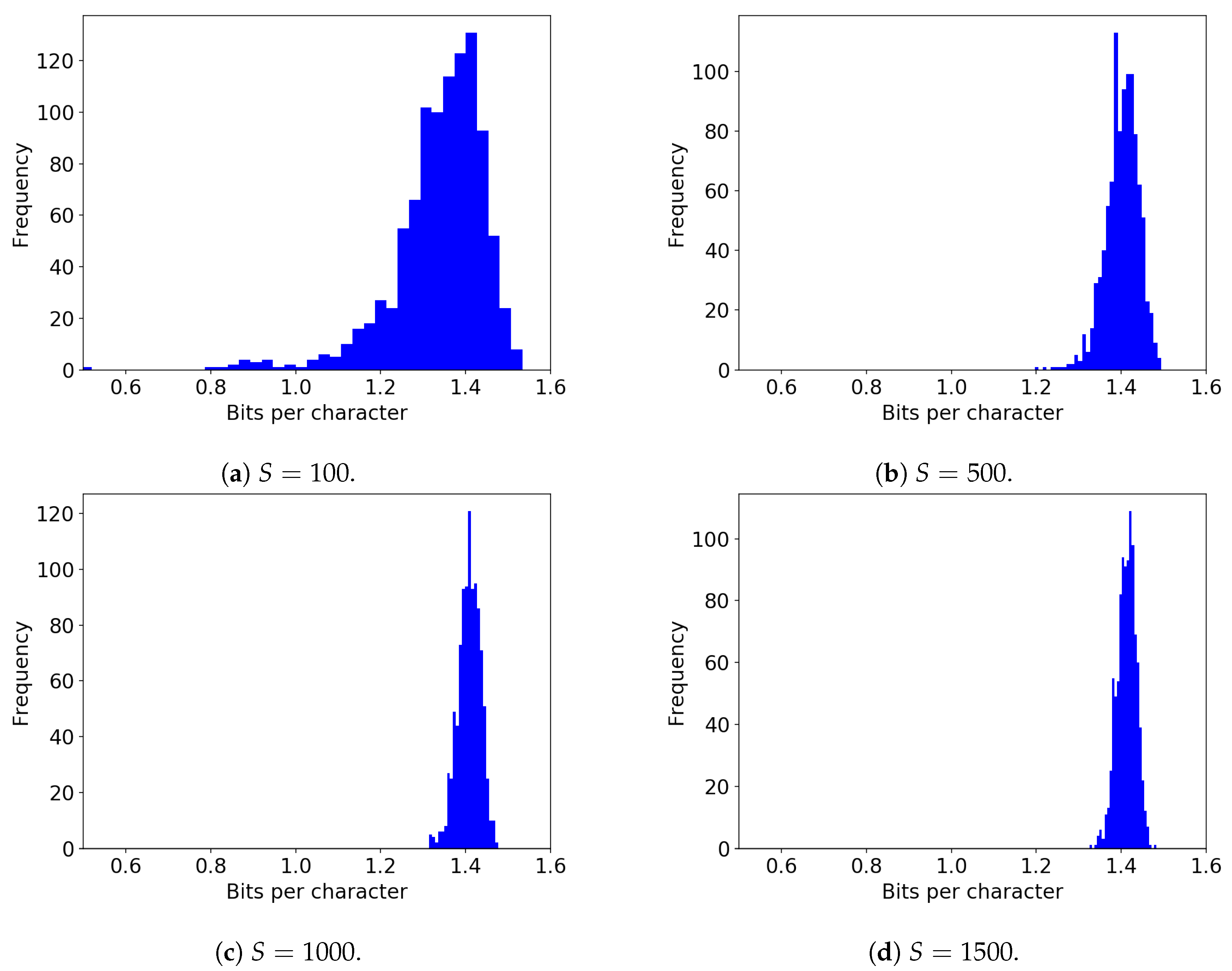
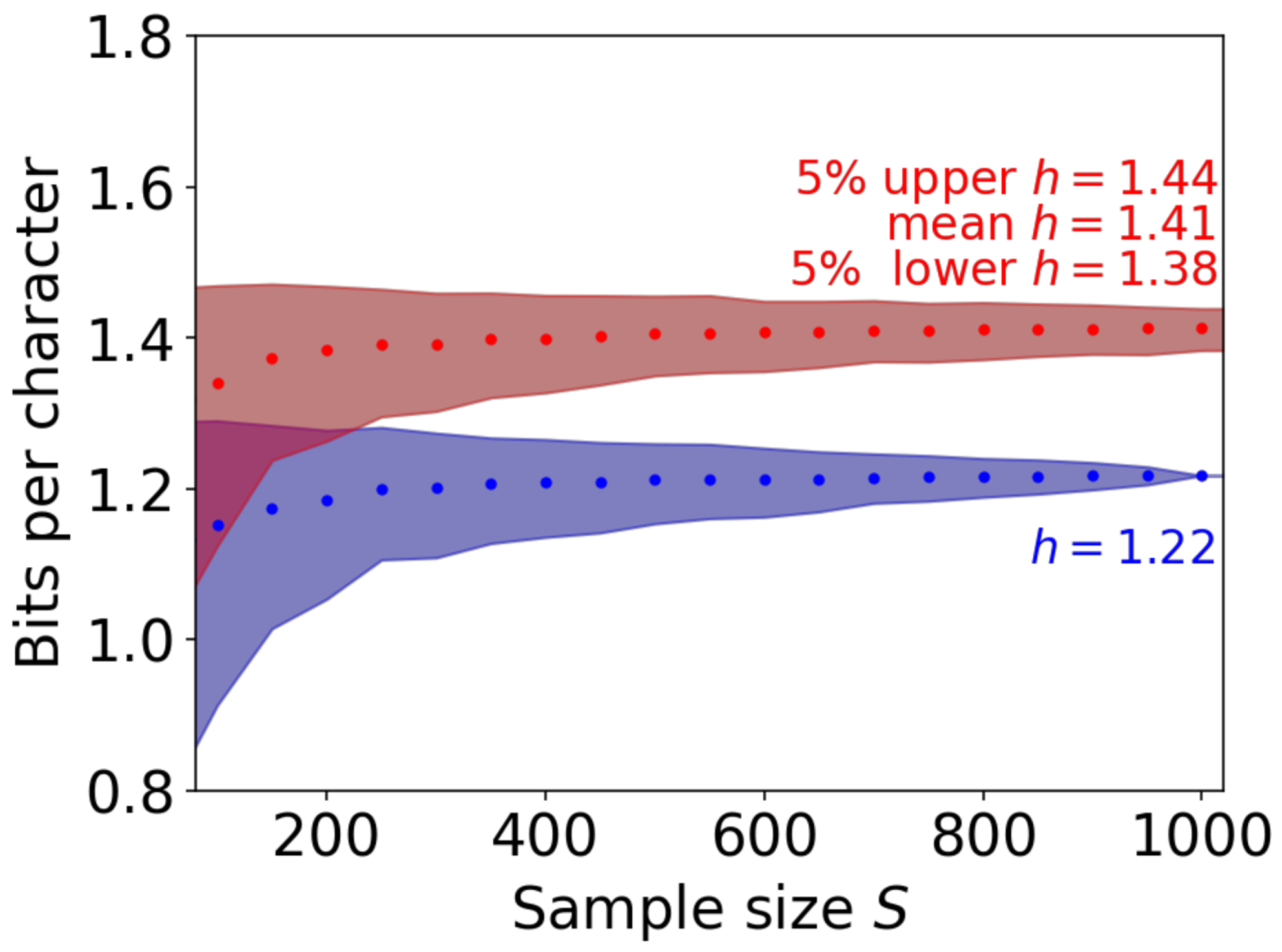
5.1. The Effect of the Sample Size
5.2. The Effect of Variation on Subjects’ Estimation Performances
6. Discussion
6.1. Computational versus Cognitive Methods
6.2. Application to Other Languages and Words
6.3. Nature of h Revealed by Cognitive Experimentation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Brown, P.F.; Pietra, S.A.D.; Pietra, V.J.D.; Lai, J.C.; Mercer, R.L. An Estimate of an Upper Bound for the Entropy of English. Comput. Linguist. 1992, 18, 31–40. [Google Scholar]
- Schümann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6, 414–427. [Google Scholar] [CrossRef] [PubMed]
- Takahira, R.; Tanaka-Ishii, K.; Dębowski, Ł. Entropy Rate Estimates for Natural Language—A New Extrapolation of Compressed Large-Scale Corpora. Entropy 2016, 18, 364. [Google Scholar] [CrossRef]
- Takahashi, S.; Tanaka-Ishii, K. Cross Entropy of Neural Language Models at Infinity—A New Bound of the Entropy Rate. Entropy 2018, 20, 839. [Google Scholar] [CrossRef]
- Manning, C.; Schutze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 2978–2988. [Google Scholar]
- Burton, N.G.; Licklider, J.C.R. Long-Range Constraints in the Statistical Structure of Printed English. Am. J. Psychol. 1955, 68, 650–653. [Google Scholar] [CrossRef] [PubMed]
- Jamison, D.; Jamison, K. A note on the entropy of partially-known languages. Inf. Control 1968, 12, 164–167. [Google Scholar] [CrossRef]
- Cover, T.M.; King, R.C. A Convergent Gambling Estimate of the Entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Moradi, H.; Grzymala-Busse, J.; Roberts, J. Entropy of English Text: Experiments with Humans and a Machine Learning System Based on Rough Sets. Inf. Sci. 1998, 104, 31–47. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kelly, J.L., Jr. A New Interpretation of Information Rate. Bell Syst. Tech. J. 1956, 35, 917–926. [Google Scholar] [CrossRef]
- Breiman, L. Optimal gambling systems for favorable games. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 65–78. [Google Scholar]
- Sorokin, A.; Forsyth, D. Utility data annotation with Amazon Mechanical Turk. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Berg, M.B.A.C.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Callison-Burch, C.; Dredze, M. Creating speech and language data with Amazon’s Mechanical Turk. In Proceedings of the NAACL HLT 2010 Workshop on Creating Speech and Language Data with Amazon’s Mechanical Turk, Los Angeles, CA, USA, 6 June 2010; pp. 1–12. [Google Scholar]
- Rajpurkar, P.; Zhang, J.; Lopyrev, K.; Liang, P. SQuAD: 100,000+ Questions for Machine Comprehension of Text. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–4 November 2016; pp. 2383–2392. [Google Scholar]
- Mason, W.; Suri, S. Conducting behavioral research on Amazon’s Mechanical Turk. Behav. Res. Methods 2012, 44, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Urbano, J.; Morato, M.M.; Martín, D. Crowdsourcing Preference Judgments for Evaluation of Music Similarity Tasks. In ACM SIGIR Workshop on Crowdsourcing for Search Evaluation; ACM: New York, NY, USA, 2010. [Google Scholar]
- Alonso, O.; Mizzaro, S. Using crowdsourcing for TREC relevance assessment. Inf. Process. Manag. Int. J. 2012, 48, 1053–1066. [Google Scholar] [CrossRef]
- Warby, S.C.; Wendt, S.L.; Welinder, P.; Munk, E.G.S.; Carrillo, O.; Sorensen, H.B.D.; Jennum, P.; Peppard, P.E.; Perona, P.; Mignot, E. Sleep-spindle detection: crowdsourcing and evaluating performance of experts, non-experts and automated methods. Nat. Methods 2014, 11, 385–392. [Google Scholar] [CrossRef] [PubMed]
- Hilberg, W. Der bekannte Grenzwert der redundanzfreien Information in Texten-eine Fehlinterpretation der Shannonschen Experimente? Frequenz 1990, 44, 243–248. [Google Scholar] [CrossRef]
- Genzel, D.; Charniak, E. Entropy Rate Constancy in Text. In Proceedings of the 40th Annual Meeting on Association for Computational Linguistics, Philadelphia, PA, USA, 7–12 June 2002; pp. 199–206. [Google Scholar]
- Levy, R.; Jaeger, T.F. Speakers optimize information density through information density through syntactic reduction. In Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 849–856. [Google Scholar]
- Berger, T. Distortion Theory for Sources with Abstract Alphabets and Memory. Inf. Control 1968, 13, 254–273. [Google Scholar] [CrossRef]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. Int. Conv. Rec. 1959, 7, 142–163. [Google Scholar]

| Total Number | Number of | Number of | Max n | Number of | |
|---|---|---|---|---|---|
| of Samples | Subjects | Phrases | for a Session | Sample Per n | |
| Shannon [1] | 1600 | 1 | 100 | 100 | 100 |
| Jamison and Jamison [9] | 360 | 2 | 50 and 40 | 100 | 50 and 40 |
| Cover and King [10] No.1 | 440 | 2 | 1 | 220 | 2 |
| Cover and King [10] No.2 | 900 | 12 | 1 | 75 | 12 |
| Moradi et al. [11] No.1 | 6400 | 1 | 100 | 64 | 100 |
| Moradi et al. [11] No.2 | 3200 | 8 | 400 | 32 | 100 |
| Our Experiment | 172,954 | 683 | 225 | 87.51 | 1954.86 |
| Rank | Word | Frequency | Two Subsequent Words | Frequency |
|---|---|---|---|---|
| 1 | market | 15 | interest rates | 4 |
| 2 | company | 13 | future contracts | 3 |
| 3 | investment | 11 | program trading | 3 |
| 4 | price | 11 | stock market | 3 |
| 5 | people | 11 | money managers | 3 |
| 6 | companies | 10 | same time | 2 |
| 7 | stock | 9 | wide variety | 2 |
| 8 | buy | 9 | time around | 2 |
| 9 | officials | 7 | higher dividends | 2 |
| 10 | growth | 7 | some firms | 2 |
| Sample Size S | Mean | 5% Upper | 5% Lower |
|---|---|---|---|
| 100 | 1.340 | 1.467 | 1.124 |
| 200 | 1.383 | 1.468 | 1.263 |
| 300 | 1.391 | 1.459 | 1.302 |
| 400 | 1.398 | 1.456 | 1.327 |
| 500 | 1.405 | 1.455 | 1.349 |
| 1000 | 1.412 | 1.438 | 1.383 |
| 1500 | 1.411 | 1.444 | 1.374 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, G.; Takahashi, S.; Tanaka-Ishii, K. Entropy Rate Estimation for English via a Large Cognitive Experiment Using Mechanical Turk. Entropy 2019, 21, 1201. https://doi.org/10.3390/e21121201
Ren G, Takahashi S, Tanaka-Ishii K. Entropy Rate Estimation for English via a Large Cognitive Experiment Using Mechanical Turk. Entropy. 2019; 21(12):1201. https://doi.org/10.3390/e21121201
Chicago/Turabian StyleRen, Geng, Shuntaro Takahashi, and Kumiko Tanaka-Ishii. 2019. "Entropy Rate Estimation for English via a Large Cognitive Experiment Using Mechanical Turk" Entropy 21, no. 12: 1201. https://doi.org/10.3390/e21121201
APA StyleRen, G., Takahashi, S., & Tanaka-Ishii, K. (2019). Entropy Rate Estimation for English via a Large Cognitive Experiment Using Mechanical Turk. Entropy, 21(12), 1201. https://doi.org/10.3390/e21121201





