Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet
Abstract
1. Introduction
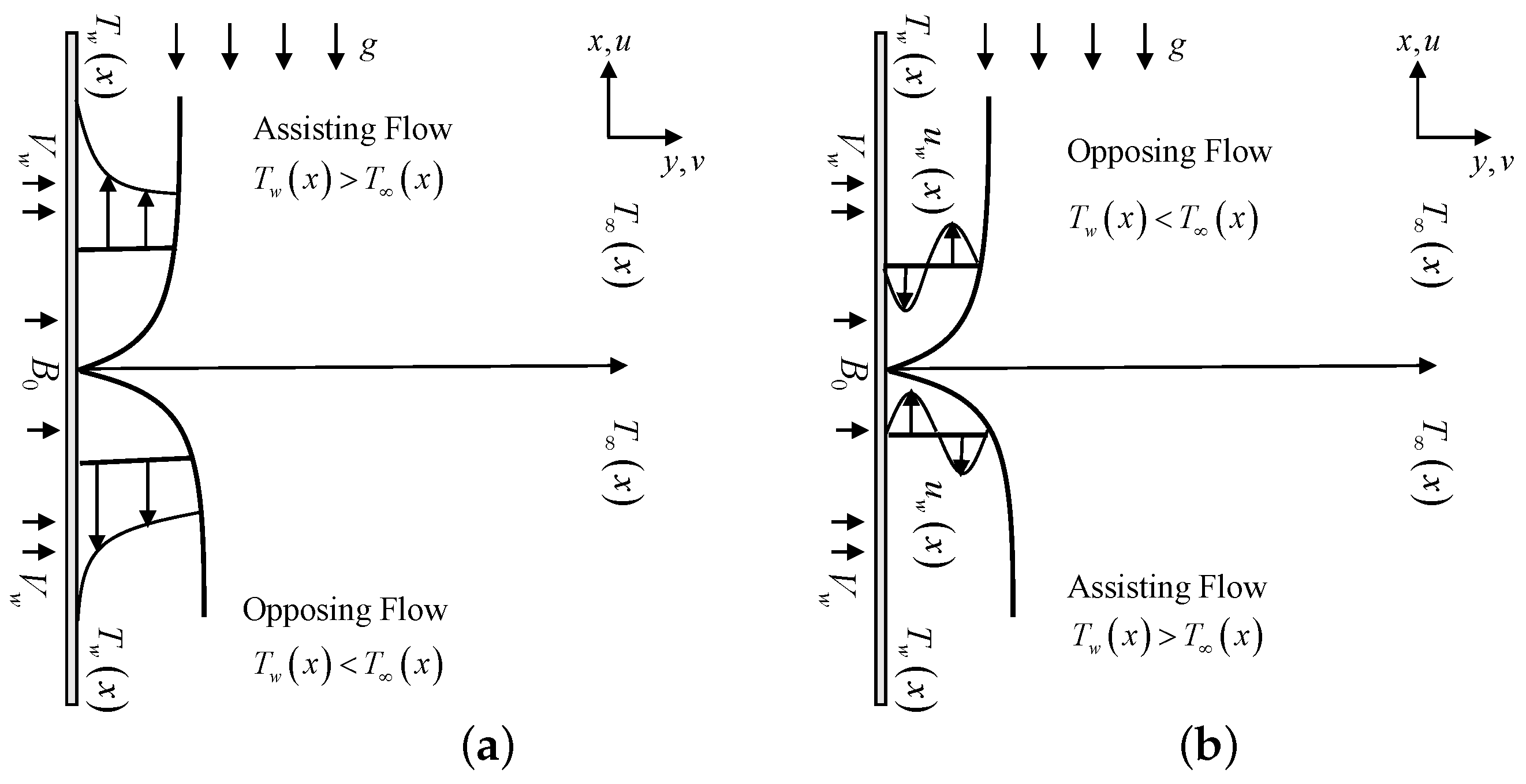
2. Mathematical Formulation
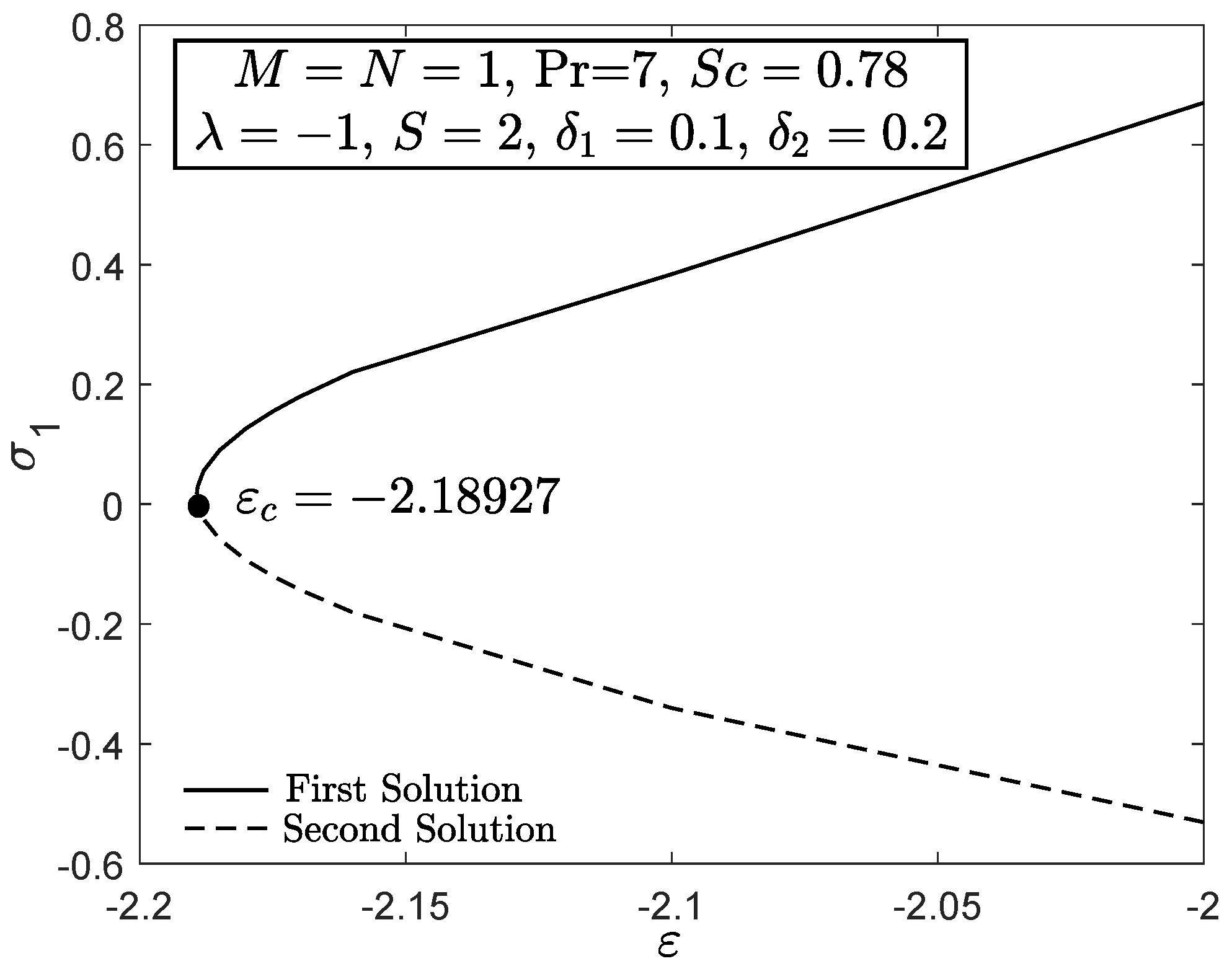
3. Stability Analysis
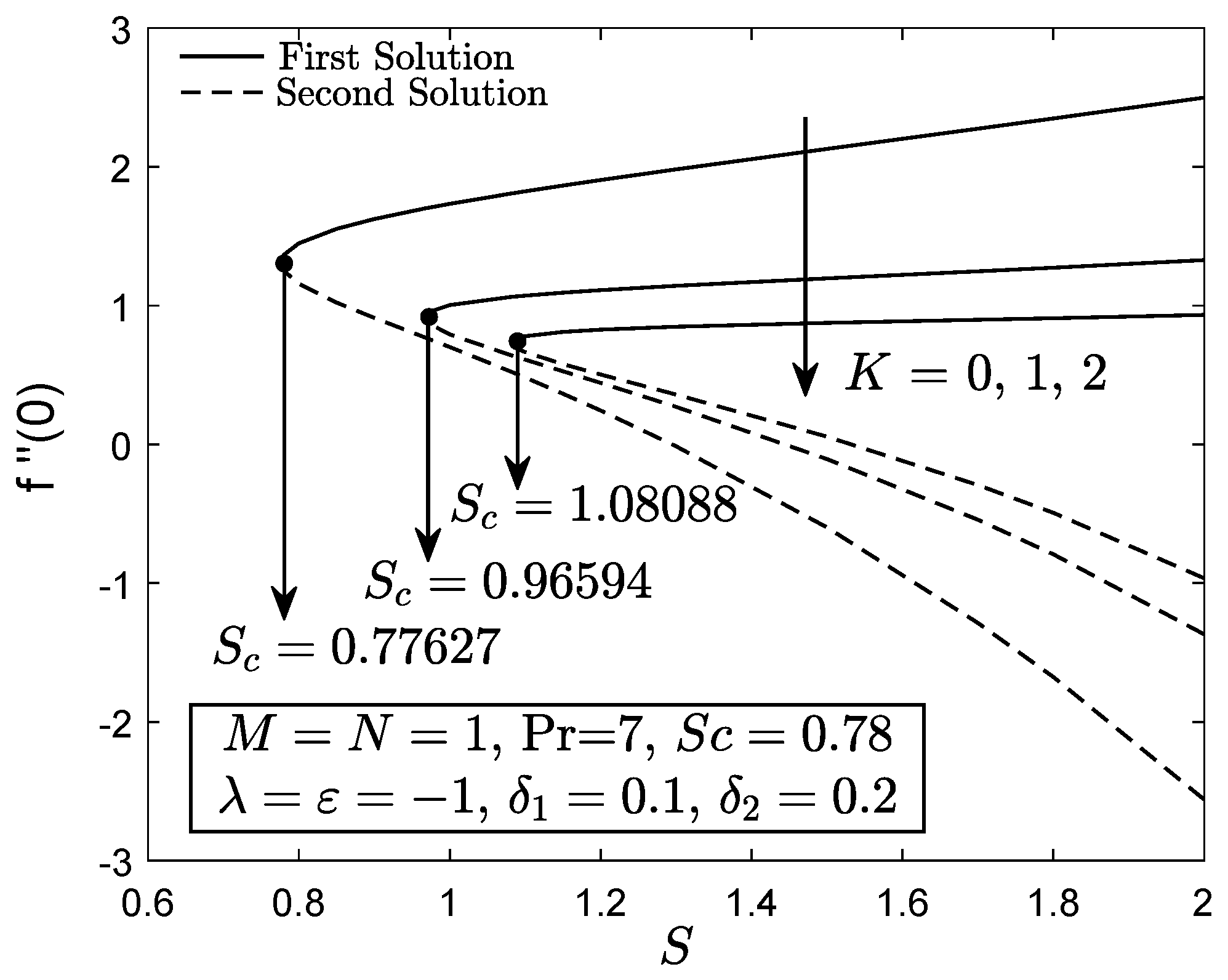
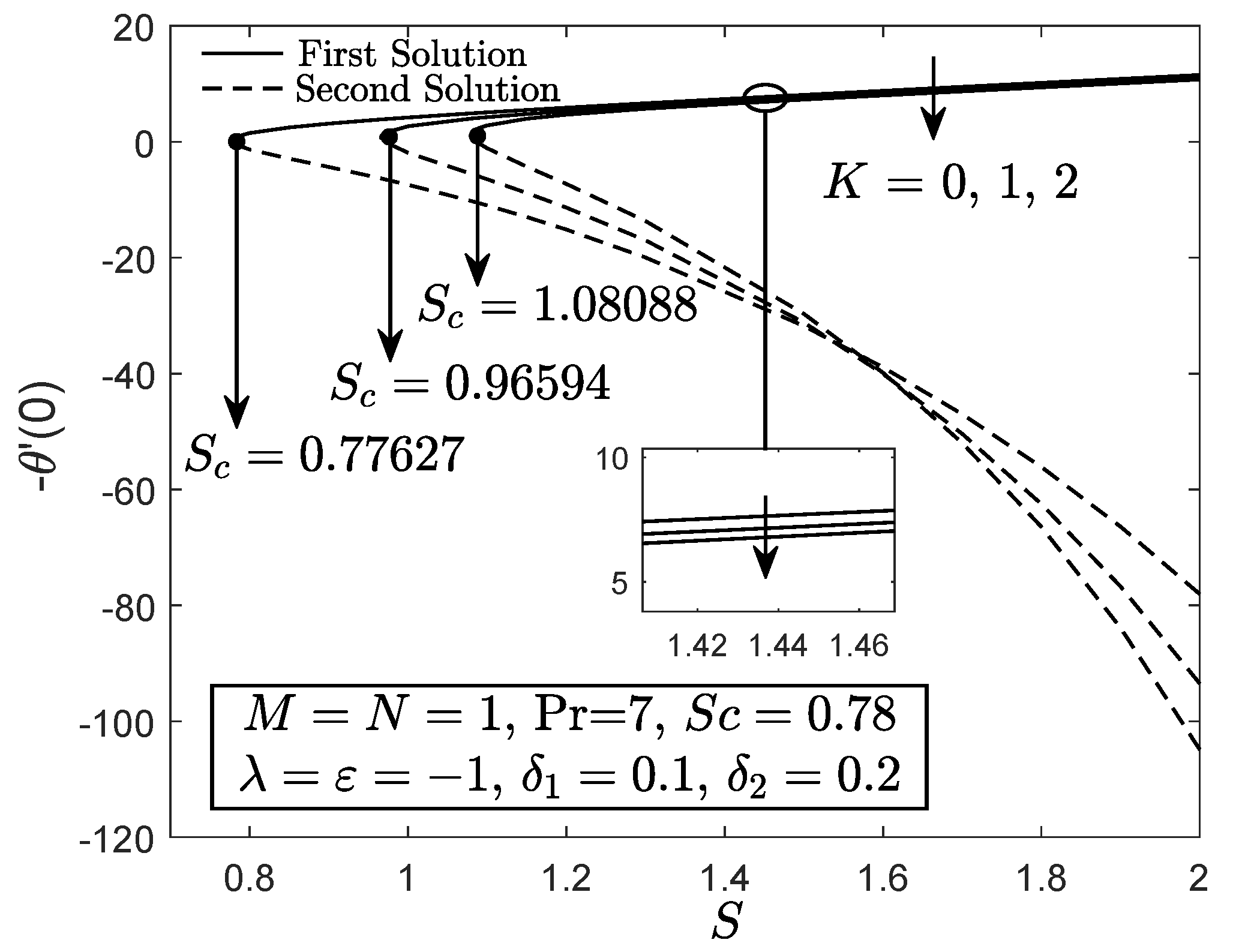
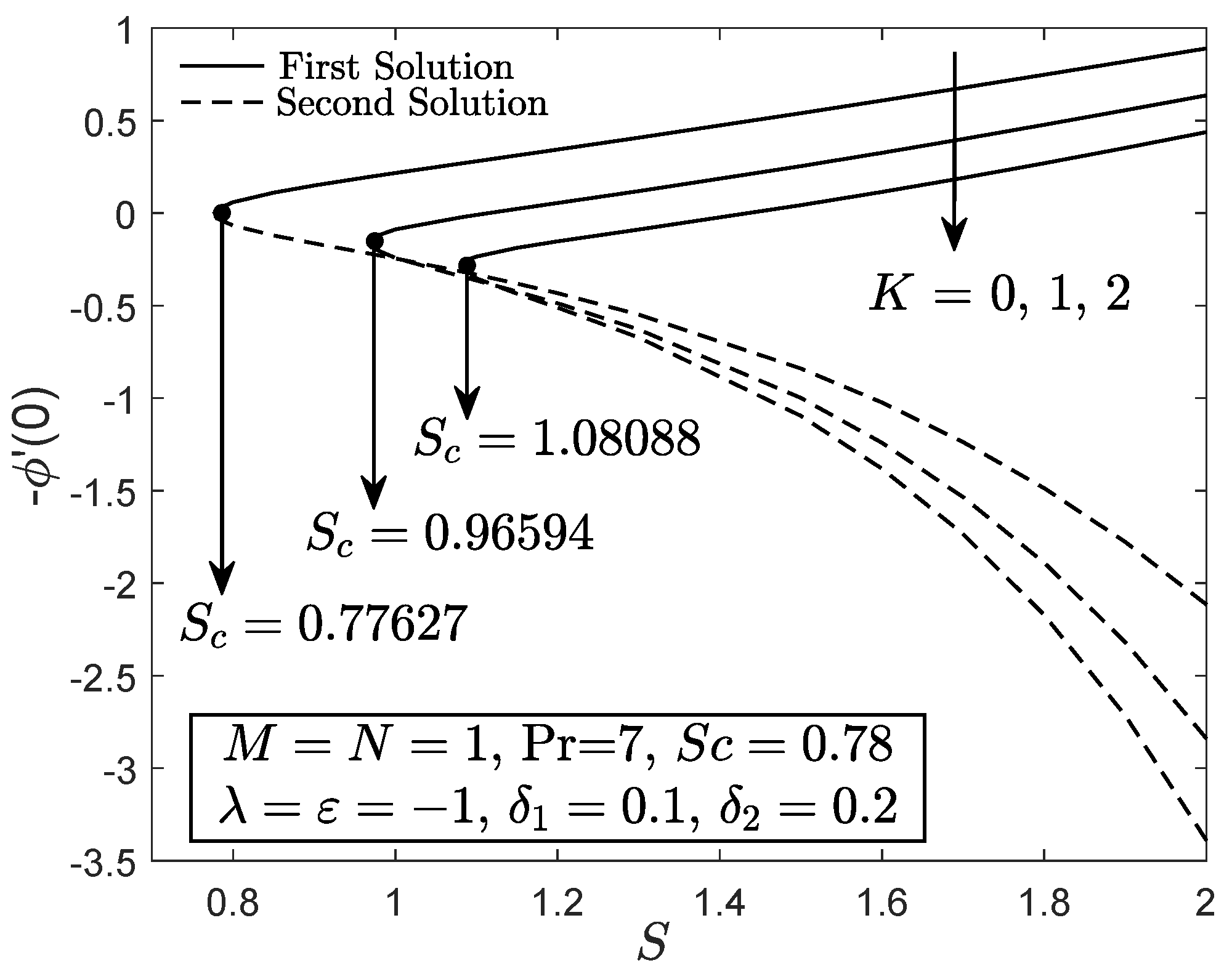
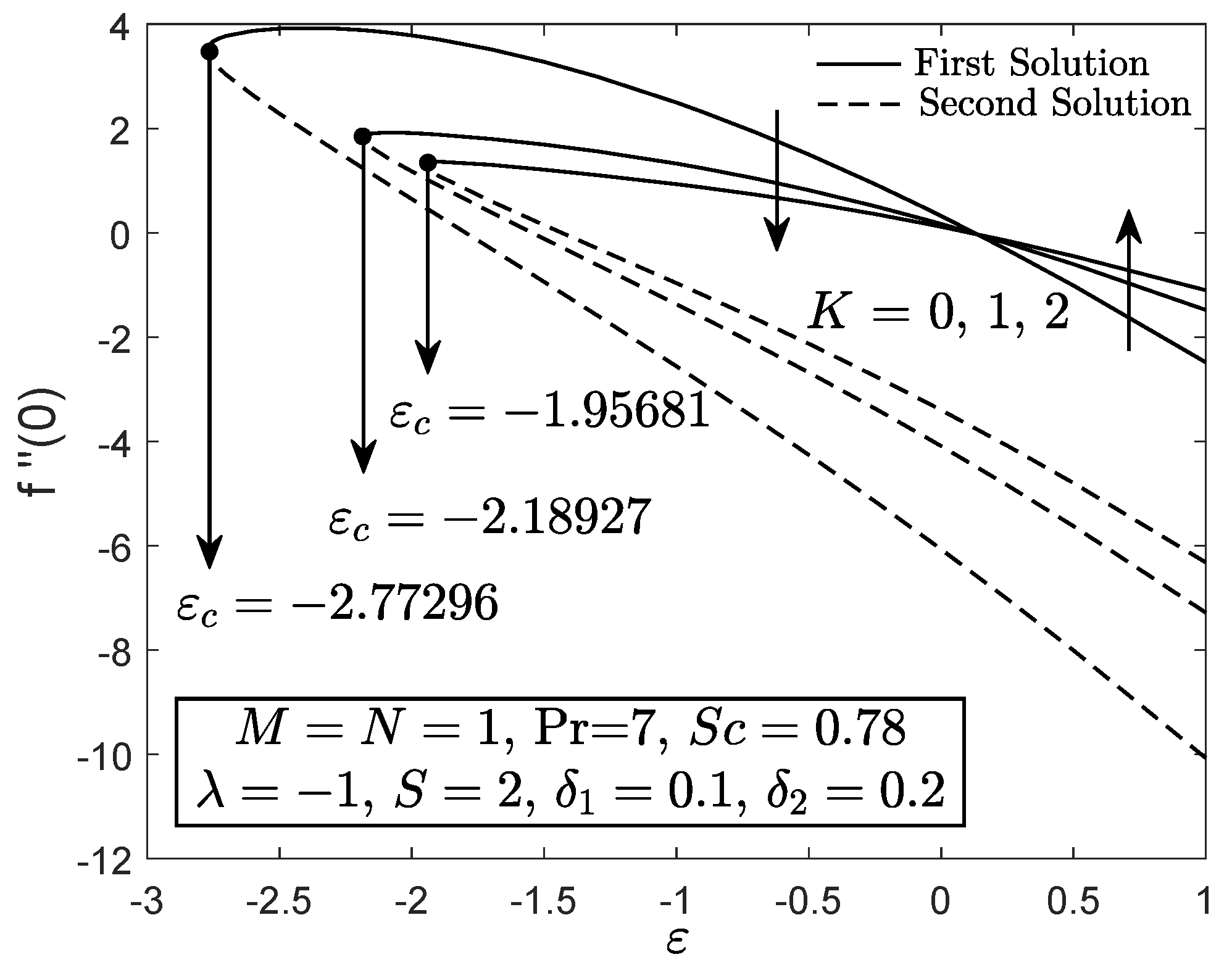
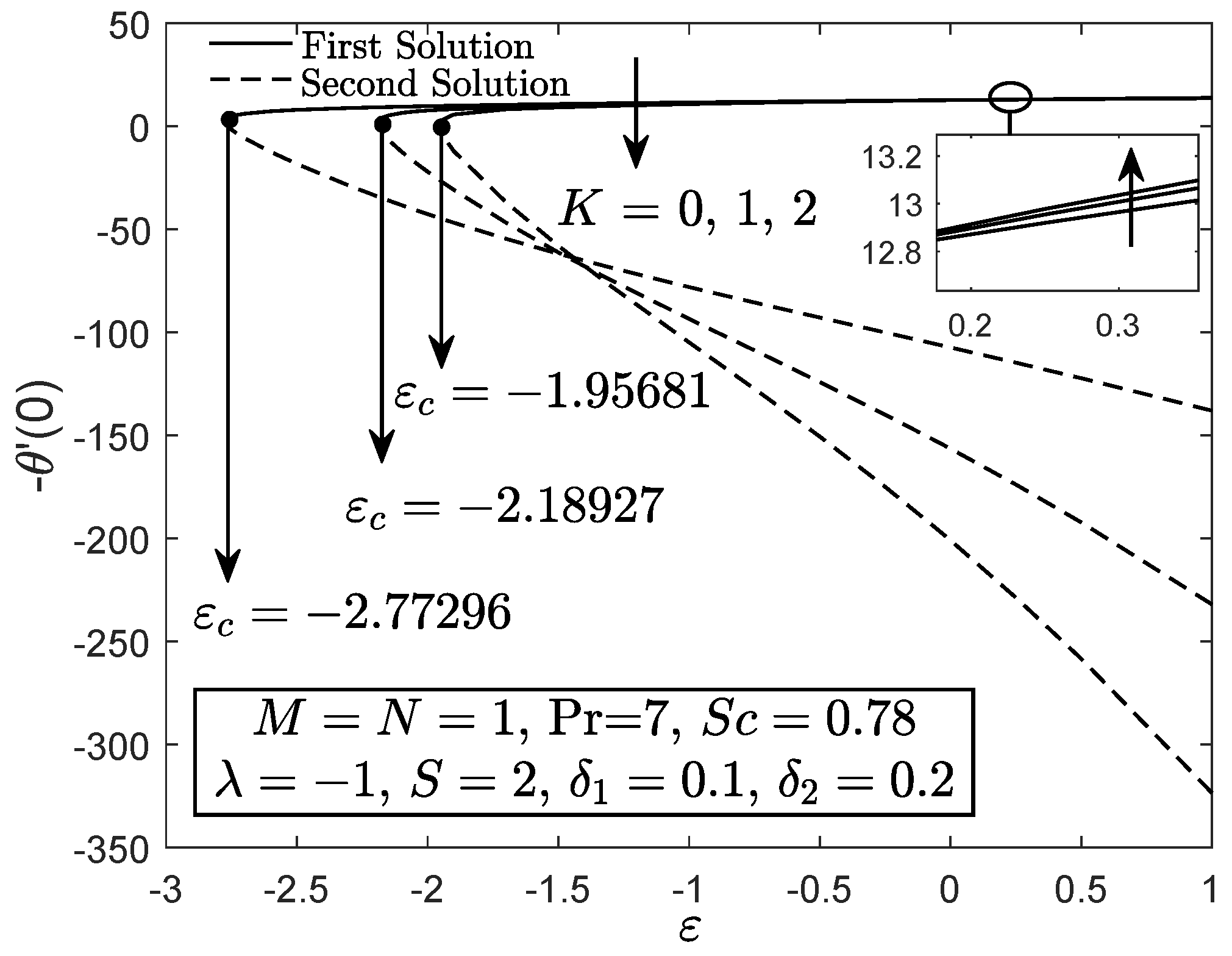
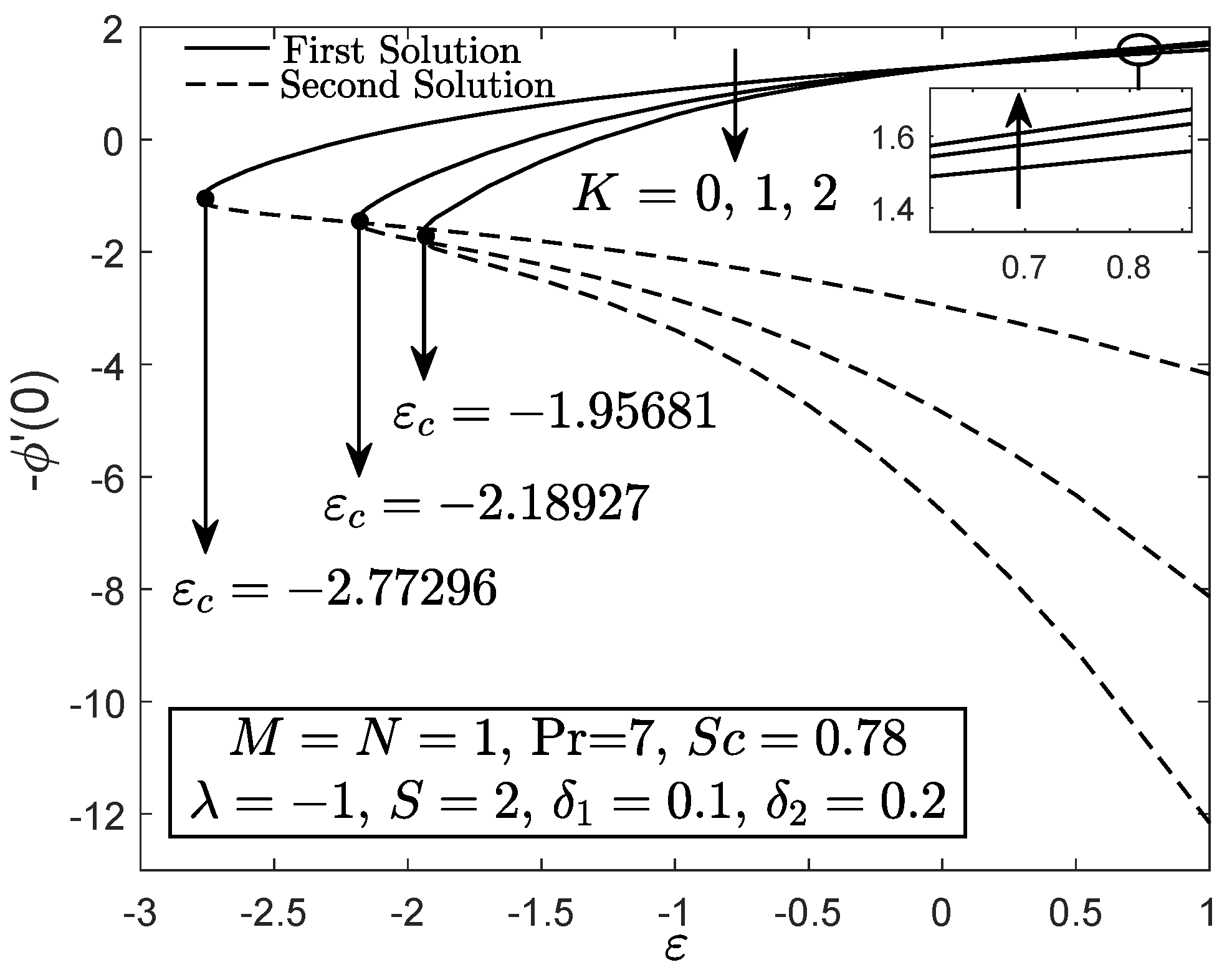
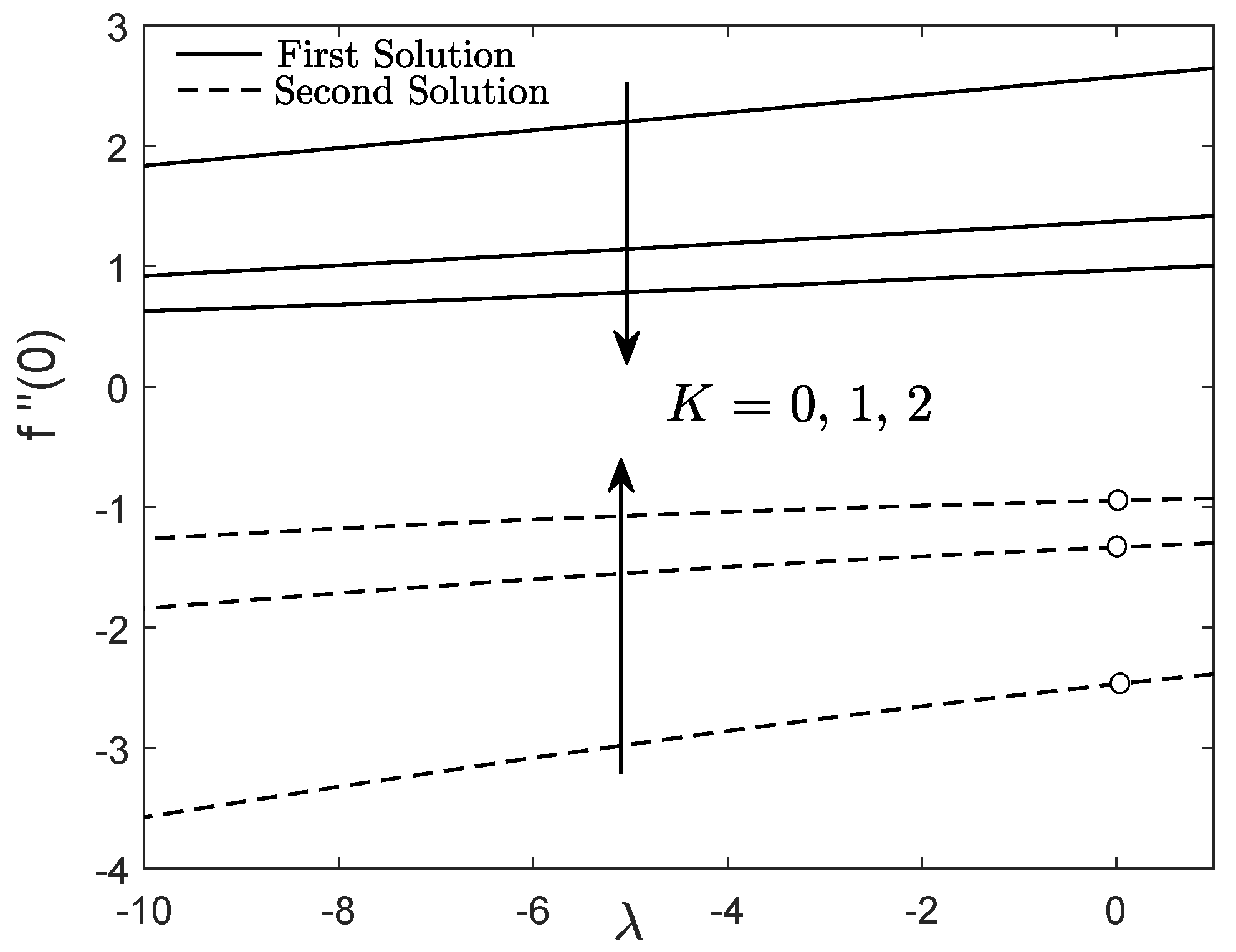
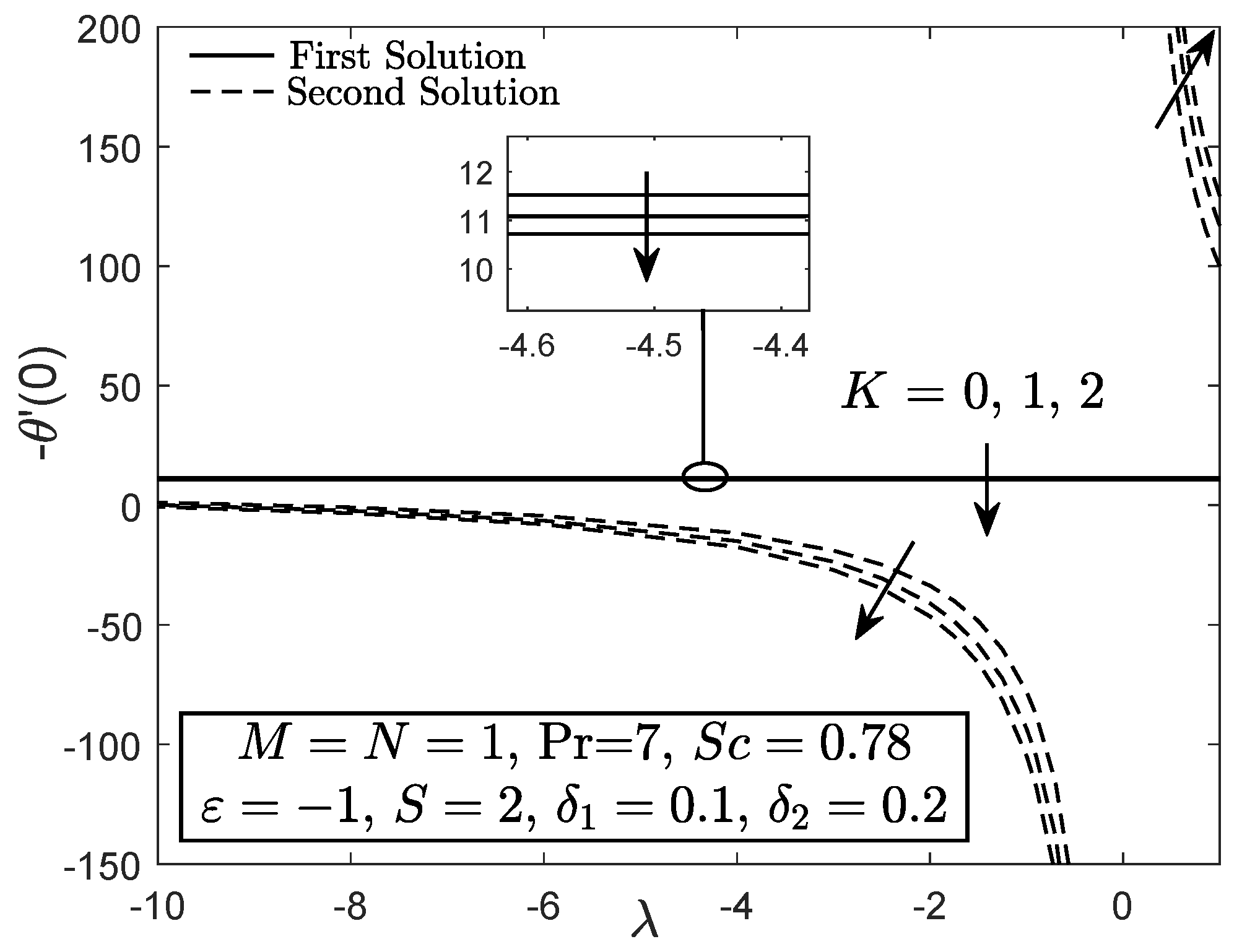
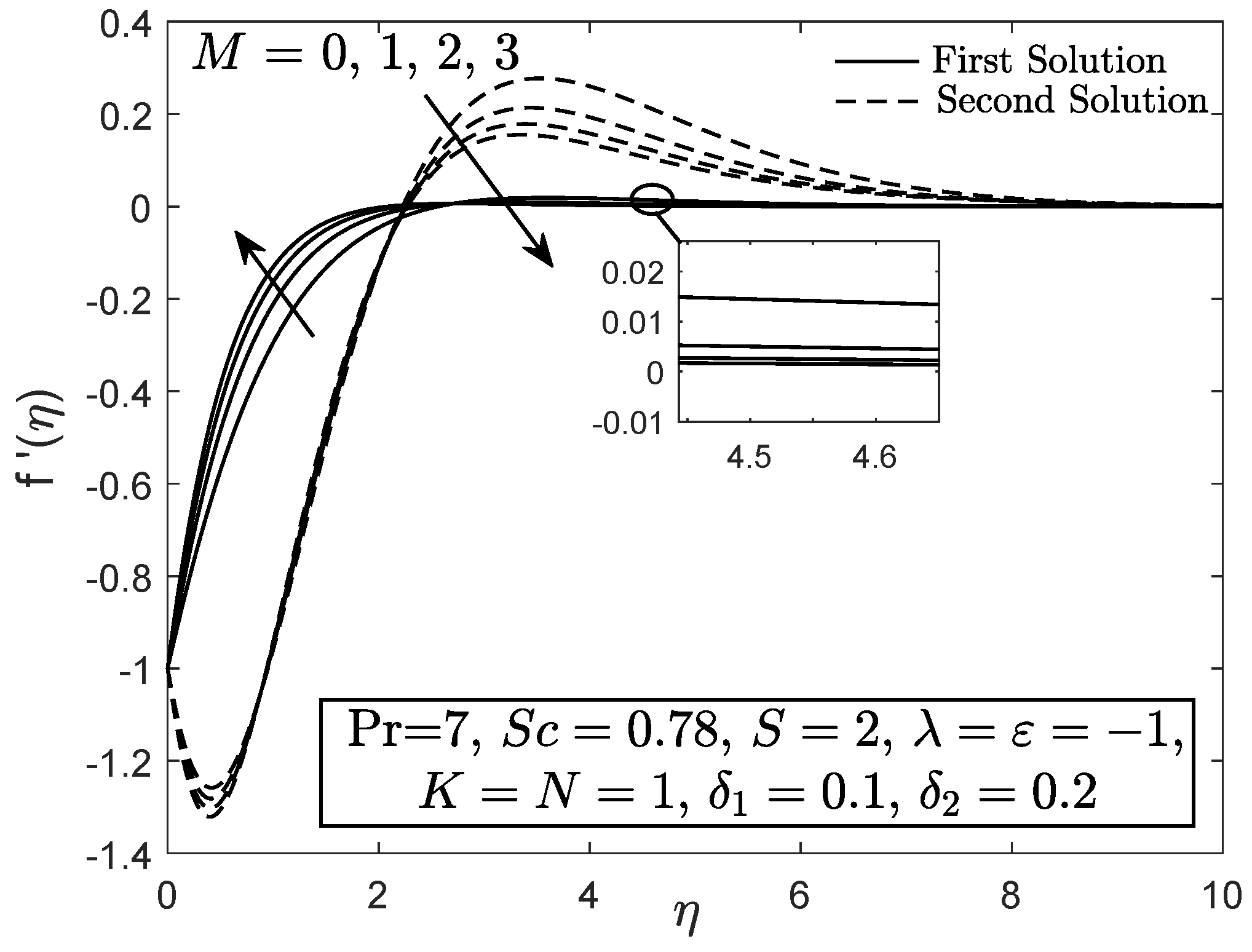
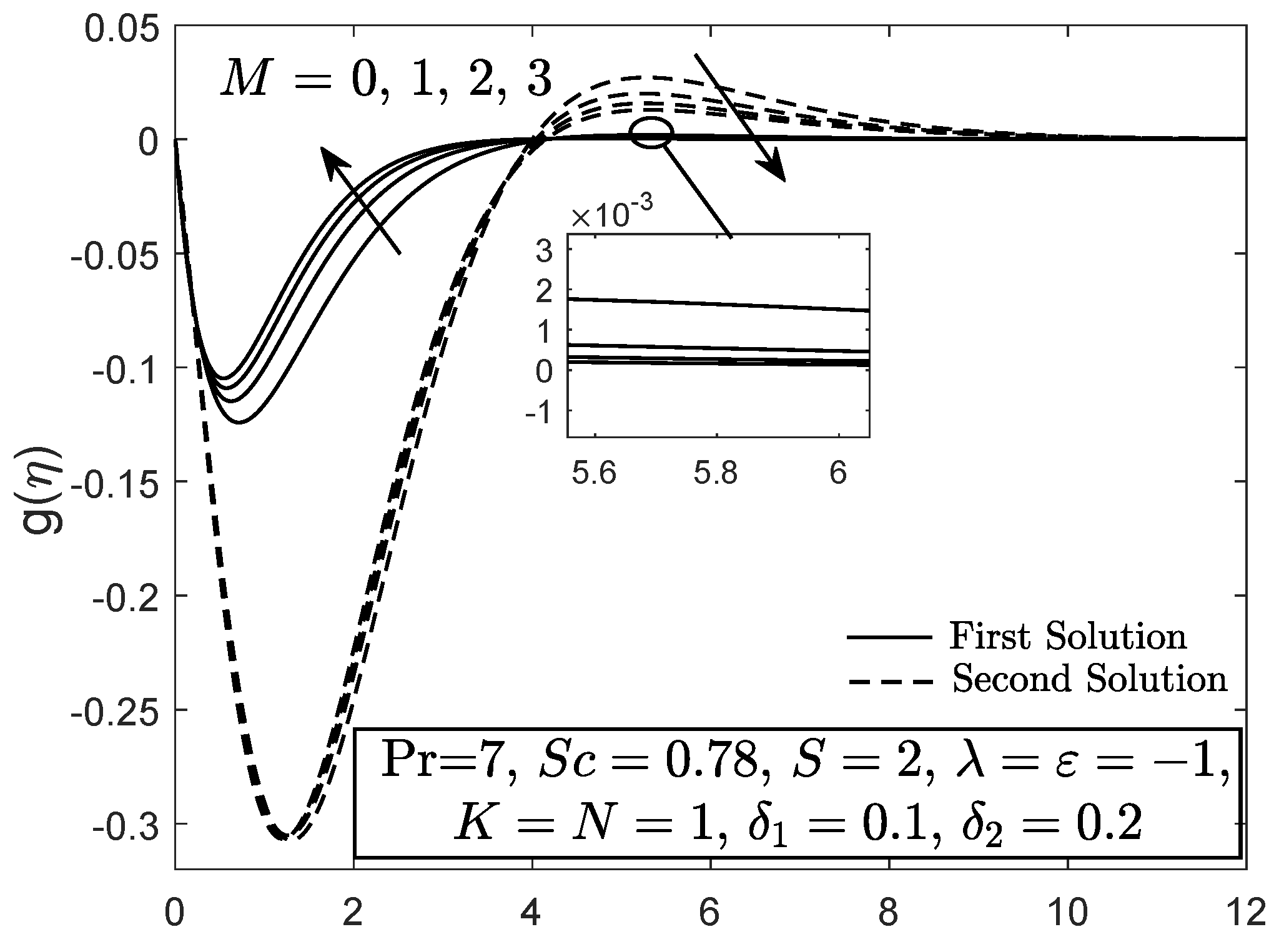
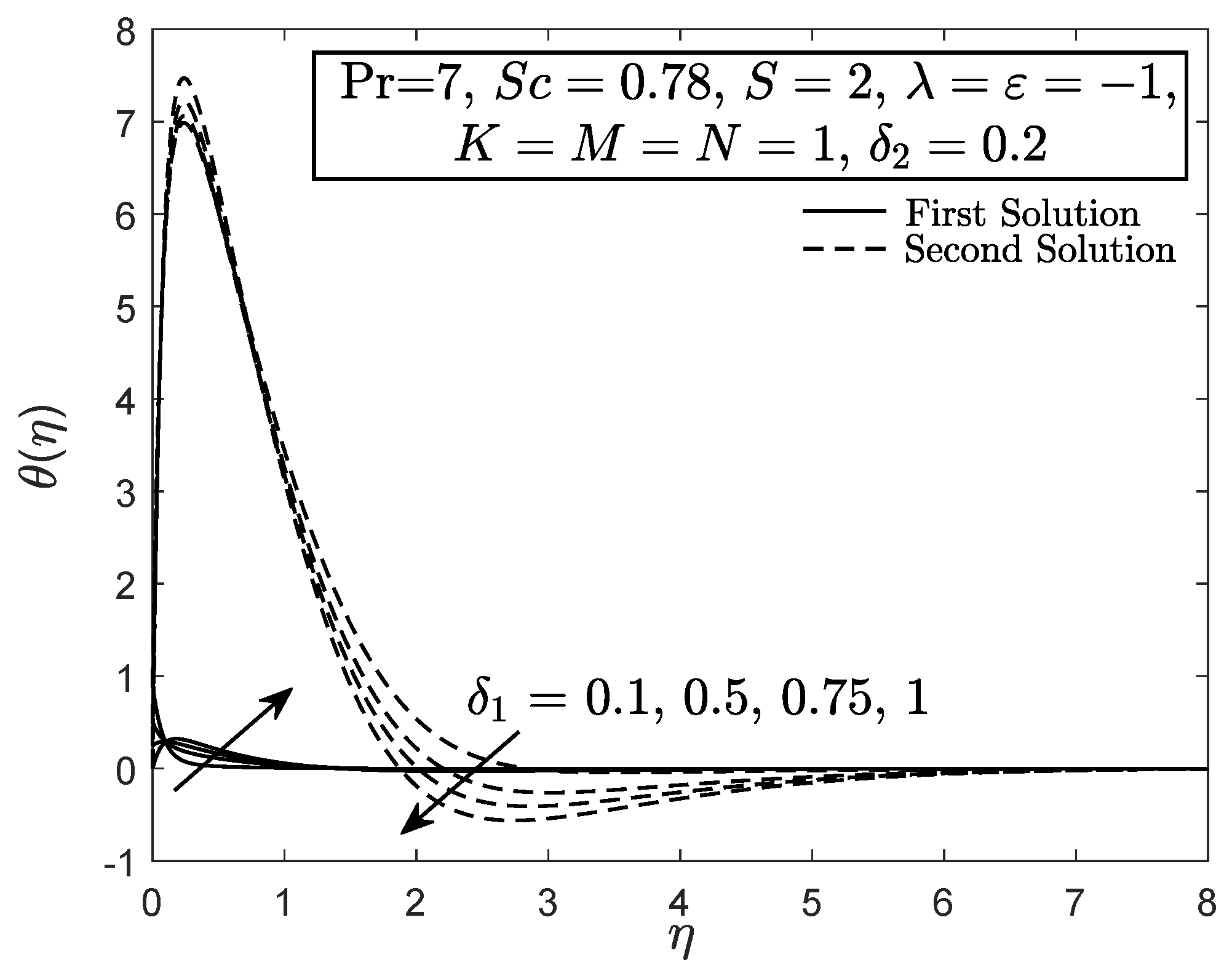
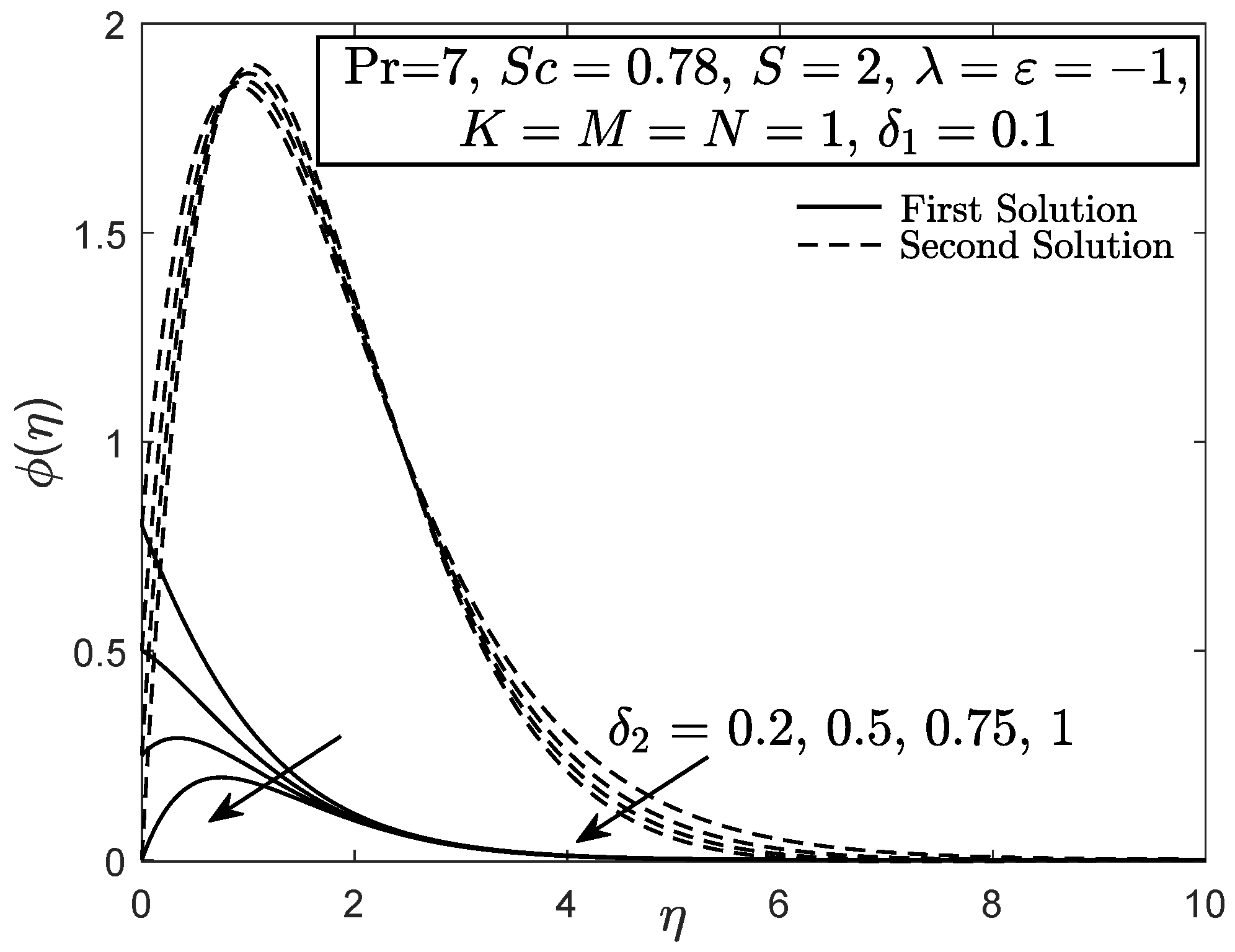
4. Results and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| magnitude of the magnetic field strength | ||
| initial ambient concentration and temperature | ||
| wall concentration and temperature | ||
| ambient concentration and temperature | ||
| K | material parameter | |
| M | magnetic parameter | |
| N | solutal buoyancy parameter | |
| Prandtl number | ||
| local Reynolds number | ||
| S | suction parameter | |
| T | fluid temperature | |
| stretching/shrinking velocity | ||
| t | time | s |
| velocities along the x-, y-directions, respectively | ||
| thermal diffusivity of the fluid | ||
| dimensionless temperature | ||
| mixed convection parameter | ||
| dynamic viscosity | ||
| kinematic viscosity | ||
| density of base fluid | ||
| unknown eigenvalue | ||
| magnetic permeability of the fluid | ||
| dimensionless time variable | ||
| ratio of the heat capacity of the nanoparticles to the base fluid | ||
| dimensionless nanoparticle volume fraction/concentration | ||
| microrotation or angular velocity |
References
- Gad-el-Hak, M. Flow control by suction. In Structure of Turbulence and Drag Reduction; Springer: Berlin/Heidelberg, Germany, 1990; pp. 357–360. [Google Scholar]
- Beck, N.; Landa, T.; Seitz, A.; Boermans, L.; Liu, Y.; Radespiel, R. Drag reduction by laminar flow control. Energies 2018, 11, 252. [Google Scholar] [CrossRef]
- Arnold, B.; Lutz, T.; Krämer, E.; Rautmann, C. Wind-Turbine Trailing-Edge Noise Reduction by Means of Boundary-Layer Suction. AIAA J. 2018, 56, 1843–1854. [Google Scholar] [CrossRef]
- Arunraj, R.; Logesh, K.; Balaji, V.; Ravichandran, T.; Yuvashree, G.K. Experimental investigation of lift enhancement by suction-assisted delayed separation of the boundary layer on NACA 0012 airfoil. Int. J. Ambient Energy 2019, 40, 243–247. [Google Scholar] [CrossRef]
- Miklavčič, M.; Wang, C. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Ellahi, R.; Rahman, S.U.; Nadeem, S.; Akbar, N.S. Influence of heat and mass transfer on micropolar fluid of blood flow through a tapered stenosed arteries with permeable walls. J. Comput. Theor. Nanosci. 2014, 11, 1156–1163. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Haroun, M.H.; El Kot, M.A. Influence of heat and chemical reactions on blood flow through an anisotropically tapered elastic arteries with overlapping stenosis. Appl. Math. 2012, 6, 281–292. [Google Scholar]
- Mekheimer, K.S.; El Kot, M.A. The micropolar fluid model for blood flow through a tapered artery with a stenosis. Acta Mech. Sin. 2008, 24, 637–644. [Google Scholar] [CrossRef]
- Bitla, P.; Iyengar, T.K. Pulsating flow of an incompressible micropolar fluid between permeable beds with an inclined uniform magnetic field. Eur. J. Mech. B-Fluid 2014, 48, 174–182. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A. Micropolar fluid flow over a shrinking sheet. Meccanica 2012, 47, 293–299. [Google Scholar] [CrossRef]
- Rosali, H.; Ishak, A.; Pop, I. Micropolar fluid flow towards a stretching/shrinking sheet in a porous medium with suction. Int. Commun. Heat Mass Trans. 2012, 39, 826–829. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. MHD Stagnation-Point Flow over a Stretching/Shrinking Sheet in a Micropolar Fluid with a Slip Boundary. Sains Malays. 2018, 47, 2907–2916. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef] [PubMed]
- Zaib, A.; Haq, R.U. Magnetohydrodynamics mixed convective flow driven through a static wedge including TiO2 nanomaterial with micropolar liquid: Similarity dual solutions via finite difference method. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2019, 233, 5813–5825. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. Int. J. 2015, 18, 738–745. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ashraf, M.; Rostami, B.; Rastegari, M.T.; Bashir, S. Mixed convection boundary-layer flow of a micropolar fluid towards a heated shrinking sheet by homotopy analysis method. Therm. Sci. 2016, 20, 21–34. [Google Scholar] [CrossRef]
- Zaib, A.; Bhattacharyya, K.; Shafie, S. Effect of partial slip on an unsteady MHD mixed convection stagnation-point flow of a micropolar fluid towards a permeable shrinking sheet. Alex. Eng. J. 2016, 55, 1285–1293. [Google Scholar]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Trans. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: Exact solutions. Int. J. Heat Mass Trans. 2017, 106, 127–134. [Google Scholar] [CrossRef]
- Patel, H.R.; Singh, R. Thermophoresis, Brownian motion and non-linear thermal radiation effects on mixed convection MHD micropolar fluid flow due to nonlinear stretched sheet in porous medium with viscous dissipation, joule heating and convective boundary condition. Int. Commun. Heat Mass Trans. 2019, 107, 68–92. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R. Effect of heat generation on mixed convection of micropolar Casson fluid over a stretching/shrinking sheet with suction. J. Phys. Conf. Ser. 2019, 1212, 012024. [Google Scholar] [CrossRef]
- Bouhal, T.; Fertahi, S.; Agrouaz, Y.; El Rhafiki, T.; Kousksou, T.; Jamil, A. Numerical modeling and optimization of thermal stratification in solar hot water storage tanks for domestic applications: CFD study. Sol. Energy 2017, 157, 441–455. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Fluid thermal stratification in a non-isothermal liquid hydrogen tank under sloshing excitation. Int. J. Hydrog. Energy 2018, 43, 22622–22635. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Mondal, I.C.; Gorla, R.S.R. Effects of thermal stratification on flow and heat transfer past a porous vertical stretching surface. Heat Mass Trans. 2012, 48, 915–921. [Google Scholar] [CrossRef]
- Khashiie, N.S.; Arifin, N.M.; Rashidi, M.M.; Hafidzuddin, E.H.; Wahi, N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2019, in press. [Google Scholar] [CrossRef]
- Khashiie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Dual stratified nanofluid flow past a permeable shrinking/stretching sheet using a non-Fourier energy model. Appl. Sci. 2019, 9, 2124. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Upendar, M. Effect of double stratification on MHD free convection in a micropolar fluid. J. Egypt. Math. Soc. 2013, 21, 370–378. [Google Scholar] [CrossRef]
- Mishra, S.R.; Pattnaik, P.K.; Dash, G.C. Effect of heat source and double stratification on MHD free convection in a micropolar fluid. Alex. Eng. J. 2015, 54, 681–689. [Google Scholar] [CrossRef]
- Rashad, A.M.; Abbasbandy, S.; Chamkha, A.J. Mixed convection flow of a micropolar fluid over a continuously moving vertical surface immersed in a thermally and solutally stratified medium with chemical reaction. Multidiscip. Model. Mater. Struct. 2019, 15, 133–155. [Google Scholar] [CrossRef]
- Koriko, O.K.; Animasaun, I.L.; Omowaye, A.J.; Oreyeni, T. The combined influence of nonlinear thermal radiation and thermal stratification on the dynamics of micropolar fluid along a vertical surface. Multidiscip. Model. Mater. Struct. 2019, 15, 133–155. [Google Scholar] [CrossRef]
- Sarojamma, G.; Lakshmi, R.V.; Sreelakshmi, K.; Vajravelu, K. Dual stratification effects on double-diffusive convective heat and mass transfer of a sheet-driven micropolar fluid flow. J. King Saud Univ.-Sci. 2018, in press. [Google Scholar] [CrossRef]
- Guram, G.S.; Smith, A.C. Stagnation flows of micropolar fluids with strong and weak interactions. Comp. Math. Appl. 1980, 6, 213–233. [Google Scholar] [CrossRef]
- Ahmadi, G. Self-similar solution of imcompressible micropolar boundary layer flow over a semi-infinite plate. Int. J. Eng. Sci. 1976, 14, 639–646. [Google Scholar] [CrossRef]
- Peddieson, J., Jr. An application of the micropolar fluid model to the calculation of a turbulent shear flow. Int. J. Eng. Sci. 1972, 10, 23–32. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Ali, F.M.; Bachok, N.; Nazar, R.; Pop, I. A Stability Analysis on Mixed Convection Boundary Layer Flow along a Permeable Vertical Cylinder in a Porous Medium Filled with a Nanofluid and Thermal Radiation. Appl. Sci. 2018, 8, 483. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Nazar, R.; Ali, F.M.; Bachok, N.; Pop, I. The effects of suction on forced convection boundary layer stagnation point slip flow in a darcy porous medium towards a shrinking sheet with presence of thermal radiation: A stability analysis. J. Porous Media 2018, 21, 623–636. [Google Scholar] [CrossRef]
- Yahaya, R.; Arifin, N.M.; Isa, S.S.P.M. Stability Analysis on Magnetohydrodynamic Flow of Casson Fluid over a Shrinking Sheet with Homogeneous-Heterogeneous Reactions. Entropy 2018, 20, 652. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M.; Pop, I. Stability analysis of mixed convection flow towards a moving thin needle in nanofluid. Appl. Sci. 2018, 8, 842. [Google Scholar] [CrossRef]
- Salleh, S.; Bachok, N.; Arifin, N.M.; Ali, F.; Pop, I. Magnetohydrodynamics flow past a moving vertical thin needle in a nanofluid with stability analysis. Energies 2018, 11, 3297. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Ishak, A.; Pop, I. Oblique stagnation slip flow of a micropolar fluid towards a stretching/shrinking surface: A stability analysis. Chin. J. Phys. 2018, 56, 3062–3072. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transport Porous Med. 2009, 77, 267–285. [Google Scholar] [CrossRef]
| M | ||||||
|---|---|---|---|---|---|---|
| Present | [28] | Present | [28] | |||
| 0.62576 | 0.62289 | 0.28162 | 0.28042 | 0.4586% | 0.4261% | |
| 0.55941 | 0.55703 | 0.23958 | 0.23895 | 0.4254% | 0.2630% | |
| 0.51257 | 0.51043 | 0.21172 | 0.21176 | 0.4175% | 0.0189% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khashi’ie, N.S.; Md Arifin, N.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet. Entropy 2019, 21, 1162. https://doi.org/10.3390/e21121162
Khashi’ie NS, Md Arifin N, Nazar R, Hafidzuddin EH, Wahi N, Pop I. Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet. Entropy. 2019; 21(12):1162. https://doi.org/10.3390/e21121162
Chicago/Turabian StyleKhashi’ie, Najiyah Safwa, Norihan Md Arifin, Roslinda Nazar, Ezad Hafidz Hafidzuddin, Nadihah Wahi, and Ioan Pop. 2019. "Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet" Entropy 21, no. 12: 1162. https://doi.org/10.3390/e21121162
APA StyleKhashi’ie, N. S., Md Arifin, N., Nazar, R., Hafidzuddin, E. H., Wahi, N., & Pop, I. (2019). Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet. Entropy, 21(12), 1162. https://doi.org/10.3390/e21121162






