Entropy Generation Assessment for Wall-Bounded Turbulent Shear Flows Based on Reynolds Analogy Assumptions
Abstract
:1. Introduction
2. Governing Equations
2.1. Turbulence Models
2.1.1. The Model
2.1.2. The Model
2.1.3. The Model
2.2. Energy Equation and Heat Transfer Model
2.3. Temperature Variance Equation
2.4. Entropy Equation
2.4.1. Entropy Production—Steady-State Calculations
2.4.2. Entropy Production—Unsteady Calculations
3. Numerical Setup
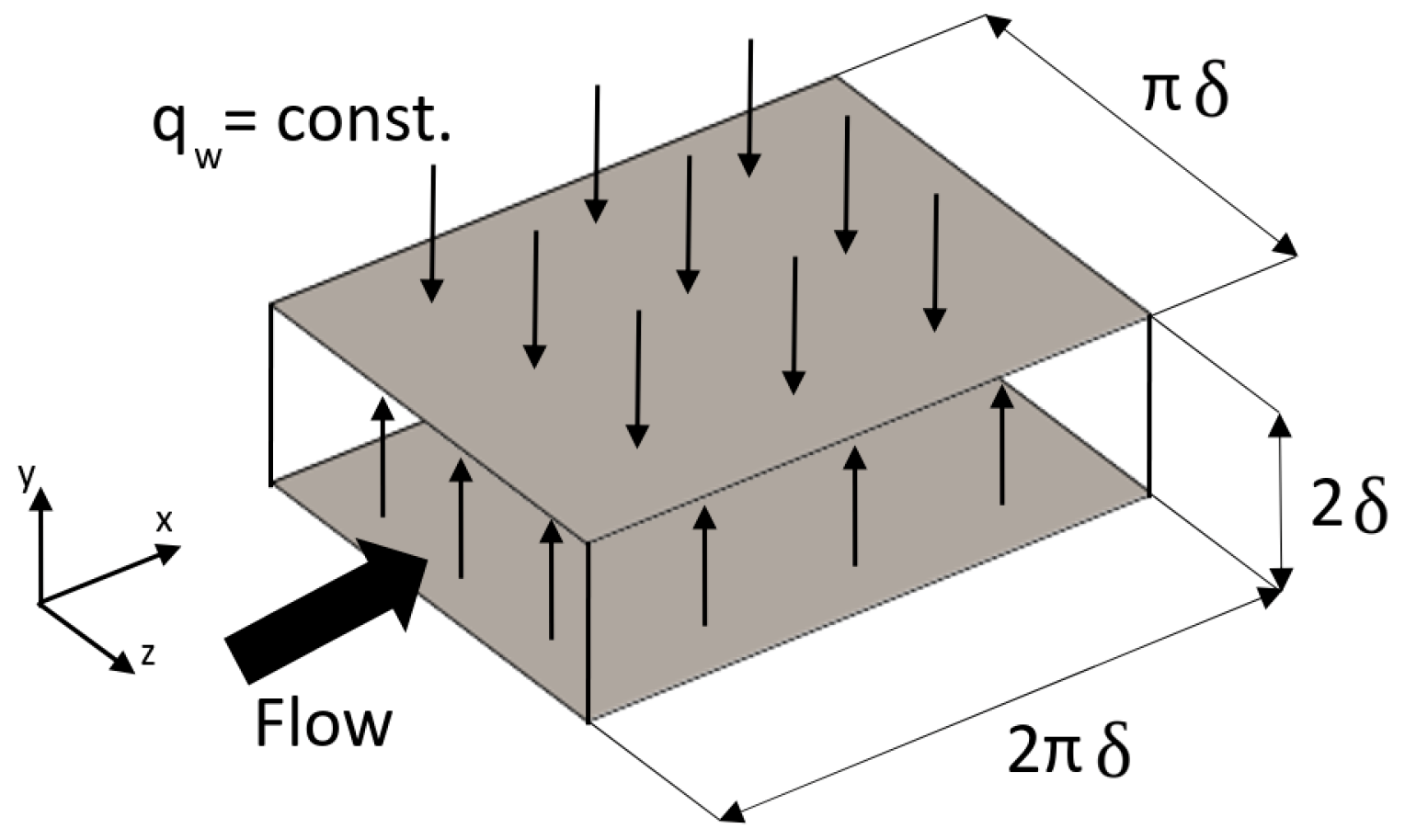
3.1. Flow Configuration
3.2. Code Description
4. Results and Discussion
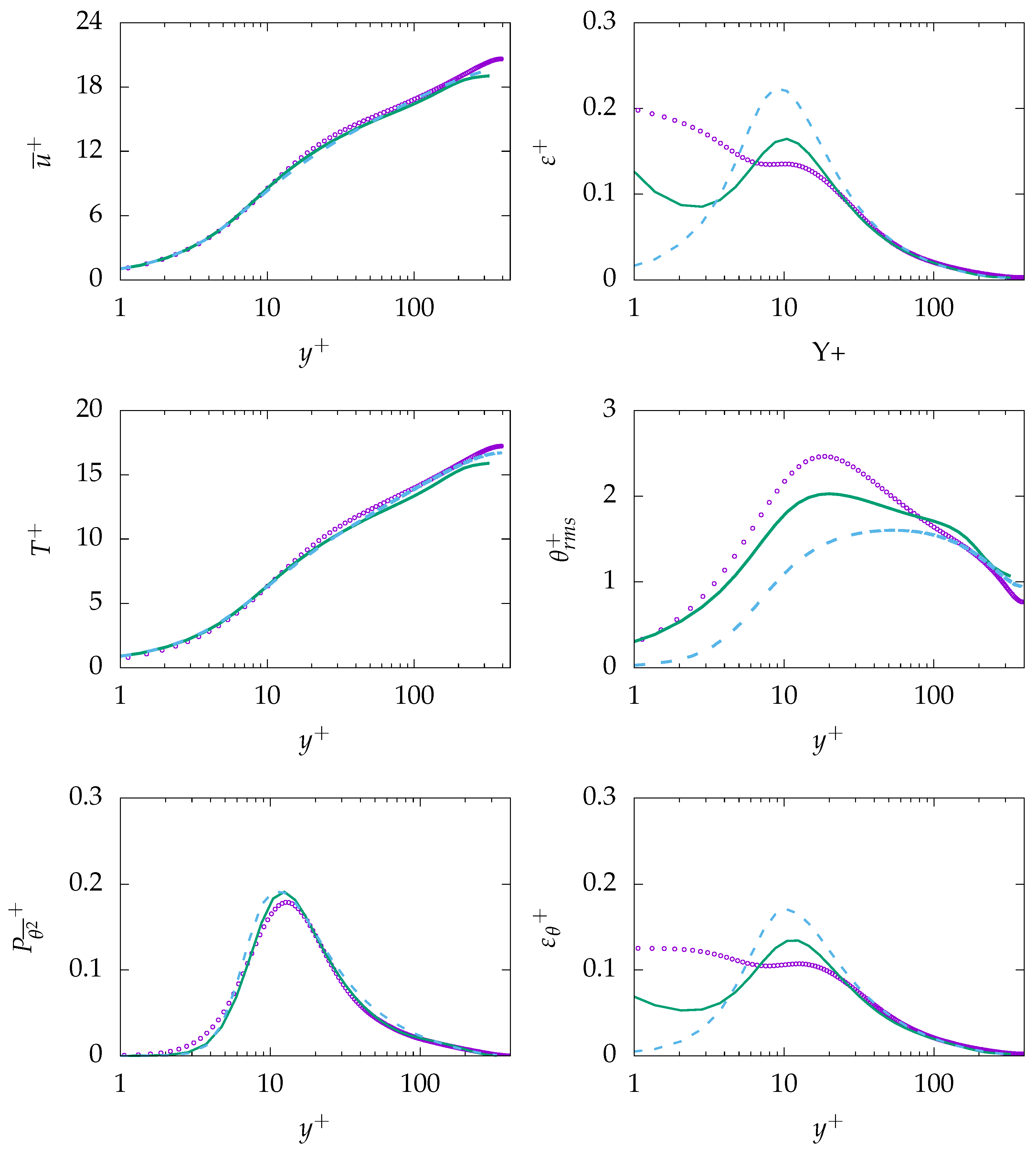
4.1. Steady-State Simulations
4.1.1.
4.1.2.
4.1.3.
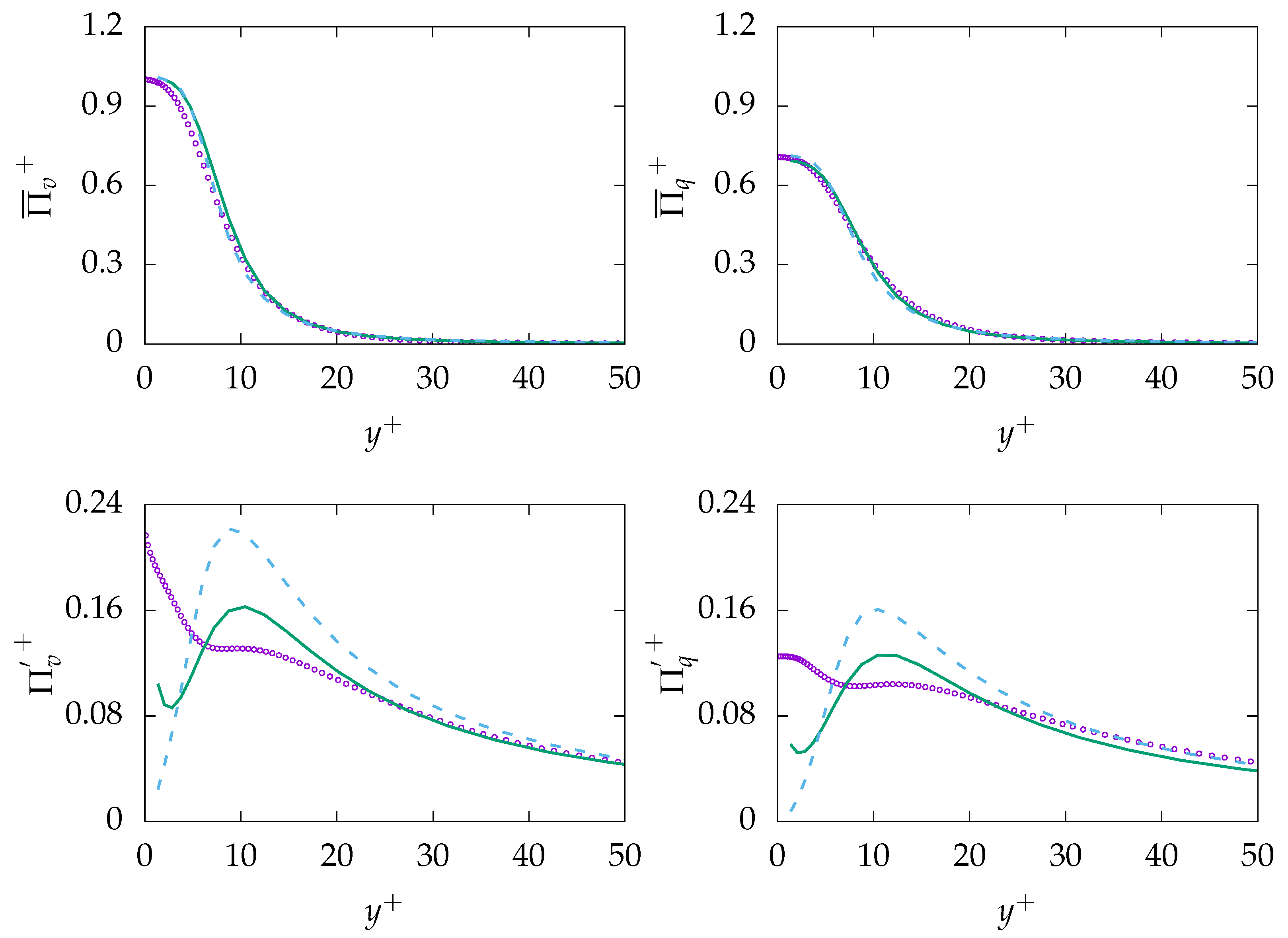
4.2. Unsteady Simulations
4.2.1.
4.2.2.
4.2.3.
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| specific heat capacity at constant pressure | |
| f | elliptic relaxation |
| k | kinetic energy |
| r | grid stretching factor in y-direction |
| s | entropy density |
| velocity fluctuations | |
| mean velocity | |
| heat flux density vector | |
| wall heat flux | |
| yPlus | |
| Prandtl | |
| mechanical to thermal time-scale ratio | |
| turbulent Reynolds number | |
| friction entropy production rate | |
| source terms in internal temperature equation | |
| T | mean temperature |
| friction temperature | |
| wall temperature | |
| friction velocity | |
| total velocity | |
| thermal diffusivity | |
| channel half height | |
| dissipation of kinetic energy | |
| dissipation of the variance of temperature fluctuations | |
| velocity scale ratio | |
| temperature fluctuations | |
| turbulent heat flux | |
| rms value of temperature fluctuations | |
| temperature variance | |
| total temperature | |
| dissipation rate of kinetic energy | |
| thermal conductivity | |
| dynamic viscosity | |
| kinematic viscosity | |
| turbulent kinematic viscosity | |
| entropy production | |
| density | |
| turbulent Prandtl number | |
| mechanical time scale | |
| thermal time scale | |
| wall shear stress | |
| sub-grid component | |
| resolved component | |
| total | |
| mean value | |
| spatial and time averaged | |
| fluctuating component | |
| normalized by wall variables |
Abbreviations
| res | resolved |
| rms | root mean square |
| sgs | sub-grid-scale |
| AFM | algebraic heat flux model |
| CFD | Computational Fluid Dynamics |
| DNS | Direct Numerical Simulation |
| EDM | Eddy Diffusivity model |
| GGDH | generalized gradient diffusion hypothesis |
| IDDES | improved delayed ettached Eddy simulation |
| SGDH | Simple Gradient Diffusion Hypothesis |
| LES | Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier Stokes equation |
| URANS | Unsteady Reynolds-Averaged Navier Stokes equation |
| THF | turbulent heat flux |
References
- Generation IV International Forum (GIF). Technology Roadmap Update for Generation IV Nuclear Energy Systems: Preparing Today for Tomorrow’s Energy Needs; OECD/NEA: Paris, France, 2014; p. 7. [Google Scholar]
- Chetal, S.C.; Balasubramaniyan, V.; Chellapandi, P.; Mohanakrishnan, P.; Puthiyavinayagam, P.; Pillai, C.P.; Raghupathy, S.; Shanmugham, T.K.; Pillai, C.S. The design of the Prototype Fast Breeder Reactor. Nucl. Eng. Des. 2006, 236, 852–860. [Google Scholar] [CrossRef]
- Kleinhans, U.; Wieland, C.; Frandsen, F.J.; Spliethoff, H. Ash formation and deposition in coal and biomass fired combustion systems: Progress and challenges in the field of ash particle sticking and rebound behavior. Prog. Energy Combust. Sci. 2018, 68, 65–168. [Google Scholar] [CrossRef]
- Paes, D.M.; Ribeiro, P.R.; Shirdel, M.; Sepehrnoori, K. Study of asphaltene deposition in wellbores during turbulent flow. J. Pet. Sci. Eng. 2015, 129, 77–87. [Google Scholar] [CrossRef]
- Schulenberg, T.; Stieglitz, R. Flow measurement techniques in heavy liquid metals. Nucl. Eng. Des. 2010, 240, 2077–2087. [Google Scholar] [CrossRef]
- Shams, A.; Roelofs, F.; Baglietto, E.; Lardeau, S.; Kenjereš, S. Assessment and calibration of an algebraic turbulent heat flux model for low-Prandtl fluids. Int. J. Heat Mass Transf. 2014, 79, 589–601. [Google Scholar] [CrossRef]
- Ries, F.; Li, Y.; Nishad, K.; Janicka, J.; Sadiki, A. Entropy Generation Analysis and Thermodynamic Optimization of Jet Impingement Cooling Using Large Eddy Simulation. Entropy 2019, 21, 129. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Makinde, O.D. Entropy Generation Due to Heat and Mass Transfer in a Flow of Dissipative Elastic Fluid Through a Porous Medium. J. Heat Transf. 2019, 141. [Google Scholar] [CrossRef]
- Keenan, J.H. Availability and irreversibility in thermodynamics. Br. J. Appl. Phys. 1951, 2, 183–192. [Google Scholar] [CrossRef]
- Wang, L.; Karimi, N.; Sutardi, T.; Paul, M.C. Numerical modelling of unsteady transport and entropy generation in oxy-combustion of single coal particles with varying flow velocities and oxygen concentrations. Appl. Therm. Eng. 2018, 144, 147–164. [Google Scholar] [CrossRef]
- Wang, L.; Karimi, N.; Paul, M.C. Gas-phase transport and entropy generation during transient combustion of single biomass particle in varying oxygen and nitrogen atmospheres. Int. J. Hydrogen Energy 2018, 43, 8506–8523. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Hussanan, A. Second law analysis of dissipative flow over a riga plate with non-linear Rosseland thermal radiation and variable transport properties. Entropy 2018, 20, 615. [Google Scholar] [CrossRef]
- Reddy, J.G.; Kumar, M.; Kethireddy, B.; Chamkha, A.J. Colloidal study of unsteady magnetohydrodynamic couple stress fluid flow over an isothermal vertical flat plate with entropy heat generation. J. Mol. Liquids 2018, 252, 169–179. [Google Scholar] [CrossRef]
- Khan, A.; ul Karim, F.; Khan, I.; Ali, F.; Khan, D. Irreversibility analysis in unsteady flow over a vertical plate with arbitrary wall shear stress and ramped wall temperature. Results Phys. 2018, 8, 1283–1290. [Google Scholar] [CrossRef]
- Makinde, O. Entropy analysis for MHD boundary layer flow and heat transfer over a flat plate with a convective surface boundary condition. Int. J. Exergy 2012, 10, 142. [Google Scholar] [CrossRef]
- Ries, F.; Li, Y.; Klingenberg, D.; Nishad, K.; Janicka, J.; Sadiki, A. Near-wall thermal processes in an inclined impinging jet: Analysis of heat transport and entropy generation mechanisms. Energies 2018, 11, 1354. [Google Scholar] [CrossRef]
- Ries, F.; Janicka, J.; Sadiki, A. Thermal transport and entropy production mechanisms in a turbulent round jet at supercritical thermodynamic conditions. Entropy 2017, 19, 404. [Google Scholar] [CrossRef]
- Okong’o, N.A.; Bellan, J. Direct numerical simulation of a transitional supercritical binary mixing layer: Heptane and nitrogen. J. Fluid Mech. 2002, 464, 1–34. [Google Scholar] [CrossRef]
- Farran, R.; Chakraborty, N. A direct numerical simulation-based analysis of entropy generation in turbulent premixed flames. Entropy 2013, 15, 1540–1566. [Google Scholar] [CrossRef]
- Jin, Y.; Herwig, H. Turbulent flow and heat transfer in channels with shark skin surfaces: Entropy generation and its physical significance. Int. J. Heat Mass Transf. 2014, 70, 10–22. [Google Scholar] [CrossRef]
- Kiš, P.; Herwig, H. Natural convection in a vertical plane channel: DNS results for high Grashof numbers. Heat Mass Transfer. 2014, 50, 957–972. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Liu, J.; Wu, Z.; Li, B.; Sundén, B. Entropy generation analysis of fully-developed turbulent heat transfer flow in inward helically corrugated tubes. Numer. Heat Transf. Part A Appl. 2018, 73, 788–805. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.C.; Yang, X.; Shi, L. Entropy generation analysis and performance evaluation of turbulent forced convective heat transfer to nanofluids. Entropy 2017, 19, 108. [Google Scholar] [CrossRef]
- Saqr, K.M.; Shehata, A.I.; Taha, A.A.; Abo Elazm, M.M. CFD modelling of entropy generation in turbulent pipe flow: Effects of temperature difference and swirl intensity. Appl. Therm. Eng. 2016, 100, 999–1006. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Diffuser and nozzle design optimization by entropy generation minimization. Entropy 2011, 13, 1380–1402. [Google Scholar] [CrossRef]
- Torabi, M.; Karimi, N.; Peterson, G.P.; Yee, S. Challenges and progress on the modelling of entropy generation in porous media: A review. Int. J. Heat Mass Transf. 2017, 114, 31–46. [Google Scholar] [CrossRef]
- Hosseinalipour, S.M.; Fattahi, A.; Afshari, H.; Karimi, N. On the effects of convecting entropy waves on the combustor hydrodynamics. Appl. Therm. Eng. 2017, 110, 901–909. [Google Scholar] [CrossRef]
- Chaouat, B. The State of the Art of Hybrid RANS/LES Modeling for the Simulation of Turbulent Flows. Flow Turbul. Combust. 2017, 99, 279–327. [Google Scholar] [CrossRef]
- Menter, F.R.; Esch, T. Elements of Industrial Heat Transfer Predictions. In Proceedings of the 16th Brazilian Congress of Mechanical Engineering (COBEM), Uberlândia, Brazil, 26–30 November 2001. [Google Scholar]
- Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES formulations for the k-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Saini, R.; Karimi, N.; Duan, L.; Sadiki, A.; Mehdizadeh, A. Entropy Effects of Near Wall Modeling in the Improved-Delayed-Detached-Eddy-Simulation (IDDES) Methodology. Entropy 2018, 20, 771. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B.E. Modelling Turbulence in Engineering and the Environment; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Kenjereš, S.; Hanjalić, K. Convective rolls and heat transfer in finite-length Rayleigh-Bénard convection: A two-dimensional numerical study. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 7987–7998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kawamura, H.; Abe, H.; Shingai, K. DNS of turbulence and heat transport in a channel flow with different Reynolds and Prandtl numbers and boundary conditions. Turbul. Heat Mass Transf. 2000, 3, 15–32. [Google Scholar]
- Bergant, R.; Tiselj, I. Near-wall passive scalar transport at high Prandtl numbers. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Sommer, T.P.; So, R.M.C.; Zhang, H.S. Heat Transfer Modeling and the Assumption of Zero Wall Temperature Fluctuations. J. Heat Transf. 1994, 116, 855. [Google Scholar] [CrossRef]
- Otić, I.; Grötzbach, G. Turbulent heat flux and temperature variance dissipation rate in natural convection in lead-bismuth. Nucl. Sci. Eng. 2007, 155. [Google Scholar] [CrossRef]
- Grötzbach, G. Challenges in low-Prandtl number heat transfer simulation and modelling. Nucl. Eng. Des. 2013, 264, 41–55. [Google Scholar] [CrossRef]
- Manservisi, S.; Menghini, F. A CFD four parameter heat transfer turbulence model for engineering applications in heavy liquid metals. Int. J. Heat Mass Transf. 2013, 69, 312–326. [Google Scholar] [CrossRef]
- Kenjereš, S.; Gunarjo, S.B.; Hanjalić, K. Contribution to elliptic relaxation modelling of turbulent natural and mixed convection. Int. J. Heat Fluid Flow 2005, 26, 569–586. [Google Scholar] [CrossRef]
- Kenjereš, S.; Hanjalić, K. Prediction of turbulent thermal convection in concentric and eccentric horizontal annuli. Int. J. Heat Fluid Flow 1995, 16, 429–439. [Google Scholar] [CrossRef]
- So, R.M.C.; Speziale, C.G. A Review of Turbulent Heat Transfer Modeling. Annu. Rev. Heat Transf. 1999, 10, 177–220. [Google Scholar] [CrossRef]
- Spurk, J.H.; Nuri, A. Strömungslehre—Einführung in die Theorie der Strömungen; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- Kock, F. Bestimmung der Lokalen Entropieproduktion in Turbulenten Stroemungen und Deren Nutzung zur Bewertung Konvektiver Transportprozesse; Shaker: Aachen, Germany, 2003. [Google Scholar]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Piller, M. Direct numerical simulation of turbulent forced convection in a pipe. Int. J. Numer. Methods Fluids 2005, 49, 583–602. [Google Scholar] [CrossRef]
- Spalart, P.R.; Venkatakrishnan, V. On the role and challenges of CFD in the aerospace industry. Aeronaut. J. 2016, 120, 209–232. [Google Scholar] [CrossRef] [Green Version]
- Sadrehaghighi, I. Mesh Generation in CFD. CFD Open Ser. 2017, 151. [Google Scholar] [CrossRef]
- Ziefuß, M.; Mehdizadeh, A. A Comprehensive Assessment of the Reynolds Analogy in Predicting Heat Transfer in Turbulent Wall-Bounded Shear Flows. Bull. Am. Phys. Soc. 2019, in press. [Google Scholar]
- Bergant, R.; Tiselj, I. On the role of the smallest scales of a passive scalar field in a near-wall turbulent flow. Heat Mass Transf. 2005, 42, 411–426. [Google Scholar] [CrossRef]
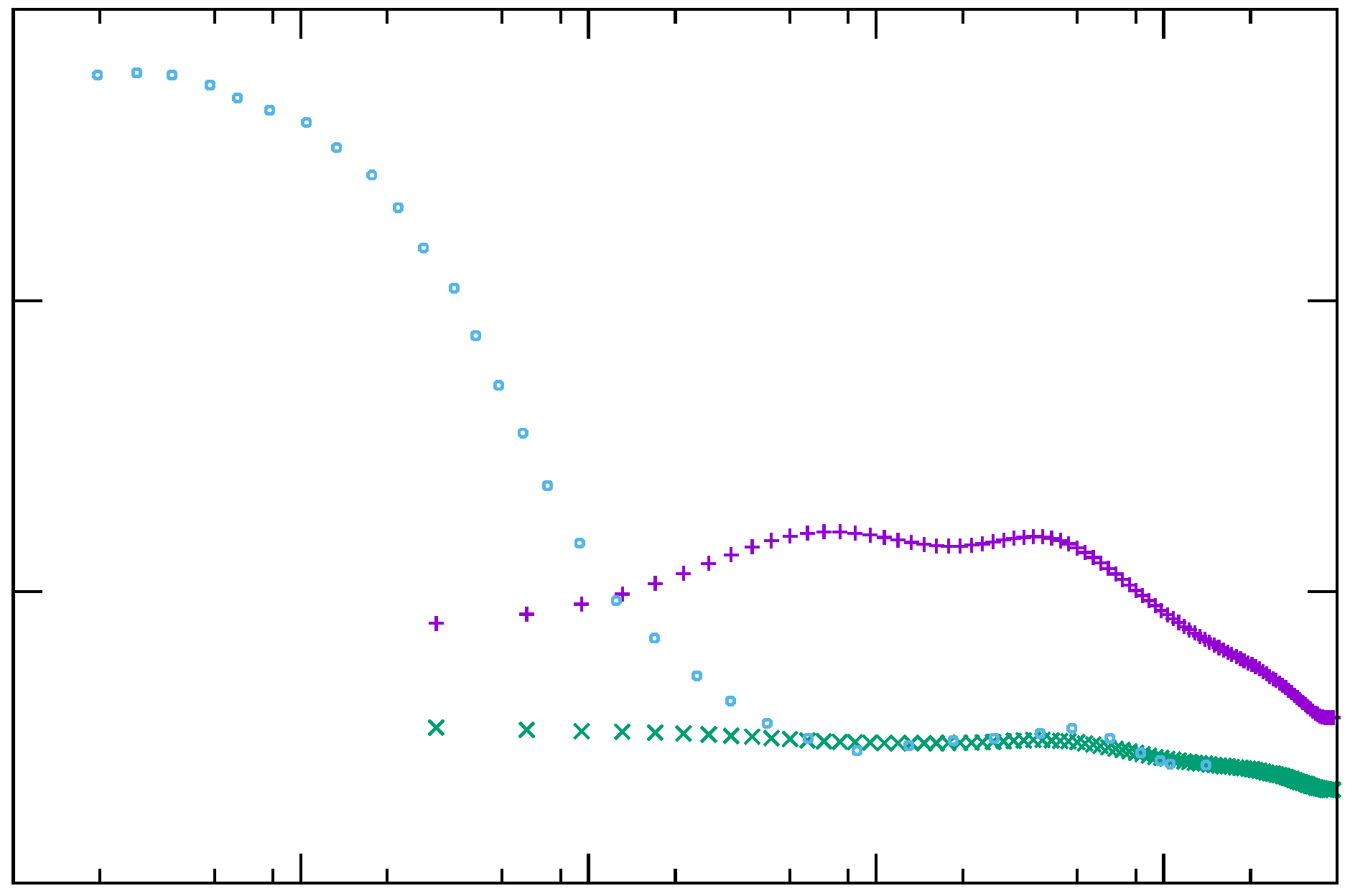
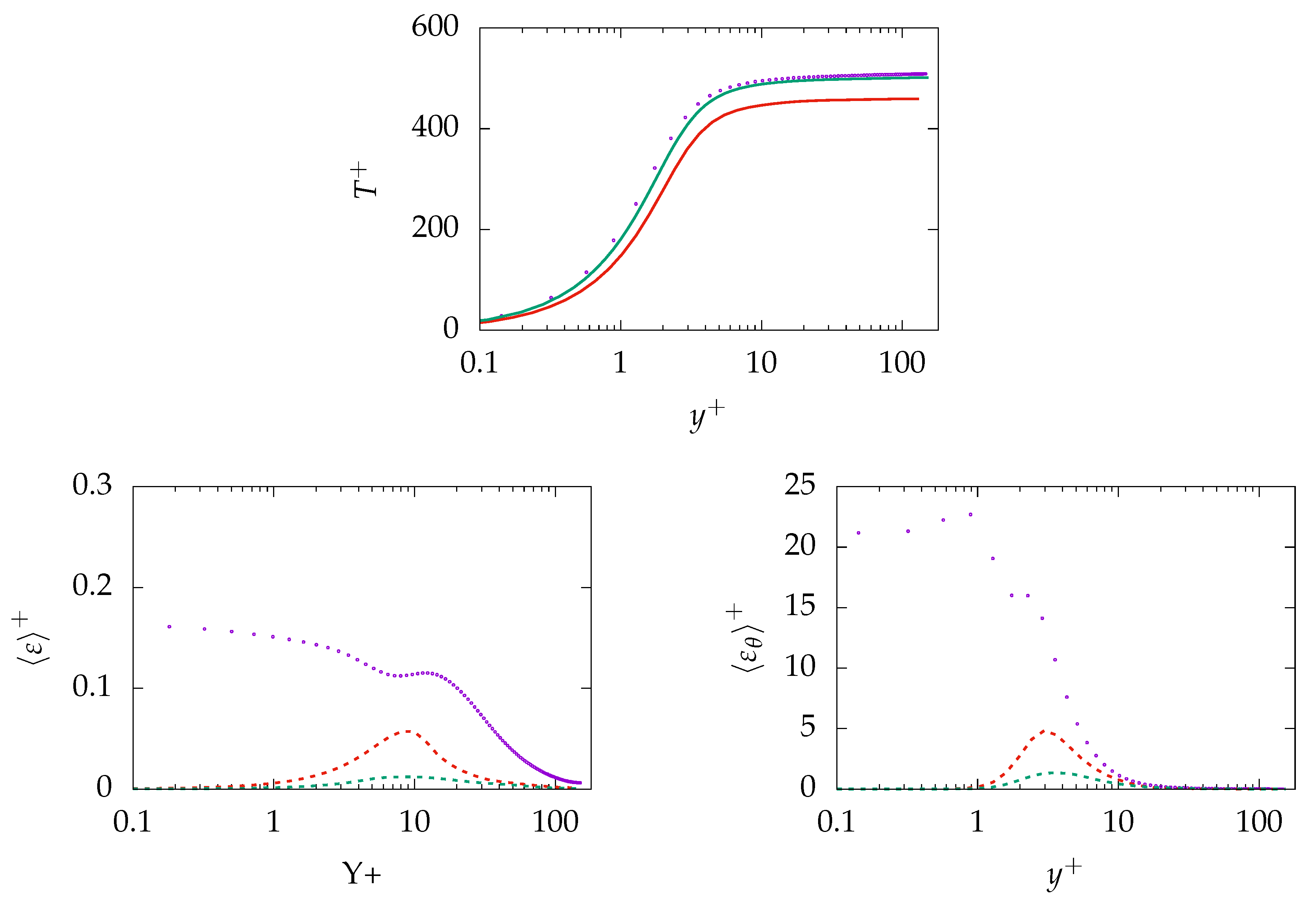
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
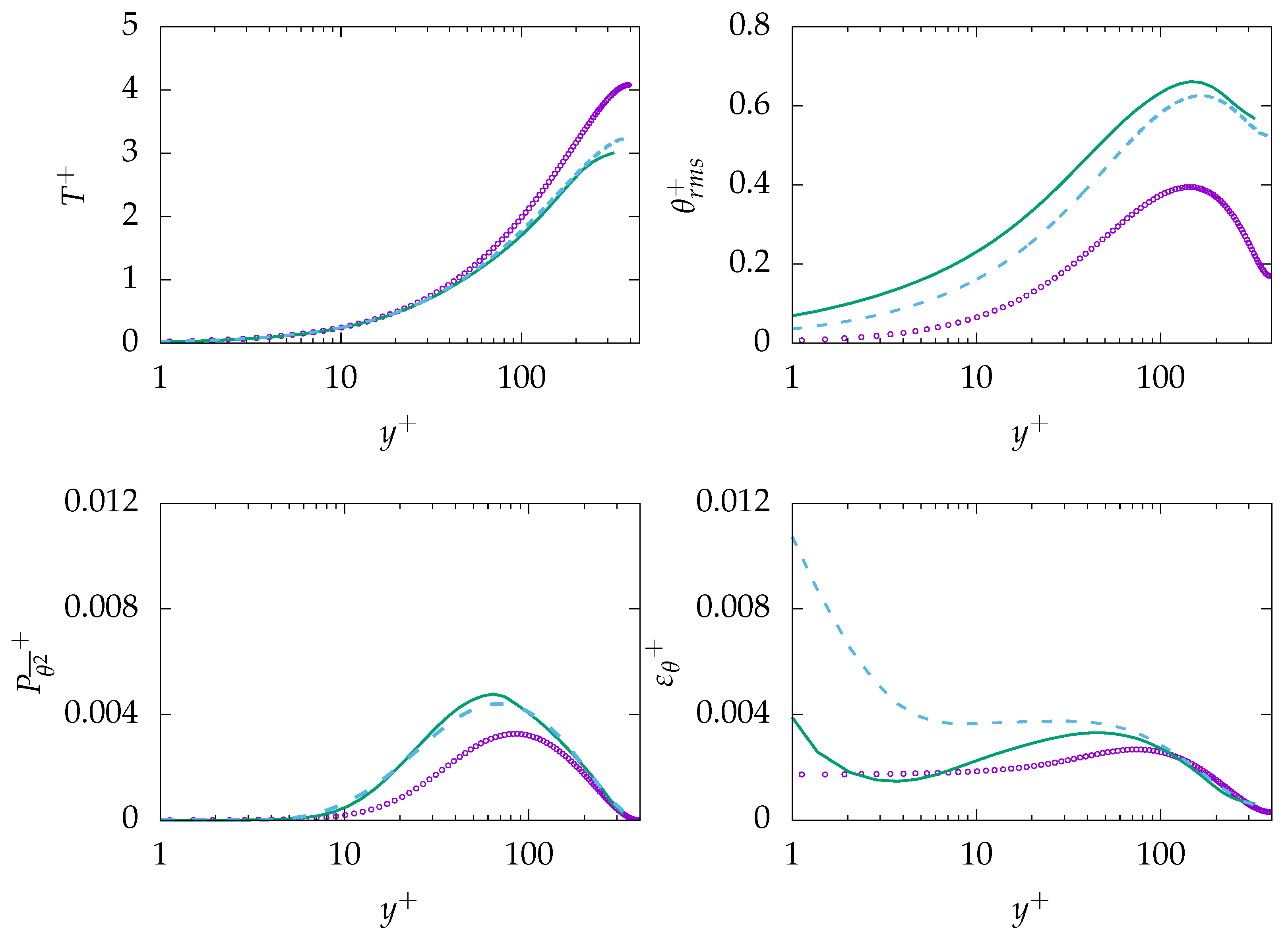
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
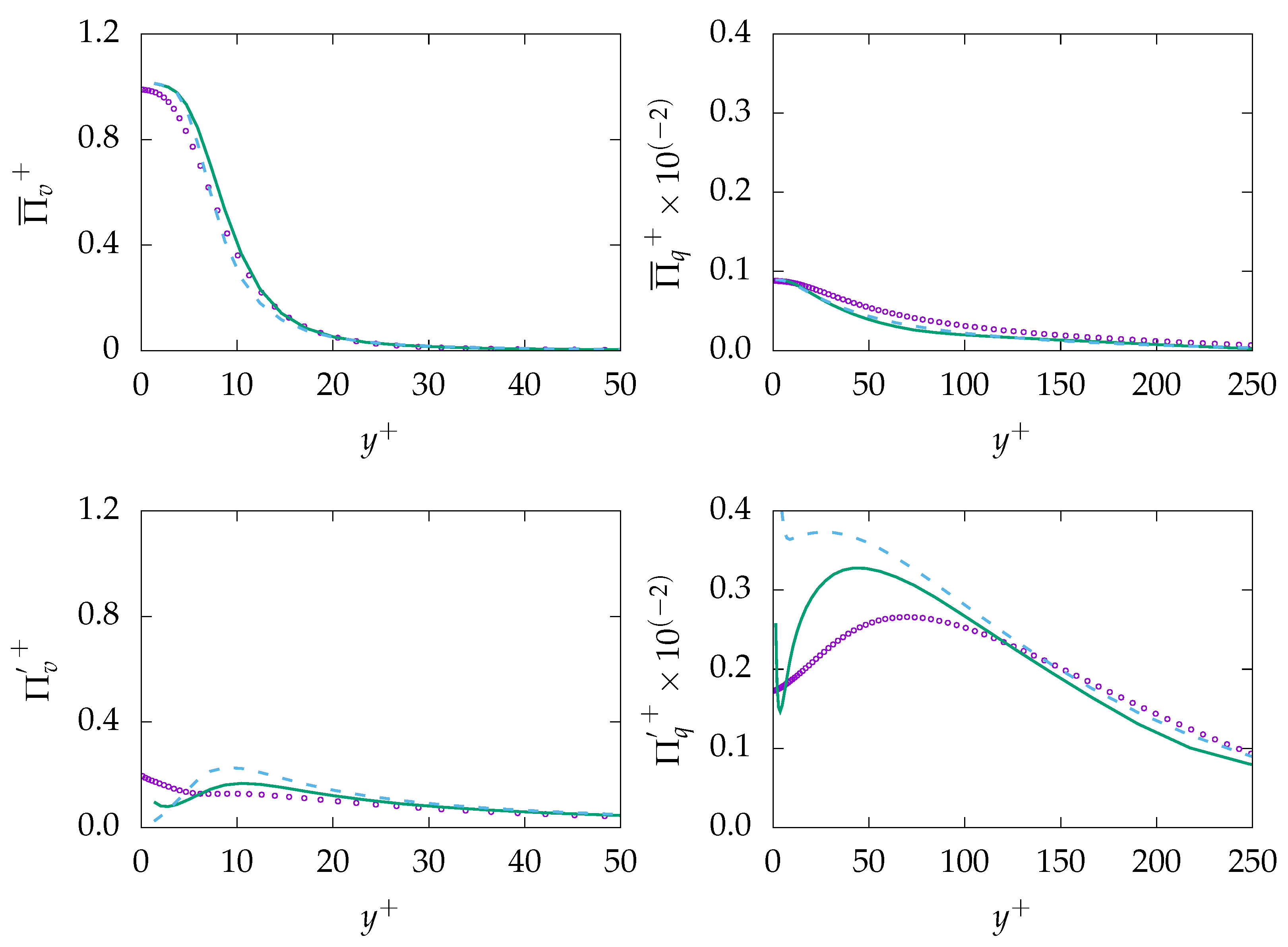
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
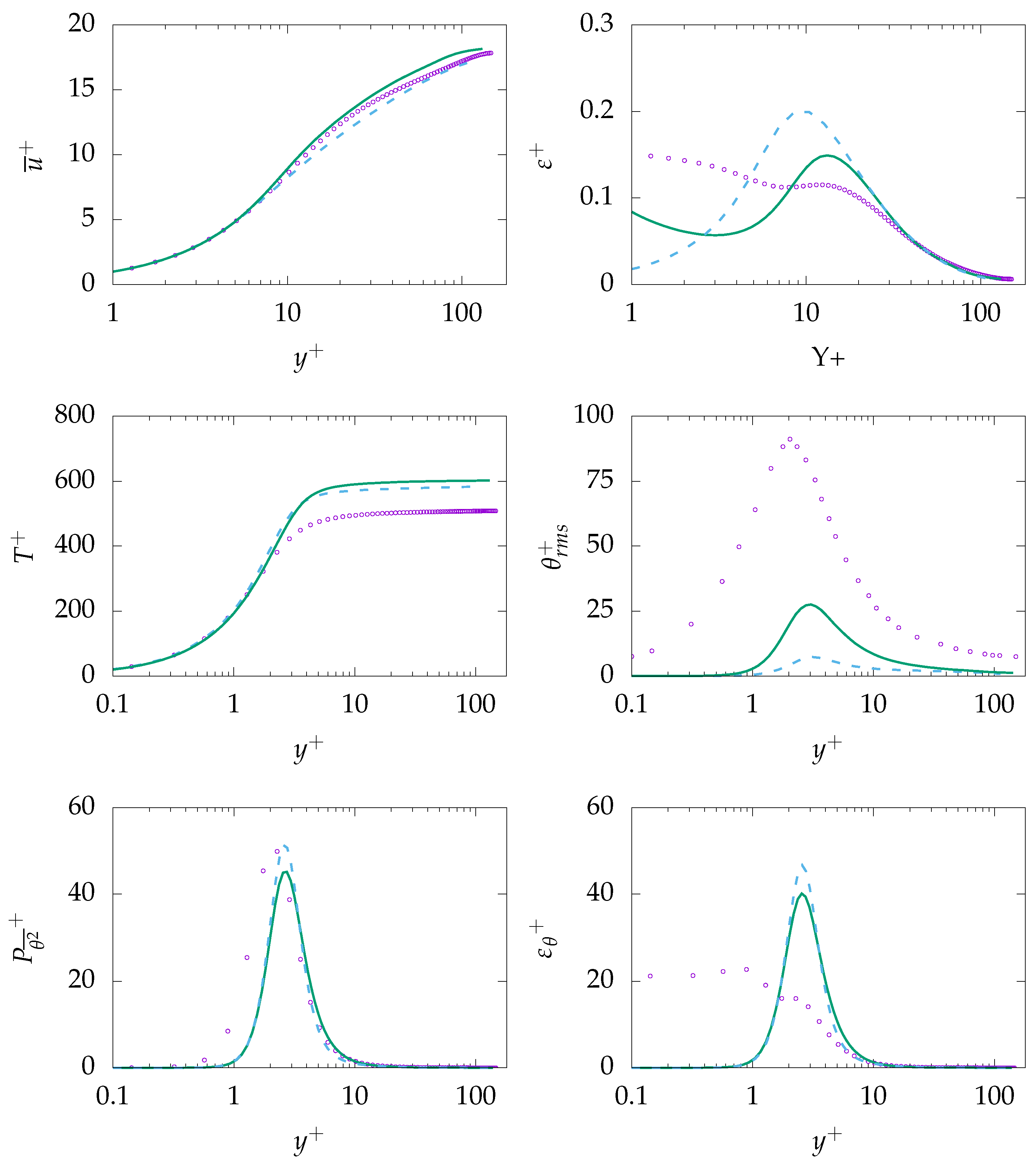
 , :
, :  , DNS:
, DNS:  .
.
 , :
, :  , DNS:
, DNS:  .
.
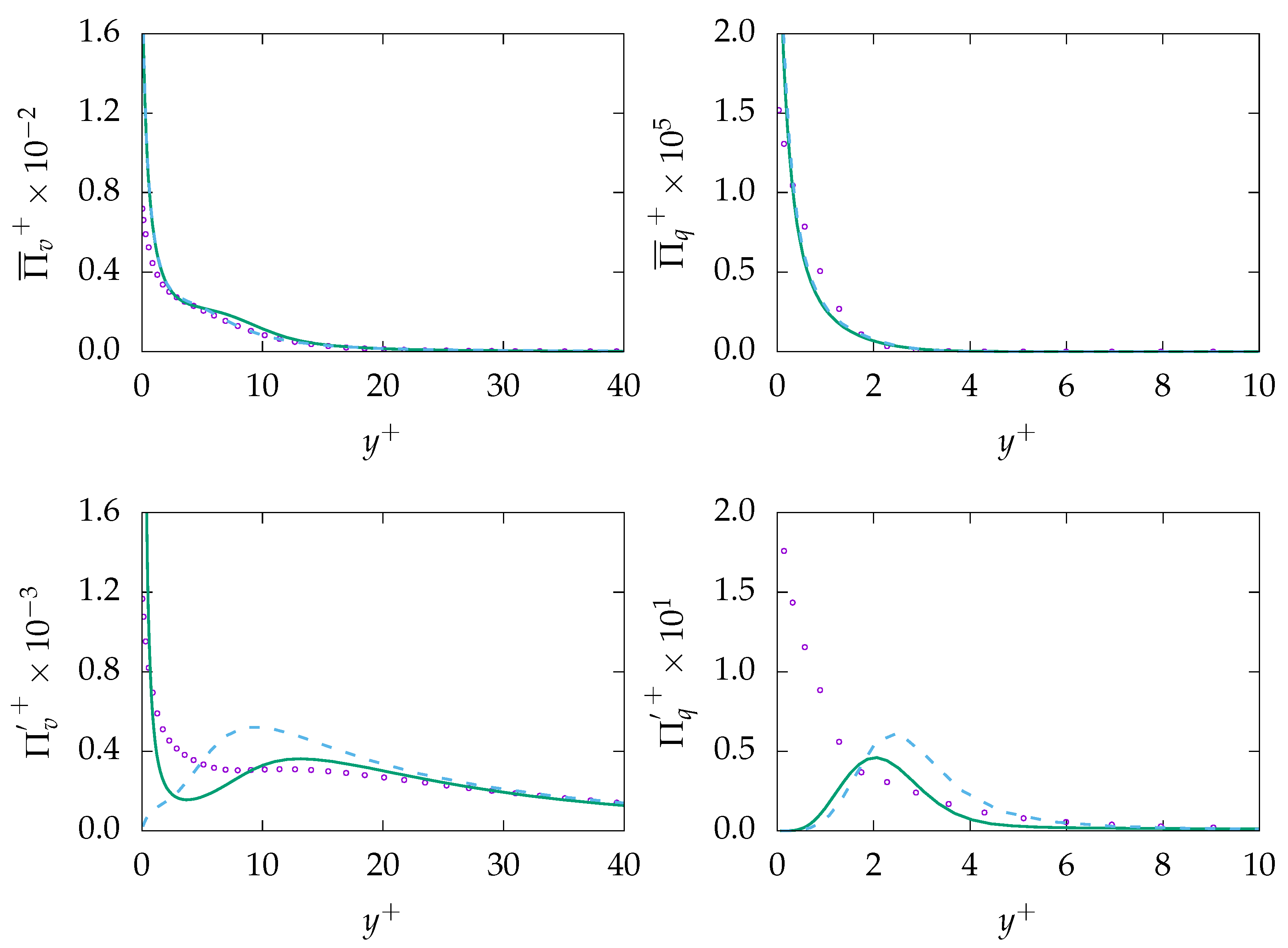
 , :
, :  , DNS:
, DNS:  .
.
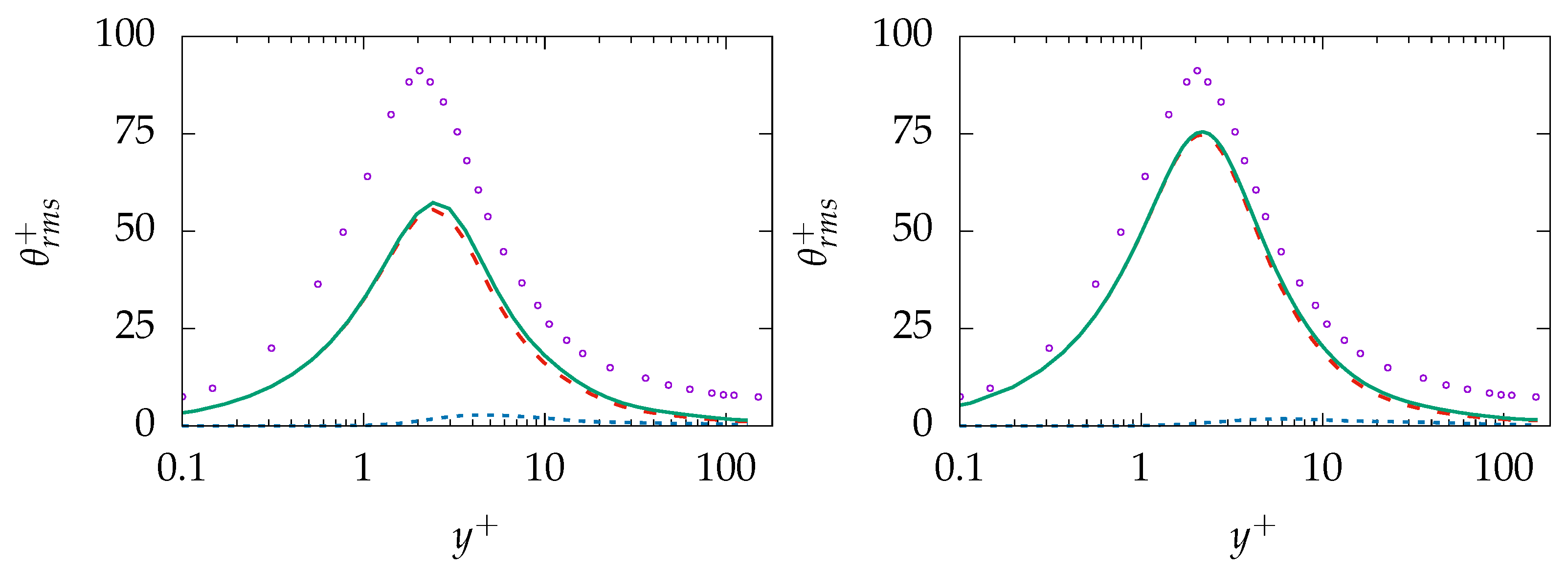
 , B-100:
, B-100:  , A-100:
, A-100:  , B-100:
, B-100:  , DNS:
, DNS:  .
.
 , B-100:
, B-100:  , A-100:
, A-100:  , B-100:
, B-100:  , DNS:
, DNS:  .
.
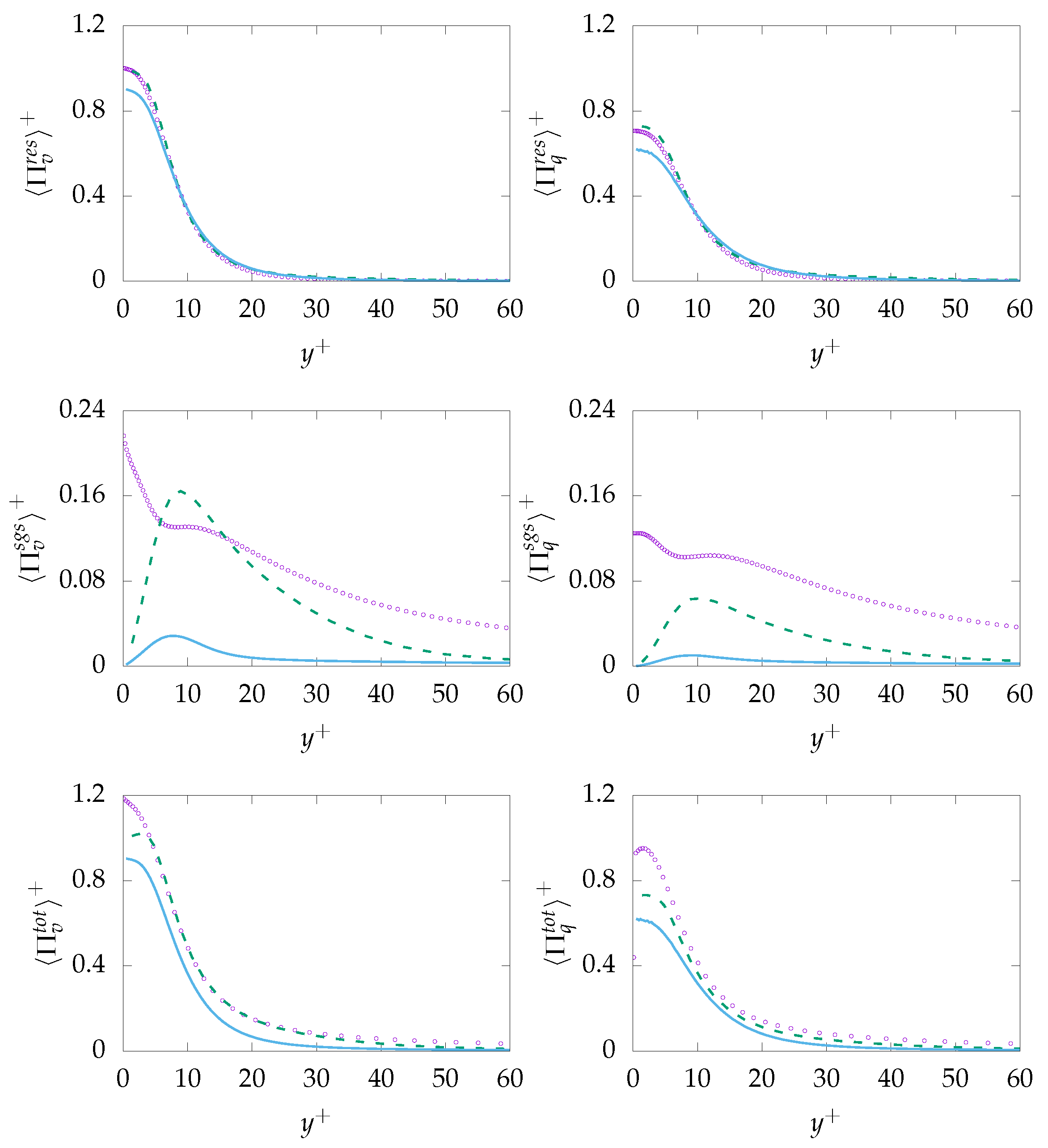
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.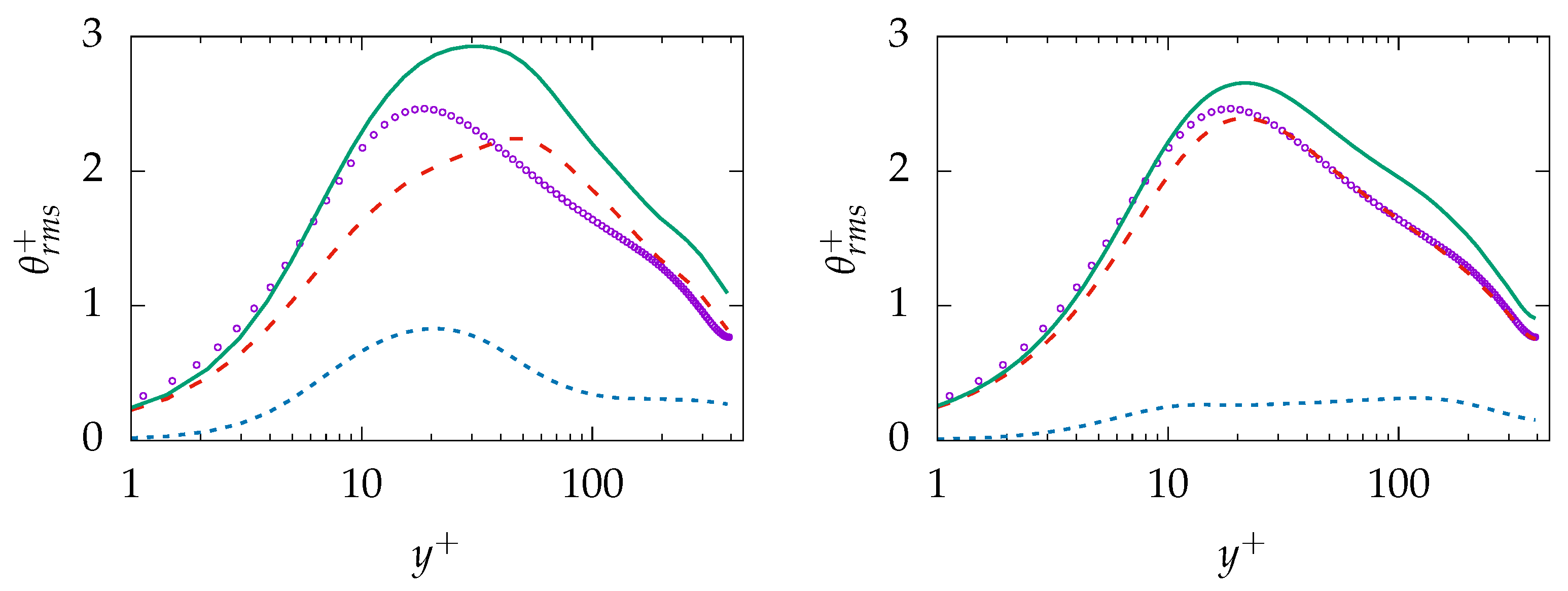
 , B-100:
, B-100:  , DNS:
, DNS:  .
.
 , B-100:
, B-100:  , DNS:
, DNS:  .
.
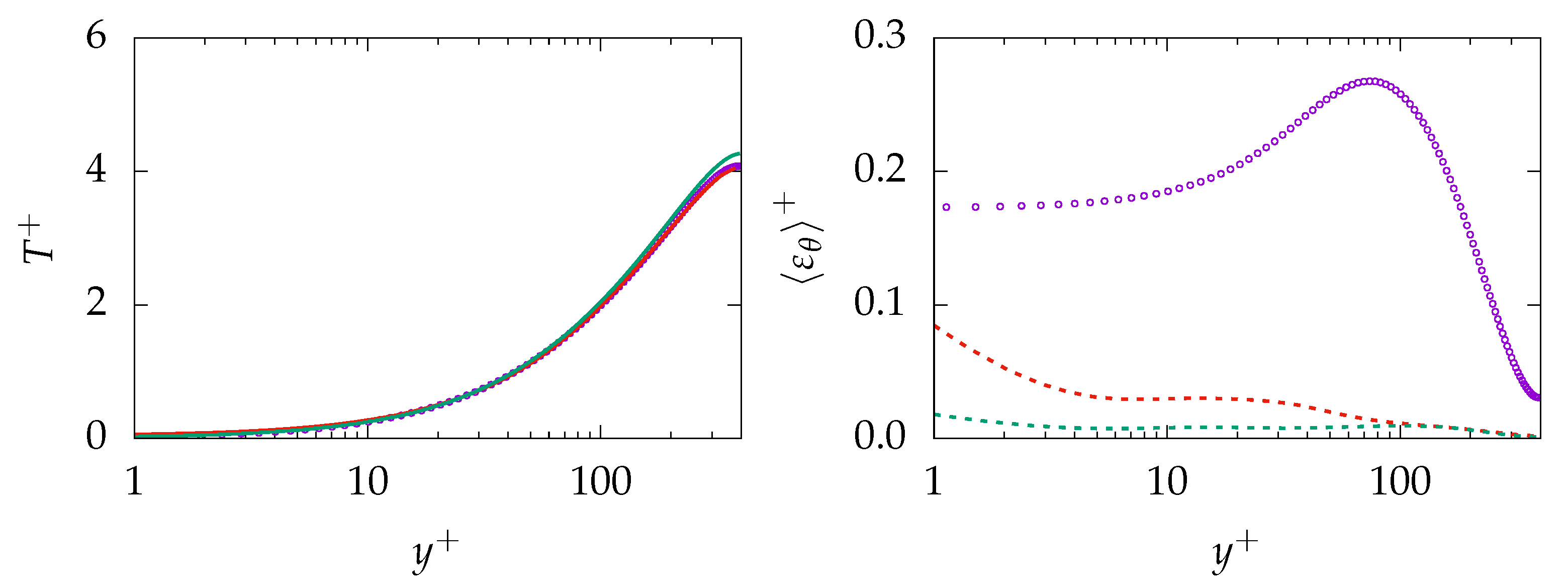
 , B-100:
, B-100:  , A-100:
, A-100:  , B-100:
, B-100:  , DNS:
, DNS:  .
.
 , B-100:
, B-100:  , A-100:
, A-100:  , B-100:
, B-100:  , DNS:
, DNS:  .
.
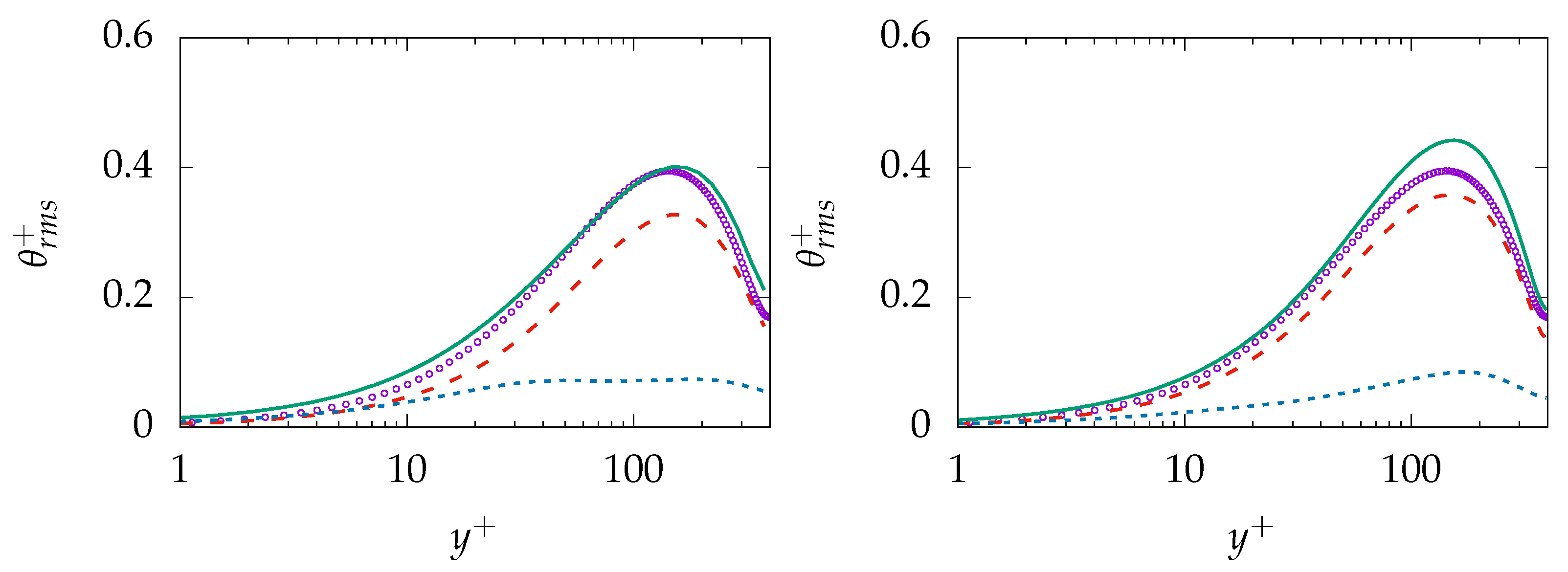
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.
 , B-100:
, B-100:  , DNS:
, DNS: 
 , B-100:
, B-100:  , DNS:
, DNS: 
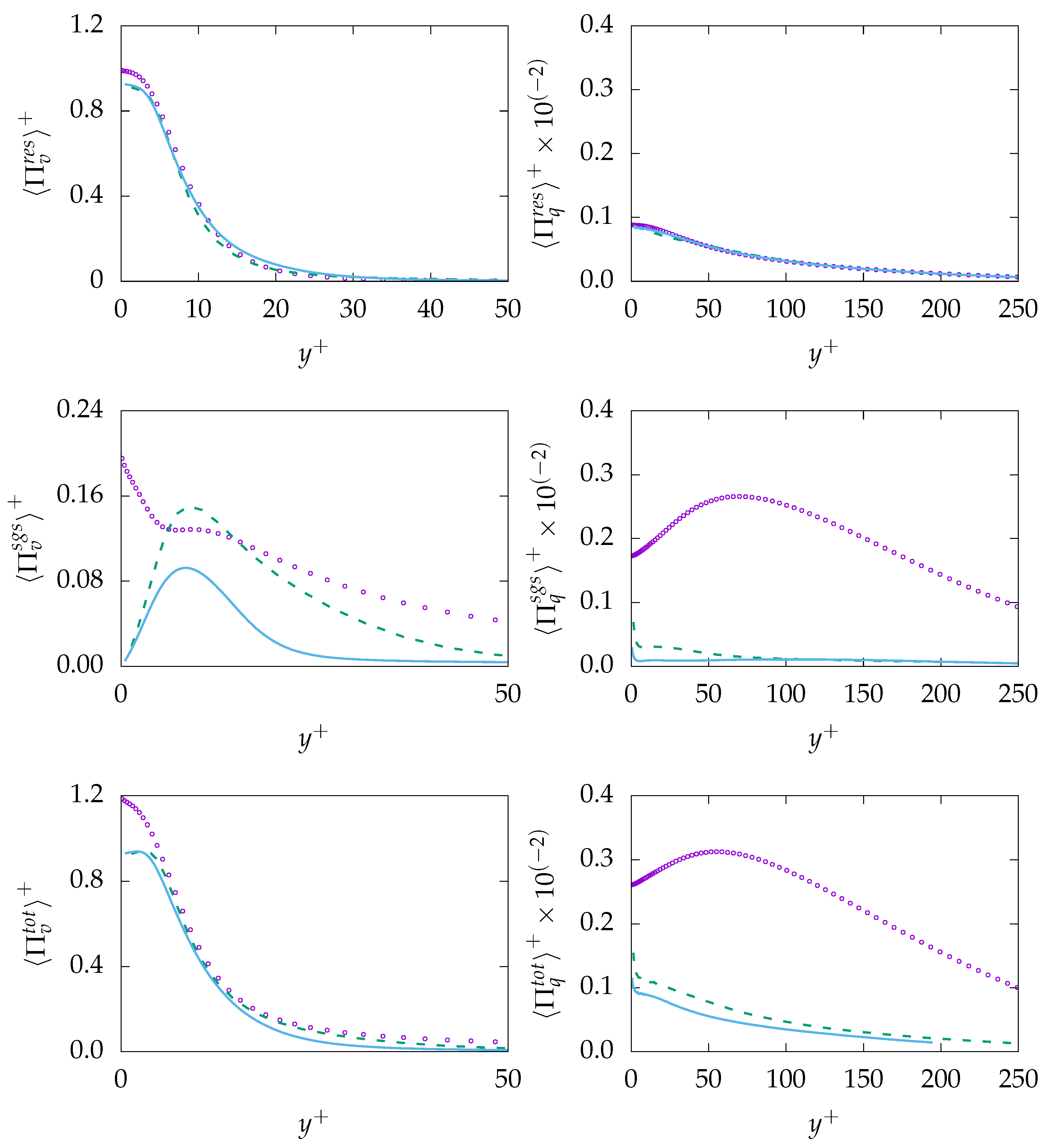
 , C-250:
, C-250:  , A-1000:
, A-1000:  , C-250:
, C-250:  , DNS:
, DNS:  .
.
 , C-250:
, C-250:  , A-1000:
, A-1000:  , C-250:
, C-250:  , DNS:
, DNS:  .
.
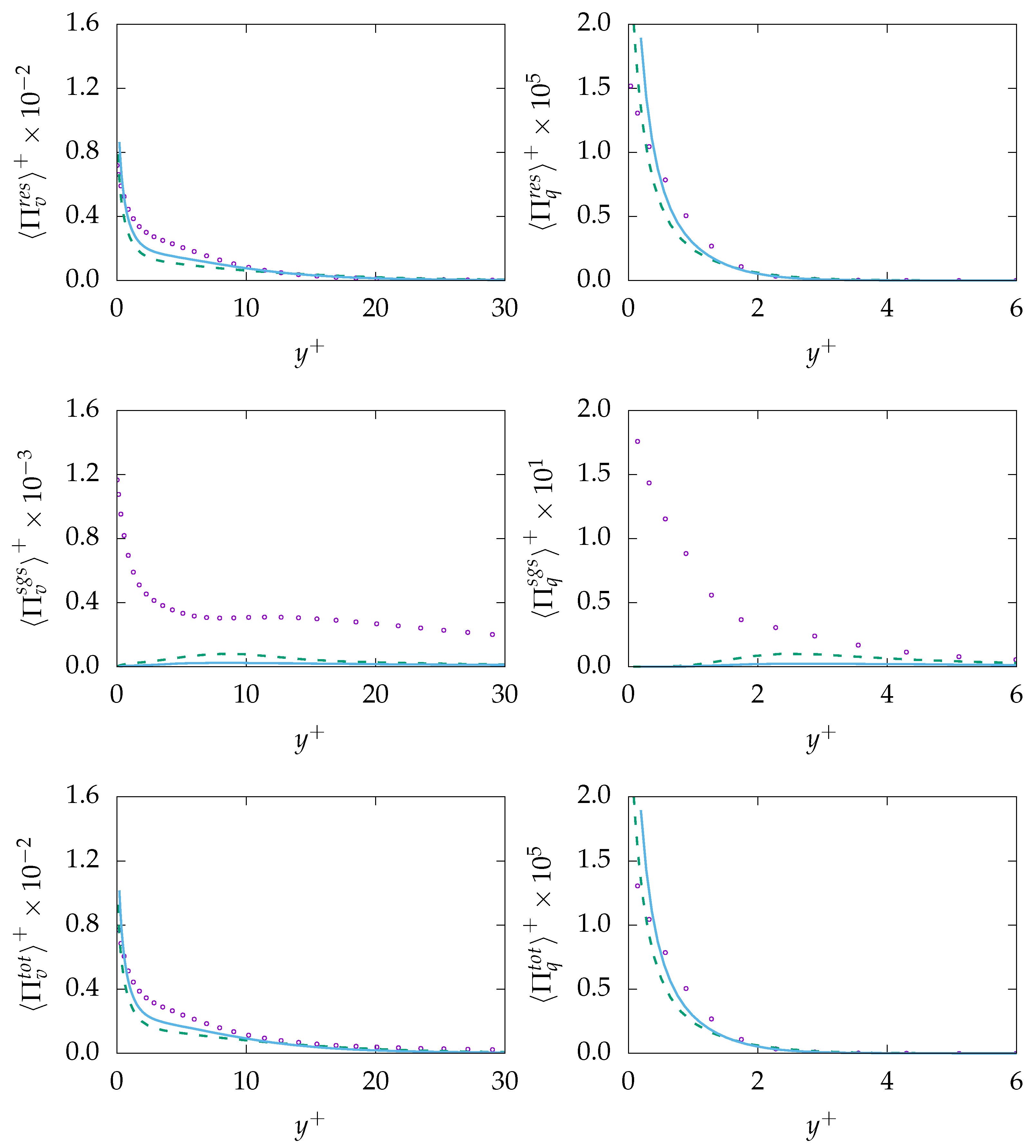
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.
 , resolved:
, resolved:  , modeled:
, modeled:  , DNS:
, DNS:  .
.
 , C-250:
, C-250:  , DNS:
, DNS:  .
.
 , C-250:
, C-250:  , DNS:
, DNS:  .
.
| Reference | Type | Resolution | Grids | ||
|---|---|---|---|---|---|
| 395 | Kawamura et al. [35] | steady | A-100 | ||
| unsteady | |||||
| unsteady | B-100 | ||||
| 395 | Kawamura et al. [35] | steady | A-100 | ||
| unsteady | |||||
| unsteady | B-100 | ||||
| 150 | 200 | Bergant et al. [36] | steady | A-1000 | |
| unsteady | |||||
| unsteady | C-250 |
| Grids | r | |||||||
|---|---|---|---|---|---|---|---|---|
| 395 | DNS [35] | 9.88 | 0.15–6.52 | 4.59 | 512 | 192 | 512 | - |
| Mesh A-100 | 51.7 | 0.49–19.1 | 25.9 | 48 | 72 | 48 | 1.14 | |
| Mesh B-100 | 19.5 | 0.19–19.0 | 128 | 192 | 1.05 | |||
| 150 | DNS [36] | 12.3 | 0.04–3.3 | 4.6 | 192 | 145 | 128 | - |
| Mesh A-1000 | 19.5 | 0.03–27.7 | 9.7 | 48 | 72 | 48 | 1.21 | |
| Mesh C-250 | 7.5 | 0.03–8.7 | 5.1 | 128 | 192 | 96 | 1.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziefuss, M.; Karimi, N.; Ries, F.; Sadiki, A.; Mehdizadeh, A. Entropy Generation Assessment for Wall-Bounded Turbulent Shear Flows Based on Reynolds Analogy Assumptions. Entropy 2019, 21, 1157. https://doi.org/10.3390/e21121157
Ziefuss M, Karimi N, Ries F, Sadiki A, Mehdizadeh A. Entropy Generation Assessment for Wall-Bounded Turbulent Shear Flows Based on Reynolds Analogy Assumptions. Entropy. 2019; 21(12):1157. https://doi.org/10.3390/e21121157
Chicago/Turabian StyleZiefuss, Matthias, Nader Karimi, Florian Ries, Amsini Sadiki, and Amirfarhang Mehdizadeh. 2019. "Entropy Generation Assessment for Wall-Bounded Turbulent Shear Flows Based on Reynolds Analogy Assumptions" Entropy 21, no. 12: 1157. https://doi.org/10.3390/e21121157
APA StyleZiefuss, M., Karimi, N., Ries, F., Sadiki, A., & Mehdizadeh, A. (2019). Entropy Generation Assessment for Wall-Bounded Turbulent Shear Flows Based on Reynolds Analogy Assumptions. Entropy, 21(12), 1157. https://doi.org/10.3390/e21121157





