Classification of Hepatitis Viruses from Sequencing Chromatograms Using Multiscale Permutation Entropy and Support Vector Machines
Abstract
1. Introduction
2. Material and Methods
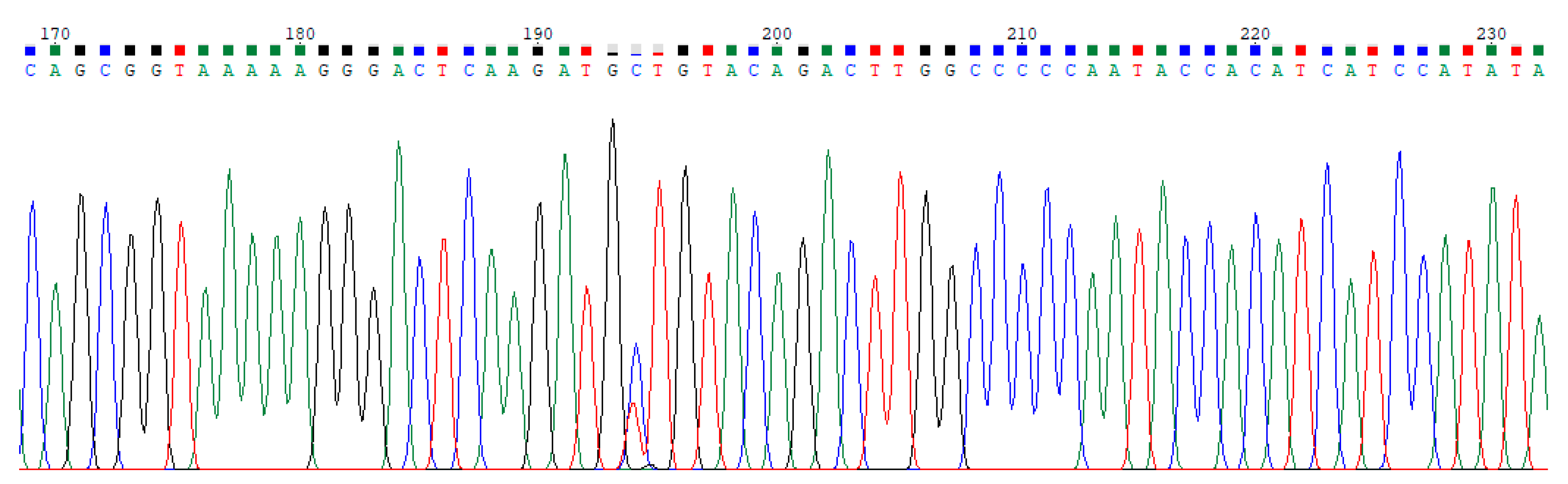
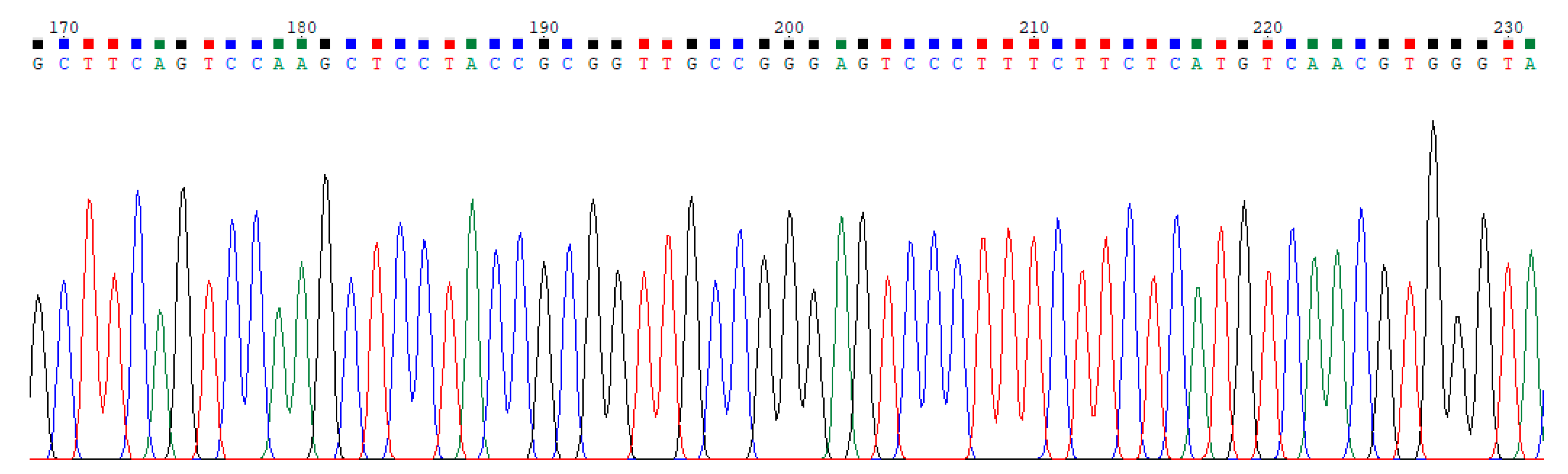
2.1. Dataset
2.2. Feature Extraction
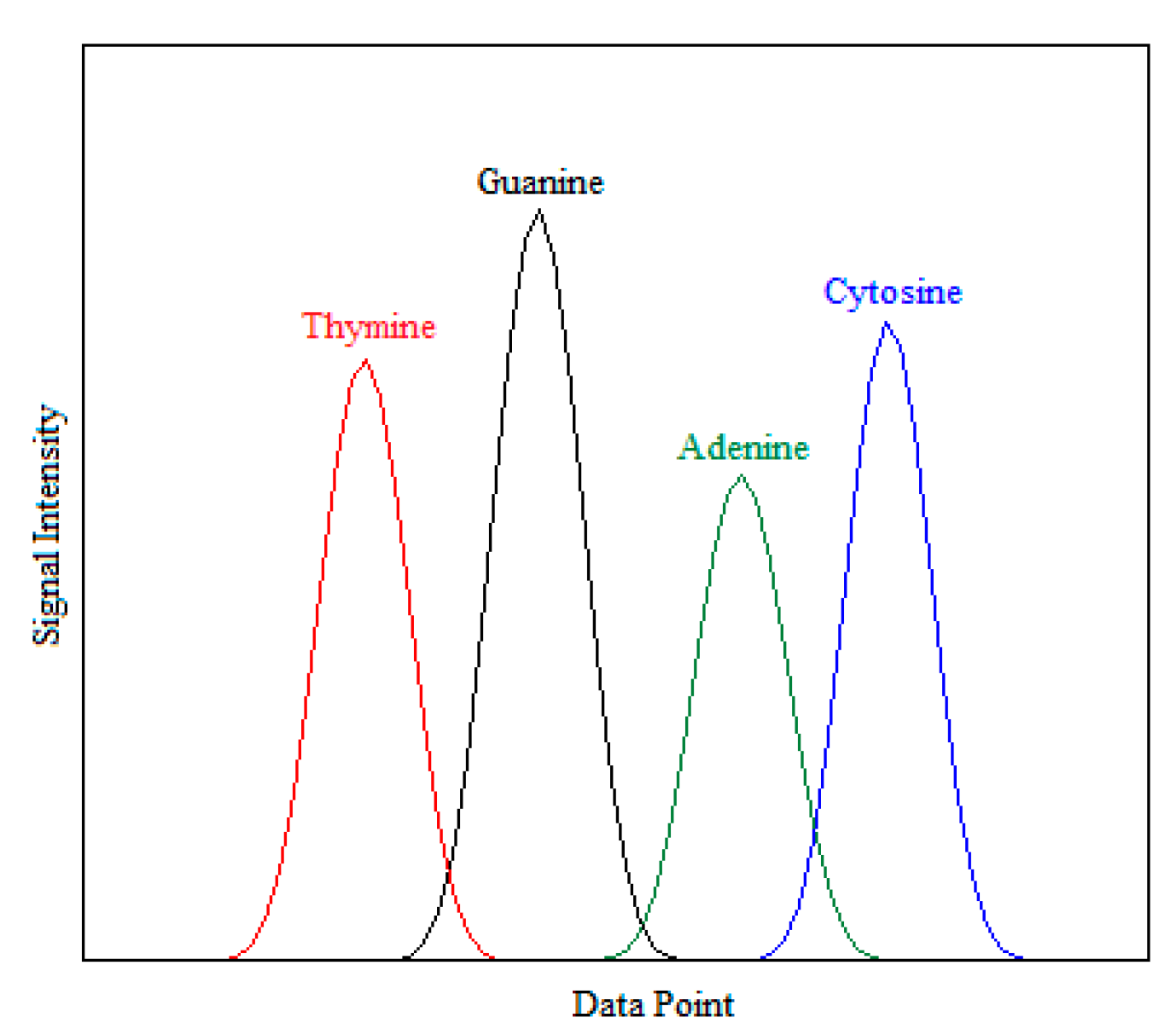
2.2.1. Statistical-Based Feature Extraction Method
2.2.2. Entropy-Based Feature Extraction Method
2.3. Support Vector Machines
2.4. Performance Evaluation
2.5. Proposed Framework
3. Results
3.1. Classification with Statistical-Based Features
3.2. Classification with Entropy-Based Features
4. Discussion
5. Conclusions
Author Contributions
Ethical Approval
Funding
Conflicts of Interest
References
- Furey, T.S.; Cristianini, N.; Duffy, N.; Bednarski, D.W.; Schummer, M.; Haussler, D. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16, 906–914. [Google Scholar] [CrossRef]
- Lander, E.S.; Linton, L.M.; Birren, B.; Nusbaum, C.; Zody, M.C.; Baldwin, J.; Devon, K.; Dewar, K.; Doyle, M.; Fitzhugh, W.; et al. Erratum: Initial sequencing and analysis of the human genome: International Human Genome Sequencing Consortium. Nature 2001, 409, 860–921. [Google Scholar] [PubMed]
- Mateos, A.; Dopazo, J.; Jansen, R.; Tu, Y.; Gerstein, M.; Stolovitzky, G. Systematic learning of gene functional classes from DNA array expression data by using multilayer perceptrons. Genome Res. 2002, 12, 1703–1715. [Google Scholar] [CrossRef] [PubMed]
- Öz, E.; Kaya, H. Support vector machines for quality control of DNA sequencing. J. Inequalities Appl. 2013, 2013, 85. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ouyang, G.; Richards, D.A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Res. 2007, 77, 70–74. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy to distinguish physiologic and synthetic RR time series. Comput. Cardiol. 2002, 29, 137–140. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait Dynamics. Phys. A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Nikulin, V.V.; Brismar, T. Comment on “Multiscale entropy analysis of complex physiologic time series”. Phys. Rev. Lett. 2004, 92, 089803. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the 9th International Multitopic Conference (INMIC ’05), Karachi, Pakistan, 24–25 December 2005; pp. 1018–1021. [Google Scholar]
- Ravelo-García, A.; Navarro-Mesa, J.L.; Casanova-Blancas, U.; Martin-Gonzalez, S.; Quintana-Morales, P.; Guerra-Moreno, I.; Canino-Rodríguez, J.M.; Hernández-Pérez, E. Application of the permutation entropy over the heart rate variability for the improvement of electrocardiogram-based sleep breathing pause detection. Entropy 2015, 17, 914–927. [Google Scholar] [CrossRef]
- Nalband, S.; Sundar, A.; Prince, A.A.; Agrawal, A. Feature selection and classification methodology for the detection of knee-joint disorders. Comput. Methods Progr. Biomed. 2016, 127, 94–104. [Google Scholar] [CrossRef]
- Nalband, S.; Prince, A.A.; Agrawal, A. Entropy-based feature extraction and classification of vibroarthographic signal using complete ensemble empirical mode decomposition with adaptive noise. IET Sci. Meas. Technol. 2018, 12, 350–359. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Ocak, H. Optimal classification of epileptic seizures in EEG using wavelet analysis and genetic algorithm. Signal Process. 2008, 88, 1858–1867. [Google Scholar] [CrossRef]
- Song, Y.; Lio, P. A new approach for epileptic seizure detection: Sample entropy based feature extraction and extreme learning machine. J. Biomed. Sci. Eng. 2010, 6, 556–567. [Google Scholar] [CrossRef]
- Labate, D.; Palamara, I.; Mammone, N.; Morabito, G.; La Foresta, F.; Morabito, F.C. SVM classification of epileptic EEG recordings through multiscale permutation entropy. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–5. [Google Scholar]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machines. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Fung, G.; Mangasarian, O.L.; Shavlik, J.W. Knowledge-based support vector machine classifiers. In Advances in Neural Information Processing Systems; Becker, S., Thrun, S., Obermayer, K., Eds.; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Öz, E.; Kurt, S.; Asyalı, M.; Yücel, Y. Feature based quality assessment of DNA sequencing chromatograms. Appl. Soft Comput. 2016, 41, 420–427. [Google Scholar] [CrossRef]
- Kurt, S.; Öz, E.; Aşkın, Ö.E.; Yücel, Y. Classification of nucleotide sequences for quality assessment using logistic regression and decision tree approaches. Neural Comput. Appl. 2018, 29, 251–261. [Google Scholar] [CrossRef]
- Seo, T.K. Classification of nucleotide sequences using support vector machines. J. Mol. Evol. 2010, 71, 250–267. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Bhat, H.F. Evaluating SVM algorithms for bioinformatic gene expression analysis. Int. J. Comp. Sci. Eng. 2017, 6, 42–52. [Google Scholar]
- Ewing, B.; Green, P. Base-calling of automated sequencer traces using phred. II. Error probabilities. Genome Res. 1998, 8, 186–194. [Google Scholar] [CrossRef]
- MATLAB, Version 9.2.0; The MathWorks Inc.: Natick, MA, USA, 2017.
- Zunino, L.; Olivares, F.; Scholkmann, F.; Rosso, O.A. Permutation entropy based time series analysis: Equalities in the input signal can lead to false conclusions. Phys. Lett. A 2017, 381, 1883–1892. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Proc. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Campbell, C.; Ying, Y. Learning with Support Vector Machines; Morgan & Claypool Publishers: San Rafael, CA, USA, 2011. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Yue, S.; Li, P.; Hao, P. SVM classification: Its contents and challenges. Appl. Math. J. Chin. Univ. 2003, 18, 332–342. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; Technical Report; Department of Computer Science and Information Engineering, National Taiwan University: Taipei City, Taiwan, 2004; Available online: http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 2 November 2019).
- Cherkassky, V.; Mulier, F.M. Learning from Data: Concepts, Theory, and Methods; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. Kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Han, H.; Jiang, X. Overcome support vector machine diagnosis overfitting. Cancer Inform. 2014, 13, CIN-S13875. [Google Scholar] [CrossRef] [PubMed]
- Amarantidis, L.C.; Abásolo, D. Interpretation of entropy algorithms in the context of biomedical signal analysis and their application to EEG analysis in epilepsy. Entropy 2019, 21, 840. [Google Scholar] [CrossRef]
- Acharya, U.R.; Molinari, F.; Sree, S.V.; Chattopadhyay, S.; Ng, K.H.; Suri, J.S. Automated diagnosis of epileptic EEG using entropies. Biomed. Signal Process. Control 2012, 7, 401–408. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sree, S.V.; Ang, P.C.A.; Yanti, R.; Suri, J.S. Application of non-linear and wavelet based features for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 2012, 22, 1250002. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Arunkumar, N.; Ramkumar, K.; Venkatraman, V.; Abdulhay, E.; Fernandes, S.L.; Kadry, S.; Segal, S. Classification of focal and non focal EEG using entropies. Pattern Recognit. Lett. 2017, 94, 112–117. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Base Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pachori, R.B.; Upadhyay, A.; Acharya, U.R. Tunable-Q wavelet transform based multiscale entropy measure for automated classification of epileptic EEG signals. Appl. Signal Process. Meth. Syst. Anal. Physiol. Health 2017, 7, 385. [Google Scholar] [CrossRef]
- Tian, P.; Hu, J.; Qi, J.; Ye, X.; Che, D.; Ding, Y.; Peng, Y. A hierarchical classification method for automatic sleep scoring using multiscale entropy features and proportion information of sleep architecture. Biocybern. Biomed. Eng. 2017, 37, 263–271. [Google Scholar] [CrossRef]
- Rodríguez-Sotelo, J.L.; Osorio-Forero, A.; Jiménez-Rodríguez, A.; Cuesta-Frau, D.; Cirugeda-Roldán, E.; Peluffo, D. Automatic sleep stages classification using EEG entropy features and unsupervised pattern analysis techniques. Entropy 2014, 16, 6573–6589. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Wang, Q.; Wang, X. Comparative analysis of different characteristics of automatic sleep stages. Comput. Methods Programs Biomed. 2019, 175, 53–72. [Google Scholar] [CrossRef]
- Michielli, N.; Acharya, U.R.; Molinari, F. Cascaded LSTM recurrent neural network for automated sleep stage classification using single-channel EEG signals. Comp. Biol. Med. 2019, 106, 71–81. [Google Scholar] [CrossRef] [PubMed]
- Vimala, V.; Ramar, K.; Ettappan, M. An intelligent sleep apnea classification system based on EEG signals. J. Med. Syst. 2019, 43, 36. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.; Wang, Y.; Hou, X. Ensemble learning algorithm based on multi-parameters for sleep staging. Med. Biol. Eng. Comput. 2019, 57, 1693–1707. [Google Scholar] [CrossRef]
- Tzimourta, K.D.; Giannakeas, N.; Tzallas, A.T.; Astrakas, L.G.; Afrantou, T.; Ioannidis, P.; Grigoriadis, N.; Angelidis, P.; Tsalikakis, D.G.; Tsipouras, M.G. EEG window length evaluation for the detection of Alzheimer’s disease over different brain regions. Brain Sci. 2019, 9, 81. [Google Scholar] [CrossRef]
- Larrañaga, P.; Calvo, B.; Santana, R.; Bielza, C.; Galdiano, J.; Inza, I.; Lozano, J.A.; Armañanzas, R.; Santafé, G.; Pérez, A.; et al. Machine learning in bioinformatics. Brief Bioinform. 2006, 7, 86–112. [Google Scholar] [CrossRef]
- Plewczynski, D.; Tkacz, A.; Wyrwicz, L.S.; Rychlewski, L.; Ginalski, K. AutoMotif server for prediction of phosphorylation sites in proteins using support vector machine: 2007 update. J. Mol. Modeling 2008, 14, 69–76. [Google Scholar] [CrossRef] [PubMed]
| Kernel | |
|---|---|
| Linear | |
| Radial basis function | |
| Polynomial |
| Classifier Prediction Value | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual Value | Positive | True positives (TP) | False negatives (FN) |
| Negative | False positives (FP) | True negatives (TN) | |
| Feature | Base Calling Signal | ||||
|---|---|---|---|---|---|
| Method | Description | Adenine | Cytosine | Guanine | Thymine |
| Statistical Based | Mean | ||||
| Median | |||||
| Standard Deviation | |||||
| Entropy Based | PE | ||||
| MPE with s = 2 | |||||
| MPE with s = 3 | |||||
| Feature | SVM | Training (10%) | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Linear | 0.983 | 0.966 | 0.969 | 1.000 | 10.9 | 0.961 | 0.923 | 0.927 | 0.999 | 0.022 |
| Poly. Kernel | 0.970 | 0.940 | 0.945 | 1.000 | 11.8 | 0.960 | 0.921 | 0.924 | 1.000 | 0.010 | |
| RBF Kernel | 0.995 | 0.989 | 0.992 | 1.000 | 15.3 | 0.980 | 0.960 | 0.987 | 0.973 | 0.015 | |
| Median | Linear | 0.793 | 0.532 | 0.669 | 0.861 | 12.9 | 0.708 | 0.425 | 0.590 | 0.844 | 0.085 |
| Poly. Kernel | 0.905 | 0.782 | 0.761 | 1.000 | 10.2 | 0.772 | 0.555 | 0.637 | 0.928 | 0.133 | |
| RBF Kernel | 0.825 | 0.618 | 0.740 | 0.891 | 17.6 | 0.718 | 0.442 | 0.613 | 0.836 | 0.107 | |
| Standard Deviation | Linear | 0.958 | 0.902 | 0.937 | 0.969 | 10.7 | 0.903 | 0.809 | 0.854 | 0.958 | 0.055 |
| Poly. Kernel | 0.980 | 0.957 | 0.979 | 0.974 | 8.9 | 0.922 | 0.846 | 0.871 | 0.979 | 0.058 | |
| RBF Kernel | 0.970 | 0.932 | 0.972 | 0.958 | 15.1 | 0.963 | 0.927 | 0.967 | 0.960 | 0.007 | |
| All Statistics | Linear | 0.992 | 0.984 | 0.985 | 0.999 | 8.9 | 0.953 | 0.906 | 0.913 | 0.996 | 0.039 |
| Poly. Kernel | 0.985 | 0.969 | 0.975 | 1.000 | 10.7 | 0.938 | 0.878 | 0.885 | 0.996 | 0.047 | |
| RBF Kernel | 0.990 | 0.979 | 1.000 | 0.977 | 15.5 | 0.972 | 0.945 | 0.994 | 0.948 | 0.018 | |
| Training (20%) | Testing | ||||||||||
| Mean | Linear | 0.981 | 0.961 | 0.963 | 1.000 | 18.4 | 0.967 | 0.935 | 0.938 | 0.999 | 0.014 |
| Poly. Kernel | 0.997 | 0.995 | 0.995 | 1.000 | 19.4 | 0.964 | 0.928 | 0.934 | 0.996 | 0.033 | |
| RBF Kernel | 0.995 | 0.989 | 0.991 | 1.000 | 30.4 | 0.983 | 0.966 | 0.990 | 0.975 | 0.012 | |
| Median | Linear | 0.801 | 0.604 | 0.621 | 0.991 | 22.5 | 0.770 | 0.547 | 0.585 | 0.971 | 0.031 |
| Poly. Kernel | 0.905 | 0.796 | 0.892 | 0.890 | 19.2 | 0.834 | 0.671 | 0.812 | 0.863 | 0.071 | |
| RBF Kernel | 0.832 | 0.661 | 0.674 | 0.982 | 27.2 | 0.773 | 0.554 | 0.620 | 0.945 | 0.059 | |
| Standard Deviation | Linear | 0.955 | 0.908 | 0.932 | 0.978 | 17.7 | 0.931 | 0.863 | 0.884 | 0.982 | 0.024 |
| Poly. Kernel | 0.987 | 0.973 | 1.000 | 0.971 | 12.7 | 0.947 | 0.895 | 0.926 | 0.970 | 0.040 | |
| RBF Kernel | 0.990 | 0.979 | 0.993 | 0.985 | 26.0 | 0.964 | 0.928 | 0.976 | 0.951 | 0.026 | |
| All Statistics | Linear | 0.989 | 0.978 | 0.979 | 1.000 | 17.0 | 0.970 | 0.941 | 0.945 | 0.998 | 0.019 |
| Poly. Kernel | 0.990 | 0.979 | 0.979 | 1.000 | 16.3 | 0.970 | 0.941 | 0.945 | 0.998 | 0.020 | |
| RBF Kernel | 0.997 | 0.994 | 1.000 | 0.993 | 30.1 | 0.975 | 0.950 | 0.995 | 0.953 | 0.022 | |
| Training (30%) | Testing | ||||||||||
| Mean | Linear | 0.986 | 0.972 | 0.974 | 1.000 | 22.7 | 0.968 | 0.937 | 0.939 | 1.000 | 0.018 |
| Poly. Kernel | 0.995 | 0.989 | 0.990 | 1.000 | 16.8 | 0.976 | 0.952 | 0.958 | 0.995 | 0.019 | |
| RBF Kernel | 0.991 | 0.983 | 0.983 | 1.000 | 43.2 | 0.984 | 0.968 | 0.991 | 0.976 | 0.007 | |
| Median | Linear | 0.807 | 0.617 | 0.638 | 0.989 | 31.0 | 0.784 | 0.574 | 0.608 | 0.976 | 0.023 |
| Poly. Kernel | 0.921 | 0.839 | 0.897 | 0.934 | 20.4 | 0.839 | 0.681 | 0.809 | 0.879 | 0.082 | |
| RBF Kernel | 0.846 | 0.696 | 0.719 | 0.990 | 36.6 | 0.764 | 0.533 | 0.564 | 0.977 | 0.082 | |
| Standard Deviation | Linear | 0.954 | 0.908 | 0.925 | 0.984 | 25.5 | 0.936 | 0.872 | 0.897 | 0.978 | 0.018 |
| Poly. Kernel | 0.988 | 0.975 | 0.993 | 0.980 | 14.6 | 0.955 | 0.909 | 0.947 | 0.963 | 0.033 | |
| RBF Kernel | 0.985 | 0.969 | 0.987 | 0.982 | 31.6 | 0.972 | 0.945 | 0.986 | 0.958 | 0.013 | |
| All Statistics | Linear | 0.990 | 0.980 | 0.981 | 1.000 | 21.3 | 0.976 | 0.952 | 0.954 | 0.999 | 0.014 |
| Poly. Kernel | 0.995 | 0.989 | 0.989 | 1.000 | 22.1 | 0.972 | 0.945 | 0.952 | 0.995 | 0.023 | |
| RBF Kernel | 0.996 | 0.993 | 0.996 | 0.996 | 41.5 | 0.980 | 0.959 | 0.995 | 0.962 | 0.016 | |
| Training (40%) | Testing | ||||||||||
| Mean | Linear | 0.984 | 0.969 | 0.970 | 1.000 | 25.0 | 0.970 | 0.941 | 0.944 | 1.000 | 0.014 |
| Poly. Kernel | 0.990 | 0.979 | 0.985 | 0.994 | 29.1 | 0.980 | 0.960 | 0.963 | 0.998 | 0.010 | |
| RBF Kernel | 0.993 | 0.987 | 0.987 | 1.000 | 57.3 | 0.990 | 0.979 | 0.991 | 0.987 | 0.003 | |
| Median | Linear | 0.818 | 0.636 | 0.651 | 0.990 | 38.5 | 0.789 | 0.586 | 0.624 | 0.975 | 0.029 |
| Poly. Kernel | 0.916 | 0.829 | 0.931 | 0.894 | 29.0 | 0.840 | 0.682 | 0.855 | 0.829 | 0.076 | |
| RBF Kernel | 0.828 | 0.661 | 0.684 | 0.989 | 48.0 | 0.827 | 0.656 | 0.678 | 0.984 | 0.001 | |
| Standard Deviation | Linear | 0.954 | 0.907 | 0.923 | 0.987 | 33.2 | 0.932 | 0.865 | 0.890 | 0.979 | 0.022 |
| Poly. Kernel | 0.995 | 0.989 | 0.997 | 0.991 | 17.1 | 0.968 | 0.936 | 0.971 | 0.964 | 0.027 | |
| RBF Kernel | 0.986 | 0.972 | 0.989 | 0.981 | 33.1 | 0.974 | 0.948 | 0.982 | 0.965 | 0.012 | |
| All Statistics | Linear | 0.992 | 0.984 | 0.985 | 1.000 | 23.8 | 0.975 | 0.951 | 0.954 | 0.999 | 0.017 |
| Poly. Kernel | 0.995 | 0.989 | 0.990 | 1.000 | 21.0 | 0.981 | 0.963 | 0.967 | 0.996 | 0.014 | |
| RBF Kernel | 0.996 | 0.992 | 0.995 | 0.997 | 41.5 | 0.984 | 0.968 | 0.983 | 0.984 | 0.012 | |
| Training (50%) | Testing | ||||||||||
| Mean | Linear | 0.987 | 0.974 | 0.975 | 1.000 | 25.4 | 0.971 | 0.941 | 0.943 | 1.000 | 0.016 |
| Poly. Kernel | 0.992 | 0.983 | 0.986 | 0.998 | 29.8 | 0.980 | 0.959 | 0.968 | 0.993 | 0.012 | |
| RBF Kernel | 0.993 | 0.985 | 0.990 | 0.995 | 73.4 | 0.989 | 0.977 | 0.988 | 0.988 | 0.004 | |
| Median | Linear | 0.817 | 0.639 | 0.655 | 0.995 | 47.8 | 0.803 | 0.611 | 0.632 | 0.987 | 0.014 |
| Poly. Kernel | 0.913 | 0.823 | 0.959 | 0.857 | 34.4 | 0.867 | 0.735 | 0.900 | 0.837 | 0.046 | |
| RBF Kernel | 0.841 | 0.679 | 0.677 | 1.000 | 54.4 | 0.802 | 0.614 | 0.643 | 0.992 | 0.039 | |
| Standard Deviation | Linear | 0.949 | 0.898 | 0.919 | 0.981 | 41.1 | 0.937 | 0.874 | 0.900 | 0.977 | 0.012 |
| Poly. Kernel | 0.984 | 0.967 | 0.990 | 0.976 | 32.2 | 0.970 | 0.939 | 0.965 | 0.974 | 0.014 | |
| RBF Kernel | 0.987 | 0.973 | 0.995 | 0.977 | 35.7 | 0.968 | 0.935 | 0.977 | 0.954 | 0.019 | |
| All Statistics | Linear | 0.995 | 0.990 | 0.991 | 1.000 | 21.3 | 0.980 | 0.961 | 0.963 | 0.999 | 0.015 |
| Poly. Kernel | 0.998 | 0.995 | 0.996 | 1.000 | 18.0 | 0.979 | 0.957 | 0.966 | 0.992 | 0.019 | |
| RBF Kernel | 0.996 | 0.991 | 0.996 | 0.995 | 37.8 | 0.991 | 0.981 | 0.989 | 0.990 | 0.005 | |
| Feature | SVM | Training (10%) | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PE | Linear | 0.944 | 0.880 | 0.984 | 0.894 | 10.8 | 0.933 | 0.867 | 0.957 | 0.909 | 0.011 |
| Poly. Kernel | 0.960 | 0.919 | 1.000 | 0.921 | 8.4 | 0.950 | 0.900 | 0.977 | 0.921 | 0.010 | |
| RBF Kernel | 0.965 | 0.928 | 1.000 | 0.931 | 16.1 | 0.950 | 0.900 | 0.994 | 0.902 | 0.015 | |
| MPE with s = 2 | Linear | 0.954 | 0.904 | 0.995 | 0.911 | 10.8 | 0.941 | 0.882 | 0.973 | 0.905 | 0.013 |
| Poly. Kernel | 0.995 | 0.990 | 1.000 | 0.990 | 9.7 | 0.945 | 0.890 | 0.954 | 0.935 | 0.050 | |
| RBF Kernel | 0.945 | 0.890 | 1.000 | 0.894 | 15.5 | 0.956 | 0.911 | 1.000 | 0.909 | 0.011 | |
| MPE with s = 3 | Linear | 0.949 | 0.894 | 0.984 | 0.909 | 11.3 | 0.937 | 0.874 | 0.963 | 0.909 | 0.012 |
| Poly. Kernel | 0.980 | 0.959 | 1.000 | 0.958 | 8.5 | 0.935 | 0.871 | 0.934 | 0.937 | 0.045 | |
| RBF Kernel | 0.955 | 0.905 | 1.000 | 0.892 | 15.6 | 0.955 | 0.909 | 1.000 | 0.907 | 0.000 | |
| All Entropies | Linear | 0.954 | 0.903 | 0.987 | 0.915 | 10.1 | 0.945 | 0.890 | 0.981 | 0.905 | 0.009 |
| Poly. Kernel | 0.980 | 0.956 | 1.000 | 0.950 | 11.0 | 0.954 | 0.908 | 0.987 | 0.919 | 0.026 | |
| RBF Kernel | 0.970 | 0.938 | 1.000 | 0.940 | 15.7 | 0.955 | 0.909 | 0.994 | 0.911 | 0.015 | |
| Training (20%) | Testing | ||||||||||
| PE | Linear | 0.945 | 0.889 | 0.990 | 0.897 | 20.6 | 0.949 | 0.899 | 0.988 | 0.908 | 0.004 |
| Poly. Kernel | 0.980 | 0.959 | 1.000 | 0.956 | 12.7 | 0.946 | 0.893 | 0.953 | 0.940 | 0.034 | |
| RBF Kernel | 0.955 | 0.906 | 1.000 | 0.896 | 31.4 | 0.953 | 0.907 | 1.000 | 0.905 | 0.002 | |
| MPE with s = 2 | Linear | 0.946 | 0.889 | 0.992 | 0.894 | 21.2 | 0.950 | 0.901 | 0.989 | 0.909 | 0.004 |
| Poly. Kernel | 0.977 | 0.954 | 0.995 | 0.958 | 16.1 | 0.947 | 0.894 | 0.989 | 0.901 | 0.030 | |
| RBF Kernel | 0.955 | 0.909 | 1.000 | 0.907 | 32.9 | 0.955 | 0.909 | 1.000 | 0.906 | 0.000 | |
| MPE with s = 3 | Linear | 0.948 | 0.894 | 0.992 | 0.904 | 20.4 | 0.950 | 0.900 | 0.989 | 0.907 | 0.002 |
| Poly. Kernel | 0.970 | 0.938 | 0.991 | 0.952 | 16.9 | 0.949 | 0.897 | 0.982 | 0.912 | 0.021 | |
| RBF Kernel | 0.965 | 0.928 | 0.993 | 0.933 | 31.2 | 0.941 | 0.883 | 0.972 | 0.910 | 0.024 | |
| All Entropies | Linear | 0.952 | 0.902 | 0.989 | 0.911 | 19.8 | 0.950 | 0.900 | 0.988 | 0.909 | 0.002 |
| Poly. Kernel | 0.987 | 0.971 | 1.000 | 0.964 | 10.6 | 0.966 | 0.932 | 0.977 | 0.955 | 0.021 | |
| RBF Kernel | 0.975 | 0.948 | 1.000 | 0.947 | 34.4 | 0.950 | 0.899 | 0.995 | 0.901 | 0.025 | |
| Training (30%) | Testing | ||||||||||
| PE | Linear | 0.949 | 0.897 | 0.989 | 0.906 | 29.4 | 0.948 | 0.896 | 0.987 | 0.906 | 0.001 |
| Poly. Kernel | 0.986 | 0.973 | 1.000 | 0.972 | 17.5 | 0.957 | 0.915 | 0.970 | 0.944 | 0.029 | |
| RBF Kernel | 0.956 | 0.911 | 1.000 | 0.905 | 49.9 | 0.954 | 0.908 | 1.000 | 0.906 | 0.002 | |
| MPE with s = 2 | Linear | 0.953 | 0.905 | 0.993 | 0.909 | 28.6 | 0.949 | 0.897 | 0.990 | 0.905 | 0.004 |
| Poly. Kernel | 0.996 | 0.993 | 0.996 | 0.995 | 11.7 | 0.964 | 0.928 | 0.970 | 0.959 | 0.032 | |
| RBF Kernel | 0.950 | 0.896 | 1.000 | 0.888 | 50.2 | 0.956 | 0.912 | 1.000 | 0.911 | 0.006 | |
| MPE with s = 3 | Linear | 0.950 | 0.899 | 0.993 | 0.904 | 30.7 | 0.950 | 0.899 | 0.989 | 0.907 | 0.000 |
| Poly. Kernel | 0.981 | 0.962 | 0.989 | 0.972 | 15.8 | 0.937 | 0.874 | 0.918 | 0.961 | 0.044 | |
| RBF Kernel | 0.963 | 0.924 | 1.000 | 0.917 | 50.0 | 0.951 | 0.902 | 1.000 | 0.901 | 0.012 | |
| All Entropies | Linear | 0.960 | 0.920 | 0.991 | 0.928 | 28.2 | 0.948 | 0.896 | 0.990 | 0.901 | 0.012 |
| Poly. Kernel | 0.996 | 0.996 | 1.000 | 0.992 | 10.6 | 0.983 | 0.967 | 0.983 | 0.983 | 0.013 | |
| RBF Kernel | 0.983 | 0.965 | 1.000 | 0.963 | 36.1 | 0.970 | 0.939 | 1.000 | 0.937 | 0.013 | |
| Training (40%) | Testing | ||||||||||
| PE | Linear | 0.951 | 0.901 | 0.989 | 0.909 | 39.0 | 0.947 | 0.893 | 0.987 | 0.903 | 0.004 |
| Poly. Kernel | 0.990 | 0.979 | 0.995 | 0.982 | 13.5 | 0.969 | 0.938 | 0.968 | 0.970 | 0.021 | |
| RBF Kernel | 0.948 | 0.896 | 1.000 | 0.891 | 70.0 | 0.959 | 0.917 | 1.000 | 0.914 | 0.011 | |
| MPE with s = 2 | Linear | 0.951 | 0.901 | 0.994 | 0.905 | 37.4 | 0.950 | 0.899 | 0.989 | 0.906 | 0.001 |
| Poly. Kernel | 0.996 | 0.992 | 1.000 | 0.991 | 14.6 | 0.961 | 0.923 | 0.960 | 0.963 | 0.035 | |
| RBF Kernel | 0.948 | 0.897 | 1.000 | 0.898 | 68.8 | 0.959 | 0.917 | 1.000 | 0.912 | 0.011 | |
| MPE with s = 3 | Linear | 0.949 | 0.896 | 0.991 | 0.903 | 40.7 | 0.951 | 0.901 | 0.990 | 0.908 | 0.002 |
| Poly. Kernel | 0.976 | 0.951 | 0.995 | 0.952 | 21.3 | 0.952 | 0.904 | 0.971 | 0.933 | 0.024 | |
| RBF Kernel | 0.956 | 0.911 | 1.000 | 0.904 | 68.4 | 0.954 | 0.908 | 1.000 | 0.907 | 0.002 | |
| All Entropies | Linear | 0.964 | 0.927 | 0.994 | 0.928 | 30.3 | 0.952 | 0.904 | 0.990 | 0.912 | 0.012 |
| Poly. Kernel | 0.993 | 0.987 | 1.000 | 0.986 | 14.0 | 0.977 | 0.954 | 0.987 | 0.967 | 0.016 | |
| RBF Kernel | 0.996 | 0.992 | 1.000 | 0.991 | 29.3 | 0.989 | 0.978 | 1.000 | 0.977 | 0.007 | |
| Training (50%) | Testing | ||||||||||
| PE | Linear | 0.948 | 0.895 | 0.990 | 0.903 | 49.5 | 0.951 | 0.901 | 0.989 | 0.909 | 0.003 |
| Poly. Kernel | 0.992 | 0.983 | 0.995 | 0.987 | 11.1 | 0.960 | 0.919 | 0.971 | 0.948 | 0.032 | |
| RBF Kernel | 0.959 | 0.917 | 1.000 | 0.916 | 76.6 | 0.955 | 0.908 | 1.000 | 0.903 | 0.004 | |
| MPE with s = 2 | Linear | 0.952 | 0.904 | 0.996 | 0.905 | 41.4 | 0.950 | 0.900 | 0.989 | 0.907 | 0.002 |
| Poly. Kernel | 0.996 | 0.991 | 0.996 | 0.995 | 13.4 | 0.972 | 0.943 | 0.966 | 0.977 | 0.024 | |
| RBF Kernel | 0.947 | 0.893 | 1.000 | 0.893 | 84.4 | 0.963 | 0.924 | 1.000 | 0.919 | 0.016 | |
| MPE with s = 3 | Linear | 0.951 | 0.902 | 0.992 | 0.907 | 46.6 | 0.949 | 0.898 | 0.991 | 0.904 | 0.002 |
| Poly. Kernel | 0.984 | 0.967 | 0.996 | 0.969 | 16.0 | 0.946 | 0.891 | 0.960 | 0.931 | 0.038 | |
| RBF Kernel | 0.954 | 0.907 | 1.000 | 0.903 | 86.4 | 0.956 | 0.911 | 1.000 | 0.909 | 0.002 | |
| All Entropies | Linear | 0.966 | 0.932 | 0.994 | 0.935 | 30.8 | 0.956 | 0.912 | 0.991 | 0.919 | 0.010 |
| Poly. Kernel | 0.999 | 0.997 | 1.000 | 0.997 | 14.6 | 0.981 | 0.962 | 0.991 | 0.971 | 0.018 | |
| RBF Kernel | 0.988 | 0.975 | 1.000 | 0.975 | 41.9 | 0.979 | 0.957 | 1.000 | 0.953 | 0.009 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Öz, E.; Aşkın, Ö.E. Classification of Hepatitis Viruses from Sequencing Chromatograms Using Multiscale Permutation Entropy and Support Vector Machines. Entropy 2019, 21, 1149. https://doi.org/10.3390/e21121149
Öz E, Aşkın ÖE. Classification of Hepatitis Viruses from Sequencing Chromatograms Using Multiscale Permutation Entropy and Support Vector Machines. Entropy. 2019; 21(12):1149. https://doi.org/10.3390/e21121149
Chicago/Turabian StyleÖz, Ersoy, and Öyküm Esra Aşkın. 2019. "Classification of Hepatitis Viruses from Sequencing Chromatograms Using Multiscale Permutation Entropy and Support Vector Machines" Entropy 21, no. 12: 1149. https://doi.org/10.3390/e21121149
APA StyleÖz, E., & Aşkın, Ö. E. (2019). Classification of Hepatitis Viruses from Sequencing Chromatograms Using Multiscale Permutation Entropy and Support Vector Machines. Entropy, 21(12), 1149. https://doi.org/10.3390/e21121149





