Adaptive Multiscale Symbolic-Dynamics Entropy for Condition Monitoring of Rotating Machinery
Abstract
1. Introduction
2. Adaptive Multiscale Symbolic-Dynamics Entropy (AMSDE)
2.1. Adaptive Coarse-Graining Algorithm
2.2. AMSDE
3. Application of AMSDE to Condition Monitoring of Rotating Machinery
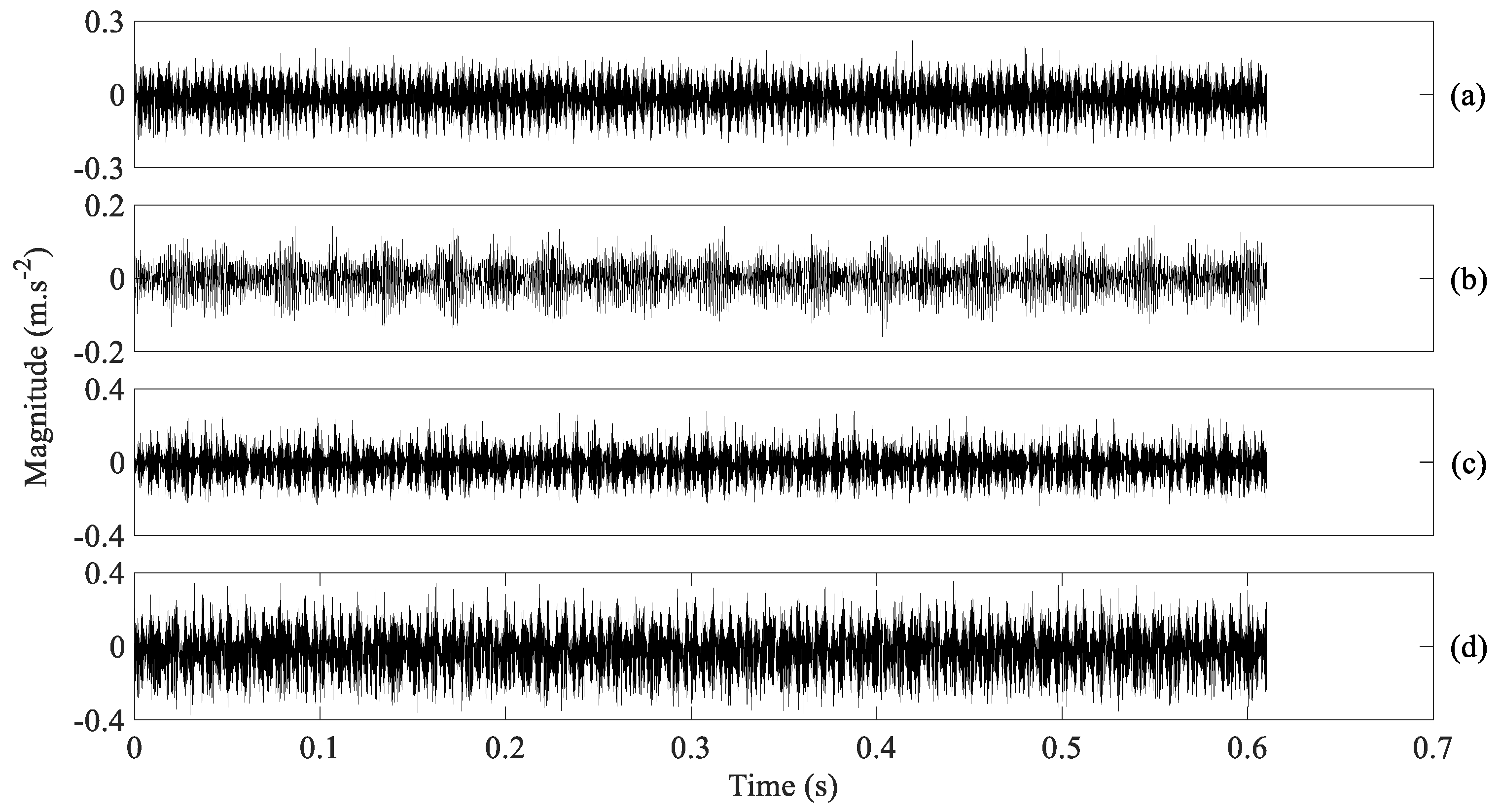
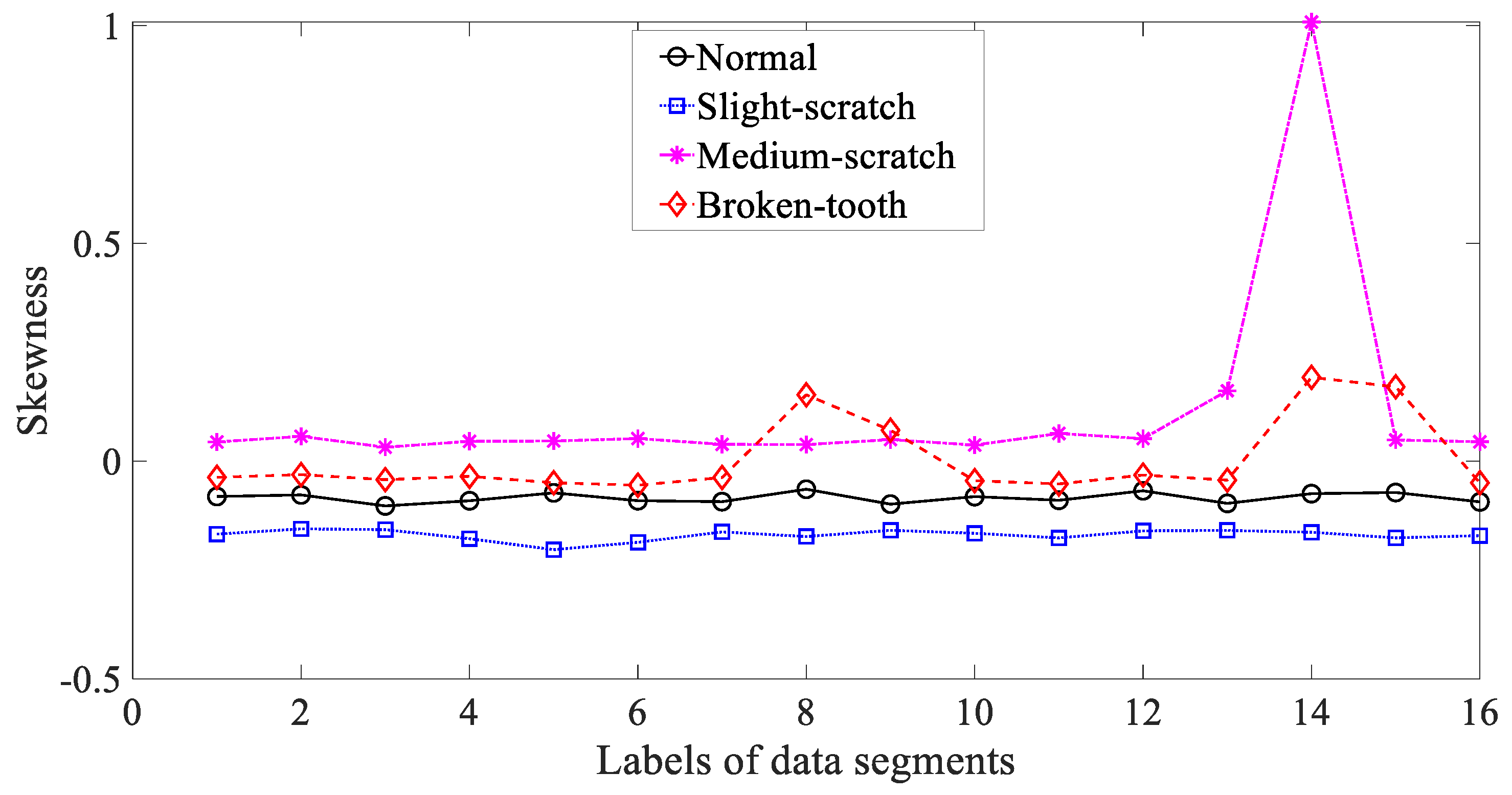
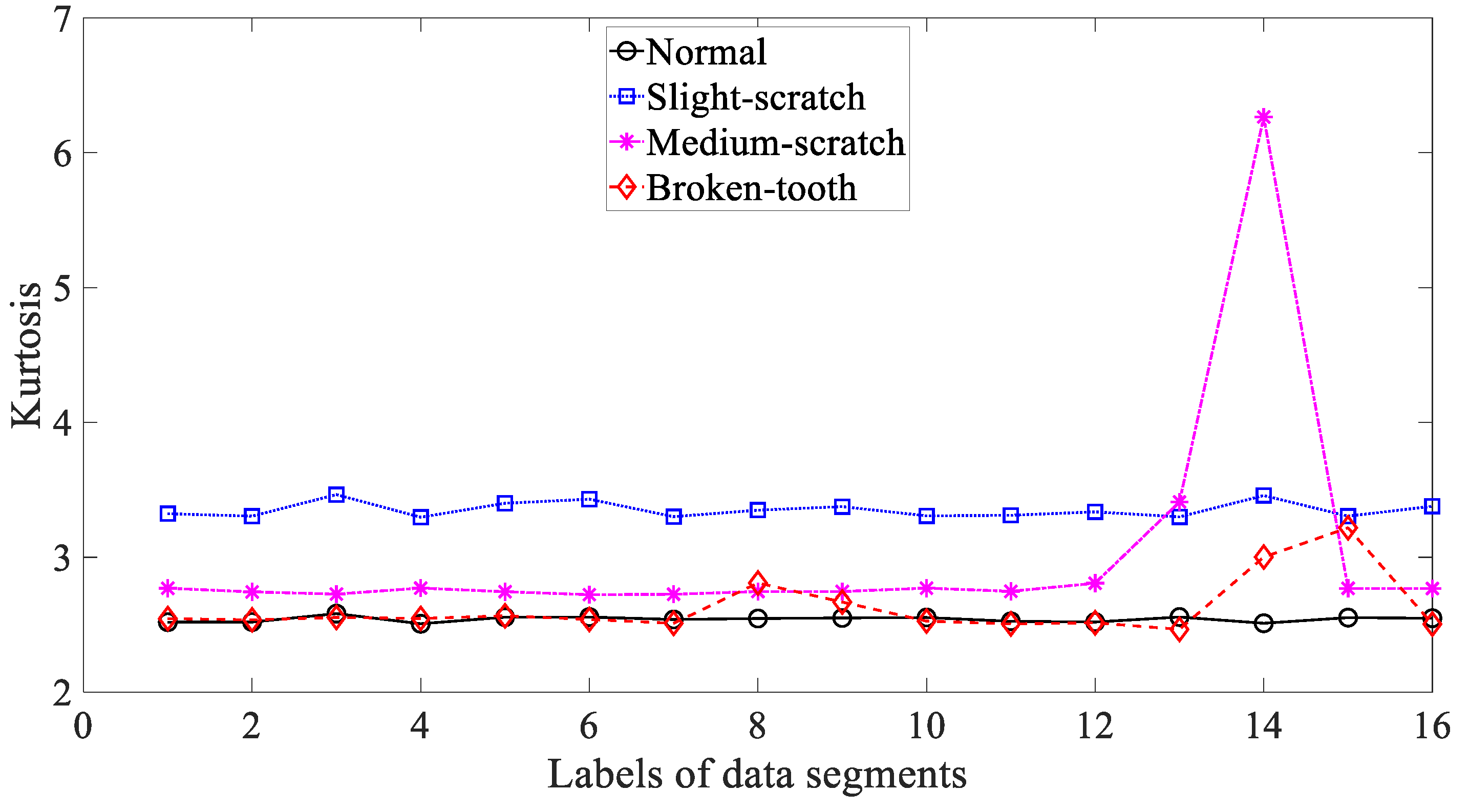
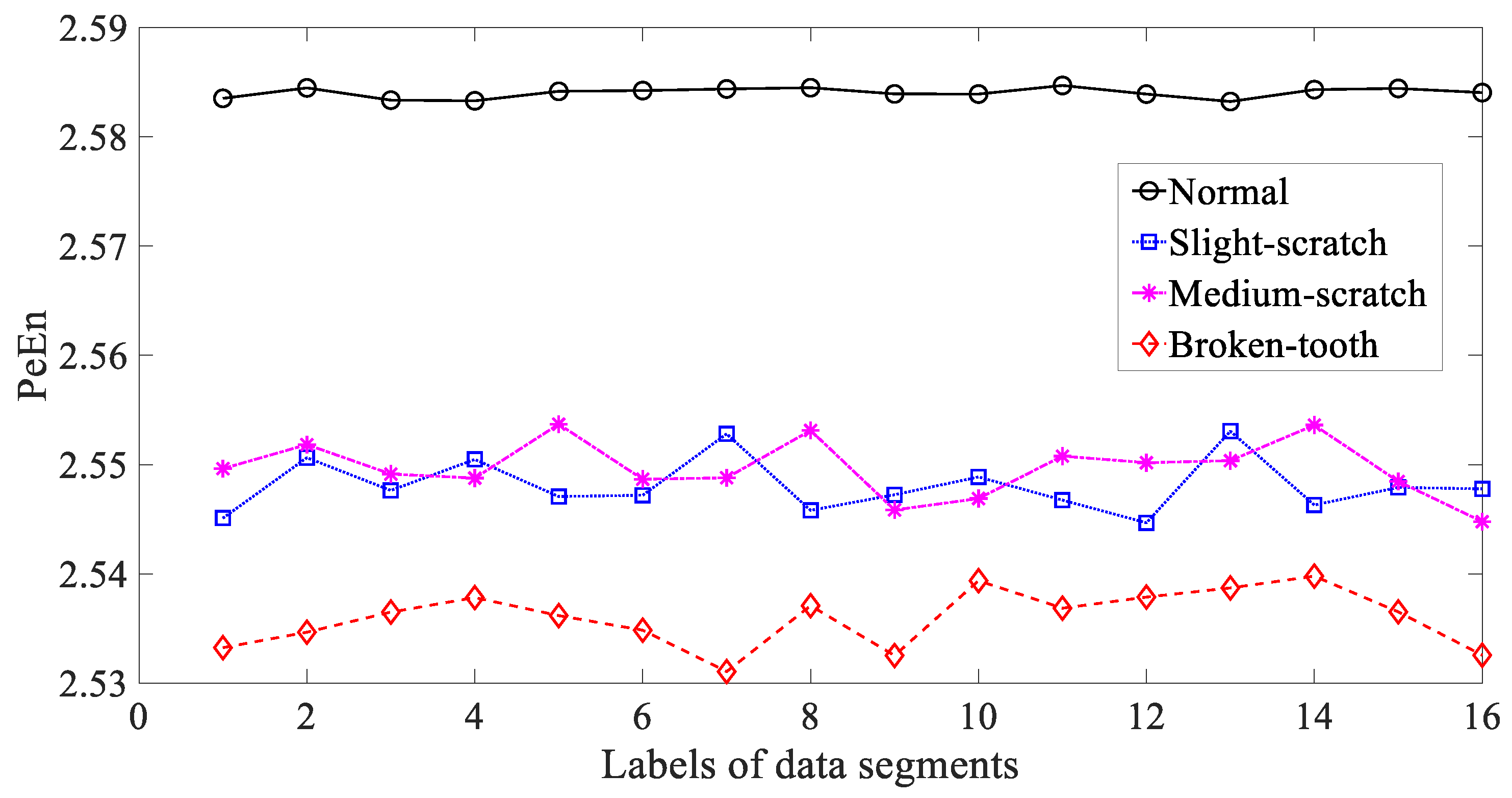
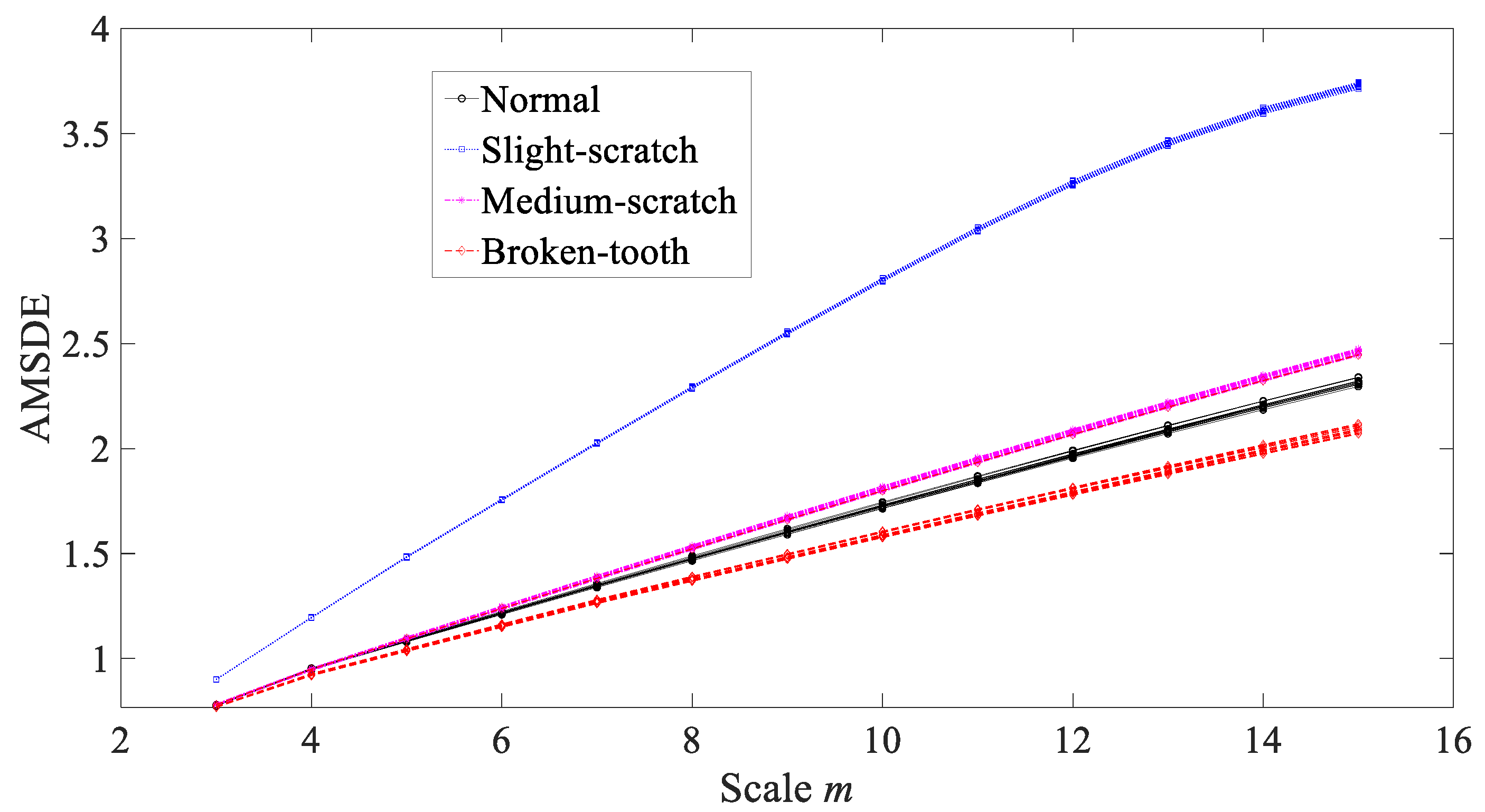
3.1. Condition Monitoring of Gears
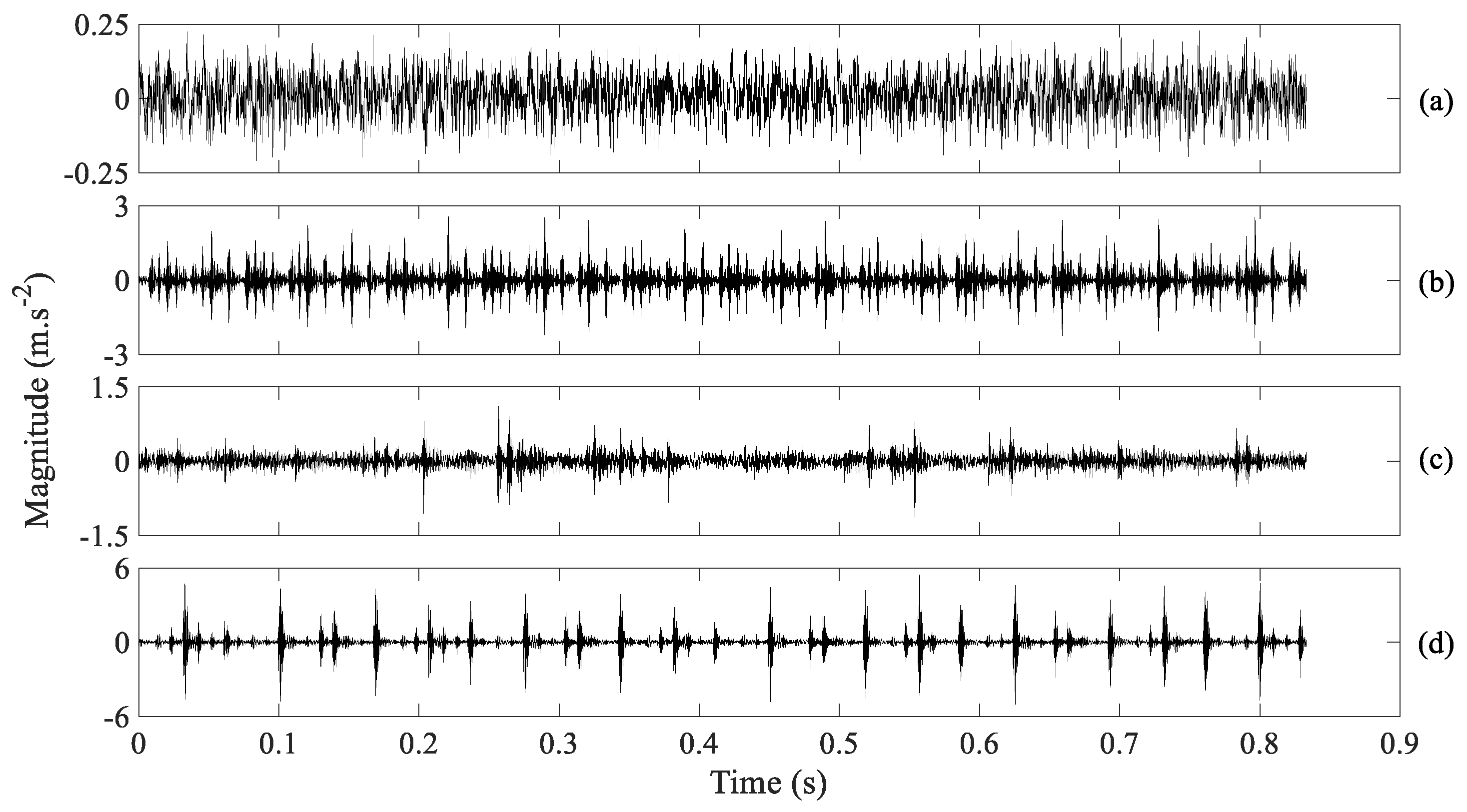
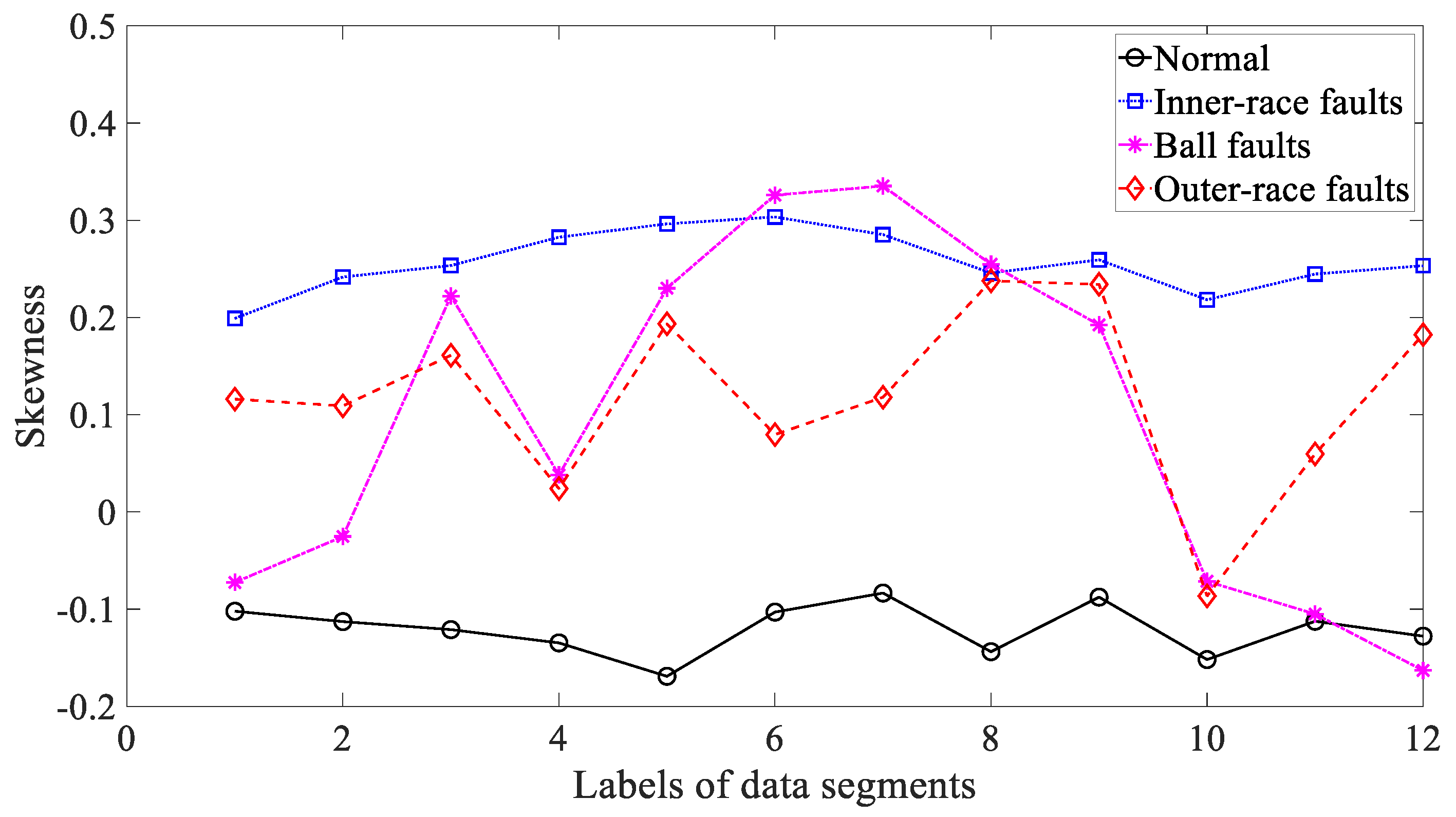
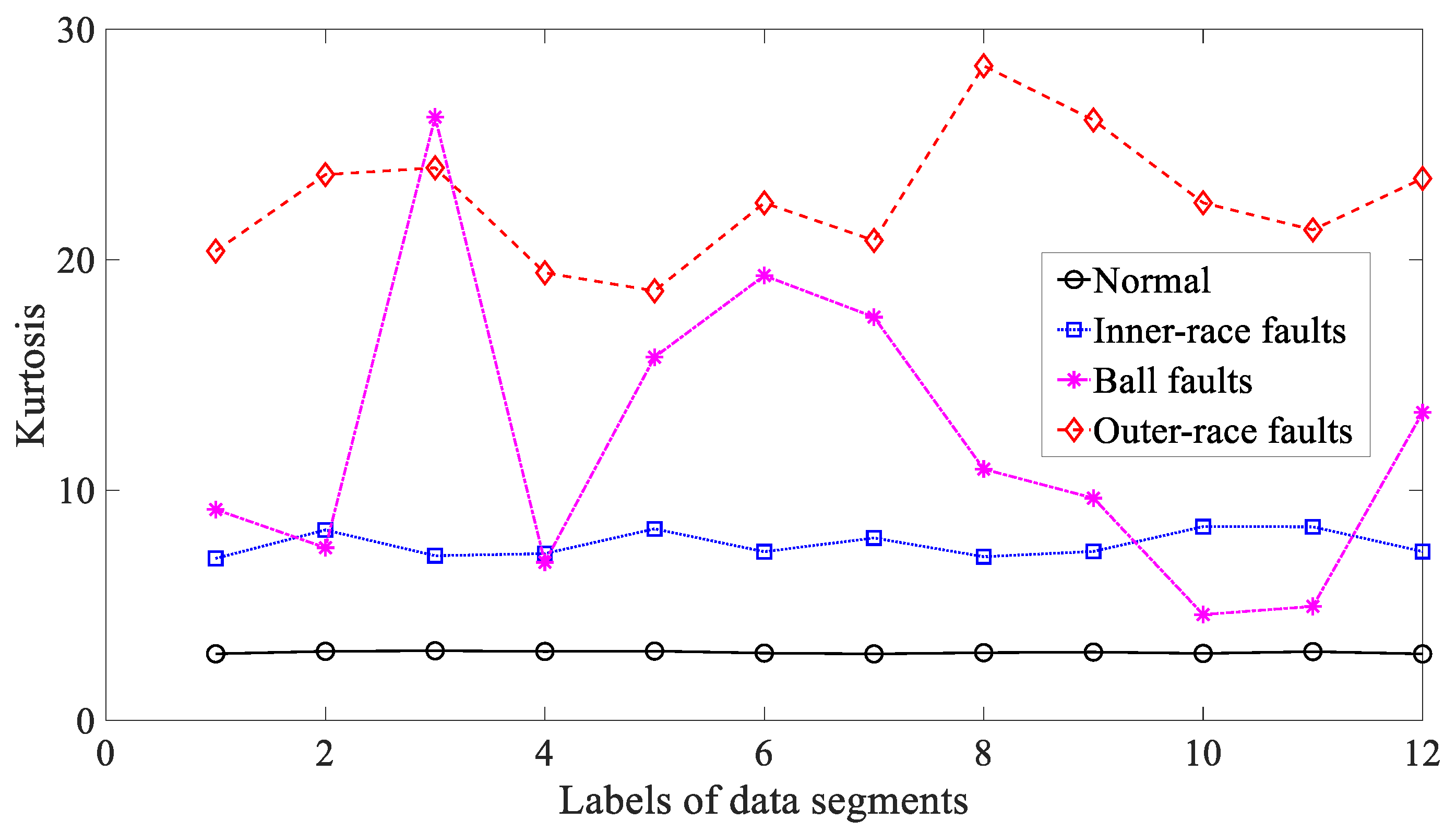
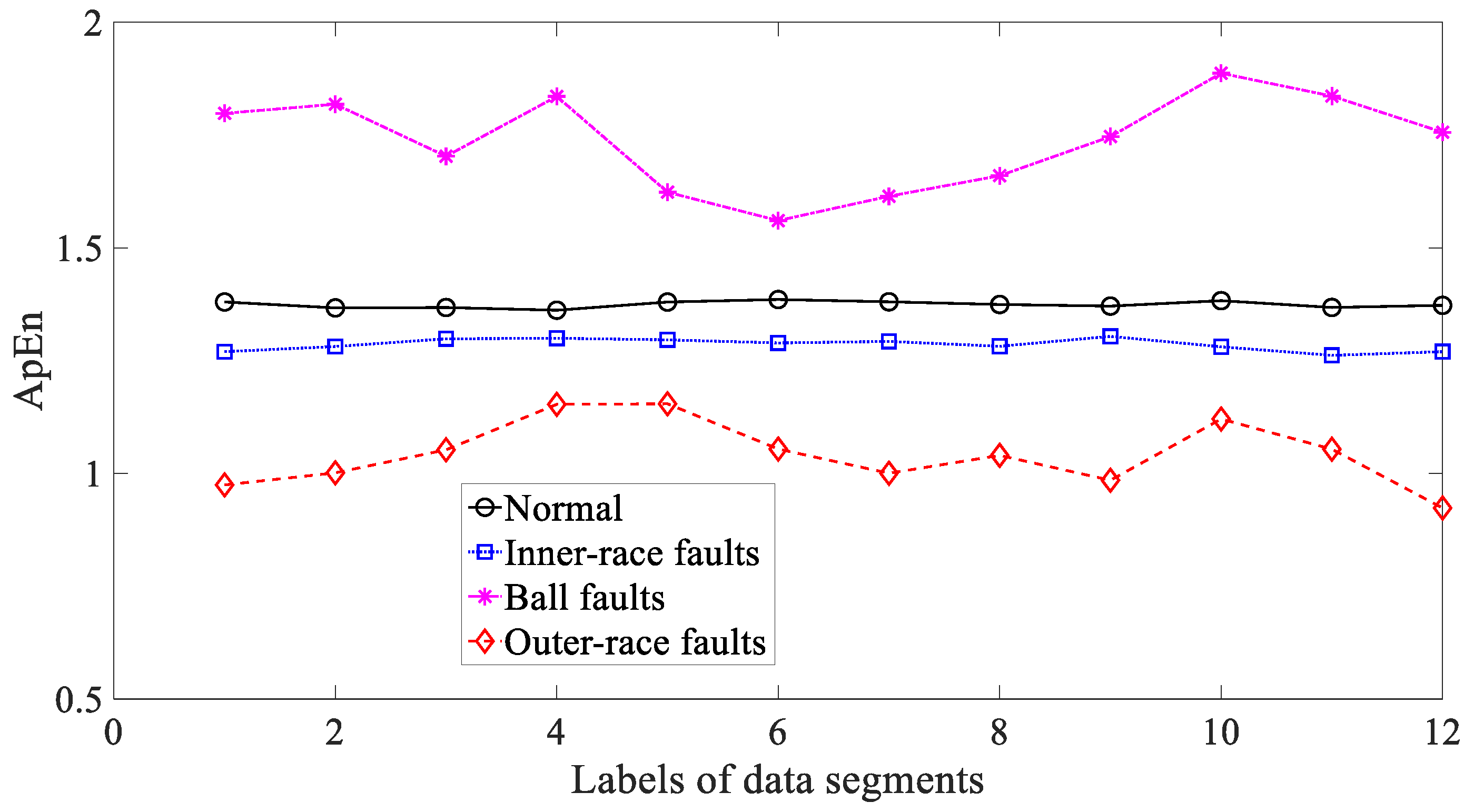
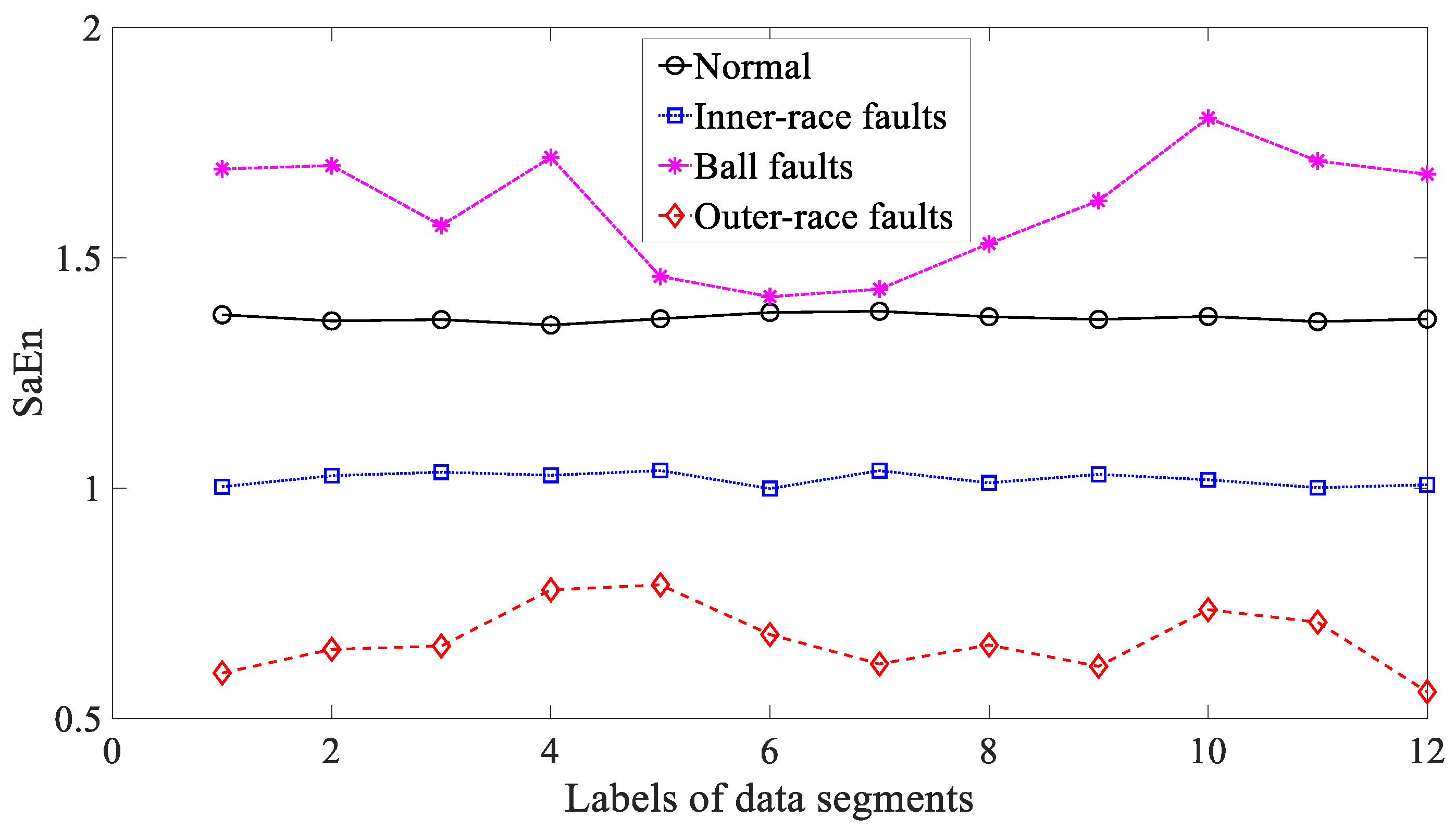
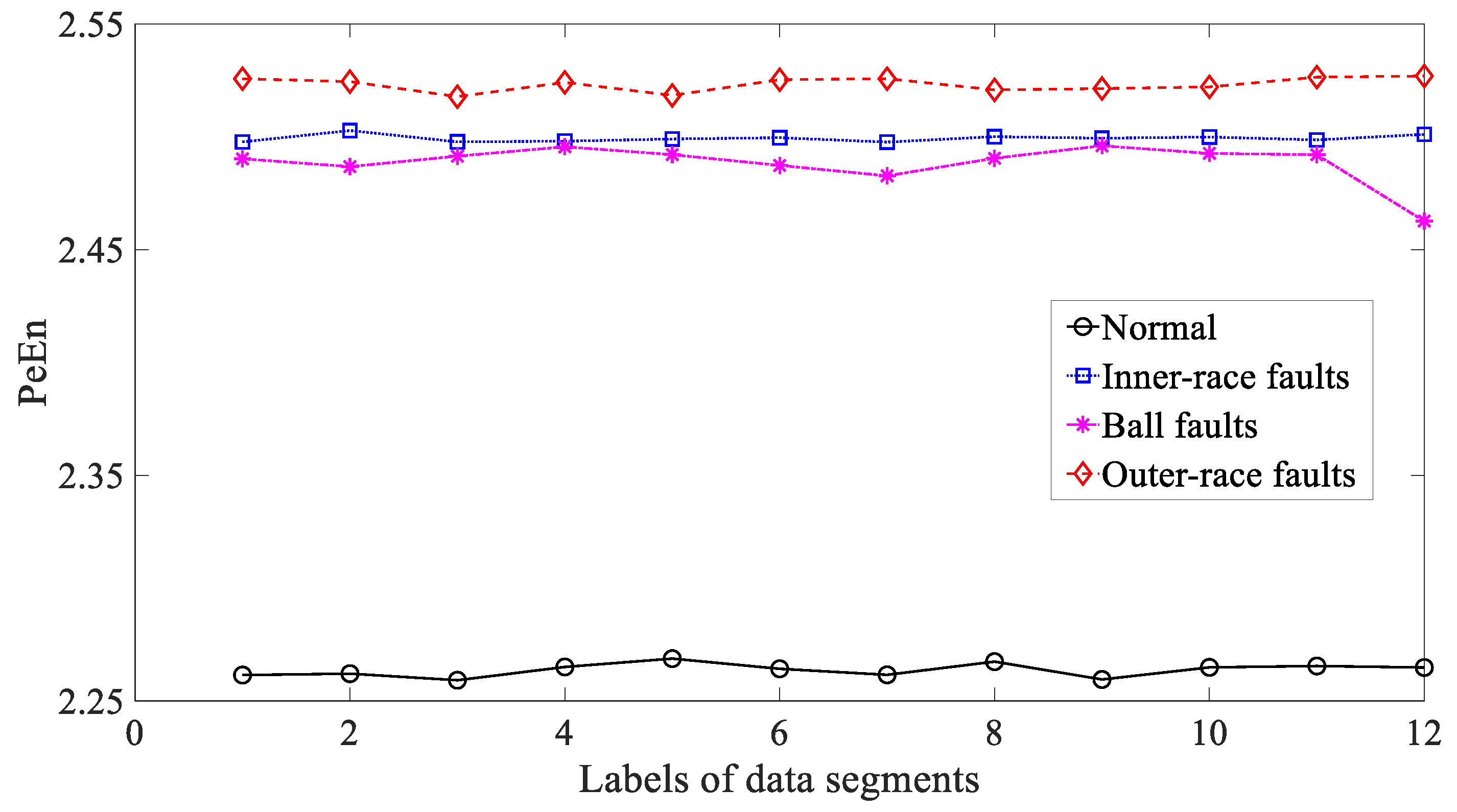
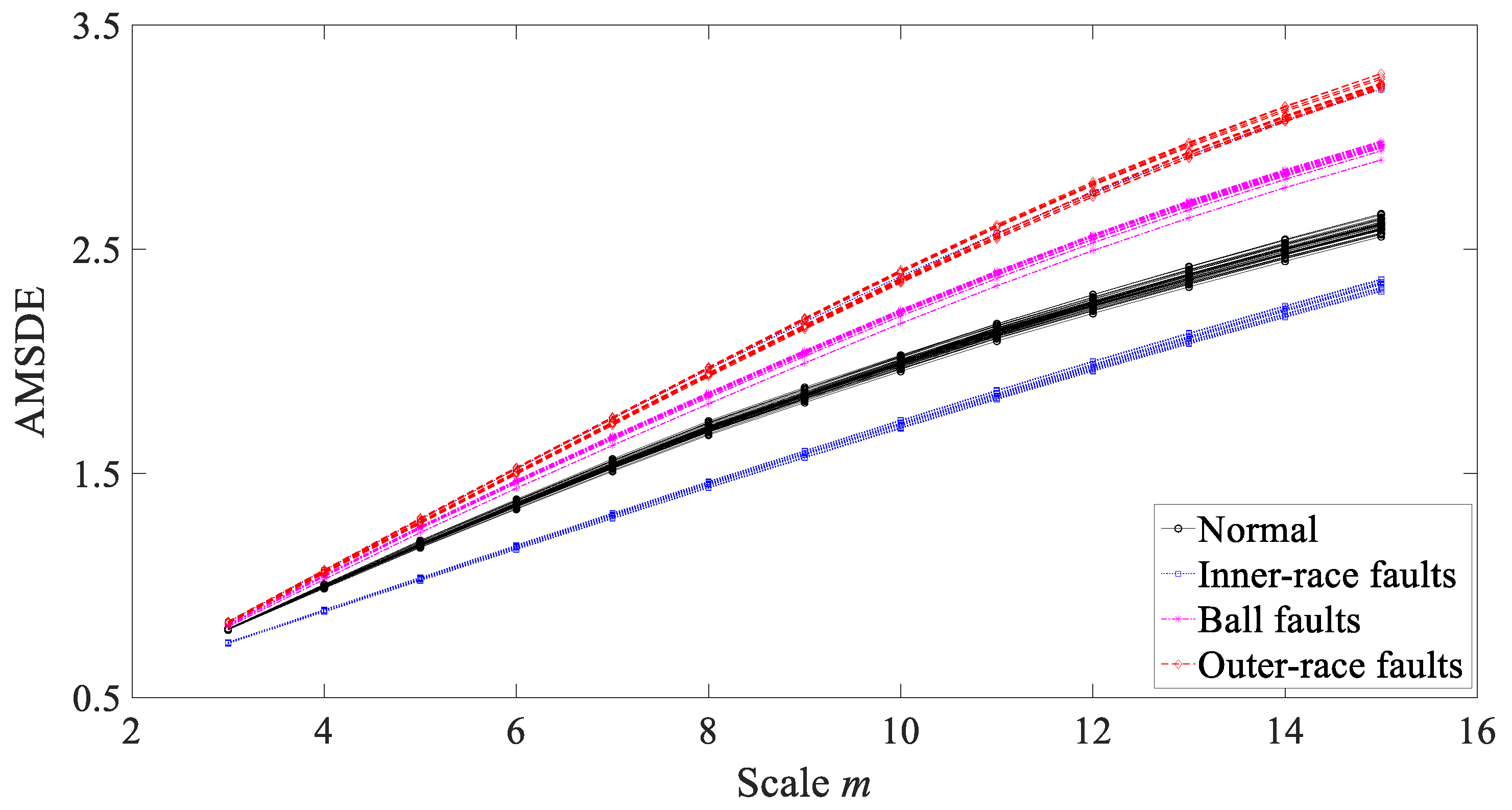
3.2. Condition Monitoring of Rolling Bearings
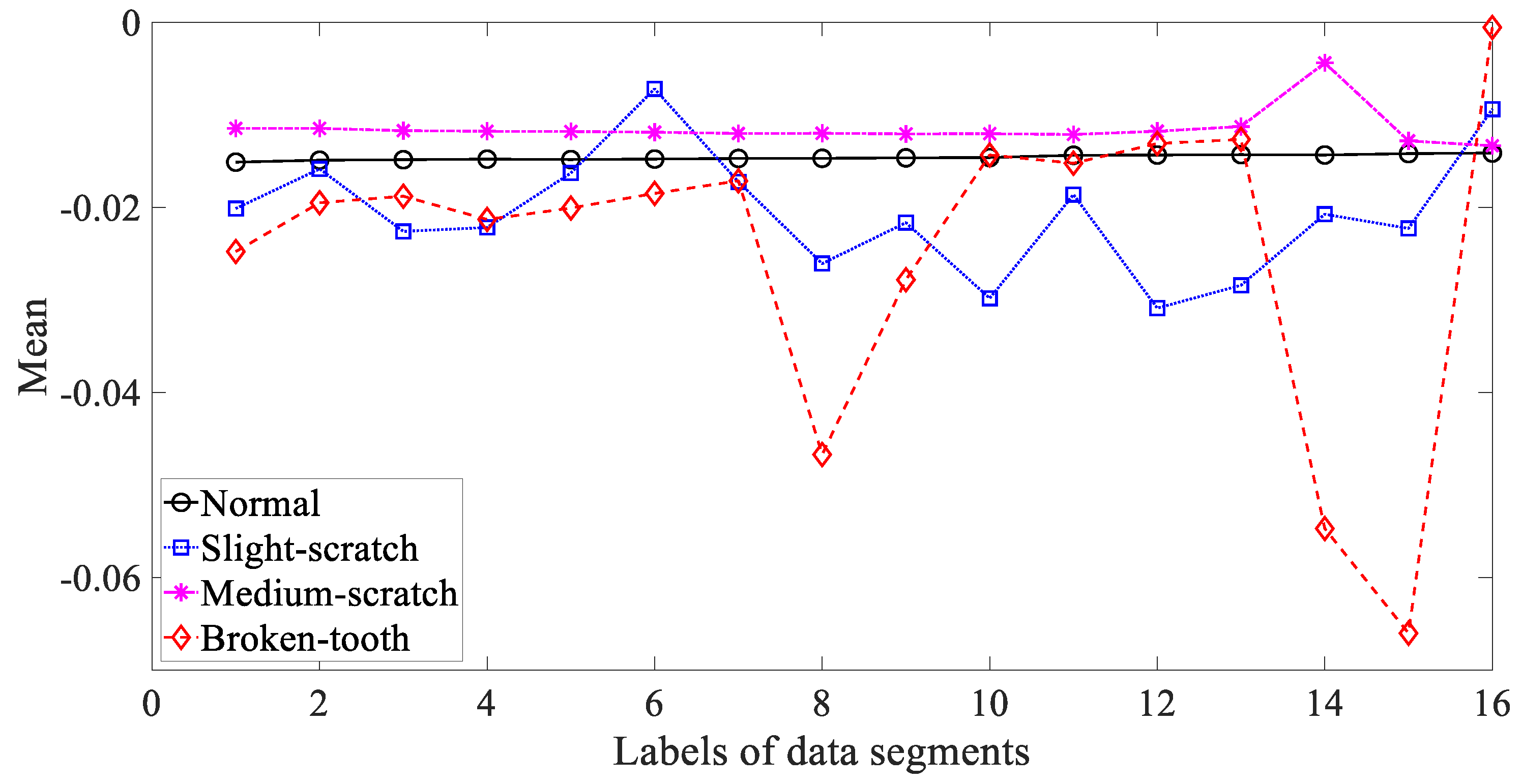
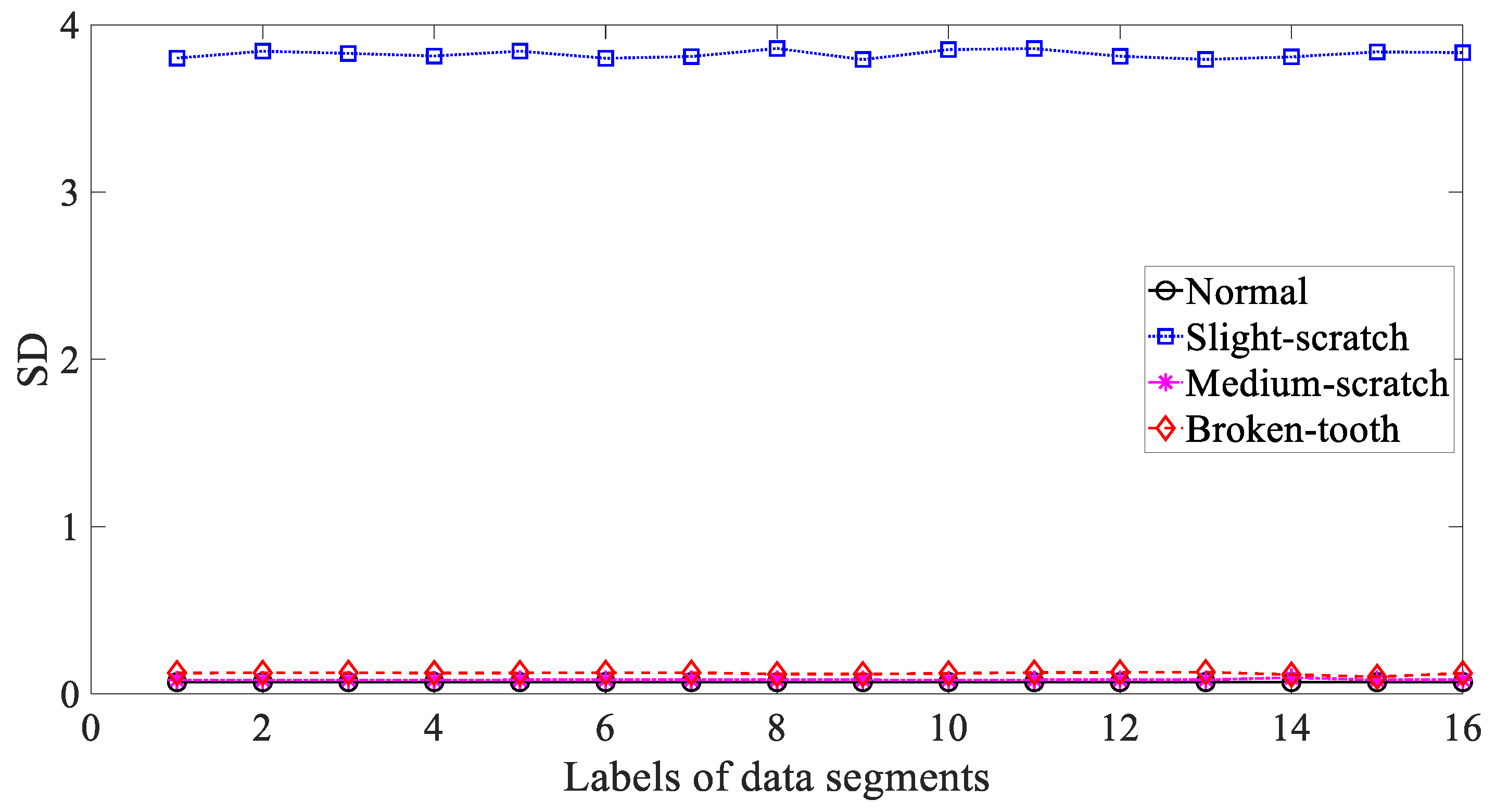
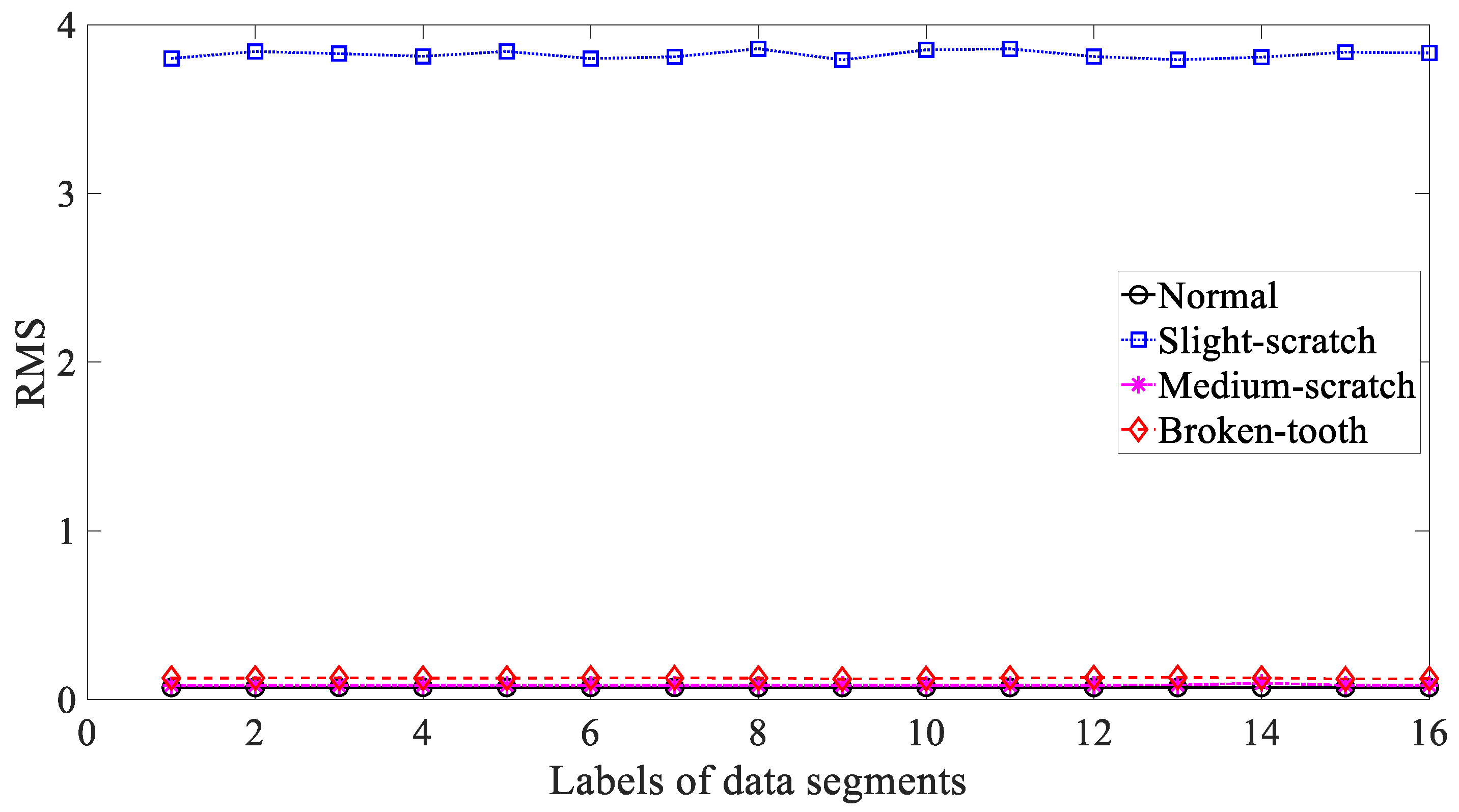
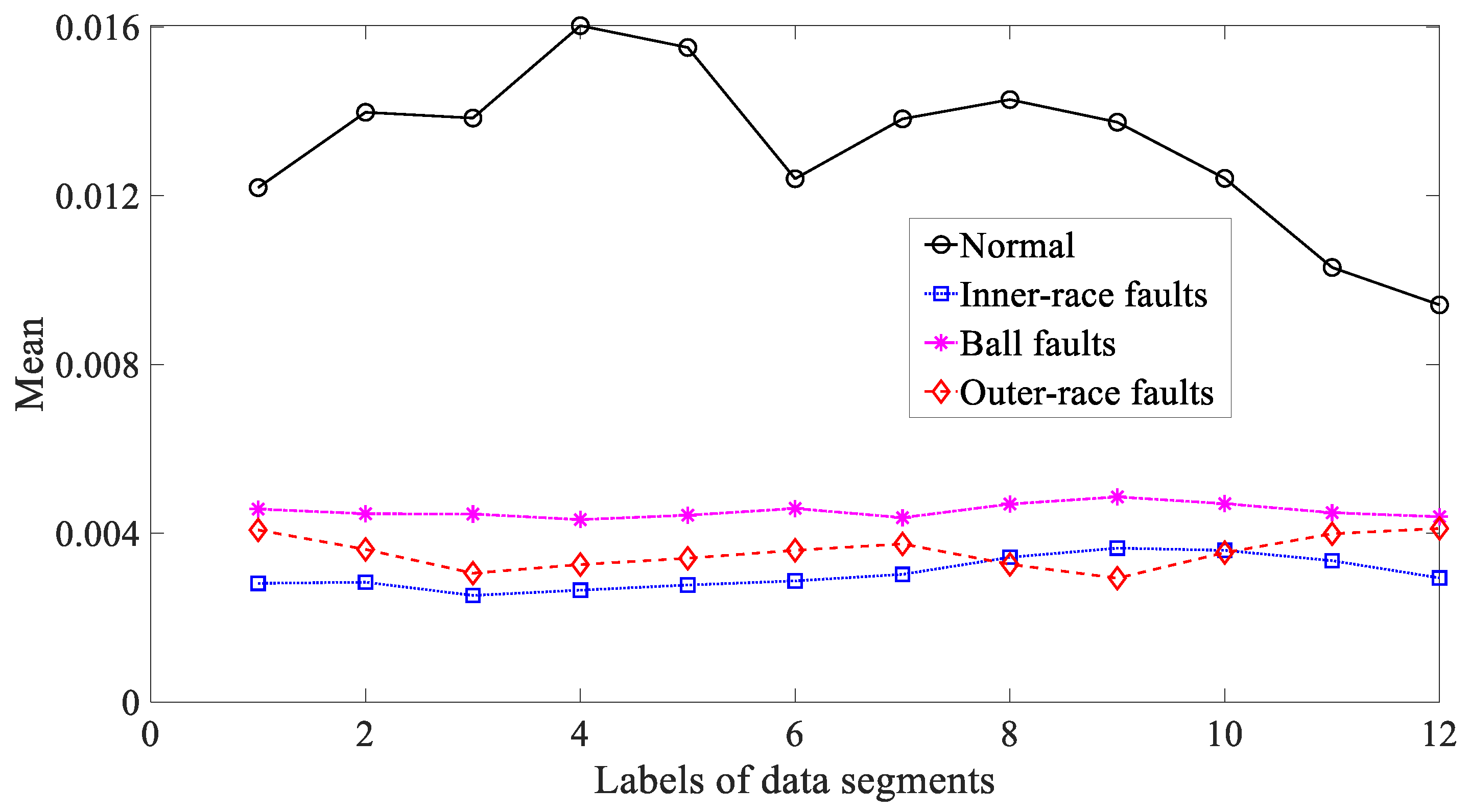
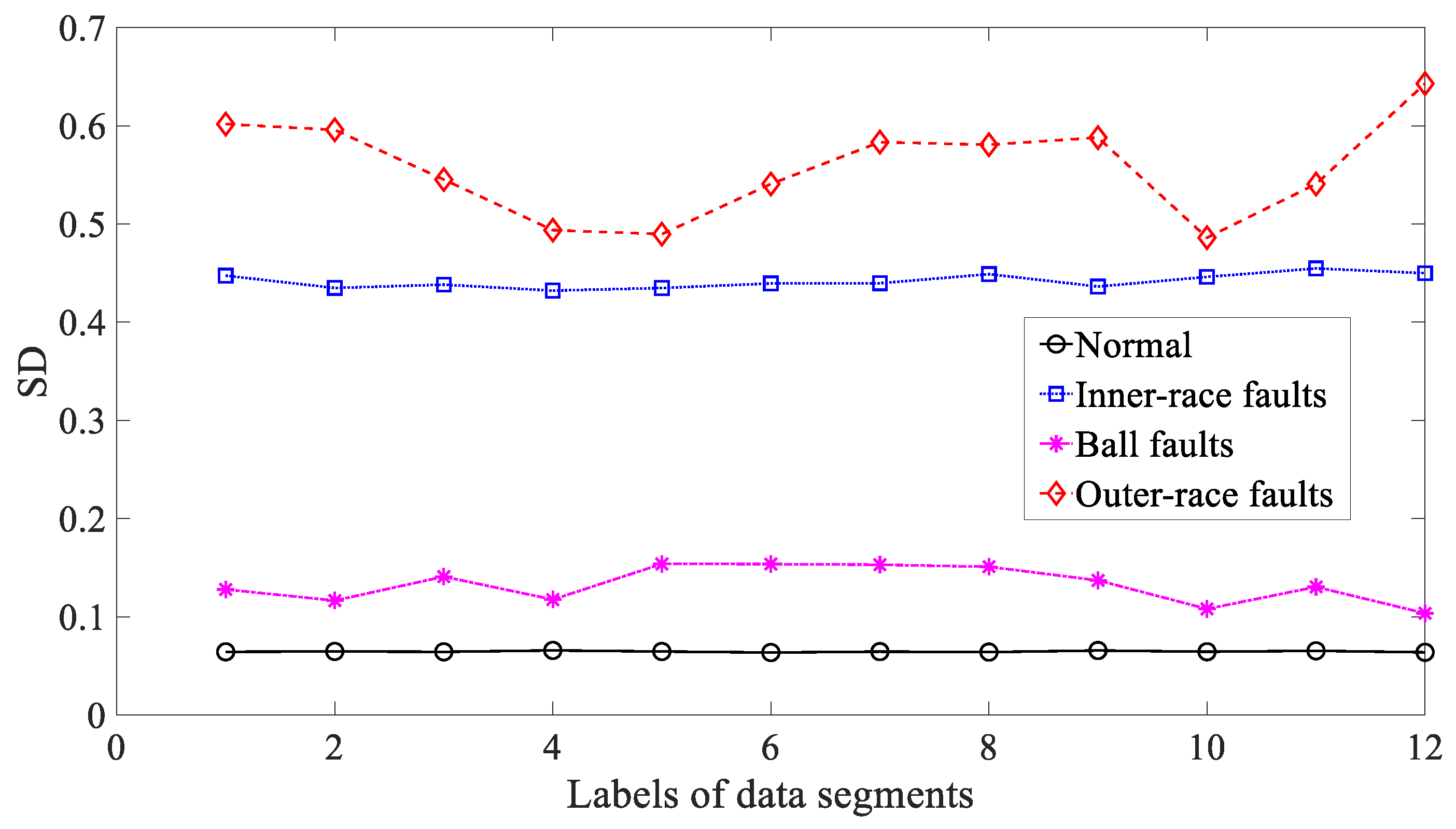
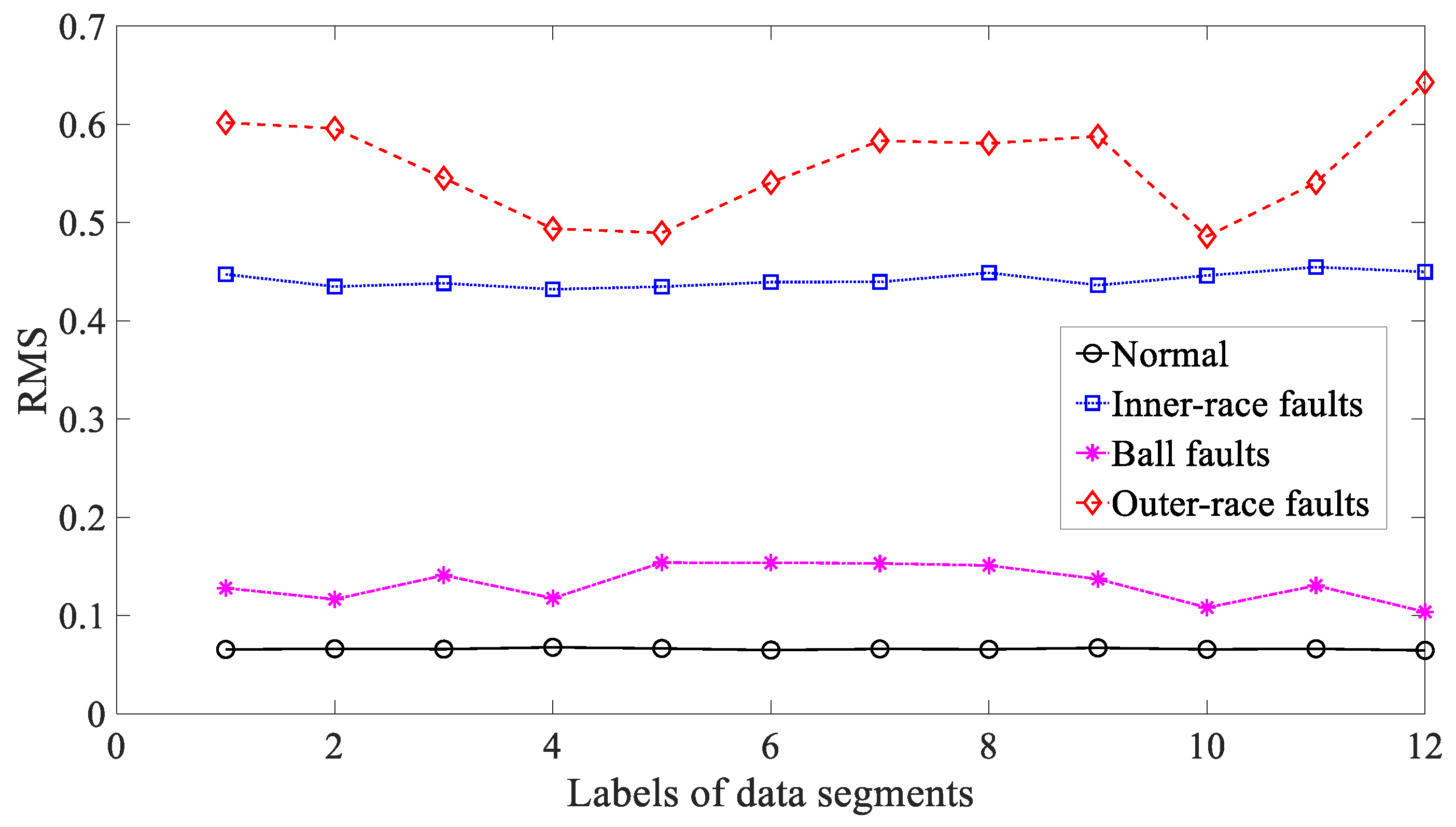
3.3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Gligorijevic, J.; Gajic, D.; Brkovic, A.; Savic-Gajic, I.; Georgieva, O.; di Gennaro, S. Online condition monitoring of bearings to support total productive maintenance in the packaging materials industry. Sensors 2016, 16, 316. [Google Scholar] [CrossRef] [PubMed]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; de Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and convolutional neural networks. IEEE-ASME Trans. Mech. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Brkovic, A.; Gajic, D.; Gligorijevic, J.; Savic-Gajic, I.; Georgieva, O.; di Gennaro, S. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Wang, Z.J.; Du, W.H.; Wang, J.Y. Research and Application of Improved Adaptive MOMEDA Fault Diagnosis Method. Measurement 2019, 140, 63–75. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, X.; Kou, L.; Qin, Y.; Zhao, Y.; Tsuib, K.-L. A simple and fast guideline for generating enhanced/squared envelope spectra from spectral coherence for bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 122, 754–768. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F.; Chu, F. HVSRMS localization formula and localization law: Localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process. 2019, 120, 608–629. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zheng, L.K.; Du, W.H. A novel method for intelligent fault diagnosis of bearing based on capsule neural network. Complexity 2019, 2019, 6943234. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J. Health assessment of rotating machinery using a rotary encoder. IEEE Trans. Ind. Electron. 2018, 65, 2548–2556. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Measurement 2016, 90, 4–19. [Google Scholar] [CrossRef]
- Venkatsubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N. A review of process fault detection and diagnosis Part II: Quantitative model and search strategies. Comput. Chem. Eng. 2003, 27, 313–326. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis Part III: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar] [CrossRef]
- Collis, W.B.; White, P.R.; Hammond, J.K. Higher-order spectra: The bispectrum and trispectrum. Mech. Syst. Signal Process. 1998, 12, 375–394. [Google Scholar] [CrossRef]
- Nikias, C.L.; Mendel, J.M. Signal processing with higher-order spectra. IEEE Signal Process. Mag. 1993, 10, 10–37. [Google Scholar] [CrossRef]
- Fackrell, J.W.A.; White, P.R.; Hammond, J.K.; Pinnington, R.J.; Parsons, A.T. The interpretation of the bispectra of vibration signals—: I. Theory. Mech. Syst. Signal Process. 1995, 9, 257–266. [Google Scholar] [CrossRef]
- Fackrell, J.W.A.; White, P.R.; Hammond, J.K.; Pinnington, R.J.; Parsons, A.T. The interpretation of the bispectra of vibration signals—: II. Experimental results and applications. Mech. Syst. Signal Process. 1995, 9, 267–274. [Google Scholar] [CrossRef]
- Akilu, Y.-K.; Sinha, J.K. Combined bispectrum and trispectrum for faults diagnosis in rotating machines. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 419–428. [Google Scholar]
- Howard, I.M. Higher-order spectral techniques for machine vibration condition monitoring. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 1997, 211, 211–219. [Google Scholar] [CrossRef]
- Rivola, A.; White, P.R. Bispectral analysis of the bilinear oscillator with application to the detection of fatigue cracks. J. Sound Vib. 1998, 216, 889–910. [Google Scholar] [CrossRef]
- Rivola, A.; White, P.R. Use of higher order spectra in condition monitoring: Simulation and experiments. In Proceedings of the DETC99, ASME, Las Vegas, NV, USA, 12–15 September 1999; pp. 1–12. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. HOS analysis of measured vibration data on rotating machines with different simulated faults. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2014; pp. 81–89. [Google Scholar]
- Sinha, J.K. Higher order spectra for crack and misalignment identification in the shaft of a rotating machine. Struct. Health Monit. 2007, 6, 325–334. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. Faults diagnosis in rotating machines using higher order spectra. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Kovach, C.K.; Howard, M.A., III. Decomposition of higher-order spectra for blind multiple-input deconvolution, pattern identification and separation. Signal Process 2019, 165, 357–379. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery health prognosis for electric vehicles using sample entropy and sparse Bayesian predictive modeling. IEEE Trans. Ind. Electron. 2016, 63, 2645–2656. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Lind, D.; Marcus, B.; Douglas, L.; Brian, M. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Daw, C.S.; Finney, C.E.A.; Tracy, E.R. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar] [CrossRef]
- Lacasa, L.; Just, W. Visibility graphs and symbolic dynamics. Phys. D 2018, 374, 35–44. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, G.; Xu, M.; Huang, W. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection. Mech. Syst. Signal Process. 2017, 91, 295–312. [Google Scholar] [CrossRef]
- Hao, B.-L. Symbolic dynamics and characterization of complexity. Phys. D 1991, 51, 161–176. [Google Scholar] [CrossRef]
- Lin, J.; Dou, C. A novel method for condition monitoring of rotating machinery based on statistical linguistic analysis and weighted similarity measures. J. Sound Vib. 2017, 390, 272–288. [Google Scholar] [CrossRef]
- Yang, A.C.-C.; Hseu, S.-S.; Yien, H.-W.; Goldberger, A.L.; Peng, C.-K. Linguistic analysis of the human heartbeat using frequency and rank order statistics. Phys. Rev. Lett. 2003, 90, 108103. [Google Scholar] [CrossRef]
- Yang, A.C.-C.; Peng, C.-K.; Yien, H.-W.; Goldberger, A.L. Information categorization approach to literary authorship disputes. Phys. A 2003, 329, 473–483. [Google Scholar] [CrossRef]
- Peng, C.-K.; Yang, A.C.-C.; Goldberger, A.L. Statistical physics approach to categorize biologic signals: From heart rate dynamics to DNA sequences. Chaos Soliton Fract. 2007, 17, 015115. [Google Scholar] [CrossRef]
- Loparo, K.A. Bearing Vibration Dataset, Case Western Reserve University. Available online: http://csegroups.case.edu/bearingdatacenter/pages/12k-drive-end-bearing-fault-data (accessed on 20 November 2019).




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, C.; Lin, J. Adaptive Multiscale Symbolic-Dynamics Entropy for Condition Monitoring of Rotating Machinery. Entropy 2019, 21, 1138. https://doi.org/10.3390/e21121138
Dou C, Lin J. Adaptive Multiscale Symbolic-Dynamics Entropy for Condition Monitoring of Rotating Machinery. Entropy. 2019; 21(12):1138. https://doi.org/10.3390/e21121138
Chicago/Turabian StyleDou, Chunhong, and Jinshan Lin. 2019. "Adaptive Multiscale Symbolic-Dynamics Entropy for Condition Monitoring of Rotating Machinery" Entropy 21, no. 12: 1138. https://doi.org/10.3390/e21121138
APA StyleDou, C., & Lin, J. (2019). Adaptive Multiscale Symbolic-Dynamics Entropy for Condition Monitoring of Rotating Machinery. Entropy, 21(12), 1138. https://doi.org/10.3390/e21121138



