Measurement Based Quantum Heat Engine with Coupled Working Medium
Abstract
1. Introduction
2. Single Temperature Measurement Driven Quantum Heat Engine without Feedback
3. Coupled Single Temperature Measurement Engine
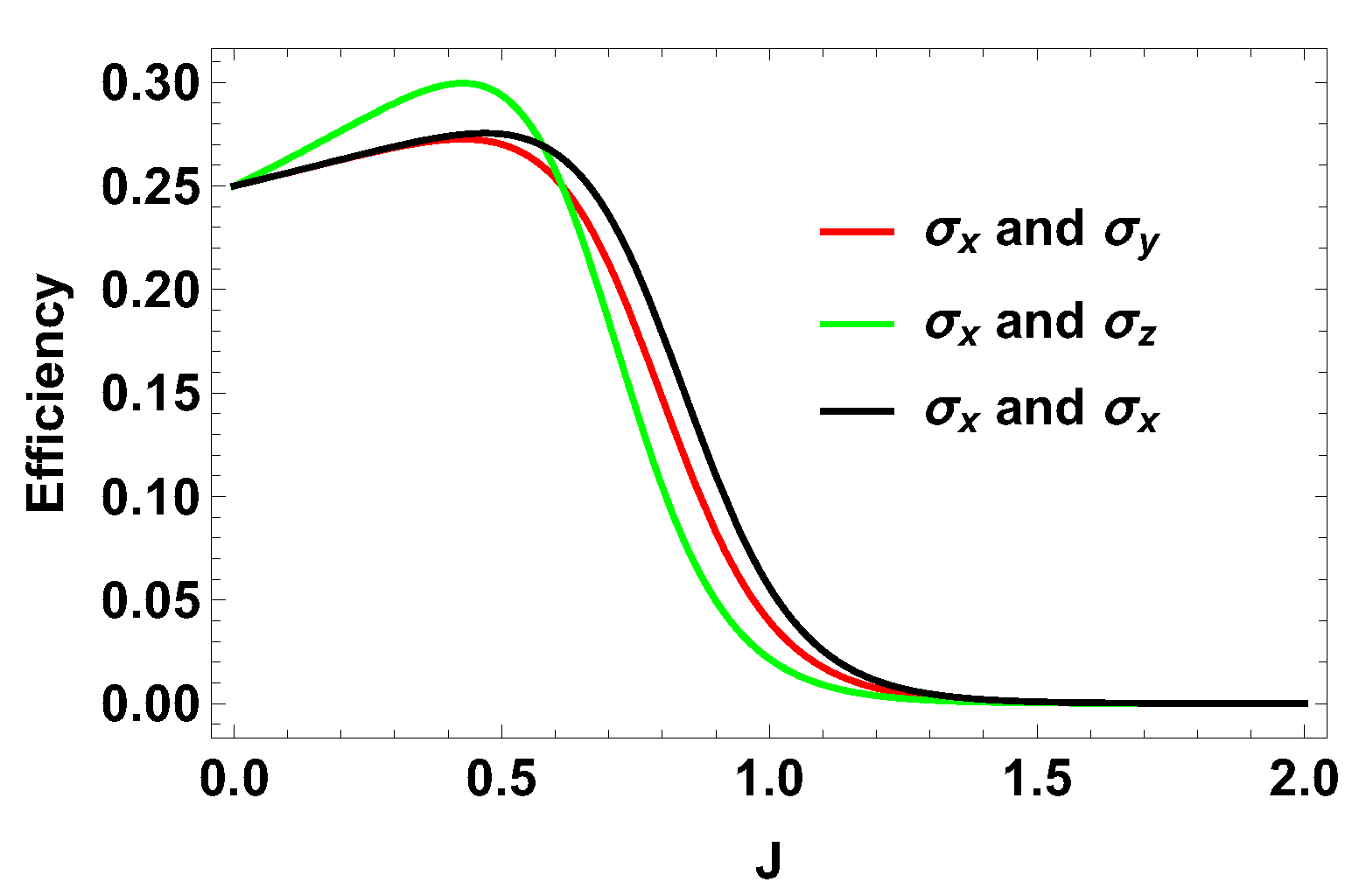
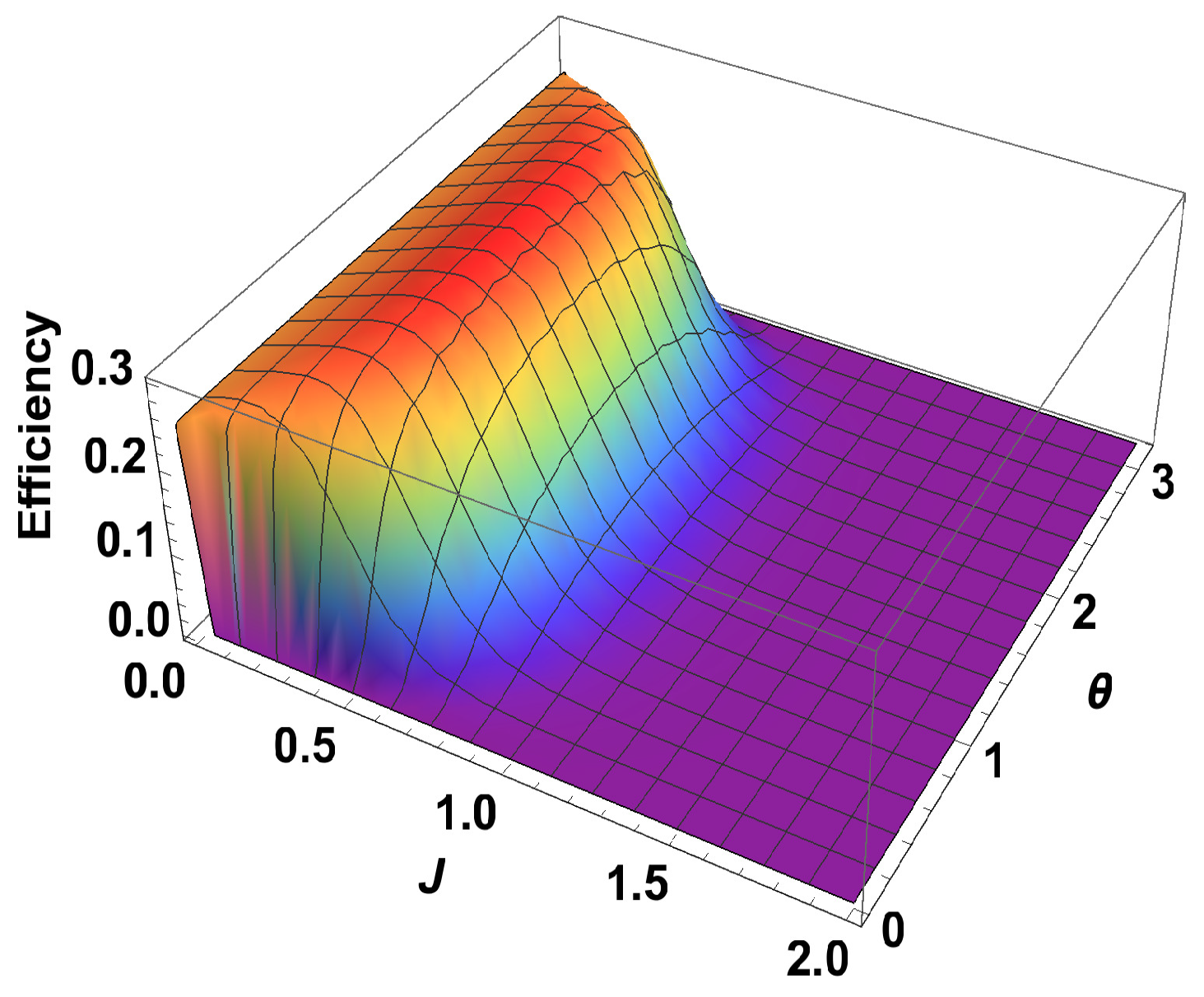
4. Efficiency of the Heat Engine, Global Analysis
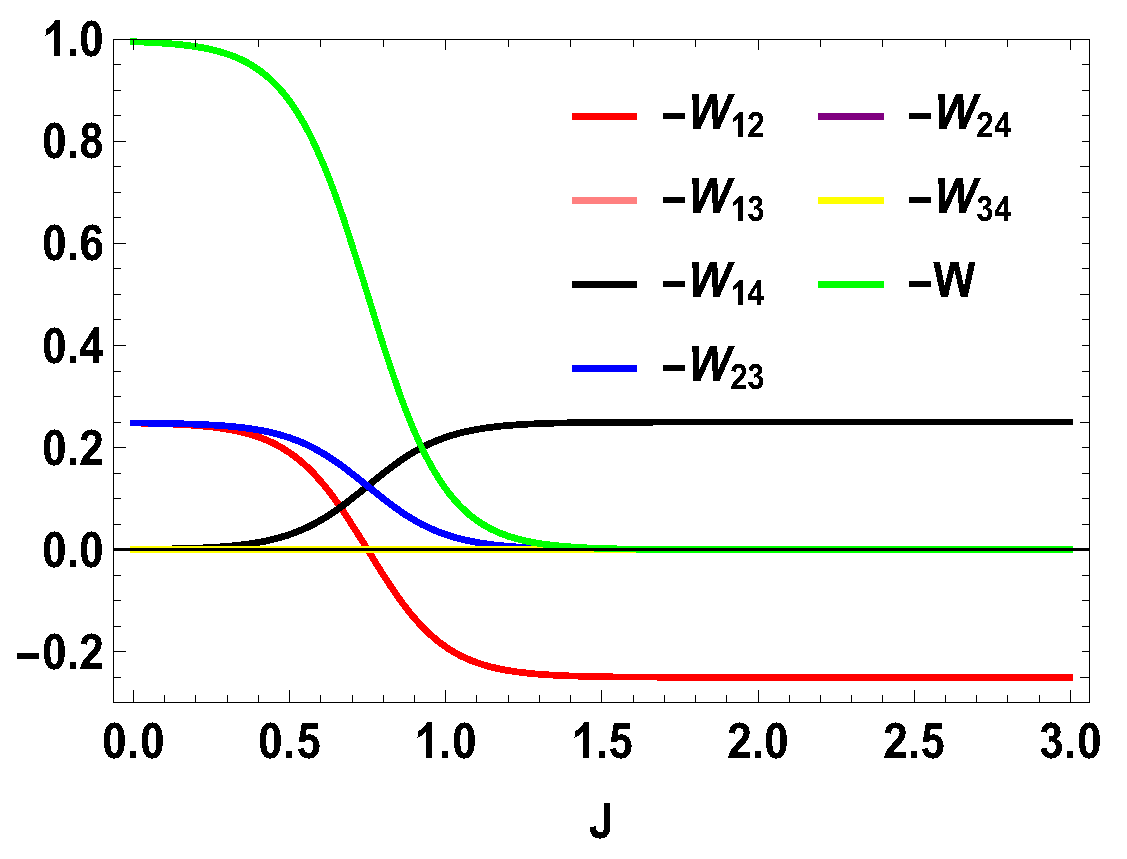
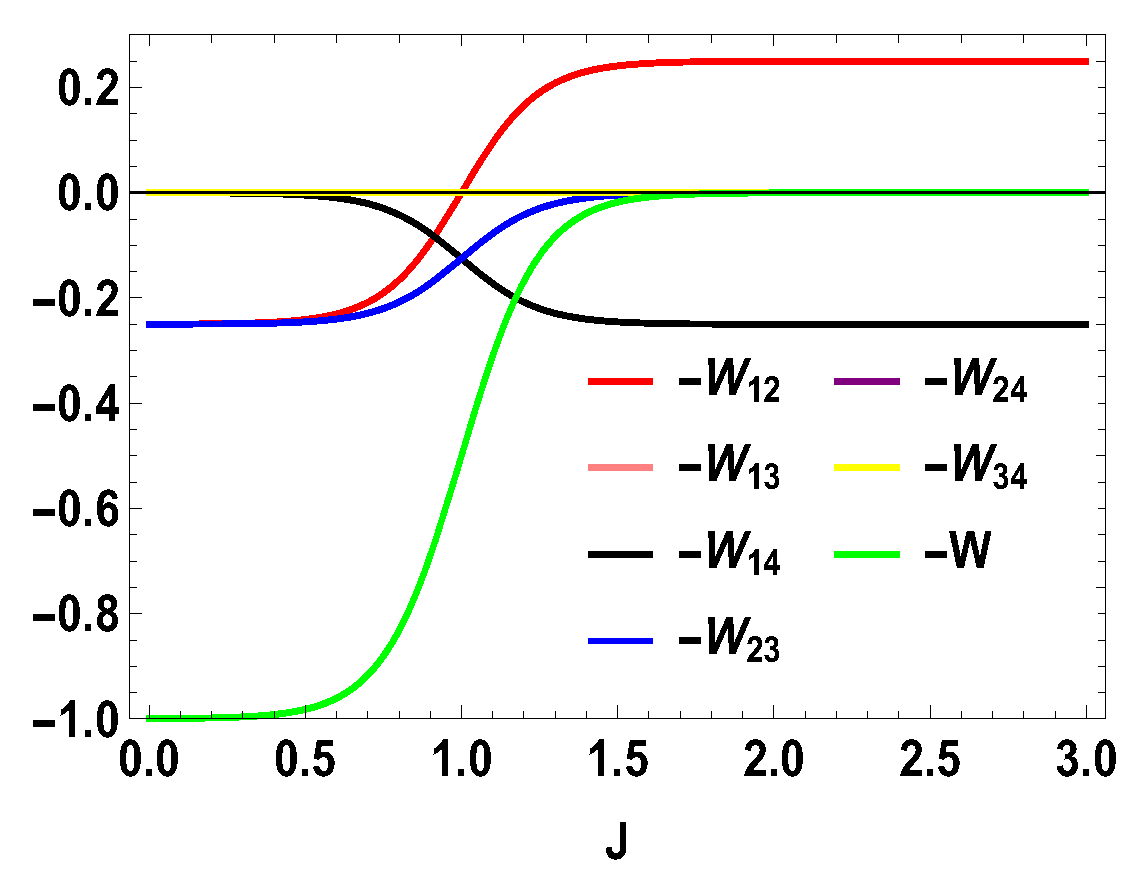
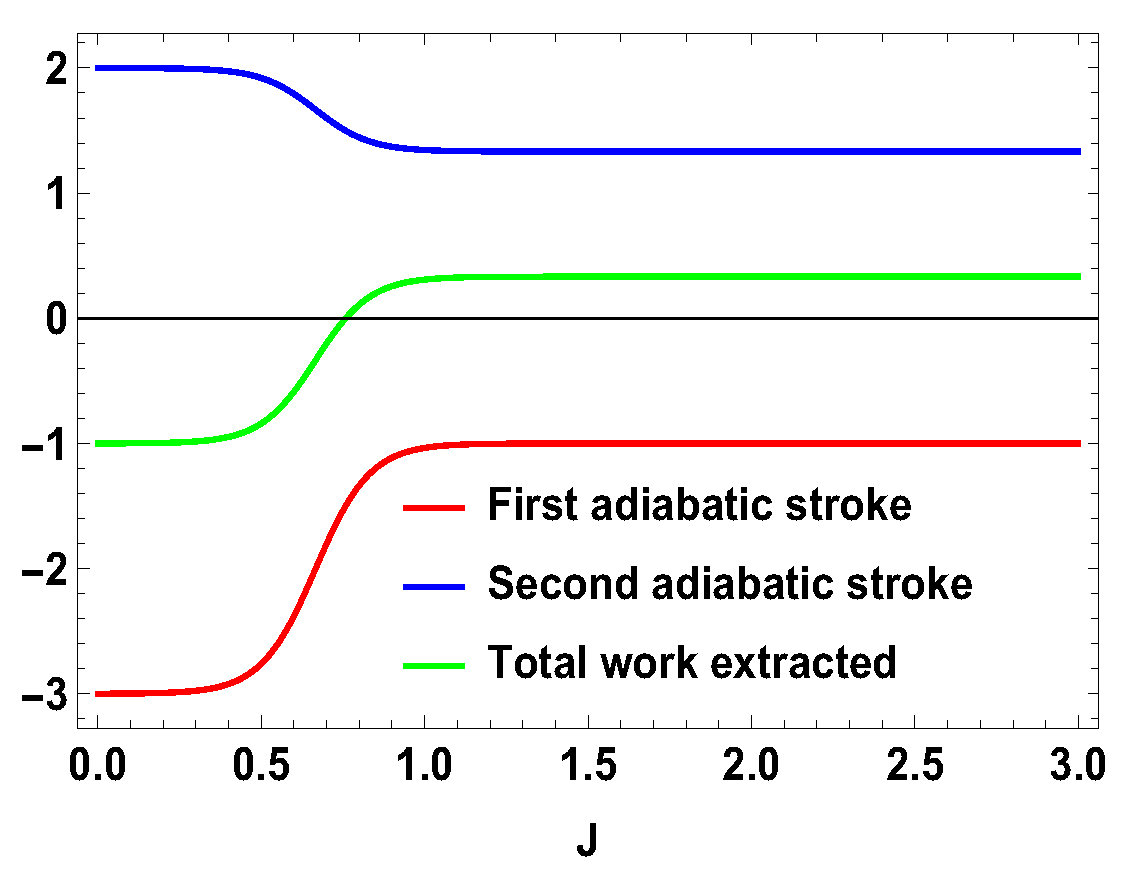
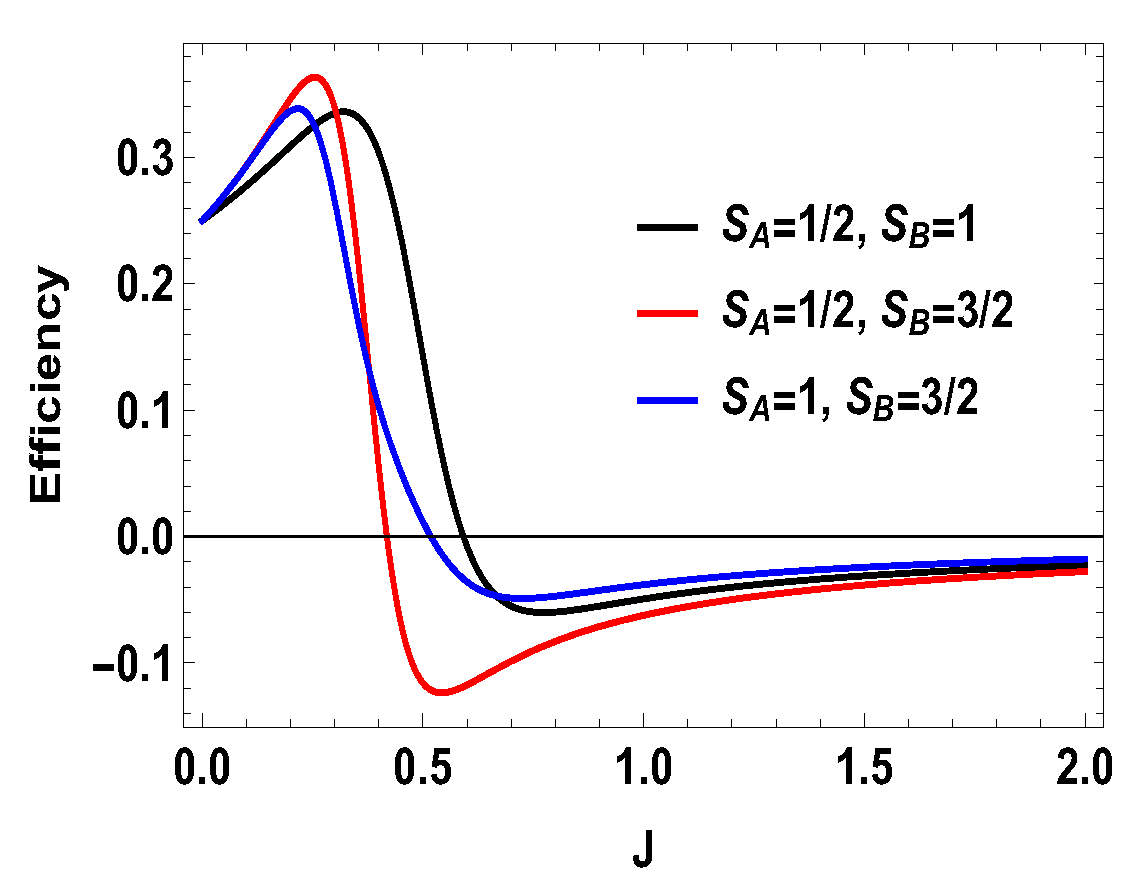
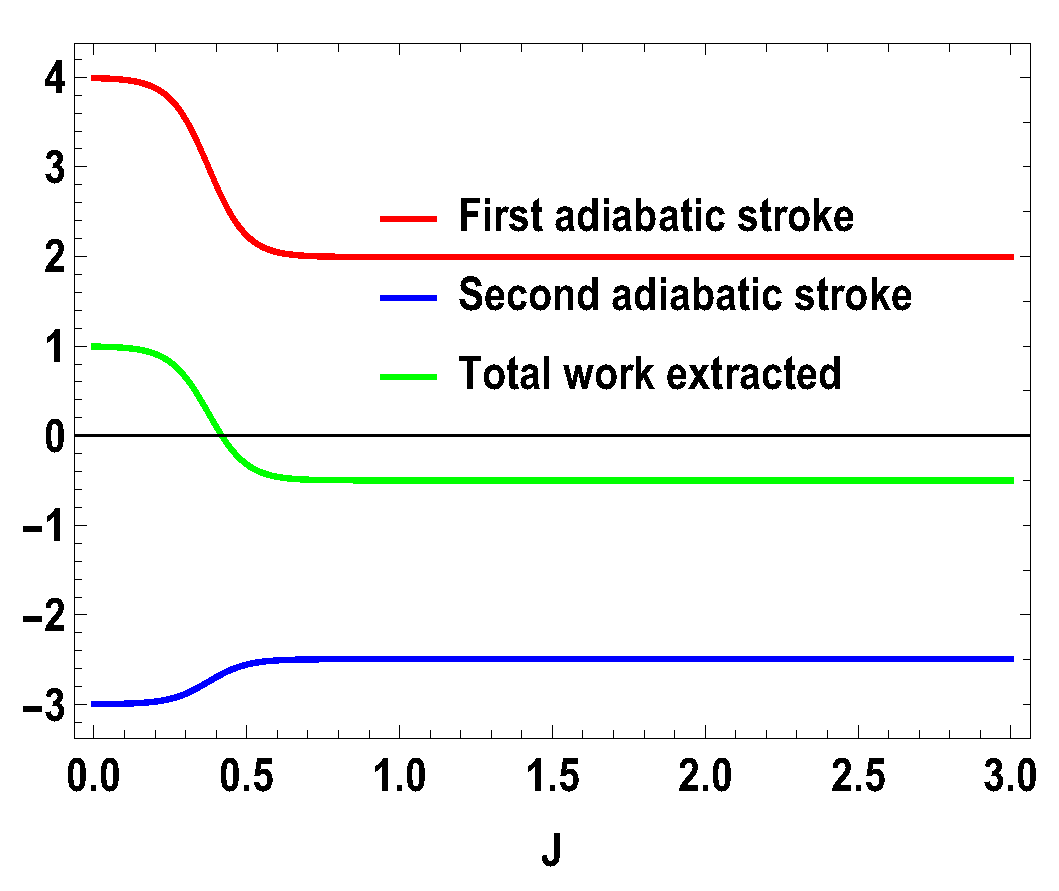
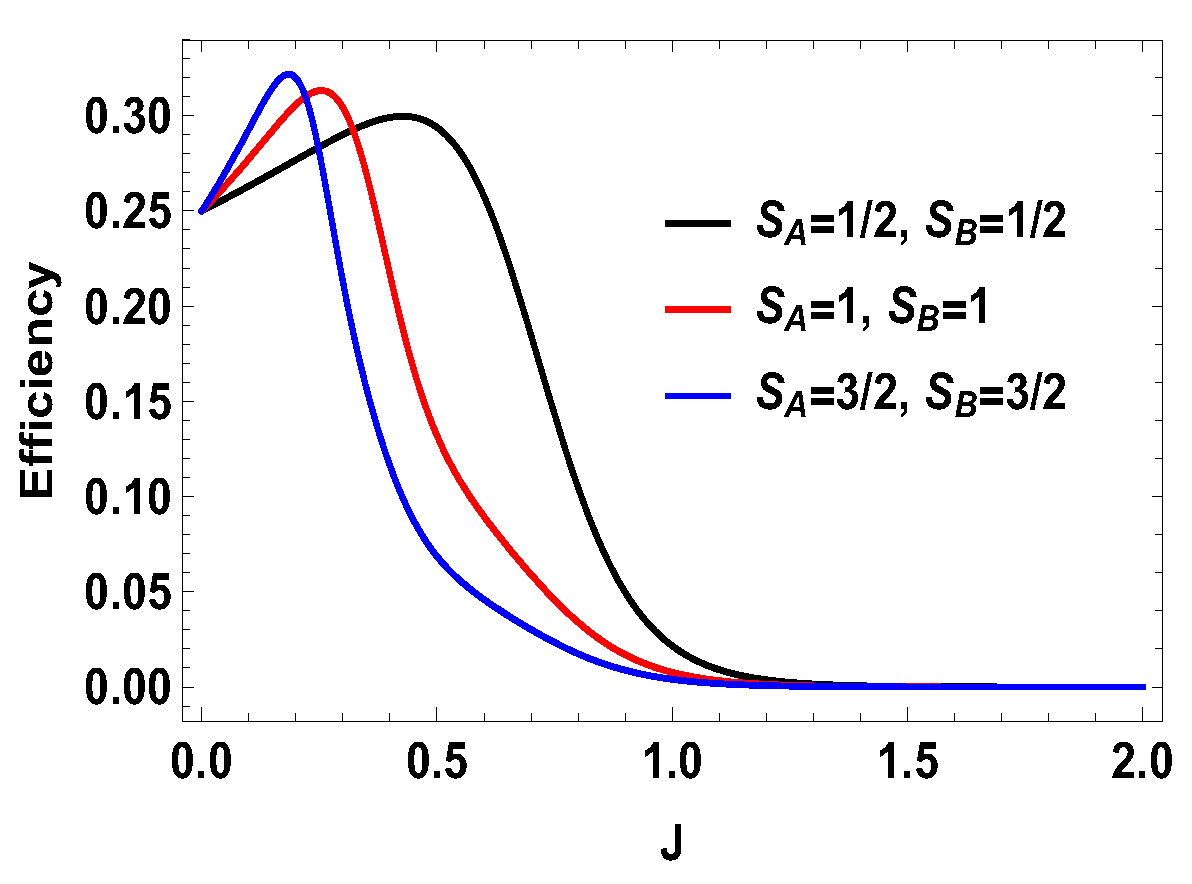
5. Higher-Dimensional Case
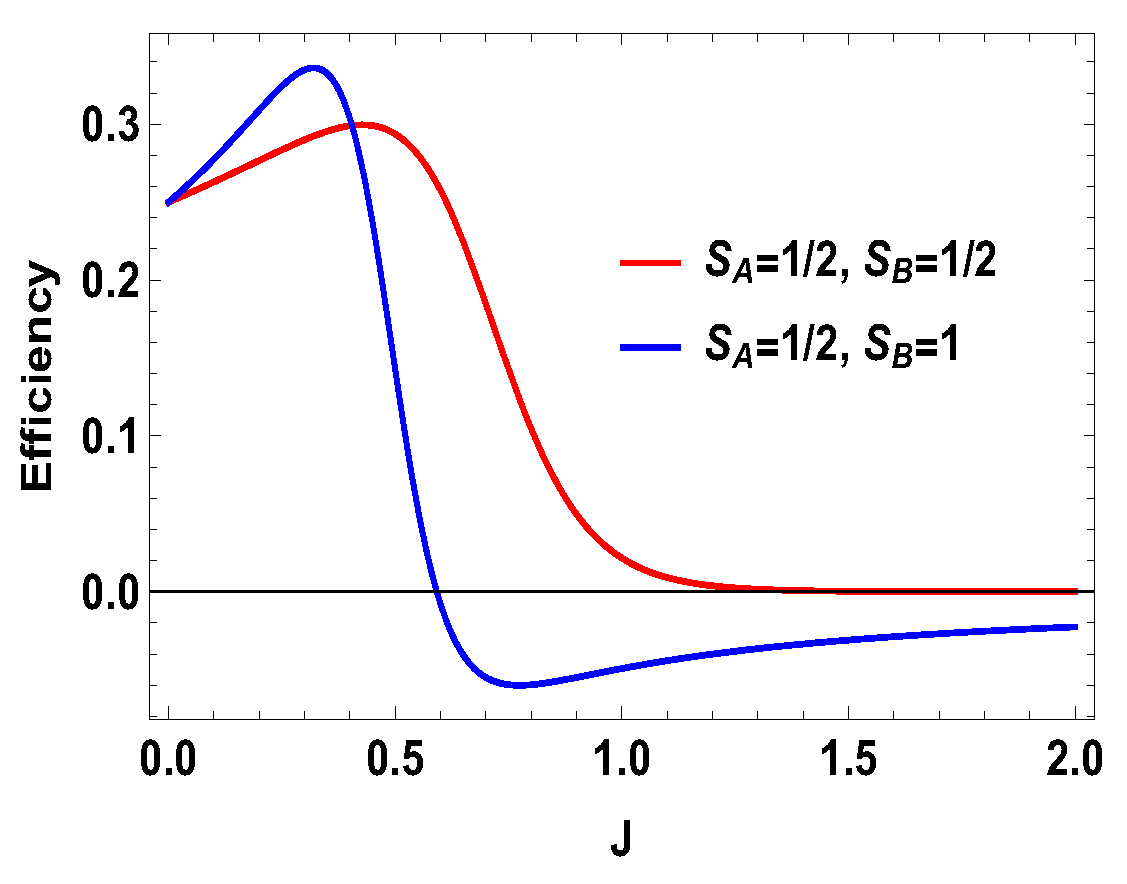
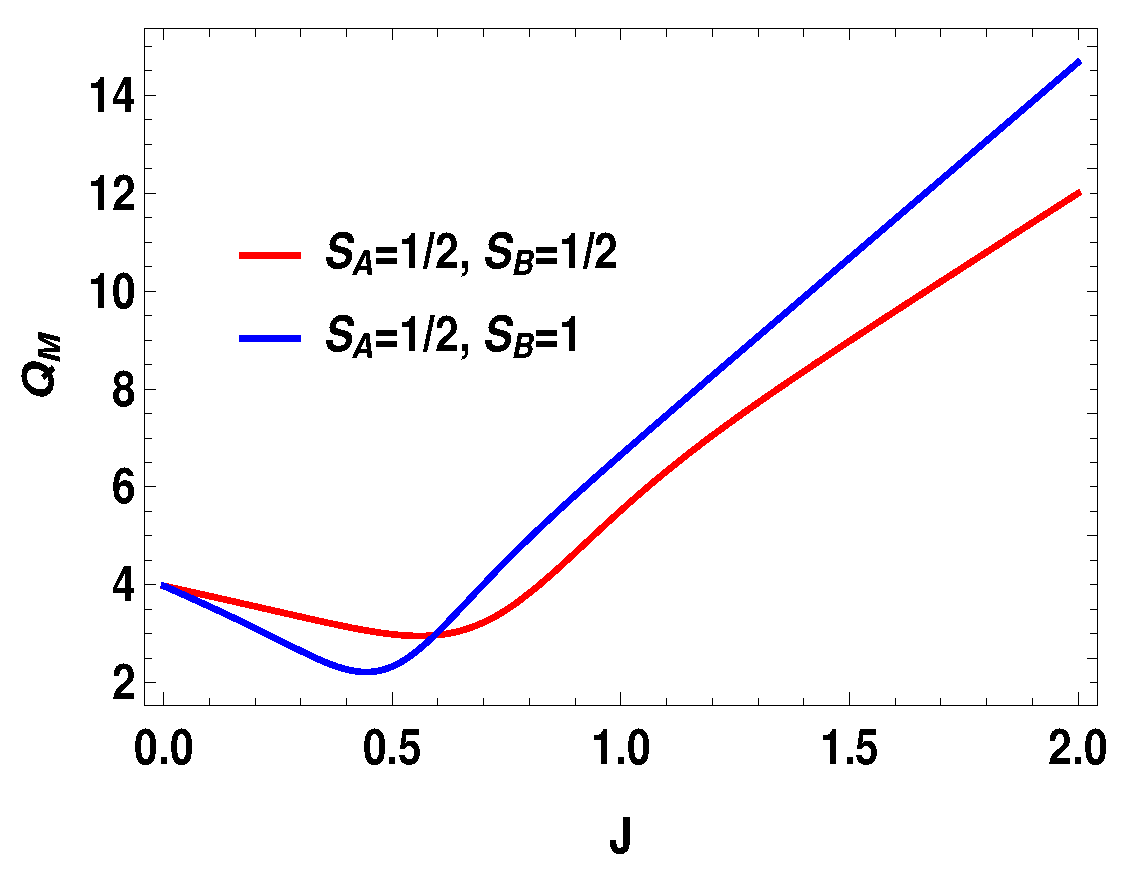
5.1. Asymmetric Case
5.2. Symmetric Case
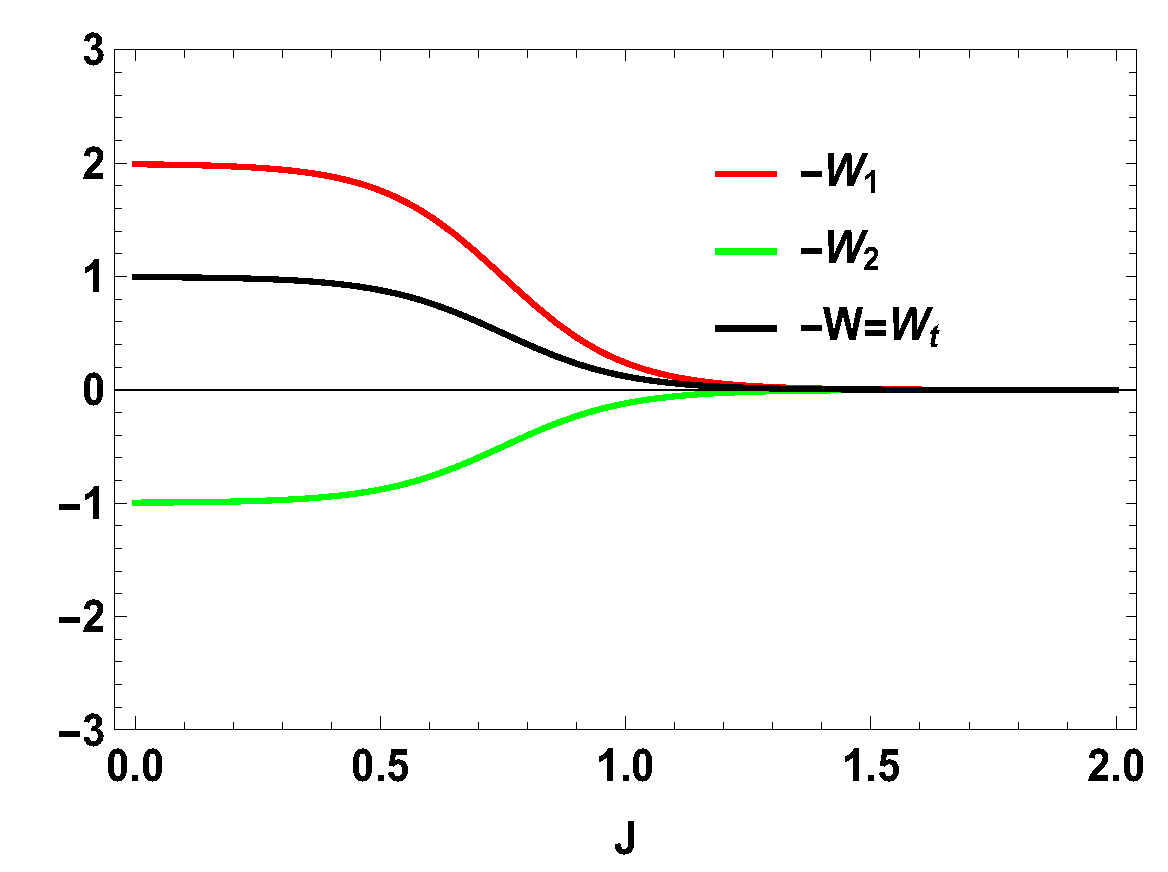
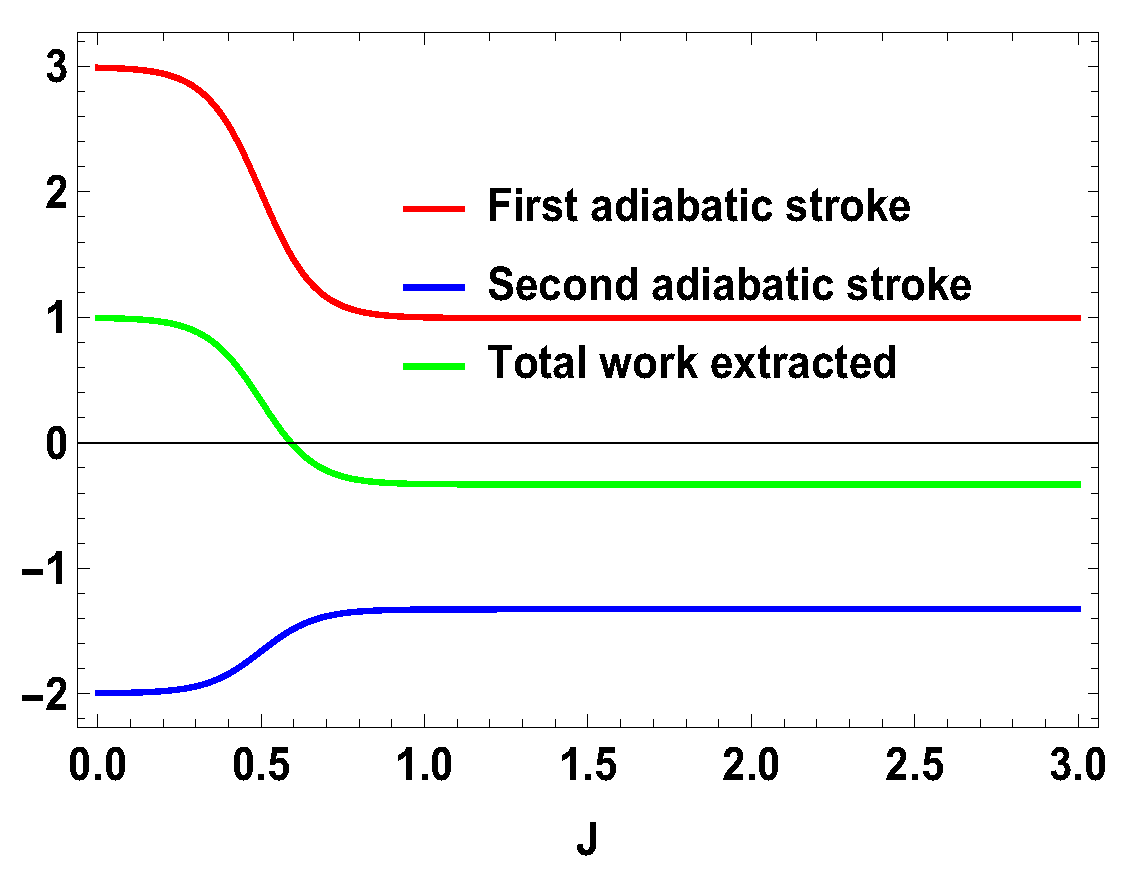
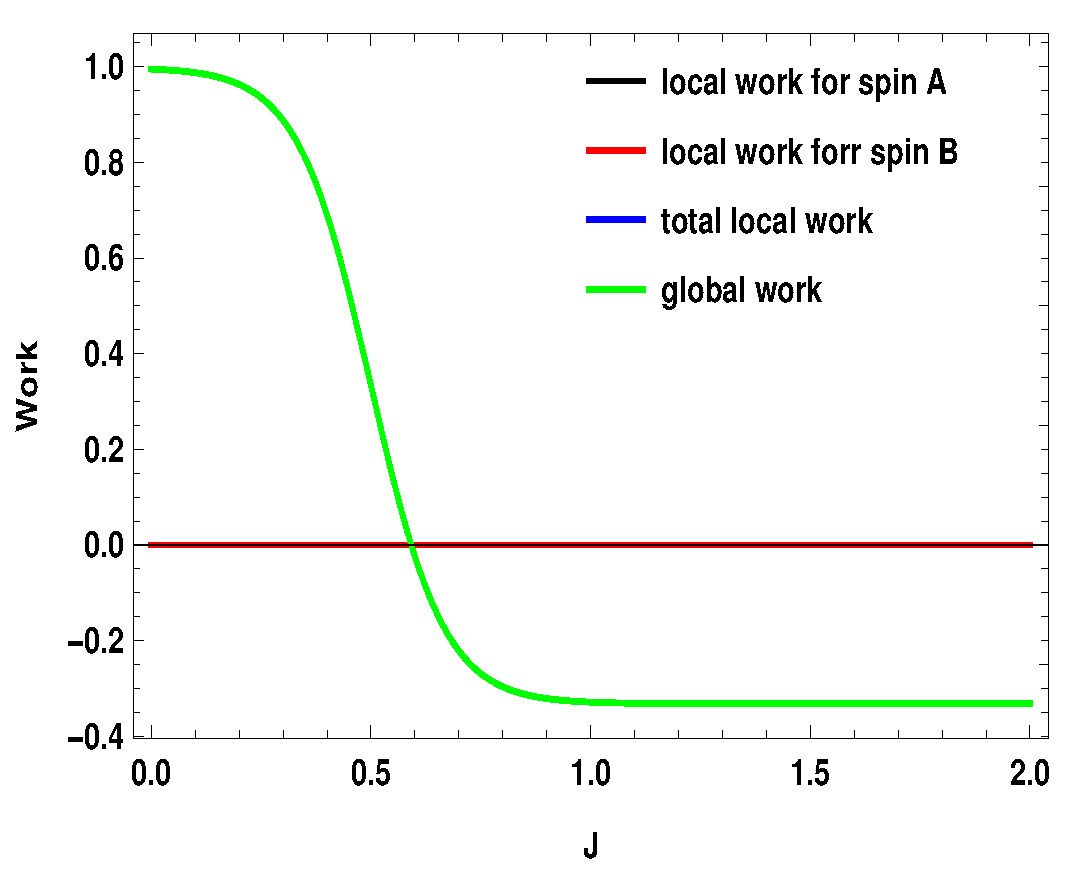
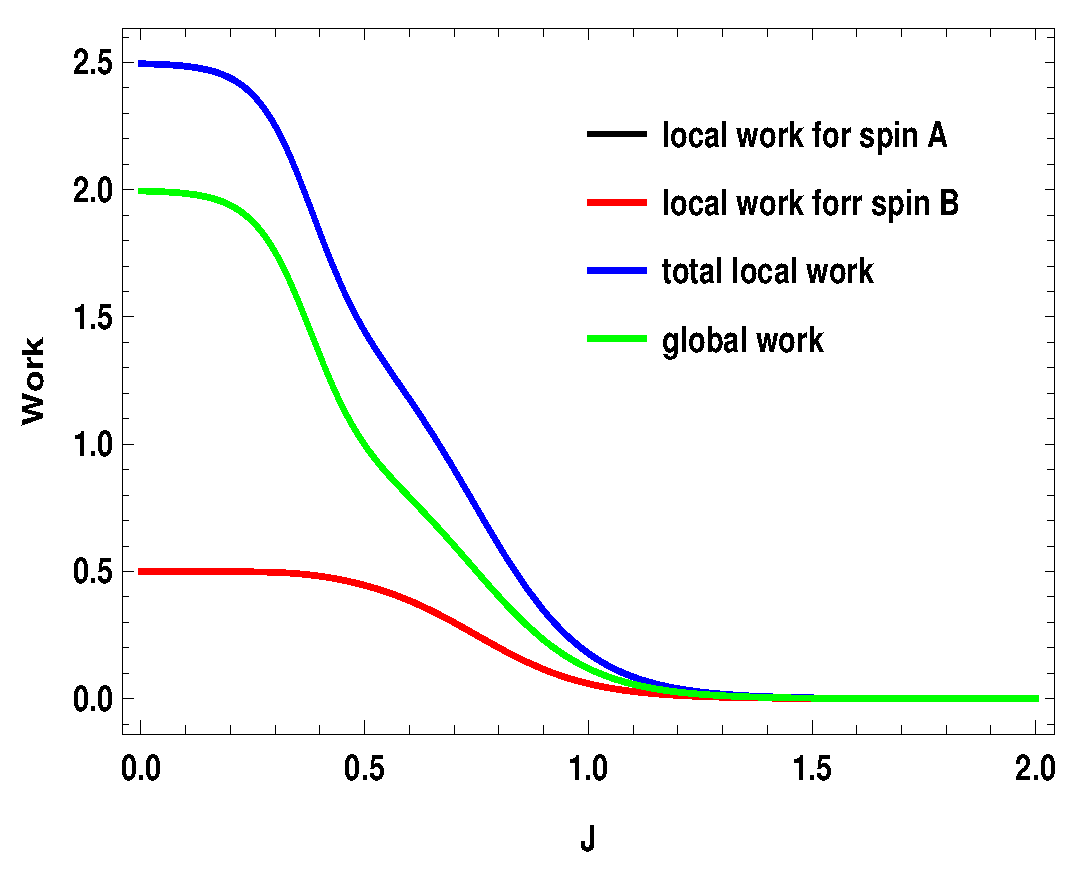
6. Local vs. Global Work
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Tables
| Eigenvalues | Eigenstates |
|---|---|
| Eigenvalues | Eigenstates |
|---|---|
| Eigenvalues | Eigenstates |
|---|---|
| Eigenvalues | Eigenstates |
|---|---|
References
- Carnot, S. Reflections on the Motive Power of Fire and on Machines Fitted to Develop that Power; Bachelier: Paris, France, 1824. [Google Scholar]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics; Willey: New York, NY, USA, 1985. [Google Scholar]
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Alicki, R.; Kosloff, R. Introduction to Quantum Thermodynamics: History and Prospects. arxiv 2018, arXiv:1801.08314. [Google Scholar]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1959, 2, 263. [Google Scholar] [CrossRef]
- Kieu, T.D. The Second Law, Maxwell’s Demon, and Work Derivable from Quantum Heat Engines. Phys. Rev. Lett. 2004, 93, 140403. [Google Scholar] [CrossRef] [PubMed]
- Quan, H.T.; Liu, Y.X.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A 1979, 12, L103. [Google Scholar] [CrossRef]
- Kosloff, R. A quantum mechanical open system as a model of a heat engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Scully, M.O. Quantum Afterburner: Improving the Efficiency of an Ideal Heat Engine. Phys. Rev. Lett. 2002, 88, 050602. [Google Scholar] [CrossRef]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. A quantum-mechanical heat engine operating in finite time. A model consisting of spin-1/2 systems as the working fluid. J. Chem. Phys. 1992, 96, 3054–3067. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Performance of discrete heat engines and heat pumps in finite time. Phys. Rev. E 2000, 61, 4774. [Google Scholar] [CrossRef] [PubMed]
- Allahverdyan, A.E.; Hovhannisyan, K.V.; Melkikh, A.V.; Gevorkian, S.G. Carnot Cycle at Finite Power: Attainability of Maximal Efficiency. Phys. Rev. Lett. 2013, 111, 050601. [Google Scholar] [CrossRef] [PubMed]
- Polettini, M.; Verley, G.; Esposito, M. Efficiency Statistics at All Times: Carnot Limit at Finite Power. Phys. Rev. Lett. 2002, 114, 050601. [Google Scholar] [CrossRef] [PubMed]
- Campisi, M.; Fazio, R. The power of a critical heat engine. Nat. Commun. 2016, 7, 11895. [Google Scholar] [CrossRef] [PubMed]
- Shiraishi, N.; Tajima, H. Efficiency versus speed in quantum heat engines: Rigorous constraint from Lieb-Robinson bound. Phys. Rev. E 2017, 96, 022138. [Google Scholar] [CrossRef] [PubMed]
- Holubec, V.; Ryabov, A. Cycling Tames Power Fluctuations near Optimum Efficiency. Phys. Rev. Lett. 2018, 121, 120601. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 292, 862–864. [Google Scholar] [CrossRef]
- Dillenschneider, R.; Lutz, E. Energetics of quantum correlations. Eur. Phys. Lett. 2009, 88, 50003. [Google Scholar] [CrossRef]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef]
- Ghosh, A.; Mukherjee, V.; Niedenzu, W.; Kurizki, G. Are quantum thermodynamic machines better than their classical counterparts? Eur. Phys. J. Special Topics 2019, 227, 2043–2051. [Google Scholar] [CrossRef]
- Alicki, R.; Fannes, M. Entanglement boost for extractable work from ensembles of quantum batteries. Phys. Rev. E 2013, 87, 042123. [Google Scholar] [CrossRef] [PubMed]
- Hovhannisyan, K.V.; Perarnau-Llobet, M.; Huber, M.; Acín, A. Entanglement Generation is Not Necessary for Optimal Work Extraction. Phys. Rev. Lett. 2013, 111, 240401. [Google Scholar] [CrossRef] [PubMed]
- Perarnau-Llobet, M.; Hovhannisyan, K.V.; Huber, M.; Skrzypczyk, P.; Brunner, N.; Acín, A. Extractable Work from Correlations. Phys. Rev. X 2015, 5, 041011. [Google Scholar] [CrossRef]
- Korzekwa, K.; Lostaglio, M.; Oppenheim, J.; Jennings, D. The extraction of work from quantum coherence. New J. Phys. 2016, 18, 023045. [Google Scholar] [CrossRef]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Hewgill, A.; Ferraro, A.; de Chiara, G. Quantum correlations and thermodynamic performances of two-qubit engines with local and common baths. Phys. Rev. A 2018, 98, 042102. [Google Scholar] [CrossRef]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nano thermodynamics. Nat. Commun. 2013, 4, 2059. [Google Scholar] [CrossRef]
- Ng, N.; Woods, M.P. Resource theory of quantum thermodynamics: Thermal operations and Second Laws. In Thermodynamics in the Quantum Regime. Fundamental Theories of Physics; Binder, F., Correa, L., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer: Cham, Switzerland, 2019; Volume 195. [Google Scholar]
- Thomas, G.; Johal, R. Coupled quantum Otto cycle. Phys. Rev. E 2011, 83, 031135. [Google Scholar] [CrossRef]
- Altintas, F.; Müstecaplıoğlu, Ö.E. General formalism of local thermodynamics with an example: Quantum Otto engine with a spin-1/2 coupled to an arbitrary spin. Phys. Rev. E 2015, 92, 022142. [Google Scholar] [CrossRef]
- Szilard, L. Zeitschrift für Physik. Z. Phys. 1929, 53, 840. [Google Scholar] [CrossRef]
- Leff, H.S.; Rex, A.F. Maxwell’s Demon 2; IOP: Bristol, UK, 2003. [Google Scholar]
- Kim, S.W.; Sagawa, T.; DeLiberato, S.; Ueda, M. Quantum Szilard Engine. Phys. Rev. Lett. 2011, 106, 070401. [Google Scholar] [CrossRef] [PubMed]
- Park, J.J.; Kim, K.H.; Sagawa, T.; Kim, S.W. Heat Engine Driven by Purely Quantum Information. Phys. Rev. Lett. 2013, 111, 230402. [Google Scholar] [CrossRef] [PubMed]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Extraction of Work from a Single Thermal Bath in the Quantum Regime. Phys. Rev. Lett. 2011, 85, 1799. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum discord and Maxwell’s demons. Phys. Rev. A 2013, 67, 012320. [Google Scholar] [CrossRef]
- Del Rio, L.; Aberg, J.; Renner, R.; Dahlsten, O.; Vedral, V. The thermodynamic meaning of negative entropy. Nature 2011, 474, 61–63. [Google Scholar]
- Funo, K.; Watanabe, Y.; Ueda, M. Thermodynamic work gain from entanglement. Phys. Rev. A 2013, 88, 052319. [Google Scholar] [CrossRef]
- Yi, J.; Talkner, P.; Kim, Y.W. Single-temperature quantum engine without feedback control. Phys. Rev. E 2017, 96, 022108. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Chand, S.; Biswas, A. Single-ion quantum Otto engine with always-on bath interaction. Eur. Phys. Lett. 2017, 118, 60003. [Google Scholar] [CrossRef]
- Chand, S.; Biswas, A. Measurement-induced operation of two-ion quantum heat machines. Phys. Rev. E 2017, 95, 032111. [Google Scholar] [CrossRef] [PubMed]
- Pozas-Kerstjens, A.; Brown, E.G.; Hovhannisyan, K.V. A quantum Otto engine with finite heat baths: Energy, correlations, and degradation. New J. Phys. 2018, 20, 043034. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.; Huard, B.; Aufféves, A. Extracting Work from Quantum Measurement in Maxwell’s Demon Engines. Phys. Rev. Lett. 2017, 118, 260603. [Google Scholar] [CrossRef] [PubMed]
- Elouard, C.; Jordan, A.N. Efficient Quantum Measurement Engines. Phys. Rev. Lett. 2018, 120, 260601. [Google Scholar] [CrossRef] [PubMed]
- Faist, P.; Dupuis, F.; Oppenheim, J.; Renner, R. The Minimal Work Cost of Information Processing. Nature Commun. 2015, 6, 7669. [Google Scholar] [CrossRef] [PubMed]
- Abdelkhalek, K.; Nakata, Y.; Reeb, D. Fundamental energy cost for quantum measurement. arxiv 2016, arXiv:1609.06981. [Google Scholar]
- Elouard, C.; Herrera-Martí, D.; Clusel, M.; Aufféves, A. The role of quantum measurement in stochastic thermodynamics. npj Quantum Inf. 2017, 3, 9. [Google Scholar] [CrossRef]
- Mohammady, M.H.; Anders, J. A quantum Szilard engine without heat from athermal reservoir. New J. Phys. 2017, 19, 113026. [Google Scholar] [CrossRef]
- Faist, P.; Renner, R. Fundamental Work Cost of Quantum Processes. Phys. Rev. X 2018, 8, 021011. [Google Scholar] [CrossRef]
- Ding, X.; Yi, J.; Kim, Y.W.; Talkner, P. Measurement-driven single temperature engine. Phys. Rev. E 2018, 98, 042122. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2015, 57, 545–579. [Google Scholar] [CrossRef]
- Jarzynski, C. Stochastic and Macroscopic Thermodynamics of Strongly Coupled Systems. Phys. Rev. X 2017, 7, 011008. [Google Scholar] [CrossRef]
- Perarnau-Llobet, M.; Wilming, H.; Riera, A.; Gallego, R.; Eisert, J. Strong Coupling Corrections in Quantum Thermodynamics. Phys. Rev. Lett. 2018, 120, 120602. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Arnesen, M.C.; Bose, S.; Vedral, V. Natural Thermal and Magnetic Entanglement in the 1D Heisenberg Model. Phys. Rev. Lett. 2001, 87, 017901. [Google Scholar] [CrossRef]
- Renes, J.M.; Blume-Kohout, R.; Scott, A.J.; Caves, C.M. Symmetric Informationally Complete Quantum Measurements. J. Math. Phys. 2004, 45, 2171. [Google Scholar] [CrossRef]
- Georgi, H. Lie Algebras in Particle Physics; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 1999. [Google Scholar]



| Eigenvalues | Eigenstates |
|---|---|
| Eigenvalues | Eigenstates |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, A.; Ghosh, S. Measurement Based Quantum Heat Engine with Coupled Working Medium. Entropy 2019, 21, 1131. https://doi.org/10.3390/e21111131
Das A, Ghosh S. Measurement Based Quantum Heat Engine with Coupled Working Medium. Entropy. 2019; 21(11):1131. https://doi.org/10.3390/e21111131
Chicago/Turabian StyleDas, Arpan, and Sibasish Ghosh. 2019. "Measurement Based Quantum Heat Engine with Coupled Working Medium" Entropy 21, no. 11: 1131. https://doi.org/10.3390/e21111131
APA StyleDas, A., & Ghosh, S. (2019). Measurement Based Quantum Heat Engine with Coupled Working Medium. Entropy, 21(11), 1131. https://doi.org/10.3390/e21111131





