2.1. Principle of MED
Equipment failure can cause a shock signal, but the original "certainty" of the shock signal is destroyed with the influence of transmission path, which leads to the increase of signal entropy. In order to restore the original shock state of the signal, it is necessary to estimate the inverse transfer function and reduce the entropy value. Assume that the fault signal expression is as follows:
Assuming that the input
is the impulse sequence of the fault signal and
is the impulse response function of the transmission path, the influence of the noise signal
on the system is neglected for the time being. The deconvolution process is to find an inverse filter
of order
, which can restore the lagged output
to the input
through the inverse filter. The expression of the deconvolution process is as follows:
Wiggins evaluates the entropy value by the sequence norm obtained after deconvolution in order to solve the optimal result. The expression is as follows:
The purpose of the MED algorithm is to find the optimal inverse filter
to minimize the entropy after filtering; that is, to maximize the norm
, and to ensure that the first derivative of the above equation is zero:
According to Equation (2),
where
is the size of the inverse filter
. We can get the derivative on both sides of Equation (5):
According to Equation (6) and further calculation of Equation (3), it can be obtained that
Let
,
,
, then Equation (7) can be written as the following matrix expression:
where
is the cross-correlation matrix of the input and output of the inverse filter,
is the Toeplitz autocorrelation matrix of the input of the inverse filter and
is the parameter of the inverse filter. According to Equation (8), the inverse filter matrix
is solved by iteration method
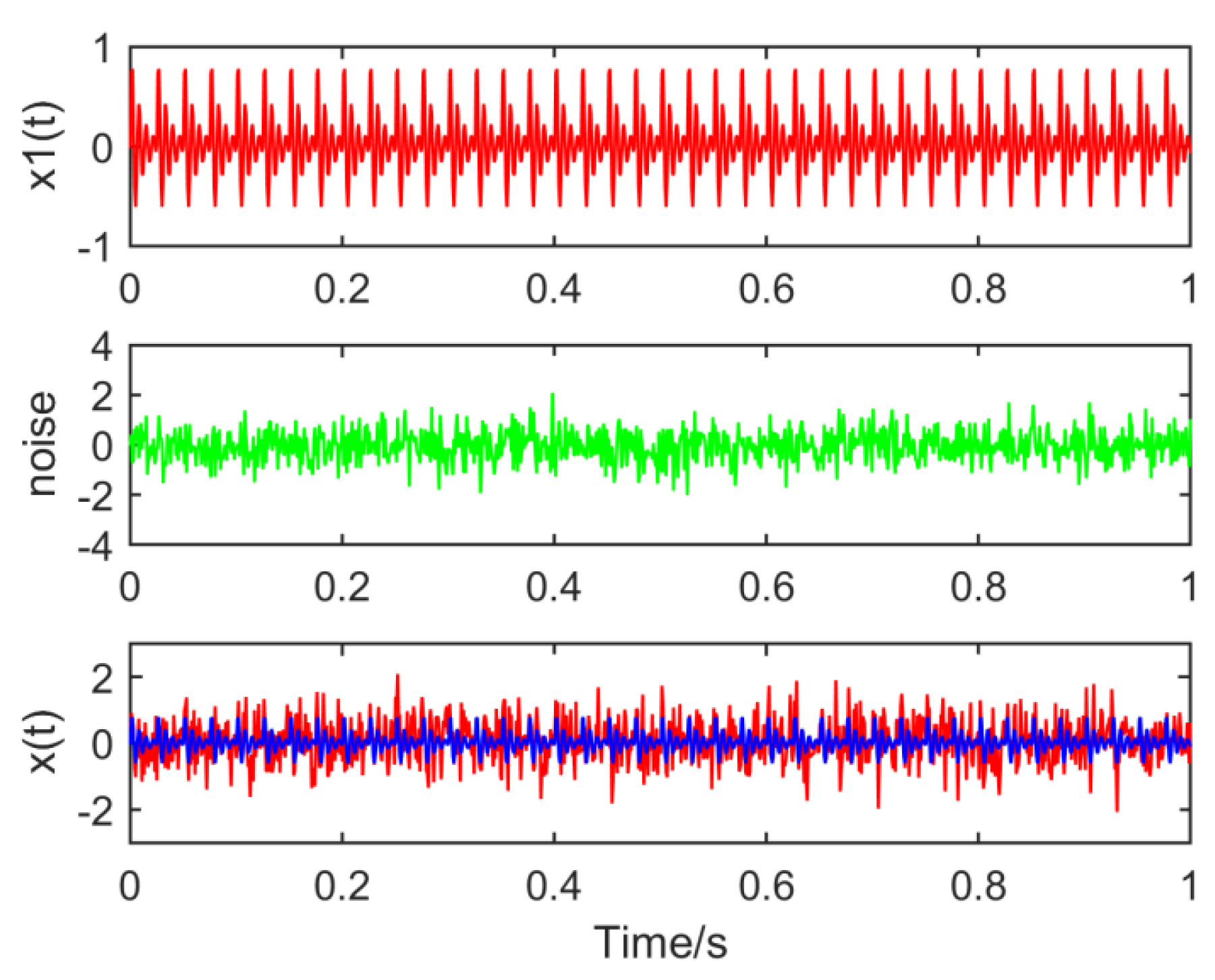
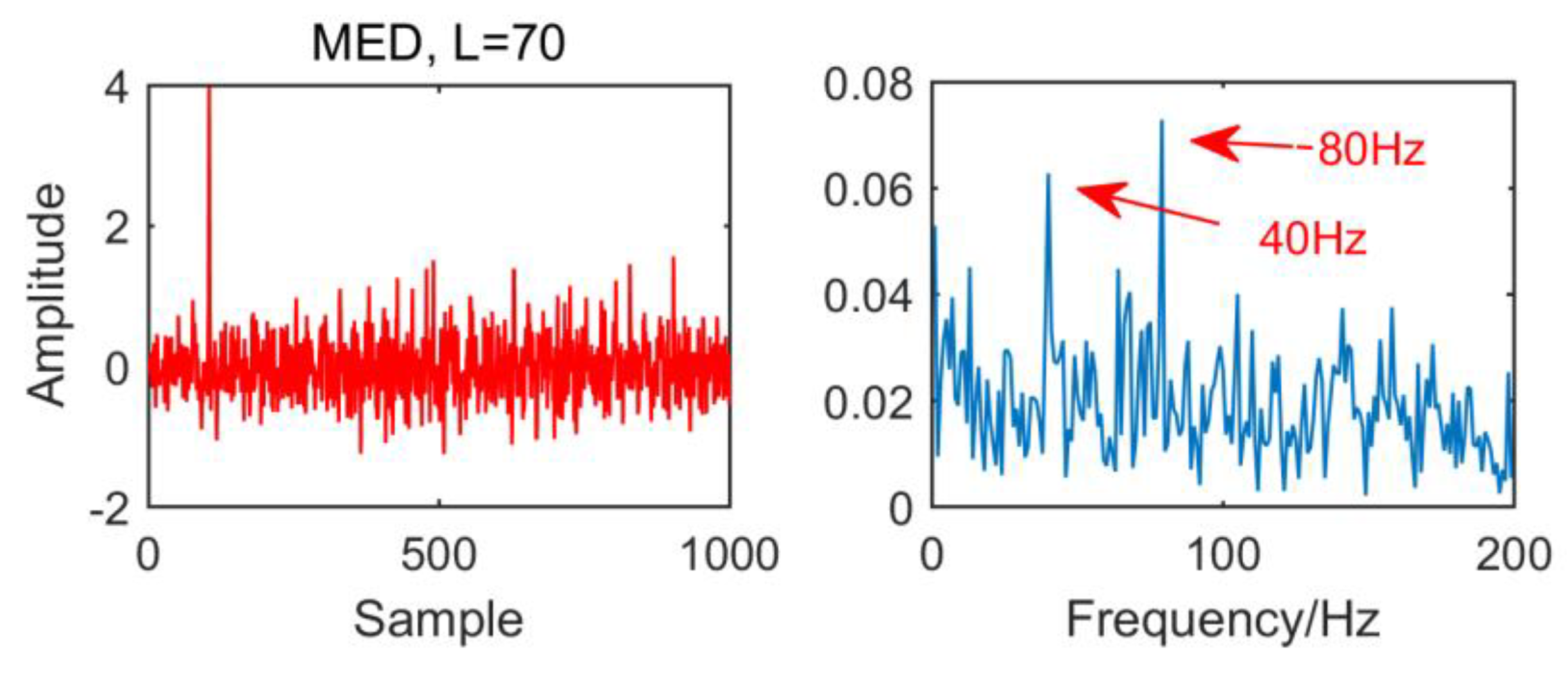
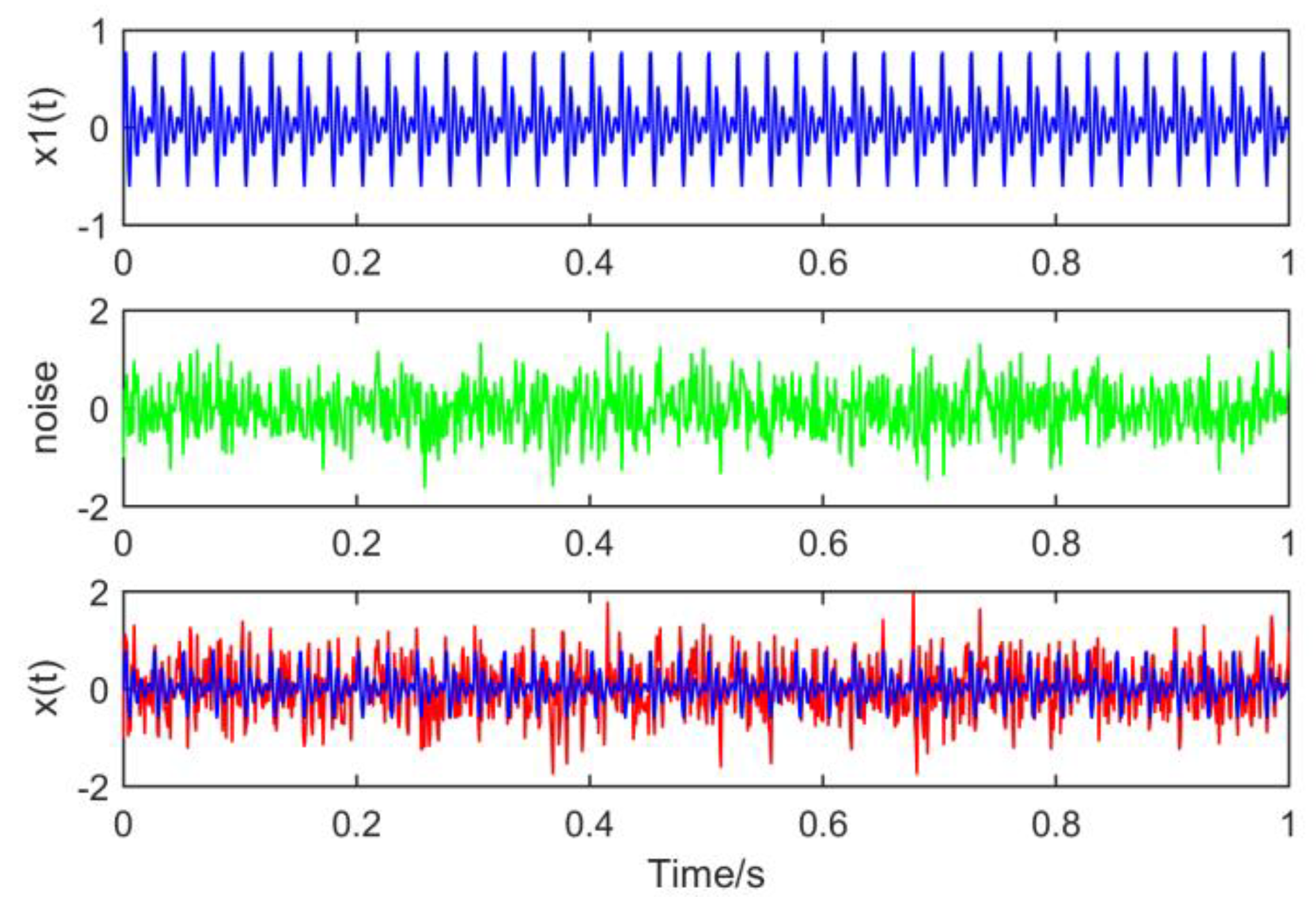
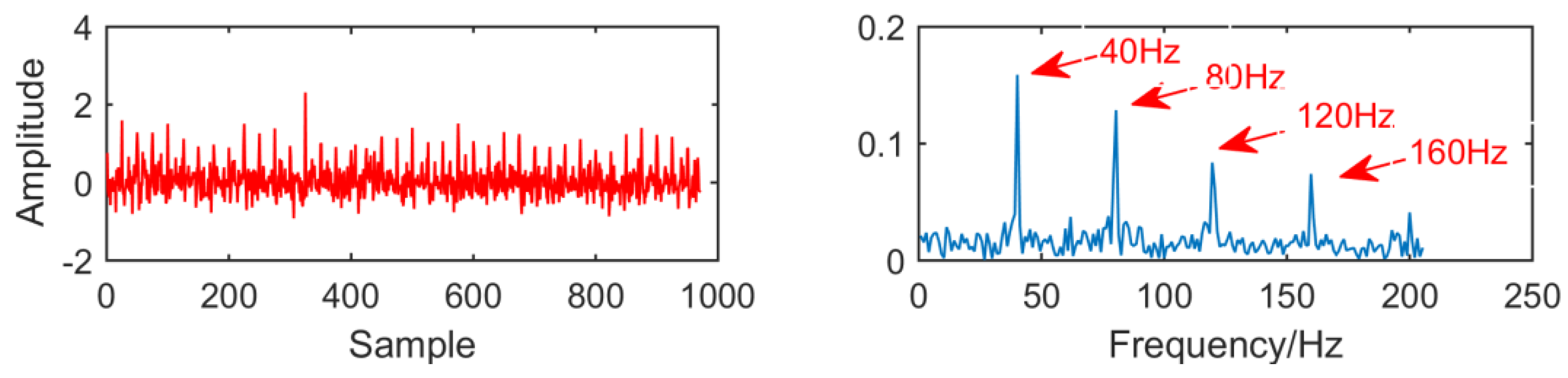
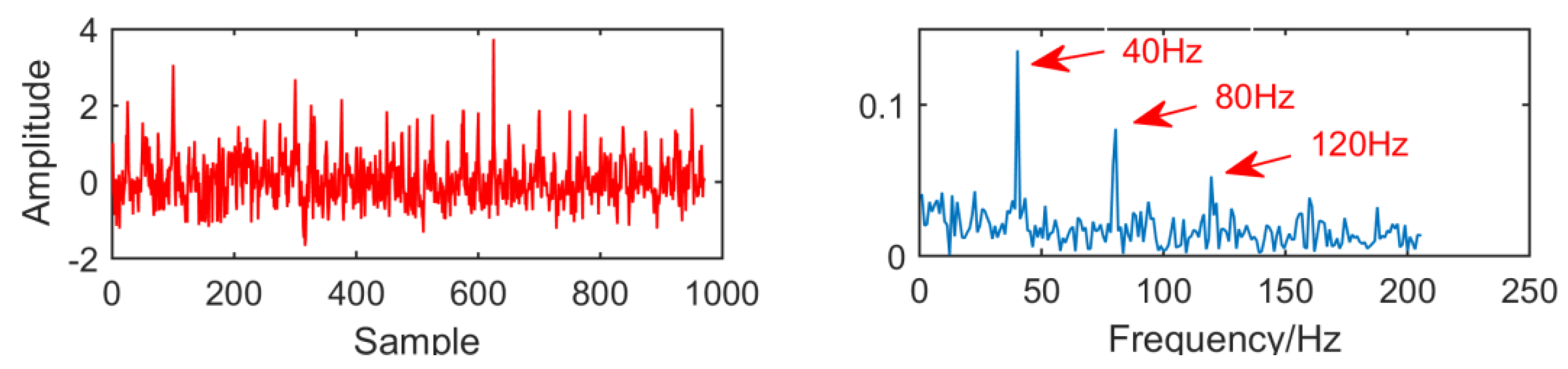
The following simulation signal is constructed to verify the necessity of optimizing the size of MED filter:
where
,
,
and the noise amplitude is 0.4, as shown in
Figure 1.
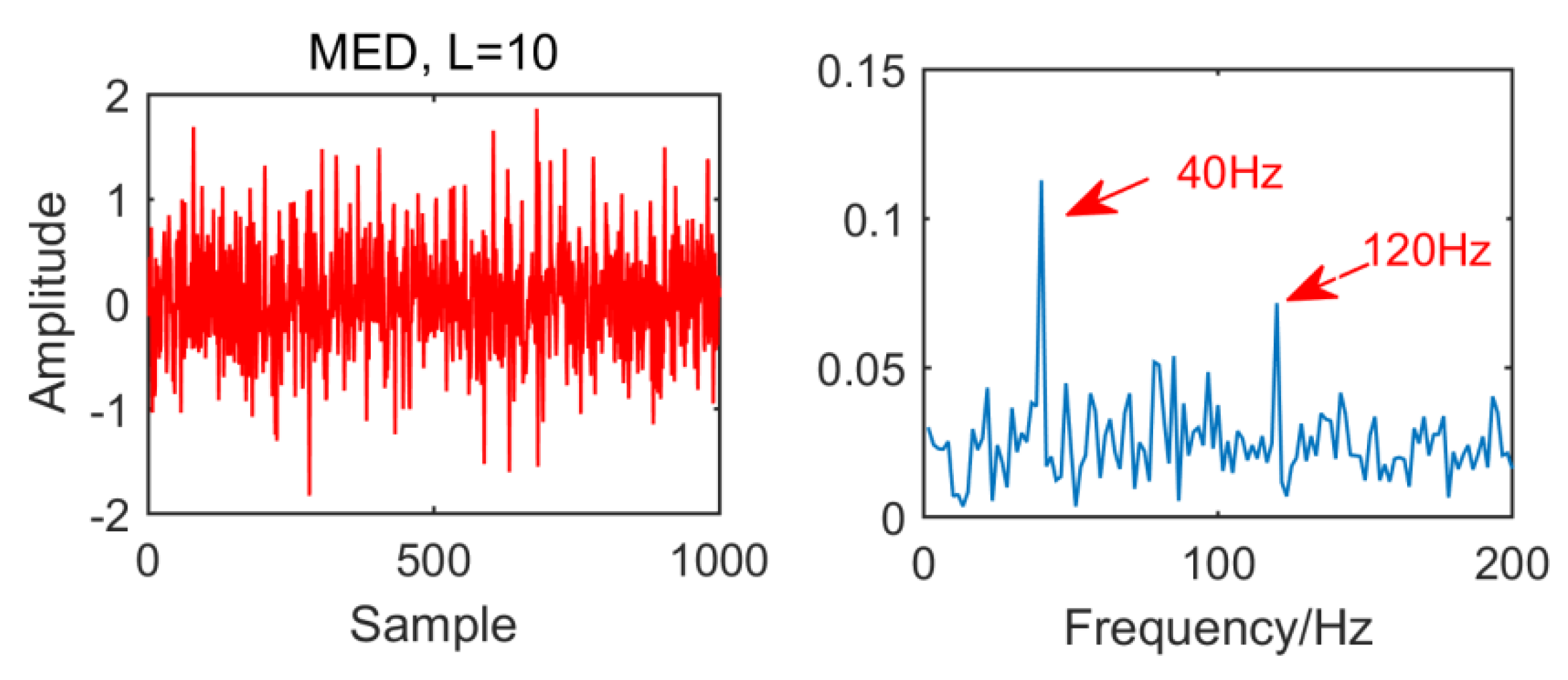
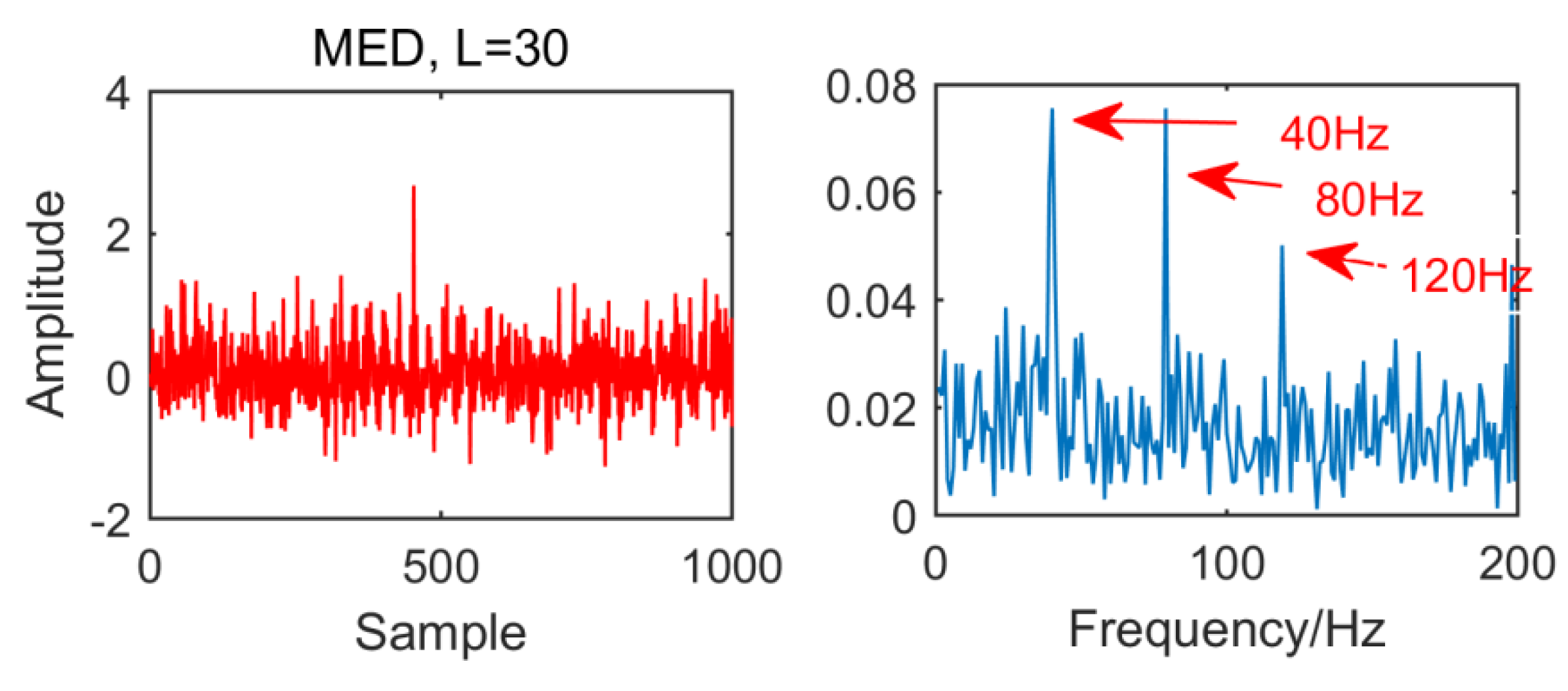
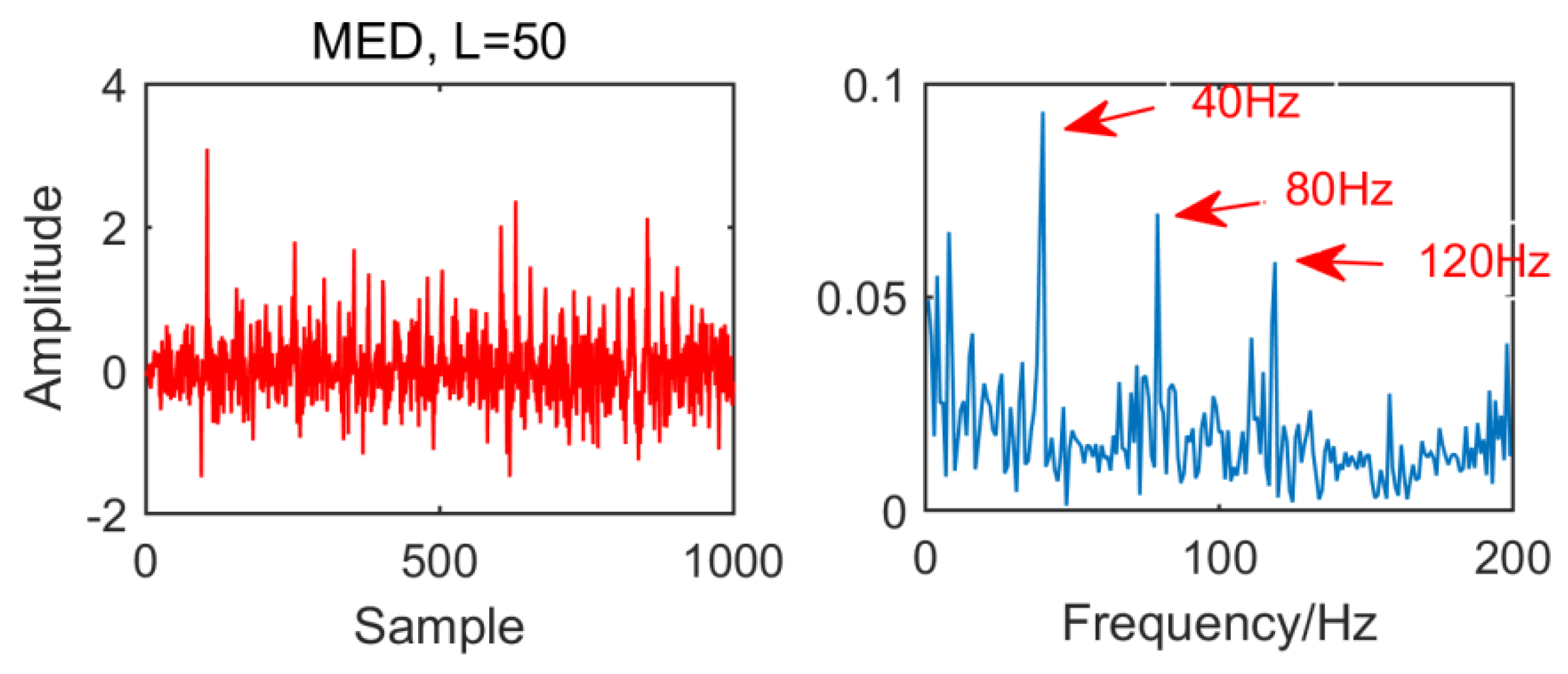
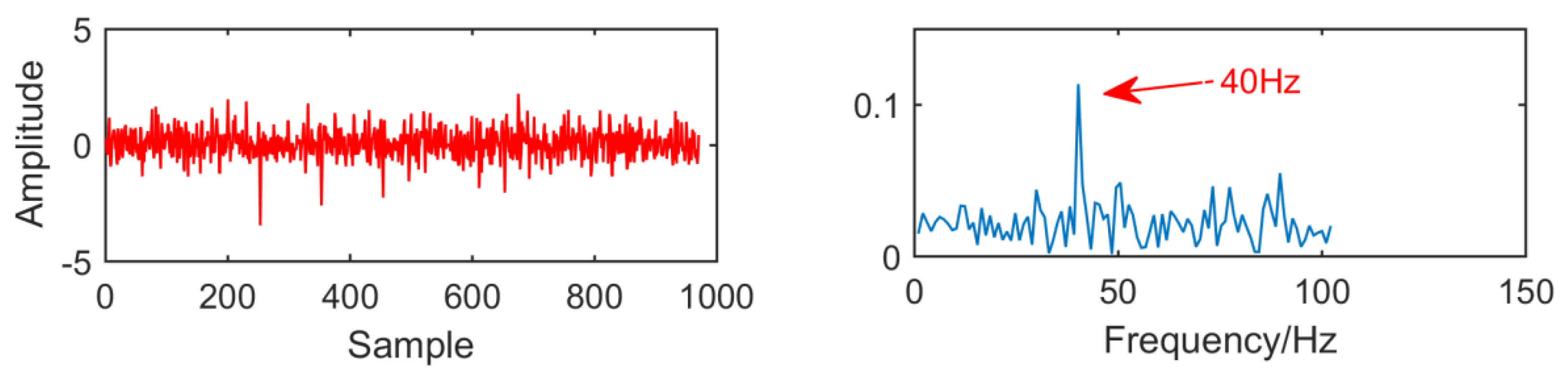
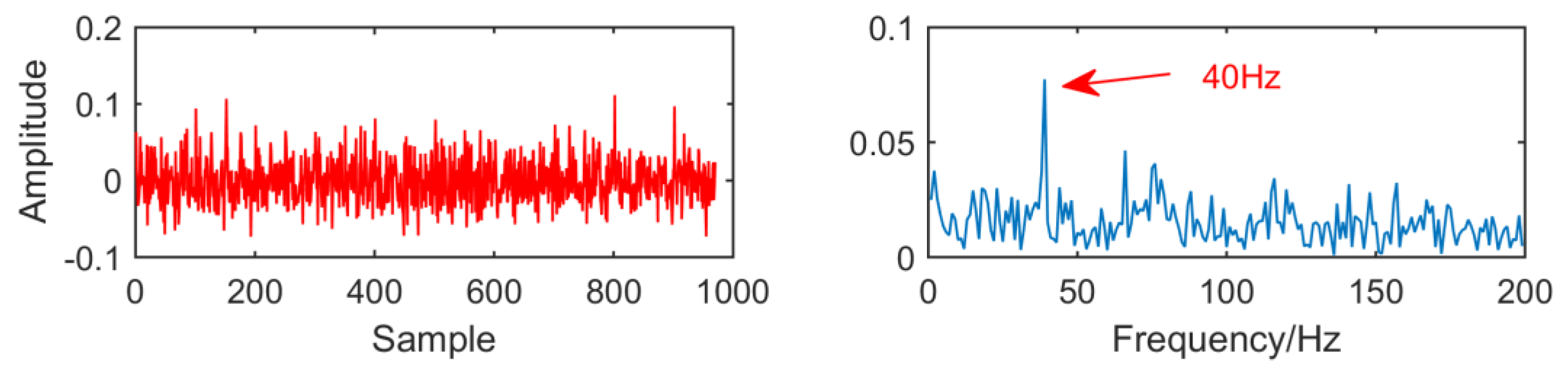
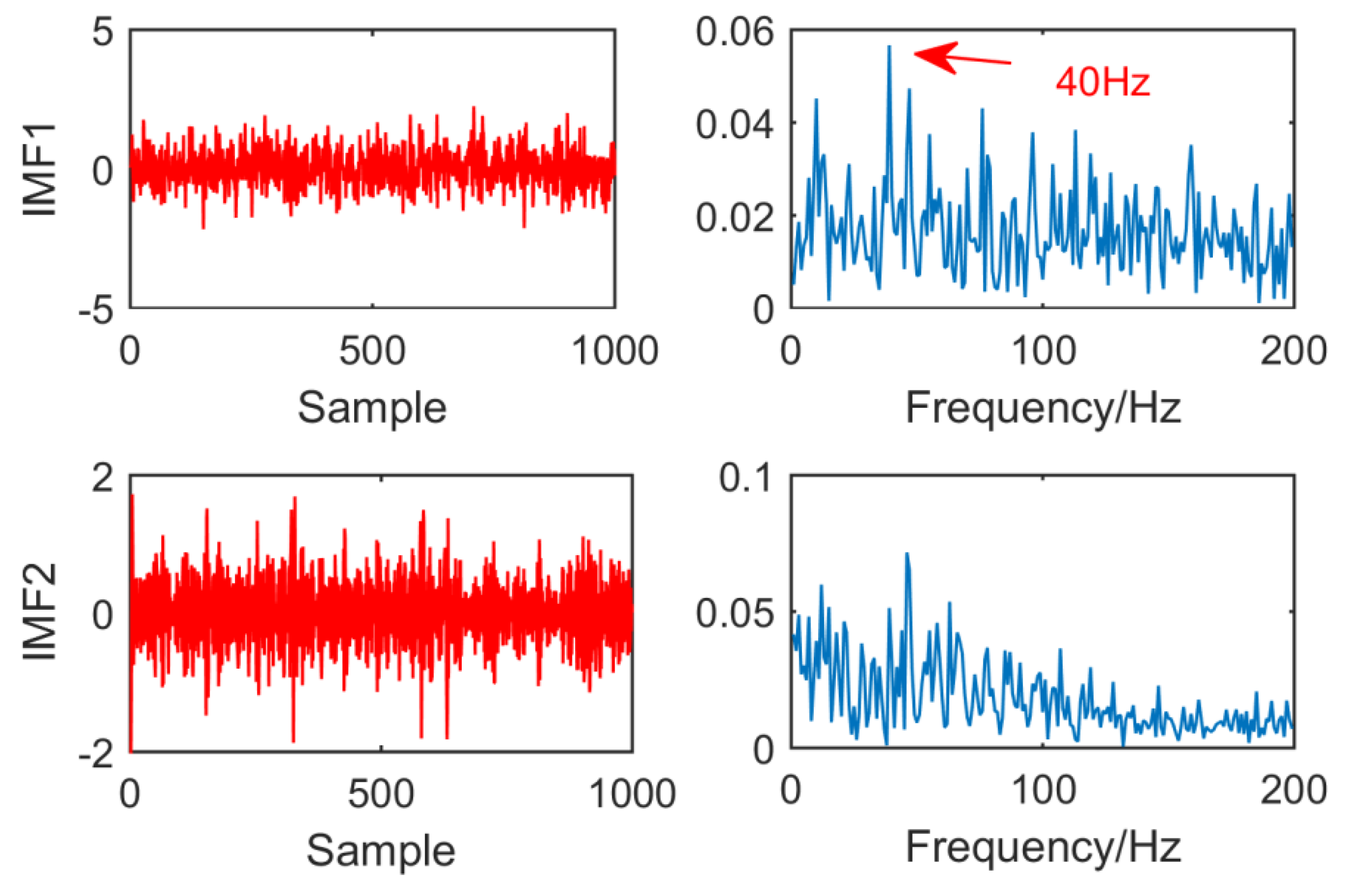
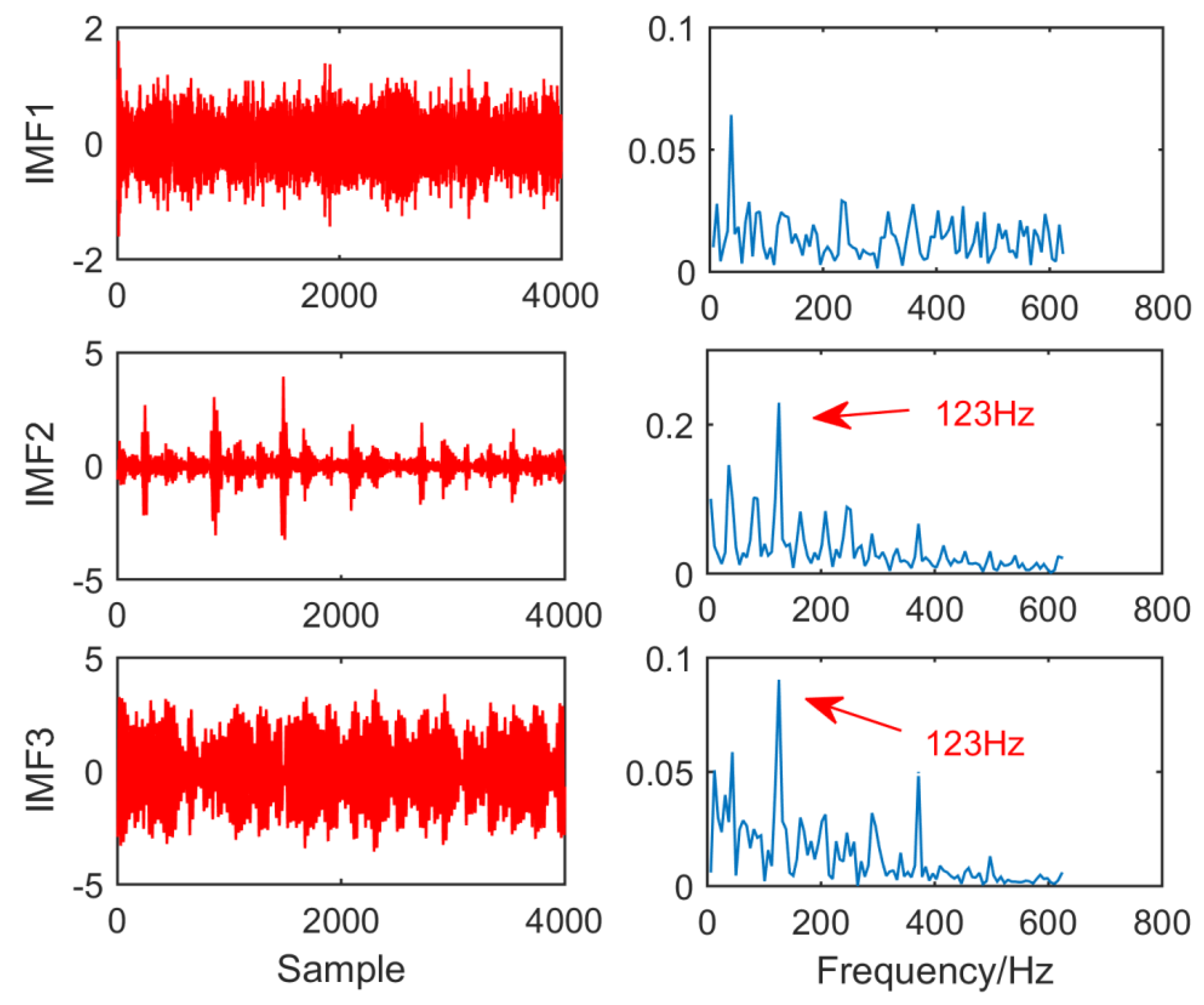
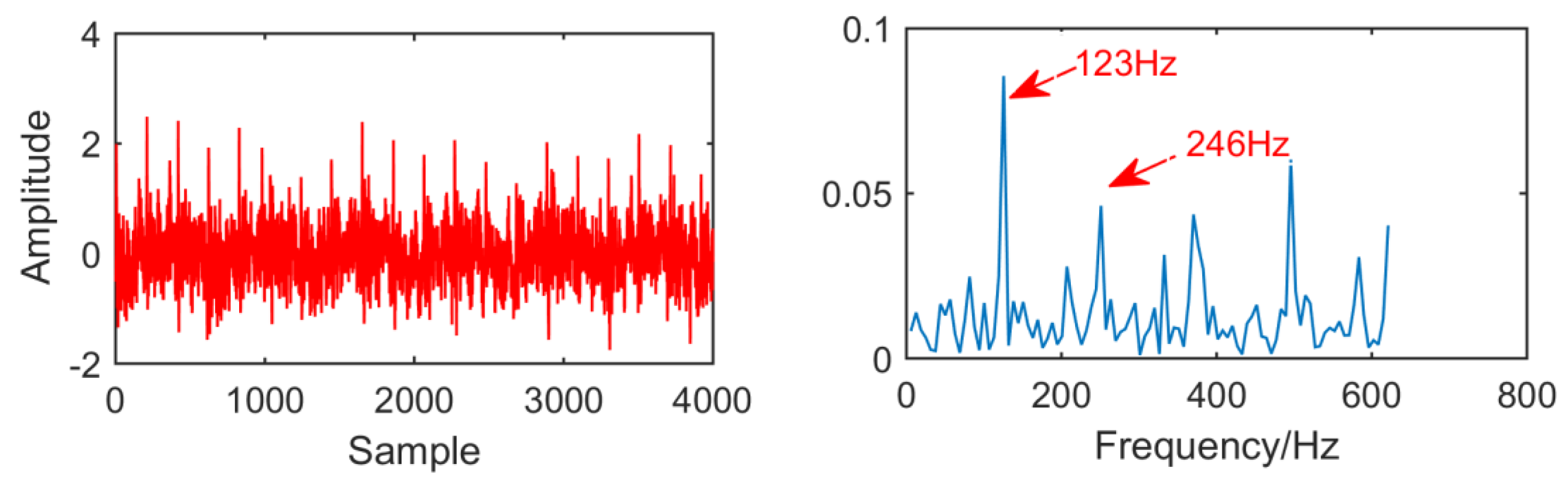
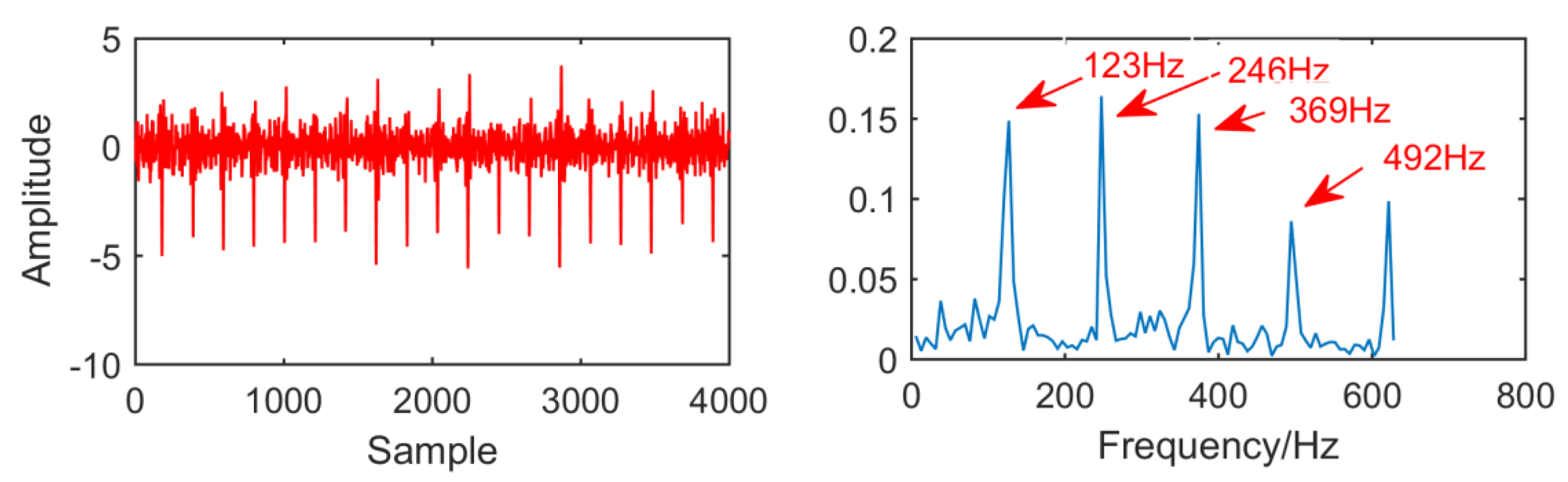
From the time domain waveform and envelope spectra in
Figure 2,
Figure 3,
Figure 4 and
Figure 5, it can be seen that when the size of the MED filter is different, the noise reduction effect of MED on the same fault vibration signal is also different. So, we can conclude that different vibration signals need to have the optimal MED filter size to achieve the best noise reduction effect. In order to improve the noise reduction and pulse enhancement effect of MED for vibration signals, it is necessary to optimize the filter size of MED so that it can choose the appropriate filter size adaptively for different vibration signals.
2.2. Principle of SSD
Singular spectral decomposition (SSD) is a new adaptive signal processing method recently proposed. It can decompose the non-linear and non-stationary signals from a high frequency to a low frequency into the sum of several singular spectral components (SSC) and residual terms. The specific process is as follows:
First, a new trajectory matrix is constructed. For a time series , its data length and embedding dimensions are N and M, respectively. It is constructed as a matrix of X of N columns and M rows, and the i-th row of matrix X is , and ; that is, matrix . Selecting , the lower-right corner of matrix X is moved to the upper-left position of matrix X, and the improved trajectory matrix is obtained. The improved trajectory matrix can enhance the vibration component of the original signal and make the residual component decrease after iteration.
The embedding dimension
M is selected adaptively. Considering the defect, SSA chooses the embedding dimension according to experience, and the adaptive rule is used to select the embedding dimension M used in the
j-th iteration. Firstly, the power spectral density (PSD) of the residual component
at the
j-th iteration is calculated, where the residual component
is
The frequency corresponding to the maximum peak value in the PSD is then estimated. In the first iteration, if the normalized frequency is less than a given threshold of 10−3, the residual is considered as a large trend term, and M is set to , where is the sampling frequency. Otherwise, when the number of iterations J > 1, the embedding dimension is set to , which improves the analysis effect of SSA.
The j-th component signal is reconstructed in the order of high frequency to low frequency. In the first iteration, if a large trend item is detected, only the first or so feature cards are used to obtain , so that and can be obtained from the diagonal average of . Otherwise, when the number of iterations J > 1, a sequence of components must be obtained to describe a time scale with a clear physical meaning. In this sense, its frequency components are mainly concentrated in the frequency band , where represents the half bandwidth of the main peak in the residual power spectral density. Therefore, a subset is created according to all the characteristic groups of the left eigenvector with prominent principal frequencies in the spectrum range and one of the characteristic groups with the greatest contribution to the principal peak energy of the selected modal components. Then the corresponding component signals are reconstructed by the diagonal averaging method of the matrix .
Setting the stop condition of an iteration. The iteratively estimated component sequence
is separated from the original signal and a residual term
is obtained. The normalized mean square deviation between the residual term and the original signal is calculated; that is, the normalized mean square deviation between the residual term and the original signal:
When the normalized mean square deviation is less than the given threshold
th = 1%, the whole decomposition process terminates. Otherwise, the residual term is used as the original signal to repeat the above iteration process until the iteration stopping condition is satisfied, and the final decomposition result is obtained:
where m is the number of component sequences obtained. It is noteworthy that after each iteration, the energy of the residual
decreases.
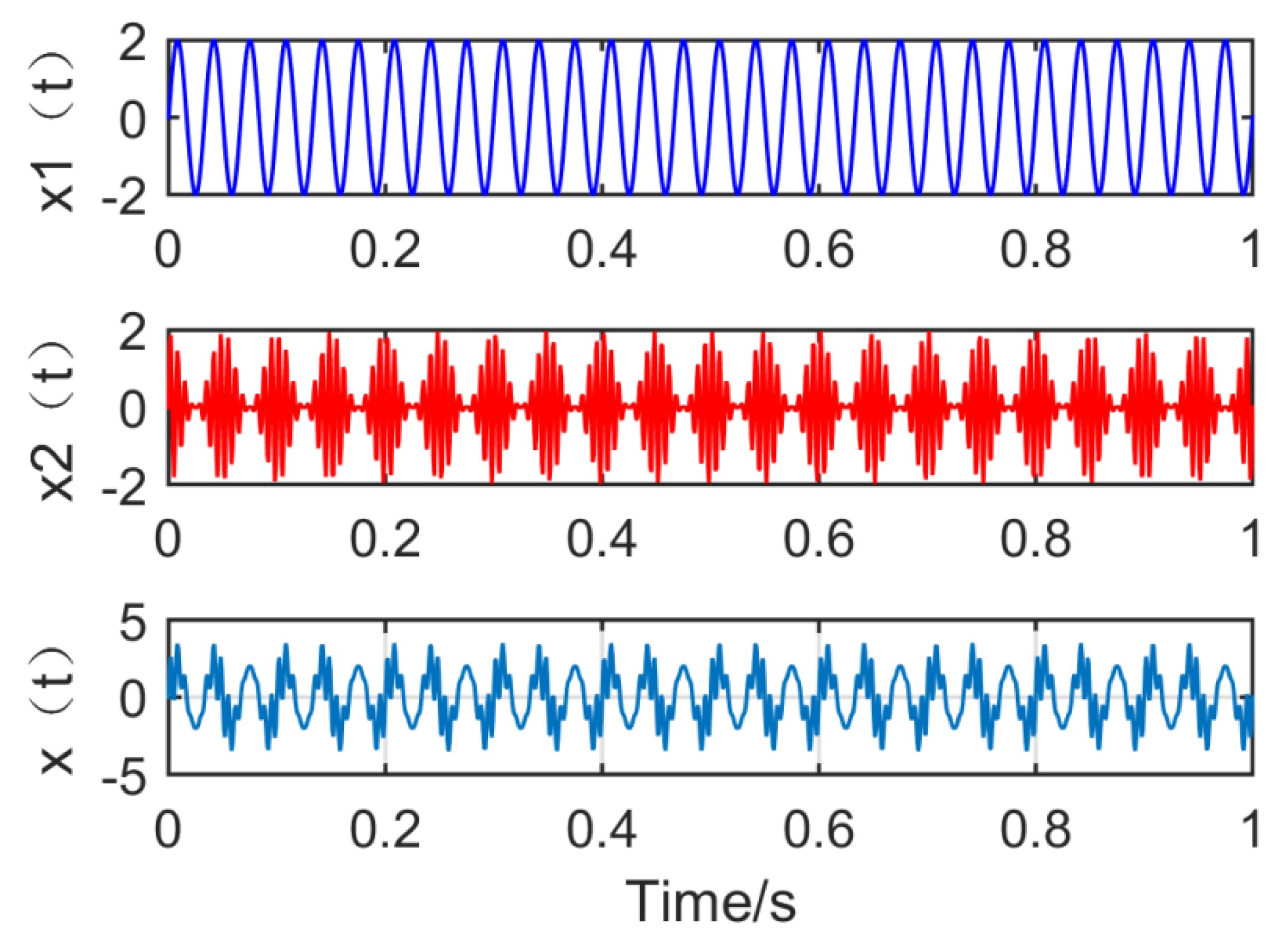
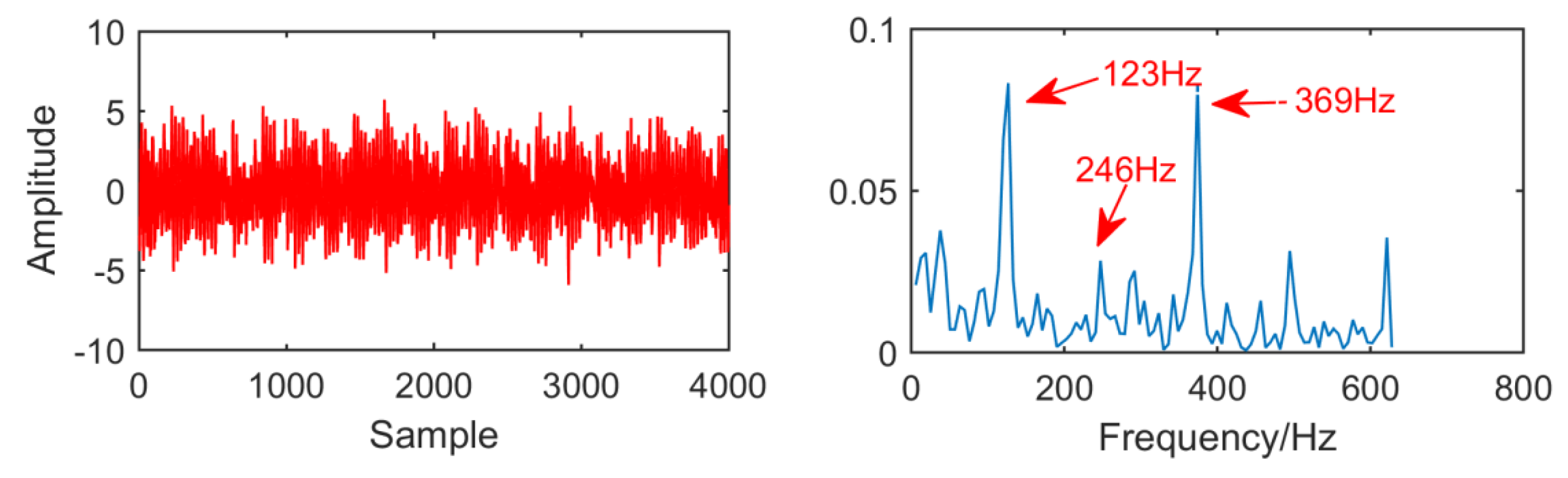
The SSD method has a higher decomposition accuracy and can better suppress the generation of modal aliasing and pseudo components. In order to compare the decomposition performance of SSD and EEMD, we construct a simulation signal, such as Equation (14), for comparison:
where
. The simulation signal consists of a sinusoidal signal and a modulation signal with a modulation source. The waveform of the simulation signal is shown in
Figure 6.
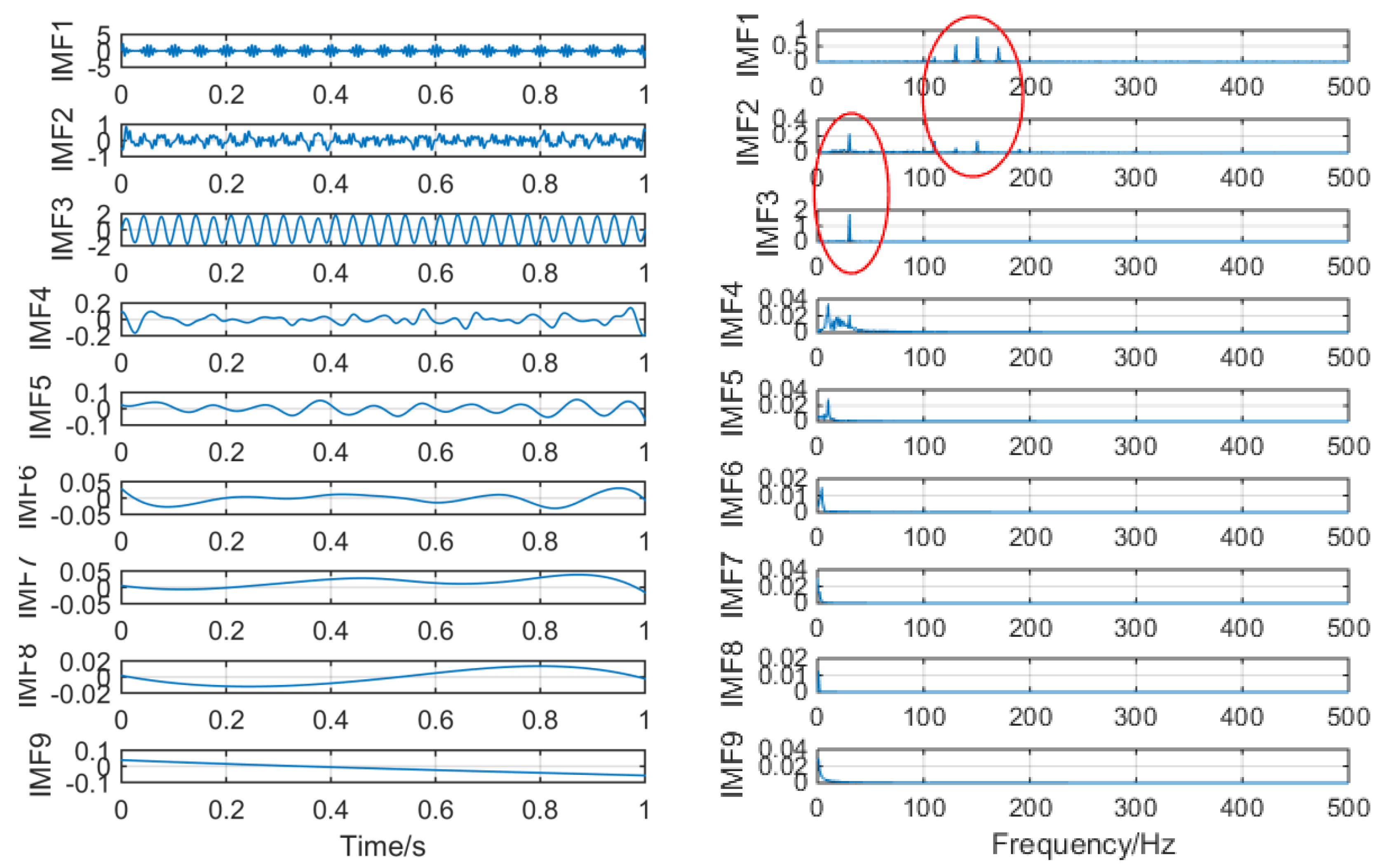
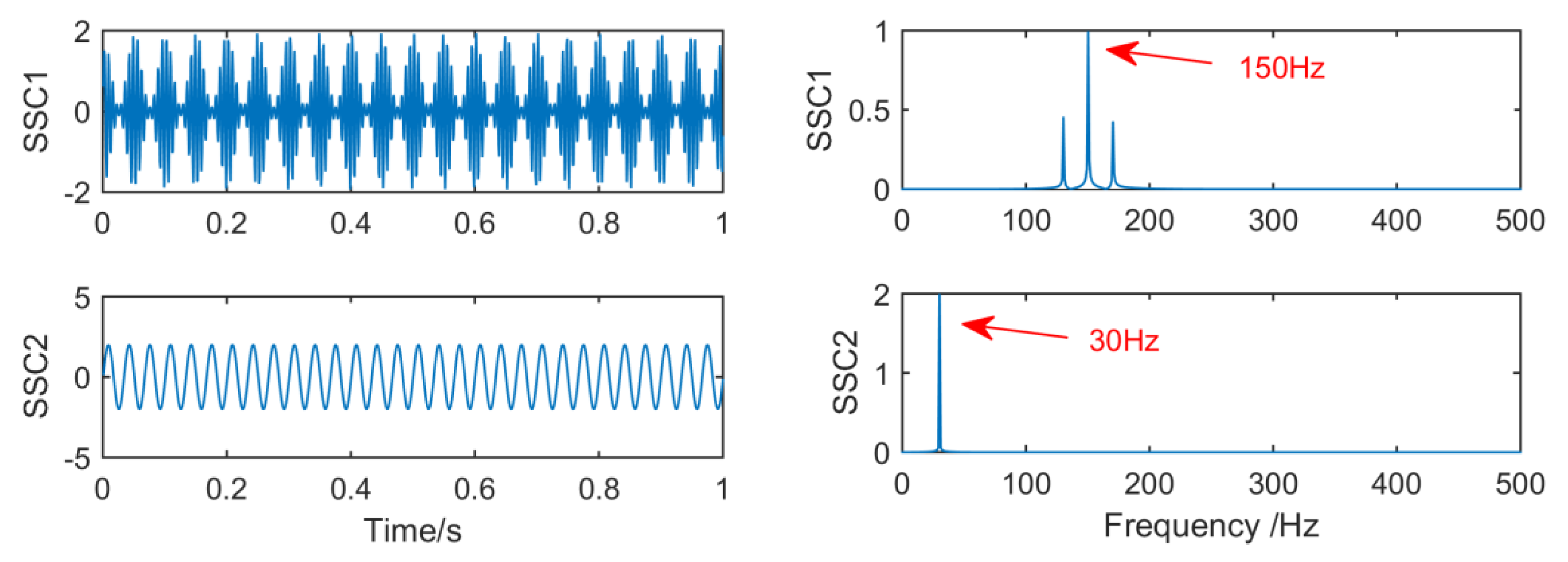
Figure 7 shows the time–frequency graph of each component of the simulation signal decomposed by EEMD, and
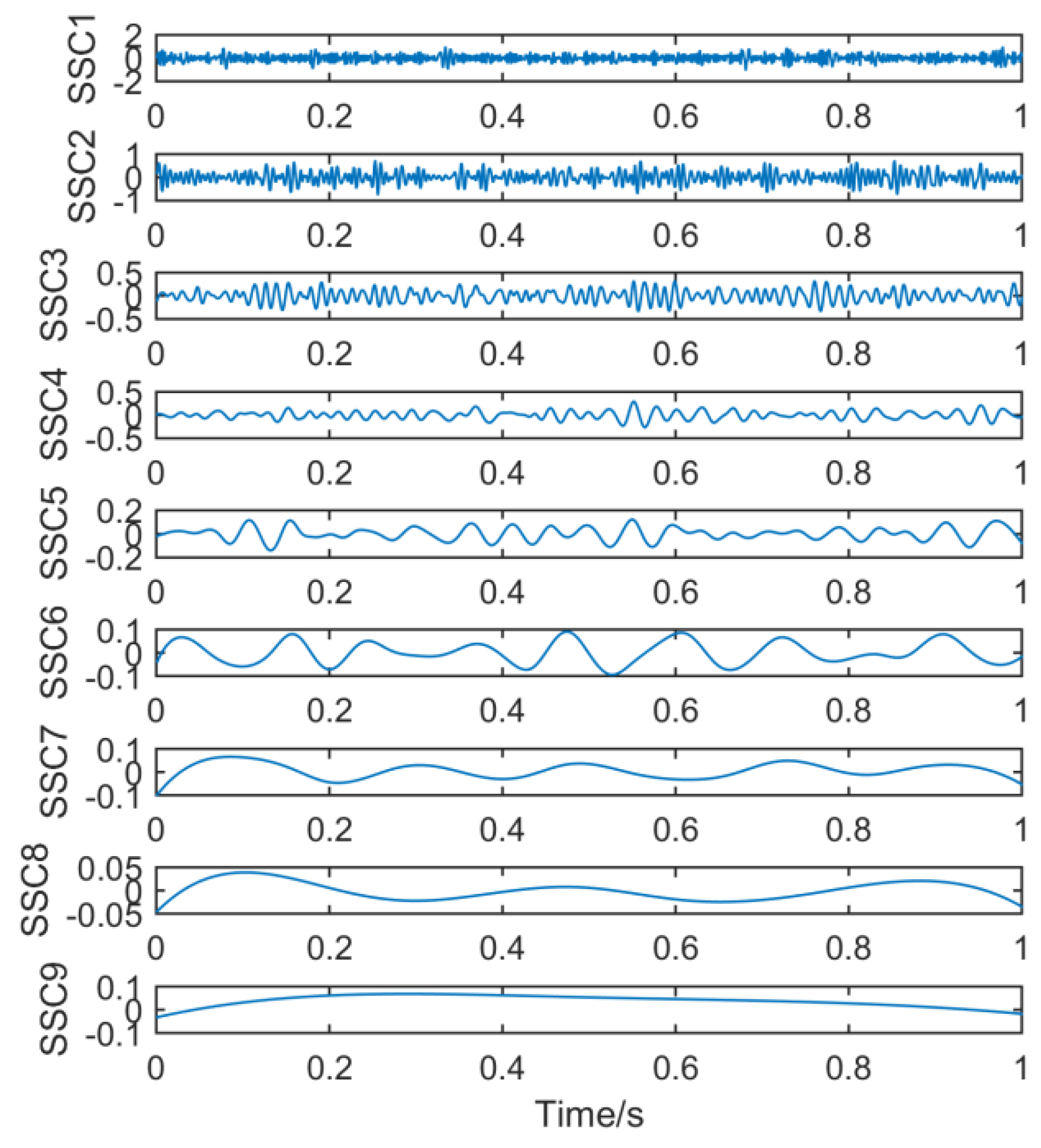
Figure 8 shows the time–frequency graph of each component of the simulation signal decomposed by SSD. It can be seen intuitively that the decomposition performance of SSD is more excellent. The decomposed components are almost identical with the simulation signals, and there is no modal aliasing and no false components. However, mode aliasing occurs in IMF, IMF2, IMF3 and IMF4 after EEMD decomposition, which shows that the decomposition performance of SSD is more reliable. Therefore, this paper chooses the SSD method to stratify the original vibration signal.
2.3. Principles of DFA
In 1994, Peng et al. [
41] proposed the DFA algorithm, which first removed the local trend and then estimated the Hurst index of the object. Initially, this method was used to analyze fractal characteristics of DNA, such as self-similarity, scale invariance and long correlation. With the continuous in-depth study, this method has been widely used in time series data analysis in different fields, such as fault diagnosis of gears and bearings through vibration signals and seismic signal analysis. The research proves that the DFA algorithm is a robust and reliable tool for analyzing non-stationary signals and time series, so this paper chooses the DFA algorithm to divide multiple signal components into noisy signal components and residual signal components. The specific process is as follows:
For the one-dimensional time series
,
. The calculation steps of detrended fluctuation analysis are as follows: Calculating the cumulative deviation
of time series
,
.
The cumulative deviation
is divided into
non-overlapping windows, where each window contains
s sampling points, thus
. Each interval can be expressed as a
p-order trend related to time t, and its corresponding trend equation can be expressed as follows:
In the equation, the coefficient is obtained by the least squares fitting method, where p is the fitting order.
Eliminate the trend term
of
of each window time series:
The second-order wave function of time series
is calculated by using the following equation:
The window size s increases with a certain step size and repeats the (12)–(14) steps to obtain the curve of function
varying with the window size s. If the curve obeys the power law relation, it exists as
It can be found from the above equation that
and
are linearly correlated, and their scaling index
is the slope that can be obtained by the least square method:
2.4. Principles of the Autoregressive (AR) Model
The AR model is widely used in signal denoising. The basic idea of an AR model is to describe the time-varying and interrelated data series by using relevant mathematical models, and to analyze and study them, so as to understand the internal structure and complexity of dynamic data in essence, so as to achieve the best prediction effect of the data. Wang et al. [
42] designed a filter based on an AR model to separate vibration impulse signals generated by local cracks in gear teeth, and used the kurtosis of prediction error signals of the AR model as fault characteristic parameters. Compared with the traditional residual vibration signal of gears, which eliminates meshing resonance frequency, an AR model’s predictive error signal can reflect the tooth defect more clearly. In this paper, an autoregressive (AR) model is used to filter the components of noisy signals. The impulse components of vibration signals are separated, and the first noise reduction is completed. The specific process is as follows:
For the zero-mean discrete sequence
,
can be linearly expressed by the first
values of the signal, and the
-th order autoregressive model
can be obtained by the idea of multiple linear regression:
where
is the
-th time series point to be predicted;
is the
-th coefficient of AR model;
is the order of AR model; and
is the white noise sequence with 0 mean variance
.
For the solution of the AR model coefficients, the autocorrelation coefficients of signals are often used. The model satisfies the Yule–Waker equation:
In the equation , , and is the number of signal points sampled.
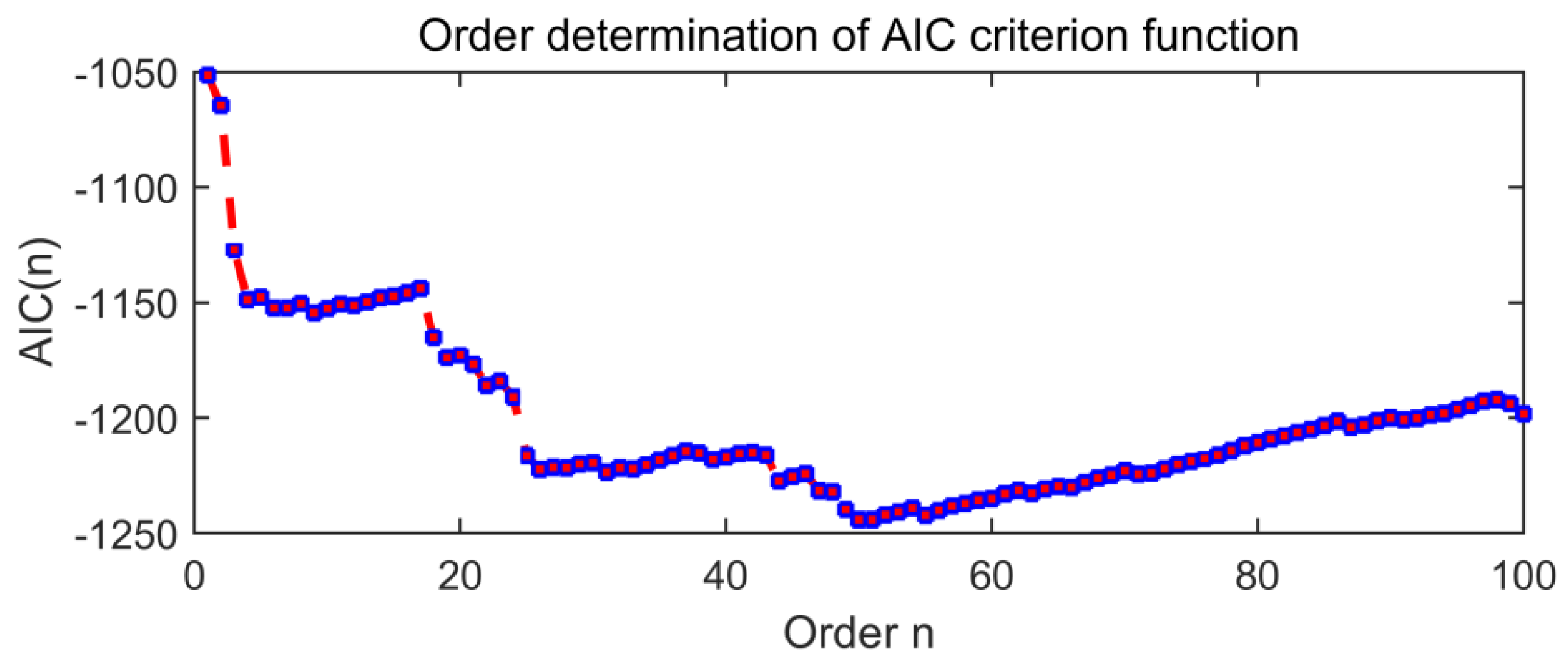
The order determination of the AR model is very important, as too large an order will produce pseudo-spectral peaks and unstable statistical values, whereas too small an order will produce the smoothing effect of spectral peaks. Minimum Information Criterion (AIC) is widely used. Its criterion function is
The value of decreases with the increase of order from 1. When the order reaches a certain order , the value of tends to be stable and is the best order of AR model.
2.5. Principles of New Methods
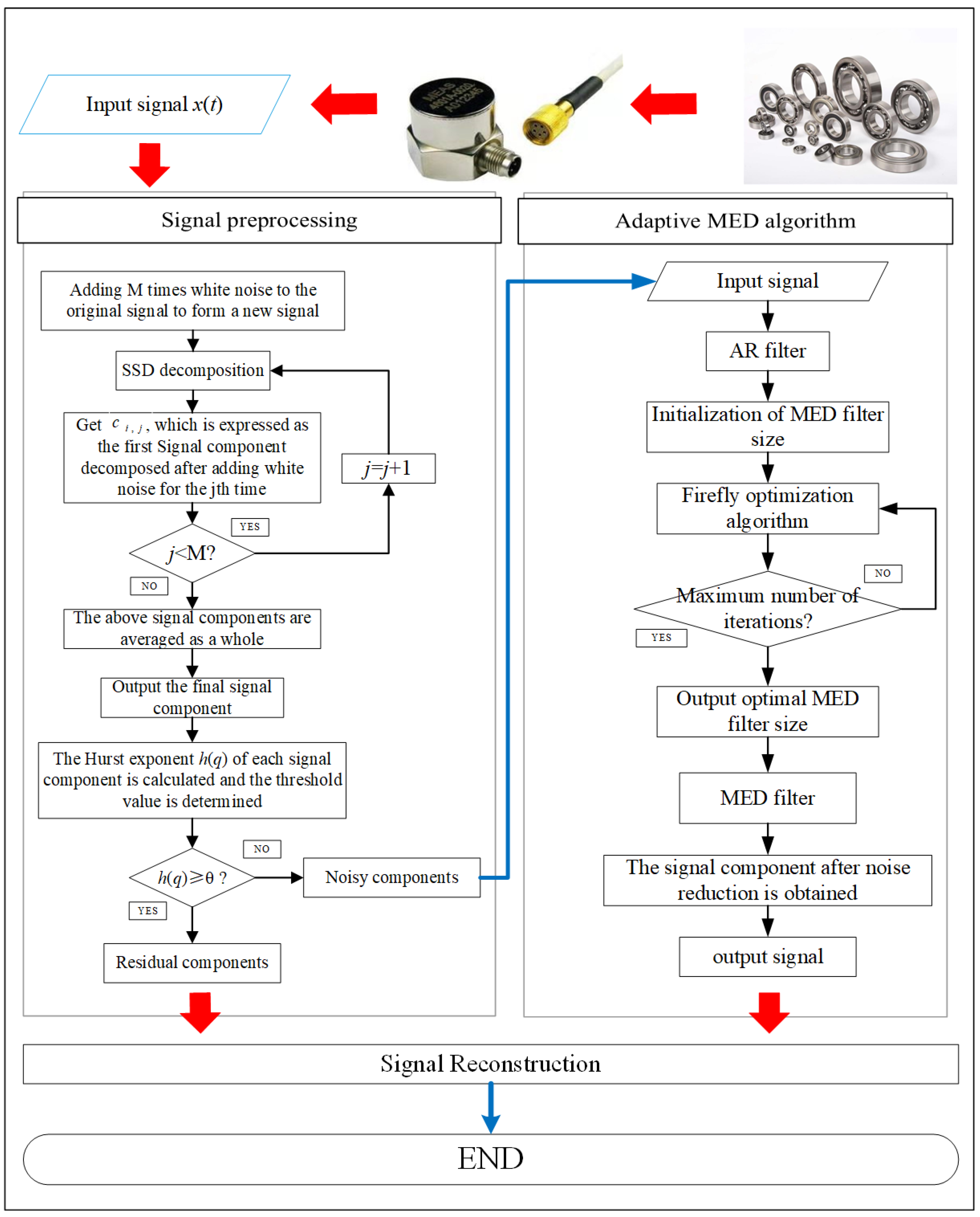
The purpose of this paper is to optimize the Med algorithm and improve the noise reduction efficiency of MED. At present, Med has two main defects; that is, poor anti-noise ability and the filter size need to be determined manually. Firstly, aiming at the defect of the bad anti-noise ability of MED, this paper proposes a preprocessing method for the original signal. The SSD algorithm has a higher decomposition accuracy than EEMD, so that the SSD algorithm is used to layer the original signal. However, it is easy to produce high-frequency pseudo components when using the SSD algorithm to process signals, and it is greatly interfered in the strong noise environment, so this paper chooses to use a Gaussian white noise assisted SSD algorithm to make up for the shortcomings of SSD. After the original signal is layered successfully, the DFA algorithm is used to distinguish the layered signal components; that is, the original signal is divided into noisy signal components with a lot of noise and residual components with less noise. After that, the noisy component is de-noising, while the residual component is less noisy. In order to ensure the integrity of the fault features, the residual component is not processed. Secondly, in order to solve the problem that the size of the MED filter is not self-adaptive, this paper proposes a method to select the optimal filter size through the optimization algorithm of firefly. Finally, the noisy and residual components are reconstructed to get the final result.
Step 1: Signal Preprocessing
The original signal is decomposed into a series of signal components by noise-assisted SSD. In SSD, modal aliasing and high-frequency pseudo components occur because of its vulnerability to noise. For this reason, adding white noise into the original signal not only makes use of the uniform distribution of the white noise spectrum to automatically distribute signals of different time scales to the appropriate reference scale, but also makes use of the zero-mean characteristic of white noise. After many times of average, the noise cancels each other, thus eliminating the influence of noise on signal components. Through this white noise processing, the problem that the SSD method is prone to generate high-frequency pseudo-components has been greatly improved. The steps are as follows: Given an original signal , white noise with a zero mean and constant standard deviation of amplitude is added, in which , M being the number of iterations.
So, the new signal is
where
,
is the standard deviation and
is the original signal.
The SSD algorithm is used to decompose the signal several times, and the result shows the first signal component decomposed in the j-th experiment. If j is less than M, repeat the previous step.
According to the principle that the statistical mean of the uncorrelated random sequence is zero, the above-mentioned signal components are averaged in general, which can eliminate the influence of multiple white noises on the signal components. Finally, the obtained signal component is
where the output
is the
i-th signal component obtained.
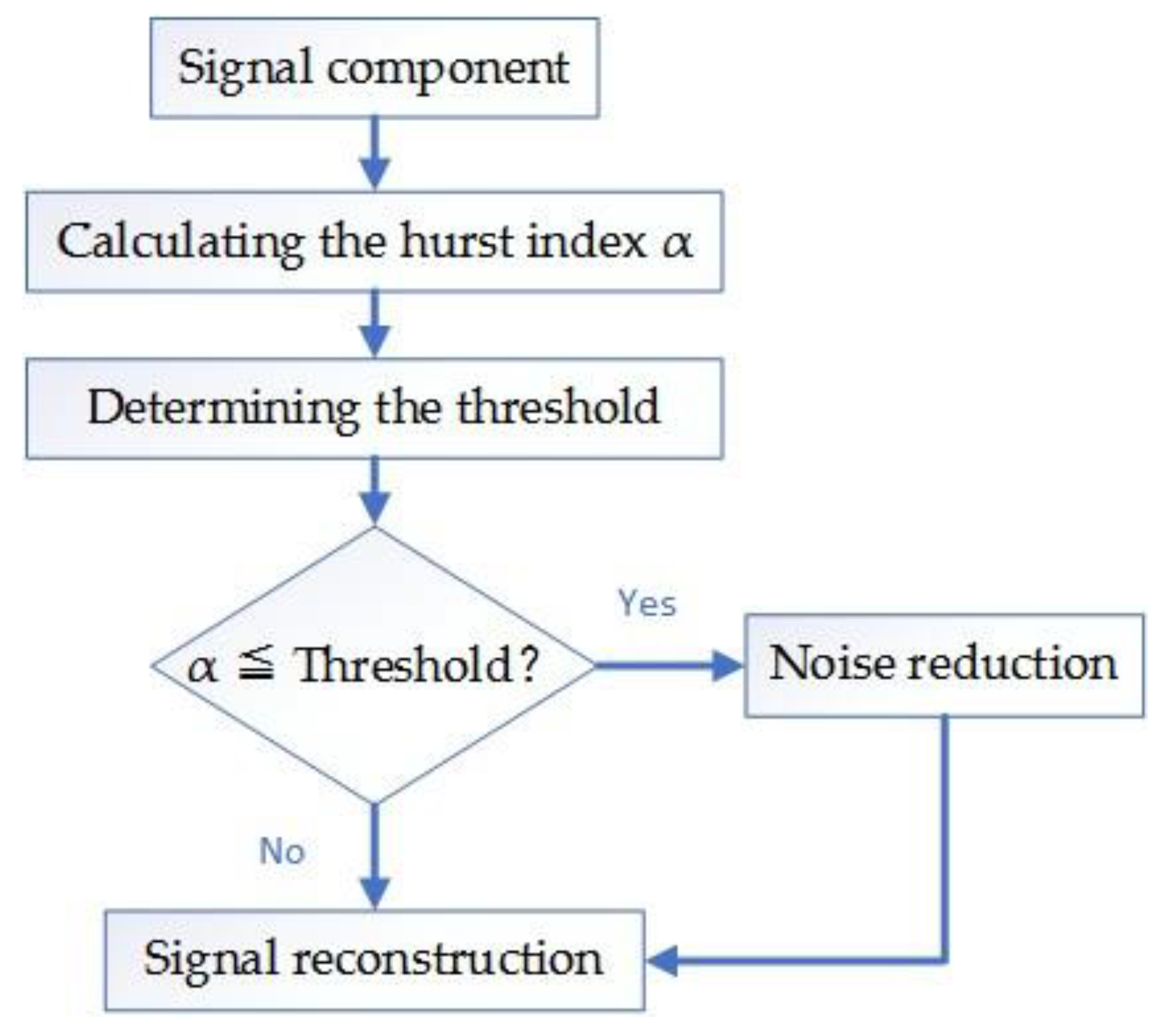
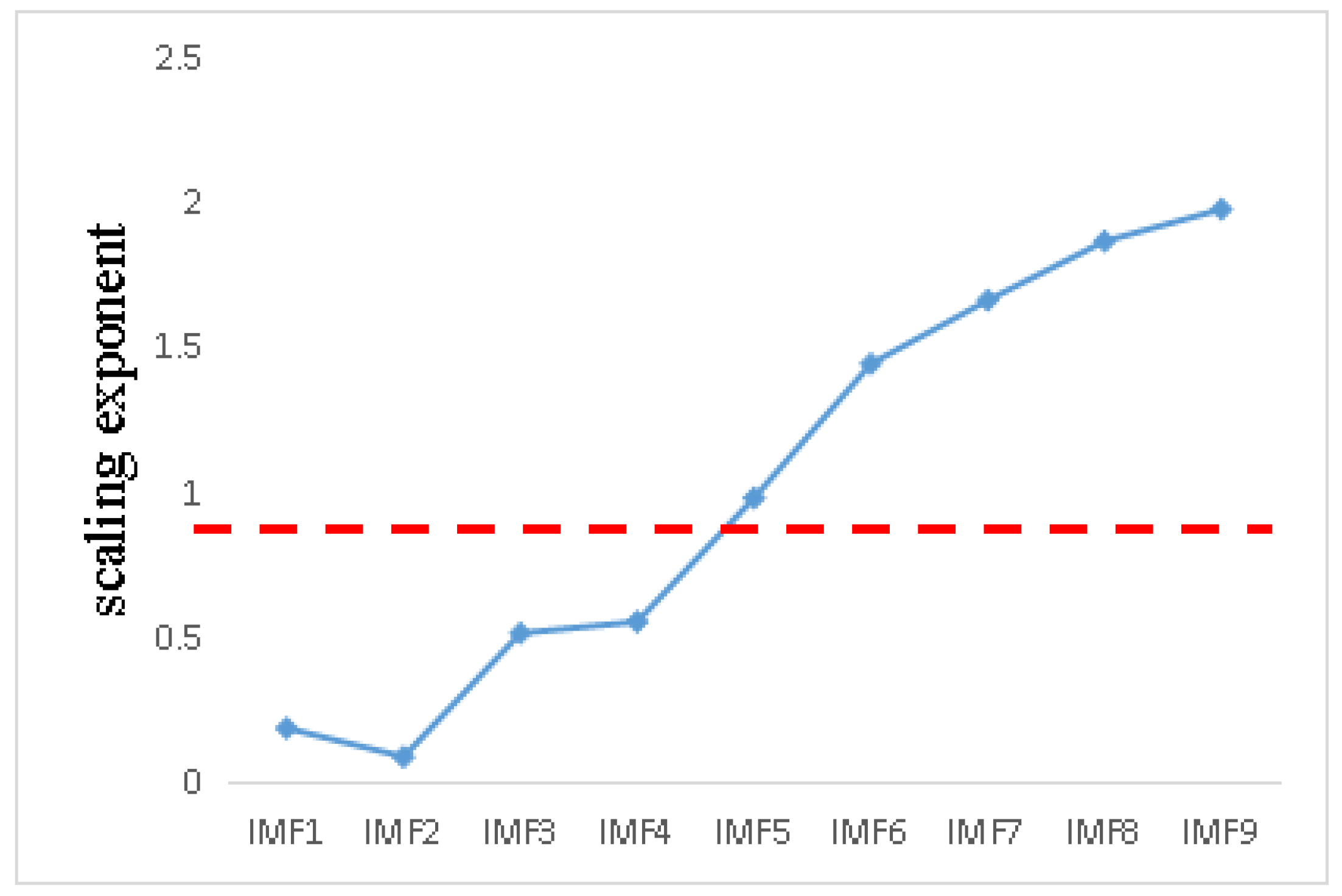
DFA is used to screen and process the signal components, and the Hurst index H(q) of each signal component is obtained. If 0 < H(q) < 0.5, the signal components have an inverse correlation; that is, the smaller the value of the friction vibration is, the stronger the inverse correlation. When H(q) = 0.5, the time series is irrelevant, and the friction vibration has no obvious forward and backward trend. When 0.5 < H(q) < 1, the time series has a correlation; that is, the larger the value, the stronger the continuity. The threshold is usually determined by the Hurst exponent of white noise .
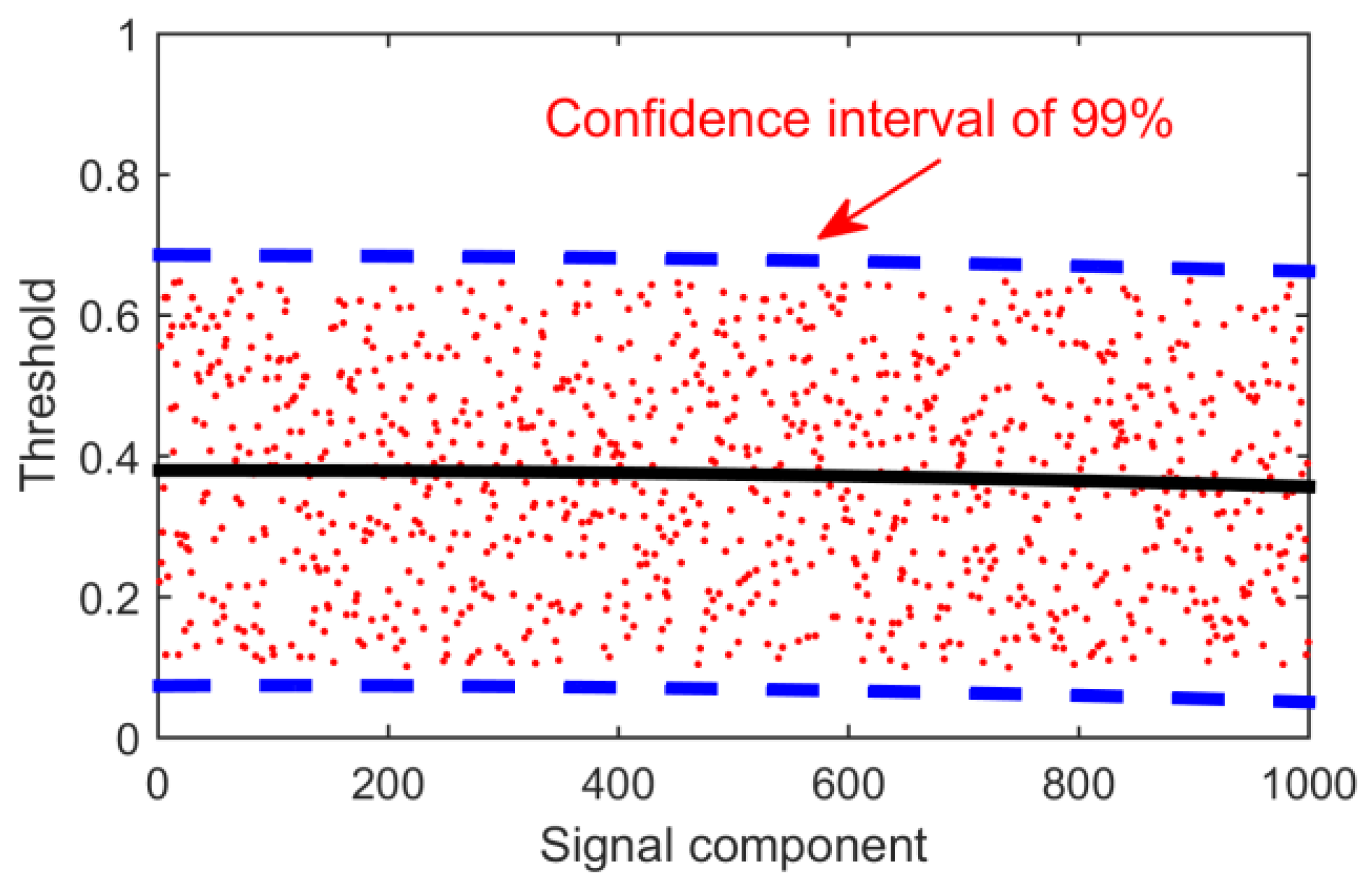
However, in many practical operations, it is found that the decomposition algorithm produces modal aliasing. In other words, the overlapping of two signal components results in multiple fault features in one signal component. So sometimes the Hurst index with a noise component is slightly larger than 0.5, ranging from 0.5 to 0.7. In order to deal with this situation, 1000 experiments were carried out in this paper. By choosing completely random signals and adding random noise, the Hurst index of the decomposed noisy signal components was calculated. Finally, the coordinate axis is established, the 1000 points are fitted by a curve, and the upper boundary of 99% confidence interval is selected as the final threshold. As shown in the following
Figure 9, the threshold should be 0.7.
The specific screening steps are as follows:
The signal component whose scale index is lower than the threshold value is the noisy component; and the signal component, whose index is higher than the threshold, is the residual component.
Finally, all the signal components are divided into two parts, as follows:
The flow chart of the screening signal component is as follows (
Figure 10):
Step 2: Adaptive MED algorithm
After processing the signal component by using the autoregressive (AR) model, the adaptive MED algorithm proposed in this paper is used to process the signal component for the second time, and then reconstruct it with the original residual signal to get the final result. The specific methods are as follows:
In this paper, envelope spectral entropy is chosen as the fitness function of the FA algorithm to optimize filter length parameters. The theory of envelope spectral entropy is as follows:
When there are local damages or defects in rolling bearings, impulsive force will be generated during the load-bearing operation, which will stimulate the high-frequency natural vibration of bearings. The inherent vibration can be regarded as the high frequency carrier of the bearing vibration signal, while the periodic shock is the low frequency modulation signal. The final vibration waveform of the bearing is a complex amplitude modulation wave. The envelope demodulation analysis based on Hilbert transform is an effective method to analyze the amplitude modulation signal.
The Hilbert transform
of signal
is defined as
and
can form new composite signals:
Envelope signal is defined as
Through envelope demodulation analysis, the low frequency modulation signal in the modulation signal, namely envelope signal, can be obtained. Envelope spectrum analysis can effectively extract the fault frequency components of rolling bearing vibration signals, which is the most widely used analysis method in rolling bearing vibration analysis. The degradation of rolling bearing performance will inevitably bring about changes in the internal characteristics of vibration signals. In order to effectively measure this change, the envelope spectrum analysis and information entropy are combined; that is, envelope spectrum entropy:
where
is the envelope spectrum of vibration signal
, and
is the envelope spectrum entropy.
To avoid the influence of data length on the results, the normalized envelope spectral entropy is defined:
It can be seen that envelope entropy measures the uniformity of frequency distribution of the envelope signal and reflects the complexity of the signal in the envelope domain. Envelope spectrum entropy depends only on the frequency distribution of the envelope signal but has nothing to do with the strength of the signal. Therefore, in order to make the denoised signal highlight a more effective continuity period, for envelope spectrum entropy, the smaller the better.
Let , the key of MED denoising is how to select the filter size L. If the filter size is different, the denoising results will be different. At the same time, it should be noted that the larger the L value selected, the longer the computation time needed for noise reduction. In this paper, the envelope spectrum entropy is used to measure the effect of signal de-noising, that is to say, the signal is de-noised by MED with different filter sizes, then the envelope signal is obtained by Hilbert transform, and then the envelope spectrum and envelope spectrum entropy are calculated.
FA optimization algorithm uses firefly individuals to simulate points in search space, and uses the phototaxis of firefly itself to transform the optimization problem into finding the brightest firefly in the firefly population. Each iteration finds the brightest firefly and updates the position of firefly through attraction and movement between fireflies.
The rule that firefly
moves and updates to brighter firefly
is
where
and
are the spatial locations of firefly
and
, respectively;
is the attraction of firefly
to firefly
;
is the distance between firefly
and
;
is the attraction of
;
is the absorption coefficient of light intensity;
is the step factor,
; and
is the interference term to avoid the FA algorithm falling into local optimum.
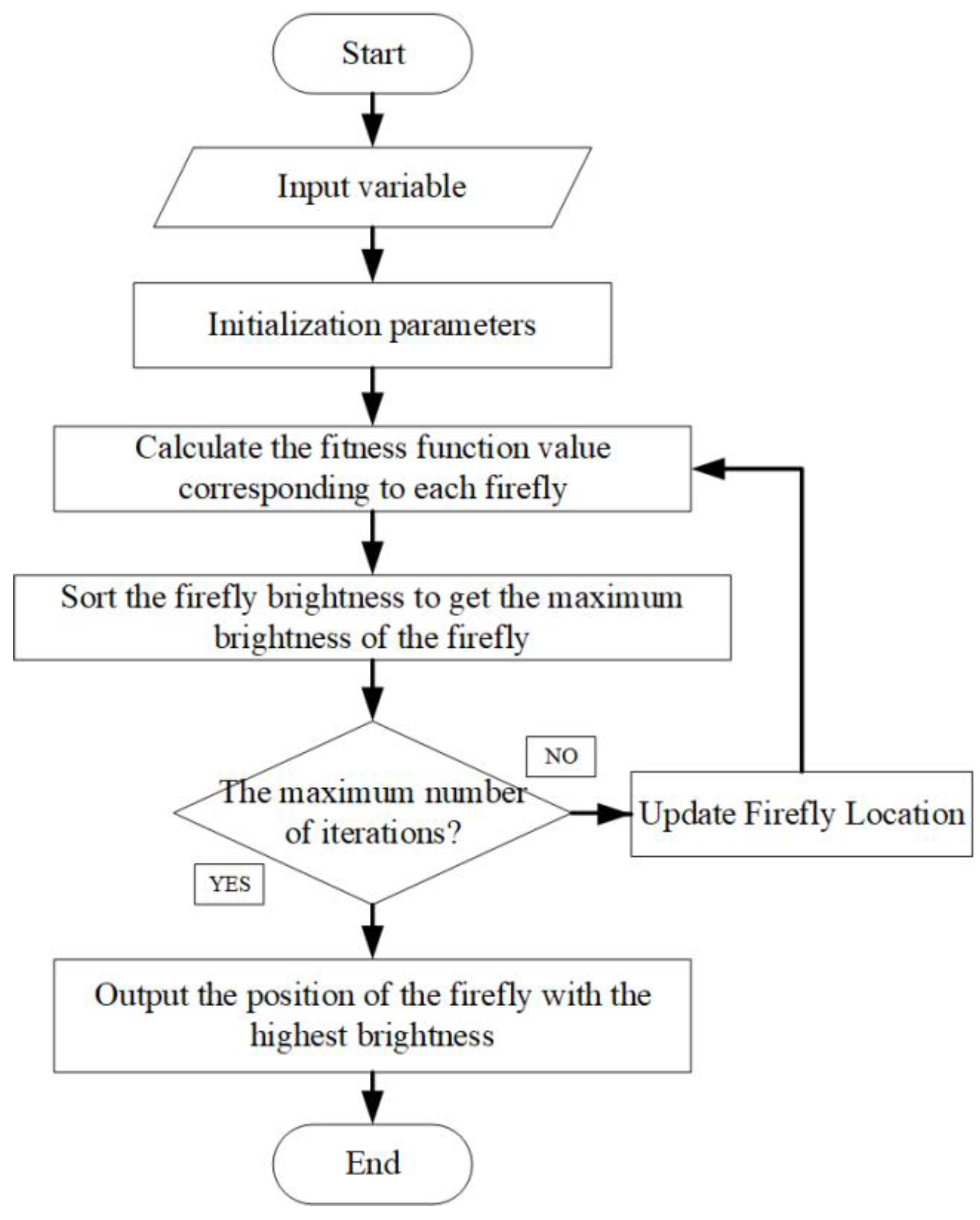
The equation is taken as the objective function of the firefly algorithm to optimize the filter size. The optimal result of the firefly algorithm is the position of the firefly with the greatest brightness. Among them, is the required filter size. The steps of filter size optimization based on the firefly algorithm are as follows:
- (1)
Initialization FA parameters: Number of fireflies , initial attractiveness , step size factor , initial position of fireflies and maximum iteration times .
- (2)
The brightness of each firefly is calculated and sorted: The fitness corresponding to each firefly is calculated, and fitness is taken as the brightness of the corresponding firefly and sorted to get the position of the firefly with the greatest brightness.
- (3)
Judging whether the iteration is over: If the algorithm reaches the maximum iteration number , then the algorithm goes to (4), otherwise it goes to (5).
- (4)
The position and brightness of the firefly with the greatest brightness are output, and the obtained is used as the optimal scale of the filter.
- (5)
Update the location of fireflies: Update the location of fireflies according to Equation (32). The flow chart of MED filter size optimization algorithm based on the firefly algorithm is shown in
Figure 11, and the flow chart of the new method is shown in
Figure 12.
The adaptive MED algorithm is used to denoise the noisy signal components and reconstruct the signal with the residual components:
The signal components m + 1 to q are the noisy signal components, and the signal components q + 1 to n are the residual components, being the final result.