1. Introduction
Information theoretic learning (ITL) [
1] methods have been shown to be efficient approaches in non-Gaussian signal processing due to their robustness against impulsive noise. The maximum correntropy criterion (MCC) [
2,
3] is one of the most popular optimization criteria in ITL due to its simplicity and robustness. Recently, it has been successfully applied in various signal processing scenarios, particularly the adaptive filtering [
4,
5,
6,
7,
8,
9,
10].
The introduction of the correntropy as a cost function into adaptive filters was proposed in Reference [
11]. The theoretical analysis in Reference [
12] has shown that the steady-state excess mean square error (EMSE) of the MCC algorithm is controlled by the step-size and the kernel width. Various kernel width selection methods for the MCC algorithm have been investigated. Adaptive kernel width adjusting methods were proposed in References [
6,
7] to improve the convergence speed of the MCC algorithm.
Just like the least mean square (LMS)-type algorithms, the MCC algorithm with fixed step-size is insufficient to achieve a good tradeoff between fast convergence and low steady-state misadjustment. The adaptive variable step-size technique is a promising way to deal with the conflicting requirements of faster learning speed and lower steady-state misadjustment error. Many varieties of variable step-size LMS-type algorithms have been proposed to improve the convergence performance [
13,
14,
15,
16]. However, many variable step-size methods based on instantaneous error cannot be directly applied in the MCC algorithm. Of course, just a few variable step-size methods for the MCC algorithm have been developed to improve the convergence performance in recent years. A convex combination of two MCC algorithms with different step-sizes was proposed in Reference [
4]. The mixing factor in this method was adaptively updated so that the MCC algorithm with larger step-size can improve the convergence speed at the beginning while the other with smaller step-size can achieve a lower misadjustment at steady state. The combinational approach can achieve desirable convergence performance but its computational complexity was more than two times higher than that of the standard MCC algorithm since two MCC algorithms were adopted in parallel. A curvature based variable step-size method for the MCC algorithm was proposed in Reference [
17]. This developed method can improve the convergence speed at the initial stage especially when the weight vector is far away from the optimal solution.
In recent years, a generalized maximum correntropy criterion (GMCC) has been proposed, which adopts the generalized Gaussian density [
18,
19,
20] function as the kernel function (not necessarily a Mercer kernel [
21]) and the type of this correntropy is called the generalized correntropy. Similar to the original correntropy with Gaussian kernel, the generalized correntropy can also be used as an optimization cost in the estimation-related problems. Under the GMCC criterion, a stochastic-gradient based adaptive filtering algorithm, called the GMCC algorithm, was developed [
21]. We can see that the GMCC algorithm was derived and based on stochastic gradient which only uses the current data sample. Although the GMCC algorithm is computationally simple and robust in the presence of impulsive noise, it suffers from high steady-state mean square deviation (MSD), which also can be verified from the next simulation.
In this paper, a smoothed GMCC algorithm (called SGMCC) is proposed to improve the performance of steady-state MSD in the presence of impulsive noise. To avoid the high steady-state MSD caused by the stochastic gradient in the GMCC algorithm, we take the GMCC algorithm as a sign algorithm with variable step-size. Then, we take the exponential weighted average of the variable step-size rather than the gradient vector, which contributes to reduce the computational complexity and further improve the convergence speed. At last, we present the convergence performance analyses of the proposed algorithm to demonstrate its robustness. The main contributions of our paper can be summarized as follows:
We propose a novel SGMCC algorithm, which can improve the performance of steady-state MSD and is robust against impulsive noise.
To demonstrate the robustness of the proposed algorithm, we derive the convergence performance analyses from three aspects including the variable step-size, mean-square stability and steady-state behavior.
Simulation results demonstrate that the proposed algorithm is robust against impulsive noise and computationally simple. Also, the SGMCC algorithm owns faster convergence speed compared with other robust adaptive algorithms.
The rest of the paper is organized as follows. In
Section 2, after a brief review of the original GMCC algorithm, a SGMCC algorithm is proposed. In
Section 3, the convergence performances of the SGMCC algorithm are studied. In
Section 4, Monte-Carlo simulation results are presented to confirm the desirable performance of the proposed algorithm. Finally, a conclusion is given in
Section 5.
2. SGMCC Algorithm
Assume the received signal
is obtained from an unknown system
where
denotes the output of the unknown system,
is the
dimension input signal vector at
nth time index and
denotes the
dimension unknown system vector that we wish to estimate. Here,
means the vector transpose operator.
In Equation (
1),
denotes the Gaussian mixture distribution noise, which is modeled as a random variable of 2-components Gaussian mixture distribution with mixed coefficient
. Its probability density function can be expressed as follows:
where the first Gaussian distribution
generates the normal Gaussian noise with probability
, the second Gaussian distribution
generates impulsive noise with probability
. Usually,
and the impulsive noise occurrence probability
is set as a number that is near but larger than 0.
and
denotes the Gaussian noise variance and the impulsive noise variance, respectively.
2.1. Review of the GMCC Algorithm
As it is well-known that MCC has been successfully applied in various non-Gaussian signal processing matters due to its robustness properties [
5,
6,
8,
22]. As a non-linear local similarity measure between two random variables
x and
y, the correntropy is defined by [
2,
3]:
where
denotes a shift-invariant Mercer kernel. The kernel function is a key factor of the correntropy that dramatically affects the similarity of two random variables. In most case, the Gaussian density function is used as kernel function, which is defined as follows:
However, for all non-Gaussian signal processing applications, the Gaussian density function is not always the best kernel function. In order to deal with this issue and take full advantage of the potential robustness properties of the correntropy, the generalized Gaussian density function was proposed as a kernel function of the correntropy in Reference [
21]. The generalized Gaussian density function with zero-mean is given by References [
18,
19] as follows:
where
is the gamma function,
denotes the shape parameter and
denotes the scale parameter. For simplicity,
is usually set as an integer value. Note that the Gaussian kernel is a special case of the generalized Gaussian density function when
.
In practice, the distribution of the data is usually unknown and only a finite number of samples are available. It is common to use these samples of the data to approximate its expectation, so the generalized corretropy can be estimated by [
21]:
Just like the correntropy, the generalized correntropy can be used as a cost function in adaptive filters. Hence, the generalized correntropy between the desired signal
and the filter output
can be shown as a cost function by [
21]:
where
is the instantaneous prediction error,
represents the normalization constant and
denotes the kernel parameter.
The goal of the adaptive filtering algorithm is to find an estimator of the unknown system vector which maximizes the generalized correntropy of
. The optimal solution of this cost maximization problem can be solved by a stochastic-gradient based adaptive algorithm, called GMCC algorithm [
21]. The update expression of the weight vector in the GMCC algorithm can be derived as [
21]
where
is the step-size parameter and
is a universal sign function. It is obvious that the GMCC algorithm can be viewed as a sign algorithm with variable step-size
.
2.2. SGMCC Algorithm
As mentioned above, although the GMCC algorithm is robust and computationally simple, it suffers from high steady-state MSD as it is derived and based on stochastic gradient which only uses the current data sample. The instantaneous prediction error fluctuates randomly with the background noise and the input vector . The random fluctuations of and can disturb the update of the weight vector and thus lead to a slow convergence speed.
To deal with this issue, it is common practice to take the average of the latest
N sample data to approximate the expectation of the gradient vector, which can statistically reduce the adverse effects caused by the randomness of
and
. Hence, the update expression of the weight vector in Equation (
8) can be rewritten as follows:
where
is the prediction error at
nth iteration for the input vector
. It is worth noting that the calculation of each instantaneous prediction error
is based on the present weight vector
, so the weight update in Equation (
9) needs
N times of computational cost and storage cost than that of Equation (
8).
In order to reduce the computational cost and the storage cost, the exponential weighted average of the gradient vector can be adopted to approximate the expectation of the gradient vector, which is shown as follows:
where
is the exponential weighted average of the GMCC gradient vector with a smoothing factor
. In this case, the update expression of the weight vector can be further expressed as
Although computational cost of Equation (
11) is much lower than that of Equation (
9), it still needs extra
N multiplications and additions than that of Equation (
8). In order to reduce the computational cost derived from gradient vector, we take the GMCC algorithm as a variable step-size sign algorithm by taking the exponential weighted average of the variable step-size instead of that of gradient vector. The exponential weighted average of the variable step-size,
, can be expressed as follows:
The replacement of the variable step-size from gradient vector can further reduce the computational cost and lead to a smoothed GMCC algorithm, namely SGMCC. The weight vector update of the SGMCC algorithm can be expressed as follows:
For convenience, the proposed SGMCC algorithm is specifically summarized in Algorithm 1.
| | Algorithm 1 SGMCC Algorithm. |
| | Input: , , , , , . |
| | Initialize: , , . |
| | while available |
| | , |
| | according to Equation (12), |
| | according to Equation (13), |
| | end while |
| | , |
| | Output: estimated unknown system . |
2.3. Computational Complexity
The complexity of the adaptive filtering algorithm is one of the important factors to measure its performance. The recursive weight updates of adaptive filtering algorithm generally include addition and multiplication operations. Since the complexity of multiplication operations is much higher than that of additive operations, in the iterative update process, the number of multiplication operations is usually used to calculate the computational complexity of the adaptive filtering algorithm. Next, we will make a comparison of the computational complexity between SGMCC and several other robust algorithms. The detail is summarized in
Table 1.
As one can see from
Table 1, the computational complexity of the proposed SGMCC algorithm and the GMCC algorithm are much lower than that of the other algorithms. The SGMCC algorithm owns almost the same the computational complexity as the GMCC algorithm. Those two algorithms require about
(usually
) multiplications, which is just about half of that required by other robust algorithms. The CMCC algorithm requires the most multiplication operations since it has to calculate two MCC algorithms with different step-sizes and update the combination parameter to combine those two MCC algorithms. The VSSA algorithm still requires more multiplication operations than the proposed SGMCC algorithm as this algorithm involves the calculation of the weighted average of the gradient vector and its square norm.
3. Convergence Performance Analysis
3.1. Analysis of the Variable Step-Size
Since the proposed SGMCC algorithm can be viewed as a variable step-size sign algorithm, it is necessary to evaluate the variable step-size theoretically. For the proposed SGMCC algorithm, the initial value of the variable step size is usually set as , so the variable step size can be expressed as
Equation (
14) shows the transient value of the variable step-size. If the transient variable step-size is positive and bounded, the adaptive algorithm can converge to steady state. It is obvious that
is positive, namely
In order to get the upper bound of the variable step size, we take the derivative of
with respect to
and set it to 0, namely
then we can obtain the variable
which maximizes
:
so the maximum of
is
Usually the shape parameter is an integer (larger than 1) and the kernel parameter , so we have
Above all, we can get the range of the variable step-size
We can see that the variable step size of the proposed algorithm is positive and bounded, so the proposed SGMCC algorithm can converge to steady state when a suitable step-size parameter is selected. When the adaptive algorithm converges to steady state, the variable step-size converges to a constant, which determines the steady-state accuracy of the adaptive filtering algorithm.
After taking the expectation for both sides of Equation (
14), we obtain
When the step-size parameter
is small enough, the weight vector
can approach very close to the optimal weight vector
and the instantaneous prediction error
is dominated by the background noise
. Assume the proposed SGMCC algorithm converges to steady state when
, Equation (
21) can be approximated as
The background noise
is usually assumed to be independent and identically distributed, so Equation (
22) can be denoted as
When
N is large enough, Equation (
23) can be further simplified as
3.2. Mean-Square Stability
The energy conservation relation (ECR) is the most widely used method to evaluate the convergence performance analysis of an adaptive filtering algorithm [
12,
16,
21,
23,
24,
25]. In this paper, we also use the ECR analysis to successively derive the mean-square stability and the steady-state behavior of the proposed SGMCC algorithm.
For the simplicity of the ECR analysis, the recursive weight update of an adaptive filtering algorithm can be denoted as
For the proposed SGMCC algorithm,
can be expressed as
where the instantaneous prediction error
can be denoted as
where
is an a priori error. Here,
represents the weight-error vector.
The performance of the adaptive filtering algorithm is usually measured by the MSD value of the weight-error vector , namely
The weight-error vector at nth iteration can be derived as
For both sides of Equation (
29), we successively take the squared-norms and expectations, then we obtain the ECR expression as follows:
To facilitate the convergence analysis of the SGMCC algorithm based on the energy conservation relationship, some commonly-used assumptions [
12,
16,
21,
23,
24,
25] are listed:
Assumption 1 (A1). The background noise sequence is independent and identically distributed (i.i.d.). Also it is independent of the input vector sequence .
Assumption 2 (A2). The filter is long enough such that is zero-mean Gaussian and independent of the background noise .
Remark 1. A1 is a valid assumption for most practical applications and is a basic assumption often used in signal processing. Moreover, it should be noted that, unlike most conventional signal processing methods that assume the background noise is Gaussian distribution, A1 does not impose any restrictions on the statistical distribution of the background noise. Based on A1, it is easy to conclude that the a priori error and background noise are independent, which is assumed by A2. According to the Central Limit Theorem, it is reasonable that the a priori error satisfies the Gaussian distribution.
Mean-square stability analysis is carried out to determine the upper bound of step-size parameter
that makes sure the SGMCC algorithm is convergent. The adaptive algorithm is convergent implies that MSD is monotonously decreasing. That is to say that the following condition exists:
Based on the ECR relation, the following inequality holds:
So, the step-size parameter that makes adaptive filtering algorithm converges to steady state would be
In our case, the scale parameter that ensures the stability of the SGMCC algorithm should meet
Because
is an exponential weighted average of
, so the correlation between
and
,
is negligible when the smoothing factor
is close to 1. Therefore, the inequality Equation (
34) can be further rewritten as follows:
Next, considering the above mentioned condition
, we obtain a smaller lower limit of the step-size parameter
:
where
is the covariance matrix of the input vector and
denotes the trace operator.
In this paper, the impulsive background noise
is modeled as a random variable that follows a 2-component Gaussian mixture distribution
. Based on the assumption A2, the Price’s theorem [
26] and References [
16,
27], we have
The Cramer-Rao [
28] bound
c is the minimum mean square error that the a priori error
of an adaptive filtering algorithm can reach, so the step-size parameter
for the SGMCC algorithm would be
3.3. Steady-State Behavior
The steady state behavior is usually measured by when the adaptive filtering algorithm converges to steady state. The steady-state value of is generally known as EMSE. Assume the adaptive filtering algorithm converges to steady state when , then EMSE can be denoted as
MSD would converge to a constant when the algorithm reaches steady-state, so we have
Based on the ECR relation, we have
For the proposed SGMCC algorithm, Equation (
41) can be expressed as
With the same reason mentioned above, the correlation between and , is negligible. Therefore, the following expression holds
As is derived in Equation (
24),
would converge to a constant when the
is small enough. Therefore, Equation (
43) becomes
The impulsive background noise is assumed to be Gaussian mixture noise that follows
. Based on the assumption A2, the Price’s theorem [
26] and References [
16,
27], we have
After substituting Equations (
44) and (
45) into Equation (
43), we obtain
When the step-size parameter
is small enough, EMSE or
S would converge to a smaller number, which is negligible comparing with the power of background noises. In this case, Equation (
46) can be approximated by
Note that the theoretical EMSE value computed by (Equation (
47)) is an approximate value that the SGMCC algorithm can achieve at steady state. The accuracy of the approximation is largely affected by the step-size parameter
. A valid approximation of EMSE can be secured with a small-enough
.
Usually,
and
, Equation (
47) can be simplified as
4. Simulation Results
To validate the theoretical analysis and evaluate the performance of the proposed SGMCC algorithm, we conduct simulations in a channel estimation [
29,
30,
31,
32] with Gaussian mixture background noise. An unknown time-varying channel with 20 multipath subchannels is randomly generated and then normalized by
. The input signals are generated by a zero-mean Gaussian distribution with unit variance. The input signals are transmitted via the above mentioned unknown channel and contaminated by impulsive background noise generated by a 2-component Gaussian mixture distribution
. The simulation results are averaged over 100 independent Monte-Carlo experiments.
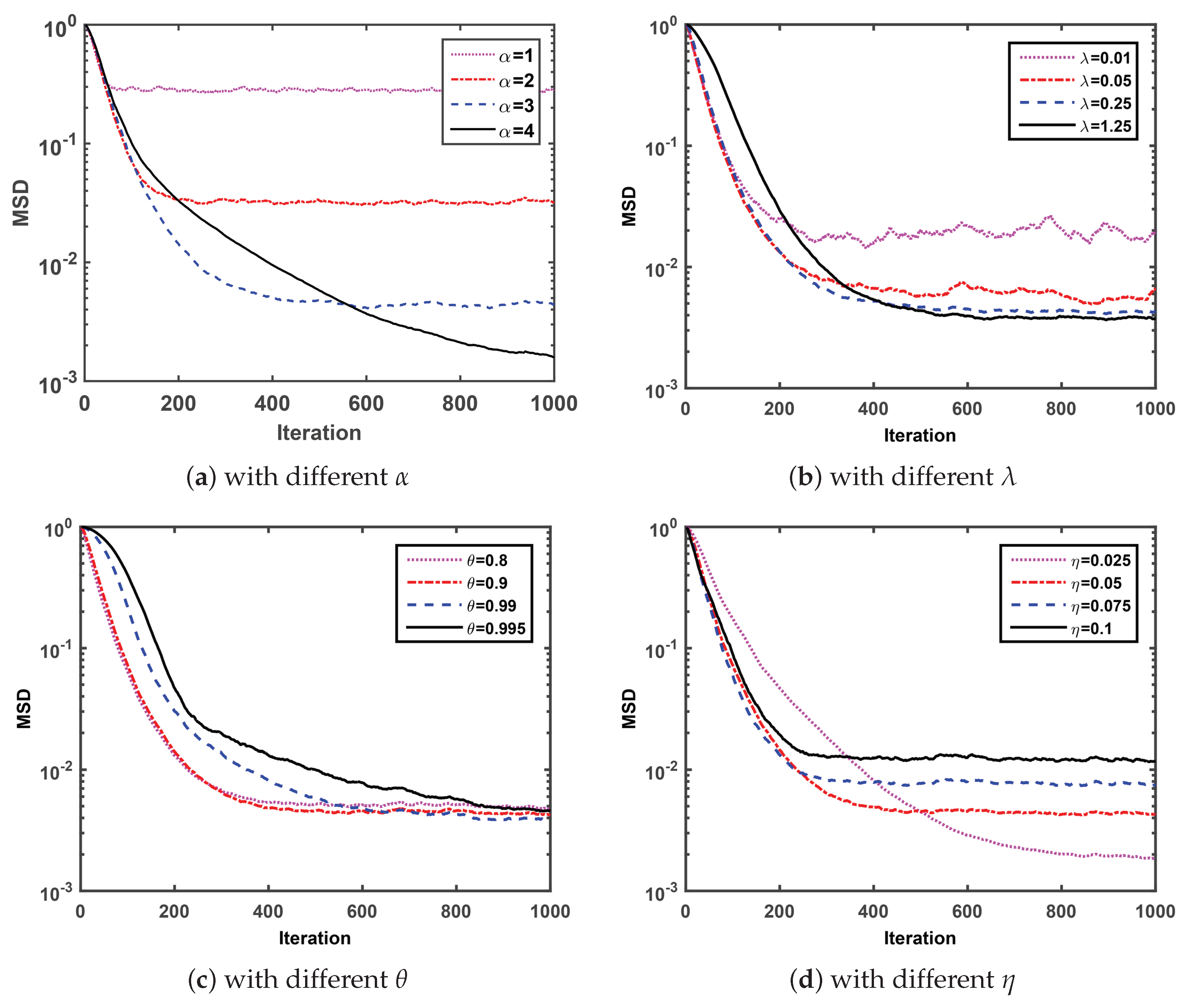
Firstly, we compare the MSD convergence curves of the proposed SGMCC algorithm with four parameters and investigate the effect of each parameter on the convergence performance of the SGMCC algorithm. Note that
Figure 1 is obtained with
,
and
. At each simulation, we set different values for a specific parameter with the other three parameters fixed and observe the effect of the parameter on the corresponding MSD convergence curve.
Under the condition of fixed parameter
,
and
,
Figure 1a shows that the SGMCC algorithm with larger shape parameter
converges slower to a lower steady-state MSD. As one can see in
Figure 1b, under the condition of fixed parameter
,
and
, the MSD convergence curve of SGMCC algorithm with smaller kernel parameter
is not smooth and fluctuates around a larger range. However, a larger kernel parameter
may lead to a slower convergence speed. As observed in
Figure 1c, under the condition of fixed parameter
,
and
, the SGMCC algorithm with different smooth factor
values converges to the almost same steady-state MSD after 1000 iterations. In addition, the SGMCC algorithm with smaller
converges faster but the improvement of the convergence speed is not obvious when
smaller than
. At last in
Figure 1d, under the condition of fixed parameter
,
and
, the SGMCC algorithm with smaller step-size parameter
can achieve lower steady-state MSD at the cost of a slower convergence speed and vice versa.
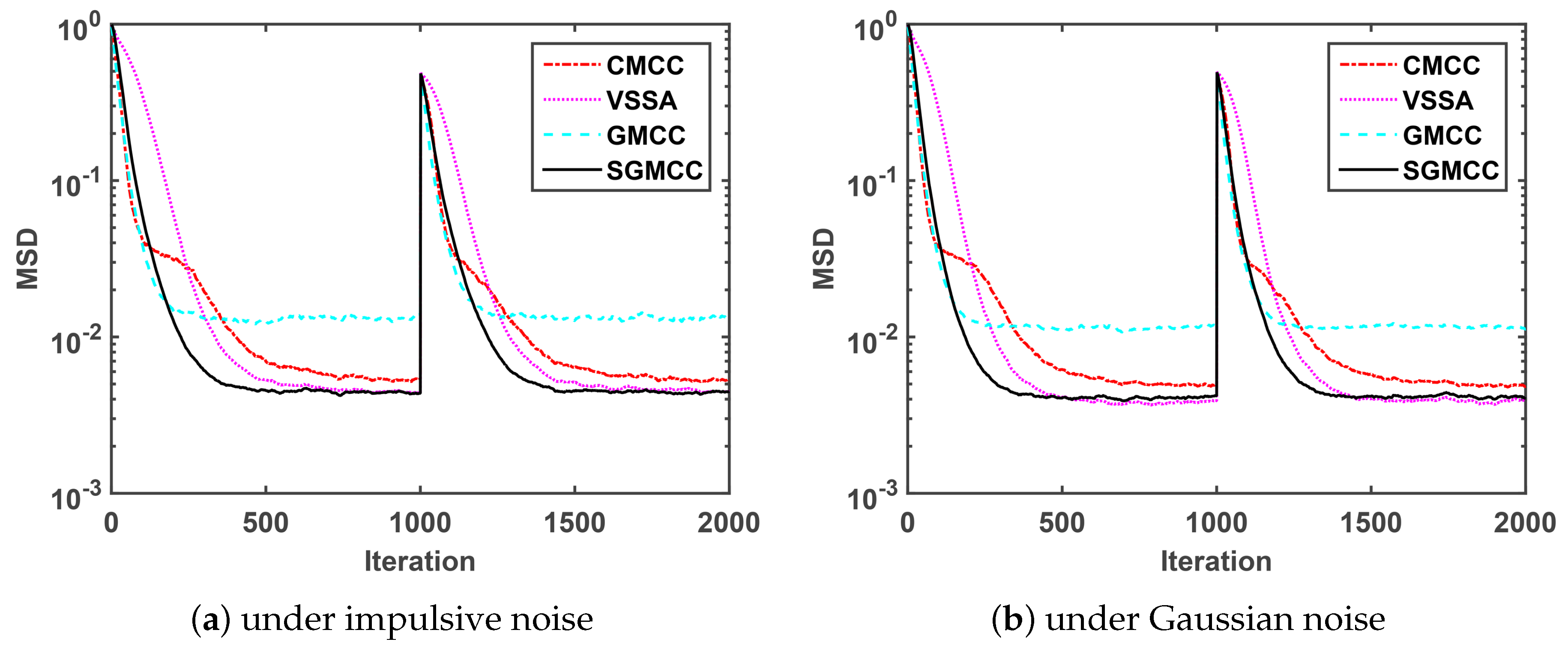
Secondly, we compare the convergence MSD performance of our proposed algorithm with several recently published algorithms to demonstrate its convergence performance. The parameters of the GMCC algorithm is set the same as that of the SGMCC algorithm. The parameters of other algorithms are carefully adopted according to the corresponding reference. The compared algorithms and their corresponding parameters were summarized in
Table 2.
Figure 2a shows a comparison of the MSD convergence curves of different algorithms under impulsive noise generated by
. As observed in
Figure 2a, the proposed SGMCC algorithm achieves a much lower steady-state MSD than the GMCC algorithm with the same parameters. The SGMCC algorithm and the VSSA algorithm converge to the same and the lowest steady-state MSD. On the other hand, the proposed SGMCC algorithm converges faster than the VSSA algorithm and the CMCC algorithm. Different from
Figure 2a simulated under impulsive noise,
Figure 2b is conducted under Gaussian noise. We can see that
Figure 2b shows the similar results with
Figure 2a. So we can conclude that, compared with the other three algorithms, the proposed SGMCC algorithm achieves the lowest steady-state MSD with a relatively fast convergence speed. Also, the proposed SGMCC algorithm is robust against both impulsive noise and Gaussian noise.
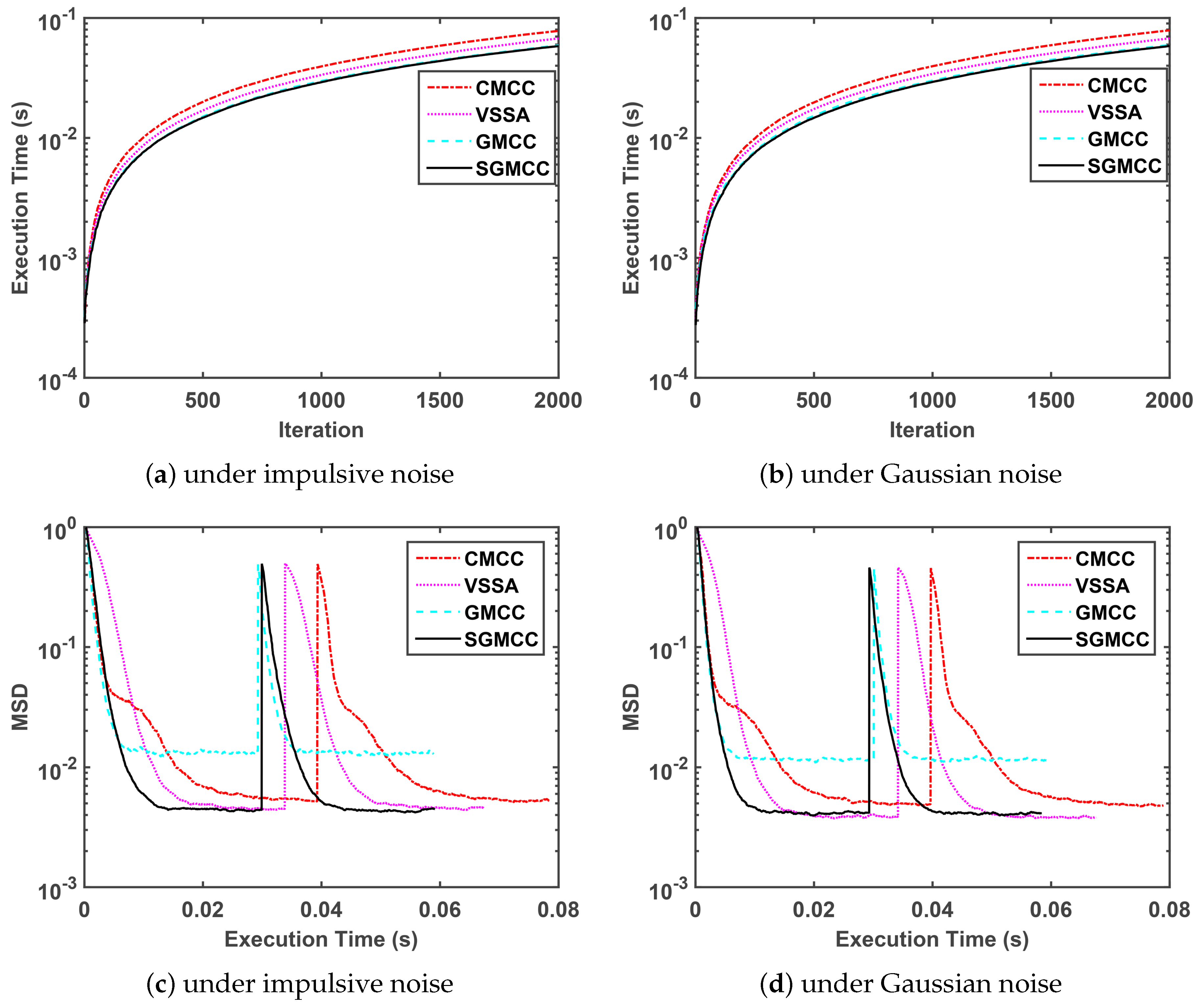
Thirdly, we compare the execution time of our proposed algorithm with several recently published algorithms in the next
Figure 3. The parameter setting of four algorithms in
Figure 3 is same with that in
Figure 2, which is shown in
Table 2. Note that the measured execution time of four algorithms is related to the running platform and specific code-programming efficiency.
Figure 3a,b shows a comparison of the execution time curves of different algorithms versus iteration under impulsive noise and Gaussian noise, respectively, and these two subfigures show the same performance trend.
Figure 3c,d shows a comparison of the steady-state MSD curves of different algorithms versus execution time under impulsive noise and Gaussian noise respectively and these two subfigures show the same performance trend. Concretely speaking,
Figure 3a,b demonstrate that the proposed SGMCC algorithm owns the shortest run time and is close to the GMCC algorithm.
Figure 3c,d demonstrate that the SGMCC algorithm owns the shortest run time by observing the length of the curve tail. Although the run time of the proposed SGMCC algorithm is also is close to that of the GMCC algorithm, the SGMCC algorithm achieves a much lower steady-state MSD. Moreover, the superiority of the SGMCC algorithm in run time can be ensured by computational complexity shown in
Table 1.
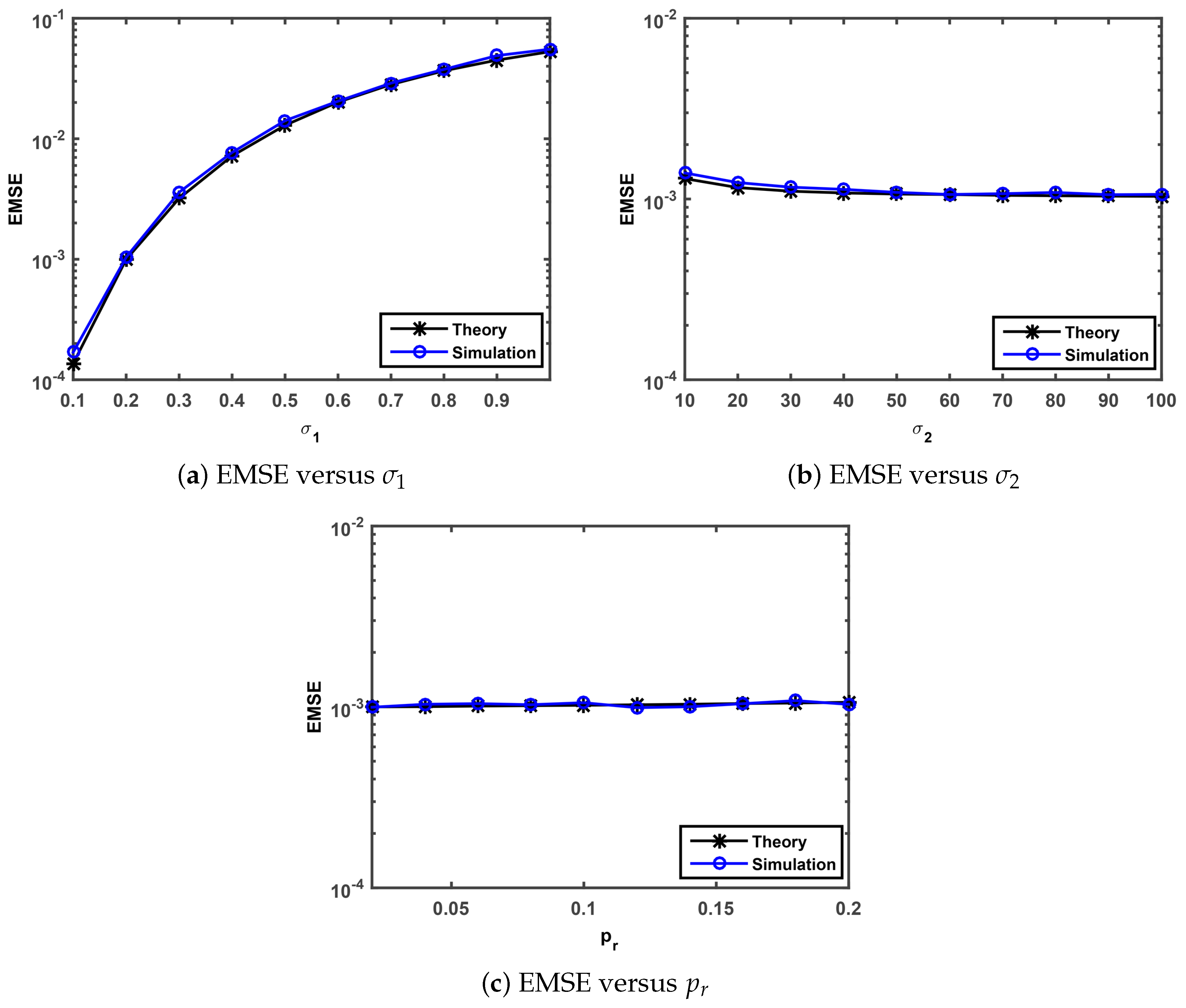
Finally, we perform simulations to confirm the steady-state behavior analysis presented in
Section 3.3. The theoretical steady-state EMSEs are evaluated by Equation (
47). The simulated steady state EMSEs were calculated as a average over the last 500 iterations of EMSE that is averaged over 50 independent Monte-Carlo simulation with 5000 iterations. We investigate the theoretical and simulated EMSEs under
versus Gaussian noise standard deviation
, impulsive noise standard deviation
, impulsive noise occurrence probability
. Note that the parameters of the SGMCC algorithm in
Figure 4 are set as
,
,
and
.
The comparisons of the theoretical and simulated value on EMSE versus
,
and
are shown in
Figure 4a–c, respectively. As observed in
Figure 4a, the simulated EMSEs match well the theoretical EMSEs computed by Equation (
47) and the simulation value grows with the increase of the parameter
. As one can see from
Figure 4b,c, the simulated EMSEs also match well the theoretical EMSEs. In
Figure 4b, the EMSE values show a very slow downward trend and no significant changes with the increase of the parameter
from 10 to 60 and from 60 to 100, respectively. In
Figure 4c, the EMSE values keep almost the same value with the range of the parameter
value from 0.02 to 0.2. This implies that the steady-state behavior analysis presented in
Section 3.3 is valid and the proposed SGMCC algorithm is robust against impulsive noise.