1. Introduction
Isotropic turbulence is an idealized form of turbulence which is defined by the invariance of the scalar correlation functions of the velocity field under translation, rotation, and reflection [
1,
2]. It is the simplest form of turbulence. It can be approximately realized when the mean flow is zero or uniform, and occurs at scales much smaller than the scale where the stirring forces are applied. The most faithful realization of the isotropic turbulence is represented by the direct numerical simulations (DNS) of turbulence [
3]. In the DNS, the Navier–Stokes equations are solved in a cubic box with periodic boundary conditions. Energy is fed in the flow at scales of the size of the box. In the recent years, high resolution DNS for (Taylor scale) Reynolds numbers larger than 1000 have appeared, see e.g., [
4,
5,
6,
7,
8]. Those DNS allow for clarification of phenomena of isotropic turbulence, such as the bottleneck effect, see e.g., [
9], as well as better determination of important characteristics of turbulence, such as the probability density function (PDF) of the distribution of the velocity derivative, including its skewness and flatness factors, as well as of the PDF of the one-point velocity distribution [
5]. The one-point velocity PDF is nearly Gaussian, with a flatness factor somewhat below 3, depending on the Reynolds number, while the velocity derivative PDF is well known to deviate significantly from the Gaussian, see e.g., [
10].
Although extensive theoretical work has been devoted to determine the one-point PDF of the velocity field (that is, the PDF of the value of the velocity field at one point), see e.g., [
10], simple direct modeling is rather sparse [
11,
12,
13]. In the present work we attempt to describe the two- and one-point PDFs (that is, the PDFs of the value(s) of the velocity field at one and two points, respectively), based on the theory of the kappa distribution which has been very useful in describing space plasmas, see e.g., [
14,
15] and the references therein. The kappa distribution has a parameter additional to temperature, called the kappa index, and coincides with the Maxwell–Boltzmann (MB) distribution for the infinite kappa index. The thermodynamic origin of the kappa distribution, and the nature of the kappa index as a second intensive parameter (thermodynamic integral) was clarified in [
16] allowing for pseudo-additivity of the entropy function. A very convenient interpretation of the kappa distribution follows from the concept of ‘superstatistics’: if the temperature of am MB system is fluctuating in a random way according to a prescribed distribution, then the system is described by kappa distribution if the inverse temperature follows a gamma distribution [
15,
17]. The physical interpretation of this construction clearly involves an ensemble of systems which are not in classical thermodynamic equilibrium. From a pragmatic point of view, the kappa distribution is a family of functions labeled by the kappa index which exhibits fatter tails than an MB distribution, and can be understood as a superposition of MB distributions.
In the present work, we attempt to model the two-point joint probability distribution of the velocity field in isotropic turbulent flows using kappa distribution and superstatistics as building blocks. The two points refer to geometric points in physical space, that is, we attempt to model the PDF for two velocity variables as a function of the distance between the observation points, given that isotropic turbulence is also homogeneous. In particular, the aim is to associate the parameters of the kappa distribution i.e., the temperature parameter and the kappa index, with fundamental quantities (functions) of isotropic turbulence. One must emphasize that in the context of the incompressible flows we are considering here, the temperature parameter does not correspond to an actual thermodynamic temperature, but rather a quantity of the proposed statistical description with formal properties quite analogous to the thermodynamic temperature, as emerges in statistical mechanics. Hence, the temperature parameter may also be referred to as statistical temperature, which is associated with the mean square of the velocity of a unit mass volume of the fluid, and it is a measure of the intensity of turbulence. On the other hand, the actual thermodynamic temperature is associated with the mean square of the velocity of the molecules of the fluid. That is, the temperature parameter refers to entirely different scales of motion from the thermodynamic temperature, i.e., the scales of the eddies of the turbulent flow.
The work of Kolmogorov [
1,
2,
18] provided the theoretical framework within which one usually thinks about isotropic turbulence (known in the literature of turbulence as K41). The Kolmogorov laws are expressed in terms of the structure functions, that is, statistical averages of integral powers
n of the velocity increment between two points, or in terms of the Fourier transform of those functions. The number
n is called the order of the structure function. As mentioned, due to isotropy and homogeneity, quantities such as the structure functions depend only on the distance between the two points. Kolmogorov’s hypotheses [
1,
2,
18] imply that, in a certain intermediate range of scales, called the inertial subrange, in which energy primarily cascades to the smaller scales with negligible viscous dissipation, the structure functions obey simple scaling laws. Those laws have been verified by numerical and actual experiments [
6,
10], although discrepancies from K41 have been found, which have been attributed to the intermittent character of turbulence in space and time (for a discussion on proposed theories see e.g., [
2]). In the small scales (which are quantified by the Kolmogorov dissipation scale), where the dissipation of energy is dominant, the Navier–Stokes equations imply that the structure functions are analytic (odd or even) functions of the distance. Certain coefficients in their expansion in power series of the distance are related to fundamental scalar quantities of isotropic turbulence, such as the skewness and the flatness factor of the velocity gradient distribution, which are clearly associated with the smallest distances. In what follows, only the general properties of the structure functions, stemming from the statistical theory of the Navier–Stokes equations, will be important, while the details of the K41 theory will mainly serve as source for certain additional comments in order to put the proposed theory in a specific context.
One may then proceed to investigate the possibility of describing isotropic turbulence with the kappa distribution and superstatistics. Reflection symmetry implies that the PDF for the values of the velocity field at two points must be invariant under an exchange of the velocity variables and a simultaneous change of their sign. This implies that the two-point PDF must be the sum of a symmetric and even part, denoted ‘se’, and an antisymmetric and odd part, denoted ‘ao’. By ‘even’ we mean that function is unchanged by a change of sign of both velocity variables, while by ‘odd’ we mean a function that changes sign under a change of sign of both velocities. The even order n structure functions, which are even functions of the separation distances, are determined from the se part, while the odd order ones are determined by the ao part and they are odd functions. Hence, the theory is naturally divided into a symmetric and an antisymmetric sector, which may be modeled independently.
The symmetric sector is easily modeled by the two-degree of freedom kappa distribution. We then learn that the temperature parameter of the kappa distribution equals the second order structure function
B2(
r), that is, it depends on the separation distance
r between the two observation points. Hence, eddies of size up to
O(
r), may be thought of as an ensemble of statistical temperature
B2(
r). For large
r, this temperature becomes 4/3 of the total energy per unit mass of flow. The fourth order structure function
B4(
r) turns out to be a function of both the temperature parameter and the kappa index. That implies that the ensemble of eddies of size up to
O(
r) have also an associated kappa index that depends on
r. From the behavior of
B4(
r) and
B2(
r) for small distances, one obtains the kappa index of small eddies as a function of the flatness factor of the velocity gradient distribution, and hence of the Reynolds number utilizing modern DNS data [
5].
The antisymmetric sector requires novel modeling, as the kappa distribution is symmetric. Guiding principles are the symmetry properties of the function ‘ao’ and a condition imposed on it following from the homogeneity of turbulence. Those restrictions are strong enough so that the simplest imaginable model (called the minimal model) that can be constructed in the context of superstatistics is effective enough. We then learn that: (i) The kappa index of the ensemble of eddies of size up to O(r) is naturally related to the third order structure function B3(r), through an important relation that involves also B2(r) and reminds one of the so-called ‘closure schemes’ of isotropic turbulence; (ii) this relation does not depend on the model, only on the superstatistics gamma distribution; (iii) the DNS data and self-consistency imply that the theory is valid for r up to ~10η, where η is the previously mentioned Kolmogorov dissipation range scale; (iv) the PDF for the velocity gradient can be derived from the two-point PDF in the limit r→0 (for the minimal model) which agrees well within six orders of magnitude with the DNS data for that quantity; (v) on the theoretical side, the Karman-Howarth equation relating the second and third order structure function of isotropic turbulence translates into a differential equation relating the temperature parameter and the kappa index functions.
Finally, the one-point PDF for the value of the velocity field can be derived. It follows from the symmetric sector alone, and it is a kappa distribution of one degree of freedom with a temperature parameter and a kappa index that depends on the ensemble of eddies of size up to O(r) for any specific scale r of interest. Taking into account the whole of the flow, i.e., r→∞, we argue that the one-point PDF should be Gaussian.
2. Structure Functions of Isotropic Turbulence
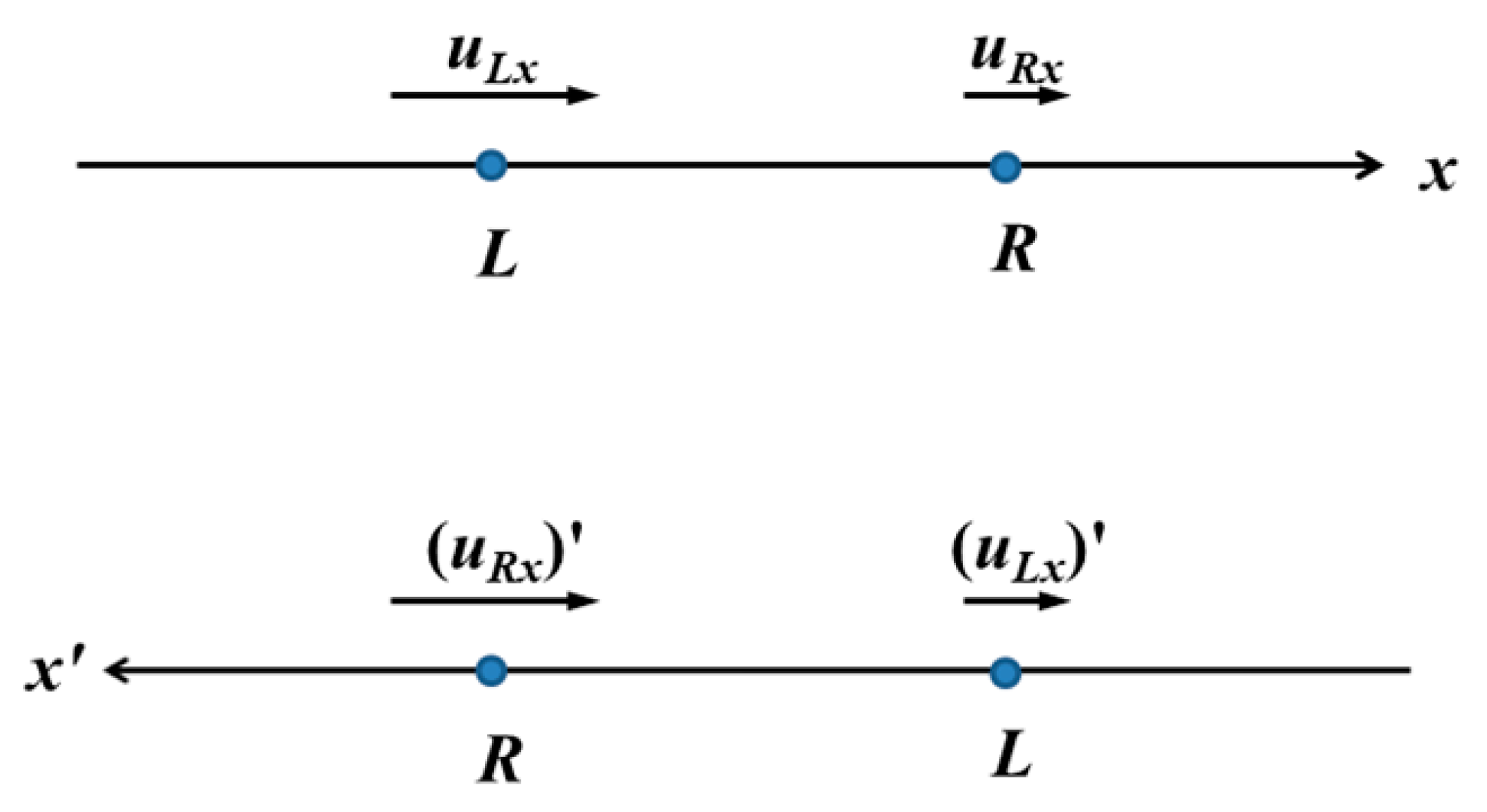
Consider an arbitrary axis in the turbulent flow, which we may call
x, and the
x-components of the velocity field at points
xL and
xR (the subscripts implying ‘left’ and ‘right’, respectively), denoted by
uLx and
uRx, respectively. The (longitudinal) structure functions of turbulence of order n are defined as
where
uRx =
ux(
xR) and
uLx =
ux(
xL). The brackets indicate an average over realizations of the turbulent velocity field. The quantity
r is the distance between the two observation points. A few cornerstone results regarding structure functions can be summarized as follows.
The function
B2 is an even function of
r, and the lowest order term in a small
r expansion is given by
where
ν [L
2T
–1] is the kinematic viscosity of the fluid, and ε [L
2T
–3] is the energy dissipation rate per unit mass of the fluid. In the so-called inertial subrange the function
B2 is given by the famous Kolmogorov result [
1,
2,
3]
where
C2 is the Kolmogorov constant, a pure number with a value around 2, that depends on the Reynolds number. The result in Equation (3) is derived essentially by scaling arguments. Important in our analysis, will be the Reynolds number of the Taylor micro-scale
λ:
The root mean square of the
ux is independent of the location on the axis
x by the homogeneity of the field. The quantity
K is the kinetic energy per unit mass of the fluid. Due to the isotropy of the flow, the kinetic energy associated with each direction is the same. Finally, for
r→∞ we have that
B2 approaches a constant:
The function
B3 is an odd and always negative function of
r, and the lowest order term in a small
r expansion is of order r
3 and it is best encoded in the following limit
which defines the skewness factor of the longitudinal derivative of the velocity field, ∂
ux/∂
x. The skewness
S is a negative pure number, which depends on the Reynolds number and is around ½ for Taylor–Reynolds numbers in the range of hundreds. In the inertial subrange the function
B3 is given by the Kolmogorov ⅘-law [
1,
2,
3]
Finally, the function
B4 is an even function of
r, whose small
r behavior is best encoded via the ratio
which defines the flatness factor of the longitudinal derivative of velocity field, ∂
ux/∂
x. The flatness
F is a positive pure number, which depends on the Reynolds number. The dependence of
S and
F on the Reynolds number is determined through direct numerical simulations of isotropic turbulence and is discussed below.
3. Two-Point Joint Probability Distribution for the Velocity Field: General Properties
The structure functions given by (1) are invariant under reflection, encoded by the transformation
The transformation of the velocity variables under reflections is explained pictorially in
Figure 1. As, we shall realize shortly, this symmetry is nearly trivial for the
n = even order structure functions, but it is fundamental for the
n = odd order structure functions. From here on we shall drop the index
x for brevity.
Consider now a joint probability density function
p(
uR,
uL) that encodes the statistics of the two velocity variables of the flow, so that
[Note: All integrations with respect to velocity variables refer to the interval (–∞, +∞)]. That means that the probability density must be invariant under reflections:
Now, the question is: what are the properties of such a probability density?
To analyze that, we first need a few definitions. Consider general functions
p(
u,
v) of two variables, and let us indicate by an index ‘
s’, functions that are symmetric under an exchange of the two variables, and by an index ‘
a’, functions that are anti-symmetric under an exchange of the two variables:
Next, by an index ‘
e’ we indicate functions which are even under a simultaneous change of sign of the two variables, and by an index ‘
o’, functions which are odd under a simultaneous change of sign of the two variables:
It is easy to see a general function
p(
u,
v) of two variables can written as
where the index ‘
se’ indicates a symmetric and even function according to the definitions above, the index ‘
so’ indicates a symmetric and odd function, and so on.
Now, it is easy to see that only the
se and
ao components are invariant under reflections, that is, they identically respect Equation (9). Hence, we have that
In all, invariance under reflections helped us specify the algebraic symmetries of the joint probability density function. We need now to clarify the implications of Equation (15).
Remark 1. By Equations (10) and (12), only the se component of the probability density specifies ‘n=even’ order structure functions, while only the ao component specifies the n=odd order ones: This is due to symmetry properties of the factor (uR–uL)n in each case, and can be verified by a suitable change of variables in the integrals, e.g., uR→uL and uL→uR. Hence, we conclude that an ao component is necessary in order to have a non-zero function B3 and therefore a non-zero skewness S, which is a fundamental property of turbulence. A most important implication of (16) is that, in terms of modeling the probability distribution, we may think and model separately the symmetric sector associated with the se component and the ‘n=even’ order structure functions, and the anti-symmetric sector associated with the ao component and the ‘n=odd’ order structure functions.
Remark 2. The ao component of the density function does not affect the normalization of the density function. Indeed,as one may verify by a change of variables such as uR→uL and uL→uR. Hence, one may only normalize the se component to the value 1. Remark 3. A non-trivial condition is imposed on the ao component by the fact that the one-variable probability distributions are the same for both L and R points, by the homogeneity of turbulence. That is, the functionsmust be the same: pR(u) = pL(u). The se part of the probability density (15) is fully consistent with the condition pR(u) = pL(u). The ao part is not. Indeed, we first note thatwhere in the first equality we changed variables as v→–v and in the second equality we used the odd-ness of the ‘ao’ component. Equation (19) implies that the part of the function pR(u) that comes from the ao part of the joint probability density is an odd function. The same can be shown for the function pL(u). Secondly, we may note also that Equation (19) can be continued with a third equalityusing the anti-symmetry of the function pao under an exchange of variables. That implies thatfor the parts of the functions coming from the ‘ao’ component of the joint probability density. Therefore, those parts do not agree and must be zero. Hence, homogeneity imposes the following condition on the ‘ao’ component of the joint probability distribution: Integration with respect to the first variable is implied by (22) via the anti-symmetry of the function.
Remark 4. Nothing in the previous conditions guaranties that the probability density (15) is everywhere non-negative. That needs to be imposed as a separate condition.
4. Modeling the Symmetric Sector: κ-Distribution and Turbulence
The proposal is that the
se component of the joint probability distribution for
uR and
uL is modeled by the two degrees of freedom kappa-distribution:
As discussed in the introduction, the kappa distribution contains two parameters: the temperature parameter θ2 and the kappa index. From that one may draw a number of implications.
The second order structure function reads
That is, the temperature parameter θ2 equals B2, which in turn depends on the distance r and the energy dissipation rate ε. The function B2 contains information about eddies of size up to the distance scale r. On this basis one may state: The ensemble of eddies of size up to O(r) is an ensemble with statistical temperature θ2 = B2(r). (Note that the constant κ0 is not involved in this relation.) Ensembles of eddies of different sizes correspond to ensembles of different statistical temperatures. Turbulence is not in equilibrium from this point of view. As mentioned in the introduction, one must emphasize that in the context of the incompressible flows we are considering here, the temperature parameter does not correspond to an actual thermodynamic temperature, which is associated with the mean square of the velocity of the molecules of the fluid, but it is a statistical parameter, associated with the randomness of the motion of the eddies in the turbulent flow.
The fourth order structure functions reads
The relation between
B2 and
B4 as implied by (24) and (25) is too simple for hold for all
r for constant
κ0. Hence, we understand that
κ0 depends on
r, along with
θ, although further information is needed to quantity that dependence:
where, as in the case of the temperature parameter
θ2 =
B2(
r), we have omitted the obvious prior dependence on the Reynolds number, i.e., on the state of turbulence. We conclude that each ensemble of eddies of size up
O(
r) has its own temperature parameter and kappa-index. We shall see below that the kappa index
κ0(
r) is associated with the third order structure function
B3(
r).
Flatness can be then immediately calculated by Equations (8) and (25) from
r→0:
Flatness is a function of
κ0 alone. In the K41 isotropic turbulence,
F can only be a function of the Reynolds number. Hence,
κ0 is indeed a function of the Reynolds number as well. Experimental data and results from direct numerical simulations imply that [
5,
19,
20]
for certain parameters
a and
α determined by best fit for a range of Reynolds numbers (up the order of 10
3), although the most recent analyses [
20] suggest that the flatness factor may asymptotically approach a constant value, in the spirit of K41. For illustration purposes, we may adopt the results of [
5], as other types of data, such as the PDF of the velocity derivative, will also be taken from the DNS covered in [
4,
5,
6,
7]:
a = 1.14 and
α = 0.34. At the same time, one should bear in mind that the simple power law (28) is barely far beyond Reynolds number ~10
3, thus it only indicates a trend.
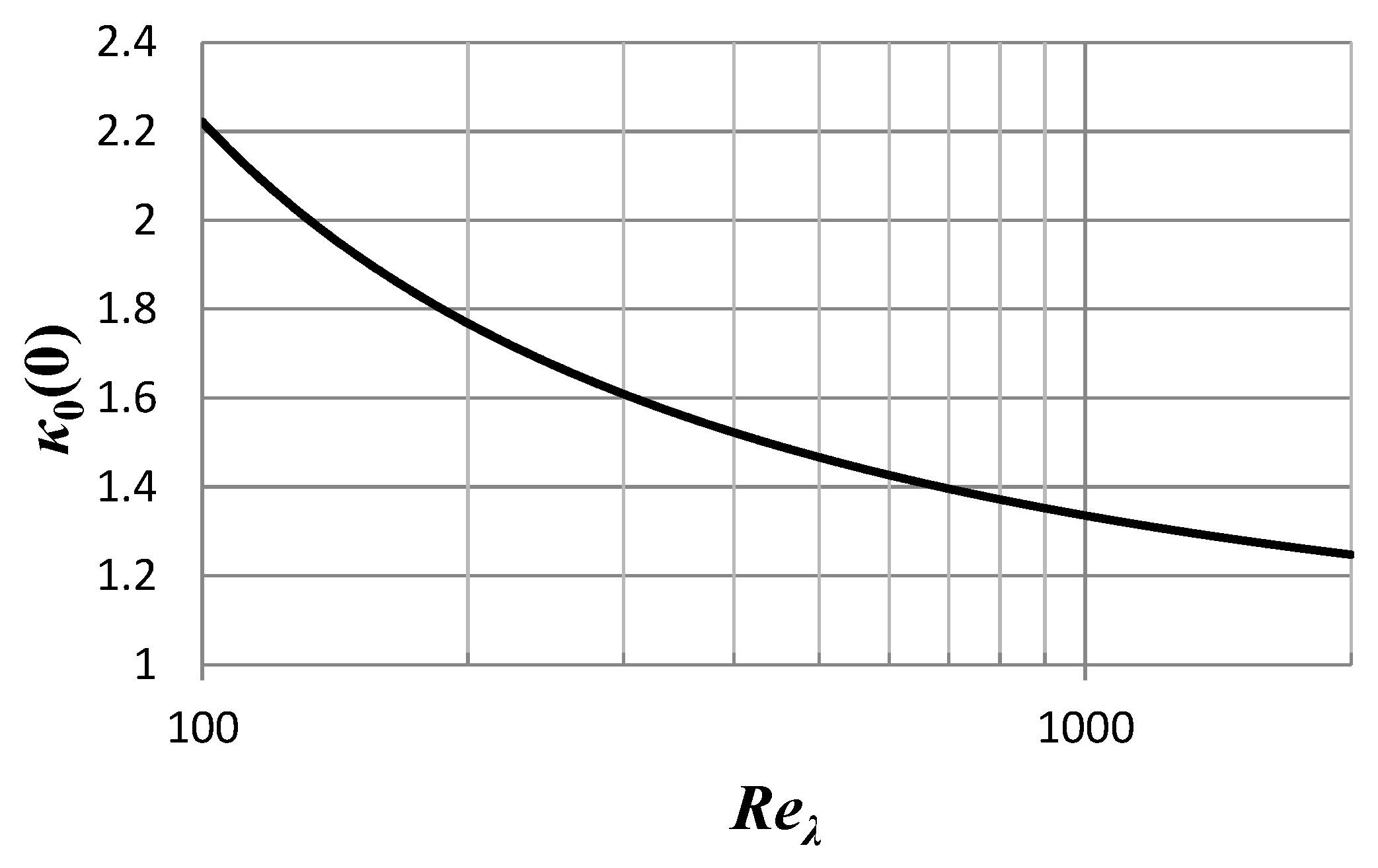
Hence, the small distances value of
κ0 can be determined and in particular, given a specific dependence on the Reynolds number of the flow:
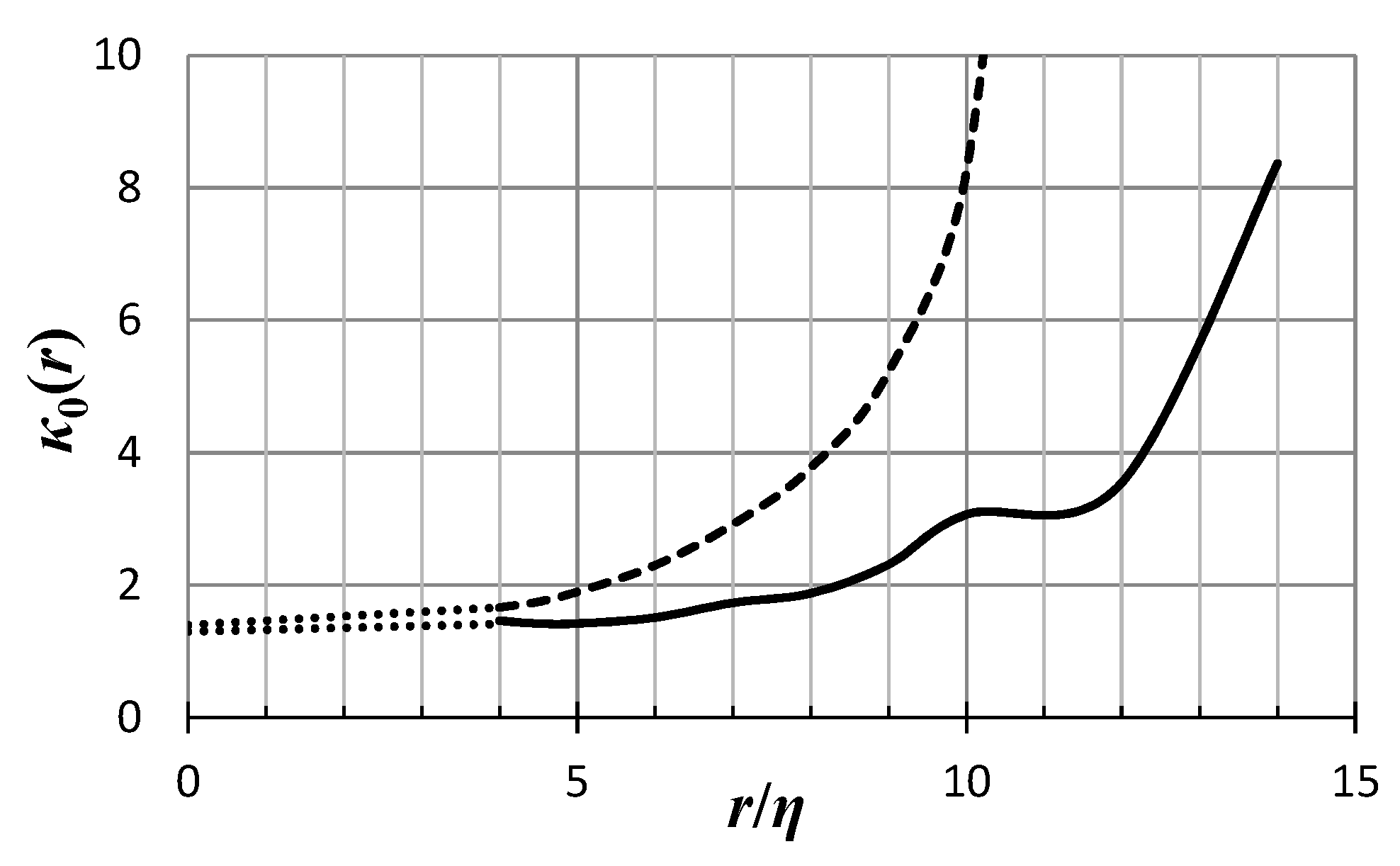
emphasizing—as above—that the explicit estimate given in the last expression is only given for illustration purposes and it is not valid for Reynolds numbers ~10
4 and larger. The magnitude and the trend of the dependence of the small distance
κ0 on the Reynolds number is given in
Figure 2: It apparently approaches asymptotically the value 1, although recent analysis [
20] suggest that the flatness factor may reach a (finite) universal value in that limit, hence
κ0(0) might approach a universal value, somewhat above unity.
6. The PDF of ux
According to the discussion of
Section 3, the PDF for the velocity
ux at any given point is given by the integration of the joint PDF for the velocity of two points given by Equation (45). The result is
which is nothing but the kappa-distribution PDF for one degree of freedom. This makes sense, as the
ao component in the two-point PDF does not contribute to result for the one-point PDF by condition (24).
One should bear in mind that both the statistical temperature and the kappa-index in (64) still carry the dependence on r, as the derivation at this stage was done within the ensemble of eddies of sizes up to O(r). That may be phenomenologically useful as in actual physical flows, e.g., space plasma, information may actually be available from a region of size r not containing the entire flow.
On the other hand, looking to answer—within our setup—the question about the one-point PDF of the velocity field in the ideal isotropic flow, it makes more sense to include the whole of the flow, that is, let
r→∞. ‘Infinite distance’ essentially means adequately larger than the integral scale of turbulence [
10], which is the length scale of the correlation of the velocity field. Then, according to Equations (5) and (24), we have
That is, we have
where
κ0(∞) is the infinite distance value of the index
κ0. Note that that
u’ is the standard deviation of
ux (Equation (4)). Equation (66) is the PDF of the normalized velocity, i.e., of unit standard deviation.
It is worth to note the following. We could have started with the one-degree of freedom PDF (64) and looked for a value for θ2 knowing nothing about the previous two-point PDF analysis. The mean value of ux according to (64) is, of course, zero, while the mean value of ux2 is ½ θ2. However, if (64) is to describe the PDF of the velocity at a point within an isotropic turbulent flow with r.m.s. value of the velocity equal to u’, or equivalently with energy per unit mass equal to (3/2)u’2, then we should identify ½ θ2 with u’2 and (64) necessarily follows. Hence, the result (64) is verified independently, within our framework.
It is now straightforward to show that the flatness of the
ux-distribution is given by
analogously to equation (27). That is,
DNS data [
5] implies that
Fu is below but near and below 3, i.e., nearly but not actually Gaussian. That means that
κ0(∞) is large and negative and large: the data of [
5] imply
κ0(∞) between −16 and −74.
Now in the previous section we found that that κ0(r) starts with positive values in the small distances and increases, although due to restrictions of the minimal model (36) we could not ‘see’ beyond r~10η. Nonetheless, for κ0(r) to become negative it is necessary for either κ0(r) to become discontinuous, or to pass through the value zero. The first case introduces a bigger unknown in the problem, regarding the nature and the size of the discontinuity, while the second case is merely physically unacceptable. Given that (64) becomes Gaussian for both infinite limits κ0(r)→±∞, and the DNS data estimates given in the previous paragraph, one concludes that the present construction essentially predicts that κ0(∞)=+∞,(∞)=+∞, as the nearest approximation to the results of the DNS explained in the previous paragraph. That is, the single-point PDF of the velocity field is Gaussian.
7. Summary and Discussion
In the present work, we construct a model for the two-point PDF of the velocity field for the ideal isotropic flow, based on the theory of the kappa distribution and the concept of superstatistics [
15]. Due to the length of the work, a summary of main points and result is given in the form of the
Table 1 below.
The main conclusions of this paper are:
The two-point PDF of the velocity field is a sum of a symmetric-even and an antisymmetric-odd part, as a result of reflection symmetry. The antisymmetric part obeys a non-trivial integral condition, as a result of the homogeneity of the flow.
The symmetric part, which gives rise to the even order structure functions, may be modeled by a kappa distribution of two degrees of freedom (DOF). The temperature parameter is given by the second order structure function. That is, the ensemble of eddies with size up to O(r) has a statistical temperature B2(r) and an r-dependence kappa index.
Using data from the DNS of isotropic turbulence and the calculated flatness factor of the velocity gradient distribution from the model, one deduces the dependence of the kappa index of the smallest eddies ensemble on the Reynolds number.
The antisymmetric part, which gives rise to the odd order structure functions, may be modeled by a minimal model constructed on the basis of symmetry properties of the antisymmetric-odd part and the non-trivial integral condition mentioned in Conclusion 2, and utilizing the superstatistics construction. The ensemble of eddies with size up to O(r) has an r-dependence kappa index that derives from third order structure function.
The fundamental Karman-Howarth equation of isotropic turbulence translates to a differential relation between the r-dependent statistical temperature and kappa-index.
The relation between B2(r), B3(r) and the r-dependent kappa index is not peculiar to the minimal model: Any model deriving from the superstatistics construction, in particular the (gamma) probability distribution of the inverse statistical temperature, results in the same relation.
By the specific form of the relation between B2(r), B3(r) and the r-dependent kappa index, the DNS data imply that the constructed model is a dissipation subrange model, not applicable e.g., in the inertial subrange, although the range of validity increases with the Reynolds number. By Conclusion 5, the only way out is the modification of the probability distribution of the inverse statistical temperature in the super-ensemble.
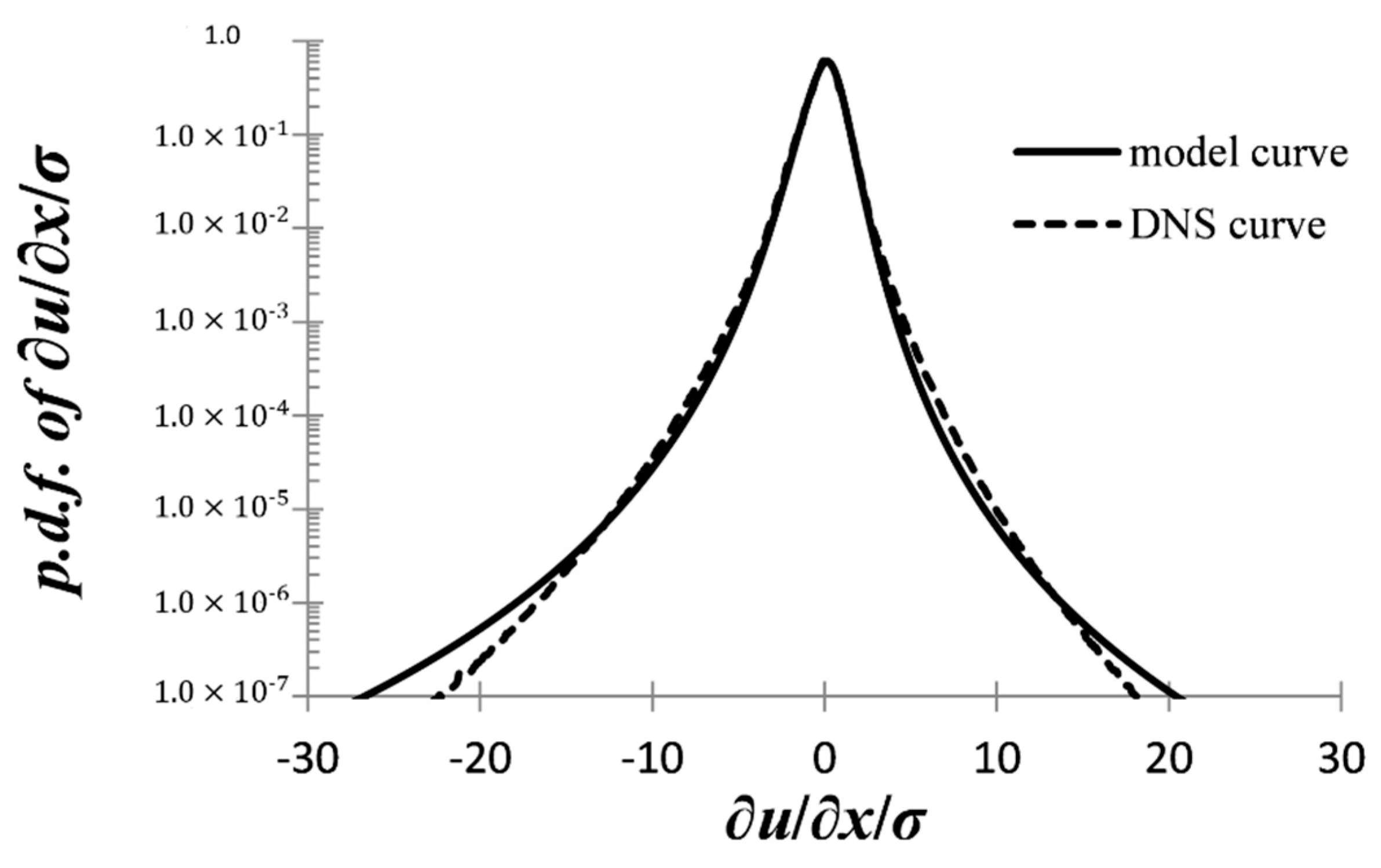
The two-point PDF of the velocity field allows the derivation of the velocity gradient PDF In the context of the minimal model, the resulting PDF agrees well within six orders or magnitude with the numerical velocity gradient PDF from the DNS.
The one-point PDF of the velocity field is a kappa distribution when defined in a finite volume, in particular, of the order of magnitude of the integral scale of turbulence, or smaller. In the ideal isotropic case of infinite volume, the most plausible deduction from the present construction is that the one-point PDF is Gaussian.
As it has been already noted, this work is only the first step in completing an effective model for the PDFs of the velocity field of isotropic turbulence, on the basis of kappa distribution and the superstatistics construction. First of all, models more complicated than the minimal model, already given in this work, need to be investigated with respect to improving further the agreement between the predicted PDF of the velocity gradient and the DNS. Secondly, on a more basic level, one needs to deal with the fact that the derived PDFs are models valid only within the dissipative subrange, due to the specific (gamma) distribution of the inverse statistical temperature in the superstatisics construction. Hence, other inverse statistical temperature distributions need to be investigated. Finally, an obvious deficiency of the proposed PDFs is that they have only very low order moments of the velocity and the velocity increment between two points, for the values of the kappa index consistent with DNS data, as the associated integrals diverge for the general moment. That cannot be correct in the context of turbulence: Arbitrarily high velocities need to be exponentially cut off, as they are associated with arbitrarily small eddies, which do not exist. That calls for a modification of the inverse statistical temperature distribution, which could simultaneously improve the agreement with the DNS data for the velocity gradient distribution, without destroying the kappa distribution-type of behavior of the PDFs for smaller values of the velocities.