Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications
Abstract
1. Introduction
2. The TIK-G Family
2.1. Main Functions
2.2. The TIKEx Distribution
3. Properties
3.1. Some Series Expansions
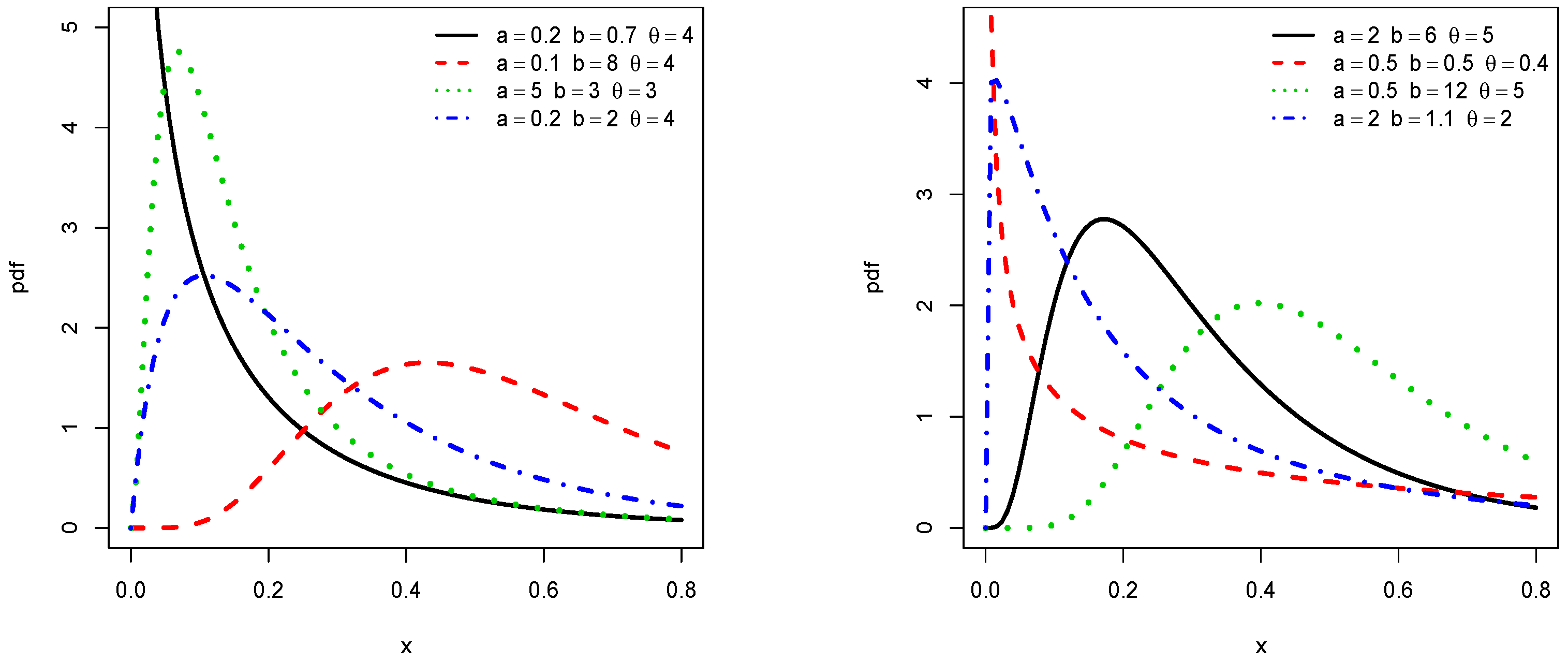
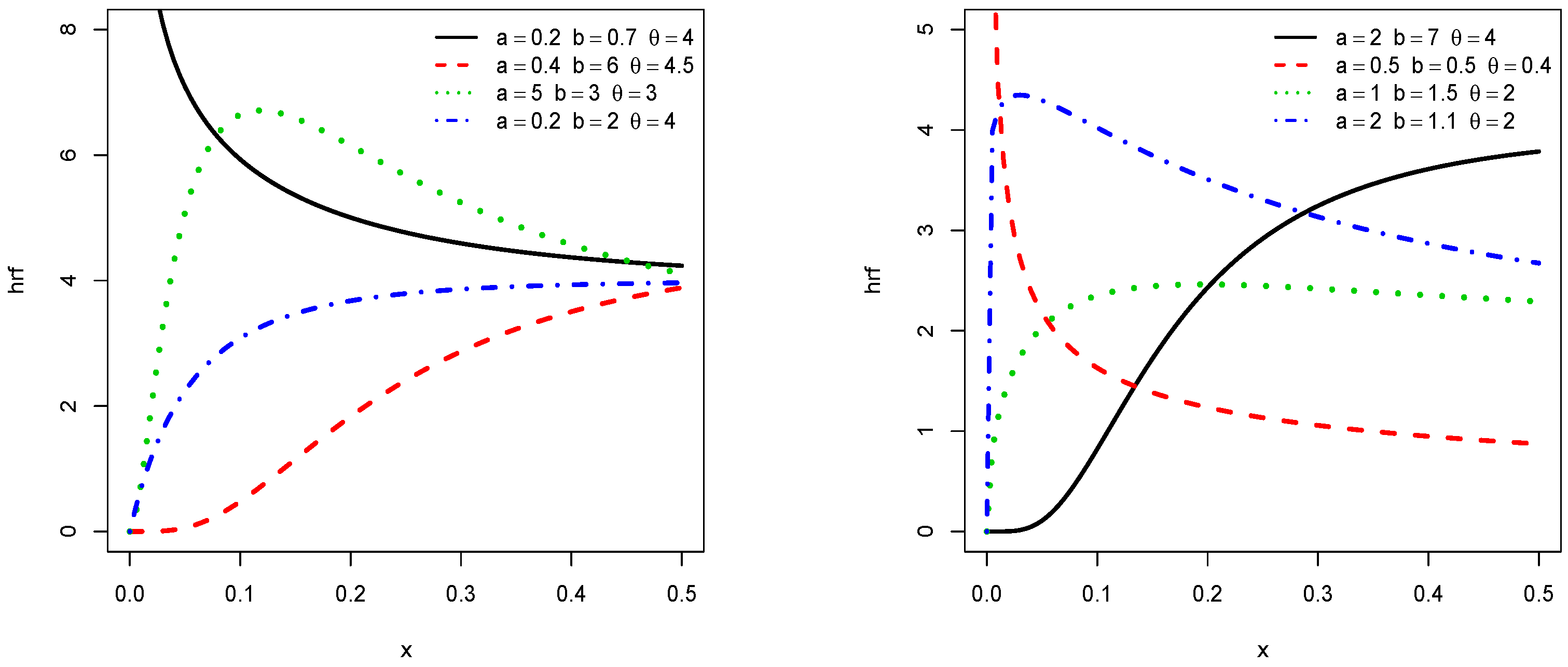
3.2. Critical Points of the pdf and hrf
3.3. Moments
3.4. Probability Weighted Moments
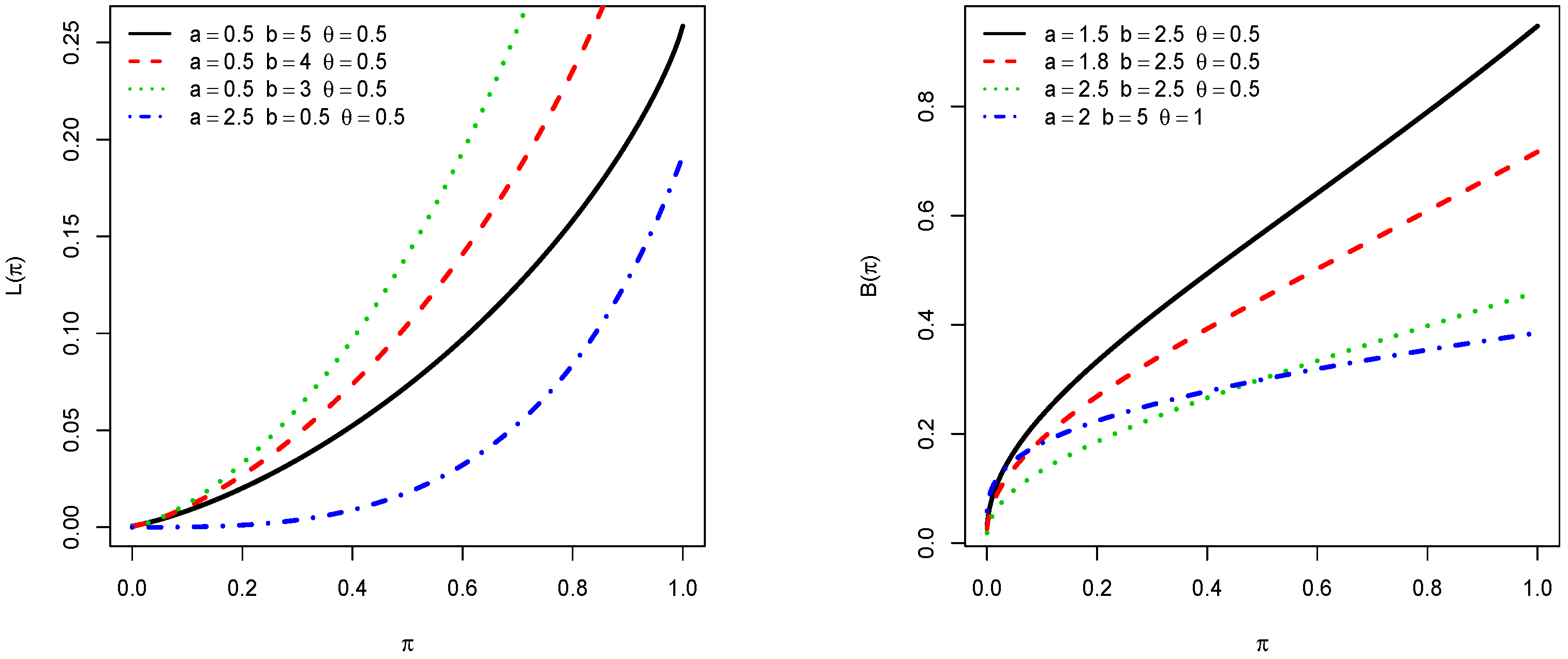
3.5. Incomplete Moments
3.6. Entropy
3.6.1. Rényi Entropy
3.6.2. Shannon Entropy
4. Maximum Likelihood Estimation
4.1. Basics on the Maximum Likelihood Method
4.2. Simulation
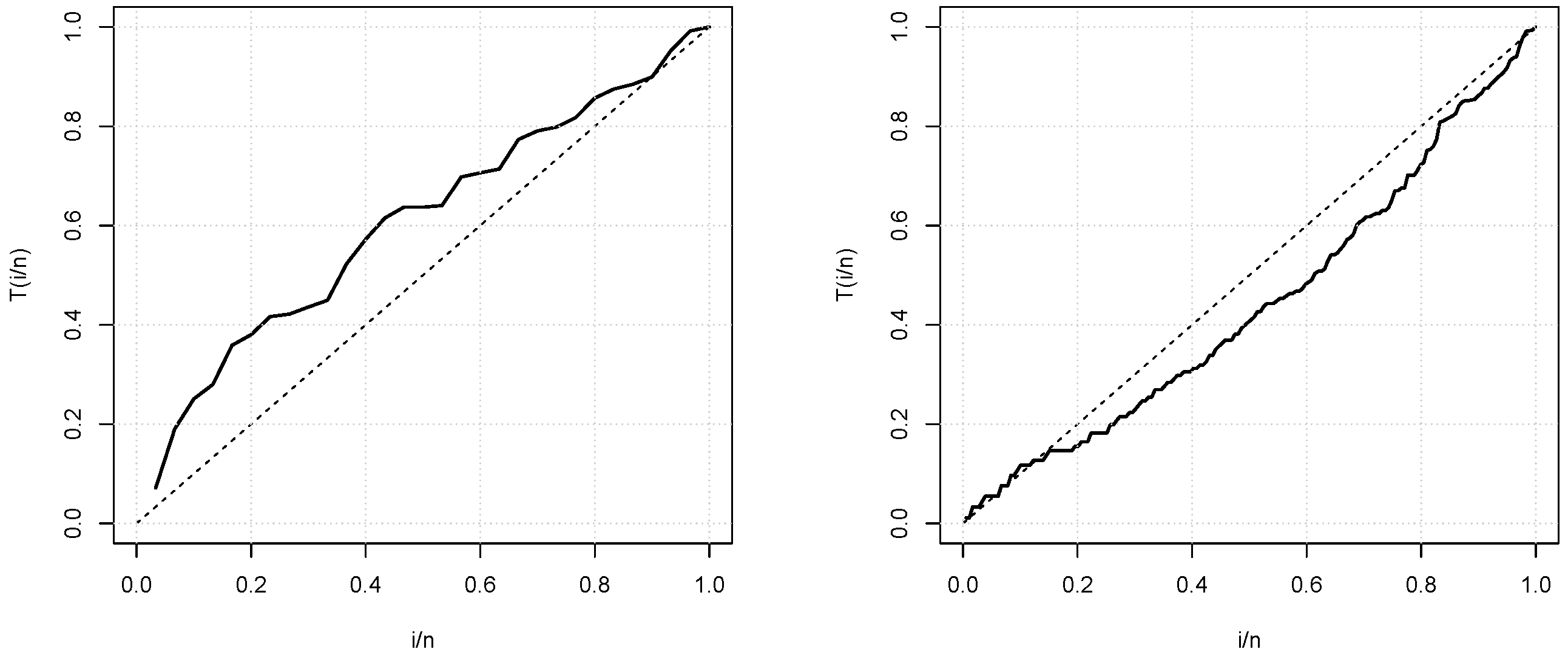
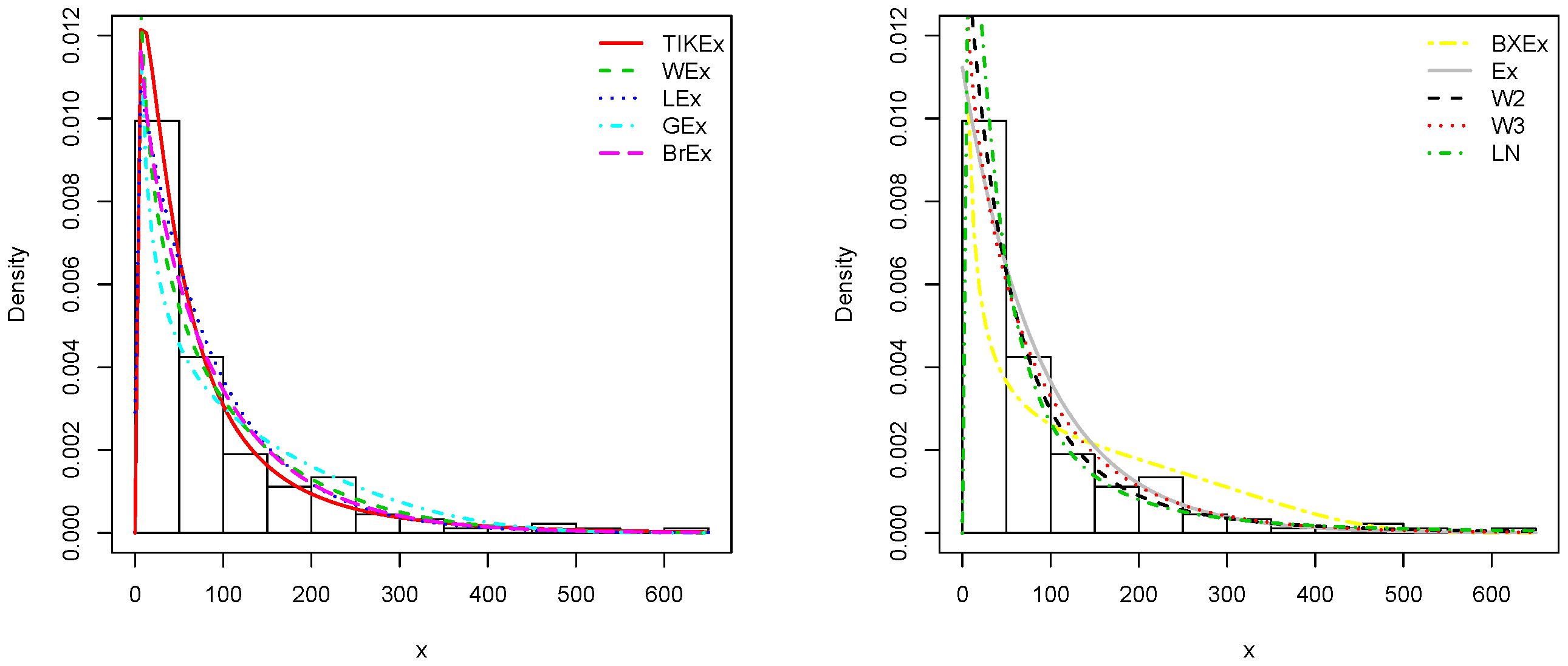
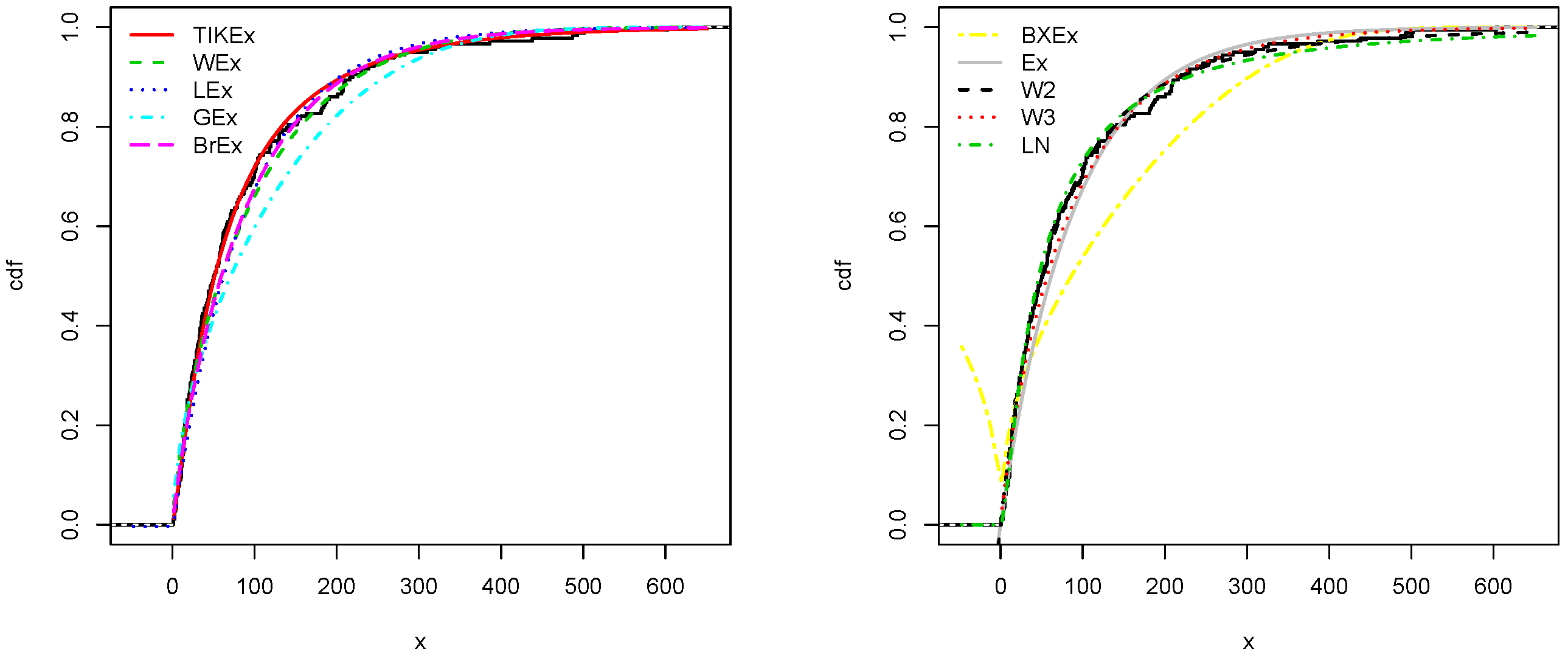
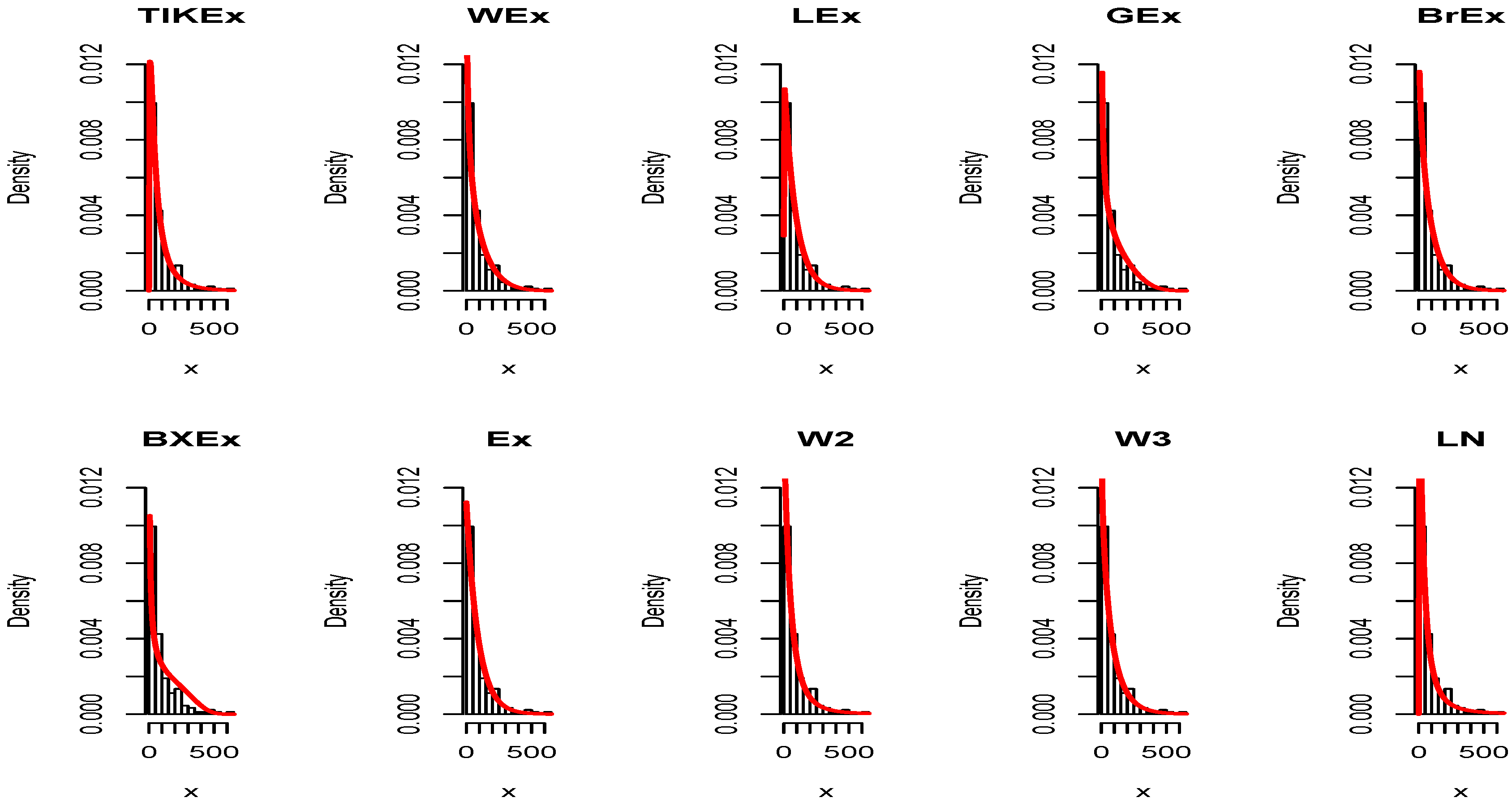
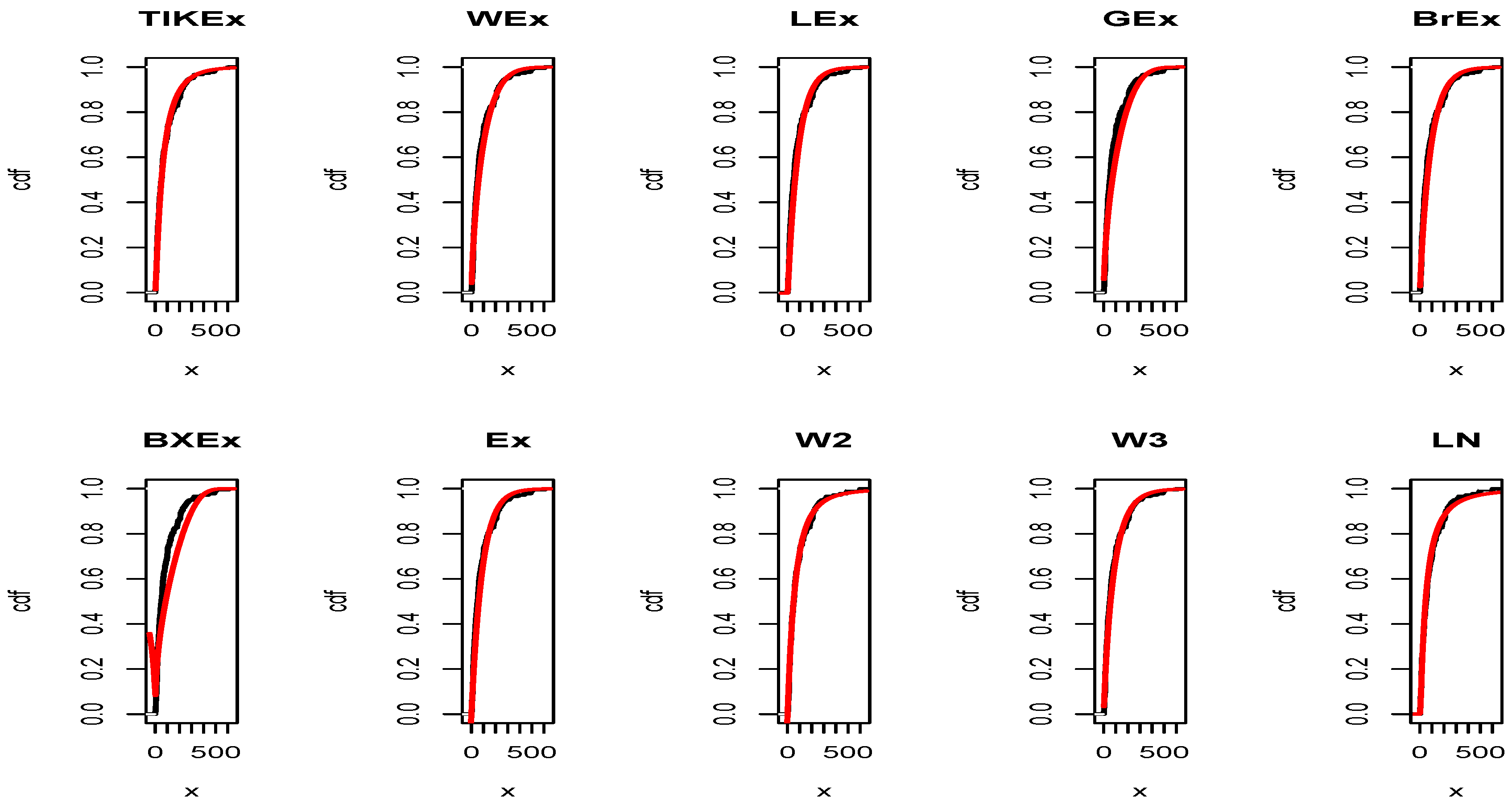
5. Applications
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abd Al-Fattah, A.M.; El-Helbawy, A.A.; Al-Dayian, G.R. Inverted Kumaraswamy distribution: Properties and estimation. Pak. J. Stat. 2017, 33, 37–61. [Google Scholar]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Abdul-Moniem, I.B.; Abdel-Hameed, H.F. On exponentiated Lomax distribution. Int. J. Math. Arch. 2012, 3, 2144–2150. [Google Scholar]
- Abid, S.H.; Abdulrazak, R.K. [0,1] truncated Fréchet-G generator of distributions. Appl. Math. 2017, 7, 51–66. [Google Scholar]
- Najarzadegan, H.; Alamatsaz, M.H.; Hayati, S. Truncated Weibull-G more flexible and more reliable than geta-G distribution. Int. J. Stat. Probab. 2017, 6, 1–17. [Google Scholar] [CrossRef]
- Jamal, F.; Bakouch, H.S.; Nasir, M.A. A truncated general-G class of distributions with application to truncated Burr-G family. RevStat 2019. to appear. [Google Scholar]
- Marshall, A.; Olkin, I. A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Kumar, D.; Sing, U.; Singh, S.K.; Mukherjee, S. The new probability distribution: An aspect to a life time distribution. Math. Sci. Lett. 2017, 6, 35–42. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biometr. J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Walti, J.R. Probability weighted moments; definition and relation to parameters of distribution expressible in inverse form. Water Resour. Res. 1979, 3, 281–292. [Google Scholar]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Giorgi, G.M.; Crescenzi, M. A look at the Bonferroni inequality measure in a reliability framework. Statistica 2001, 61, 571–583. [Google Scholar]
- Amigo, J.M.; Balogh, S.G.; Hernandez, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; The Regents of the University of California: California, CA, USA,, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Brooks/Cole Publishing Company: Pacific Grove, CA, USA, 1990. [Google Scholar]
- Oguntunde, P.E.; Balogun, O.S.; Okagbue, H.I.; Bishop, S.A. The Weibull-exponential distribution: Its properties and applications. J. Appl. Sci. 2015, 15, 1305–1311. [Google Scholar] [CrossRef]
- Golzar, N.H.; Ganji, M.; Bevrani, H. The Lomax-exponential distribution, some properties and applications. J. Stat. Res. Iran 2016, 13, 131–153. [Google Scholar] [CrossRef][Green Version]
- Ristić, M.M.; Balakrishnan, N. The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 2012, 82, 1191–1206. [Google Scholar] [CrossRef]
- Umar, N.; Damisa, S.; Abdulkadir, Y. Odd Burr III-Exponential distribution: Its theory and application. In Proceedings of the Conference: Nigeria Mathematical Society 37th Annual International Conference, Bayero University Kano, Kano, Nigeria, 8–11 May 2018. [Google Scholar]
- Oguntunde, P.E.; Adejumo, A.O.; Owoloko, E.A.; Rastogi, M.K.; Odetunmib, O.A. The Burr X-exponential distribution: Theory and applications. In Proceedings of the World Congress on Engineering 2017 Vol I WCE 2017, London, UK, 5–7 July 2017. [Google Scholar]
- Teimouri, M.; Gupta, K.A. On three-parameter Weibull distribution shape parameter estimation. J. Data Sci. 2013, 11, 403–414. [Google Scholar]
- Murthy, D.N.P.; Xie, M.; Jiang, R. Weibull Models, Wiley Series in Probability and Statistics; John Wiley and Sons: New York, NY, USA, 2004. [Google Scholar]
- Kus, C. A new lifetime distribution. Comput. Stat. Data Anal. 2007, 51, 4497–4509. [Google Scholar] [CrossRef]
- Reyad, H.; Korkmaz, M.C.; Afify, A.Z.; Hamedani, G.G.; Othman, S. The Fréchet Topp Leone-G Family of Distributions: Properties, Characterizations and Applications. Ann. Data Sci. 2019. [Google Scholar] [CrossRef]
- Aarset, M.V. How to identify bathtub hazard rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
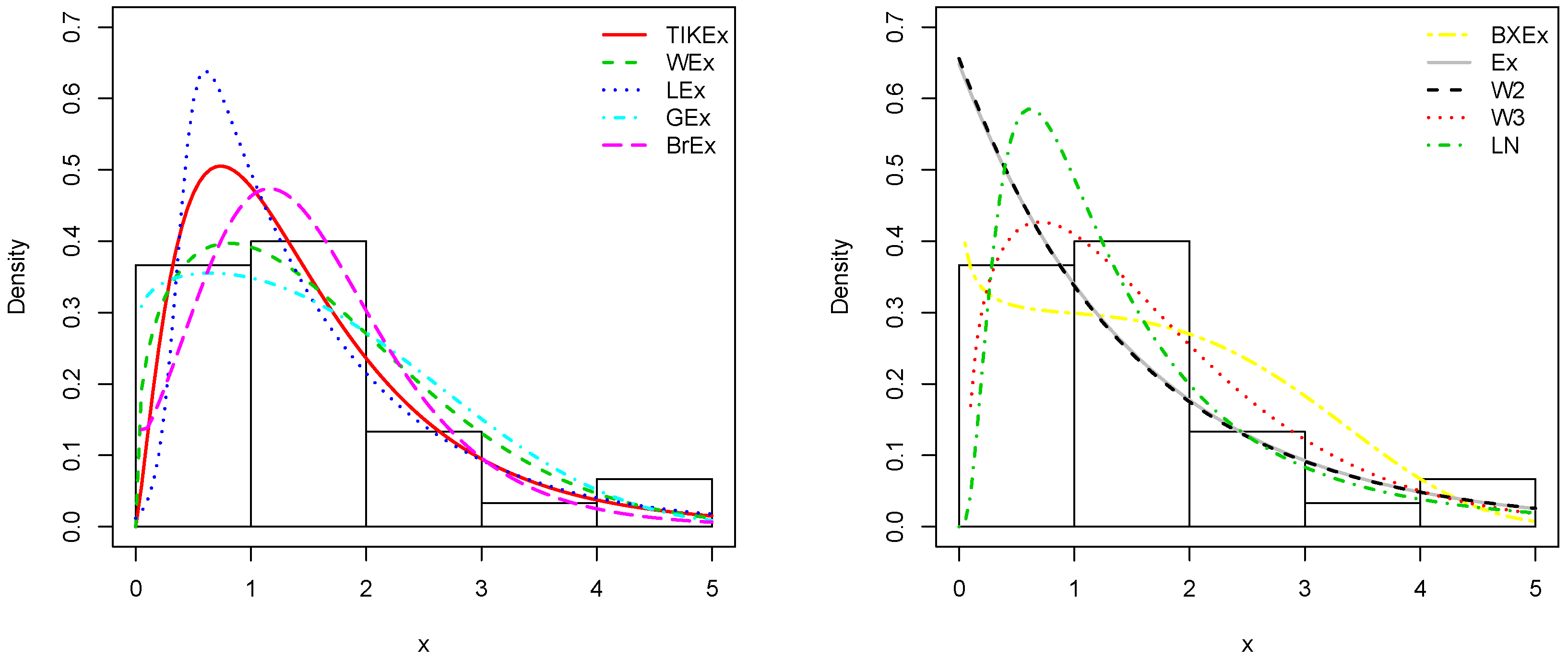
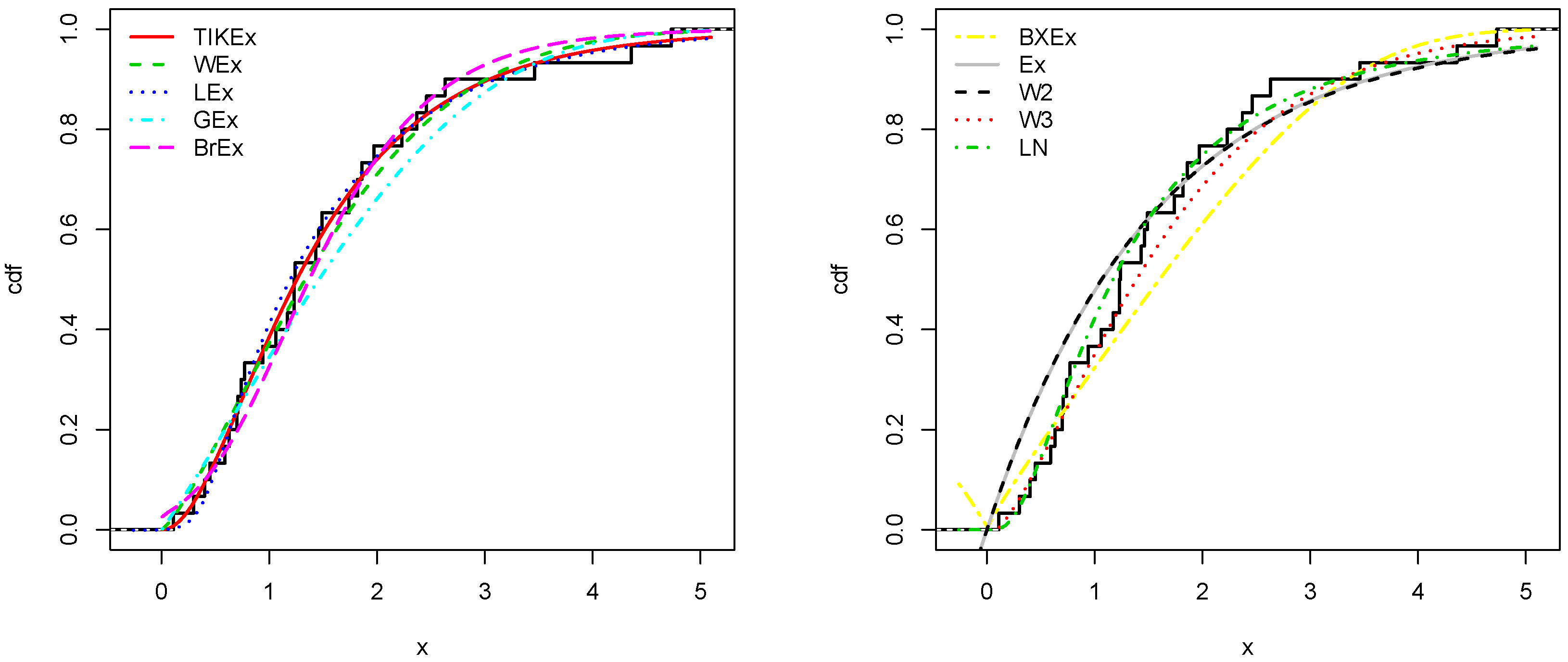
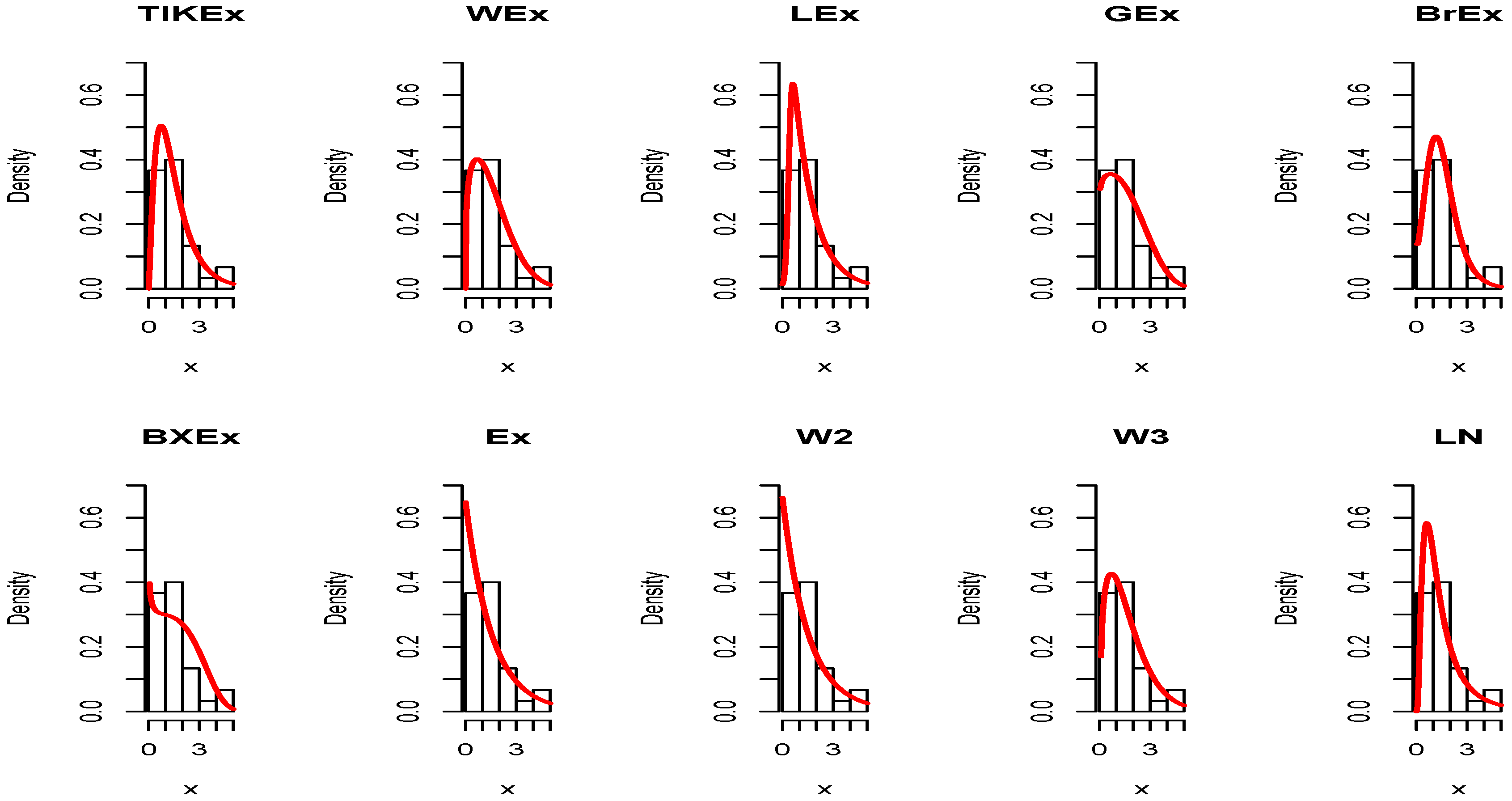
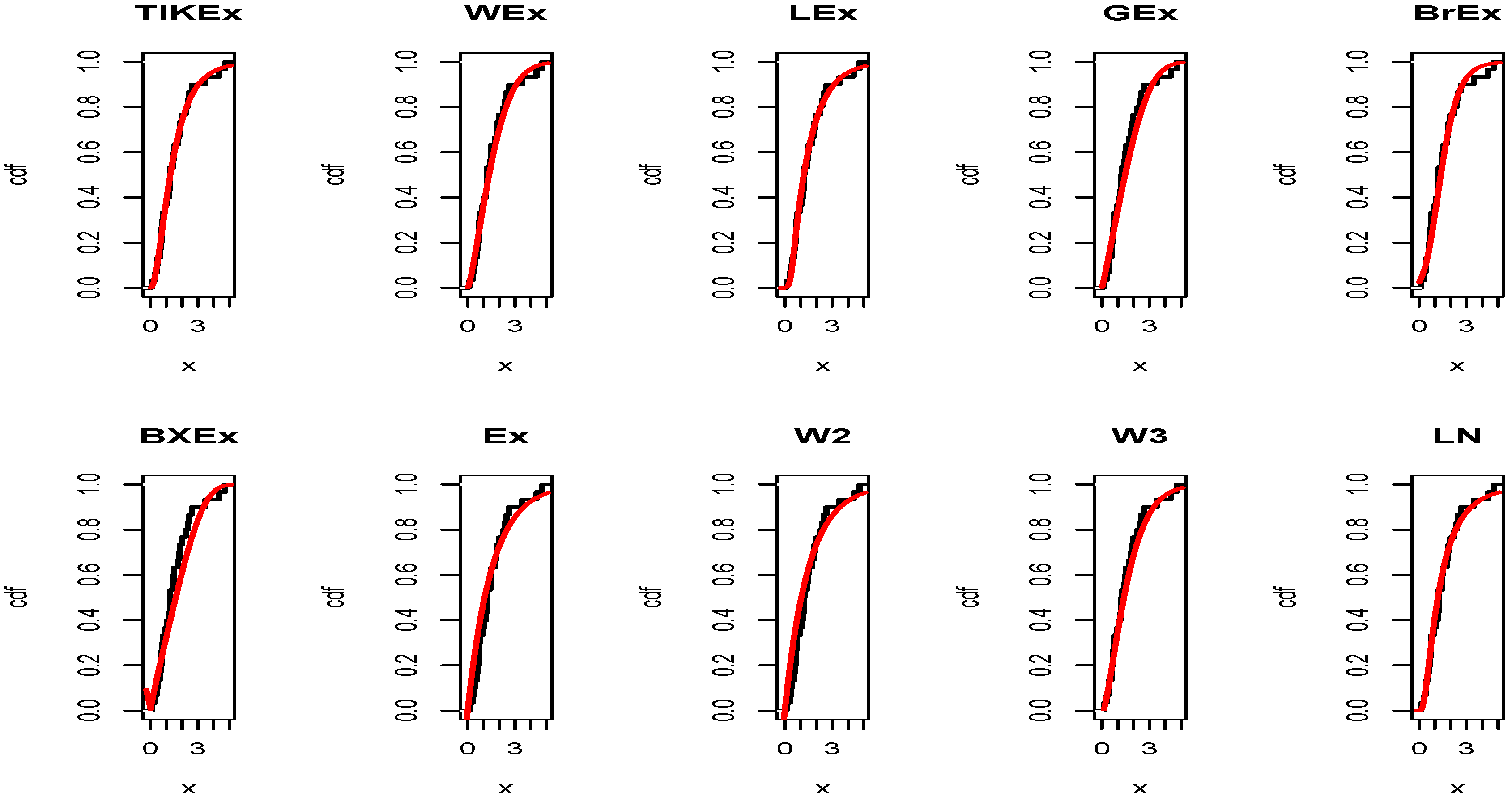
| (a, b, ) | Med | CV | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (0.5, 0.5, 0.5) | 0.7309 | 0.9175 | 2.8803 | 15.6847 | 120.2783 | 2.0384 | 3.1958 | 19.4201 | 1.5559 |
| (1.5, 0.5, 0.5) | 0.1954 | 0.7433 | 2.1122 | 11.0235 | 83.0045 | 1.5596 | 3.6627 | 24.8965 | 1.6800 |
| (2.5, 0.5, 0.5) | 0.1128 | 0.5980 | 1.5117 | 7.4977 | 55.2596 | 1.1541 | 4.2044 | 32.3790 | 1.7964 |
| (5.0, 0.5, 0.5) | 0.0548 | 0.3507 | 0.6128 | 2.5498 | 17.4948 | 0.4898 | 5.8093 | 63.5770 | 1.9955 |
| (0.5, 1.0, 0.5) | 3.0081 | 1.5291 | 5.3943 | 30.5369 | 237.7203 | 3.0561 | 2.4223 | 12.5090 | 1.1432 |
| (0.5, 0.5, 1.0) | 0.3654 | 0.4587 | 0.7200 | 1.9605 | 7.5173 | 0.5096 | 3.1958 | 23.2365 | 1.5559 |
| (1.0, 0.5, 1.0) | 0.1541 | 0.4134 | 0.6187 | 1.6507 | 6.2740 | 0.4477 | 3.4198 | 25.7699 | 1.6184 |
| (1.0, 0.5, 2.0) | 0.0770 | 0.2067 | 0.1546 | 0.2063 | 0.3921 | 0.1119 | 3.4198 | 33.4255 | 1.6184 |
| (5.0, 0.5, 2.0) | 0.0137 | 0.0876 | 0.03830 | 0.0398 | 0.0683 | 0.0306 | 5.8093 | 79.7019 | 1.9955 |
| (5.0, 0.5, 5.0) | 0.0054 | 0.0350 | 0.0061 | 0.0025 | 0.0017 | 0.0048 | 5.8093 | 111.9517 | 1.9955 |
| (5.0, 1.0, 5.0) | 0.0122 | 0.0598 | 0.0117 | 0.0050 | 0.0034 | 0.0082 | 4.5217 | 97.2774 | 1.5136 |
| (5.0, 3.0, 5.0) | 0.0225 | 0.1229 | 0.0314 | 0.0146 | 0.0103 | 0.0163 | 3.2159 | 100.9527 | 1.0407 |
| (5.0, 5.0, 5.0) | 0.0258 | 0.1637 | 0.0482 | 0.0237 | 0.01707 | 0.0214 | 2.7876 | 111.0229 | 0.8945 |
| a | b | Rényi Entropy | ||
|---|---|---|---|---|
| 0.5 | 0.5 | 0.5 | 0.5 | −0.76558 |
| 0.5 | 1.0 | 0.5 | 0.5 | −0.7256 |
| 0.5 | 5.0 | 0.5 | 0.5 | −0.37040 |
| 0.5 | 5.0 | 1.0 | 0.5 | −0.5772 |
| 0.5 | 5.0 | 5.0 | 0.5 | −0.9030 |
| 0.5 | 5.0 | 5.0 | 1.0 | −0.5564 |
| 0.5 | 5.0 | 5.0 | 5.0 | 0.2482 |
| 0.5 | 0.5 | 0.5 | 5.0 | 0.3857 |
| 0.5 | 2.0 | 0.5 | 5.0 | 0.5099 |
| 0.5 | 2.0 | 0.5 | 5.0 | 0.7808 |
| 2.0 | 2.0 | 1.0 | 0.5 | 0.6079 |
| 2.0 | 2.0 | 2.0 | 0.5 | 1.2298 |
| 2.0 | 2.0 | 5.0 | 0.5 | 1.6593 |
| 2.0 | 5.0 | 5.0 | 0.5 | 1.0207 |
| 2.0 | 5.0 | 5.0 | 2.0 | −0.3655 |
| 2.0 | 5.0 | 5.0 | 5.0 | −1.2818 |
| 5.0 | 5.0 | 5.0 | 1.0 | 0.3039 |
| 5.0 | 5.0 | 5.0 | 5.0 | −6.1337 |
| a | b | Shannon Entropy | |
|---|---|---|---|
| 2.0 | 5.0 | 0.5 | 1.8957 |
| 2.0 | 5.0 | 1.0 | 1.2025 |
| 2.0 | 5.0 | 3.0 | 0.1039 |
| 2.0 | 5.0 | 5.0 | −0.4068 |
| 0.5 | 1.0 | 0.5 | 1.4128 |
| 1.0 | 1.0 | 0.5 | 1.3068 |
| 3.0 | 1.0 | 0.5 | 0.8544 |
| 5.0 | 1.0 | 0.5 | 0.4170 |
| 5.0 | 2.0 | 0.5 | 0.9045 |
| 5.0 | 5.0 | 0.5 | 1.3442 |
| 5.0 | 5.0 | 1.0 | 0.6510 |
| 5.0 | 5.0 | 3.0 | −0.4475 |
| 5.0 | 5.0 | 5.0 | −0.9583 |
| Set 1: | (0.5, 0.5, 2) | Set 2: | (1.5, 0.5, 2) | Set 3: | (2, 0.5, 2) | Set 4: | (1.5, 1.5, 2) | |
| n | Estimates | RMSEs | Estimates | RMSEs | Estimates | RMSEs | Estimates | RMSEs |
| 50 | 0.872 | 1.632 | 1.029 | 1.780 | 1.213 | 2.046 | 1.213 | 2.160 |
| 0.485 | 0.122 | 0.563 | 0.157 | 0.595 | 0.202 | 1.535 | 0.442 | |
| 2.201 | 0.716 | 2.099 | 0.962 | 2.015 | 0.624 | 1.988 | 0.789 | |
| 100 | 0.794 | 1.093 | 1.202 | 1.384 | 1.475 | 1.486 | 1.533 | 1.291 |
| 0.490 | 0.092 | 0.525 | 0.117 | 0.562 | 0.150 | 1.562 | 0.333 | |
| 2.164 | 0.499 | 1.970 | 0.374 | 1.973 | 0.443 | 2.129 | 0.501 | |
| 200 | 0.670 | 0.901 | 1.360 | 1.248 | 1.477 | 1.224 | 1.385 | 1.205 |
| 0.497 | 0.073 | 0.513 | 0.104 | 0.535 | 0.097 | 1.513 | 0.275 | |
| 2.087 | 0.335 | 1.994 | 0.286 | 1.894 | 0.315 | 1.975 | 0.367 | |
| 500 | 0.419 | 0.609 | 1.098 | 0.996 | 1.885 | 0.936 | 1.225 | 0.910 |
| 0.503 | 0.042 | 0.524 | 0.073 | 0.506 | 0.072 | 1.549 | 0.186 | |
| 1.981 | 0.222 | 1.895 | 0.249 | 1.959 | 0.221 | 1.946 | 0.262 | |
| 1000 | 0.291 | 0.447 | 1.080 | 0.858 | 1.712 | 0.832 | 0.943 | 0.837 |
| 0.510 | 0.030 | 0.525 | 0.056 | 0.520 | 0.066 | 1.594 | 0.158 | |
| 1.949 | 0.145 | 1.905 | 0.248 | 1.940 | 0.189 | 1.868 | 0.222 | |
| Set 5: | (0.5, 1.5, 2) | Set 6: | (2, 1.5, 2) | Set 7: | (2, 2, 2) | Set 8: | (1.5, 2, 2) | |
| n | Estimates | RMSEs | Estimates | RMSEs | Estimates | RMSEs | Estimates | RMSEs |
| 50 | 1.020 | 2.135 | 1.869 | 1.913 | 1.829 | 2.128 | 1.329 | 2.259 |
| 1.514 | 0.409 | 1.609 | 0.492 | 2.155 | 0.703 | 2.094 | 0.641 | |
| 2.425 | 1.204 | 2.041 | 0.559 | 2.144 | 0.839 | 2.060 | 0.607 | |
| 100 | 1.056 | 1.303 | 1.747 | 1.598 | 2.403 | 1.607 | 1.617 | 1.389 |
| 1.451 | 0.275 | 1.622 | 0.421 | 1.965 | 0.512 | 2.047 | 0.454 | |
| 2.259 | 0.555 | 2.002 | 0.442 | 2.138 | 0.470 | 2.154 | 0.457 | |
| 200 | 0.621 | 0.887 | 1.840 | 1.218 | 1.778 | 1.061 | 1.340 | 1.004 |
| 1.487 | 0.218 | 1.573 | 0.296 | 2.089 | 0.387 | 2.059 | 0.339 | |
| 2.052 | 0.321 | 2.009 | 0.345 | 1.980 | 0.303 | 1.992 | 0.314 | |
| 500 | 0.645 | 0.616 | 1.744 | 0.852 | 2.015 | 0.811 | 1.449 | 0.714 |
| 1.484 | 0.125 | 1.560 | 0.192 | 2.005 | 0.272 | 2.031 | 0.240 | |
| 2.069 | 0.259 | 1.968 | 0.219 | 2.013 | 0.205 | 1.998 | 0.208 | |
| 1000 | 0.556 | 0.484 | 1.823 | 0.716 | 1.975 | 0.572 | 1.450 | 0.558 |
| 1.499 | 0.094 | 1.552 | 0.157 | 2.010 | 0.187 | 2.003 | 0.157 | |
| 2.042 | 0.188 | 1.979 | 0.182 | 2.013 | 0.148 | 1.971 | 0.172 |
| n | Mean | Median | Standard Deviation | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|
| First data set | 30 | 1.54 | 1.23 | 1.13 | 1.23 | 1.04 |
| Second data set | 179 | 89.13 | 51 | 105.56 | 2.21 | 5.64 |
| Model | a | b | ||||
|---|---|---|---|---|---|---|
| TIKEx | 40.5241 | 2.2765 | 0.0271 | - | - | - |
| (2.7618) | (0.6944) | (0.0446) | - | - | - | |
| WEx | - | - | - | 0.1013 | 8.4803 | 1.3238 |
| - | - | - | (0.0470) | (6.2815) | (0.1776) | |
| LEx | 69.2568 | 11.1652 | 0.0755 | - | - | - |
| (8.2345) | (6.1143) | (0.01261) | - | - | ||
| GEx | - | - | - | 0.9649 | 0.3993 | 1.1085 |
| - | - | - | (0.4346) | (0.1894) | (0.5843) | |
| BrEx | 38.7695 | 0.0365 | 5.2164 | - | - | - |
| (9.9407) | (0.1128) | (1.2006) | - | - | - | |
| BXEx | - | - | 0.4261 | 0.2399 | - | - |
| - | - | (0.0852) | (0.0237) | - | - | |
| Ex | - | - | 0.6482 | - | - | - |
| - | - | (0.1183) | - | - | - | |
| W2 | - | - | - | - | 66.0352 | 43.2275 |
| - | - | - | - | (4.44084) | (3.51546) | |
| W3 | - | - | 0.0794 | - | 1.3441 | 1.7189 |
| - | - | (0.0622) | - | (0.2322) | (0.2767) | |
| LN | - | - | - | - | 0.1628 | 0.8014 |
| - | - | - | - | (0.1463) | (0.1033) |
| Model | AIC | BIC | W | A | KS | p-Value (KS) | |
|---|---|---|---|---|---|---|---|
| TIKEx | 39.6679 | 85.3358 | 89.5394 | 0.0174 | 0.1287 | 0.0631 | 0.9998 |
| WEx | 40.2139 | 86.4278 | 90.6314 | 0.0365 | 0.2729 | 0.0973 | 0.9388 |
| LEx | 40.3989 | 86.7978 | 91.0014 | 0.0353 | 0.2236 | 0.0864 | 0.9784 |
| GEx | 41.3196 | 88.6392 | 92.8428 | 0.0711 | 0.5068 | 0.1239 | 0.7459 |
| BrEx | 41.5335 | 89.0670 | 93.2706 | 0.0449 | 0.3360 | 0.1097 | 0.8631 |
| BXEx | 42.9933 | 89.9866 | 92.7890 | 0.1187 | 0.8107 | 0.1649 | 0.3877 |
| Ex | 43.5300 | 89.0600 | 90.4611 | 0.0189 | 0.1439 | 0.1845 | 0.2589 |
| W2 | 43.1745 | 90.3491 | 93.1515 | 0.0183 | 0.1395 | 0.1889 | 0.2344 |
| W3 | 39.7242 | 85.4484 | 89.6520 | 0.0246 | 0.1962 | 0.0979 | 0.9358 |
| LN | 40.7353 | 85.4707 | 88.2731 | 0.0391 | 0.2737 | 0.0970 | 0.9399 |
| Model | a | b | ||||
|---|---|---|---|---|---|---|
| TIKEx | 2.2601 | 1.2920 | 0.0073 | - | - | - |
| (1.0398) | (0.1740) | (0.0014) | - | - | - | |
| WEx | - | - | - | 2.9055 | 0.7768 | 0.0024 |
| - | - | - | (0.4138) | (0.0441) | (0.0002) | |
| LEx | 3.9060 | 1.0496 | 0.0108 | - | - | - |
| (4.5170) | (0.5452) | (0.0056) | - | - | ||
| GEx | - | - | - | 0.7496 | 0.0044 | 0.7989 |
| - | - | - | (0.1327) | (0.0007) | (0.1188) | |
| BrEx | 0.0112 | 0.9459 | 0.9739 | - | - | - |
| (0.0024) | (0.1413) | (0.2126) | - | - | - | |
| BXEx | - | - | 0.4261 | 0.2399 | - | - |
| - | - | (9.5 × ) | (.0017) | - | - | |
| Ex | - | - | 0.0112 | - | - | - |
| - | - | (0.0008) | - | - | - | |
| W2 | - | - | - | - | 210.6370 | 3.2537 |
| - | - | - | - | (4.6020) | (0.9242) | |
| W3 | - | - | - | 0.3540 | 0.9100 | 85.2728 |
| - | - | - | (0.3317) | (0.0364) | (6.5928) | |
| LN | - | - | - | - | 3.8393 | 1.2405 |
| - | - | - | - | (0.0927) | (0.0655) |
| Model | AIC | BIC | W | A | KS | p-Value (KS) | |
|---|---|---|---|---|---|---|---|
| TIKEx | 977.4752 | 1960.9500 | 1970.5130 | 0.0501 | 0.3418 | 0.0470 | 0.8237 |
| WEx | 985.8205 | 1977.6410 | 1987.2030 | 0.2669 | 1.6410 | 0.0755 | 0.2588 |
| LEx | 982.0106 | 1970.0210 | 1979.5830 | 0.1416 | 0.8632 | 0.0926 | 0.0927 |
| GEx | 997.0995 | 2000.1990 | 2009.7610 | 0.4779 | 2.9176 | 0.1279 | 0.0057 |
| BrEx | 982.1473 | 1970.2950 | 1979.8570 | 0.1918 | 1.1773 | 0.0746 | 0.2712 |
| BXEx | 1015.6880 | 2035.3750 | 2041.7500 | 0.7582 | 4.6283 | 0.1899 | 4.9 × |
| Ex | 985.7355 | 1973.4710 | 1976.6583 | 0.1894 | 1.1638 | 0.0864 | 0.1380 |
| W2 | 980.2322 | 1964.4640 | 1970.8390 | 0.0751 | 0.5026 | 0.0576 | 0.5910 |
| W3 | 982.1508 | 1970.3020 | 1979.8640 | 0.1724 | 1.0704 | 0.05841 | 0.5745 |
| LN | 980.8582 | 1965.7164 | 1972.0911 | 0.0535 | 0.4329 | 0.0400 | 0.9360 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bantan, R.A.R.; Jamal, F.; Chesneau, C.; Elgarhy, M. Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications. Entropy 2019, 21, 1089. https://doi.org/10.3390/e21111089
Bantan RAR, Jamal F, Chesneau C, Elgarhy M. Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications. Entropy. 2019; 21(11):1089. https://doi.org/10.3390/e21111089
Chicago/Turabian StyleBantan, Rashad A. R., Farrukh Jamal, Christophe Chesneau, and Mohammed Elgarhy. 2019. "Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications" Entropy 21, no. 11: 1089. https://doi.org/10.3390/e21111089
APA StyleBantan, R. A. R., Jamal, F., Chesneau, C., & Elgarhy, M. (2019). Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications. Entropy, 21(11), 1089. https://doi.org/10.3390/e21111089







