Feature Extraction of Ship-Radiated Noise Based on Intrinsic Time-Scale Decomposition and a Statistical Complexity Measure
Abstract
1. Introduction
2. Basic Theory
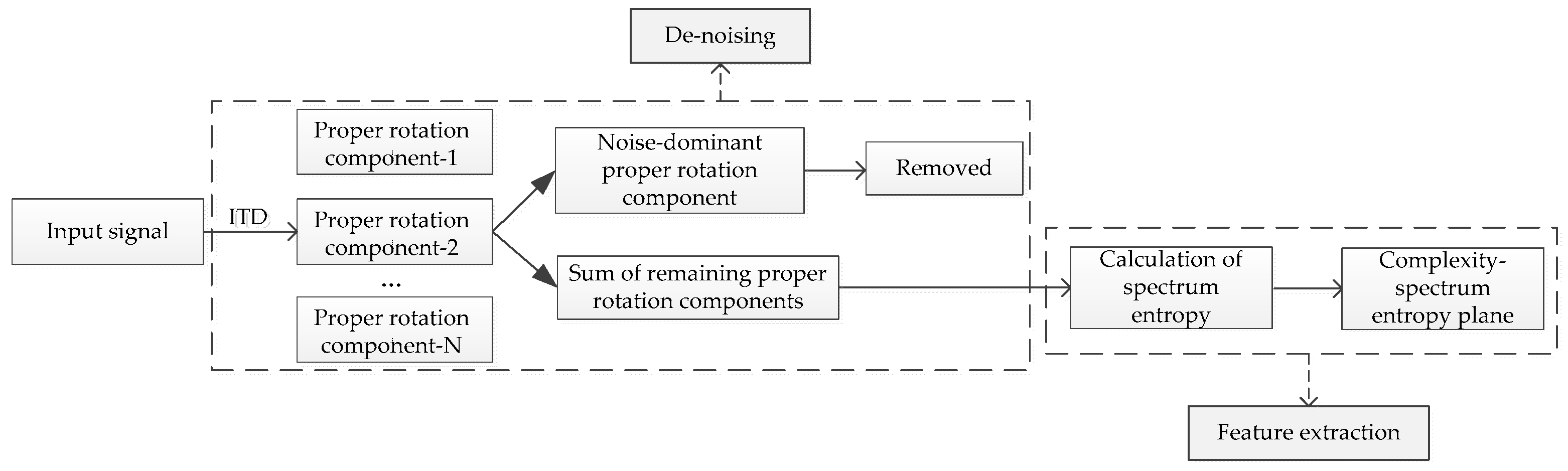
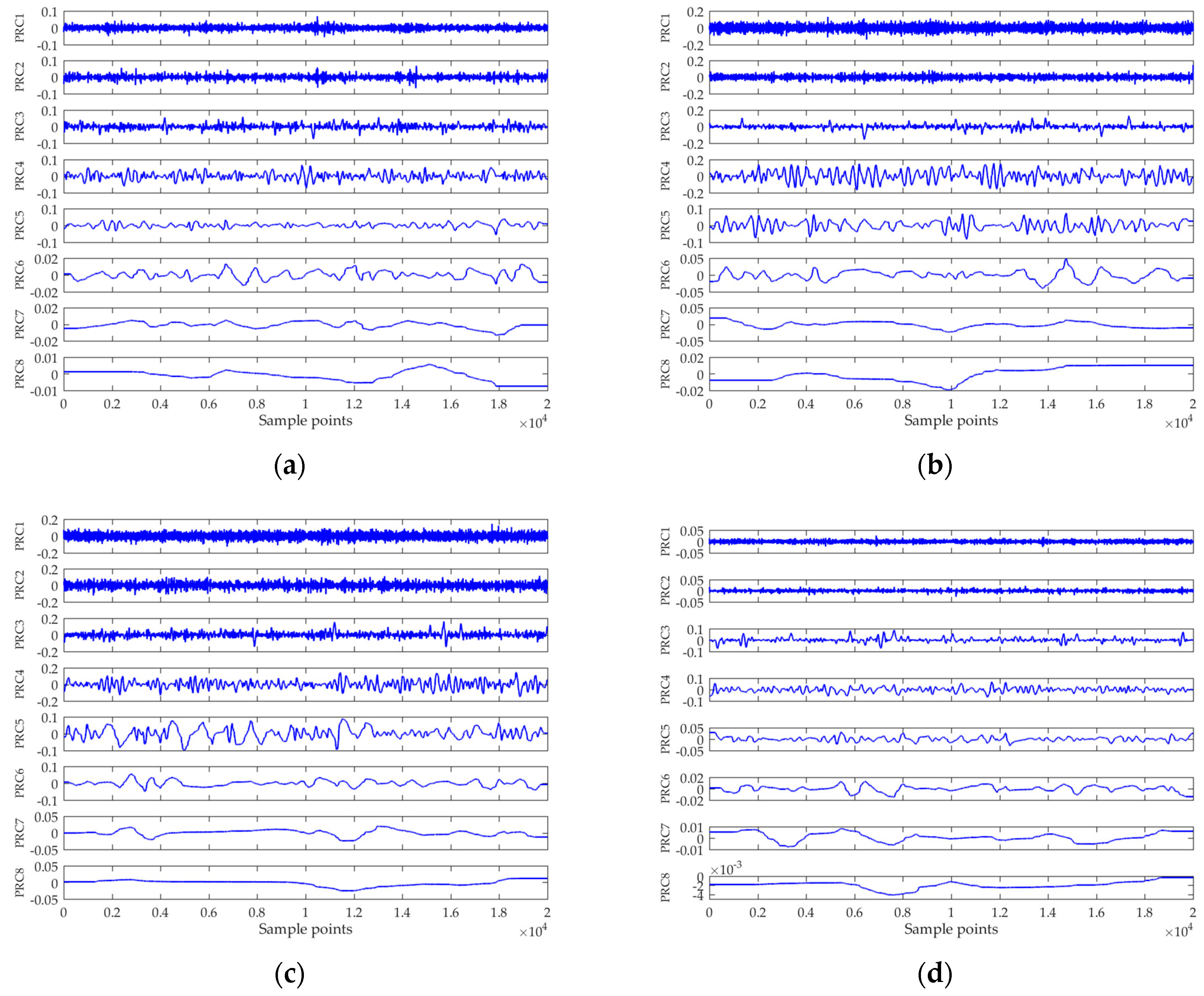
2.1. Intrinsic Time-Scale Decomposition (ITD)
- Let be the local extrema of at time index . Suppose that is available on and that is defined on interval . Then, on the interval can be computed using:where:According to Frei and Osorio [27], the constant is typically fixed at .
- Set the obtained as the input signal and continue the iteration until the terminal condition is reached. In our study, once the energy of was less than 1% of , the iteration was stopped.
- Finally, the ITD of can be expressed as:where denotes the obtained PRC after k + 1 iterations, and is the monotonic trend (if the terminal condition is reached before the monotonic trend is obtained, represents the lowest frequency baseline). ITD is a fully data-driven method; the produced PRCs are adaptively arranged in order from high frequency to low frequency in the frequency domain. In general, the kth PRC will be “noisier” than that of the (k + 1)th [26,36]. Hence, in this study, the first PRC of the ship-radiated noise is regarded as a noise-dominant component, and is removed.
2.2. LMC Complexity Measure
2.3. Complexity–Spectrum Entropy Plane
- Transform the input signal to the frequency domain using:where is the Fourier transform of , is a frequency point of , and is the length of .
- The probability distribution of can be computed using:
- The spectrum entropy and its normalized version are then, respectively, defined as:
- Compute the disequilibrium using Equations (10)–(12), where the distance between and are calculated using the Jensen divergence:
- Define the new complexity as:
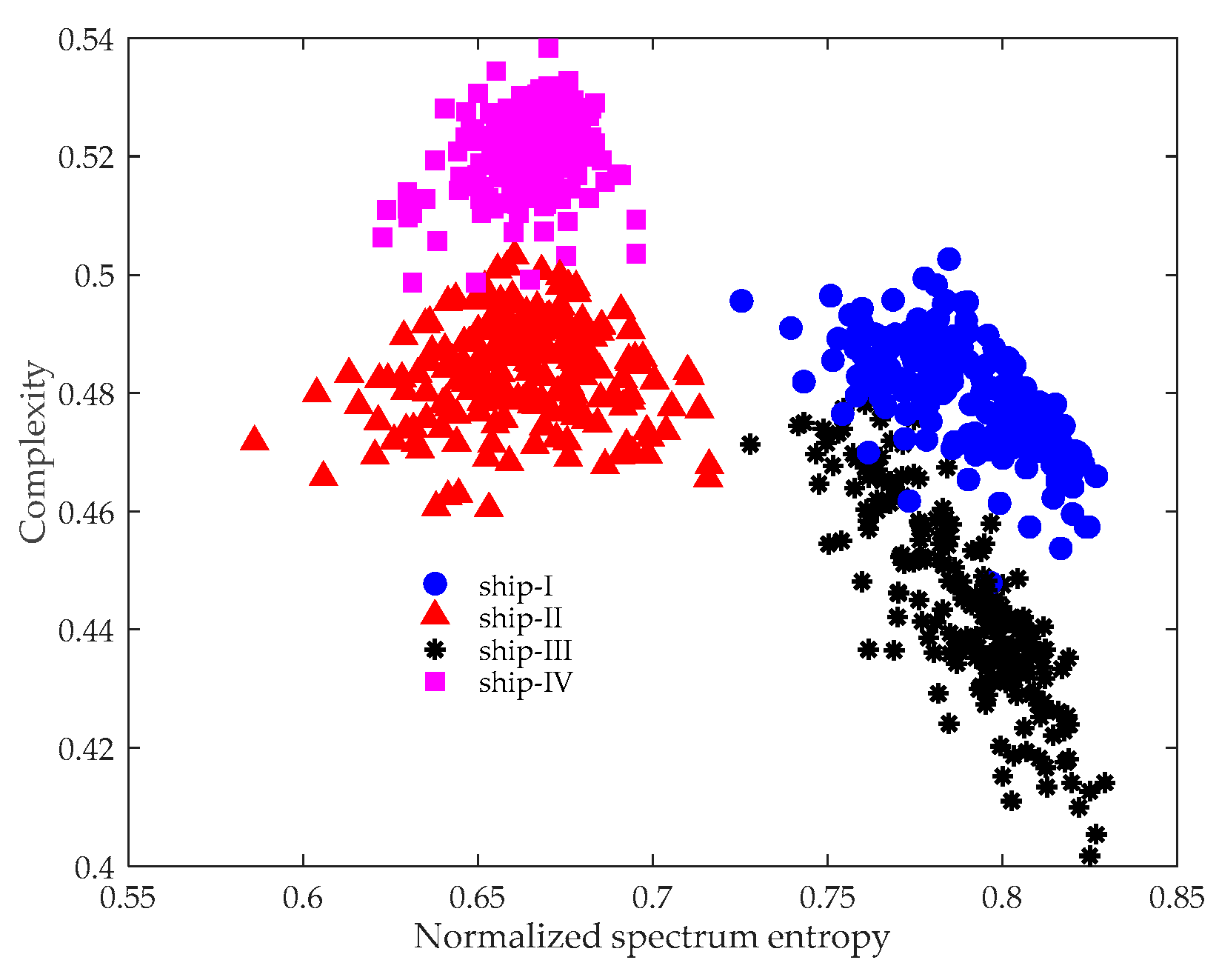
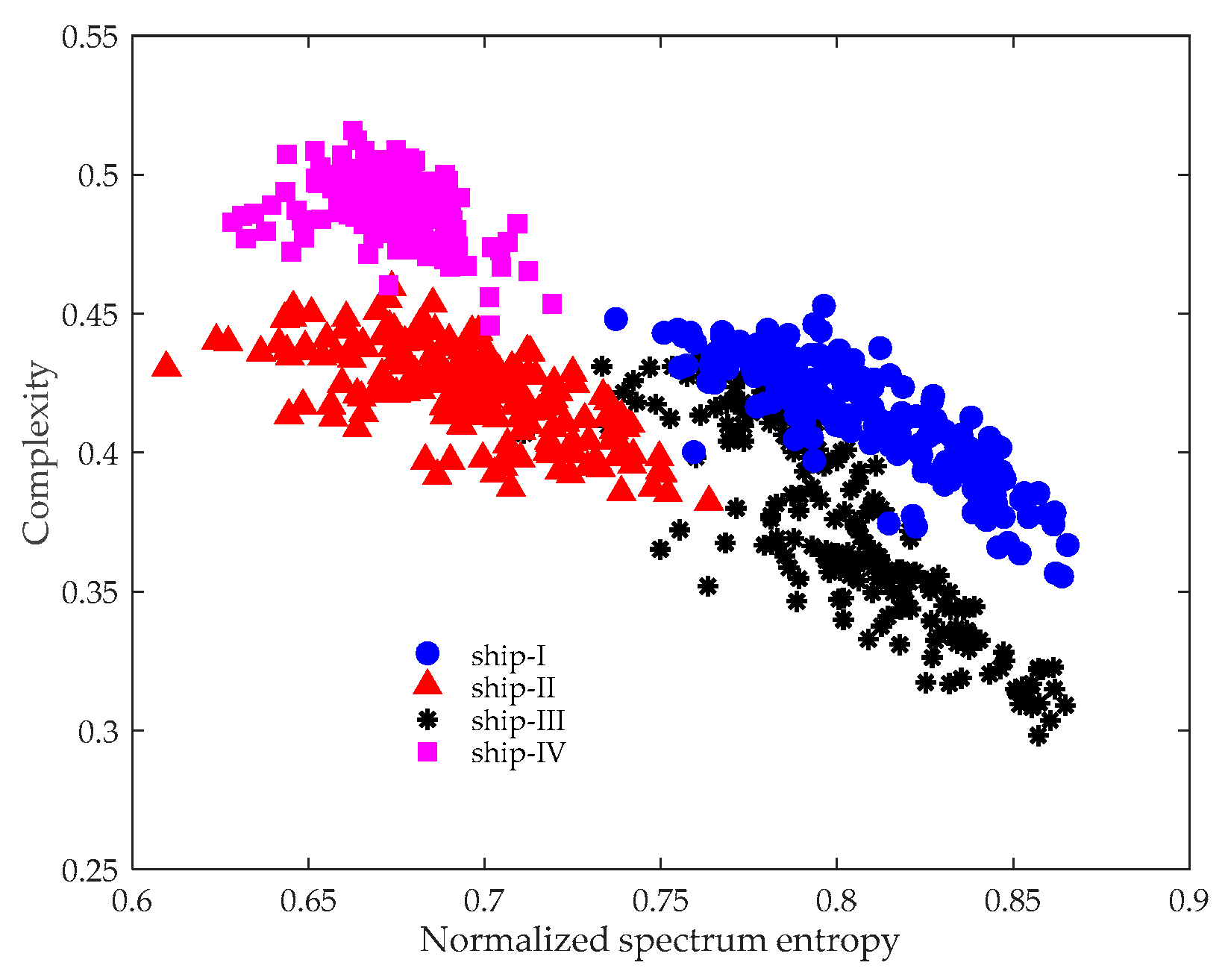
- Finally, the two-dimensional plane composed of and is called the CSEP, which can be used to discriminate different types of ship-radiated noise according to their location (i.e., the (,) points).
3. Results and Discussion
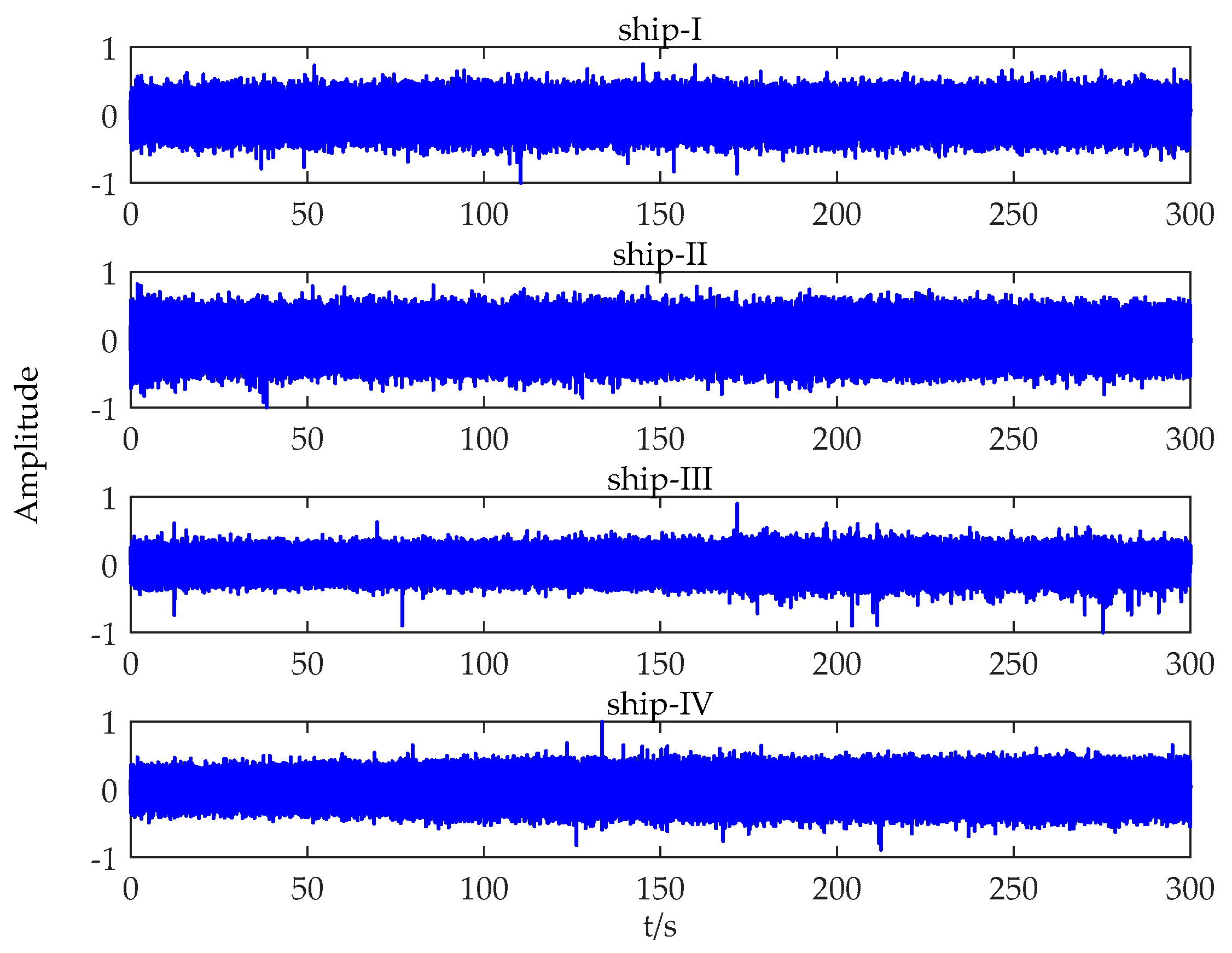
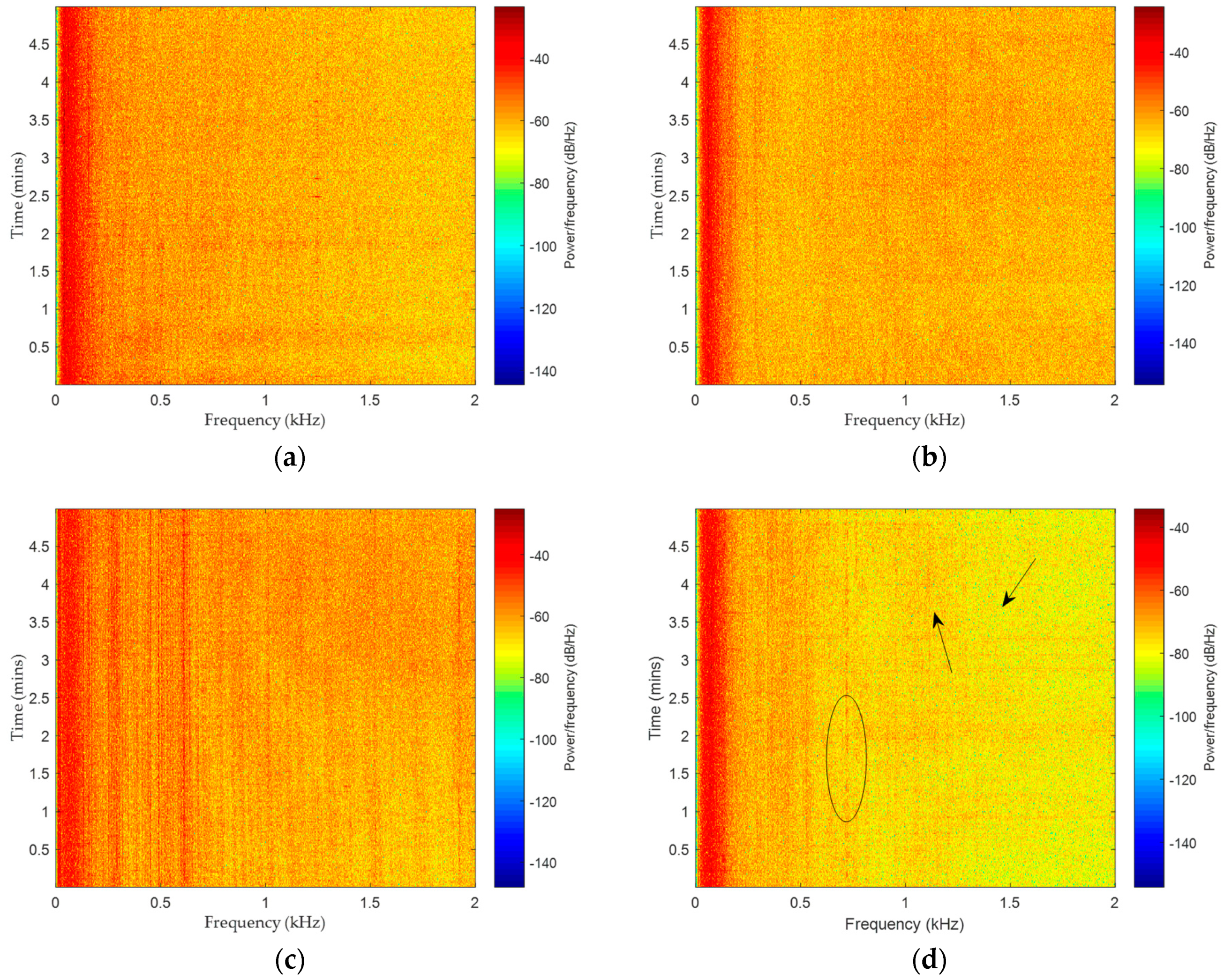
3.1. Data Description
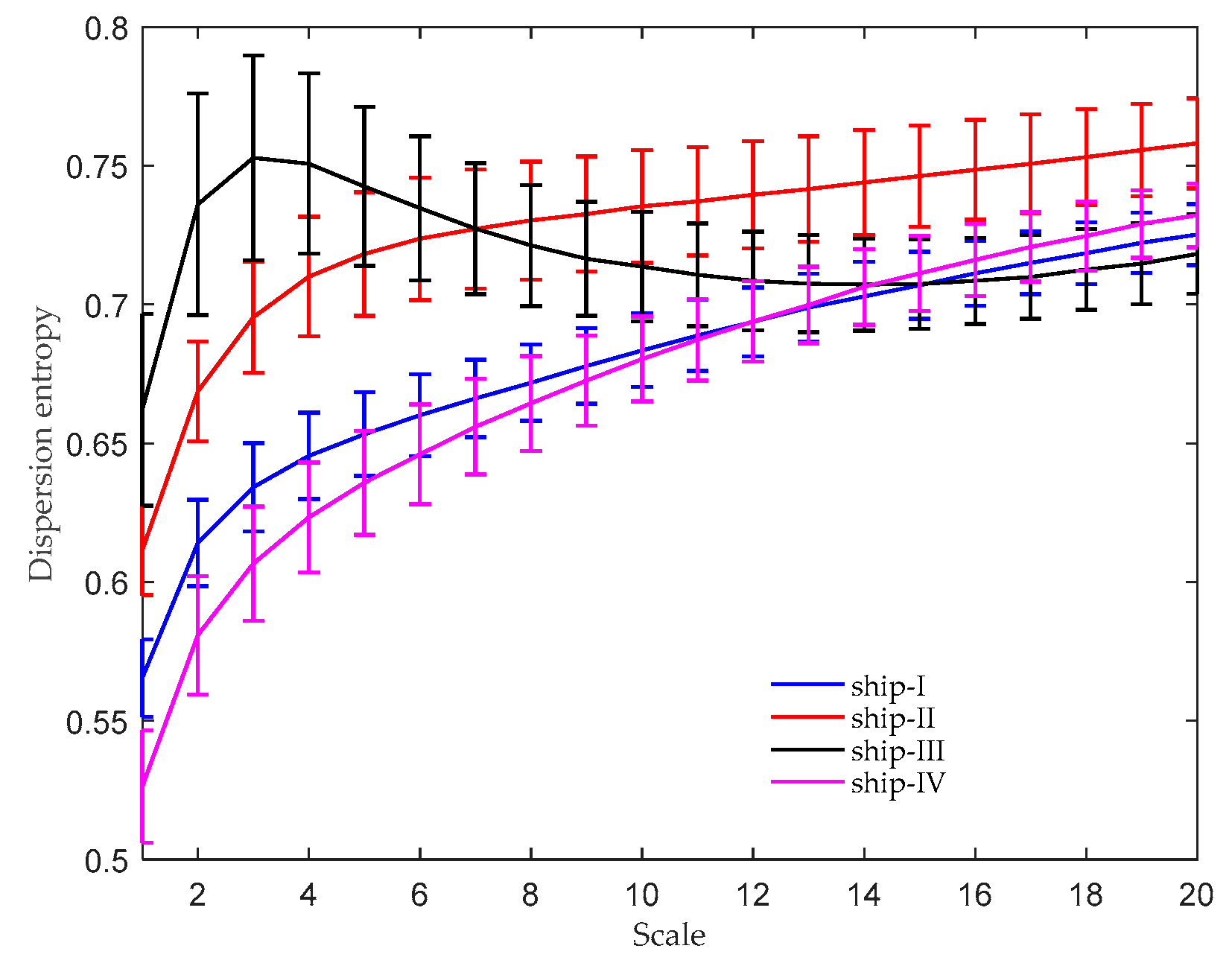
3.2. Complexity Feature Extraction of Ship-Radiated Noise
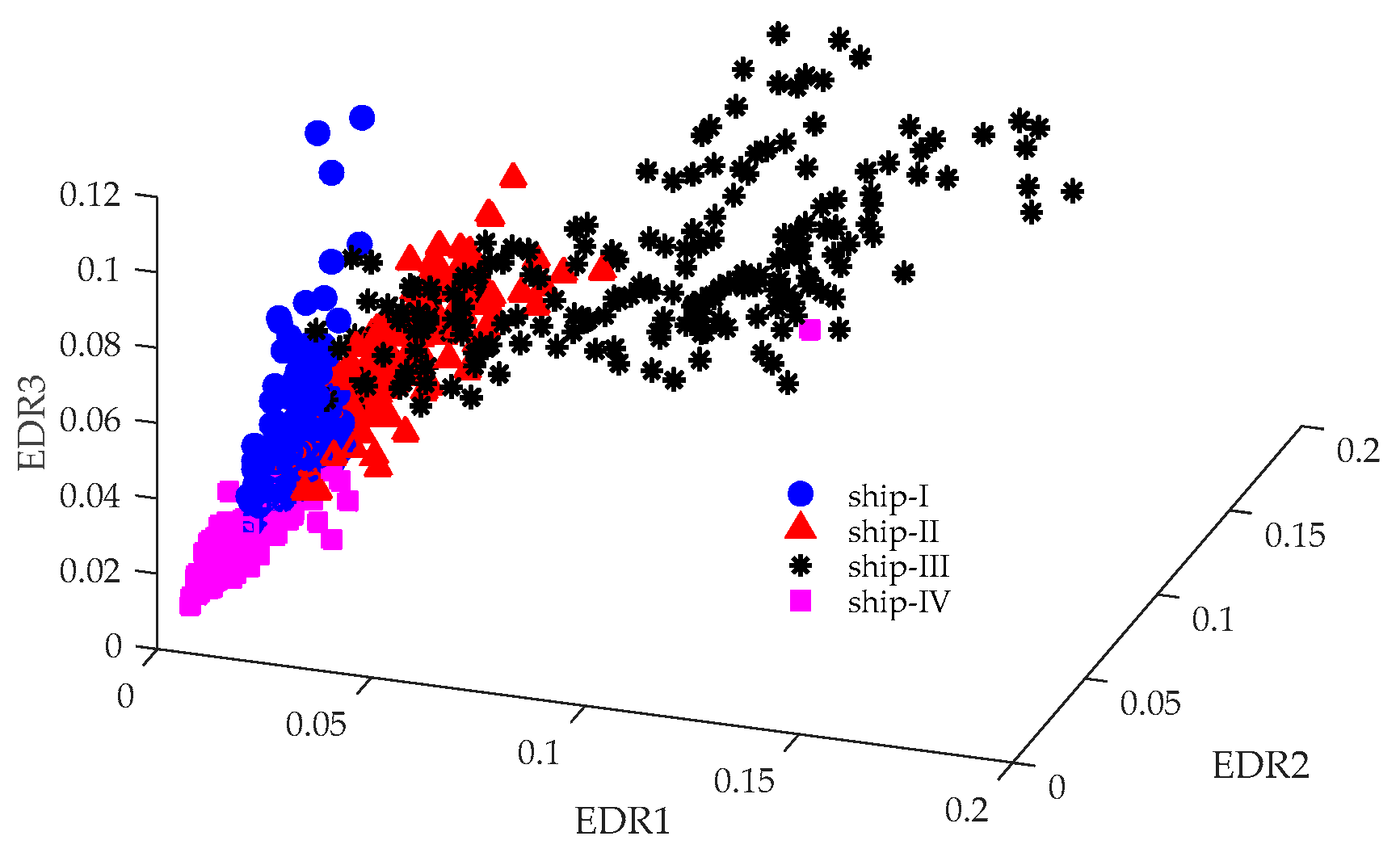
4. Pattern Recognition
5. Conclusions
- The proposed algorithm was fast. It only required 81.82 s to process all 1200 pieces of data while the MDE and SN-EMD-EDR needed 528.27 s (scale = 1–20) and 825.6 s, respectively.
- Unlike MDE and VMD whose performance may be influenced by parameter selection, the ITD-CSEP is completely free of parameters.
- The ITD-CSEP features are unique for different types of ships. The ship classification experiment proves that the recognition rate of the proposed method achieved 94%, which was much higher than other traditional feature extraction methods.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.G.; Zeng, X.Y. Robust underwater noise targets classification using auditory inspired time-frequency analysis. Appl. Acoust. 2014, 78, 68–76. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, X.Y.; Wang, L.; Wang, H.T.; Cai, H.H. Passive moving target classification via spectra multiplication method. IEEE Signal Process Lett. 2017, 24, 451–455. [Google Scholar] [CrossRef]
- Bao, F.; Li, C.; Wang, X.L.; Wang, Q.F.; Du, S.P. Ship classification using nonlinear features of radiated sound: An approach based on empirical mode decomposition. J. Acoust. Soc. Am. 2010, 128, 206–214. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Li, Z.S.; Wang, X.L. Ship recognition via its radiated sound: The fractal based approaches. J. Acoust. Soc. Am. 2002, 112, 172–177. [Google Scholar] [CrossRef]
- David, S.D.; Soledad, T.G.; Antonio, C.L.; Antonio, P.G. ShipsEar: An underwater vessel noise database. Appl. Acoust. 2016, 113, 64–69. [Google Scholar]
- Chen, Z.; Li, Y.Y.; Liang, H.T.; Yu, J. Hierarchical cosine similarity entropy for feature extraction of ship-radiated noise. Entropy 2018, 20, 425. [Google Scholar] [CrossRef]
- Das, A.; Kumar, A.; Bahl, R. Marine vessel classification based on passive sonar data: The cepstrum-based approach. Iet Radar Sonar Navig. 2013, 7, 87–93. [Google Scholar] [CrossRef]
- Richardson, A.M.; Hodgkjiss, W.S. Bispectral analysis of underwater acoustic data. J. Acoust. Soc. Am. 1994, 96, 828–837. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, J.C.; Lin, L.J. Feature extraction of ship-radiated noises based on wavelet transform. Acta Acust. 1997, 22, 139–144. [Google Scholar]
- Hodges, R.P. Underwater Acoustics: Analysis, Design and Performance of Sonar, 1st ed.; Wiley: West Sussex, UK, 2010; pp. 183–184. [Google Scholar]
- Waite, A.D. Sonar for Practicing Engineers, 3rd ed.; Wiley: West Sussex, UK, 2002; pp. 126–127. ISBN 0471497509. [Google Scholar]
- Chang, S.H.; Wang, F.T. Application of the robust discrete wavelet transform to signal detection in underwater sound. Int. J. Electron. 2003, 90, 361–371. [Google Scholar] [CrossRef]
- Chen, C.H.; Lee, J.D.; Lin, M.C. Classification of underwater signals using wavelet transform and neural networks. Mathl. Comput. Model. 1998, 27, 47–60. [Google Scholar]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application on electroencephalogram recordings. Biomed. Signal Process. Control 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude- and fluctuation-based dispersion entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef]
- Shashidhar, S.; Li, Y.A.; Guo, X.J.; Chen, X.; Zhang, Q.F.; Yang, K.D.; Yang, Y.X. A complexity-based approach for the detection of weak signals in ocean ambient noise. Entropy 2016, 18, 101. [Google Scholar]
- Chen, Z.; Li, Y.A.; Liang, H.T.; Yu, J. Improved permutation entropy for measuring complexity of time series under noisy condition. Complexity 2019, 2019, 1403829. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature extraction of ship-radiated noise based on permutation entropy of the intrinsic mode function with the highest energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Li, Y.X.; Wang, L.; Li, X.; Yang, X. A novel linear spectrum frequency feature extraction technique for warship radio noise based on complete ensemble empirical mode decomposition with adaptive noise, duffing chaotic oscillator, and weighted-permutation entropy. Entropy 2019, 21, 507. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, K.; Li, G.H. A new ship-radiated noise feature extraction technique based on variational mode decomposition and fluctuation-based dispersion entropy. Entropy 2019, 21, 235. [Google Scholar] [CrossRef]
- Niu, F.; Hui, J.; Zhao, A.B.; Cheng, Y.; Chen, Y. Application of SN-EMD in mode feature extraction of ship radiated noise. Math. Prob. Eng. 2018, 2018, 2184612. [Google Scholar] [CrossRef]
- Li, Z.X.; Li, Y.A.; Zhang, K. A feature extraction method of ship-radiated noise based on fluctuation-based dispersion entropy and intrinsic time-scale decomposition. Entropy 2019, 21, 693. [Google Scholar] [CrossRef]
- Frei, M.G.; Osorio, I. Intrinsic time-scale decomposition: Time–frequency–energy analysis and real-time filtering of non-stationary signals. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 321–342. [Google Scholar] [CrossRef]
- Calbet, X.; Ricardo, L.R. Tendency towards maximum complexity in a non-equilibrium isolated system. Phys. Rev. E 2001, 63, 066116. [Google Scholar] [CrossRef]
- Ricardo, L.R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 2010, 209, 321–326. [Google Scholar]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical complexity measures: Geometrical and analytical properties. Phys. A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Rosso, O.A.; Luciana, D.M.; Larrondo, H.A.; Martin, M.T.; Plastino, A. Generalized statistical complexity measure. Int. J. Bifurc. Chaos 2010, 20, 775–785. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.A.; Martin, M.T. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, H.V.; Jauregui, M.; Zunino, L. Characterizing time series via complexity-entropy curves. Phys. Rev. E 2017, 95, 062106. [Google Scholar] [CrossRef] [PubMed]
- Jauregui, M.; Zunino, L.; Lenzi, E.K. Characterization of time series via Rényi complexity-entropy curves. Physica A 2018, 498, 74–85. [Google Scholar] [CrossRef]
- Restrepo, J.M.; Venkataramani, S.; Comeau, D.; Flaschka, H. Defining a trend for time series using the intrinsic time-scale decomposition. New J. Phys. 2014, 16, 085004. [Google Scholar] [CrossRef]
- Specht, D.F. Probability neural networks and the polynomial Adaline as complementary techniques for classification. IEEE Trans. Neural Netw. 1990, 1, 111–121. [Google Scholar] [CrossRef]
| ITD | VMD | |
|---|---|---|
| Computation time | 0.8 s | 557.8 s |
| Type | Recognized as | Accuracy | |||
|---|---|---|---|---|---|
| Ship-I | Ship-II | Ship-III | Ship-IV | ||
| Ship-I | 83 | 6 | 4 | 7 | 83% |
| Ship-II | 0 | 99 | 1 | 0 | 99% |
| Ship-III | 4 | 0 | 96 | 0 | 96% |
| Ship-IV | 0 | 2 | 0 | 98 | 98% |
| In total | - | - | - | - | 94% |
| Type | Recognized as | Accuracy | |||
|---|---|---|---|---|---|
| Ship-I | Ship-II | Ship-III | Ship-IV | ||
| Ship-I | 74 | 0 | 26 | 0 | 74% |
| Ship-II | 0 | 97 | 2 | 1 | 97% |
| Ship-III | 34 | 1 | 65 | 0 | 65% |
| Ship-IV | 0 | 2 | 0 | 98 | 98% |
| In total | - | - | - | - | 83.5% |
| Type | Recognized as | Accuracy | |||
|---|---|---|---|---|---|
| Ship-I | Ship-II | Ship-III | Ship-IV | ||
| Ship-I | 96 | 3 | 0 | 1 | 96% |
| Ship-II | 10 | 82 | 8 | 0 | 82% |
| Ship-III | 0 | 0 | 100 | 0 | 100% |
| Ship-IV | 26 | 1 | 0 | 73 | 73% |
| In total | - | - | - | - | 87.75% |
| Type | Recognized as | Accuracy | |||
|---|---|---|---|---|---|
| Ship-I | Ship-II | Ship-III | Ship-IV | ||
| Ship-I | 83 | 13 | 4 | 0 | 83% |
| Ship-II | 6 | 58 | 36 | 0 | 58% |
| Ship-III | 0 | 0 | 100 | 0 | 100% |
| Ship-IV | 8 | 0 | 1 | 91 | 91% |
| In total | - | - | - | - | 83% |
| Type | Recognized as | Accuracy | |||
|---|---|---|---|---|---|
| Ship-I | Ship-II | Ship-III | Ship-IV | ||
| Ship-I | 61 | 0 | 9 | 30 | 61% |
| Ship-II | 0 | 99 | 1 | 0 | 99% |
| Ship-III | 0 | 48 | 52 | 0 | 52% |
| Ship-IV | 38 | 0 | 1 | 61 | 61% |
| In total | - | - | - | - | 68.25% |
| ITD-CSEP | MDE (scale = 1–20) | MDE (scale = 1–10) | SN-EMD-EDR | PSD | |
|---|---|---|---|---|---|
| Computation time | 81.82 s | 528.27 s | 390.87 s | 825.6 s | 3.19 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, Z. Feature Extraction of Ship-Radiated Noise Based on Intrinsic Time-Scale Decomposition and a Statistical Complexity Measure. Entropy 2019, 21, 1079. https://doi.org/10.3390/e21111079
Wang J, Chen Z. Feature Extraction of Ship-Radiated Noise Based on Intrinsic Time-Scale Decomposition and a Statistical Complexity Measure. Entropy. 2019; 21(11):1079. https://doi.org/10.3390/e21111079
Chicago/Turabian StyleWang, Junxiong, and Zhe Chen. 2019. "Feature Extraction of Ship-Radiated Noise Based on Intrinsic Time-Scale Decomposition and a Statistical Complexity Measure" Entropy 21, no. 11: 1079. https://doi.org/10.3390/e21111079
APA StyleWang, J., & Chen, Z. (2019). Feature Extraction of Ship-Radiated Noise Based on Intrinsic Time-Scale Decomposition and a Statistical Complexity Measure. Entropy, 21(11), 1079. https://doi.org/10.3390/e21111079




