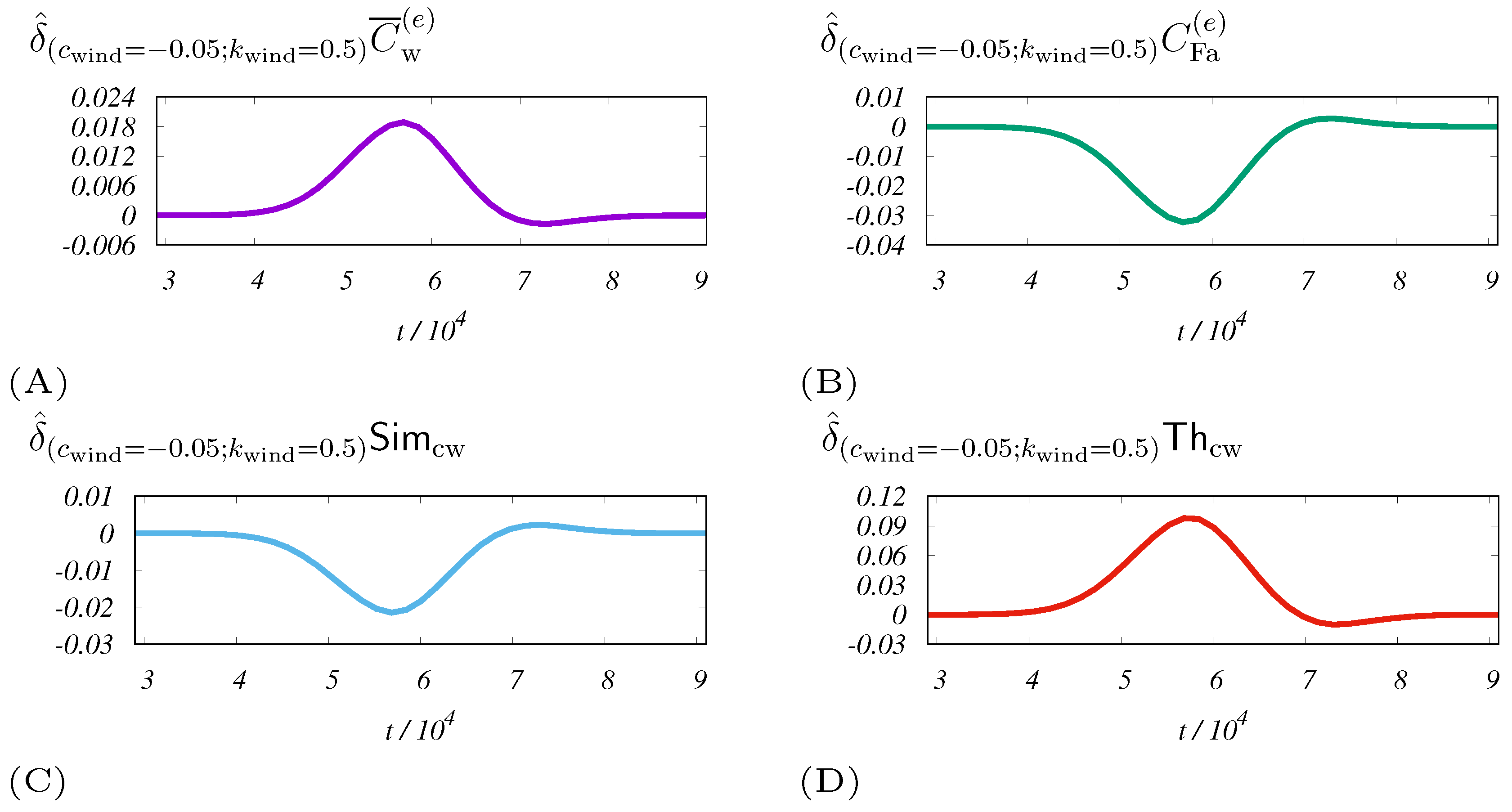1. Introduction
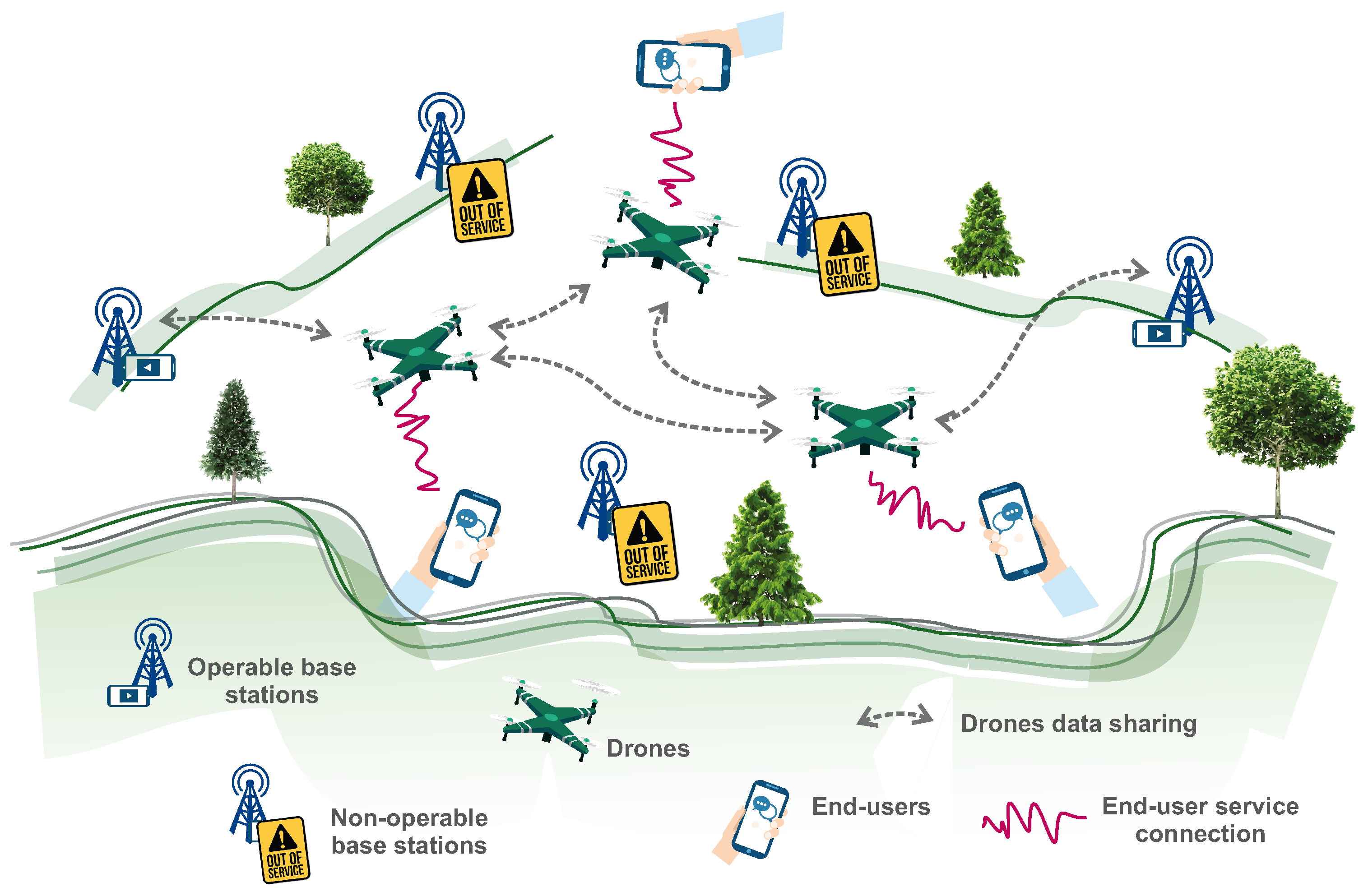
Modern wireless communication systems are shifting the conventional paradigm of terrestrial-based deployment towards hybrid terrestrial/aerial network deployment. The reasons underlying the transition are the rapidly growing number of users and continuously increasing service requirements. Moreover, traffic demand is not typically uniform over the coverage area, so it is common to observe a peak load in some areas, while other areas are not loaded at all [
1].
Therefore, the conventional infrastructure of ground base stations (BSs), small cells and relays requires massive redundancy in order to handle the peak network load in a cost-effective manner. Promising candidates for the aerial communication networks are unmanned aerial vehicle mounted base stations (i.e., drones), which are characterized by low manufacturing costs, high flexibility in terms of speed, reconfiguration capability and mobility control mechanisms, and good signal propagation characteristics towards user equipment (UE) with a strong line-of-sight component [
2]. These features make drones more attractive alternatives than other solutions in the air, such as high-altitude platforms or helikites. As a result, we are currently observing a growing interest in hybrid cellular networks assisted by mobile drones from both industry and academia. For convenience, the remainder of this paper uses the term “drone” to mean an unmanned aerial vehicle (UAV) with a mounted base station.
In general, there are multiple options for deployment of hybrid cellular networks. Very common use cases are drones that are deployed as partially static aerial BSs to support coverage for massive long-lasting social events or military operations [
3]. An alternative option is that drones can serve to track the mobility pattern of UEs and dynamically recompute their flying trajectories in order to provide better coverage quality [
4]. In both cases, the functionality of drones strongly resembles the activity of the conventional BSs with the additional degree of freedom in terms of dynamic location. Nevertheless, such a new degree of freedom increases the complexity of network topology optimization. Moreover, the limited flight time and dynamic trajectories of drones have a direct impact on network performance. Thus, the complexity of the drones’ trajectories is caused by multiple factors such as terrain impairments, interference between drones, UE mobility and the limited lifetime of drones. Despite several benefits and practical applications of using drones as aerial base stations, it is important to address many technical challenges such as performance analysis, deployment, air-to-ground channel modeling, user association, and flight trajectory optimization.
In this paper, we propose a dynamic model of self-organized behavior of drones that takes into account the conditions of the network environment, such as the mobility of UEs and the spatial drone flying constraints, to solve the problem of disaster recovery in mobile networks. The novelty of the proposed approach is that we simulate the interaction between drones based on the analogy of condensed matter physics, i.e., crystallization of molecular structures. However, these original models were also improved and addressed through feedback and adaptability.
The major contributions of this paper are as follows:
A specific drone-assisted mobile network deployment is designed for fast coverage recovery in the case of terrestrial BS failures, taking into account the mobility or activity of UEs, the limited flying time of the drones and the optimal drone trajectories.
A model of drones’ interaction based on the Langevin dynamics (LD) [
5] is proposed to simulate the swarm dynamic of the fleet of drones.
Simulations of the proposed system are conducted and overall performance is discussed. Potential suggestions for progress in model construction have been made.
Although there is much research regarding trajectory and coverage optimization of drone-assisted mobile networks, most of this is actually simplified to a very small number of issues, such as trajectory or coverage optimization of drones. This strategy of limited interest could provide a good indication regarding the possible performance evaluation of such a network, although with restricted practical deployment recommendations. It has been proven that the deployment of the wireless networks belongs to the computationally NP-hard problems, which makes the complexity of deterministic algorithms troubling for both the time and space aspects. It is clear that, with the increasing complexity of networks, scientists are beginning to prefer heuristic methods to technological problems that cannot be solved by traditional deterministic algorithms.
As can be seen from our brief representative list of references, the actual state-of-the-art computing can be simply partitioned into deterministic and heuristic algorithms focusing on drone trajectory planning and, in part, optimizing coverage. Thus, we begin our literature review by referring to the deterministic methods used for adjusting the drone coverage and their flight paths. First, the argument in [
6] is for the effective construction of drones with overall trajectory limitations in order to maximize their energy efficiency. Another critical element of aerial communication networks is the conservation of energy. This research was further extended by Yang et al. [
7], who performed work on the Pareto optimal trade-off between BS emission energy and drone trajectory specification. Further, the authors of [
8] proposed the optimization problem covering joint the horizontal location, vertical location and coverage radius of UAVs. They showed that the joint optimization of these aspects results in the performance gain of such defined system. However, no specific system dynamics were considered in this study.
In addition, attempts to optimize the drone trajectory carried out in [
9] are based on maximizing UE throughputs. It has been shown that, if the initial problem is transformed into a pair of convex problems, an iterative algorithm can be proposed to address the shape of the drone trajectory. Mozaffari et al. proposed the method to optimize the path of the drones by calculating the optimum number of the stop points in [
10]. The goal was to maximize the probability of coverage.
It has also been shown that intelligent trajectory design could significantly reduce the total power required to operate drones. For this reason, we must reconcile a number of trade-offs [
11]. The most important factors to mention are data delay, power unit behavior and network throughput. Therefore, further procedures should be based on the assumption that all identified measures are reaching a sufficient level. The advantage of artificial intelligence has been exploited in [
12], where the authors proposed a proportional-integral-derivative (PID) motion controller capable of maintaining proportions in critical factors. An analogous method was proposed by Razmi [
13]. The work uses an adaptive sliding mode controller based on a neural network for flight altitude control. A recommendation testing of drone pathways suggests that parametric uncertainties may tend to increase the learning process’s effectiveness.
While optimization efforts are being presented as precursors to our work, we are not trying to focus on optimization directly. Instead, in our version of the swarm model, we rely on the concept of swarm adaptability, which means that we are dealing with a less demanding or different task than optimizing the entire trajectory. Our article also highlights the factors of uncertainty in post-disaster deployment and therefore the type of different problems that need to be addressed.
The remainder of this paper is structured as follows.
Section 2 defines the main model issues, separating its dynamics into exogenous and endogenous components. It explains how the trajectory of drones determines the problems of user demand and coverage.
Section 3 introduces more details about the model structure. One of the essential features is the hybrid terrestrial/aerial network deployment. In the framework of self-organizing LD-based processes,
Section 4 clarifies the suggested drone interaction model.
Section 5 devotes attention to the characteristics of drones that are organized into swarms.
Section 7 presents numerical results with an emphasis on sensitivity analysis and careful selection of systemic measures. Finally, conclusions are presented with findings on an extension and other possible directions of study. To be more informative on the issues presented, two appendices are also available.
Appendix A addresses the robustness of the swarm deployment under wind conditions. In
Appendix B, the parameters, symbols, and variables used in the article are thematically organized and roughly defined.
3. Model of Endogenous Drones Dynamics in UAV-Assisted Mobile Network
Before delving into the details of dynamics, it is worth noting that the interactions listed below are mainly computationally useful indirect tools that facilitate the creation of relevant dynamic geometric relationships between drones. Virtual forces therefore constitute an intermediate step in encoding actual move strategies.
3.1. Self-Organizing Swarms of Drones
The swarm entity paradigm applied to a group of organized drones is largely consistent with
active matter physics and multi-agent systems using local interactions [
16], which is a generalization analogous to condensed matter physics. Perhaps the most recognized example of the active matter is the spontaneous self-organization of autonomous mobile “agents” into ordered swarms through elementary local relationships similar to the comparative location and determination rules [
17].
The properly organized and often geometrically or topologically highly ordered configurations of drone swarms can be created through interaction/communication effects. The inspiration in this situation borrows from the qualitative resemblance of condensation or even crystallization in molecular samples. For our work, it is very important that self-organized configurations can also be generated through properly selected “interaction forces” determined by the on-board computer systems of UAVs. This means that we focus primarily on describing swarms created by drones without very invasive centralized control schemes.
In this case, however, we may assume, for example, that a centrally authorized access would have the right to affect the choice of the swarm parameterization depending on the degree of variability of the external conditions. Therefore, it is also strategically important to assume that the proposed system should allow occasional receipt of key messages from the central data storage and computational facilities.
3.2. Types of Drones Interaction in UAV-Assisted Mobile Network
We use the upper
index indicating the corresponding autonomous swarm variables in line with the [
15] literature, from which we derive our greatest technical inspiration. Therefore, in all the variables where we have this label, we are reminded to consider drones as members of the “swarm family”.
Let us now switch from a single separate drone to the assembly of interacting drones. If only the type of the robotic interaction is considered, the result is a system of multiple robots that in principle might behave in a self-organized way. To capture the reality studied, more details and therefore more interactions must be taken into account.
For example, the extra terms are presumed to occur between the selected drones and the points representing a pair of terrestrial (ground) immobile stations. The effects have been included in the modeling, taking into consideration the influence of two base stations , . Clearly, with a sufficient strength of , the robotic movement zone becomes restricted, which means that “soft” or “elastic” bonds are formed.
As we plan to address the issue of signal coverage by drones, we assume that virtual interaction must be defined in such a way as to link members to the end users described by the respective variables formally labeled by . The corresponding interaction is called . To achieve a sufficiently large lower limit of the quasi-equilibrium distances between and , the specific force parameter settings for interaction forces of are needed. On the other hand, there is a requirement for the sustainable transfer of information from to nodes and vice versa. This can be achieved by well-tuned virtual forces (their parameters), which represent an attempt to set distances indirectly. Therefore, the rate of drop in transmission will also depend on the virtual forces of , indirectly related to how far the planar projections will be within the plane.
For a comprehensive overview of current information, we integrate types of interaction forces into the tuple set
where
is used to label 3D vectors of the real components corresponding to the interaction forces. We specify the interactions in detail in the next section.
3.2.1. Inter-Drone Interaction
The pair interaction of type
that coordinates drones with positions marked with
k,
i is described by force
For the relative position of the drone
the respective distance
is given by the Euclidean norm
. The positive real-valued parameters
,
,
, and
have been used to define the scalar function
written here for some general distance
r. The function
serves as a template for the introduction of interactions; the subscript
A is used for the parameters
;
is related to the mutual attraction; and index
R labels the parameters for the repulsion description. The exponents
are universally selected, as shown in the entire paper.
3.2.2. Drone to User Interaction
In this project, we aim to develop an integrated swarm model with enhanced adaptive capacity to deal with environmental change. Suppose that if interactions are also applied in non-stationary temporary epochs, then forces parameterized with only constant parameters may not be sufficiently effective. For instance, one might be concerned regarding how heavily the interactions that determine robot preferences in choosing certain nodes can reduce their effect on the rest of the nodes.
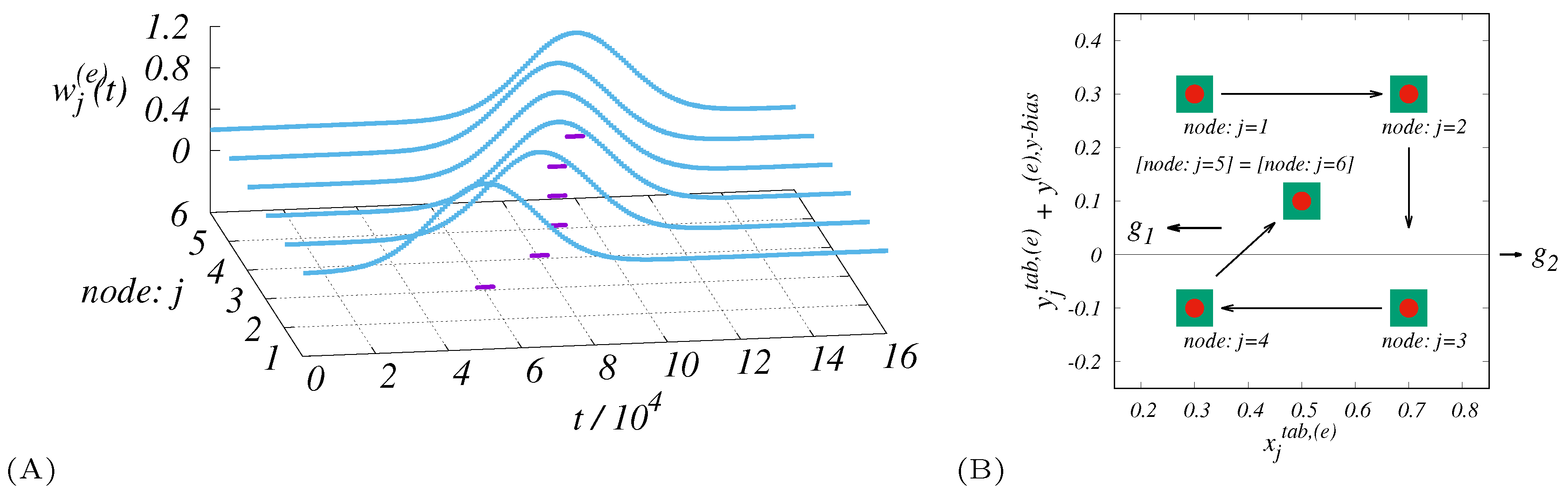
This brings us to the feedback proposition which, in a multiplicative way, modifies some of the chosen constant parameters. We focus on quantifying whether a specific adaptive approach is strong enough to favourably modify the desired transmission characteristics. The weights , …, , represent priorities of the respective end users. The basic conceptual prerequisite for the system adaptability is that drones should be mainly attracted high-weight nodes. Nevertheless, as mentioned above, it is not recommended to focus solely on enhancing the attractiveness of the node, since a collision of the drones must be avoided.
If we focus on signal coverage in particular, the actual can provide the swarm with important feedback information. This goes beyond the standard LD. However, with this modification, there is a possible loss of the strictly pairwise nature of the interactions. As a result, more global data exchange must be resolved at the cyber-physical systemic level. In our specific model, we have taken the instant mean = as the scaling term that is used for calculating of the virtual interdronal forces.
The LD factors can be taken into account to modulate or “renormalize multiplicatively” (even though the analogy with renormalization is rather exaggerated) the forces between the population nodes
and
drones. The respective forces with the feedback are defined by
Here, the notation
is equivalent to
. In the adaptive model, the force includes the pair of factors
which exploit the free parameters
and
, and the scaled argument
with the instant mean
. The key hypothesis included in
and
is that drone adjustment trends should be lowered as demand
declines. The relative position
is used to connect the
ith drone with the respective projection
of the
jth population node. For reasons of aviation safety, the greater
,
of the pair of the parameters
,
that comprise the requirements of the permanent terrestrial base stations
,
has been chosen.
Importantly, the heights and related altitudes are also drone targets. Moreover,
is the only one of the coordinates in Equation (
9) that does not describe the end user positions explicitly. In addition, by analogy with the
type,
interactions not only make the 2D coordinates of end-user node images (at the height
) attractive to UAVs but also cause some canonical virtual repulsion on the small scales. We have introduced two new constant parameters
and
that offer additional freedom and may enhance the attractiveness of the targets.
It should also be noted that the way in which adaptive parameters (their factors) are introduced is inspired by the general philosophy of the field theory accompanied by the multiplicative renormalization group technique [
18]. By this powerful standard procedure, the original constants are replaced with appropriate impulse-dependent (i.e.,
-dependent in our case) factors to fulfill asymptotic (mostly large-scale and long-term) conditions.
3.2.3. Drone to Terrestrial Base Station Interaction
To arrive at the description of a more complex but communication-friendly form of configuration, we focus on building a “flexible but anchored swarm”. Here, too, interactions are indirect tools for maintaining adequate distances between drones. As shown below, the results of our numerical procedures justify the usefulness of the idea of determining successive movements based on virtual interaction forces.
The additional interactions proposed for this purpose are categorized as
. The swarm can primarily achieve its telecommunications goals through
interactions. The anchored form should not, however, trigger conflicts with the more elementary swarm configuration. Its additional role is stabilizing the geometric distance between the swarm and the pair of base stations [
2].
Let us formally specify that two of the UAVs
interact with the ground nodes
defined by the 3D Cartesian coordinates
As already mentioned, the transmission and flight safety constraints are the primary limitations on the flight heights
(see Equation (
9)). The persistent
can be associated with the instantaneous
by means of the vector
Together with the
≡
abbreviation, the positions serve to build the virtual forces
Again, the default is used as for the case, but two new parameters are . The attraction should be strong enough to guarantee tighter coupling to terrestrial sources.
4. Model of Drones Swarms Behavior Based on the Langevin Dynamics
Langevin dynamics (LD) is an advanced and comprehensive concept of theorizing and simulation with an important position of the stochastic variables. Initially, it was intended to recognize correlations at the molecular scales only. Later developments have included mesoscopic scales as well. Much later, there have been numerous extra modifications on the track from the initial LD to modified LD variants that reflect some specific requirements [
19] that are currently the subject of extensive research of
stochastic systems.
The experience and findings have supported the dissemination of stochastic modeling trends across many disciplines. Due to intricate development, LD-inspired stochastic dynamics often occur under different names. In economics and technology, as shown by a large number of examples, a highly productive variety of new phenomena were modeled that operated at the interface between determinism and stochastics. The popular optimization strategy has become stochastic Langevin dynamics with the Bayesian concept and mini-batch stochastic gradient in the background [
20].
Since the macroscopic applications are more relevant to our problem, we wish to move away from the original molecular scales. Instead, we deal with engineering applications that involve the development of a very particular model. The project is inspired by the multirobotic ideas of distributed design [
17]. The LD formulation has also been used in the mixtures of primitive robots [
19]. This paper describes the LD formulation of drone dynamics that is characterized by virtual pair forces with an algebraic framework similar to the introduction of 3D molecular forces. This means that we are moving towards macroscopic LD applications in the engineering sciences. Our stochastic model for the swarms of drones expresses a methodological opinion that the stochastic description is often very unique in its enrichment of the original determinism. Moreover, while the stochastic approach could lead to realism, it also necessitates the probabilistic treatment of trajectories.
However, stochastic functionality is not the only means of adding relatively new aspects to the original self-organization and robustness of the drone swarm. Moreover, this work involves a type of endogenous adaptive mechanism that responds to the actual nodal weights encoding the activity of the end users. For the sake of clarity, we specify that the adaptability refers here to the role of the specific systemic unit that should allow an efficient reaction to the changing telecommunication load.
From the point of view of references, it should also be noted that there is a functional similarity between the present LD proposal and the Vicsek model [
16] applied to the description of the flock within theoretical biology. If an iterative discrete Euler formula is used to implement LD numerically, the results obtained are similar to the Vicsek formulation in many respects (including stochastic terms). Despite significant modifications in their areas of implementation, both modeling methods are almost compatible. Certain unique features such as collision prevention were carried out with improved variants of comparable algorithms [
21]. Similarly, Yuan et al. [
22] used a decentralized predictive control algorithm in the broadcast network mode with the ability to form a certain equilibrium range, analogous to virtual force models.
4.1. Swarm Self-Organization Based on Langevin Dynamics
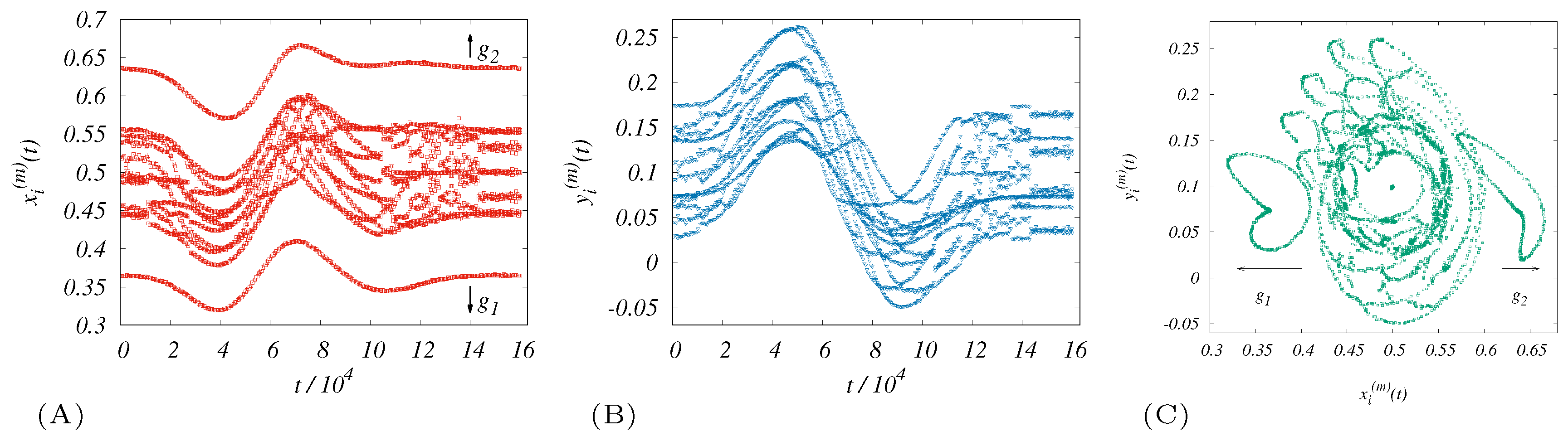
It is worth noting that our specific intuition in relation to the consequences of LD derives from experience regarding the effects of nonlinearities and (virtual) interactions with stochasticity. Competitive objects calculated within LD often show that they are capable of generating flexible configurations rather close to attractors, as demonstrated in multiple studies [
23]. This concept can be considered equivalent to the self-organization mechanism because there is also an attraction towards the trajectories of the dynamic system. Consequently, if the virtual interaction action is linked to the activity of the sensors, this binding can be considered a methodical means that implicitly solves a known problem such as avoiding drone collisions [
24]. Interference effects are not specifically recalculated in our model, but we deal with them indirectly, assuming that the distance between drones is controlled by repulsive virtual interactions that are strong enough to reduce interference. Similarly, the combination of propulsion technology with modeling software may of course be limited, particularly in terms of the speed, range and capacity of reliably executable flight maneuvers.
For example, the deployment of a hybrid swarm control system with virtual LD forces will require coordinated on-board computing [
25] with propulsion and sensory design. It is also natural to suppose that the navigation system of each drone will also have limited access to data from a centralized acquisition server. Each particular drone should be equipped with an ongoing quantification of data importance to avoid congestion due to excessive information flows. Of course, high signal transmission quality and efficiency of the drone propulsion system [
26] are also required for the technical implementation.
4.1.1. Impact of Stochastic Environments on the Swarm Self-Organization
In multirobotic applications [
27], stochastic and nonlinear features are not unusual. On the sensory level, noises can be induced at the interfaces where on-board computers interact with avionics subsystems. If the noise intensity is too high, for example, it can significantly affect any distance detection device, causing feedback that leads to invalid calculations and faulty mechanical behavior.
This is, however, no major problem, as stochastic external factors associated with climatic and weather conditions in urban or rural environments may be significant for certain drone missions [
28]. The safety aspect of drones in turbulent conditions is a more important aspect of stochasticity that partially motivated our work. Improvements can be necessary to migrate simple stochastic models to possible realistic variants. If buildings display complicated boundaries, our virtual force version will not succeed. In addition, the approximation of white noise is not adequate for intermittent turbulence–laminar transitions that are present in the atmosphere. This kind of realism is only mentioned in our current work but was not technically achieved because of the preparation of its distinctive focus.
4.1.2. Virtual Forces Lead to a Path of Discrete Segments
As a compromise, we present an over-damped LD variant, which is directly approximated by a form based on the explicit Euler’s first-order numerical method. According to this, the positions
of drones,
… at the time
are calculated by the iterative process
Here,
is the kinetic factor that determines the strength of virtual deterministic (virtual) forces. The additive term
stands for the Gaussian zero mean noise components of
variance. The deterministic factors are integrated within the total force
It consists of the additive contributions
5. Systemic Averages and Characteristics
When evaluating the swarm dynamics obtained with the given LD, we considered it necessary to implement tools, measures, and characteristics to distinguish appropriate and less suitable LD parameterizations, and stages with different levels of adaptivity.
In the scenarios examined, a drone signal is transmitted into the plane () of the temporally active nodes. A formula can thus be derived that quantifies the coverage in the representation of the population nodes.
The derivation is based on three key assumptions. First, the main assumption is that many critical events are so local that they can be quite satisfactorily reduced down to the structural nodes. Second, the coverage between drones and customer nodes decreases monotonically with geometric distance (for example as ). The complement to this is the idea of scaling that assumes that coverage decreases nearly as minus the first power of . Our third phenomenological assumption is that the multiplicative effect of demographic and geometric factors can be used for the coverage evaluation for a node system.
The algebraic representation of the above assumptions gives rise to a local (node) coverage
that, if written for the node
, may be postulated as follows:
where
and
,
are very small parameters of regularization used to avoid the rare but possible singular effects. Although the decrease with the minus first power of the
distance expresses a standard assumption about propagation from a point (sole drone isotropic) source, more specific models (see, e.g., [
29]) exist that can be reconsidered in a similar manner. To carry out the particular calibration (normalization),
having the dimension of length was introduced. Its structure is elucidated by the additional assumptions involved in the next subsection.
Calibration of Coverage Quality
Generally, through calibration and related operations, we are able to understand the relationships of the intrinsic units comprehensively. Using some limits or idealizations seems to be useful in this process. As an extreme idealization, let us assume for a moment that all drones are permanently operating at a certain unique height over the single selected ground node that encompasses the entire end-user population . Let us assume also that all drones work near the only active node . The remaining nodes function under normal, safe circumstances, and the requirements for services are small. The assumption results in the consequence
Then, by imposing of the calibration condition
we obtained the typical length of the problem
which decreases with the number of drones increasing. To characterize the total efficiency, the mean weighted coverage is defined by
In addition to global quantification by means of Equation (
17), adequate description of the diversity in coverage is required. In this respect, our objective is to provide a specific coverage-related measure to evaluate how fairly the transmission reaches population nodes with the demands of end users. In keeping with the previous formulation, the following version of Jain’s fairness index can be presented as
Let us focus on the specific scenario of that measure to make it more understandable. When turning to the highly located end-user system with a single node , we have obtained the fairness . The explanation of this paradox is merely that has no inner structure so that ideal fairness is trivially achieved when a signal is transferred to the single node.
We also examined a distinct limit situation in order to understand the main elements of the model, deciding to abandon a preliminary assumption of only one particular active node. More specifically, one can obtain → (uniform for all j) with the highest for the presumed homogeneity of users’ activity . The results also indicate the need for a wider range of measures to complement the characteristics of the system. As we continue, we put forward additional candidate measures.
6. Simulations and Performance Analysis
First, we reintroduce the specific
Theil T index. Its multiple applications in the field of economic [
30,
31], social or software assessment [
32] have been developed. The specificity of our telecommunications application is that we are interested in nodal inequalities seen through
. For the purposes of evaluating the system under consideration, it is natural to evaluate the diversity of service satisfaction by taking into account nodal weights. Consequently, the modified expression is the form
It can be seen as an alternative that integrates issues of end-user satisfaction with the quality of redistribution of drone signal coverage. We should also note that the cw indices in are defensible and related to coverage and weighting.
The complementary measure
is introduced, which is based on the definition of devaluation using
. This factor reflects the disparities between the quality of services provided to end users. Analogously to the economic and social literature [
33], we propose
Here,
is the parameter that controls the impact of diversity, while
plays role of the efficiency amplitude. However, there is also an alternative formulation
that is far better known from the theories of societal welfare. This function reflects not only the individual but also the social aspect and the often analyzed fundamental question regarding the extent to which economic welfare can be achieved if certain groups are not sufficiently met. The exponential term here represents the so-called aversion to inequality. In this context, the wireless industry and the associated service sector are only specific areas where the effect of customer-perceived inequality can be discussed. The space of new measures
can be built on previous foundations. This is an example that integrates two measures of heterogeneity through a single scalar homotopy parameter
.
Although the function above is exponential (not the power form), the combination of inputs (of similar nature, i.e., similar “units”) resembles by its structure
Cobb–Douglas aggregate production functions [
34] with the elasticities
and
. The transformation
=
not only shows a clear link to the Cobb–Douglas formula but also demonstrates how different measures could be combined to achieve a scalar output that is suitable for clearly interpretable multi-objective problems. Although this paper does not tackle the multi-objective drone swarm problem, the form
reflects a progressive step in that regard, as it incorporates two customer views. It is designed in the classical framework in which a single scalar function embodies several demands. This integrated formulation can be considered as multi-objective scalarization [
35].
If we want to make further progress in understanding the swarm system, we believe that this can be done by comparing and grouping existing measures together. At the beginning, we give the specific modification in the cosine measure extracted from trigonometry. The applications [
36,
37] could serve as an example of some universal features. The similarity measure
is defined in order to analyze population weight and local coverage relationships. The similarity of this type evaluates the degree to which coverage is consistent with the service demands (∼
). The use of other ways of thinking on research components, such as hierarchical entropy and cosine correlation, is also very useful [
38].
8. Conclusions
In post-disaster situations, the routing of autonomous facilities should not be environmental specific and should be designed to avoid unnecessary handling of redundant information. The article proposes a swarming strategy for UAVs with an adaptive multiplication of selected dynamic parameters based on the continuous monitoring of internal swarm geometry and the environment. An adequately advanced sensor system integrated with a remote center is, without doubt, a requirement for these considerations. On-board computers are expected to provide interpolations that may be required as inputs for the Langevin model. Otherwise, the model may not be applied, for example due to transmission delay.
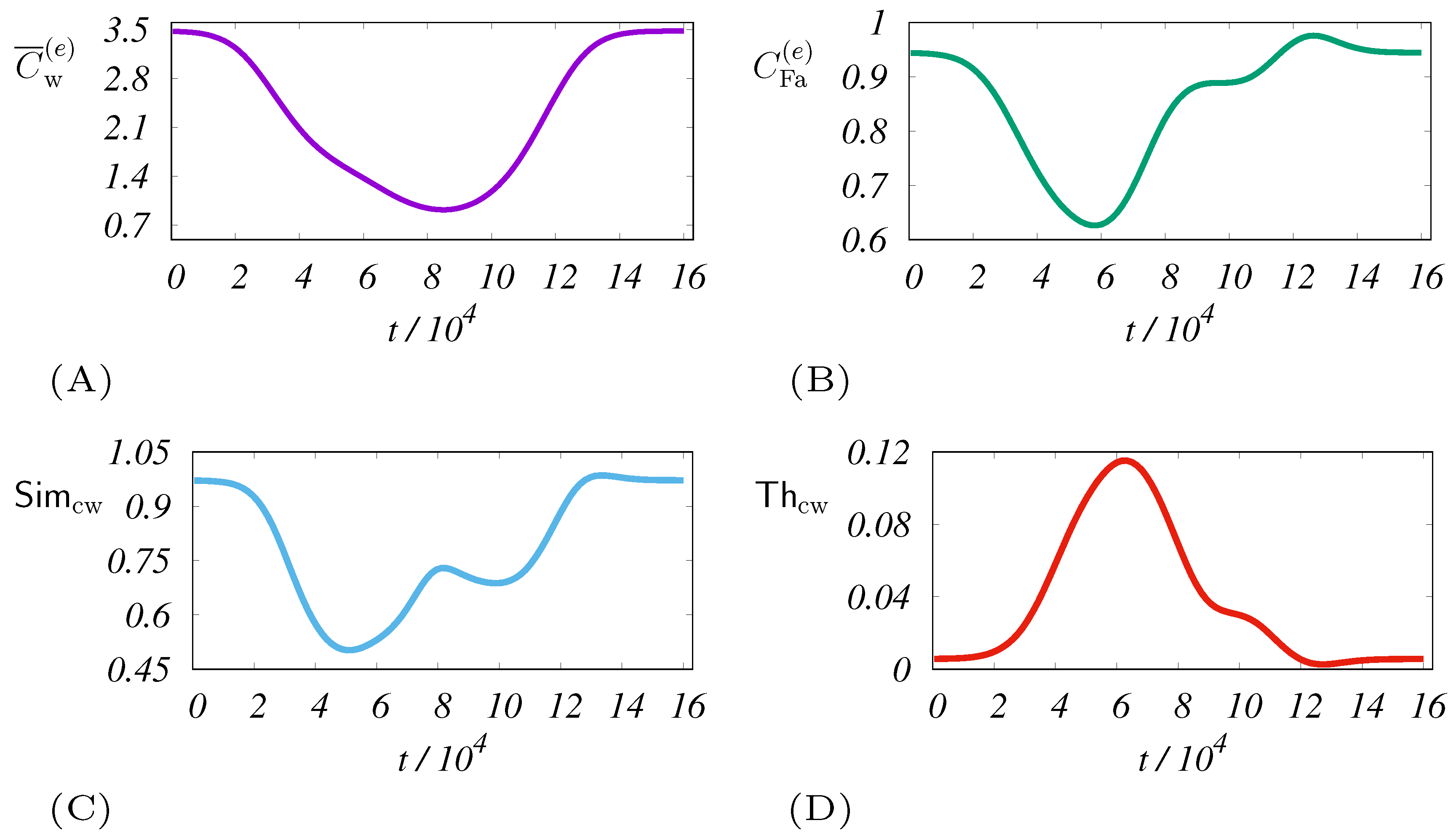
By numerical simulation, we illustrated that the dynamics of a swarm consisting of uniform swarms mapped to some systemic measures show different sensitivities with respect to adaptivity parameters according to the types of the measures we decided to analyze. Four hypothetical types of measures , , , and were selected and tested for sensitivity. It should be noted that we consider each measure to be a specific projection of swarm information, but we recommended focusing specifically on the coverage factor considered by the telecommunications sector. As each measure has expanded from a specific scientific field, our work is also integrative. The conclusion supported by Theil index and fairness is that they are very sensitive to parameter changes responsible for adaptability. In terms of detailed analytical form, the Theil index is approaching entropy, so it would be better to investigate why specific entropic measures could also promote swarm adaptability. The most sensitive measures , are linked to the heterogeneity of coverage. Thus, we hypothesize that a stronger mastery of heterogeneity/homogeneity is a key to better performance. In particular, if we monitor the coverage represented by the customized Theil index, this may be the base of a plan to achieve higher adaptability.
The problem of modeling, which is insufficiently discussed in this study, seems to be how far we can go in developing an appropriate general strategy for semi-autonomous UAVs operating in the disaster conditions. In our work, we are contributing to eliminating this conceptual uncertainty by creating an alternative adaptivity basis which is tested for specially selected environmental scenarios. In this context, it may seem that the main disadvantage of our approach is the lack of empirical support in the event of disasters. On the other hand, we are well aware that empiricism will probably not be the only way to improve adaptability unless we also consider unexpected scenarios. For example, mergers with the Monte Carlo strategy can be very successful.